1 Introduction

State space models are widely used to analyse dynamic data in a wide range of scientific disciplines, e.g. in finance, reservoir modelling, weather forecasting, and signal processing. A general state space model consists of an unobserved process \(\{x^t\}_{t=1}^{T}\) and a corresponding observed process \(\{y^t\}_{t=1}^{T}\) where \(y^t\) is a partial observation of \(x^t\). The unobserved \(x^{t}\)-process, usually called the state process, is assumed to be a first-order Markov process, and the observations \(y^1, \dots , y^T\) of the observed process are assumed to be conditionally independent given \(\{x^t\}_{t=1}^{T}\) with \(y^t\) only depending on \(x^t\). The main objective of state space modelling is some type of inference about the state process given the observations. There are many inference procedures associated with state space models, among which one of the most common is filtering. Filtering, which is the problem addressed in the present article, refers to the task of computing, for each time step \(t=1, \dots , T\), the distribution of the state \(x^{t}\) given all observations \(y^{1:t} = (y^1, \dots , y^t)\) available at time t. In some fields, filtering is known as sequential data assimilation. Other common terms are history matching and online inference. However, in the present article, we use the term filtering throughout.

Because of the particular dependency structure of the general state space model, the series of filtering distributions can be computed recursively according to a recursion which alternates between a forecast step and an update step. Generally, however, apart from a few simple special cases, the exact solution to the filtering recursions is intractable due to complex and/or high-dimensional integrals. Approximate strategies are therefore required, and simulation-based methods, or ensemble methods, represent the most popular approach. An ensemble-based solution may, similarly to the original filtering recursions, alternate between a forecast step and an update step. Instead, however, of computing the forecast and filtering distributions explicitly, the distributions are represented empirically with an ensemble of realisations. The main challenge in this context is the update step where, at time step t, an ensemble of (approximate) realisations from the so-called forecast distribution \(p_{x^{t} |y^{1:t-1} }(x^{t} | y^{1:t-1})\) needs to be conditioned on the new observation \(y^t\) so that an updated ensemble of (approximate) realisations from the filtering distribution \(p_{x^{t} |y^{1:t} }(x^{t} | y^{1:t})\) is obtained. Since there is no straightforward way to approach this task, ensemble methods require approximations in the update step. This ensemble updating problem is the core focus of the present paper. In particular, we address the problem of updating an ensemble of categorical state vectors and present in detail an approximate ensemble updating method for this situation.

Among the ensemble filtering methods that have currently been proposed in the literature there are two main categories; particle filters (Gordon et al. 1993; Doucet et al. 2001) and ensemble Kalman filters (EnKFs) (Burgers et al. 1998; Evensen 2003; Tippett et al. 2003). Particle filters are based on importance sampling while EnKFs rely on a linear-Gaussian assumption about the underlying state space model. Particle filters have the advantage of being asymptotically exact in the sense that as the ensemble size goes to infinity, the filters converge to the exact filtering solution. In practical applications, however, computational resources often restrict the ensemble size to be quite small, and particle filters are known to collapse unless the ensemble size is very large compared to the state dimension (Snyder et al. 2008). For the EnKF, the solution is always biased unless the underlying state space model really is linear-Gaussian. Despite this fact, the EnKF often performs remarkably well also in non-linear, non-Gaussian situations and, unlike the particle filter, also scales well to problems with very high-dimensional states. The filter is, however, inappropriate in situations with categorical vectors, as considered in the present paper.

Loe and Tjelmeland (2021b), in a follow-up study to Loe and Tjelmeland (2021a), present an alternative solution to the ensemble updating problem based on a generalised view of the EnKF. Specifically, they describe a general updating framework where the idea is first to introduce assumed models for the intractable forecast and filtering distributions and thereafter to update the prior samples by simulating samples from a distribution which, under the assumption that the assumed forecast distribution is correct, preserves the corresponding assumed filtering distribution. To make the update robust against the assumptions of the assumed forecast and filtering models, the distribution from which the posterior samples are simulated is also required to be optimal with respect to a chosen optimality criterion. More specifically, the updating distribution is required to minimise the expected value of a certain distance, or norm, between a prior (forecast) and posterior (filtering) ensemble member. The framework is Bayesian in the sense that the parameters of the forecast distribution are also treated as random variables. Uncertainty about these parameters are thereby incorporated into the updating. Two particular applications of the proposed framework are investigated, one continuous and one categorical. In the continuous case, the assumed forecast and filtering models are chosen as Gaussian distributions and the optimality criterion is to minimise the expected Mahalanobis distance between a prior and posterior ensemble member. The framework then leads to a Bayesian version of square root EnKF (Bishop et al. 2001; Whitaker and Hamill 2002; Tippett et al. 2003). In the categorical case, the assumed forecast and filtering distributions are instead chosen as first-order Markov chains and the optimality criterion is to minimise the expected number of variables of a prior state vector that change their values. An optimal transition matrix for simulating a posterior ensemble member from a corresponding prior ensemble member is constructed using a combination of dynamic and linear programming.

There are three important limitations to the updating procedure for categorical state vectors proposed in Loe and Tjelmeland (2021b). Firstly, the procedure is difficult to implement except in the binary case where there are only two possible values for each variable of the state vector. Consequently, the authors only demonstrate the method in binary numerical experiments. Secondly, the approximation to the forecast distribution is restricted to be a first-order Markov chain. This means that models with higher-order interactions, for example a higher-order Markov chain, cannot be considered. Thirdly, the procedure is not applicable in two- or three-dimensional problems since it requires that the state vector has a one-dimensional spatial arrangement. In the present article, we address the first and second of these three issues. Specifically, we present a modified and improved version of the updating procedure applicable also for \(K > 2\) classes and which allows the use of a higher-order Markov chain as the approximate forecast distribution. In the procedure described in Loe and Tjelmeland (2021b), a directed acyclic graph (DAG) is put forward to update each prior realisation. The chosen structure of the DAG allows the corresponding optimal solution to be computed recursively using a dynamic programming algorithm where a piecewise-linear programming problem is solved in each recursive step. In the present article, the starting point is, instead of a DAG, an undirected graphical model (UGM). This UGM has a more flexible structure than the DAG in the sense that we can more easily consider different types of dependency properties without overcomplicating the computation of the optimal solution. The underlying graph is decomposable and this gives the UGM many convenient computational properties. The optimal updating distribution is computed by solving a linear program derived from a series of local computations on the UGM.

The remains of this paper take the following outline. In Sect. 2, we review state space models and the associated filtering problem in more detail, and we also present some basic graph theory required to understand the proposed approach. In Sect. 3, we present a slightly modified version of the general ensemble updating framework in Loe and Tjelmeland (2021b), restricting the focus to categorical state vectors. In Sect. 4, we describe in detail how the general framework can be applied when a Markov chain model is adopted for the assumed forecast distribution. Thereafter, we present in Sect. 5 a simulation example where each element of the state vector can take \(K=3\) values. Finally, we finish off with a few closing remarks in Sect. 6.

2 Preliminaries

This section describes the filtering problem in more detail and also reviews some graph-theoretic concepts related to the proposed approach. The section also introduces notations that we use throughout the paper.

2.1 The filtering problem

A general state space model consists of an unobserved process \(\{x^t\}_{t=1}^{T}, x^t \in \Omega _x\), called the state process, and a corresponding observed process \(\{y^t\}_{t=1}^{T}, y^t \in \Omega _y\), called the observation process, where \(y^{t}\) is a partial observation of \(x^{t}\) at time t. The unobserved state process \(\{x^t\}_{t=1}^{T}\) is modelled as a first-order Markov chain with initial distribution \(p_{x^1}(x^1)\) and transition probabilities \(p_{x^t | x^{t-1}}(x^t | x^{t-1})\), \(t=2, \dots , T\). Throughout this paper, we use the notations \(x^{s:t} = (x^s, \dots , x^t)\) and \(y^{s:t} = (y^s, \dots , y^t)\), \(s \le t\), to denote the vector of all states and the vector of all observations, respectively, from time s to time t. The joint distribution of \(x^{1:T}\) follows from the Markov chain assumptions as

$$\begin{aligned} p_{x^{1:T}}(x^{1:T}) = p_{x^1}(x^1) \prod _{t=2}^T p_{x^{t}| x^{t-1} }(x^t | x^{t-1}). \end{aligned}$$

For the observation process, it is assumed that the observations are conditionally independent given \(x^{1:T}\), with \(y^t\) only depending on \(x^{t}\). The conditional distribution of \(y^{1:T}\) given \(x^{1:T}\) thereby follows as

$$\begin{aligned} p_{y^{1:T} | x^{1:T}}(y^{1:T} | x^{1:T}) = \prod _{t=1}^T p_{y^{t} | x^{t}}(y^{t} | x^{t}). \end{aligned}$$

It is possible to adjust the model so that observations are only recorded at a subset of the time steps \(\{1, \dots , T\}\). However, for the sake of simplicity, we assume in this work that an observation is recorded at every time step \(t=1, \dots , T\).

The objective of the filtering problem is, for each time step \(t=1, \dots , T\), to compute the so-called filtering distribution, \(p_{x^{t} | y^{1:t}}(x^{t} | y^{1:t})\), i.e. the distribution of the latent state \(x^{t}\) given all the observations \(y^{1:t} \) available at time t. Because of the particular structure of the state space model, the series of filtering distributions can be computed recursively according to a recursion which alternates between a forecast step,

$$\begin{aligned} p_{x^t | y^{1:{t-1}}}(x^t | y^{1:{t-1}}) = \int _{\Omega _x} p_{x^t | x^{t-1}}(x^{t} | x^{t-1}) p_{x^{t-1} | y^{1:t-1}}(x^{t-1} | y^{1:t-1}) \text {d} x^{t-1}, \end{aligned}$$
(1)

and an update step,

$$\begin{aligned} p_{x^{t} | y^{1:t}}(x^{t} | y^{1:t}) = \dfrac{ p_{x^{t} | y^{1:t-1}}(x^{t} | y^{1:t-1})p_{y^{t}|x^{t}}(y^{t}|x^{t})}{p_{y^{t} | y^{1:t-1}}(y^{t} | y^{1:t-1}) }, \end{aligned}$$
(2)

where

$$\begin{aligned} p_{y^{t} | y^{1:t-1}}(y^{t} | y^{1:t-1}) = \int _{\Omega _x} p_{x^{t} | y^{1:t-1}}(x^{t} | y^{1:t-1})p_{y^{t}|x^{t}}(y^{t}|x^{t}) \text {d} x^{t}. \end{aligned}$$
(3)

The distribution \(p_{x^t | y^{1:{t-1}}}(x^t | y^{1:{t-1}}) \) computed in the forecast step is called the forecast distribution of \(x^t\). In the update step, this distribution is conditioned on the new observation \(y^t\) in order to compute the filtering distribution of \(x^t\), \(p_{x^{t} | y^{1:t}}(x^{t} | y^{1:t}) \). The update step is essentially a standard Bayesian inference problem with the forecast distribution becoming the prior and the filtering distribution the posterior.

There are two important special cases where the filtering recursions can be computed exactly. The first is the linear-Gaussian model where the initial distribution \(p_{x^1}(x^1)\) is Gaussian and where \(p_{x^t | x^{t-1}}(x^t | x^{t-1})\) and \(p_{y^{t} | x^{t}}(y^{t} | x^{t})\) are Gaussian with mean vectors being linear functions of \(x^{t-1}\) and \(x^{t}\), respectively. The forecast and filtering distributions are then also Gaussian and Eqs. (1) and (2) lead to the famous Kalman filter (Kalman 1960). The second situation where the filtering recursions are tractable is the finite state space hidden Markov model for which the state space \(\Omega _x\) consists of a finite number of states. The integrals in Eqs. (1) and (3) then reduce to finite sums. If, however, the number of states in \(\Omega _x\) is large, for example if \(x^{t}\) is a high-dimensional vector of categorical variables, the summations become too computer-demanding to cope with, and the filtering recursions are left computationally intractable.

Generally, the integrals in Eqs. (1) and (3) make the recursive solution to the filtering problem intractable, and approximate solutions therefore become necessary. The most popular approach is the class of ensemble-based methods, where a set of samples, an ensemble, is used to empirically represent the sequence of filtering distributions. A great advantage of the ensemble context is that it simplifies the forecast step. Specifically, if an ensemble \(\{{\widetilde{x}}^{t,(1)}, \dots , \widetilde{x}^{t,(M)}\}\) of independent realisations from the filtering distribution \(p_{x^t | y^{1:t}}(x^t | y^{1:t})\) is available, a forecast ensemble \(\{x^{t+1,(1)}, \dots , x^{t+1,(M)}\}\) with independent realisations from the forecast distribution \(p_{x^{t+1}|y^{1:t}}(x^{t+1}|y^{1:t})\) can be obtained by simulating

$$\begin{aligned} x^{t+1,(i)} | \widetilde{x}^{t,(i)} \sim p_{x^{t+1} | x^t}(\cdot | \widetilde{x}^{t,(i)}) \end{aligned}$$

independently for \(i=1, \dots , M\). The consecutive updating of the ensemble, however, remains challenging. There is simply no straightforward way to condition the forecast ensemble \(\{x^{t+1,(1)}, \dots , x^{t+1,(M)}\}\) on the new observation \(y^{t+1}\) so that a new filtering ensemble \(\{\widetilde{x}^{t+1,(1)}, \dots , \widetilde{x}^{t+1,(M)}\}\) of independent realisations from the filtering distribution \(p_{x^{t+1} | y^{1:t+1}}(x^{t+1} | y^{1:t+1})\) is obtained. In the present article, we propose an approximate way to do this when the elements of the state vector are categorical variables.

2.2 Decomposable graphical models (DGMs)

This section introduces decomposable graphical models (DGMs), a certain type of undirected graphical models, or Markov random fields (Kindermann and Snell 1980; Cressie 1993; Cowell et al. 1999). For simplicity, the focus is restricted to discrete DGMs. In the following, we start with a brief review of some basic theory on undirected graphs in Sects. 2.2.1 and 2.2.2. Thereafter, discrete DGMs are introduced in Sect. 2.2.3, while Sects. 2.2.4 and 2.2.5 consider simulation from discrete DGMs. A more thorough introduction to graph theory and graphical models can be found in, e.g., Cowell et al. (1999).

2.2.1 Undirected graphs

An undirected graph G is an ordered pair \(G = (V, E)\) where V is a set of vertices, or nodes, and \(E \subset \{ V \times V \}\) is a set of edges. The elements of the edge set E are pairs of distinct nodes, \(\{i,j\}\), \(i,j \in V\), \(i \ne j\). If \( \{ i, j\} \in E\) then node i and node j are said to be neighbours, or adjacent. Figure 1 illustrates a simple undirected graph with four vertices where, as per convention, vertices are represented by labelled circles and edges by lines between the circles. For this graph we have \(V = \{1,2,3,4\}\) and \(E = \left\{ \{1,2\}, \{1,3\}, \{2,3\}, \{3,4\}\right\} \).

Fig. 1
figure 1

An undirected graph with four vertices

Full size image

If there is an edge between every pair of nodes in a graph G, the graph is said to be complete. A subgraph of G is a graph \(G_A = (A, E_A)\) where \(A \subseteq V\) and \(E_A \subseteq E~\cap \{ A \times A \} \). If a subgraph \(G_A = (A, E_A)\) of G is complete, its set of nodes A is called a clique. A clique is called a maximal clique in G if it is not a subset of another clique. Throughout this article, we denote the set of maximal cliques by C. For the graph pictured in Fig. 1, the empty set \(\emptyset \) and \( \{1\}, \{2\}, \{3\}, \{4\}, \{1,2\}, \{1,3\}, \{2,3\}, \{3,4\},\) and \(\{1,2,3\}\) are cliques, while \(\{1,2,3\}\) and \(\{3,4\}\) are maximal cliques.

A path of length n from node i to node j is a sequence \((\alpha _0, \dots , \alpha _n)\) of distinct nodes where \(\alpha _0=i\) and \(\alpha _n = j\) and \(\{ \alpha _{k-1}, \alpha _{k} \} \in E\), \(k = 1, \dots , n\). Note that if there is a path from node i to node j in an undirected graph, there is also a path from node j to node i. For the graph pictured in Fig. 1, there are two paths from node 1 to node 4: (1, 2, 3, 4) and (1, 3, 4). Two nodes i and j are said to be connected if there is a path from node i to node j, and an undirected graph is said to be connected if every pair of vertices are connected. A tree is a connected undirected graph with the additional property that the path between every pair of vertices is unique. The graph in Fig. 1 is thus not a tree since there are different paths between some of the vertices.

2.2.2 Decomposable graphs and junction trees

An undirected graph \(G=(V,E)\) is said to be decomposable if the set of maximal cliques can be ordered in a way so that all elements in maximal clique number i (say) that are also in any later maximal cliques, are all contained in one of the later maximal cliques. If an undirected graph is decomposable, a so called junction tree for the maximal cliques can be defined, which in turn allow efficient computations of many properties.

Mathematically, the requirement for an undirected graph to be decomposable can be formulated as follows. Let \(C = \{c_1, \dots , c_{|C|}\}\) denote the set of maximal cliques of an undirected graph \(G=(V,E)\), where |C| denotes the number of maximal cliques. The graph is then decomposable if the elements of C can be ordered as \((c_1, \dots , c_{|C|})\) so that for each \(i=1, \dots , |C|-1\) there is a \(j > i\) such that

$$\begin{aligned} s_i = c_i \cap (c_{i+1} \cup \cdots \cup c_{|C|}) \subseteq c_j. \end{aligned}$$
(4)

The property in Eq. (4) is called the running intersection property, and the sets \(s_1, \dots , s_{|C|-1}\) are called the separators of the graph. The set of all separators, \(S = \{s_1, \dots , s_{|C|-1}\}\), and the set of maximal cliques, C, are uniquely determined by the structure of the graph G; however, the ordering \((c_1, \dots , c_{|C|})\) is generally not unique. Figure 2a shows a simple decomposable graph with six vertices. The maximal cliques of this graph are \(\{1,2,3\}\), \(\{3,4,5\}\) and \(\{4,5,6\}\), and there are two orderings of these that fulfil the running intersection property, namely \((\{1,2,3\},\{3,4,5\},\{4,5,6\})\) and \((\{4,5,6\},\{3,4,5\},\{1,2,3\})\). In the following we use the first of these orderings, \((c_1, c_2, c_3) = (\{1,2,3\}, \{3,4,5\},\{4,5,6\})\). The separators are \(s_1 = \{3\} = \{1,2,3\} \cap (\{3,4,5\} \cup \{4,5,6\}) \subseteq c_2\) and \(s_2 = \{4,5\} = \{3,4,5\} \cap \{4,5,6\} \subseteq c_3. \)

Fig. 2
figure 2

(a) A decomposable graph, and b a corresponding junction tree representation

Full size image

From a decomposable graph, a corresponding junction tree can be derived. A junction tree J for a decomposable graph G is a tree with \(C = \{c_1, \dots , c_{|C|}\}\) as its node set and the additional property that for every pair \(c_i, c_j \in C\) every node on the unique path between \(c_i\) and \(c_j\) in J contains the intersection \(c_i \cap c_j\). In a visual representation of a junction tree, it is common to include the separators as squared labels on the edges. This is illustrated in Fig. 2b which shows one of the possible junction tree representations for the decomposable graph in Fig. 2a.

A junction tree is a nice way to organise a decomposable graph, and many computations are easier to perform on the junction tree. Depending on the structure of the graph, however, it can be a complicated task to construct a corresponding junction tree. There exist several algorithms for this purpose, see Cowell et al. (1999). In all the examples we encounter in the present article, the decomposable graph under study has a structure which makes it particularly simple to construct a junction tree, and therefore we do not focus on the problem of constructing junction trees in this paper.

2.2.3 Discrete decomposable graphical models

A discrete decomposable graphical model (DGM) is a probabilistic model consisting of a decomposable graph \(G = (V,E)\), a random vector \(x = (x_i, i \in V)\) of categorical variables \(x_i \in \{0, 1, \dots , K-1\}\), and a probability distribution \(p_x(x)\). Alternatively, a discrete DGM can be defined as a discrete Markov random field whose underlying graph is decomposable. In the following, the notation \(x_A\) is used to denote the variables of x associated with subset \(A \subseteq V\), and \(\Omega _{x_A} \subseteq \Omega _x\) is the sample space of \(x_A\). Taking \(0/0 = 0\), the distribution \(p_x(x)\) of a discrete DGM can always be expressed as

$$\begin{aligned} p_x(x) = \frac{\prod _{c \in C} p_{x_c}(x_c)}{ \prod _{s \in S} p_{x_s}(x_s) }, \end{aligned}$$
(5)

where C is the set of maximal cliques in G and S is the set of separators (Cowell et al. 1999). This expression can easily be shown using basic probability rules and the Markov properties assumed for a DGM. Intuitively, the numerator in Eq. (5) includes the distribution of the elements in x that are in one or more separators more than once, and this is corrected for by the product in the denominator.

DGMs support several efficient algorithms and are fundamental for the work of this article. In particular, it should be noted that, if \((c_1, \dots , c_{|C|})\) is an ordering of the maximal cliques fulfilling the running intersection property in Eq. (4) and \((s_1, \dots , s_{|C|-1})\) is the corresponding ordering of the separators, we have

$$\begin{aligned} p_{x_{s_i}}(x_{s_i}) = \sum _{x_{c_i \setminus s_i}} p_{x_{c_i}}(x_{c_i}) = \sum _{x_{c_{i+1} \setminus s_i}} p_{x_{c_{i+1}}}(x_{c_{i+1}}) \quad \text { for all } x_{s_i} \in \Omega _{x_{s_i}}. \end{aligned}$$
(6)

2.2.4 Simulation from discrete DGMs

Consider a discrete DGM \(p_x(x)\) with respect to a graph \(G = (V,E).\) To simulate a realisation from \(p_x(x)\), a recursive procedure can be adopted, which goes as follows. First, \(p_x(x)\) is decomposed into \(p_{x_i | x_{V\setminus \{i\}}}(x_i | x_{V\setminus \{i\}})\) and \(p_{x_{V\setminus \{i\}}}(x_{V\setminus \{i\}})\) for some \(i \in V\). Thereafter, \(p_{x_{V\setminus \{i\}}}(x_{V\setminus \{i\}})\) is decomposed into \(p_{x_j | x_{V\setminus \{i, j\}}}(x_j | x_{V\setminus \{i, j\}})\) and \(p_{x_{V\setminus \{i,j\}}}(x_{V\setminus \{i,j\}})\) for some \(j \in V\setminus \{i\}\). Then, \(p_{x_{V\setminus \{i,j\}}}( x_{V\setminus \{i,j\}} )\) is decomposed into \(p_{x_k | x_{V\setminus \{i, j,k\}}}(x_k | x_{V\setminus \{i, j,k\}})\) and \(p_{x_{V\setminus \{i,j,k\}}}( x_{V\setminus \{i,j,k\}})\) for some \(k \in V\setminus \{i,j\}\). Continuing in this manner, we ultimately end up with only one variable \(x_l\) and corresponding marginal distribution \(p_{x_l}(x_l)\). A realisation \(x \sim p_x(x)\) can then be generated by recursively simulating from the series of conditional distributions, in the reverse order as they were computed. Without loss of generality, suppose that the vertex set is \(V = \{1, \dots , n\}\) and that the nodes have been numbered so that nodes are removed in the order from n to 1. This means that we make us of the following factorisation of \(p_x(x)\):

$$\begin{aligned} p_x(x) = p_{x_1} (x_1) \prod _{i=2}^n p_{x_i | x_{1:i-1}} (x_i | x_{1:i-1}). \end{aligned}$$
(7)

Having computed all the factors in Eq. (7), simulation from \( p_x(x)\) follows easily by first simulating \(x_1 \sim p_{x_1}(x_1)\), thereafter \(x_2 | x_1 \sim p_{x_2 | x_1} (x_2 | x_1)\), and so on. The recursive procedure described above, as well as the factorisation in Eq. (7), is general and holds for any distribution \(p_x(x)\), not necessarily a discrete DGM. However, for many models, it is inconvenient to factorise \(p_x(x)\) in this manner, since it can be a complicated task to compute all the factors. If the model is a DGM, however, and a corresponding junction tree J is available, computations can become particularly easy and efficient, as we discuss in the following.

First, note that the distribution in Eq. (5) can be expressed as

$$\begin{aligned} p_x(x) \propto \exp \left\{ \sum _{c \in C} V_{c} ( x_{c}) \right\} , \end{aligned}$$
(8)

where \(V_{c} (x_{c}) \) in this context is called a potential function for clique c. With the junction tree J given, it is convenient to start the decomposition of \(p_x(x)\) in a leaf of J. Denote the clique to which the chosen leaf corresponds by \(c^*\). Since \(c^*\) is a leaf of J, there is at least one node \(i \in V\) which is only present in \(c^*\). Suppose, without loss of generality, that the nodes have been numbered so that this is the case for node n, i.e. that node n is only contained in clique \(c^*\). We can then easily decompose \(p_x(x)\) into \(p_{x_n | x_{1:n-1}}({x_n | x_{1:n-1}})\) and \(p_{x_{1:n-1}} (x_{1:n-1})\) as follows. Since node n is only contained in clique \(c^*\), the variable \(x_n\) only enters the right-hand-side expression in Eq. (8) through the potential function \(V_{c^*} (x_{c^*})\). This means that \(p_{x_n | x_{1:n-1}}(x_n | x_{1:n-1}) \) can be computed as

$$\begin{aligned} p_{x_n | x_{1:n-1}}(x_n | x_{1:n-1}) = \dfrac{ \exp \left\{ V_{c^*} (x_{c^*} ) \right\} }{\sum _{x_n}\exp \left\{ V_{c^*} (x_{c^*} ) \right\} }. \end{aligned}$$
(9)

The other part, \(p_{x_{1:n-1}} (x_{1:n-1})\), can be computed, up to a constant of proportionality, by summing out \(x_n\) from Eq. (8),

$$\begin{aligned} p(x_{1:n-1}) \propto \sum _{x_n} \left( \exp \left\{ \sum _{c \in C \setminus c^*} V_{c} (x_{c}) \right\} \exp \left\{ V_{c^*} (x_{c^*}) \right\} \right) . \end{aligned}$$
(10)

Using that node n is only contained in clique \(c^*\), we can rewrite this expression as

$$\begin{aligned} p_{x_{1:n-1}}(x_{1:n-1} ) \propto \exp \left\{ \sum _{c \in C \setminus c^* } V_{c} (x_{c}) \right\} \sum _{x_n} \exp \left\{ V_{c^*} (x_{c^*}) \right\} . \end{aligned}$$
(11)

That is, we only need to sum over \(x_n\) in \(\exp \left\{ V_{c^*} (x_{c^*}) \right\} \). Now, if we define a new potential function for the clique \(c^* \setminus \{n\}\),

$$\begin{aligned} V_{c^* \setminus \{n\} } (x_{c^* \setminus \{n\} }) = \log \left( \sum _{x_n} \exp \left\{ V_{c^*} (x_{c^*}) \right\} \right) , \end{aligned}$$

we can rewrite Eq. (11) in the more convenient form

$$\begin{aligned} p_{x_{1:n-1}}(x_{1:n-1} ) \propto \exp \left\{ \sum _{c \in C \setminus c^* } V_{c} (x_{c}) \right\} \exp \left\{ V_{c^* \setminus \{n\} } (x_{c^* \setminus \{n\} }) \right\} . \end{aligned}$$
(12)

It is not necessary to compute the normalising constant in Eq. (12) in order for the remaining computations to proceed.

Next, we want to decompose \(p_{x_{1:n-1}}(x_{1:n-1} )\) into \(p_{x_{n-1}|x_{1:n-2}}(x_{n-1} | x_{1:n-2} )\) and \(p_{x_{1:n-2}}(x_{1:n-2} )\). For this, consider first the junction tree \(J_{V\setminus \{n\}}\) we obtain after removing node n from \(c^*\) in J. Removing node n from \(c^*\) can affect the structure of \(J_{V\setminus \{n\}}\) in two different ways: either \(J_{V\setminus \{n\}}\) has the same number of nodes as J, or it has one node less. To understand why, consider the clique \(c^* \setminus \{n\}\) that we obtain after removing node n from \(c^*\). Moreover, let \({\tilde{c}}\) denote the neighbour of \(c^*\) in J and let \(G_{V\setminus \{n\}}\) denote the graph obtained by removing node n from G. For the clique \(c^*\setminus \{n\}\), there are now two possibilities: either it is a subset of \({\tilde{c}}\), i.e. \(c^*\setminus \{n\} \subseteq {\tilde{c}}\), or it is not a subset of \({\tilde{c}}\), i.e. \(c^*\setminus \{n\} \not \subseteq \tilde{c}\). If \(c^*\setminus \{n\} \not \subseteq {\tilde{c}}\), then \(c^*\setminus \{n\}\) is a maximal clique in the graph \(G_{V\setminus \{n\}}\), and \(J_{V\setminus \{n\}}\) is essentially the same tree as J except that \(c^*\) is replaced with \(c^* \setminus \{n\}\). The clique \(c^*\setminus \{n\}\) then represents a leaf in \(J_{V\setminus \{n\}}\), and we can decompose \(p_{x_{1:n-1}}(x_{1:n-1} )\) into \(p_{x_{n-1}|x_{1:n-2}}(x_{n-1} | x_{1:n-2} )\) and \(p_{x_{1:n-2}}(x_{1:n-2} )\) in the same manner as we decomposed \(p_{x}(x)\) above. If, on the other hand, \(c^* \setminus \{n\} \subseteq {\tilde{c}}\), we must merge \(c^* \setminus \{n\}\) and \({\tilde{c}}\) before we can proceed. Specifically, this entails that we need to add the potential functions of the two cliques together,

$$\begin{aligned} {\widetilde{V}}_{ {\tilde{c}} } (x_{{\tilde{c}}} ) = V_{{\tilde{c}}} (x_{{\tilde{c}}}) + V_{c^* \setminus \{n\} } (x_{c^* \setminus \{n\} }). \end{aligned}$$

We can then rewrite Eq. (12) as

$$\begin{aligned} p_{x_{1:n-1}}(x_{1:n-1} ) \propto \exp \left\{ \sum _{c \in C \setminus \{ c^*, {\tilde{c}}\} } V_{c} (x_{c}) \right\} \exp \left\{ {\widetilde{V}}_{{\tilde{c}} } (x_{{\tilde{c}} }) \right\} . \end{aligned}$$
(13)

After merging the cliques, we can decompose \(p_{x_{1:n-1}}(x_{1:n-1} )\) in Eq. (13) into \(p_{x_{n-1}|x_{1:n-2}}(x_{n-1} | x_{1:n-2} )\) and \(p_{x_{1:n-2}}(x_{1:n-2} )\) in the same manner as we decomposed \(p_x(x)\) into \(p_{x_n | x_{1:n-1}}(x_n | x_{1:n-1}) \) and \(p_{x_{1:n-1}}(x_{1:n-1} )\). Notice, however, that it is possible that \({\tilde{c}}\) is not a leaf in \(J_{V\setminus \{n\}}\). If so, we must move to a clique which does represent a leaf, and decompose \(p_{x_{1:n-1}}(x_{1:n-1} )\) by removing a node and corresponding variable from this clique.

Ultimately, we end up computing \(p_{x_1}(x_1)\). A realisation from \(p_x (x)\) can then be obtained by first simulating \(x_1 \sim p_{x_1}(\cdot )\), thereafter \(x_2 | x_1 \sim p_{x_2 | x_1}(\cdot | x_1)\), then \(x_3 | x_1, x_2 \sim p_{x_3 | x_1, x_2}(\cdot | x_1, x_2)\), and so on.

2.2.5 Conditional simulation from discrete DGMs

Suppose again that \(p_x(x)\) is a discrete DGM with respect to a graph \(G = (V,E), \) and let J be a junction tree for G. In the previous section, we described how to simulate from \(p_x(x)\). Now, we address the closely related problem of how to simulate from the conditional distribution \(p_{x_A | x_{V\setminus A} }(x_A | x_{V\setminus A} )\), \(A \subset V\). First, Bayes rule gives

$$\begin{aligned} p_{x_A | x_{V\setminus A} }(x_A | x_{V\setminus A} ) \propto p_{x_A, x_{V\setminus A} }(x_A, x_{V\setminus A} ) = p_x(x). \end{aligned}$$
(14)

By inserting values for \( x_{V\setminus A}\) in Eq. (14), we obtain an expression for \(p_{x_A | x_{V\setminus A} }(x_A | x_{V\setminus A} ) \) up to a constant of proportionality. Thus, since \(p_{x_A | x_{V\setminus A} }(x_A | x_{V\setminus A} )\) is also a discrete DGM, we can simulate from \(p_{x_A | x_{V\setminus A} }(x_A | x_{V\setminus A} )\) using the recursive procedure described in Sect. 2.2.4, as this procedure only requires that \(p_{x_A | x_{V\setminus A} }(x_A | x_{V\setminus A} )\) is known up to a constant of proportionality. Before starting the computations, however, a new graph \( G_{ A}\) and corresponding junction tree \(J_{ A }\) must be constructed for \(p_{x_A | x_{V\setminus A} }(x_A | x_{V\setminus A} )\), and the clique potentials for the maximal cliques of \(G_A\) must be computed. The graph \(G_{A }\) is simply obtained by removing the nodes \(V\setminus A\) from V and all edges \(\{i,j\}\) from E where \(i \in V\setminus A\) and/or \(j\in V\setminus A\).

As an illustrative example, consider a DGM with respect to the graph in Fig. 2a. Suppose values for \(x_3\) and \(x_4\) are given and that we want to simulate from the conditional distribution \(p(x_{1}, x_2, x_5, x_6 | x_{3}, x_{4})\),

$$\begin{aligned}&p_{x_1, x_2, x_5, x_6 | x_3, x_4}({x_1, x_2, x_5, x_6 | x_3, x_4}) \\&\quad \propto \exp \left\{ V_{\{1,2,3\}} (x_1, x_2, x_3)+ V_{\{3,4,5\}}(x_3, x_4, x_5) + V_{\{4,5,6\}}(x_4, x_5, x_6) \right\} . \end{aligned}$$

For this toy example, we have \(A= \{1,2, 5, 6\}\) and \(V\setminus A = \{3,4\}\). The graph \(G_{A }\) is shown in Fig. 3a and the junction tree \(J_{A }\) is shown in Fig. 3b. The graph \(G_{A }\) only has two maximal cliques, \(\{1,2\}\) and \(\{5,6\}\), and the separator is simply the empty set \(\emptyset \). The potential functions corresponding to the maximal cliques \(\{1,2\}\) and \(\{5,6\}\) become, respectively,

$$\begin{aligned} {\widetilde{V}}_{\{1,2\}}(x_1, x_2) = V_{\{1,2,3\}}(x_1, x_2, x_3) \end{aligned}$$

and

$$\begin{aligned} {\widetilde{V}}_{\{5,6\}}(x_5, x_6) = V_{\{3,4,5\}}(x_3, x_4, x_5) + V_{\{4,5,6\}}(x_4, x_5, x_6), \end{aligned}$$

where now \(x_3\) and \(x_4\) are constant values. With \(G_{A }\), \(J_{A }\) and these potential functions given, we can simulate from

$$\begin{aligned} p_{x_1, x_2, x_5, x_6 | x_3, x_4}({x_1, x_2, x_5, x_6 | x_3, x_4}) \propto \exp \left\{ {\widetilde{V}}_{\{1,2\}}(x_1, x_2) + \widetilde{V}_{\{5,6\}}(x_5, x_6) \right\} \end{aligned}$$

using the procedure described in Sect. 2.2.4.

Fig. 3
figure 3

(a) The graph \(G_{A}\) with \(A = \{1,2,5,6\}\) for the graph in Fig. 2, and b the corresponding junction tree \(J_{A}\)

Full size image

3 Updating framework for categorical vectors

In this section we present our framework for the ensemble updating of categorical state vectors. The framework is a modified version of what is presented in Loe and Tjelmeland (2021b). Our focus is all the time on the updating of one specific ensemble member, number i say. We start in Sect. 3.1 by formulating an assumed Bayesian model for all quantities involved in the updating of ensemble number i. Next, in Sect. 3.2.1, we characterise a class of updating procedures that is correct under this assumed Bayesian model. This class of updating procedures is computationally hard to work with, so our next step, in Sect. 3.2.2, is to formulate a class of updating procedures that is only approximately correct under the assumed Bayesian model, but which is computationally simpler to work with. The last step in our framework, which we discuss in Sect. 3.3, is to define a criterion for identifying, within the class of updating procedures that are (approximately) correct under the assumed model, an updating procedure that is robust against the assumptions made in the assumed Bayesian model. In Sect. 4 we develop the computational details of the resulting updating procedure when the assumed Bayesian model is based on a \(\nu \)’th order Markov chain model.

3.1 Assumed Bayesian model

A graphical illustration of our assumed Bayesian model for the variables involved in the updating of the forecast sample \(x^{t,(i)}\) to a filtering sample \(\widetilde{x}^{t,(i)}\) is shown in Fig. 4.

Fig. 4
figure 4

Graphical illustration of the assumed Bayesian model for the updating of \(x^{t,(i)}\) to \(\widetilde{x}^{t,(i)}\)

Full size image

The model includes an unknown parameter vector \(\theta ^t \in \Omega _{\theta }\) for which a prior model \(f_{\theta ^t}(\theta ^t)\) is adopted. Moreover, the latent state vector \(x^t\) and the prior samples \(x^{t, (1)}, \dots , x^{t, (M)}\) are all assumed to be conditionally independent and identically distributed given \(\theta ^t\), i.e.

$$\begin{aligned} f_{x^t, x^{t, (1)}, \dots , x^{t, (M)} | \theta ^t }(x^t, x^{t, (1)}, \dots , x^{t, (M)} | \theta ^t ) = f_{x^t|\theta ^t}(x^t | \theta ^t) \prod _{i=1}^{M} f_{x^t|\theta ^t}(x^{t, (i)} | \theta ^t), \end{aligned}$$

where \(f_{x^t|\theta ^t}(x^t|\theta ^t)\) is an assumed prior model for \(x^t | \theta ^t\). The observation \(y^t\) is assumed to be conditionally independent of \(\theta ^t\) and \(x^{t, (1)}, \dots , x^{t, (M)}\) given \(x^t\), and distributed according to an assumed likelihood model \(f_{y^t|x^t}(y^t|x^t)\). Given \(x^{t, (i)}\), \(\theta ^t\) and \(y^t\), the posterior realisation \(\widetilde{x}^{t, (i)}\) is conditionally independent of \(x^{t, (1)}, \dots , x^{t, (i-1)}, x^{t, (i+1)}, \dots , x^{t, (M)}\) and \(x^t\). For simplicity, we denote in the following the set of prior samples except the sample \(x^{t,(i)}\) by \(x^{t, -(i)} \), i.e.

$$\begin{aligned} x^{t, -(i)} = \{x^{t, (1)}, \dots , x^{t, (i-1)}, x^{t, (i+1)}, \dots , x^{t, (M)}\}. \end{aligned}$$

Conceptually, the assumed models \(f_{x^t | \theta ^t}(x^t | \theta ^t)\) and \(f_{y^t|x^t}(y^t|x^t)\) can be any parametric distributions. In order for the framework to be useful in practice, however, they must be chosen so that the corresponding posterior model

$$\begin{aligned} f_{x^t | \theta ^t, y^t}(x^t | \theta ^t, y^t) \propto f_{x^t | \theta ^t}(x^t | \theta ^t) f_{y^t|x^t}(y^t|x^t) \end{aligned}$$
(15)

is tractable. Moreover, \(f_{\theta ^t}(\theta ^t)\) should be chosen as conjugate for \(f_{x^t | \theta ^t}(x^t | \theta ^t)\).

3.2 Class of updating distributions

Based on the assumed Bayesian model defined above we characterise in this section a class of updating procedures for generating the filtering ensemble element \(\widetilde{x}^{t,(i)}\) from forecast ensemble member \(x^{t,(i)}\). First, we derive in Sect. 3.2.1 a class of updating distributions which are exact in the sense that, under the assumption that the forecast samples are distributed according to the assumed Bayesian model, the posterior sample \(\widetilde{x}^{t,(i)}\) is distributed according to the resulting posterior model in Eq. (15). Thereafter, we introduce in Sect. 3.2.2 a class of updating procedures that are only approximately correct under the assumed Bayesian model, but which is computationally simpler to deal with.

3.2.1 Derivation of a class of updating distributions

A natural minimal restriction for the updating of \(x^{t,(i)}\) to \(\widetilde{x}^{t,(i)}\) is to require that the procedure is consistent with the assumed model. One can then say that the updating is correct under the assumed model. In addition one would naturally also like the updating to be robust against the assumptions made in the assumed Bayesian model, but this is not the main focus in this section.

A naïve updating procedure that is consistent with the assumed model is simply to set \(\widetilde{x}^{t,(i)}\) equal to a sample from \(f_{x_t|x^{t,(1)},\ldots ,x^{t,(M)},y^t}(\cdot |x^{t,(1)}, \ldots ,x^{t,(M)}, y^t)\). This procedure may, however, be very sensitive to the assumptions of the assumed model. To get a more robust updating procedure, a better alternative is to generate \(\widetilde{x}^{t,(i)}\) as a modified version of \(x^{t,(i)}\), as indicated by the graph in Fig. 4. In such a setup, the role of \(x^{t,(i)}\) is as a source of randomness in the generation of \(\widetilde{x}^{t,(i)}\). One should therefore remove \(x^{t,(i)}\) from the conditioning set in the naïve updating procedure and instead require that \(\widetilde{x}^{t,(i)}\) is a sample from \(f_{x^t|x^{t,-(i)},y^t}(\cdot | x^{t,-(i)},y^t)\) under the assumed model. Thus, the updating of \(x^{t,(i)}\) to \(\widetilde{x}^{t,(i)}\) should be such that

$$\begin{aligned} f_{\widetilde{x}^{t,(i)}|x^{t,-(i)},y^t}(x^t|x^{t,-(i)},y^t) = f_{x^t|x^{t,-(i)},y^t}(x^t|x^{t,-(i)},y^t) \end{aligned}$$
(16)

for all \(x^t\), \(x^{t,-(i)}\) and \(y^t\). In the following we study what implications the restriction in Eq. (16) have on how to generate \(\widetilde{x}^{t,(i)}\) from \(x^{t,(i)}\).

Introducing the parameter vector \(\theta ^t\), the distribution on the left hand side of Eq. (16) is obtained by marginalising out \(\theta ^t\) from the joint distribution \(f_{\theta ^t, \widetilde{x}^{t, (i)} | x^{t, -(i)}, y^t} (\theta ^t, x^t | x^{t, -(i)}, y^t)\). Rewriting the distribution on the right hand side of Eq. (16) in a similar way it follows that Eq. (16) can be rewritten as

$$\begin{aligned} \int _{\Omega _{\theta ^t}} f_{\theta ^t, \widetilde{x}^{t, (i)} | x^{t, -(i)}, y^t} (\theta ^t, x^t | x^{t, -(i)}, y^t) \text {d}\theta ^t = \int _{\Omega _{\theta ^t}} f_{\theta , x^{t} | x^{t, -(i)}, y^t} (\theta ^t, x^t | x^{t, -(i)}, y^t)\text {d}\theta ^t. \nonumber \\ \end{aligned}$$
(17)

Writing each of the joint distributions in these two integrands as a product of the marginal distribution for \(\theta ^t\) and the conditional distribution for the other variable given \(\theta ^t\), the restriction reads

$$\begin{aligned}&\int _{\Omega _{\theta ^t}} f_{\theta ^t | x^{t, -(i)}, y^t} (\theta ^t | x^{t, -(i)}, y^t) f_{\widetilde{x}^{t,(i)} | \theta ^t, y^t }(x^t | \theta ^t, y^t) \text {d}\theta ^t\nonumber \\&\quad =\int _{\Omega _{\theta ^t}} f_{\theta ^t | x^{t, -(i)}, y^t} (\theta ^t | x^{t, -(i)}, y^t) f_{x^{t} | \theta ^t, y^t }(x^t | \theta ^t, y^t) \text {d}\theta ^t . \end{aligned}$$
(18)

A sufficient condition for this relation to hold is that the two integrands are equal for each \(\theta ^t\). From this it follows that a sufficient condition for Eq. (18) to hold is that

$$\begin{aligned} f_{\widetilde{x}^{t,(i)} | \theta ^t, y^t }(x^t | \theta ^t, y^t) = f_{x^{t} | \theta ^t, y^t }(x^t | \theta ^t, y^t) \end{aligned}$$
(19)

for all \(x^t, \theta ^t\) and \(y^t\). Thereby, we understand that \(x^{t,(i)}\) can be updated by first simulating

$$\begin{aligned} \theta ^{t,(i)} | x^{t,-(i)}, y^t \sim f_{\theta ^{t} | x^{t,-(i)}, y^t} (\cdot | x^{t,-(i)}, y^t) \end{aligned}$$

and thereafter simulate

$$\begin{aligned} \widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t \sim f_{\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t } (\cdot | x^{t,(i)}, \theta ^{t,(i)}, y^t ), \end{aligned}$$

where \( f_{\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t } (\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t )\) is a distribution which fulfils Eq. (19). Generally, a class of updating distributions \(f_{\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t } (\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t )\) consistent with the requirement in Eq. (19) exists. The simplest option is to use the assumed posterior model \( f_{x^{t} | \theta ^{t,(i)}, y^t }(x^t | \theta ^{t,(i)}, y^t)\) and simulate \(\widetilde{x}^{t,(i)}\) independently of \(x^{t,(i)}\). However, this means that we possibly lose valuable information from \(x^{t,(i)}\) about the true forecast and filtering distributions that we may not have been able to capture with the assumed model. To preserve more of this information from \(x^{t,(i)}\), it is important to simulate \(\widetilde{x}^{t,(i)}\) conditionally on \(x^{t,(i)}\).

Conceptually, an updating distribution \( f_{\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t } (\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t )\) can be constructed by first constructing a joint distribution \( f_{x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t } (x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t )\), and thereafter condition this distribution on \(x^{t,(i)}\). The joint distribution\( f_{x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t } (x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t )\) can be factorised as

$$\begin{aligned}&f_{x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t } (x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t )\nonumber \\&\quad = f_{x^{t} | \theta ^{t,(i)}}(x^{t,(i)} | \theta ^{t,(i)} ) f_{\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t } (\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t ). \end{aligned}$$
(20)

To be consistent with the requirement in Eq. (19), \(f_{x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t } (x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t )\) must fulfil

$$\begin{aligned} \sum _{x^{t,(i)}} f_{x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t } (x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t ) = f_{x^{t} | \theta ^{t,(i)}, y^t }(\widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t), \end{aligned}$$
(21)

that is, when marginalising out \(x^{t,(i)}\) we end up with the assumed posterior model. To be consistent with the model assumptions, and so that the factorised form in Eq. (20) holds, the distribution must also fulfil

$$\begin{aligned} \sum _{\widetilde{x}^{t,(i)}} f_{x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t } (x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t ) = f_{x^{t} | \theta ^{t,(i)}}(x^{t,(i)} | \theta ^{t,(i)} ), \end{aligned}$$
(22)

that is, when marginalising out \(\widetilde{x}^{t,(i)}\) we end up with the assumed prior model. In principle, infinitely many distributions \(f_{x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t } (x^{t,(i)}, \widetilde{x}^{t,(i)} | \theta ^{t,(i)}, y^t )\) consistent with the requirements in Eqs. (21) and (22) exist. In practice, however, it is generally difficult to assess one of these distributions, except the naïve solution where \(f_{\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^{t,(i)}, y^t } (\cdot | x^{t,(i)}, \theta ^{t,(i)}, y^t )\) is set equal to the assumed posterior model \( f_{x^{t} | \theta ^{t,(i)}, y^t }(\cdot | \theta ^{t,(i)}, y^t)\). Therefore, we must resort to approximations, which we consider in more detail below.

3.2.2 A class of approximate updating distributions

In this section we propose an approximation to \(f_{x^{t,(i)},\widetilde{x}^{t,(i)}|\theta ^{t,(i)},y^t}(x^{t,(i)},\widetilde{x}^{t,(i)}|\theta ^{t,(i)},y^t)\), which we denote by \(q(x^{t,(i)},\widetilde{x}^{t(i)}|\theta ^{t,(i)},t^t)\). Like \(f_{x^{t,(i)},\widetilde{x}^{t,(i)}|\theta ^{t,(i)},y^t}(x^{t,(i)},\widetilde{x}^{t,(i)}|\theta ^{t,(i)},y^t)\), also the approximation \(q(x^{t,(i)},\widetilde{x}^{t,(i)}|\theta ^{t,(i)},y^t)\) defines a joint distribution for \(x^{t,(i)}\) and \(\widetilde{x}^{t,(i)}\) for given values of \(\theta ^{t,(i)}\) and \(y^t\). However, whereas \(f_{x^{t,(i)},\widetilde{x}^{t,(i)}|\theta ^{t,(i)},y^t}(x^{t,(i)},\widetilde{x}^{t,(i)}|\theta ^{t,(i)},y^t)\) defines a conditional distribution for the two variables consistent with the assumed Bayesian model, we do not require this for \(q(x^{t,(i)},\widetilde{x}^{t(i)}|\theta ^{t,(i)},t^t)\). We define a class of allowed distributions \(q(x^{t,(i)},\widetilde{x}^{t(i)}|\theta ^{t,(i)},t^t)\) by replacing the restrictions in Eqs. (21) and (22) with two weaker restrictions, which we detail in the following.

Let \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) be a DGM with respect to a graph G with vertex set \(V = \{1, \dots , 2n\}\) and maximal clique set \(C = \{c_1, \dots , c_{|C|}\}\) where |C| is the number of maximal cliques. Associate the n variables of \(x^{t,(i)}\) with the nodes \(1, \dots , n\) and the n variables of \(\widetilde{x}^{t,(i)}\) with the nodes \(n+1, \dots , 2n\), so that, for \(j=1, \dots , n\), the variable \(x_j^{t,(i)}\) is associated with node j and the variable \(\widetilde{x}_j^{t,(i)}\) is associated with node \(j+n\). Next, let \(A_1, \dots , A_{|C|}\), \(B_1, \dots , B_{|C|}\) denote a sequence of subsets of \(V_{1:n} = \{1, \dots , n\}\) such that the nodes of V that are associated with \((x_{A_j}^{t,(i)}, \widetilde{x}_{B_j}^{t,(i)})\) form clique \(c_j\). Mathematically, that is

$$\begin{aligned} A_j = \{i \in c_j; i \le n\} \end{aligned}$$
(23)

and

$$\begin{aligned} B_j =\{i-n; i \in c_j, i > n\}. \end{aligned}$$
(24)

Thereby, \(q(x_{A_j}^{t,(i)}, \widetilde{x}_{B_j}^{t,(i)}| \theta ^{t,(i)}, y^t)\) represents the distribution of the variables \((x_{A_j}^{t,(i)}, \widetilde{x}_{B_j}^{t,(i)})\) associated with clique \(c_j\), \(j=1, \dots , |C|\). For example, if \(c_1 = \{1,2,n+1\}\), then \(A_1 =\{1,2\}\) and \(B_1 = \{1\}\), and \(q(x_{1:2}^{t,(i)}, \widetilde{x}_{1}^{t,(i)}| \theta ^{t,(i)}, y^t)\) represents the distribution for the variables \((x_1^{t,(i)}, x_2^{t,(i)}, \widetilde{x}_1^{t,(i)})\) associated with the nodes of clique \(c_1\).

From Sect. 2.2 we know that since \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) is a DGM it is fully specified by its clique probabilities and can be expressed as

$$\begin{aligned} q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t) = \frac{ \prod _{j=1}^{|C|} q( x^{t,(i)}_{A_j}, \widetilde{x}^{t,(i)}_{B_j}| \theta ^{t,(i)}, y^t) }{ \prod _{j=1}^{|C|-1} q( x^{t,(i)}_{A_j \cap A_{j+1}}, \widetilde{x}^{t,(i)}_{B_j \cap B_{j+1}}| \theta ^{t,(i)}, y^t) }. \end{aligned}$$

Hence, in order to specify \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t) \), all we need to do is to appropriately specify each of the clique probabilities \(q( x^{t,(i)}_{A_j}, \widetilde{x}^{t,(i)}_{B_j}| \theta ^{t,(i)}, y^t)\), \(j=1, \dots , |C|\). Recall that the goal is to specify \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) such that it approximately represents the joint distribution in Eq. (20) subject to the constraints in Eqs. (21) and (22). To construct such a \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\), we replace the requirements in Eqs. (21) and (22) by

$$\begin{aligned} \sum _{x_{A_j}^{t,(i)}} q( x^{t,(i)}_{A_j}, \widetilde{x}^{t,(i)}_{B_j}| \theta ^{t,(i)}, y^t) = f_{x^{t}_{B_j} | \theta ^{t,(i)} , y^t }(\widetilde{x}_{B_j}^{t,(i)} | \theta ^{t,(i)}, y^t ), \quad j = 1, \dots , |C|, \nonumber \\ \end{aligned}$$
(25)

and

$$\begin{aligned} \sum _{\widetilde{x}_{B_j}^{t,(i)}} q( x^{t,(i)}_{A_j}, \widetilde{x}^{t,(i)}_{B_j}| \theta ^{t,(i)}, y^t) = f_{x^{t}_{A_j} | \theta ^{t,(i)} , y^t }(x_{A_j}^{t,(i)} | \theta ^{t,(i)} ), \quad j = 1, \dots , |C|, \end{aligned}$$
(26)

respectively. That is, instead of requiring that \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) fully preserves \(f_{x^t | \theta ^t}(x^t | \theta ^t)\) and \(f_{x^t | \theta ^t}(x^t | \theta ^t, y^t)\), as required in Eqs. (21) and (22), we only require that the marginal distributions \(f_{x_{A_j}^t | \theta ^t}(x_{A_j}^t | \theta ^t)\) and \(f_{x_{B_j}^t | \theta ^t, y^t}(x_{B_j}^t | \theta ^t, y^t)\) are preserved. Another constraint we need to take into account when specifying \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) is that the clique probabilities must be consistent in the sense that, if we let \((c_1, \dots , c_{|C|})\) denote an ordering of the cliques in C which fulfils the running intersection property in Eq. (4), the probabilities for two consecutive cliques \(c_j\) and \(c_{j+1}\) must return the same marginal distribution for the separator \(s_j = c_j \cap c_{j+1}\). Mathematically, this can be written as

$$\begin{aligned}&\sum _{x^{t,(i)}_{A_j \setminus A_{j+1}}} \sum _{\widetilde{x}^{t,(i)}_{B_j \setminus B_{j+1}}} q( x^{t,(i)}_{A_j}, \widetilde{x}^{t,(i)}_{B_j}| \theta ^{t,(i)}, y^t)\nonumber \\&\quad = \sum _{x^{t,(i)}_{A_{j+1} \setminus A_j}} \sum _{\widetilde{x}^{t,(i)}_{B_{j+1} \setminus B_j}} q( x^{t,(i)}_{A_{j+1}}, \widetilde{x}^{t,(i)}_{B_{j+1}}| \theta ^{t,(i)}, y^t). \end{aligned}$$
(27)

Assuming we are able to construct a DGM \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) consistent with the requirements discussed above, we can condition this DGM on \(x^{t,(i)}\) and simulate \(\widetilde{x}^{t,(i)} | x^{t,(i)}\) as described in Sect. 2.2.5.

3.3 Defining an optimal solution

There may be infinitely many distributions \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) which fulfil the requirements in Eqs. (25)–(27). In this section we formulate a criterion that can be used to identify an update distribution within the class defined above, that is robust with respect to the assumed Bayesian model. To preserve as much information from \(x^{t,(i)}\) as possible in \(\widetilde{x}^{t,(i)}\), we define the optimal \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) as the one which maximises the expected number of elements in \(x^{t,(i)}\) that remain unchanged, i.e. the \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) that maximises

$$\begin{aligned} g(x^{t,(i)}, \widetilde{x}^{t,(i)}) = \text {E} \left[ \sum _{j=1}^n 1 \left( x_j^{t, (i)} = \widetilde{x}_j^{t, (i)} \right) \right] , \end{aligned}$$
(28)

where the expectation is taken over \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\). Intuitively, this is a reasonable optimality criterion for categorical variables which should make the update robust. By making minimal changes to \(x^{t, (i)}\), the updated sample \(\widetilde{x}^{t,(i)}\) may be able to capture properties of the true filtering distribution \(p(x^t | y^{1:t})\) that we may not have captured with the posterior distribution \(f(x^t | \theta ^t, y^t)\) resulting from the assumed Bayesian model. The key steps of the resulting updating procedure are summarised in Algorithm 1.

figure a

4 Updating procedure using a Markov chain assumed prior

Using the updating framework introduced above, we in this section develop the resulting updating procedure when the assumed Bayesian model is based on a \(\nu \)’th order Markov chain model. In particular we propose to choose the maximal cliques of the DGM \(q(x^{t,(i)}, \widetilde{x}^{t, (i)}| \theta ^{t}, y^t)\) in such a way that the optimal solution can be computed by solving a linear optimisation problem.

4.1 Model specifications

Assuming the vector \(x^t\) to have a one-dimensional spatial arrangement, we choose the assumed prior distribution \(f_{x^t | \theta ^t}(x^t | \theta ^t)\) to be a Markov chain of order \(\nu \ge 1\),

$$\begin{aligned} f_{x^t | \theta ^t}(x^t | \theta ^t ) = f_{x^t_{1:\nu } | \theta ^t} (x_{1:\nu }^t | \theta ^t) \prod _{j=\nu +1}^n f_{x^t_j | x^t_{j-\nu :j-1}, \theta ^t} (x_j^t | x^t_{j-\nu :j-1}, \theta ^t). \end{aligned}$$

For the likelihood model \(f_{y^t | x^t}(y^t|x^t)\), we assume that \(y^t = (y_1^t, \dots , y_n^t)\) contains n conditionally independent observations, with \(y_j^t\) depending only on \(x_j^t\),

$$\begin{aligned} f_{y^t | x^t} (y^t | x^t) = \prod _{j=1}^{n} f(y_j^t | x_j^t). \end{aligned}$$
(29)

This choice of assumed prior and likelihood yields a posterior model \(f_{x^t|\theta ^t, y^t}(x^t | \theta ^t, y^t)\) which is also a Markov chain of order \(\nu \). The initial and transition probabilities of this posterior Markov chain can be computed efficiently with the forward filtering-backward smoothing algorithm for hidden Markov models (e.g., Künsch , 2000).

The parameter vector \(\theta ^t\) should define the initial and transition probabilities of the assumed prior Markov chain. A Markov chain of order \(\nu \) is specified by \(n-\nu +1\) transition matrices, each matrix consisting of \(K^{\nu }\) rows and K columns. Denote in the following these transition matrices by \( \theta _1^t, \dots , \theta ^t_{n-\nu +1}\). Furthermore, let \(\theta _0\) be a vector representing the initial probabilities of the Markov chain, and consider

$$\begin{aligned} \theta ^t = (\theta _0^t, \theta _1^t, \dots , \theta ^t_{n-\nu +1}). \end{aligned}$$

Following the recommendations of Section 3.1, we choose \(f_{\theta ^t}(\theta ^t)\) as conjugate for \(f_{x^t | \theta ^t}(x^t | \theta ^t)\). Here, this entails adopting a Dirichlet distribution for \(\theta _0^t\) and a Dirichlet distribution for each of the \(K^{\nu }\) row vectors in each transition matrix \(\theta ^t_j\), \(j= 1, \dots , n-\nu +1\), and to let all these Dirichlet distributed parameters be a priori independent. For simplicity, the remaining technical details of the specification of \(f_{\theta ^t}(\theta ^t)\) are presented in Appendix A, whereas how to simulate from \(\theta ^t | x^{t, -(i)}, y^t \sim f_{\theta ^t | x^{t, -(i)}, y^t}(\theta ^t | x^{t, -(i)}, y^t)\) we discuss in Appendix B.

4.2 Class of updating distributions

Having specified the distributions \(f_{\theta ^t}(\theta ^t)\), \(f_{x^t|\theta ^t}(x^t | \theta ^t)\) and \(f_{y^t|x^t}(y^t|x^t)\) of the assumed Bayesian model, the next task is to characterise the class of DGMs \(q(x^{t, (i)}, \widetilde{x}^{t, (i)}| \theta ^t, y^t)\) introduced in Sect. 3.2. For this, we need to specify the cliques of the underlying decomposable graph of \(q(x^{t, (i)}, \widetilde{x}^{t, (i)}| \theta ^t, y^t)\) or, equivalently, the \(A_j\) and \(B_j\)-sets in Eqs. (23) and (24). For some integer \(d\ge 1\), the \(A_j\) and \(B_j\)-sets are specified as

$$\begin{aligned} A_j = B_j = \{j, j+1, \dots , j+d-1\} \end{aligned}$$
(30)

for \(j=1, \dots , n-d+1\). Visually, the decomposable graph G can then be represented as a two-dimensional grid with two rows and n columns, or as a \(2 \times n\) matrix. The first row is associated with the nodes \(1, \dots , n\) and the second row is associated with the nodes \(n+1, \dots , 2n\). Each maximal clique is formed by d consecutive columns, hence we call it a \(2 \times d\) clique. The variables associated with each \(2 \times d\) clique are \(x_{j:j+d-1}^{t,(i)}\) and \(\widetilde{x}_{j:j+d-1}^{t,(i)}\). Figures 5a and 6a illustrate G when \(d=2\) and \(d=3\), respectively, when the state vector \(x^t\) contains \(n=5\) variables. Figures 5b and 6b show corresponding junction tree representations. The chosen graphical structure makes it fairly trivial to construct corresponding junction trees.

Fig. 5
figure 5

a Underlying graph for the DGM \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t}, y^t)\) of Sect. 4 when \(d = 2\), b a corresponding junction tree representation

Full size image
Fig. 6
figure 6

a Underlying graph for the DGM \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t}, y^t)\) of Sect. 4 when \(d=3\), b a corresponding junction tree representation

Full size image

The criteria in Eqs. (25)–(27) can now be rewritten as

$$\begin{aligned} \sum _{x^{t,(i)}_{j:j+d-1}} q( x^{t, (i)}_{j:j+d-1} ,\widetilde{x}^{t, (i)}_{j:j+d-1}| \theta ^{t,(i)}, y^t)= & {} f_{x_{j:j+d-1}^t | \theta ^{t,(i)}, y^t}(\widetilde{x}_{j:j+d-1}^{t,(i)} | \theta ^{t,(i)}, y^t), \qquad \end{aligned}$$
(31)
$$\begin{aligned} \sum _{\widetilde{x}^{\, t,(i)}_{j:j+d-1}} q( x^{t, (i)}_{j:j+d-1} ,\widetilde{x}^{t, (i)}_{j:j+d-1}| \theta ^{t,(i)}, y^t)= & {} f_{x_{j:j+d-1}^t | \theta ^{t,(i)}}(x_{j:j+d-1}^{t,(i)} | \theta ^{t,(i)}), \end{aligned}$$
(32)

and

$$\begin{aligned} \sum _{x^{t,(i)}_{j} } \sum _{\widetilde{x}^{t,(i)}_{j} } q( x^{t,(i)}_{j:j+d-1}, \widetilde{x}^{t,(i)}_{j:j+d-1}| \theta ^{t,(i)}, y^t) = \sum _{x^{t,(i)}_{j+d} } \sum _{x^{t,(i)}_{j+d} } q( x^{t,(i)}_{j+1:j+d}, \widetilde{x}^{t,(i)}_{j+1:j+d}| \theta ^{t,(i)}, y^t), \qquad \end{aligned}$$
(33)

respectively.

4.3 Computing the optimal solution

When the maximal cliques of the DGM \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) are as specified in Sect. 4.2, the optimal solution of \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\), i.e. the solution which maximises the expected value in Eq. (28), can be computed by solving a linear optimisation problem where the unknowns are all the clique probabilities \(q (x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)} ; \theta ^t, y^t)\), \(j=1, \dots , n-d+1\). To see this, notice first that the objective function in Eq. (28) can be rewritten as

$$\begin{aligned}&\text {E} \left[ \sum _{j=1}^{n} 1 \left( x_j^{(i)} = \widetilde{x}_j^{(i)} \right) \right] \nonumber \\&\quad = \sum _{k=0}^{K-1} \sum _{j=1}^{n} q( x_j^{t, (i)} = k, \widetilde{x}_j^{t, (i)} = k | ~\theta ^{t,(i)}, y^t) \nonumber \\&\quad = \sum _{k=0}^{K-1} \left( \sum _{j=1}^{n-d} q (x_j^{t, (i)} = k, \widetilde{x}_j^{t, (i)} = k; ~\theta ^{t,(i)}, y^{t})\right. \nonumber \\&\qquad \left. + \sum _{j=n-d+1}^n q( x_j^{t, (i)} = k, \widetilde{x}_j^{t, (i)} = k| ~ \theta ^{t,(i)}, y^{t}) \right) . \end{aligned}$$
(34)

All the terms in Eq. (34) can be computed by summing out variables from a corresponding clique distribution \(q (x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)} ; \theta ^{t,(i)}, y^t)\). More precisely, term number j in the sum from 1 to \(n-d\) in Eq. (34) can be computed by summing out variables from \(q (x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)} ; \theta ^{t,(i)}, y^t)\), while each term in the sum from \(n-d+1\) to n can be computed by summing out variables from \(q ({x_{A_{n-d+1}}^{t, (i)}, \widetilde{x}_{A_{n-d+1}}^{t, (i)} ; \theta ^{t,(i)}, y^t} )\). This leads to an objective function which is a linear function of \(q (x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)} ; \theta ^{t,(i)}, y^t)\), \(j=1, \dots , n-d+1\). The objective function is to be maximised subject to the constraints in Eqs. (31) to (33), which are also linear functions of \(q (x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)} ; \theta ^{t,(i)}, y^t)\). Because \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) is a probability distribution, we must also include the constraint that \(q( x^{t,(i)}_{A_j}, \widetilde{x}^{t,(i)}_{A_j}| \theta ^{t,(i)}, y^t)\) sums to one,

$$\begin{aligned} \sum _{x_{A_j}^{t, (i)}} \sum _{\widetilde{x}_{A_j}^{t, (i)}} q(x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)}| \theta ^{t,(i)}, y^t) = 1, \end{aligned}$$
(35)

and that it can only take values between zero and one,

$$\begin{aligned} 0 \le q(x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)}| \theta ^{t,(i)}, y^t) \le 1. \end{aligned}$$
(36)

These constraints are also linear functions of \(q (x_{A_j}^{t, (i)}, \widetilde{x}_{A_j}^{t, (i)} ; \theta ^{t,(i)}, y^t)\). Thus, we have a linear optimisation problem, or a linear program, which can be efficiently solved with standard linear programming techniques.

5 Simulation example

In this section, the updating procedure described in Sect. 4 is demonstrated in a simulation example. The example involves a filtering problem where the unobserved Markov process \(\{x^t\}_{t=1}^{T}\) consists of \(T=100\) time steps, the dimension n of \(x^t\) is \(n=200\), and there are three classes for each element \(x_j^t\) of \(x^t\): 0, 1, and 2.

5.1 Experimental setup

Our simulation experiment is a modified version of the binary simulation scheme in Loe and Tjelmeland (2021b). As for the example in that article, we let us inspire from the process when water comes through to an oil producing well in a petroleum reservoir. It should be stressed, however, that we do not claim our setup to be a realistic description for this process.

The t in \(x_j^t\) represents time and j the location in the well, with \(j=1\) being at the top of the well and \(j=n\) at the bottom. We let the events \(x^t_j=0\) and \(x_j^t=1\) represent the presence of porous sand stone filled with oil and water, respectively, in location j of the well at time t, while the event \(x^t_j=2\) represents non-porous shale in the same location. One should note that the spatial distribution of sand stone and shale does not change with time, whereas the fluid in a sand stone may change.

We start by simulating a reference, or true, sequence of states, \(x^1,\ldots ,x^T\). We simulate these as a Markov chain with an initial distribution for \(x^1\) and a forward model for generating \(x^2\ldots ,x^T\). The precise initial and forward models we are using are defined in Appendix C. The simulated reference states are shown in Fig. 7a.

Fig. 7
figure 7

Simulation experiment: a The generated reference process \(\{x^t\}_{t=1}^{100}\), b the first coordinate \(\{ (y_{j,1}^t, j=1, \dots , 200) \}_{t=1}^{100}\) of the observation process \(\{y^t\}_{t=1}^{T}\), and (c) the second coordinate \(\{ (y_{j,2}^t, j=1, \dots , 200) \}_{t=1}^{100}\). In (a) yellow is shale and green and blue are sand stone filled with water and oil, respectively. In (b) and (c) the colours represent the values of the continuous distributed observation processes

Full size image

The horizontal and vertical axes in the figure is time and depth, respectively. The yellow is shale and the green and blue are sand stone filled with water and oil, respectively. The initial and forward models are constructed so that at time \(t=0\) all the sand stone is filled with oil, whereas at time \(t=T\) most of the sand stone is filled with water.

Given the reference states \(x^1,\ldots ,x^T\) shown in Fig. 7a we simulate corresponding observations \(y^1,\ldots ,y^T\). At each time t we assume the elements of \(y^t\) to be conditionally independent given \(x^t\). To avoid that the likelihood effectively induces an ordering of the three possible values for each \(x^t_j\), we let \(y_t^j\) be a vector of two conditionally independent normally distributed components, and choose the mean values and variances of these normal distributions to obtain a likelihood that has full symmetry between the three possible values of \(x^t_j\). A detailed description of the likelihood function used is given Appendix C. Images of the two components of the simulated \(y_1,\ldots ,y^T\) are shown in Fig. 7b and c. As in Fig. 7a, the horizontal and vertical axes represent in these figures time and depth, respectively, whereas the colours represents real values as shown by the associated colour bars.

Having generated values for \(y^1,\ldots ,y^T\) we consider these as observed values and the underlying reference process as unknown. We then run the proposed filtering procedure proposed above. To generate the initial ensemble \(\{x^{1,(1)},\ldots ,x^{1,(M)}\}\) we generate independent samples from the same distribution we used to generate the reference state at time \(t=0\). Moreover, in the filtering procedure we use the same forward model as we used when generating the reference state at times \(t>0\), and same likelihood function as we used to generate \(y^1,\ldots ,y^T\) from the reference states.

When running the proposed updating procedure, we need to set a value for \(\nu \), i.e. the order of the assumed Markov chain model \(f_{x^t|\theta ^t}(x^t | \theta ^t)\), and a value for the integer d in Eq. (30) which determines the structure of \(q(x^{t,(i)},\widetilde{x}^{t,(i)} | \theta ^t, y^t)\). High values for \(\nu \) and d, and high values for d especially, make the construction of \(q(x^{t,(i)},\widetilde{x}^{t,(i)} | \theta ^t, y^t)\) computer-demanding. Below, we investigate the two values \(\nu =1\) and \(\nu =2\), and for each of these we consider the three values \(d=1\), \(d=2\) and \(d=3\). Thereby, we have six combinations, or cases, for \((\nu , d)\). For each of these six cases, we perform five independent runs, using ensemble size \(M=20\). The hyper-parameters \(a_0^t(0), \dots , a_0^t(K^{\nu }-1)\), \(a_i^{t,j}(0), \dots , a_i^{t,j}(K-1)\) of the prior distribution \(f_{\theta ^t}(\theta ^t)\) for \(\theta ^t\) (cf. Appendix A) at each time step t are all set equal to one, and 500 iterations are used in the MCMC simulation of \(\theta ^{t,(i)} | x^{t, -(i)}, y^t\) (cf. Appendix B).

5.2 Results

To evaluate the performance of the proposed approach, we first compute, for each of the five runs of each of the six combinations of \((\nu , d)\), the maximum a posteriori probability (MAP) estimate \({\hat{x}}_t^j\) of \(x_j^t\), \(t=1, \dots , T\), \(j=1, \dots , n\),

(37)

where

$$\begin{aligned} {\hat{p}}_j^t(k) = \frac{1}{M} \sum _{i=1}^{M} 1(\widetilde{x}_j^{t,(i)}=k), \quad k=0, 1, 2, \end{aligned}$$
(38)

is an estimate of the marginal filtering probability \(p_{x_j^t | y^{1:t}}(k | y^{1:t})\). Figure 8 shows images of the computed MAP estimates \(\{{\hat{x}}_j^t, j=1, \dots , n\}_{t=1}^{T}\) from one of the five runs performed for each of the six cases. From a visual inspection, it seems that we in all cases manage to capture the main characteristics of the true \(x^t\)-process in Fig. 7a, but the MAPs shown in Fig. 8a and d, which are obtained using \(d=1\), are possibly a bit noisier than the others.

Fig. 8
figure 8

Results from simulation experiment: MAP estimates of \(\{ x_j^{t}, j=1, \dots , 200\}_{t=1}^{100}\)

Full size image
Table 1 Results from simulation experiment: proportion of correctly classified variables \(x_j^t\) obtained with the MAP estimates in Eq. (37) computed in five independent runs
Full size table

Table 1 lists the ratio of correctly classified variables \(x_j^t\) based on the MAPs obtained from the five independent runs of each case.

According to Table 1 we classify around 85-90\(\%\) of the variables correctly, and we obtain the best results when using the combinations \(\nu = 1, d=2\) and \(\nu =1, d=3\). This may suggest that adopting a first-order Markov chain (i.e., \(\nu =1\)) for \(f_{x^t | \theta ^t}(x^t| \theta ^t)\) and using 2\(\times \)2- or 2\(\times \)3-cliques (i.e., \(d=2\) or \(d=3\)) in the construction of \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) is a robust strategy.

To further investigate the performance of the proposed approach, we estimate for each j and t the probability that \(\widetilde{x}_j^{t,(i)}\) is equal to the true value \(x_j^t\), and we do this for each of the classes \(k=0, 1, 2\). Specifically, for each run and for each \(j=1, \dots , n\), \(t =1, \dots , T\), we compute, if \(x_j^t = 0\),

$$\begin{aligned} \pi _{0|0} = \frac{1}{M} \sum _{i=1}^{M} 1(\widetilde{x}_j^{t,(i)}=0), \end{aligned}$$

while if \(x_j^t = 1\), we compute

$$\begin{aligned} \pi _{1|1} = \frac{1}{M} \sum _{i=1}^{M} 1(\widetilde{x}_j^{t,(i)}=1), \end{aligned}$$

and if \(x_j^t = 2\), we compute

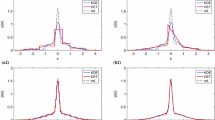
$$\begin{aligned} \pi _{2|2} = \frac{1}{M} \sum _{i=1}^{M} 1(\widetilde{x}_j^{t,(i)}=2). \end{aligned}$$

There are, in the latent \(x^t\)-process shown in Fig. 7a, 11929 variables \(x_j^t\) taking the value 0, 7271 variables taking the value 1 and 800 variables taking the value 2. Thereby, since we run each of the six \((\nu , d)\) combinations five times, we obtain for each \((\nu , d)\) combination \(5 \cdot 11929\) samples of \(\pi _{0|0}\), \(5 \cdot 7271\) samples of \(\pi _{1|1} \) and \(5 \cdot 800\) samples of \(\pi _{2|2} \). We denote the corresponding sample means by \({\bar{\pi }}_{0|0}\), \({\bar{\pi }}_{1|1}\) and \(\bar{\pi }_{2|2}\), and we let \({\bar{\pi }} = \frac{1}{3} \left( \bar{\pi }_{0|0} + {\bar{\pi }}_{1|1} + {\bar{\pi }}_{2|2} \right) \). Figure 9

Fig. 9
figure 9

Results from the simulation experiment: Histograms of \(\pi _{0 | 0}\) (left), \(\pi _{1 | 1}\) (middle) and \(\pi _{2 | 2}\) (right)

Full size image

presents histograms constructed from the samples of \(\pi _{0|0}\), \(\pi _{1|1}\) and \(\pi _{2|2}\) for each case, and Table 2

summarises the corresponding computed values for \({\bar{\pi }}_{0|0}\), \({\bar{\pi }}_{1|1}\), \({\bar{\pi }}_{2|2}\) and \({\bar{\pi }}\). The values for \({\bar{\pi }}\) indicate that, again, we obtain the best results using \(\nu = 1, d=2\) and \(\nu =1, d=3\). Computationally, using \(d=3\) is more demanding, and since the improvement it offers over \(d=2\) is only minor, the best approach may be to use \(\nu =1, d=2\).

6 Closing remarks

An ensemble updating method for categorical state vectors is proposed. The proposed procedure is an improved version of the updating procedure for categorical vectors described in Loe and Tjelmeland (2021b). What is new is mainly in how the optimal solution of \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^t, y^t)\) is computed. Loe and Tjelmeland (2021b) construct the conditional distribution \(q(\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^t, y^t)\) directly based on a directed acyclic graph (DAG) for \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^t, y^t)\). The chosen structure of the DAG allows the optimal solution of \(q(\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^t, y^t)\) to be computed recursively using a combination of dynamic and linear programming. This strategy works well when the elements of \(x^t\) are binary, but the algorithm is difficult to generalise to situations with more than two classes. Moreover, only one particular dependency structure for \(q(\widetilde{x}^{t,(i)} | x^{t,(i)}, \theta ^t, y^t)\) is considered, and it is difficult, or essentially impossible, to generalise the algorithm to cope with more complicated structures allowing for higher-order interactions. In the present article, we take a different approach which in the end results in a more flexible and general procedure. Instead of a DAG, the starting point is an undirected graphical model for \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^t, y^t)\), specifically a DGM. When specifying the maximal cliques of this DGM one has a certain level of flexibility, which makes it possible to study different dependency structures between \(x^{t,(i)}\) and \(\widetilde{x}^{t,(i)}\). The optimal solution is computed by solving a single linear program which is both easier to implement and computationally more efficient than the dynamic programming algorithm proposed in Loe and Tjelmeland (2021b). Moreover, we can easily consider more than two classes. The proposed procedure is demonstrated in a simulation example with three classes, and the results look promising.

Table 2 Results from simulation experiment: Estimated probabilities for observing \(\widetilde{x}_j^{t,(i)}\) equal to the true value \(x_j^t\) for each class \(k=0,1,2\)
Full size table

In Sect. 3.2, we introduced an exact and an approximate class of distributions for the updating of the prior sample \(x^{t,(i)}\). Although it may seem disadvantageous to pursue an approximate approach over an exact one, we believe that in this case the approximate approach actually provides better results. The constraints of the approximate approach are less restrictive and allows the optimality criterion to affect the solution to a larger extent, which may result in an optimal updating distribution which is more robust against the assumptions of the assumed Bayesian model. That is, even if the assumed Markov chain model is far from the truth, the optimal model \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^{t,(i)}, y^t)\) still provides reasonably good results.

Future work naturally includes to extend the proposed procedure to two dimensions. Assuming \(x^t\) is defined on a two-dimensional grid, a possible choice of model for \(f_{x^t | \theta ^t}(x^t | \theta ^t)\) is then a Markov mesh model (Abend et al. 1965). However, when it comes to the construction of the DGM \(q(x^{t,(i)}, \widetilde{x}^{t,(i)}| \theta ^t, y^t)\), the two-dimensional situation causes trouble, and we probably need to introduce some sort of approximations to overcome this.