1 Introduction

In the design of a mechanical assembly, tolerance allocation is the choice of tolerance values for selected dimensions of parts [1,2,3]. This task is performed jointly for all dimensions involved in a same functional requirement (a clearance, interference or any other type of geometric relationship between parts). These are arranged in a dimension chain, where their contributions to the requirement can be calculated. Tolerances on part dimensions (or design tolerances) must satisfy the stackup condition, i.e. the deviation of the requirement must not exceed a specified amount of variation (or assembly tolerance).

The problem has infinite solutions, because the same assembly tolerance can result from different combinations of design tolerances. Not all solutions are equivalent, because each tolerance influences the manufacturing cost of the related part. Therefore, the allocation aims to find a set of tolerances that keeps the total cost reasonably close to the minimum. This goal requires the designer to know the impact of each tolerance on cost. Since this knowledge is generally not explicitly available, the allocation is often done with heuristic methods [4,5,6]: design tolerances are given initial values in suitable proportions or from assumptions on manufacturing processes, and then scaled to the desired assembly tolerance. The calculation is straightforward but does not directly account for cost, so the result is obviously not optimal.

The alternative to scaling methods is a cost-based optimization, in which tolerances are the the solution of a constrained optimization problem. The objective function to minimize is the sum of the costs associated with the individual tolerances; each of these is estimated with a cost-tolerance function assumed for the corresponding geometric feature [4, 7, 8]. The constraint is the stackup equation, i.e. the relationship between assembly tolerance and design tolerances. In literature, several methods have been proposed for tolerance optimization, each based on a different formulation of the problem (stackup equation, cost-tolerance function, possible additional constraints) and on different algorithms for the search of the optimal solution [3].

The optimization ensures a reduction in manufacturing costs, but involves more complex procedures that are rarely adopted in industry. This suggests a question, which this paper seeks to answer: what is the expected economic benefit from cost-based optimization compared to traditional allocation methods? If an optimal solution allowed to significantly lower the cost of a product, the additional calculation effort would be more likely to be made in a manufacturing company especially in large-volume production.

With this objective in mind, a procedure is proposed for a comparison of the two approaches. It consists in expressing the cost differences between optimal and heuristic solutions as functions of some design data regarding parts and geometric features. The procedure is based on a previously proposed cost-tolerance function [9], which allows the analytical solution of the optimization problem for a linearized stackup equation. The application to simple cases suggests how to recognize the actual economic worth of optimization depending on the properties of the dimension chain.

Section 2 briefly reviews the main tolerance allocation methods. Section 3 defines the comparison problem and the underlying assumptions. Section 4 describes the proposed procedure, highlighting its additional contribution to previous results. Section 5 presents the application of the procedure to some examples of dimension chains. Section 6 discusses the conditions that influence the economic benefits of optimization and a possible way of predicting them. Section 7 makes some final considerations about the scope and results of the comparison.

2 Background

Tolerance allocation has been extensively studied for several decades. It was initially formulated for a broad class of problems and often referred to as statistical tolerancing: for a set of random variables of a response function, find the distributions that determine a given output distribution satisfying some optimality criteria [10,11,12]. Soon enough, it was applied to the design of mechanical assemblies [13,14,15], where the response is typically an assembly dimension and the input variables are part dimensions. This started a long discussion on which formulations could be best suited to the practical needs of manufactured products. Only the results most directly related with the objectives of this work will be recalled here, while detailed accounts of the available methods are provided by several reviews. Following the evolution of the research on the topic, these have focused first on formulations and general approaches [4,5,6], then on increasingly sophisticated methods [1, 2], and finally on all the developments emerged under the pressure of industrial applications [3].

Allocation is also regarded as the inverse problem of tolerance analysis [16, 17], where the distribution of the assembly dimension is to be calculated from given distributions of part dimensions. Again, different assumptions have led to formulations and methods of varying complexity, ranging from statistical equations to numerical simulations; one of those methods is usually embedded in allocation as a validity check for candidate solutions. This paper will refer to a basic formulation based on a single linear dimension chain, which covers most cases of practical interest (1D stackup problems [18]) and can be adapted to advanced tolerancing problems (2D and 3D stackup). In the latter cases, a nonlinear response function is linearized using either an explicit equation, the finite-difference method, or direct linearization from geometric relationships between part features [19,20,21].

For linear dimension chains, traditional allocation methods based on a scaling approach are straightforward and widely used in practice. Tentative values for tolerances are set according to a heuristic rule, then their stackup is calculated and compared with the specified assembly tolerance; a uniform scaling is finally done to satisfy the stackup condition. Some scaling methods are reviewed in [4,5,6]; these use simple heuristic rules, such as proportionality to a given power of nominal dimensions, or compatibility with predefined machining processes. As an exception, a scaling method mentioned in [13] is based on a difficulty factor related to design variables (material, manufacturing process, shape and size of the toleranced features), although no details are provided on how the factor is evaluated. Overall, scaling methods provide reasonable combinations between design tolerances but do not take into explicit account their impact on manufacturing cost.

In principle, better allocations could be done by solving a cost-based optimization problem. This consists in minimizing the cost associated with design tolerances subject to a stackup constraint, i.e. the specified assembly tolerance. The cost is estimated for the dimension chain as the sum of cost-tolerance functions for individual part dimensions. A cost-tolerance function is a mathematical relationship between the tolerance on a dimension and the tolerance-dependent cost of manufacturing the corresponding part feature, usually by a machining process. Several expressions of the cost-tolerance function have been proposed in literature and reviewed in [4, 7, 8]. As highlighted in some comparative studies [22,23,24,25,26,27], the choice of the function is generally a trade-off between accuracy and simplicity. The former allows a better approximation of cost data from literature or industrial experience, while the latter makes the optimization problem easier to solve.

With a sufficiently simple cost-tolerance function, the constrained optimization problem can be solved in closed form. Beside reducing the computational effort, this can provide the result as a function of some data of the allocation problem. The method of Lagrange multipliers [28,29,30] has a closed-form solution under restrictive assumptions on the dimensions (independent, normally distributed without mean shift, in statistical control with equal process capabilities) and using simple yet sufficiently accurate cost-tolerance equations such as the reciprocal power function [31] and the exponential function [28, 32]. For more general assumptions, the method has allowed numerical solutions using both deterministic [33,34,35] and stochastic algorithms [23, 36,37,38,39]. This work uses a closed-form solution of Lagrange multipliers with a cost-tolerance function proposed in [9] as an extended form of the reciprocal power function. The extension puts the parameters of the original function in explicit relationship with some properties of part features, so that the same function could be consistently used for all the dimensions of a chain.

Cost minimization is not the only available approach to tolerance optimization. Based on considerations originally made by Taguchi [40], quality can be considered in addition to cost: tighter tolerances might be preferred with the aim to reduce the variability on assembly-level requirements, thus avoiding additional costs incurred in case of deviations from the desired functionality. Quality measures have been introduced in both the objective function and the constraints of the optimization problem. One approach defines the objective function as the sum of the manufacturing cost and the quality loss, and solves the optimization problem with designed experiments [41,42,43,44,45,46]; alternatively, cost and quality loss are minimized in a multiobjective problem, e.g. [47]. Another approach minimizes cost with a constraint on the non-conforming rate, which is evaluated by Monte Carlo simulation wrapped into a numerical search method [48,49,50,51,52]. Many variants and additions to the above formulations have been proposed; the most recent developments include the use of metaheuristics [53, 54], surrogate models [55,56,57,58] and machine learning [59].

Beyond the few representative studies cited here, increasingly sophisticated formulations and solution methods are being proposed with the aim to cover a broader spectrum of assumptions of the allocation problem. On the application side, such choice is methodologically sound and paves the way for the development of software tools capable of effectively supporting design choices. At the same time, however, it may discourage the practice of tolerance optimization, which would require simple manual or spreadsheet-based calculations. In fact, designers seem to prefer scaling methods in their daily design tasks, in the belief that marginal improvements achievable with optimization are not worth any additional effort.

According to the above considerations, this paper aims to evaluate the economic benefits of cost-based optimization compared to traditional allocation methods. To this end, it proposes a procedure to estimate the cost differences between the optimal solution and those provided by some scaling methods. The procedure defines a comparison factor that can be evaluated similarly between the alternative methods; this is equivalent to treating optimization as a special scaling method. Through application to some examples, the procedure suggests the conditions under which the cost differences are actually significant and the heuristics should be replaced by an optimization approach.

In literature, previous studies have proposed comparisons between scaling methods and optimization by Lagrange multipliers [5, 30]. In estimating cost differences, however, these comparisons set the cost-tolerance parameters for specific examples without any explicit reference to feature properties; therefore, they do not allow conclusions on the actual economic worth of optimization in general cases. Other comparison studies have focused on alternative stackup criteria [60], or on optimization methods capable of overcoming some restrictive assumptions of closed-form Lagrange multiplier solutions [61, 62].

3 Objective and assumptions

The paper deals with the tolerance allocation problem for a single dimension chain on an assembly of rigid parts. A dimension chain is a geometric relationship between an assembly dimension y and a set of design dimensions xi (i = 1, …, n) on individual parts. The relationship is described by the response function

$$y=y\left({x}_{1}, \dots ,{x}_{n}\right)$$
(1)

which can be known or, more generally, evaluated by querying a geometric database (e.g. a CAD model of the assembly) or by measurements on physical samples. The design dimensions have nominal values Xi, which determine a nominal value Y for the assembly dimension. On an assembly built from a random set of manufactured parts, the deviations δxi result into a deviation δy through a linearized stackup equation:

$$\delta y=\sum_{i=1}^{n}{S}_{i}{\delta x}_{i}$$
(2)

where Si are the sensitivities of y with respect to the xi. These can be calculated either as ∂y/∂xi if (1) is an explicit equation, or with one of the available methods of tolerance analysis.

The deviation δy must be within a specified assembly tolerance ± TY. Consequently, design tolerances ± Ti must be assigned to deviations δxi in order to satisfy the stackup condition:

$${T}_{Y}=c\sqrt{{\sum }_{i=1}^{n}{S}_{i}^{2}{T}_{i}^{2}}$$
(3)

where c ≥ 1 is an inflation factor that corrects the root sum square (RSS) of the tolerances to take into account possible violations of the assumptions on which it is based [63]. These include the independence of the δxi and their distribution (normal with zero mean and standard deviation in a fixed ratio with Ti).

In the following it will be assumed that all tolerances Ti are unknowns of the allocation problem. If some tolerances in the dimension chain are fixed (e.g. for stock parts), the number n does not include them while their stackup terms in (3) are subtracted from the square of TY.

As recalled in Sect. 2, a widespread criterion for the selection of the Ti requires that the total manufacturing cost of the parts is the minimum among all the choices that satisfy (3). In an attempt to get close to such condition, scaling methods choose tolerance values proportional to appropriate parameters Fi. Their solution to the allocation problem is

$${T}_{i}={T}_{Y}\frac{{F}_{i}}{{F}_{Y}}$$
(4)

where

$${F}_{Y}=c\sqrt{{\sum }_{i=1}^{n}{S}_{i}^{2}{F}_{i}^{2}}$$
(5)

The following scaling methods will be considered below, each with a different choice of parameters Fi:

  • equal tolerances: all dimensions have the same tolerance;

  • precision factor: tolerances are proportional to the cubic root of nominal dimensions Xi, assuming equal IT tolerance grades according to the ISO standard [64]; this should give similar results to another practical method cited in [4,5,6], i.e. the proportional scaling of initial tolerances set according to typical tolerance ranges of predefined machining processes;

  • proportional to nominal: tolerances are proportional to nominal dimensions Xi; this is equivalent to assume that all features will be manufactured with the same process, at a natural tolerance in a fixed percentage of the dimension; such assumption is less likely to be satisfied, and is included in the study for reference only.

Hence

$$\begin{array}{l}{\left({F}_{i}\right)}_{et}=1 \, \text{(equal tolerances)}\\ {\left({F}_{i}\right)}_{pf}={X}_{i}^{1/3} \, \text{(precision factor)}\\ {\left({F}_{i}\right)}_{pn}={X}_{i} \, \text{(proportional to nominal)}\end{array}$$
(6)

Unlike scaling methods, cost-based optimization usually assumes a continuous cost-tolerance function for each dimension:

$${C}_{i}={C}_{i}\left({T}_{i}\right)$$
(7)

and uses the total cost as the objective function of an optimization problem constrained by the stackup condition:

$$\begin{array}{l}\text{min}C=\sum_{i=1}^{n}{C}_{i}\left({T}_{i}\right)\\ \text{s.t.} {T}_{Y}^{2}={c}^{2}\sum_{i=1}^{n}{S}_{i}^{2}{T}_{i}^{2}\end{array}$$
(8)

This study regards each Ci as a cost-tolerance function for combined processes, i.e. an envelope of functions related to different manufacturing processes for the same feature (e.g. rough machining, finish machining and grinding). This implies that the processes are to be chosen after the allocation under the condition that all dimensions are made with equal and very small non-conforming rates. It is also assumed that suitable processes are always available, therefore the optimization problem (8) does not need additional constraints specifying the allowable tolerance ranges.

Solving (8) with the method of Lagrange multipliers [28, 29], it is found that the optimal tolerances are proportional to

$${F}_{i}=\frac{\partial {C}_{i}}{\partial {T}_{i}}{S}_{i}^{-2}$$
(9)

The focus of the paper is in estimating the difference in the total cost C between the solution of the optimization problem (8) and the solutions calculated with the three scaling methods. This may seem a trivial task since, on any specific case, the costs could be easily estimated from (4) and (5) using the same cost-tolerance functions (7) and appropriate parameters Fi for the different methods from (6) and (9). However, the objective here is to develop a meaningful expression for the cost differences, which can show their dependence on some design variables. These are related to individual parts (e.g. material, shape and size of features) and to their contribution to the dimension chain (sensitivities).

4 Method

The solutions of the allocation methods described in Sect. 3 consist of different tolerance values, which determine different total costs. These can be calculated using the same cost-tolerance function as in the optimization problem. To help understand the effect of design variables on cost differences, a cost-tolerance function must satisfy two conditions: allow the analytical solution of the optimization problem, and express the cost as a function of the properties of the toleranced feature (as well as of the tolerance itself). Such a function is introduced below by recalling the results of previous studies. Then the function is used to estimate the costs of the solutions of optimization and scaling methods. Finally the cost expressions are compared and the cost differences are characterized.

4.1 Prior work

Several optimization methods express the cost-tolerance relationship by the reciprocal power function [31]:

$${C}_{i}\left({T}_{i}\right)={a}_{i}+\frac{{b}_{i}}{{T}_{i}^{k}}$$
(10)

which is simple enough to allow the closed-form solution of problem (8) by Lagrange multipliers. In the optimal allocation the tolerances Ti are proportional to

$${\left({F}_{i}\right)}_{opt}={\left({b}_{i}{S}_{i}^{-2}\right)}^{\frac{1}{k+2}}$$
(11)

As noted in [27], a few different values have been used in literature for the coefficients ai, bi and k in (10). Explanations on the sources of those values are rarely provided, although they probably come from cost data published in handbooks [65] or collected in specific production settings. As a result, the effects of design variables on optimal tolerances cannot usually be evaluated. To overcome this limitation, an extended version of the reciprocal power function was proposed in [9]:

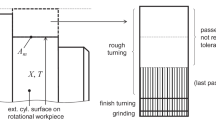
$${C}_{i}\left({T}_{i}\right)=\frac{{b}_{i}}{{T}_{i}^{k}}\text{ , }{b}_{i}=\beta {f}_{Mi}{f}_{Fi}{f}_{Ai}{X}_{i}^{k/3}$$
(12)

It drops the fixed term ai of (10), which is particularly difficult to evaluate and has no effect on the result (11) of the allocation. This means that the cost-tolerance function is mostly related to the last manufacturing steps on the toleranced feature (finish machining, grinding). The remaining coefficients were set through regression analysis of machining costs estimated with a feature-based method available in literature [66]. In detail, the tolerance exponent has a constant value k = 0.55, while the variable cost factor bi is the product of the following elements:

  • β = 0.4 ⋅ 10–3, which allows Ci to be indirectly expressed in minutes of machining on multifunctional computer numerically controlled (CNC) machine tools; the time estimate is readily converted into a variable machining cost assuming a suitable shop rate;

  • a parameter fMi related to the material of the part, inversely proportional to its machinability;

  • a parameter fFi related to the type of feature;

  • a parameter fAi equal to the surface area of the feature in cm2;

  • a small power of the nominal dimension Xi, which accounts for its relatively flat effect on cost.

Figure 1 illustrates the evaluation of parameters fMi, fFi and fAi. Like (10), the extended reciprocal power function (12) allows the closed-form solution of (8) with the same result (11), where bi is replaced with its detailed expression in (12) and the constant β is omitted in the proportionality factor:

Fig. 1
figure 1

Evaluation of cost parameters related to design variables

Full size image
$${\left({F}_{i}\right)}_{opt}={\left({f}_{Mi}{f}_{Fi}{f}_{Ai}{X}_{i}^{k/3}{S}_{i}^{-2}\right)}^{\frac{1}{k+2}}$$
(13)

The advantage is that the optimal tolerances and the total cost can now be calculated with an explicit evaluation of the effects of design variables (materials, feature types and sizes, nominal dimensions).

4.2 Comparison of allocation methods for a dimension chain

As shown above, all the described allocation methods give results expressed in the same form by Eqs. (4) and (5). The parameters Fi are evaluated differently; the simple expressions in (6) for the heuristic methods are replaced by the more detailed (13) for the optimization with the extended reciprocal power function. Similar expressions are now to be found for the costs associated with the tolerances.

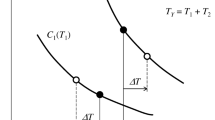
First, the costs Ci of the individual tolerances Ti calculated by one of the heuristic methods are compared with the costs (Ci)opt of the optimal tolerances (Ti)opt. The cost ratio

$${M}_{i}=\frac{{C}_{i}}{{\left({C}_{i}\right)}_{opt}}$$
(14)

is not necessarily ≥ 1 for any i, although it is certainly C ≥ Copt. Equation (12) implies that

$$\frac{{C}_{i}}{{\left({C}_{i}\right)}_{opt}}=\frac{{\left({T}_{i}\right)}_{opt}^{k}}{{T}_{i}^{k}}$$
(15)

Substituting (4) and (5), (14) becomes

$${M}_{i}={{\left(\frac{{F}_{Y}}{{F}_{i}}\right)}^{k}\left(\frac{{F}_{i}}{{F}_{Y}}\right)}_{opt}^{k}={\left(\frac{{\left({F}_{i}\right)}_{opt}}{{F}_{i}}\frac{\sqrt{{\sum }_{i=1}^{n}{S}_{i}^{2}{F}_{i}^{2}}}{\sqrt{{\sum }_{i=1}^{n}{S}_{i}^{2}{\left({F}_{i}\right)}_{opt}^{2}}}\right)}^{k}$$
(16)

or, equivalently:

$${M}_{i}=\frac{{G}_{i}}{{\left({G}_{i}\right)}_{opt}}$$
(17)

where

$${G}_{i}={\left(\frac{\sqrt{{\sum }_{i=1}^{n}{S}_{i}^{2}{F}_{i}^{2}}}{{F}_{i}}\right)}^{k}$$
(18)

and (Gi)opt has the same expression with (Fi)opt.

Using (13) and the generic solution in (4) and (5), the costs are calculated as

$${C}_{i}=\frac{{b}_{i}}{{T}_{i}^{k}}=\frac{{b}_{i}{F}_{Y}^{k}}{{T}_{Y}^{k}{F}_{i}^{k}}=\frac{{b}_{i}{c}^{k}}{{T}_{Y}^{k}}{\left(\frac{\sqrt{{\sum }_{i=1}^{n}{S}_{i}^{2}{F}_{i}^{2}}}{{F}_{i}}\right)}^{k}=\frac{{c}^{k}}{{T}_{Y}^{k}}{b}_{i}{G}_{i}$$
(19)

So the optimal costs are

$${\left({C}_{i}\right)}_{opt}=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}{f}_{i}{X}_{i}^{k/3}{\left({G}_{i}\right)}_{opt}$$
(20)

where

$${f}_{i}={f}_{Mi}{f}_{Fi}{f}_{Ai}$$
(21)

and the cost difference between the heuristic method and the optimization is

$$\Delta {C}_{i}=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}{f}_{i}{X}_{i}^{k/3}{\left({G}_{i}\right)}_{opt}\left({M}_{i}-1\right)$$
(22)

For the dimension chain, the total cost difference is finally

$$\Delta C=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}\sum_{i=1}^{n}{f}_{i}{X}_{i}^{k/3}{\left({G}_{i}\right)}_{opt}\left({M}_{i}-1\right)$$
(23)

Equations (4), (5) and (18) also give the result of the allocation in a simple form:

$${T}_{i}=\frac{{T}_{Y}}{c}{\left(\frac{1}{{G}_{i}}\right)}^{1/k}$$
(24)

where the Gi are calculated separately for the different methods.

5 Results

The comparison described in Sect. 4 is now applied to some examples in order to demonstrate the procedure and get actual figures for the cost differences. Costs may be interpreted either as machining minutes or in a generic currency unit (CU), assuming a shop rate of 60 CU/h (reasonable for either USD, EUR and GBP at the time of writing). Dimensions and tolerances are in mm and the RSS inflation factor is always set to c = 1.2.

5.1 Simple cases

Three low-carbon steel bars with the same rectangular section 60×30 and lengths 100, 50 and 20 are placed end-to-end. A tolerance TY =  ± 0.1 is specified on the total length.

Table 1 shows the results of the different allocation methods, as well as the data on the three dimensions. These include the sensitivities Si, the nominal dimensions Xi, and the factors fi from (21). All bars have fMi = 1 for the given material, fFi = 1.5 (flat surfaces of prismatic parts), and fAi = 36 (total area in cm2 of the two opposite ends of each bar). The factors (Gi)opt, (Gi)et, (Gi)pf and (Gi)pn are calculated from (18) using the appropriate Fi. The corresponding tolerances (Ti)opt, (Ti)et, (Ti)pf and (Ti)pn are calculated from (24).

Table 1 Simple stack: tolerance allocations
Full size table

Table 2 shows the costs associated with the alternative allocations. The costs (Ci)opt are calculated from (20). The cost ratios (Mi)et, (Mi)pf and (Mi)pn for the heuristic methods are calculated from (17) and then substituted in (22) to get the costs (Ci)et, (Ci)pf and (Ci)pn of the sub-optimal allocations. The total costs C and their differences ΔC from the optimal one (here shown as percentages of Copt) are finally calculated adding the contributions of the three tolerances.

Table 2 Simple stack: tolerance costs
Full size table

The results suggest that the optimization does not allow any significant cost reduction compared to two of the heuristic methods. With equal tolerances, the allocations are actually very close to the optimal ones. The precision factor gives looser tolerances for larger nominal dimensions, offsetting the cost disadvantage on the tightest tolerance with an almost equal advantage on the loosest one. Differently, the proportional-to-nominal method results into a wider tolerance range, with a strong cost penalty for the excessively tight tolerance on the smallest dimension.

A ∅40×40 hole and shaft on medium-carbon steel parts are connected in a cylindrical fit. The variation allowed on the clearance is TY =  ± 0.02, approximately corresponding to IT tolerance grades between 7 and 6.

In Table 3, the indices i = 1, 2 refer to the hole and the shaft respectively (y = x2 – x1). In feature data, fM1 = fM2 = 1.3 (common material), fF1 = 1.25 and fF2 = 1 (external and internal cylindrical surfaces on rotational parts, respectively), and fA1 = fA2 = 50.3 (area in cm2 of a cylindrical surface with diameter 40 and length 40). Cost estimates are made as for the previous example, limiting the comparison to the equal tolerance method. In fact, Eqs. (18) show that the other allocation methods have the same comparison factor Gi (depending only on sensitivities and nominal dimensions), therefore they result in the same tolerances and costs.

Table 3 Cylindrical fit: tolerance allocations and costs
Full size table

The optimal allocation is nearly identical to the result of the heuristic methods, with no appreciable cost reduction. As in the previous case, this seems due to the fact that the mating features have similar properties: equal sensitivities, materials and sizes, with the only difference in the type of cylindrical surface (internal, external). The forthcoming examples will check whether more complex chains give better opportunities for a cost-based approach.

5.2 Overrunning clutch

In a classic example from [13], the overrunning clutch mechanism in Fig. 2 includes a hub, a cage and four rollers: all parts have a height of 30 and are made of medium-carbon steel. For the needs of unidirectional transmission of rotary motion from the hub to the cage, the angle Y = 6.5° between the normals to the contact points of each roller with the cage and the hub must be controlled at a variation TY =  ± 0.5° =  ± 8.75 • 10–3 rad. The angular assembly dimension depends on three linear design dimensions: the distance X1 = 54.5 between two parallel flats of the hub, the diameter X2 = 22.5 of the rollers, and the diameter X3 = 100 of the cage.

Fig. 2
figure 2

Overrunning clutch

Full size image

The dimension chain has an explicit equation:

$$y=\text{arccos}\frac{{x}_{1}+{x}_{2}}{{x}_{3}-{x}_{2}}$$
(25)

which is linearized with the following sensitivities:

$${S}_{1}=\frac{\partial y}{\partial {x}_{1}}=-\frac{1}{\sqrt{1-{\left(\frac{{X}_{1}+{X}_{2}}{{X}_{3}-{X}_{2}}\right)}^{2}}}\frac{1}{{X}_{3}-{X}_{2}}=-0.114$$
(26)
$${S}_{2}=\frac{\partial y}{\partial {x}_{2}}=-\frac{1}{\sqrt{1-{\left(\frac{{X}_{1}+{X}_{2}}{{X}_{3}-{X}_{2}}\right)}^{2}}}\frac{{X}_{1}+{X}_{3}}{{X}_{3}-{X}_{2}}=-0.227$$
(27)
$${S}_{3}=\frac{\partial y}{\partial {x}_{3}}=\frac{1}{\sqrt{1-{\left(\frac{{X}_{1}+{X}_{2}}{{X}_{3}-{X}_{2}}\right)}^{2}}}\frac{{X}_{1}+{X}_{2}}{{\left({X}_{3}-{X}_{2}\right)}^{2}}=0.113$$
(28)

The dimension data in Table 4 take into account the material (fMi = 1.3), the feature types (fF1 = 1.5 for planar surfaces on a prismatic part, fF2 = 1 for an external cylindrical surface on a rotational part, fF3 = 1.25 for an internal cylindrical surface), and the feature areas (fA1 = 42 for four flat rectangular areas with approximate size 35×50 each, fA2 = 84 for four ∅22.5×30 external cylindrical surfaces, fA3 = 94 for a ∅100×30 internal cylindrical surface).

Table 4 Overrunning clutch: tolerance allocations and costs
Full size table

The allocations and the corresponding costs are also shown in Table 4. Compared to the cases in subSect. 5.1, the optimal tolerances are spread in a wider range, achieving a cost reduction of about 10% compared to the equal tolerance allocation. The tolerance T2 on the rollers is especially tight mainly due to its greater sensitivity, while the tolerance T3 on the hub is looser due to several possible factors (large nominal dimension, large area, internal surface). Although these differences are not captured by the heuristic methods, tolerances turn out to increase with nominal dimensions, making the optimal cost closer to those calculated for the precision factor and proportional-to-nominal methods. In absolute terms, however, the optimization gives almost negligible cost reductions with respect to all heuristic methods, with an average estimate of about 0.1 CU (or min) per unit; possible reasons for that include the small size of the assembly, the relatively loose assembly tolerance, and the few dimensions in the chain.

5.3 Ball slide

Figure 3 shows another example adapted from [13]. A ball slide mechanism allows the translational motion of a carriage relative to a linear guide that includes a frame and a keeper. All parts are made of medium carbon steel. The carriage and the guide have lengths 100 and 500 respectively in the direction of motion. A set of balls is placed between the carriage and the guide, two on the keeper side and two on the frame side. The assembly is preloaded with screws (not shown) driven from the keeper side into threaded holes in the frame. For a correct tightening of the screws without deformation of the connected parts, the clearance y between the contact surfaces of the keeper and the frame must be controlled at an assembly tolerance TY =  ± 0.1 compared to its nominal value Y = 1.

Fig. 3
figure 3

Ball slide

Full size image

The part drawings show that the positions of the V-guide surfaces on the keeper (x1), carriage (x2) and frame (x3) are defined so that they could be inspected using measuring pins. These have diameter d (with negligible deviation) nominally equal to the diameter of the spheres (x4). The assembly dimension can be easily calculated as a function of five auxiliary dimensions zi:

$$y={z}_{1}+{z}_{2}+{z}_{3}+{z}_{4}-{z}_{5}$$
(29)

Simple geometric considerations give

$${z}_{1}={x}_{1}+\frac{\sqrt{2}}{4}{x}_{41}-\frac{1+\sqrt{2}}{2}d$$
(30)
$${z}_{2}=\frac{\sqrt{2}}{2}{x}_{41}$$
(31)
$${z}_{3}={x}_{2}+\frac{\sqrt{2}}{4}\left({x}_{41}+{x}_{42}\right)-\left(1+\sqrt{2}\right)d$$
(32)
$${z}_{4}=\frac{\sqrt{2}}{2}{x}_{42}$$
(33)
$${z}_{5}={x}_{3}-\frac{\sqrt{2}}{4}{x}_{42}+\frac{1+\sqrt{2}}{2}d$$
(34)

where x41 and x42 are respectively the diameters of the balls on the keeper side and on the frame side, which come from the same production batch. The assembly dimension is therefore expressed as a function of actual design dimensions:

$$y={x}_{1}+{x}_{2}-{x}_{3}+\sqrt{2}{x}_{41}+\sqrt{2}{x}_{42}-2\left(1+\sqrt{2}\right)d$$
(35)

As d has assumedly zero tolerance, the assembly tolerance is

$${T}_{Y}=c\sqrt{{T}_{1}^{2}+{T}_{2}^{2}+{T}_{3}^{2}+2\cdot 2{T}_{4}^{2}}=c\sqrt{{T}_{1}^{2}+{T}_{2}^{2}+{T}_{3}^{2}+4{T}_{4}^{2}}$$
(36)

Hence

$$\left|{S}_{1}\right|=\left|{S}_{2}\right|=\left|{S}_{3}\right|=1\text{ , }\left|{S}_{4}\right|=2$$
(37)

The nominal dimensions are X1 = 22, X2 = 75, X3 = 60, X4 = d = 18. The corresponding tolerances T1, T2, T3 and T4 are the unknowns of the allocation problem.

In Table 5, the above data are listed together with the parameters fi calculated taking into account the material (fMi = 1.3), the types of features (fF1 = fF2 = fF3 = 1.5 for flat surfaces on prismatic parts, fF4 = 1 for external rotational surface), and the areas of the features (with the dimensions in Fig. 3 and assuming a width of 15 for each of the two surfaces of each V-shaped guide); the area of the balls is calculated for the whole set of four parts.

Table 5 Ball slide: tolerance allocations and costs
Full size table

Unlike in the previous cases, the results show very different allocations between the optimization and the three heuristic methods. The main reason is that the features have very different sizes, which have a strong influence on finish machining times and costs. Heuristic methods do not directly take cost into account, so they ignore size differences in the allocation. Compared to these, the optimization gives looser tolerances T1 and T3 and a tighter tolerance T2; this reduces the machining cost of the long guide surfaces on the keeper and on the frame more than it increases the corresponding cost of the short guide surfaces on the carriage. Consequently, the optimization allows a significant cost reduction compared to the other methods: consistently with the above considerations, the cost ratios Mi have high values especially for the most expensive tolerances (T1 and T3). Equal tolerances and precision factor have cost penalties around 20%; again, proportional to nominal has the worst performance with a cost about 30% higher than optimization. In absolute terms, the cost differences are in the range 1–1.5 CU (or min) per unit, which may be relevant for large production volumes.

6 Discussion

The examples in Sect. 5 help identify situations where cost-based optimization may be a real improvement over traditional allocation methods. Since the tolerance-dependent fraction of manufacturing cost is predominantly associated with the required amount of finish machining, the cost reduction is greater when the part features tend to require very different machining times. This involves part properties such as material as well as feature type and size; these are represented by the parameters fi of the cost-tolerance function used in this work.

Furthermore, the optimization takes sensitivities Si into account more correctly. In traditional methods, the presence of features with different sensitivities modifies the stackup condition and brings to a uniform scaling of all tolerances. In optimization, each tolerance depends on the associated sensitivity; for example, a tolerance with higher sensitivity increases the stackup of deviations but not the cost, therefore it tends to be narrower than other tolerances.

The role of the above variables can be highlighted by reviewing Eqs. (14) and (17), which define the comparison factors Gi proportional to the costs Ci of the individual tolerances. These are calculated by (18), where the Fi have different expressions for the different methods: (6) for the heuristic methods and (13) for the optimization. In the special case where Si = S and Fi = F for i = 1, … n, all dimensions have the same Gi:

$${G}_{i}={\left(\frac{\sqrt{n{S}^{2}{F}^{2}}}{F}\right)}^{k}={\left(S\sqrt{n}\right)}^{k}$$
(38)

hence Mi = 1, that is, all methods including optimization give the same result without any cost differences. This condition occurs approximately in the example of the cylindrical fit (Table 3).

If the dimensions of the chain have very different fi and Si, heuristic methods stay further away from the optimal cost (i.e. have higher Mi) if their Fi are lower than the corresponding (Fi)opt for the optimization. The expressions (6) and (13) of Fi show that this occurs when a feature has either a high fi or a low Si compared to other features. The former condition applies to the frame of the ball slide (i = 3 in Table 5), while the latter applies to the hub of the overrunning clutch (i = 1 in Table 4).

The presence of very different nominal dimensions Xi in the chain can also influence the performance of the different methods. This is especially true for proportional to nominal, where the tolerances depend on Xi much more than in optimization: a feature with a low Xi compared to the others ends up having too tight a tolerance with an excessive increase in its cost. This situation applies to the shortest bar of the stack (i = 3 in Table 2) and to the rollers of the clutch (i = 2 in Table 4). The effect of nominal dimensions is almost negligible with precision factor and equal tolerances, as suggested by the exponents of Xi in the respective expressions of Fi.

Two reference cases will now be discussed to get a rough idea of the cost savings provided by optimization. In one, the only difference between the dimensions is in the parameters fi that determine the required amount of finish machining. In the other, the only difference is in the sensitivities Si.

In the first case, let a chain be given with the same sensitivity S and nominal value X for all n dimensions and

$${f}_{i}={\varphi }_{i}f\text{ , }f=\frac{1}{n}\sum_{i=1}^{n}{f}_{i}$$
(39)

where φi are the parameters fi normalized on their arithmetic mean f. From (13) and (21) it is

$${\left({F}_{i}\right)}_{opt}={{\varphi }_{i}}^{\frac{1}{k+2}}{\left(f{X}^{k/3}{S}^{-2}\right)}^{\frac{1}{k+2}}$$
(40)

and (18) is worked out into

$${\left({G}_{i}\right)}_{opt}={S}^{k}{{\varphi }_{i}}^{-\frac{k}{k+2}}{\left(\sum_{i=1}^{n}{{\varphi }_{i}}^{\frac{2}{k+2}}\right)}^{k/2}$$
(41)

Since Gi is given by (38), all heuristic methods have equal cost ratios:

$${M}_{i}={n}^{k/2}{{\varphi }_{i}}^{\frac{k}{k+2}}{\left(\sum_{i=1}^{n}{{\varphi }_{i}}^{\frac{2}{k+2}}\right)}^{-k/2}$$
(42)

According to definitions (13) and (21), the variable cost factors are

$${b}_{i}=\beta {\varphi }_{i}f{X}^{k/3}$$
(43)

Substituting (41), (42) and (43) in (22), the individual cost differences become

$${\Delta C}_{i}=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}f{X}^{k/3}{S}^{k}\left[{n}^{k/2}{\varphi }_{i}-{{\varphi }_{i}}^{\frac{2}{k+2}}{\left(\sum_{i=1}^{n}{{\varphi }_{i}}^{\frac{2}{k+2}}\right)}^{k/2}\right]$$
(44)

Summing (44) for the n dimensions gives

$$\Delta C=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}f{X}^{k/3}{S}^{k}\left[{n}^{k/2}\sum_{i=1}^{n}{\varphi }_{i}-{\left(\sum_{i=1}^{n}{{\varphi }_{i}}^{\frac{2}{k+2}}\right)}^{\frac{k+2}{2}}\right]$$
(45)

Since it is

$$\sum_{i=1}^{n}{\varphi }_{i}=n$$
(46)

Equation (45) becomes

$$\Delta C=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}f{X}^{k/3}{S}^{k}{n}^{\frac{k+2}{2}}{g}_{f}\left({\varphi }_{i},n\right)$$
(47)

where

$${g}_{f}\left({\varphi }_{i},n\right)=1-{\left(\frac{1}{n}\sum_{i=1}^{n}{{\varphi }_{i}}^{\frac{2}{k+2}}\right)}^{\frac{k+2}{2}}$$
(48)

To get a simpler expression for gf, a further hypothesis is that it is related with the normalized range of the fi:

$${r}_{f}={\left({\varphi }_{i}\right)}_{\text{max}}-{\left({\varphi }_{i}\right)}_{\text{min}}$$
(49)

Figure 4 shows the result of a simulation on 5000 random instances of dimension chains. These were generated by sampling n from a uniform distribution between 4 and 10, and the φi from uniform distributions so as to satisfy the property in (46). It can be noted that gf varies approximately in a fraction between 0.01 and 0.02 of rf squared. Therefore, an estimated interval for the cost reduction due to rf is

Fig. 4
figure 4

Simulation of the effect of the range of fi on the cost reduction

Full size image
$${\Delta C}_{f}=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}f{X}^{k/3}{S}^{k}{n}^{\frac{k+2}{2}}{r}_{f}^{2}\cdot \left[0.01\div 0.02\right]$$
(50)

In the second case, let a chain be given with the same f and X for all n dimensions and

$${S}_{i}={\sigma }_{i}S\text{ , }S=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{S}_{i}^{2}}$$
(51)

where σi (not meant as standard deviations) are the sensitivities Si normalized on their mean square S. The following property is easy to recognize:

$$\sum_{i=1}^{n}{\sigma }_{i}^{2}=n$$
(52)

With similar calculations as above, the cost reduction is expressed as

$$\Delta C=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}f{X}^{k/3}{S}^{k}{n}^{\frac{k+2}{2}}{g}_{S}\left({\sigma }_{i},n\right)$$
(53)

where

$${g}_{S}\left({\sigma }_{i},n\right)=1-{\left(\frac{1}{n}\sum_{i=1}^{n}{{\sigma }_{i}}^{\frac{2k}{k+2}}\right)}^{\frac{k+2}{2}}$$
(54)

The coefficient gS in (54) is related with the normalized range of the Si:

$${r}_{S}={\left({\sigma }_{i}\right)}_{\text{max}}-{\left({\sigma }_{i}\right)}_{\text{min}}$$
(55)

Figure 5 shows the result of a simulation similar to the one in the previous case, this time with the σi generated from uniform distributions while satisfying (52). It appears that gS is a fraction between 0.04 and 0.10 of rS squared. Therefore, an interval for the cost reduction due to rS is

Fig. 5
figure 5

Simulation of the effect of the range of Si on the cost reduction

Full size image
$${\Delta C}_{S}=\frac{{\beta c}^{k}}{{T}_{Y}^{k}}f{X}^{k/3}{S}^{k}{n}^{\frac{k+2}{2}}{r}_{S}^{2}\cdot \left[0.04\div 0.10\right]$$
(56)

Equations (50) and (56) allow a quick prediction of the savings expected from optimization due to the variation of either fi or Si. For example, in the ball slide of subSect. 5.3, the following data are easily calculated from Table 5: X = 45, f = 300, rf = 1.8, S = 1.3, rS = 0.8. It results that ΔCf = [0.2÷0.4] and ΔCS = [0.15÷0.4]. On the average, the two separate effects cover about half the total cost difference between the optimization and the two heuristic methods with the best performances (around 1 CU). The balance may depend on the possibile interaction effect of fi and Si (not evaluated here) as well as on differences in nominal dimensions Xi.

The same equations highlight other variables that can influence the economic advantage of the optimization. This should be especially relevant for for large-sized assemblies, considering that f increases with the square of the dimensional scale (and X also increases marginally); however, the relative effect might be offset by the simultaneous increase of tolerance-independent costs (e.g. material and rough machining). The positive effect of S also suggests that, in a typical rotating mechanism, the optimization should be more worthy for axial clearances (which usually have S = 1) than for radial clearances (typically S = 0.5). Finally, it is not surprising that the need to control a functional requirement to a tighter tolerance TY is an additional incentive for optimization.

Along with the method described in Sect. 4, the above results define a possible workflow for tolerance allocation. Faced with the task of allocating tolerances to a dimension chain, the designer can proceed with the following steps:

  • collection of data on the individual dimensions (Si, Xi and fi) and choice of the functional specification TY on the assembly tolerance;

  • verification of the basic precondition for a choice of the optimization approach, i.e. a sufficiently wide range of Si and fi;

  • use of Eqs. (50) and (56) to get a rough estimate of the economic worth of optimization, and evaluation of its impact on the expected production volume;

  • possible refinement of the estimate with a spreadsheet based on the more detailed Eq. (23), as in the tables presented in Sect. 5 for the different examples;

  • decision on the best allocation route (scaling or optimization), and calculation of the tolerances with the same spreadsheet;

  • as an alternative, use of the above allocations for comparison with the results of a different optimization method based on corporate standards.

The examples in Sect. 5 only include tolerances on part dimensions. The allocation problem obviously also arises for assemblies with parts designed according to modern tolerancing standards. For such parts, dimensional tolerances are used along with geometric tolerances that control form, orientation, and position errors on features arranged in datum reference systems. The propagation of geometric deviations is often described by complex mathematical models, which are used to repeatedly evaluate the assembly deviation during the iterative solution of the optimization problem (see [3] for detailed approaches). However, these models can be always linearized into an approximate stackup Eq. (2). In principle, this allows to streamline the allocation using both scaling and closed-form optimization by Lagrange multipliers. Therefore, the method proposed here for comparing these methods can be used in all situations in which the cost-tolerance function (12) is valid. The most common ones are illustrated in Fig. 6, which shows a possible geometric specification on the parts of the overrunning clutch in Fig. 2. Specifically:

  • for the hub, the nominal dimension X1 coincides with a basic dimension and the tolerance T1 is equal to half the location tolerances on the pairs of parallel flats, while the perpendicularity tolerance does not influence the dimension chain;

  • for the rollers, it is not easy to separately allocate the dimensional tolerance TS2 and the straightness tolerance TG2 specified at maximum material condition (MMC); however, as reported in [67], the two tolerances are jointly equivalent to a dimensional tolerance T2 = 3TS2 + TG2; once allocated, T2 can be apportioned to TS2 and TG2 by experience without further optimization.

  • for the cage, similarly, the dimensional tolerance TS3 and the perpendicularity tolerance TG3 specified regardless of feature size (RFS) are equivalent to a dimensional tolerance T3 = TS3 + TG3.

Fig. 6
figure 6

Geometric tolerance specification on the parts of the overrunning clutch

Full size image

Less frequently, orientation tolerances may be involved in dimension chains involving angles. As suggested in [9], the function (12) also applies to angular dimensions if an equivalent nominal angle is calculated with an appropriate expression of the lengths of adjacent edges.

7 Conclusions

The paper has proposed an economic comparison between tolerance optimization and some well-known heuristic methods of tolerance allocation, which are customarily used due to their simplicity. The chosen optimization method, based on the extended reciprocal power cost-tolerance function, is bound to restrictive assumptions but has two main advantages. First, it allows to carry out the constrained optimization of cost in closed form; as a consequence, the cost reduction is estimated directly even before the tolerances are explicitly calculated (although these have been shown here for the sake of completeness). Second, it allows to easily recognize how the cost reduction is influenced by the properties of part features. A further advantage, from the perspective of industrial application, is the ease of calculation: through the use of parameters (Fi)opt, the optimization is performed as a scaling procedure quite similar to the heuristic methods.

The comparison on some examples suggests that the optimization is not always economically justified compared to traditional methods. If the features involved in a functional requirement are similar in material, shape, size and nominal dimension, the different approaches converge to about the same allocation without actual cost differences. On the contrary, the optimization leads to significantly less expensive solutions if the features in a dimension chain have very different properties. Specifically, features that are larger or more difficult to machine (due to material and required machining process) or with lower sensitivity on the requirement are less effectively treated by heuristic methods, which do not account for most of these cost drivers. The optimization tends to selectively loosen the corresponding tolerances, achieving cost reductions that are not offset by the necessary tightening of other tolerances in the chain. Under these conditions, cost reductions may be relevant for quantity production of large-sized, high-precision assemblies.

Qualitatively, these results are consistent with what was expected. As a further decision tool, obtaining cost estimates is subject to the availability of a cost-tolerance function with appropriate characteristics. As a required condition, the function should be based on a single cost model suitable for many different types of part features. The one used in this work is based on literature data relating to CNC machining processes, which cover a wide diversity of applications with medium–high production volumes. A company may want to improve the accuracy of the function by using its own cost data. This involves a preparatory activity that might be considered too expensive for the sole purpose considered here, but it is nevertheless useful for making the economic implications of tolerancing explicit and immediately understandable to designers and manufacturing engineers. Regarding the possible concern regarding the confidentiality of cost data, the risks are mitigated by the fact that tolerances influence only a marginal fraction of manufacturing costs (the variable cost with respect to tolerance, usually associated with finish machining).

Another assumption of the proposed comparison method is related to the formulation of the optimization problem, which involves only the cost objective and the stackup constraint without considering other possible criteria (use of available equipment, minimization of quality loss, variable process capabilities, etc.). In principle, the above conclusions should also apply to more sophisticated optimization methods, which may be needed when dealing with less restrictive assumptions. However, the cost differences between optimization and scaling may be smaller due to the additional constraints. On the other hand, the method could be extended to the comparison of higher-level tolerance specifications, such as the choice of functional dimensions or geometric tolerance schemes. The mentioned properties of the cost-tolerance function could also be useful for that task, while the cost differences between alternative choices could be expressed as a function of new parameters, such as the ranges of nominal dimensions or the types of datum reference frames.