1 Introduction

Advancements in metal additive manufacturing (AM) technology have greatly expanded the range of applications for AM processes, particularly in the healthcare industry. These advancements have led to the creation of highly optimised, custom-designed orthopaedic implants that have significantly improved the lifespan and performance of prostheses [1,2,3,4,5]. For example, typical total hip replacement (THR) implants have a lifespan of about 15 years. These surgeries are typically performed on patients between the ages of 60 and 80. However, recent data from the World Health Organization shows that global life expectancy has been on the rise for the past 20 years, which may have an impact on the longevity of these implants [6, 7], making the lifetime of current implants less effective. This trend has been shown to lead to an increase in the number of revision surgeries, which typically come at a cost of around £12,000 per procedure [8]. Extending the lifespan of implants would not only provide significant benefits to patients but also greatly reduce the environmental impact of waste and scrap. According to data from Sandwell General Hospital in West Bromwich, England, an estimated 2% of the annual implant budget is spent on disposing of scrap and waste due to the complex sterilisation and disposal processes associated with biomedical waste [9].

Manufacturers of conventional total hip replacement implants typically offer cementless designs that rely on biological fixation [10]. These designs are considered the standard option. Cemented designs, on the other hand, are typically only used for patients with reduced osteogenic cells [11]. Current implant geometries are fabricated using conventional manufacturing processes and have a surface coating applied to enhance osseointegration. Osseointegration is the structural and functional bonding between living bone and the surface of a load-bearing implant. However, stress shielding, which occurs when the implant has a higher stiffness than the surrounding bone, can negatively impact implant performance. This can lead to decreased stress on the adjacent bones, causing decreased bone density, implant loosening and ultimately failure of the implantation process [12, 13]. This phenomenon is outlined in Wolff’s Law [14] and further explored in the literature [15].

Previous research has shown that around 66% of medical implants fail due to aseptic loosening and instability. However, these negative outcomes can be mitigated by reducing stress shielding and increasing osseointegration [16, 17]. Lattice structures can be utilised in the fabrication of the implants to effectively control and optimise these factors. The porous structure of the lattice allows for improved bone growth and also decreases the elastic modulus of the implant, thereby limiting stress shielding. Lattice structures are open-celled, 3-D structures which contain ordered pores due to their construction of repeated unit cells. Lattices can be strut-based, created as a wireframe with a constant-diameter swept cylinder applied, or truss-based, known as triply periodic minimal surfaces (TPMS) structures, that are modelled and manipulated using mathematical formulae [18]. Due to their complex curvature and organic shape, TPMS lattice structures can be challenging to model using traditional CAD software, such as SolidWorks, and require specialised software. However, the surface curvature of the TPMS lattice allows for enhanced bone growth, improved osseointegration and greater energy absorption when compared to strut-based designs [19,20,21,22].

The mechanical behaviour of lattice structures is defined by their stretch-dominated or bending-dominated performance; stretch-dominated behaviour occurs in stiffer structures, while bending-dominated behaviour is more common in open-celled, ductile structures [23]. Lattice structures can be mechanically categorised according to their Maxwell number, M, which is dependent on the number of struts, s, and nodes, n [18], and could be determined as follows:

$$M=s-3n+6$$
(1)

If M < 0, the structure is bending-dominated, meaning that there are not enough struts to balance external forces. Conversely, if M ≥ 0, the structure is stretch-dominated, indicating that external forces are in equilibrium.

Laser powder bed fusion (LPBF) is a key additive manufacturing technique that uses a laser beam to selectively fuse metal powder according to a digital design. Also known as selective laser melting (SLM), the process is repeated layer by layer until a 3D object is produced. This technique is now widely used for creating complex designs and components, particularly lattice structures, from various Fe, Al and Ti alloys for applications in transportation and healthcare. While major implant manufacturers have not adopted it yet, a lot of recent research has investigated the use of AM technology to create implants, especially towards the acetabular cup component involved in a total hip replacement (THR). AM still utilises the conventional Ti6Al4V (α + β)-type titanium alloy due to its high biocompatibility, corrosion resistance, lack of toxicity, and high specific strength [24, 25]. However, Ti6Al4V alloy has an elastic modulus of 114 GPa, which is seven times larger than that of the cortical bone of the femur. This would cause the solid Ti6Al4V prosthesis to be significantly susceptible to failure by stress shielding.

Several studies about the application of LPBF for the printing of metallic cellular structures were found in the literature. Their focus was mainly on the investigation of the manufacturability of such periodic structures as well as the examination of their mechanical performance. In earlier research, efforts had been directed towards the investigation of the mechanical behaviour of PBF-fabricated cellular structures from different titanium and steel alloys such as body centre cubic [26] and Schoen gyroid [27] lattice structures. Their main focus was on the determination of the effect of unit cell design on its properties. In other research, like those carried out in the literature [28, 29], the influence of PBF process parameters was examined. In these studies, the substantial impact of laser parameters on the characteristics of the fabricated lattices was demonstrated. Recent studies were also carried out by Hassanin [30], El-Sayed [23] and Bittredge [31] to study and optimise Ti6Al4V lattice structures for the fabrication of cellular-based lattice-structured orthopaedic implants that could be effectively used in trabecular bone and total shoulder-replacement surgeries.

The existing literature review lacks to provide a dedicated research focus on the development and optimisation of graded lattice structures for the femoral stem, a pivotal component in total hip replacement implants. This gap is significant as the femoral stem directly impacts the implant’s stability, load-bearing capacity and susceptibility to stress shielding, highlighting the need for targeted investigation in this specific area. Several earlier research has failed to simultaneously improve the osseointegration and reduce the stress shielding of these implants. Additionally, while the unique surface curvature of TPMS lattice structures has been shown to enhance osseointegration, it may also increase the cost of modelling and design. This work aims to cover such a gap through the designing and 3D modelling of a strut-based lattice structure with a novel unit cell and optimised curvature. The lattice structure will also be functionally graded to enhance the performance of the orthopaedic implant. This approach would eliminate stress concentrations and improve biomedical performance while maintaining the designability of the medical prosthesis.

2 Methodology

2.1 Design and modelling

In this study, two simple strut-based unit cell designs were considered: simple cubic (SC) and body-centred cubic (BCC). The strut length and diameter were 0.32 mm and 0.35 mm, respectively. Comparable design parameters were reported by earlier studies [32, 33]. For each of the lattice topologies, fillets were added to horizontal and vertical struts to investigate the effect of increasing the surface curvature on the biomedical and mechanical performance of the cellular structure. This resulted in two new unit cells, named filleted SC and filleted BCC. The geometry of the four lattices was created in Solidworks 2018 (Dassault Systems, Velizy-Vilacoublau, France) and is presented in Fig. 1.

Fig. 1
figure 1

CAD models of different strut-based lattice geometries: (a) standard BCC, (b) filleted BCC, (c) standard SC and (d) filleted SC

Full size image

As seen in Fig. 1, the application of fillets to standard strut-based lattice designs was found to significantly improve the surface curvature, with only small areas of sharp creases that could lead to stress concentrations. While this solution does not fully emulate TPMS unit cells, it demonstrated a noticeable improvement. To determine the expected performance of the lattice structure, the Maxwell number for each lattice design was calculated using Eq. (1), and the results are presented in Table 1. The number of struts (s) of the SC and BCC structures was 12 and 8, respectively, while the number of nodes (n) was 8 and 9, respectively. The two unit cells exhibited negative Maxwell numbers of − 6 and − 13, respectively, indicating that both structures were bending-dominated. This means that the structures were expected to have linear-elastic behaviour up to an elastic limit, where cell edges might begin to yield, buckle or fracture [34].

Table 1 Maxwell number calculation for the different lattice unit cells
Full size table

2.2 Unit cell testing

Finite element analysis (FEA) simulation was used to evaluate the different lattice designs described above by simulating a simple compression test. Since the application of surface curvature was proposed to enhance the performance of the lattice, the two modified lattice designs, filleted BCC and filleted SC (Fig. 1b,d, respectively), were first modelled using FEA to assess the compressive behaviour of each of the two unit-cell designs. The best design was then compared against the unmodified unit cell to quantify the effect of strut design modification on the mechanical properties of the lattice structure.

A standard cubical BCC lattice structure, with a strut length of 0.32 mm and strut diameter of 0.35 mm, was fabricated and validated against the corresponding FEA model. Ti6Al4V gas-atomized powder, with a particle size of d50 = 40 μm, supplied by TLS Technik GmbH, was used. The lattice structure was fabricated using a Renishaw RenAM 500 M Additive Manufacturing system (Renishaw plc, Wot ton-under-Edge, UK). The lattice was produced using standard process parameters for Ti6Al4V: a laser power of 200 W, a scanning speed of 1200 mm/s and a layer thickness of 20 microns. The samples were produced on a titanium plate and under argon control down to O2 < 100 ppm. The manufactured BCC lattice sample is shown in Fig. 2. The compression properties of the lattices were examined using a Zwick/Roell universal testing machine with a speed of 0.1 mm/min. The lattice was placed in the centre of the loading plate to ensure an even distribution of the compressive force during the test.

Fig. 2
figure 2

Fabricated Ti6Al4V lattice in body-centred cubic (BCC) configuration prepared for compression testing

Full size image

It should be emphasised that, for simplicity, the four unit-cell designs were compared using finite element analysis based on cubical models. This allows for an analogous comparison between the four designs in terms of mechanical behaviour without complicating the design. However, the selected unit cell design was further developed and optimised using a cylindrical model as it resembles the geometries being used in biomedical applications.

2.3 Strategy to grade the unit cell design

The optimised lattice design, created in Solidworks and shown in Fig. 2, was then imported into nTopology software (nTopology, NY, USA) to apply the unit cell grading. This software allows for the creation of complex geometries and optimization of lattice structures, making it an ideal tool for the design of implant structures. The relative density of the lattice unit cell was first evaluated using both Solidworks and nTopology to confirm the matching of the values of the relative density. This would minimise the error when transferring the unit cell design between software. Then, the completed unit cell was stored as a function in nTopology as a ‘custom implicit unit cell’ before the geometry of the lattice structure was created. Earlier studies showed that the diameter of a femoral stem implant would be 15 mm [35, 36]. In the current model, a cylinder was extruded with a depth of 10 mm to mimic a small section of the implant. The cylindrical section was copied with a + 1 mm offset applied before the unit cell and then mapped across the implicit body. This was to ensure that the cylindrical volume would be fully filled with the unit cell.

Ramped parameters were applied to decrease the strut diameter of the unit cell based on a user-defined scale factor (SF) towards the centre of the cylinder to create an initial grading effect. To achieve a lattice grading with a constant strut diameter, the structure was then remapped with an SF acting in the opposite direction to scale the x and y data by 1, at the outer edge, to SF at a user-defined radius, the ‘high-porosity zone radius’, rHP (mm). Figure 3 gives an example of the grading of a BCC lattice structure. The initial grading obtained by the reduction of the strut diameter towards the centre is shown in Fig. 3a, while the lattice obtained through grading the lattice using an SF and rHP of 2 mm and 0 mm, respectively, is shown in Fig. 3b. No grading was applied to the z-axis.

Fig. 3
figure 3

Examples of the lattice designs obtained through nTopology lattice grading: (a) strut diameter reduction towards the centre and (b) graded lattice with SF = 2, rHP = 0 mm

Full size image

2.4 Grading the lattice structure

During the lattice optimisation setup, three design parameters were considered: the strut diameter (D), SF and rHP. Through a preliminary study where D, SF and rHP were changed from 0.2 to 0.5 mm, from 1 to 3, and from 1 to 5 mm, respectively, only three conditions were able to be graded successfully and accordingly, and three different lattice designs were achieved, which are shown in Table 2. Pore size was calculated as the largest sphere that can fit inside the unit cell [37]. Each lattice was exported to Abaqus 2017 (Dassault Systemes, Velizy-France) and examined in a theoretical compression test to determine the effect of different design parameters on the compressive properties of the lattice.

Table 2 The lattice topologies considered in the current study with their corresponding parameters
Full size table

The unit cell design parameters, defined for each of the three lattices, were imported into nTopology to produce the FGLS. The lattice geometries produced were then exported to Abaqus to conduct FEA and evaluate their compressive performance. To reduce model complexity and decrease the number of nodes in the orphan mesh, the cylinder was quartered and trimmed to two cells thick in the z-axis, as per Fig. 4a. A simple compression test was then applied to this geometry. With the lattice imported into Abaqus, a reference point was placed at the centre of the lattice surface. A 3D discrete-rigid, shelled die was created using an extruded cylinder with a reference point applied at the centre of one of the circular faces. The test was assembled by translating the instances using the described reference points to place a die above and below the lattice, as shown in Fig. 4b. The material properties and plasticity data of the Ti6Al4V titanium alloy obtained from [38] and presented in Table 3 were applied to the lattice section of the model. As shown, Ti6Al4V has unique mechanical properties with a density, elastic modulus and Poisson’s ratio of 4430 kg/m3, 110 GPa and 0.33, respectively.

Fig. 4
figure 4

(a) Finite element analysis model representing the reduced size lattice and (b) assembly configuration during the compression test, as simulated in Abaqus

Full size image
Table 3 Ti6Al4V alloy mechanical properties [38]
Full size table

A 3-s static displacement step was used to simulate a static compression test. The initial step increment was set at 0.02 s in order to decrease computational time. Three interactions were applied, including two surface-to-surface contact interactions and one self-contact interaction. The surface-to-surface contacts were applied at the top and bottom interfaces between the die surfaces and the lattice, with the die surface serving as the master surface. Each interaction was created at the initial step and propagated to subsequent steps, using a tangential penalty contact with a friction coefficient of 0.125 to promote better convergence. Instead of applying load, it was controlled using boundary conditions (BC). A fixed BC was applied to the reference point at the lower surface of the bottom die at the initial step, and the encastré condition was used to fix the die. To fix the model on the cut edges, axisymmetric BCs were also applied for the x and y axes. This approach simplifies the model for simulation and allows for obtaining results for the complete geometry. The final BC was applied to the reference point at the lower surface of the top die at the displacement step.

To create a single displacement in the z-axis, the BC was initialized as follows: U3 =  − 0.0001; U1 = U2 = UR1 = UR2 = UR3 = 0. The value assigned to U3 was determined through trial and error to find the point where the lattice plastically deforms. To reduce simulation time, U3 was set to the minimal value. The assembly (lattice and die) was then meshed using a simple R3D4. For each sample, the simulation was run, and 100 data points for the reaction force and displacement were extracted. The data was then plotted to obtain engineering stress–strain diagrams for different lattice designs. The Gibson-Ashby model [33], seen in Eq. (2), was used to predict the effect that changing the relative density \(\frac{{\rho }^{*}}{{\rho }^{s}}\) of a lattice structure they had on its elastic modulus E.

$$\frac{{E}^{*}}{{E}^{s}}=C{\left(\frac{{\rho }^{*}}{{\rho }^{s}}\right)}^{n}$$
(2)

The superscript ‘*’ symbolises the lattice structure, and the subscript ‘s’ refers to the solid region of the material. C and n are constant values dependent on the unit cell topology and are experimentally derived. By using this model, an improved design can be obtained once initial results are obtained [39].

3 Results

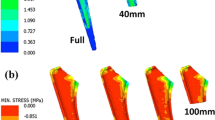
The FEA compression test results for the modified SC, modified BCC and standard BCC lattice structures are presented in Fig. 5a–c, respectively. The Von Mises stress results were analysed to identify potential stress concentration locations within the examined lattice. The modified unit cell lattices (Figs. 5a and 4b) showed that the highest stresses were observed at the interfaces between the lattice structure and the dies, where inter-lattice stresses were reduced and distributed over the surface curvature, as indicated by the large green zones. Overall, the modified BCC lattice exhibited better performance compared to the modified BC structure. This was revealed by the lower von Mises stress and the way loads were spread throughout the structure rather than being concentrated at the vertical members. This is a crucial aspect in the design of implant structures, as it ensures the distribution of loads over a larger surface area, reducing the risk of failure at a single point.

Fig. 5
figure 5

Von Mises stress distribution during the compression test for different lattice designs: (a) modified SC, (b) modified BCC and (c) standard BCC

Full size image

To further evaluate its performance, the modified BCC structure was tested against the unmodified BCC structure. As shown in Fig. 5c, while stress appeared to be lower with larger blue regions, the highly stressed areas at the unit cell interfaces had experienced significantly higher stress concentrations. This is an indication that the unmodified BCC structure is not suitable for implant design as it presents high-stress concentration at specific points, increasing the risk of failure. This effect justifies the application of surface curvature to amend the struts of lattice unit cell design, providing a rational for the employment of the modified BCC structure for the implant design. The results of this test revealed that the modified BCC structure is better suited for implant design, as it provides lower stress concentration and better load distribution. The design model of the modified BCC lattice structure is shown in Fig. 6

Fig. 6
figure 6

Schematic illustration of the modified BCC lattice structure, designed to eliminate stress concentration and improve load distribution

Full size image

The reaction forces and displacement data extracted from FEA compression test results of the three lattice designs (given in Fig. 5) were used to plot the compressive stress–strain diagrams for different lattice structures, which are presented in Fig. 7. The experimental stress–strain diagram for the additively manufactured standard BCC lattice is also plotted at the same axes in Fig. 7. It could be indicated that the modified BCC lattice structure experienced the highest ultimate compressive strength (UCS) of about of about 440 MPa, which was significantly higher than that of either the standard BCC lattice or the modified SC lattice structures. In order to validate the FEA predictions, the compressive stress–strain diagrams of fabricated and modelled standard BCC lattices were compared. As shown, the respective errors in the FEA model prediction were found to be less than 10%, suggesting an acceptable accuracy of the model in estimating the mechanical properties of the lattice structures in this study.

Fig. 7
figure 7

Stress vs strain curves obtained from FEA for various lattice designs, alongside the stress–strain profile of the conventionally printed standard body-centred cubic (BCC) lattice structure

Full size image

To design a modified (graded) BCC unit cell identical to that shown in Fig. 1b, nTopology was used. Then, the values chosen for the lattice unit cell design parameters, shown in Table 2, were used to generate three lattices of modified BCC structures, which are presented in Fig. 8. This allowed for further examination and comparison of the performance of the modified BCC structure against other lattice structures. It also allowed the investigation of the effect of varying the design parameters on the performance of the structure. The results of these simulations can be used to guide the design of implant structures, ensuring that they are optimised for load distribution and stress concentration reduction.

Fig. 8
figure 8

(a–c) The three lattice geometries achieved through nTopology gradings, employing the parameters outlined in Table 2 for lattices 1, 2 and 3, respectively

Full size image

Figure 9 shows the compressive stress–strain diagram, based on the data obtained from Abaqus, for graded filleted BCC lattices 1, 2 and 3 (presented in Figs. 8a–c, respectively). Through examination of these diagrams, the yield strength, modulus of elasticity and ultimate compressive strength were calculated for each of the three lattice structures. The FEA was also implemented to calculate the pore size of each lattice design, and these results are presented in Table 4. A plot of the mechanical properties of the lattice against its pore size is also presented in Fig. 10.

Fig. 9
figure 9

Stress vs. strain curves derived from finite element analysis (FEA) for the lattice designs depicted in Fig. 8

Full size image
Table 4 Results of the pore size and mechanical properties of different lattice structures presented in Fig. 8
Full size table
Fig. 10
figure 10

Pore size vs. compressive properties of the graded lattice structures described in Table 4

Full size image

As shown in Table 4, the pore size of all studied lattices lied within the desired range for biomedical applications that was reported to vary from 400 to 700 µm [40, 41]. For lattice 1, the standard grading resulted in a low modulus, good yield strength and acceptable compressive strength with a lattice pore size of 550 µm. However, increasing both the strut diameter and the high-porosity zone radius (lattice 2) had significantly increased the elastic modulus and compressive strength by factors of about 0.92 and 0.55, respectively, while showing a slight reducing effect on the yield strength and the resulting pore size was 600 µm. In contradiction, increasing the scale factor (lattice 3) had reduced (compared to lattice 1) the elastic modulus, yield strength and compressive strength by about 40%, 31% and 16%, respectively. This grading strategy was also shown to reduce the lattice pore size to 400 µm.

In terms of pore size, the results in Fig. 10 showed a consistent improvement of both the elastic modulus and the UCS of the lattice with increasing pore size. Increasing the pore size by a factor of 0.5 caused the elastic modulus and UCS to increase by about 220% and 84%, respectively. Increasing the lattice pore size from 400 to 550 µm was also associated with an increase in the yield strength from 120 to 175 MPa (about 46%). However, the additional increase of the pore size to 600 µm did not result in any further improvement of the strength. In contradiction, it caused the property to decrease slightly to 162 MPa.

Therefore, the design parameters of lattice 3 were considered insufficient to achieve the intended lattice compressive performance, especially since the small pore size makes it difficult to modify using the Gibson-Ashby model while maintaining the desired relative density.

The von Mises stress data at the increment of the ultimate compressive strength (UCS) was analysed to determine the load distribution across different lattice structures, given in Fig. 11. It was shown that the unit cell design of lattice 1 exhibited a higher effectiveness in dispersing the stress throughout the whole cellular structure rather than having it concentrated close to the edges. Therefore, the design of lattice 1 (with a pore size of 550 µm and mechanical properties listed in Table 4) was chosen to apply the Gibson-Ashby model grading.

Fig. 11
figure 11

Von Mises stress distributions for the lattice structures whose designs are shown in Fig. 8 and whose mechanical properties are listed in Table 4: (a) lattice 1 and (b) lattice 2

Full size image

From the modelling results of lattice 1, the density and elastic modulus of the lattice were determined to be 1629 kg/m3 (a relative density of 0.368) and 12.5 GPa, respectively. The Gibson-Ashby model, Eq. (2), was applied to lattice 1, where the Gibson-Ashby constant was found to be 0.84. The constant was then used to find the ideal relative density of the grading to produce a lattice structure with an appropriate elastic modulus for a medical implant. The elastic modulus of the cortical bone of the femur was reported to be between 15 and 21 GPa [42, 43]. An average value of 18 GPa was substituted in Eq. (2) along with the Gibson-Ashby constant to calculate the corresponding optimal density and relative density of the structure, which were found to be 1955 kg/m3 and 0.441. The unit cell of lattice 1 was then re-graded using nTopology to achieve the optimal relative density. Then, the adjusted lattice 1 structure was re-modelled and re-tested to verify the improvement. A comparison between the original and adjusted lattice 1 structures is given in Fig. 12. Due to the pore size limit, the highest achievable relative density of the adjusted structure was 0.411, and the corresponding predicted elastic modulus was 15.7 GPa.

Fig. 12
figure 12

Schematic illustration of the graded BCC lattice structure: (a) original grading and (b) Gibson-Ashby–adjusted grading of lattice 1

Full size image

The standard BCC unit cell lattice structure (without the fillets applied to increase curvature) was also modelled and tested. The results were compared to those corresponding to the adjusted lattice 1 structure and presented in Table 5 and Fig. 13. As shown, there was a noticeable improvement in the mechanical properties.

Table 5 The mechanical properties of adjusted lattice 1 against the standard BCC unit cell lattice design
Full size table
Fig. 13
figure 13

A comparison of stress–strain curves between the standard and Gibson-Ashby–modified body-centred cubic (BCC) lattice structures

Full size image

Compared to the standard BCC unit cell design, the FEA results of the Gibson-Ashby–modified design showed a reduction in the elastic modulus (by about 21%), a good rise of both the yield strength and UCS by about 26% and 28%, respectively. Figure 14 shows the von Mises stress distribution for the improved Gibson-Ashby structure. With respect to the lattice 1 unit cell design, the adjusted structure allowed a better distribution of the stress and also eliminated the distortion of the graded cells.

Fig. 14
figure 14

Von Mises stress distribution of the Gibson-Ashby–graded lattice structure

Full size image

4 Discussion

4.1 Comparison of initial graded runs

Table 4 presents a comparison of the compressive performance of different lattice topologies designed using varied strut diameter, scale factor and high-porosity zone radius, whose grading details are presented in Table 2. While lattice 1, where the resulting pore size was 550 µm, does not have a high effective modulus, the yield strength is appealing for its relative density. Such good performance is likely to be a result of the smoothly graded structure allowing for effective load transfer between lattice cells. These findings were confirmed by the von Mises stress results shown in Fig. 11a that suggested a greater ability of lattice 1 design to spread the applied load over a larger proportion of the structure. On the other hand, although lattice 2 structure (with 600 µm pore size) exhibited a significantly doubled stiffness compared to lattice 1, the harsher transition between low and high-porosity zones was shown to act as a barrier of stress conveyance which centralised most of the load endured by the structure at the 2.5-mm-thick low-porosity ring around the circumference of the cylinder. The drastic transition also caused a severe distortion to the unit cells which had also affected the ability of the structure to transfer loads. This resulted in about 7% reduction of the yield strength due to the premature buckling of this region of the structure. Despite its enhanced stiffness, the application potential of lattice 2 is limited in the context of biomedical orthopaedic implants due to the adverse stress distribution caused by the abrupt transition.

The unit cell design of lattice 3, where a 400-µm pore size was achieved, was shown to be the worst as the admission of a relatively large scale factor to increase the porosity has resulted in a significant decrease of the strut diameter towards the centre of the lattice. This brought about a significant retrogradation of the mechanical properties, especially the yield strength, due to the lack of material in the central region of the lattice, decreasing its energy absorption capability and making it weaker against buckling. Since the design also exhibited the lowest pore size of 400 µm, it would be rather difficult to increase the relative density to optimise the properties, and therefore, lattice 3 was not included during the subsequent analysis in this study.

Considering the von Mises stress data (shown in Fig. 11), the poor stress distribution associated with the design of lattice 2 caused it to be also excluded. Therefore, the design of lattice 1 with a pore size of 550 µm and mechanical properties listed in Table 4 was chosen to apply the Gibson-Ashby model grading. This positions lattice 1 as a favourable choice for biomedical orthopaedic implants, where improved mechanical strength and matching elastic modulus to human bones are essential.

4.2 Gibson-Ashby model discussion

Comparing the mechanical properties of lattice 1 design before and after the Gibson-Ashby model grading (given in Table 4 and 5, respectively) revealed a notable improvement of the elastic modulus by about 25%, making it closer to that of human bones. The increase in the elastic modulus with a change in the relative density was a confirmation of the results obtained by Benedetti et al. [33]. In addition and considering that the UCS and yield strength of the femur are 205 MPa and 115 MPa, respectively [44], the Gibson-Ashby model grading has increased both the UCS and yield strength to 530 MPa and 296 MPa, respectively, with a safety factor of more than 2.5 each, compared to the target values of the femur. This is ideal for better implant survivability with a reduced chance of requiring expensive revision surgery.

With regards to the standard BCC unit cell, the Gibson-Ashby adjustment of the lattice 1 design resulted in a good improvement of both the yield strength and UCS. On the other hand, the adjustment has reduced the elastic modulus of the structure. However, it still lies within the appropriate range for the cortical bone of the femur [42].

Overall, the optimally (Gibson-Ashby) graded lattice structure obtained in this study would be suitable for a femoral stem implant design. Nevertheless, and since the relative density cannot be further increased with the current grading input parameters, further investigation might be performed to increase the strut diameter aiming at improving the compressive performance (as realised by the lattice 2 results) while maintaining the lattice 1 grading with the smooth grade transition.

The porosity of the Gibson-Ashby–adjusted lattice 1 structure was determined to be 58.9% (corresponds to a relative density of 0.411) which is within the porosity range of 30–60% found in the upper region of the femur [45]. Traxel et al. [46] tested a uniform BCC lattice under compression using Ti6Al4V. For a lattice structure with a porosity of about 60%, they obtained an elastic modulus of 15.1 GPa and a yield strength of 229.7 MPa and a UCS of 325 MPa. Therefore, the graded structure provides an improvement of 5%, 29% and 63% over uniform structure modulus, yield strength and UCS values, respectively. This might be reasoned to the optimised lattice topology as well as the modified surface curvature of the unit cell that allowed for enhanced distribution of the applied stress through the whole structure, eliminated stress concentrations and in turn improved the mechanical performance of the cellular structure.

The FEA results of the current study suggested that the adjustment of Ti6Al4V BCC lattice design through both the application of strut surface curvature and porosity grading within the cellular structure had succeeded in producing a structure that would be suitable for a graded implant design of a femoral stem implant. The higher curvature increased the effectiveness of stress distribution throughout the structure which resulted in an overall amelioration of the mechanical properties, especially the stiffness. Along with the expected improvement to osseointegration, the modified BCC sees several performance improvements over the standard design while still maintaining designability.

5 Conclusions

The research introduces a novel grading strategy for a Ti6Al4V body-centred cubic lattice structure specifically designed for hip implants, with the aim of enhancing both osseointegration and addressing stress shielding issues in the prosthetic component. This grading involved the systematic adjustment of various unit cell design parameters within the lattice structure. Subsequent finite element analysis was conducted to evaluate the mechanical performance of the graded lattices, leading to the following key conclusions.

  1. 1.

    Von Mises stress analysis demonstrated the effectiveness of the BCC lattice compared to the standard body-centred (BC) structure. Notably, structural modification through filleting the struts was found to enhance the performance of both lattice geometries.

  2. 2.

    Increasing the BCC lattice pore size from 400 to 600 µm resulted in a nearly twofold increase in the ultimate compressive strength (UCS) of the lattice. Additionally, this adjustment was associated with a substantial threefold increase in the elastic modulus and a modest 35% rise in yield strength.

  3. 3.

    The optimised BCC lattice, achieved through Gibson-Ashby model grading, features a 400-µm pore size, aligning effectively with osseointegration needs. This design has an elastic modulus of 15.7 GPa, a porosity of 58.9% and effectively mitigating stress shielding. Furthermore, the optimised structure exhibits a yield strength and UCS of 296 MPa and 560 MPa, respectively, surpassing femur properties by more than double.

The performance of the developed designs contributes valuable insights into lattice structure optimization. However, it is important to recognise the need for further associated study in vivo conditions. Patient variations in terms of anatomy, physiological responses, and implant interactions may pose challenges not included in the study.