1 Introduction

Auxetics make possible to enhance already existing structures and create new mechanically improved ones [1, 2]. As the shift towards the use of auxetics occurs, methodologies must be defined for the process of designing these geometries to allow their production through additive manufacturing processes. To further explore variations of auxetic structures, functional gradients are used in this work. This inclusion of methods to gradually apply variability is motivated by the possibility of obtaining different performances in different sections of a structure, which promotes highly adapted characteristics of different elements within the same structure [3].

The idea of designing graded gyroid cell structures is attracting the awareness of researchers. Jung and Buehler [4] worked on the mechanical properties of the graphene TPMS unit cell, proving excellent and adjustable load-bearing properties. Yang et al. [5] studied the comportment of functionally graded gyroid structures subjected to quasi-static uniaxial compression. The results showed that, compared to uniform ones, there is no effect in deformation conduct when graded density is introduced normal to the loading direction compared to uniform ones. However, they observed a layer-by-layer collapse behaviour for structures with a density gradient parallel to the loading direction. Afshar et al. [6] found analogous effects on other TPMS cell structures.

In classical elasticity theory, it is stated that the Poisson ratio is within the [− 1,0.5] range for an isotropic material. For a material in the upper limit of this range, when subjected to deformation, the body volume is preserved. For all other values, there is an increase in volume when the material is pulled apart in one direction and a decrease in volume when compressed. In this aspect, even though the volume change is more accentuated when the Poisson ratio has a negative value, the fundamental behaviour is preserved throughout the range of values [7]. At the lower limit of the range, shape is preserved, but as the Poisson ratio value strays further away from the value (− 1), the shape after deformation becomes less proportionate to the original shape [8].

When most materials are compressed along a given direction, the transverse dimension increases. This behaviour occurs in materials with a positive value of the Poisson ratio (PR), and this property is defined by Eq. (1).

$$\nu =-\frac{{\varepsilon }_{\mathrm{Tran}}}{{\varepsilon }_{\mathrm{Load}}}$$
(1)

where \({\varepsilon }_{\mathrm{Tran}}\) represents the transverse direction strain and \({\varepsilon }_{\mathrm{Load}}\) the loading direction strain [7].

Unlike most materials, auxetic metamaterials are characterized by a non-positive Poisson’s ratio (NPR). This forces the material to shrink transversely when compressed longitudinally and, when stretched in one direction, it expands in the direction transverse to the loading direction. According to Lim [8], there are five landmarks of Poisson’s ratio for isotropic solids, whose values have different physical significance, namely preservation of area (\(\nu =1\)), preservation of volume (\(\nu =0.5\)), preservation of cross section (\(\nu =0\)), preservation of moduli, E = G, (\(\nu =-0.5\)), and preservation of shape (\(\nu =-1\)). The material’s behaviours for different PR values are presented in Fig. 1.

Fig. 1
figure 1

Schematic of undeformed and deformed comparison between materials with positive, negative, and null Poisson ratio (adapted from [8])

Full size image

Deformation mechanisms are essential for the auxetic comportment to manifest [9]. These deformation mechanisms characterize how the changes in elements and units occur. Units or unit cells are constituents of material structures. The shape of these units can lead to different deformation mechanisms. The fragments that compose these units are the elements.

Two mechanisms that commonly prompt the auxetic behaviour are hinging and a combination of buckling and stretching. Hinge like comportment in structures can enable the rotation of either elements or units. A mechanism that causes the rotation of elements, can be found in re-entrant cells’ structures. The unit cells of these structures have re-entrant elements. The re-entrant shape of the unit cells is responsible for the auxetic behaviour [10]. When the re-entrant cell is compressed, the values of the angles will decrease. This change occurs due to the rotational movement of the two elements on the upper section and the two elements on the lower section of the cell.

A hinging mechanism that causes the rotation of units is found in rotating units’ structures. These structures are characterized by that mechanism. The hinging points connecting units allow for the rotation of those units. Figure 2 shows an example of a rotating units’ structure where the expansion of the structure is linked to the rotation of the units around the hinging points, which is accompanied by an increase in the value of the angle θ.

Fig. 2
figure 2

Rotating units’ structure behaviour throughout the full range of rotation of its units: (a) θ=0°; (b) θ=30°; (c) θ=60°; (d) θ=90°; (e) θ=120° [11]

Full size image

In other auxetic structures, a combination of buckling and stretching of the composing elements of the structure enables the auxetic behaviour. An example where this buckling and stretching mechanism is present can be found in structures such as the chiral quadratic lattice shown in Fig. 3. Comparing the schematic in Fig. 3a with the one in Fig. 3b, it is visible that when the structure is compressed, the elements will buckle. If the presented structured is pulled apart, the composing elements would be stretched [12].

Fig. 3
figure 3

Chiral quadratic lattice: a before and b after being deformed showing auxetic behaviour (adapted from [12])

Full size image

The gyroid is a minimal surface (meaning that in every point of its domain, it has zero mean curvature) that belongs to a family of associated minimal surfaces known as P-G-D. From a topological perspective, the surfaces of this family are the simplest examples of triply periodic minimal surfaces, that are free of self-intersections and have cubic lattice symmetry [13, 14].

The current work is part of a larger ongoing effort from our research team to design, simulate, fabricate, and characterize a range of mechanical metamaterials for biomedical and structural applications. Along with concurrent work where such metamaterials are designed via topology optimization [15], the methodology hereby proposed should serve as the basis for the transition from a purely empirical design approach, where pre-existing structure designs are modified to achieve the intended behaviour [16], to one where the metamaterial’s architecture is tailored a priori to exhibit the best results, behaviour-wise.

This work proposes a method that allows modelling of tailored complex functionally graded auxetic structures, achieved through modifications in the equations defining the basic surfaces that characterize the structures, to obtain specific equations for each situation. The methodology proposed in this paper also includes the simulation studies performed by means of the finite element method. The capabilities of the methodology using complex geometries were exemplified trough the gyroid surface, from which to form the auxetic structures, and applied on geometries with different gradient types and steepness’s to obtain comprehensive data that allows to infer on the accuracy of the method.

2 Modelling methodology

Figure 4 shows a unit cell of the gyroid surface which can be approximated using Eq. (2) [17], with x, y, and z varying in [− π, π], a = 1 and b = 0.

Fig. 4
figure 4

Unit cell of the gyroid surface

Full size image
$$\mathrm{cos}\left(x/a\right)\bullet \mathrm{sin}\left(y/a\right)+\mathrm{cos}\left(y/a\right)\bullet \mathrm{sin}\left(z/a\right)+\mathrm{cos}\left(z/a\right)\bullet \mathrm{sin}\left(x/a\right)=b$$
(2)

To alter the geometry of the gyroid, adjustments can be made to the values of the coefficients a and b [18]. The value of a influences the size of the unit cell. In Fig. 5, three gyroid surfaces modelled with different values for a are represented. The surface in Fig. 5a was modelled with a = 1, that in Fig. 5b with a = 0.75 and the one in Fig. 5c with a = 1.25. Comparing the three surfaces, one can observe that an increase in the value of a causes the size of the unit cells to increase and vice-versa.

Fig. 5
figure 5

Gyroid surfaces modelled with a = 1, b a = 0.75, and c a = 1.25

Full size image

Changes in the value of the coefficient b influence the density throughout the geometry. Figure 6 presents three gyroid surfaces that were modelled with (a) b = 0, (b) b =  − 0.75, and (c) b = 0.75. A comparison between the surfaces discloses that changes in the value of b influence not the density of the whole geometry but only the local density. These changes result in alternating higher and lower density areas on the gyroid surface. A shift from a negative value of b to its absolute value results in the variation of the density to occur in the opposite way, with high-density areas becoming low-density areas and vice-versa.

Fig. 6
figure 6

Gyroid surfaces modelled with a b = 0, b =  − 0.75, and c b = 0.75

Full size image

To model the base surfaces, software capable of generating 3D geometries based on their descriptive equations was used. MathMod and Matlab were employed in this work to complete this step. The surface model can be altered in this part of the process, through changes in the equations. In the case of the gyroid, the changes are done by altering the values of the coefficients a and b in Eq. (2). As previously shown, the values of the coefficients can be changed in a discrete way. Alternatively, their values may also be varied continuously through the introduction of functional gradients, as detailed further along in this work.

When the surface model is exported using the OBJ or the STL file formats, the shape of the surface is approximated by using polygons to define it. In the case of STL, the triangular shape is the only polygon shape available, while in the OBJ format, other polygon shapes can be used.

The exported model is a faceted body that lacks thickness; thus, the next step is to grant thickness to the model. This can be achieved by using purposefully built-in tools such as “Solidify” in Blender or “Thicken” in Fusion 360 and Ansys SpaceClaim. After granting thickness to the surface, the resulting body is converted into a solid. In the current work, the tool “Convert to solid” from Ansys SpaceClaim was used.

Even though the process explained above can be sufficient to produce satisfying results in simulation studies, further refinements are possible. With the model as a faceted body, the number of polygons that define the geometry can be reduced, making the simulations easier to solve and thus requiring less computational power. Built-in tools can regularize facets or detect and fix irregularities in the geometries such as holes, self-intersections, and sharp and over-connected edges and vertices. With the model now in the form of a solid body, using built-in tools to detect and fix duplicate faces, inexact and split edges, and removing extra edges, its quality can be improved. The tools mentioned in this paragraph are all available in Ansys SpaceClaim.

2.1 Functional gradient

A functional gradient is a controlled variation, throughout the structure, of either the geometrical parameters or the inherent properties of its constitutive materials. In this work, the functional gradients were obtained through the variation of the geometrical parameters that define the structure. Such parameters are altered in a continuous way to avoid deficiencies in the geometrical continuity and cellular connectivity. These shortcomings can derive from abrupt transitions in a structure formed by joining unit cells with slightly different values of geometrical parameters.

Due to the disruptive influence that non discrete modifications of the parameter a have on the gyroid shape, within the context of the current work, the decision was made to focus on modifying the parameter b in Eq. (2). This disruptive influence results in surfaces that are outside of the context of the current work.

2.1.1 Linear gradient

The most basic example of gradient is the linear. To generate it in the gyroid surface, the coefficient b is to be replaced with the sum of the space defining variables x, y, and z. Equation (3) can be used to define a surface with a linear gradient that is made up of gyroid cells, in which c, d, and e can be changed to further modify the shape of the surface.

$$\mathrm{cos}\left(x/a\right)\bullet \mathrm{sin}\left(y/a\right)+\mathrm{cos}\left(y/a\right)\bullet \mathrm{sin}\left(z/a\right)+\mathrm{cos}\left(z/a\right)\bullet \mathrm{sin}\left(x/a\right)=c\bullet x+d\bullet y+e\bullet z$$
(3)

Figure 7a is the graphical representation of a gyroid-based surface model defined by Eq. (3) with x, y, and z varying in [− 15,15], a = 1, c = -0.1, and d = e = 0. The modelled surface has a linear gradient parallel to the x axis because only c is non-null among the coefficients c, d, and e. An increase in the absolute value of coefficient c will lead to a steeper gradient along the related direction.

Fig. 7
figure 7

a Gyroid surface with linear gradient parallel to the x axis. b Gyroid surface with a linear gradient equal in magnitude in the x, y, and z directions

Full size image

It should be noted that a linear gradient can still be obtained through a virtually infinite number of combinations of values of the c, d, and e coefficients, which may assume values other than zero in a simultaneous way. This is illustrated in Fig. 7b, which shows a gyroid surface modelled with x, y, and z in the range [− 10,10] and c = d = e = 0.06. The resulting linear gradient is parallel to the bisector of the first and seventh octants. Consequently, the magnitude of the linear gradient is equal in the three main directions.

2.1.2 Sinusoidal gradient

This gradient was created from the linear gradient with the objective of inducing periodic density changes within the gyroid structure. Equations (4) and (5) were obtained by altering Eq. (3) and can be used to define gyroid-based surfaces with alternative sinusoidal gradients. The coefficient a was set in the terms of each equation that define the gradient to preserve the matching period between the gradient and the surface, even when the value of a is changed. In both equations, changes in the values of c, d, and e affect the steepness of the gradients.

$$\mathrm{cos}\left(x/a\right)\bullet \mathrm{sin}\left(y/a\right)+\mathrm{cos}\left(y/a\right)\bullet \mathrm{sin}\left(z/a\right)+\mathrm{cos}\left(z/a\right)\bullet \mathrm{sin}\left(x/a\right)=c\bullet x\bullet \mathrm{sin}\left(x/a\right)+d\bullet y\bullet \mathrm{sin}\left(y/a\right)+e\bullet z\bullet \mathrm{sin}\left(z/a\right)$$
(4)
$$\mathrm{cos}\left(x/a\right)\bullet \mathrm{sin}\left(y/a\right)+\mathrm{cos}\left(y/a\right)\bullet \mathrm{sin}\left(z/a\right)+\mathrm{cos}\left(z/a\right)\bullet \mathrm{sin}\left(x/a\right)=c\bullet x\bullet \mathrm{cos}\left(x/a\right)+d\bullet y\bullet \mathrm{cos}\left(y/a\right)+e\bullet z\bullet \mathrm{cos}\left(z/a\right)$$
(5)

Figure 8a and b compare two different views of a modelled gyroid surface with a sinusoidal gradient defined using the sine function. The view in Fig. 8a is normal to the x–z plane, while the view in Fig. 8b is normal to the x–y plane. This surface is defined by Eq. (4) with x, y, and z varying in the range [− 10,10], a = 1, c = 0.1, and d = e = 0.

Fig. 8
figure 8

Gyroid surface with a sinusoidal gradient in the x direction: a and b sine, view normal to the x–z plane and x–y plane, respectively; c and d cosine, view normal to the x–z plane and x–y plane

Full size image

The sinusoidal gradient can be observed in Fig. 8a, the x–z plane. In Fig. 8b, even though there is a slight distortion of the voids, the changes in the surface caused by the gradient are too minor to be easily observed.

Similarly, Fig. 8c and d show two views of a modelled gyroid surface with a sinusoidal gradient defined using the cosine function. The view in Fig. 8c is normal to the x–z plane, while the one in Fig. 8d is normal to the x–y plane. This surface is defined by Eq. (5) with x, y, and z varying within [− 10,10], a = 1, c = 0.1, and d = e = 0.

The differences caused by the gradient are imperceptible in Fig. 8c, while in Fig. 8d, the effect of the gradient in the surface becomes noticeable.

2.1.3 Radial gradient

A gyroid-based surface with radial gradient can be defined by Eq. (6). To that purpose, either two (in the case of a cylindrical gradient around a linear axis) or three (to generate a spherical gradient around a single point) values of the c, d, and e parameters must be different from zero.

$$\mathrm{cos}\left(x/a\right)\bullet \mathrm{sin}\left(y/a\right)+\mathrm{cos}\left(y/a\right)\bullet \mathrm{sin}\left(z/a\right)+\mathrm{cos}\left(z/a\right)\bullet \mathrm{sin}\left(x/a\right)=c\bullet {x}^{2}+d\bullet {y}^{2}+e\bullet {z}^{2}$$
(6)

Figure 9a shows a surface with a planar gradient modelled using Eq. (6) with x, y, and z varying in the range [− 15,15], a = 1, c = d = 0.0075 and e = 0. Because the coefficient e is null, the gradient in the surface is cylindrical; i.e., it is independent of the z coordinate.

Fig. 9
figure 9

a Gyroid surface with a planar radial gradient. b Gyroid surface with a spatial radial gradient

Full size image

To model a gyroid surface with a spherical gradient, the values of all three gradient defining coefficients must be different from zero. Figure 9b shows a gyroid surface modelled with spherical gradient using Eq. (6) with x, y, and z varying within [− 15,15], a = 1 and c = e = d = 0.0075.

It should be noted that if the values of the c, d, and e parameters are non-null and different from each other, the resulting gradients have the shape of ellipses or ellipsoids.

3 Simulation

In this work, the finite element method (FEM) was used to simulate the mechanical behaviour of the previously modelled structures. The domain of the problem is decomposed into several subdomains, and in each of those subdomains, the equation that defines the problem is approximated by a variational method. This approximation leads to a significant reduction in the computational power required to solve the problem. The downside is that the approximation of the problem runs to an approximated solution.

To overcome the error introduced by using the FEM, a mesh convergence analysis was done. With this analysis, several ways of refining the mesh were considered to improve the obtained results. Refinements of the mesh are classified in three types: h-refinement, p-refinement, and r-refinement [19]. H-refinement is based on the decomposition of the problem domain into more subdomains than before. Essentially, the size of the elements decreases due to an increase in the quantity of elements. With p-refinement, the degrees of the shape functions are increased, which improves the interpolation of data between nodes. R-refinement consists in rearranging the mesh. In sections where a mesh with better resolution is advantageous for better results, more nodes can be placed. However, as to not increase the number of nodes in the mesh, the resolution is worsened in sections where lower resolution is sufficient. In this work, the three types of refinement were adopted, considering their intrinsic characteristics. However, the h-refinements were performed up to the limit (128,000 elements) of the software license and the highest degree functions available were quadratic. Because of these limitations imposed by the license of the software used (Ansys), the extent of the h- and p-refinements performed was severely limited. These limitations hinder the accuracy of the method.

Due to the high deformation inflicted to the structures, the study was performed considering the finite strain theory instead of the simpler infinitesimal strain theory. This consideration took place because of the 10% limit of deformation, associated with the use of infinitesimal strain theory for engineering applications [20].

On the gyroid-based structures where the first simulation studies were performed, an effect related to structural instability was observed (Fig. 10). Figure 10a presents an unsupported and undeformed gyroid-based structure; in Fig. 10b, it is noticeable the lack of support in the extremities of the structure causing them to flare. However, in structures with a higher number of unit cells, this non-uniform deformation would not affect the behaviour of the inner cells.

Fig. 10
figure 10

Unsupported gyroid-based structure: a before and b after deformation

Full size image

Because of this effect, simulations performed in structures with a low number of unit cells would not be useful for inferring about the comportment of structures with a high number of unit cells.

To surpass this question, instead of increasing the number of unit cells in the structure, which would ultimately result in an increase in the complexity of the simulation, slabs were added at both the top and the bottom ends of the structures. This eliminates the possibility of lateral movements in the ends of the structure under load. Due to the low resistance to deformation and large elastic range of the material used, these deformation constraints should not be effective beyond the cells to which the slabs are directly connected.

4 Experimental procedure

The experimental procedure was divided in two stages: material characterization and structure testing. In the material characterization stage, samples of the chosen material were tested to collect data to be used in the simulation phase. The structure testing stage was performed with the objective of creating a benchmark, to which the simulations’ results were to be compared for validation. All material samples and structures were 3D printed in FilaFlex UltraSoft 70A TPE filament, using a Prusa i3 MK3S printer.

4.1 Material characterization

The testing methodology used in this stage was based on the ASTM D638-14 standard test method for the determination of tensile properties of plastics. Ten samples were used, with five of them being printed with 0° orientation and the other with a 90° orientation. By orienting the samples like this and orienting each infill layer orthogonally relative to the previous and next layers, the effects of the anisotropy inherent to the 3D printing process on the collected data, and the surface roughness are reduced [21]. The five samples for each printing orientation were tested with an elongation rate of 5 mm/min, up to a strain of 300%. Figure 11 presents the graphical representation of the stress–strain curves obtained from the ten tensile tests on the material samples.

Fig. 11
figure 11

Stress–strain curves of tensile tests on the material samples

Full size image

4.2 Structure testing

In the validation testing stage, the structures corresponding to the models used in the simulations were compressed up to 15% with an elongation rate of 1 mm/min. At 15% compression, the auxetic behaviour of the structures is already observable. In fact, from preliminary tests, it was found that for strain levels above 15% deviations between the predicted and the experimentally observed deformation behaviour could no longer be ignored. Furthermore, for practical applications, the sought after auxetic behaviour essentially pertains to the domain of small deformations.

To emulate the effect of the slabs introduced in the models used in simulations, the top and bottom ends of each printed structure were fixed against sheets, which were fixed onto both the base plate and the compression plate of the testing machine. Consequently, the restriction in lateral movement imposed at the top and bottom of the models in the simulations, is also established in the experiments.

Images from two viewpoints (90° apart) of the structures undergoing deformation were acquired during the tests, for subsequent comparison with the simulation results.

A universal testing machine Shimadzu AG was used along its corresponding software, TRAPEZIUM 2, for the mechanical testing.

5 Results and discussion

The proposed methodology for modelling and simulation of tailored 3D functionally graded auxetic metamaterials is underlined in Fig. 12.

Fig. 12
figure 12

Flowchart representing the proposed methodology

Full size image

Regarding the comparation performed, the distances between reference points in the tested structures and in the simulated models were measured using the JMicroVision software. Due to the difference in resolution between the images of the tested structures and the simulated models, all the distances were relativized to a distance that is common in both the tested structures and the simulated models. After, the values of the distances in both the undeformed and the deformed geometries were compared, to establish the real and the simulated deformation. The error associated to the method was calculated from the obtained values of deformation.

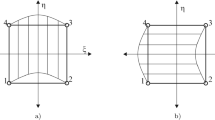
For the geometries that are not cylindrically shaped, the chosen reference points were inflexion points in the curved edges and points at the end of the curved edges on the sides. Figure 13a and b show sides 1 and 2, respectively, of the undeformed non-graded gyroid-based structure with the reference points on each side numbered from 1 to 12. These reference points are equivalent in the other non-cylindrically shaped structures. For the geometries that are cylindrically shaped, the chosen reference points were inflexion points in the curved edges. Figure 13c and d show the reference points numbered up to 6 and 5 on sides 1 and 2, respectively, of the undeformed non-graded gyroid-based structure with a cylindrical shape. Figure 13e and f show the reference points numbered up to 4 on sides 1 and 2, respectively, of the undeformed radially graded gyroid-based structure with a cylindrical shape.

Fig. 13
figure 13

Reference points: a on side 1 and b on side 2 of the gyroid-based structure with no gradient; c on side 1 and d on side 2 of the gyroid-based structure with a cylindrical shape and no gradient; e on side 1 and f on side 2 of the gyroid-based structure with a cylindrical shape and radial gradient

Full size image

Since the points were manually located, it was decided that all distances would be measured between points at least one unit cell apart instead of consecutive points, to minimize the influence that the misplacement of the points has on the results.

Figures 14 and 15 depict the summary of the results obtained, by comparing simulation and experimental images with no gradient and with gradient, respectively, showing the two sides for each geometry after compression.

Fig. 14
figure 14

Comparison between experimental and simulation results of gyroid-based structures with no gradient

Full size image
Fig. 15
figure 15

Comparison between experimental and simulation results of gyroid-based structures with different gradients

Full size image

Figure 16 presents the values of the average error for each geometry and for all geometries combined. The data shows that the method is, on average, below the 10% mark, which is a reference value for simulation error in engineering applications.

Fig.16
figure 16

Average error for each geometry

Full size image

Even though the data from Fig. 16 is necessary for evaluating the method, it is not sufficient for a complete evaluation. Data relative to the dispersion of the error values makes possible to infer more precisely about the consistency of the method. Figure 17 shows the quantity of error values, in each geometry and in all geometries combined, for the presented ranges. The quantities are also shown in a percentage relative to the total amount of measurements.

Fig. 17
figure 17

Quantity of error values that are within the four presented ranges, for each geometry and for all geometries combined

Full size image

Figure 17 shows that in the worst-case scenario for the tested geometries (No gradient), the method is predicting the deformation with enough accuracy since 68.8% of the measurements have sufficient precision. Moreover, the data also shows that in the large no gradient geometry, 97.2% of all the error values are below the 10% mark, and in two of the geometries, 100% of the error values are below that mark. Looking at the combined data for all geometries, 84.4% of the measurements have sufficient precision.

6 Conclusions

This work focused on developing a methodology capable of modelling complex 3D functionally graded auxetic structures simulating their mechanical behaviour when under load. The necessary steps to model successfully were described, along with ways to improve the models to better their performance. Three different gradient types were presented, and comparisons between variations of the same types of gradients were performed.

Regarding the simulation, refinements of the mesh and the influence of software limitations on the results were addressed, namely the limit of the h-refinements and the fact that the highest degree functions available were quadratic. Considerations regarding strain theories and structural instability were also presented such as the need to relativize the image measured distances and the restriction in lateral movement established in the experiments. The obtained results demonstrate that even for large deformations (> 10%), the simulations concur with the experimental results.

Based on the good agreement between computational and experimental results, the results show that the developed methodology can realistically perform in the intended way, meaning that the proposed objectives were accomplished for gyroid-based structures and, with right adaptation, can be used further for other auxetic structures.