Model of force interaction for stability prediction in turning of thin-walled cylindrical workpiece

Abstract

Turning of the thin-walled cylindrical workpiece is technologically highly demanding process due to the high flexibility of the workpiece. In this paper, a mathematical treatment of integral-based model of the cutting force which takes into account feed, cutting speed, depth of cut and tool nose radius leading to a model of tool-workpiece interaction is presented. The force interaction together with the compliant workpiece dynamics leads to a machining stability formulation. The effect of the aforementioned parameters on characteristic exponents is calculated and validated by comparison with experimentally identified exponents. One of the outputs with immediate practical value is identification of the process damping, which is in the studied case shown to be significantly higher than structural damping of the workpiece itself. This means that without loss of reliability in stability prediction the experimental modal analysis of a given workpiece may be omitted and workpiece’s dynamics may be described only by mass and stiffness matrices which can be easily and reliably obtained by a finite element analysis.

1 Introduction

Finishing highly compliant thin-walled workpieces is one of the most technologically demanding operations, particularly due to the high risk of regenerative vibration. Tuning the cutting process by testing different conditions is very costly for larger parts and the parts are often unique. Successful machining requires the use of one of the techniques to avoid chatter [30]. In practice, this is usually addressed either by reducing the dynamic compliance of the workpiece by additional reinforcement [12], damping with active or passive dampers, or by appropriate intervention in the force action of the process — either by disrupting the regenerative principle or by reducing the magnitude of the force response. In case of disturbance of the regenerative principle, either the use of gaps between lobes in high-speed machining (especially in milling [24]), speed variation in low-speed machining [2, 16, 20] or one of the newer methods such as regenerative compensation by active control [23], machining with ultrasonic vibration [33] or the method of time-varying longitudinal workpiece stiffness due to external force [6].

These approaches contribute to stabilizing the system only to a certain extent. Since the dynamic stiffness of the structure is typically very low, instability can be built up by a very small force response from the cutting process, which places higher demands on the accuracy of its modelling. The force response is determined by the physical effects caused by the vibration of the workpiece against the tool — either the usually dominant ones, such as chip thickness regeneration [37], or the less commonly considered ones, such as the change in tool-workpiece engagement at the circular tool tip [15] or the process damping associated with the velocity-dependent orientation of the cutting forces and the geometry of the cutting process [3]. Understanding the behavior of the cutting process as a function of process parameters and its mathematical model will allow reliable technological design of cutting conditions that can ensure the elimination of chatter.

The problem of turning thin-walled cylindrical parts is a challenging problem where relatively complex workpiece dynamics interact with the cutting process. One of the dominant themes in the literature is the focus on the dynamic behavior of the workpiece itself, where the cutting force itself is mostly modelled only schematically. Lorong [22] and Chanda [11] consider a stability problem involving the motion of the point force on the workpiece and a Kienzle model of the cutting force. Chanda’s follow-up papers [9, 10] focus on the link between the structural nonlinearity of the workpiece and the regenerative effect. Khasawneh and Otto [21, 31] consider the effect of interaction of eigenshapes on the cylinder and mutual indentation on stability in machining with circular inserts. Similarly, Yan [38] considers the effect of indentation on machining stability. Gerasimenko [17, 18] describes the workpiece using shell models and investigates the effect of gradual material removal on the evolution of eorkpiece compliance. The thin-walled workpiece deformation in radial direction in combination with damping due to rubbing between the tool flank and the machined workpiece surface was considered by Mehdi [25]).

Another group of authors focuses on the cutting process in relation to tool geometry. A frequent topic is the detailed calculation of forces at the tip radius [8, 21, 26, 34]; however, Eynian [15] considered the effect of changing the girdling during vibration on the stability of the process. He demonstrated this consideration computationally in the case of a Colwell model parameterizing the geometry of the cutting edge by the length of its chord and the chip area. One of the contributions of the paper we present is the representation of this effect in Montgomery’s [28] cutting force model based on the integration of the specific force along the cutting edge. In contrast to Colwell’s model, this model is more versatile and is able to capture the variable local geometry of the cutting edge in the engagement.

Another phenomenon considered when modelling the interaction of structure and cutting process is the modelling of process damping. This damping is modelled in several ways. One focuses on the damping associated with the contact between the tool back and the workpiece [1, 3, 7, 29]. This problem is fundamentally nonlinear and is not considered in this study as it would play a role in studying the onset of chatter in tools that are only worn, where even small vibrations could result in contact between the tool back and the workpiece. The second approach, which complements or modifies the statically identified models, is an approach aiming at capturing the rapid harmonic change of the tool-workpiece interfacial position by identifying the cutting coefficients during forced tool vibration [14, 35]. Another approach, which is also used in this paper, follows the research of Das and Tobias [13], who showed that even static models can be used to model process damping by more accurately considering the geometry of the cut with respect to the instantaneous direction of the cutting speed including vibration. This approach was applied, for example, by Molnar and Bachrathy [4, 27] to cylindrical milling. One of the main complications of this approach, which this paper aims to address, is the integration of damping contributions for geometrically complex cutting edges where the local face and blade inclination angles change gradually. A related issue is the correct representation of this geometry using practically available data from catalogues on the orientation of the tool in space, which has been addressed in a separate paper by, for example, Campocasso [8].

The article is structured as follows. In the first part, the problem of the force response of the cutting process to vibration is formulated considering chip regeneration, vibration-dependent girding and process damping. In the second part, the coupling of the cutting process to the structure is formulated leading to the formulation of the stability problem. In the third part, an experimental verification of the theory is carried out on the machining of a dimensional thin-walled cylindrical workpiece. This case study has shown interesting findings that can simplify the stability calculation on similar problems. It is well established that most of the structural damping comes from effects at the interfaces. In the case of workpieces with low structural damping, the interface between the tool and the workpiece in the cut can be the region where the vibration energy is dissipated dominantly. This has the advantage of eliminating the need to experimentally identify damping, which is a major source of uncertainty in the prediction of structural dynamics by the finite element method.

2 Tool-workpiece force interaction

In this section, a model of tool-workpiece interaction for a thin-walled cylinder during turning will be presented. The theory is based on Eynian [15] and Otto’s [32] approach, where the total force between tool and workpiece is constructed taking into account the effect of position disturbance (current and delayed by a revolution) and speed. From this total force, the Jacobian of the cutting force with respect to the deflection and deflection speed is obtained by linearization. The main difference to previous work is the application of the Eynian approach derived for the simple Colwell model to a force model based on the integration of the elementary contributions of the cutting force along the cutting edge. These force contributions are defined using empirical models of the cutting force per unit chip width, which is probably the most commonly used approach in machining stability analysis today. The basic idea of the approach is that the calculation of the cutting edge engagement takes into account not the nominal position of the tool relative to the workpiece, but the position including deviations from the nominal path. Similarly, the model of the forces on the cutting edge element is calculated from empirical model of the local geometric parameters of the cutting process (rake angle, inclination angle). The parameters are defined relative to a coordinate system defined by physical parameters — the tangency of the cutting edge and the direction of its instantaneous velocity (including the relative vibration velocity of the tool and workpiece). This coordinate system is based on real quantities, not nominal quantities, and is therefore more physically justifiable. The force acting on the cutting edge element, which results from the empirical model, is also expressed relative to this coordinate system. Although it might appear that the vibrations are small and therefore negligible, this is not true, because what is important from the stability formulation viewpoint is not the magnitude of the force, but its change with the variation of the relative trajectory of the tool and workpiece, which can be formally expressed in the Jacobians of the cutting force, with respect to the displacement, the relative displacement per revolution, and the velocity of the displacement.

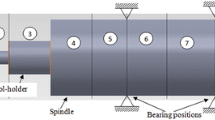
At first the geometry of the cutting process is described. The cutting edge consists of a round part of radius $\rho$ and a straight part with cutting edge setting angle $\kappa _0$. The geometry of the cutting edge and the contact is in Fig. 1. It should be noted that as the forces are calculated from local increments, the tool-workpiece contact must also be identified locally. It means that the local rake angle $\alpha$ and inclination angle $\lambda$ need to be calculated from orientation of the insert rake plane (defined technologically by side and end rake angled for the holder and insert combination) with respect to cutting edge and tool-workpiece relative velocity, as shown in the figure. The cylindrical workpiece is machined along its Z-axis as shown in Fig. 2 showing the simplified geometry of the workpiece and detail on its contact with the cutting insert. The contact is specified by the depth of cut $a_p$ and feed per revolution $f_e$.

Fig. 1

Local geometry and specific cutting force coordinate system on the cutting edge. The gray color gives an idea how the model components are affected by workpiece vibration

Fig. 2

Scheme of the cutting edge in contact with workpiece and local coordinate system at the contact

The force interaction on the tool-workpiece contact is based on empirical models of specific force per chip width and in detail described in the following section.

2.1 Specific cutting force model

The Montgomery and Altintas model [28] is based on integration of elementary forces acting on infinitesimal element of the cutting edge of width ${\text {d}}\!{w}$

$$\mathrm d{\boldsymbol F}_{\mathrm c}=\mathbf f\left(\mathrm h,\;\mathrm\lambda,\;\mathrm\alpha,\;\mathrm v\right)\mathrm{dw}$$

(1)

where $\mathbf {f}$ is an empirical model of specific force per unit chip width w dependent on the undeformed chip thickness h, the local rake angle $\alpha$, the inclination angle $\lambda$ and the cutting velocity magnitude v. The components of the model force are related to tangential $\mathbf {t}$, normal $\mathbf {n}$ and binormal (often also called axial) $\mathbf {b}$ local coordinate system basis vectors.

There is an issue of choice of the specific force model. Various models were considered from the comprehensive list of models that was summarized by Bachrathy [5]. In the current study the empirical model of specific force per unit chip width is assumed in a form

$$\begin{aligned} \begin{aligned} \mathbf {f}(h,\lambda ,\alpha ,v)=&\mathbf {K}_0(\lambda ,\alpha ,v)+\mathbf {K}_1(\lambda ,\alpha ,v)h+\mathbf {K}_2(\lambda ,\alpha ,v)h^2\\ \mathbf {K}_i(\lambda ,\alpha ,v)=&\mathbf {K}_{i0}+\mathbf {K}_{i1}\alpha + \mathbf {K}_{i2}\lambda +\mathbf {K}_{i3}\lambda ^2+\mathbf {K}_{i4} v \end{aligned} \end{aligned}$$

(2)

Experimentally identified coefficients for the presented case are in (30), Appendix A1. Example of the force behavior with respect to a few chosen parameters is shown in Fig. 3.

Fig. 3

Example of the experimentally identified cutting force model and its dependence on the rake angle, the inclination angle and the chip thickness

The reasons for the particular choice were the following. Firstly, the model can be easily identified by linear regression. Secondly, the model needs to be extrapolated to zero chip thickness on the round tool nose of the insert. The higher order polynomial models often lead to wrong and erroneous estimations when extrapolated.

The cutting force dependence on other parameters than undeformed chip thickness was more significant than expected. Although the studied case is rather extreme with respect to process damping, which plays unusually important role in the stability prediction, it casts some doubt on the often seen approach to sideline the process damping as a less important effect than the regeneration. It also highlights the issue of possible lack of accuracy of typical empirical cutting force models which often oversight other process parameters than undeformed chip thickness.

2.2 Total cutting force and its gradient

The total (dynamic) cutting force acting on the contact is calculated as an integral along the cutting edge parametrized by s

$$\begin{aligned} \mathbf {F}&=\int _{s_1}^{s_2} \mathbf {T}\, \mathbf {f}(h,\lambda ,\alpha ,v)\frac{dw}{ds}\, {\text {d}}\!{s} \end{aligned}$$

(3)

where the integration limits ${s_1},{s_2}$ are enter and exit angles for the cutting edge, see Fig. 2, $\mathbf {f}$ is a specific force per unit chip width, w is chip width. The engagement defining integral limits are determined by constraints following from tool and workpiece shape and requirement of positive chip thickness. Generally, almost all parameters of the integral are affected by a variation of the tool-workpiece relative motion. The machining stability calculation requires linearization (gradients) of the dynamic cutting force with respect to small perturbation of the tool-workpiece trajectory parameters (actual and delayed displacement and vibration velocity) as described by Otto [32]. For practical reasons the gradients are expressed in the way used by Otto which linearizes the force with respect to relative displacement between two consecutive revolutions $\Delta (t)=u(t)-u(t-\tau )$.

Tool-workpiece displacement (including its history) affects

• the undeformed chip thickness via the regenerative effect

• the tool-workpiece engagement represented here by the integration limits.

The tool-workpiece relative velocity affects

• the transformation matrix $\mathbf {T}$ between global coordinate system and local coordinate system of the empirical force model on the cutting edge,

• local geometry (rake angle $\alpha$ and inclination angles $\lambda$) on the tool-workpiece contact, because the coordinate system of the specific cutting force is derived from actual cutting velocity, i.e., including vibration velocity ($\mathbf {v}_0+ \dot{x}$), and the geometry is measured with respect to this coordinate system.

The elementary chip width is defined as a projection of the elementary cutting edge length into a plane perpendicular to the actual velocity, so generally it also depends on actual tool/workpiece relative velocity, but it is not difficult to show that the effect is negligible unless the inclination angle is high.

Due to dominant compliance in the radial direction only the radial component is considered $F_r= \mathbf {e}_r\cdot \mathbf {F}$ to simplify the calculations, but the approach can be applied in a similar way to geometrically more complicated case. The main obstacle is dominantly in the definition of the process geometry parameters (tool-workpiece engagement, rake and inclination angles) with respect to the dynamical perturbations rather than in the linearization itself.

The dependence of the scalar parameters ($s_1, s_2, h,\lambda ,\alpha$) and the transformation matrix $\mathbf {T}$ on tool-workpiece relative motion will be calculated in the following paragraphs. It will be shown in the next part that the lower integration limit $s_1$ and the chip thickness h depend on the relative position of the tool and workpiece after one spindle revolution period $\Delta =u(t)-u(t-\tau )$ and the upper limit $s_2$ depends on instantaneous relative position of the tool and workpiece u(t).

2.2.1 Vibration-dependent undeformed chip thickness

First of all, the most usual source of instability is the undeformed chip thickness regeneration. The formula for the dynamic chip thickness in the case of considered tool geometry is a standard one (e.g., [15])

$$\begin{aligned} h=f_e \sin \kappa (s)+\Delta \cos \kappa (s) \end{aligned}$$

(4)

where $\kappa (s)$ depends on the cutting edge parameter s as follows

$$\begin{aligned} \kappa (s)={\left\{ \begin{array}{ll} s &{}a_p\le \rho (1-\cos \kappa _0), \\ \kappa _0 &{} a_p>\rho (1-\cos \kappa _0). \end{array}\right. } \end{aligned}$$

(5)

The parameters are shown in Fig. 2.

2.2.2 Vibration-dependent tool engagement

The second effect treated here is the dependence of the tool-workpiece engagement on the tool-workpiece displacement, which is in the formula 3 represented by the integration limits. These are rarely considered in dynamic interaction models. Their effect on stability is calculated from conditions on cutting edge engagement. The condition that determines engagement on the tool tip is zero chip thickness. The upper limit is based on the intersection of the cutting edge and the outer surface of the workpiece. The limits may be approximated for small displacement as

$$\begin{aligned} s_1&\approx -\arctan \frac{ u (t)-u(t-\tau )}{f_e}\end{aligned}$$

(6)

$$s_2\approx {\left\{ \begin{array}{ll} \arccos \left( 1-\frac{a_p-u}{\rho }\right) &{}a_p\le \rho (1-\cos \kappa _0) \\ \kappa +\arctan \left( \frac{a_p+u-\rho (1-\cos \kappa ))}{\rho \sin \kappa }\right) &{} a_p>\rho (1-\cos \kappa _0) \end{array}\right. }$$

(7)

For the tool engagement scheme see Figs. 2 and 5 and the derivation of the both formulas is in Appendix A2. Figure 5 shows schematically how the displacement in the actual and previous groove affects the cutting edge engagement. The change in cutting force with the change in the relative position of the tool and workpiece (including the history of the path) is important for stability. The greatest effect on the change in force is the change in blade length in the engagement at point s1 (red dashed curve). Since the chip thickness is close to zero around this point, the change in force will only occur for the non-zero edge component of the force given by the coefficients $\mathbf {K}_0$. As can be seen from the formulae, the smaller the displacement and the larger the tool radius, the greater the extension of the cutting edge in the engagement at the same relative deflection (u-ut). Around the $s_2$ limit, the chip thickness is non-zero, but typically this term is negligible (see factor $A_s$ in comparison to $A_r$ in Table 2) and, moreover, is proportional only to the actual workpiece displacement u and not to the regenerative workpiece displacement $(u-u_\tau )$ which is behind the feedback that destabilizes the cutting process.

2.2.3 Vibration-dependent transformation matrix and tool geometry

The matrix ${\mathbf {T}}$ that determines relation between global coordinate system and local coordinate system n the cutting edge is affected by vibration velocity. The geometric parameters of the process (rake and inclination angles) are dependent on the coordinate system so they are also affected by vibration velocity (Fig. 4).

Fig. 4

Sketch of the cutting edge parameter limits depending on the relative tool-workpiece vibration

The basis vectors of the local coordinate system on the cutting edge are tangential $\varvec{t}$ — determined by local velocity of the cutting edge element $\varvec{v}$, normal $\varvec{n}$ defined by normal to surface generated by moving cutting edge, i.e., normal to both actual velocity and tangent to the curve $\gamma$ describing the cutting edge, and their orthogonal complement — binormal vector $\varvec{b}$. The transformation matrix between local a global coordinate system is composed of the basis vectors, so we have

$$\begin{aligned} \mathbf {t}&=\frac{\mathbf {v}}{\Vert \mathbf {v}\Vert } \end{aligned}$$

(8)

$$\begin{aligned} \mathbf {n}&=\frac{\mathbf {v}\times \varvec{\gamma }'}{\Vert \varvec{v}\times \varvec{\gamma }'\Vert }\end{aligned}$$

(9)

$$\begin{aligned} \mathbf {b}&=\mathbf {t}\times \mathbf {n} \end{aligned}$$

(10)

The difference with the conventional approach is that here we consider both the nominal tool to workpiece velocity $\varvec{v}_0$ and its change related to the relative deformation rate $\Delta \mathbf {v}$ of the tool and workpiece, see Fig. 1. The local basis vectors can be formally split to nominal local basis $\mathbf {t}_0,\, \varvec{n}_0,\,\varvec{b}_0$ based on the nominal cutting velocity $\varvec{v}_0$ and its perturbation. The transformation matrix is

$$\begin{aligned} {\mathbf {T}}&=\begin{bmatrix} \varvec{t}&\varvec{n}&\varvec{b} \end{bmatrix}. \end{aligned}$$

(11)

In the studied case the nominal velocity is dominantly in circumferential direction, velocity perturbation due to cylinder vibration is dominantly in radial direction and the curve $\varvec{\gamma }(s)$ describing the cutting edge are

$$\begin{aligned} \varvec{v}_0&=v_0 \varvec{e}_\varphi \end{aligned}$$

(12)

$$\begin{aligned} \Delta v&=\dot{u} \varvec{e}_r\end{aligned}$$

(13)

$$\begin{aligned} \varvec{\gamma }(s)&= \rho \sin s\, \varvec{e}_r+ \rho \cos s\, \varvec{e}_z . \end{aligned}$$

(14)

Due to dominant compliance in radial direction, the dependence of the transformation matrix can be reduced to its projection to radial direction. The transformation from model coordinate system to the radial direction can therefore be defined as

$$\begin{aligned} \varvec{e}_r^T{\mathbf {T}}&= \begin{pmatrix} \frac{\dot{u}}{v_0},&\cos s,&\sin s \end{pmatrix} \end{aligned}$$

(15)

Tool geometry on a tool-workpiece contact is described by an inclination angle and (normal) rake angle, which are related to a coordinate system determined by actual velocity (including velocity of the vibrations), see Figs. 1 and 5. The normal rake angle is an angle between normal vector $\varvec{n}$, which defines the machined surface normal, and the plane defining the rake face.

$$\begin{aligned} \alpha _n(s)&=\lambda _0\cos \varphi + \alpha _0\sin \varphi -\frac{\dot{u}}{v_0} \cos s \end{aligned}$$

(16)

Fig. 5

Global coordinate system of the workpiece and local coordinate system on the cutting edge. GAMO is orthogonal rake angle and LAMS inclination angle of the cutting insert which are used for local rake and inclination angle determination, as shown in the detail. The local basis vectors $\varvec{t},\, \varvec{n},\, \varvec{b}$ are defined by actual tool-workpiece velocity, i.e., including velocity of workpiece vibrations

Similarly the inclination angle is defined as an angle between the cutting edge and vector $\varvec{b}$.

$$\begin{aligned} \lambda (s)&=\lambda _0\sin s + \alpha _0\cos s+\frac{\dot{u}}{v_0}\sin s \end{aligned}$$

(17)

The chip width w is defined as

$$\begin{aligned} \frac{\partial {w}}{\partial {s}}={\left\{ \begin{array}{ll} \rho &{} s\le \kappa _0 \\ \frac{\rho }{\cos ^2 (s-\kappa _0)} &{} s>\kappa _0 \end{array}\right. } \end{aligned}$$

(18)

After describing the dynamic behavior of the cutting force parameters the cutting force gradients can be calculated in order to obtain the linearized dynamical cutting force which is crucial for the following stability analysis.

2.3 Cutting process stiffness and damping

The previous formulas presented the dependence of the cutting force on the parameters which allowed the cutting force linearization. The following formula summarizes the cutting force dependence on the displacement and actual velocity variations

$$\begin{aligned} F_r(u,\Delta ,\dot{u})&=\int \limits _{s_1(\Delta )}^{s_2(u)} \mathbf {e}_r\cdot \mathbf {T}(\dot{u})\, \mathbf {f}(h(\Delta ),\lambda (\dot{u}),\alpha (\dot{u}))\frac{dw}{ds}\, {\text {d}}\!{s}\ . \end{aligned}$$

(19)

The linearization of the previous expression for dynamic cutting force with respect to the perturbations $u,\Delta ,\dot{u}$ can be formally written

$$\begin{aligned} F_r(u,\Delta ,\dot{u})\approx F_{r0}-A_r \Delta -A_s u-A_d\dot{u} \end{aligned}$$

(20)

where the unperturbed force and respective gradients are denoted

$$\begin{aligned} F_{r0}&= F_r|_{u\equiv 0}\end{aligned}$$

(21)

$$\begin{aligned} A_r&=-\left. \frac{\partial { F_r}}{\partial {\Delta }}\right| _{u\equiv 0}\end{aligned}$$

(22)

$$\begin{aligned} A_s&= -\left. \frac{\partial { F_r}}{\partial { u}}\right| _{u\equiv 0}\end{aligned}$$

(23)

$$\begin{aligned} A_d&=-\left. \frac{\partial { F_r}}{\partial {\dot{u}}}\right| _{u\equiv 0} \end{aligned}$$

(24)

The gradient $A_r$ with respect to relative displacement between two consecutive revolutions (often also called a directional matrix) can be physically interpreted as a regenerative process stiffness, and cutting force gradient with respect to the actual velocity is interpreted as a process damping.

Most of the derivatives are straightforward except for the calculation of the derivatives related to the displacement-dependent integration limits. However, the Leibniz integral formula overcomes the problem for most of the specific force models. The derivative of the integral splits it into term that is based on derivative of an integrand and terms containing derivatives of the integral limits. The formula and resulting terms related to displacement-dependent engagement are in Appendix A2.

The exception from the usual models is the Kienzle model due to the non-existent derivative at zero undeformed chip thickness $h(s_0)=0$. Solution to the problem will be briefly discussed in the section below.

The calculated process stiffness of process parameters described in the case study below is shown in Fig. 6. The surface plots demonstrate the dependence on various process parameters. There is near linear increase of the stiffness with the nose radius for given feed and depth of cut, sharp increase of stiffness near zero feed, and insensitivity of the stiffness to the depth of cut once the depth of cut is higher than tool nose radius.

Fig. 6

Process stiffness dependence on feed, depth of cut and insert nose radius

The process damping dependence on the parameters is shown in Fig. 7. Both depth of cut and feed increase the damping. This can be explained by the friction force acting on the rake face, which is projected into the radial direction when the workpiece is vibrating. The nose radius on the other hand affects the damping only marginally.

Fig. 7

Process damping dependence on feed, depth of cut and insert nose radius

3 Dynamics of tool-workpiece interaction

The section is focused on formulation of workpiece dynamics loaded by the dynamic cutting force. The effect of material removal will be considered only stepwise — slow change of dynamic properties due to material removal during one test is neglected.

The dynamic behavior of the system under a dynamic load acting on the workpiece is mathematically described in the time domain by a set of delay differential equations originating from FE discretization of the workpiece. This leads to

$$\begin{aligned} {\mathbf {M}}\ddot{\varvec{y}}&+{\mathbf {C}}\dot{\varvec{y}}+\mathbf {K}\mathbf {y}=\varvec{P} \varvec{F} (t, \mathbf {P}^T\varvec{y},\mathbf {P}^T\varvec{\dot{y}},\mathbf {P}^T\varvec{y}_\tau ,) \end{aligned}$$

(25)

where $\varvec{y}$ is a $3n\times 1$ vector of displacements at workpiece nodes (n is number of nodes). $\mathbf {M}$ is a mass matrix, $\mathbf {C}$ is a damping matrix and $\mathbf {K}$ is a stiffness matrix, $\mathbf {F}$ is $3\times 1$ cutting force vector. $\mathbf {P}$ is a $3n\times 3$ matrix of $3\times 3$ zero matrices and $3\times 3$ identity matrix which specify nodal position of the force load on the workpiece. To simplify the problem, we apply the modal reduction $\mathbf {y}=\varvec{\Psi } \mathbf {q}$, which leads to

$$\begin{aligned} \begin{aligned} \ddot{\mathbf {q}}&+2\varvec{\zeta }\varvec{\Omega }\dot{\mathbf {y}}+\varvec{\Omega }^2\mathbf {y}\\&=\varvec{\Psi }^T\mathbf {P} \mathbf {F} (t, \mathbf {P}^T\varvec{\Psi } \mathbf {q},\mathbf {P}^T\varvec{\Psi }\mathbf {\dot{q}},\mathbf {P}^T\varvec{\Psi } \mathbf {q}_\tau ) \end{aligned} \end{aligned}$$

(26)

where $\varvec{\Omega }$ is a diagonal matrix of angular eigenfrequencies and $\varvec{\Psi }$ are corresponding mass/normalized eigenvectors of the workpiece (contain values of all workpiece DOFs at all nodes). The general solution $\mathbf {q}$ can be divided into static part $\mathbf {q}_s$, which is not important for stability analysis as it affects depth of cut only negligibly, and dynamic part $\mathbf {q}_d$ which affects the system feedback. Since it is excited at one point in the grid and also depends on the deflection at the same point, it is not necessary to work with the whole matrix of eigenvectors. This is represented by the matrix $\mathbf {P}$. It is therefore sufficient to select the column of the matrix corresponding to the position of contact between the tool and the workpiece. In addition, we select only the radial DOF from this column, since the workpiece is dominantly compliant in this direction. In this respect, we follow the stability analysis of flexible workpiece turning described in a paper by Stepan [36]. The column vector $\varvec{\psi }$ denotes radial DOF of eigenvectors at node with Z-coordinate corresponding to tool-workpiece contact. Circumferential position of the node is not important due to mode-degeneracy described in the section 4.1.

After application of the force gradients (see Eq. 22) and transformation to Laplace domain we get

$$\begin{aligned} \begin{aligned} (\eta ^2 \mathbf {I}+2\eta \varvec{\zeta }\varvec{\Omega }+\varvec{\Omega ^2}) \mathbf {V}(\eta )=\\ - \left( A_r (1-\exp (-\eta \tau ))+A_s+\eta A_d\right) \varvec{\psi }\varvec{\psi }^T \mathbf {V}(\eta ) \end{aligned} \end{aligned}$$

(27)

where $\mathbf {V}$ is a Laplace transform of a vector of displacements in modal coordinates. The formula is typical problem for machining stability with process damping. When the lobe diagrams are investigated the constraint of zero real part of the Laplace parameter $\eta =\lambda _c+i \omega _c$. The real part $\lambda _c$ of the parameter called the characteristic exponent determines whether and how fast the vibration grow. This parameter is used in the experimental validation below to distinguish between stable and unstable machining.

This generalized eigenvalue problem is transformed into numerically more convenient form and solved by Newton-based method developed by Harrar [19] for eigenvalues $\eta$ and eigenvectors $\mathbf {V}$

$$\begin{aligned} \begin{aligned} \begin{pmatrix} 0&{}- \varvec{\Omega }\\ \varvec{\Omega }+(A_r+A_s)\varvec{\Omega }^{-1}\varvec{\psi }\varvec{\psi }^T &{} 2\varvec{\zeta }\varvec{\Omega }\mathbf {V} + A_d\varvec{\Omega }^{-1}\varvec{\psi }\varvec{\psi }^T\end{pmatrix}\mathbf {V}=\\ \begin{pmatrix} \eta \mathbf {I}&{}0\\ -A_r\exp (-\eta \tau ))\varvec{\Omega }^{-1}\varvec{\psi }\varvec{\psi }^T &{} \eta \mathbf {I}\end{pmatrix} \mathbf {V} \end{aligned} \end{aligned}$$

(28)

Short description of the method is in Appendix A4. This dependence of the predicted characteristic exponents on the process stiffness and damping based on the workpiece model presented in the case study is in Fig. 8. The graph shows in detail expected behavior that in order to have stable machining high process damping and low process stiffness is desired. However, how to achieve low process stiffness and high damping is more complex problem. As was shown in the previous section in Figs. 6 and 7 the stiffness and damping depend on process geometry and technological parameters in a complex way so the goal is not easy to be achieved.

Fig. 8

Dependence of the characteristic exponent for a given workpiece dynamics on process stiffness and damping. The red surface corresponds to positive exponent which signalizes unstable machining

4 Experimental validation

Validation of the theory described above is done on BASICTURN 2000 C2 by TOSHULIN. Effect of various technological parameters on machining process stability was tested with aim to validate the presented approach to process stiffness and damping calculation.

The machined workpiece is a thin-walled cylinder of height 767 mm, outer diameter 1210 mm and wall thickness 15 mm made of structural steel C45. The operation was vertical turning, see scheme Fig. 2.

Experimental modal analysis of the workpiece was done before the tests and repeated after each ca 20 mm z-direction shift of the tool-workpiece contact. The aim of these measurements was to determine the initial workpiece compliance and its change due to material removal. A uni-axial accelerometer Bruel& Kjaer 4517 and a modal hammer Bruel& Kjaer 8206-003 were used for this purpose. The experimental setup and area of machining on the workpiece are shown in Figs. 9, 10. Three inserts with different radii (0.4 mm, 0.8 mm, 1.6 mm) of the nose were used, see Fig. 11.

The identified eigenfrequencies and modal damping values are in Table 1. Notice the low values of modal damping.

Table 1 Modal properties of the workpiece identified by modal testing

The vibration of the workpiece during 36 machining tests was measured by a Doppler laser vibrometer placed in front of the workpiece (at a distance of 3.8 m from the workpiece). The vibrometer measured oscillation speed of the top of the workpiece in the Y direction both for workpiece dynamic compliance measurement and during turning tests. If chatter occurred, control system integrated spindle speed variation was turned on and machining was stabilized. This action ensured the following test was not affected by a force variation due to chatter marks.

Fig. 9

The photo (a) shows range of the machining experiment on the workpiece bounded by dashed red lines and Z parameter defining position of the test relatively to the upper edge of the workpiece. The second photo (b) shows a detail of the machined surface (b)

Fig. 10

The experimental setup. (a) The first machining test, (b) the vibrometer with detail of accelerometer and laser spot during experimental modal analysis of the workpiece

Fig. 11

The inserts with different tool nose radii: (a) 0.4 mm — insert DNMG 15 06 04-MF 2015, (b) 0.8 mm — insert DNMG 15 06 08R-K 4325, (c) 1.6 mm — insert CNMG 19 06 16-QM 4325

The machining tests were done in a range from ca 70 mm to 200 mm from the upper edge of the cylinder. The distance from the upper edge, process parameters and tool geometries of the tests are in Table 2.

Table 2 Measured and theoretical data

4.1 Workpiece simulation model

Based on the drawing documentation a FE was created using SW Ansys. The model consists of Solid-Shell type elements, which are suitable for modelling thin-walled structures. The model has about $4.10^6$ degrees of freedom (Fig. 12a). Cross-section of the workpiece is in Fig. 12b. The effect of material removal is modelled via thin shell layer. The boundary conditions reflect the four supports and four jaws fixing the workpiece, see photo in Fig. 9a and scheme in Fig. 13. A vector of eigenvalues and matrix of eigenvectors was obtained by modal analysis of the FE model. The model was supplemented by experimentally identified modal damping values and frequency response functions (FRFs) were generated for comparison with the experimentally identified FRFs.

Fig. 12

FE mesh (a) and workpiece cross-section (b)

Fig. 13

A scheme FE boundary conditions of the clamped supported workpiece (a view from below)

The modal damping of the FE model was tuned using measured FRFs at the state before machining, see comparison at position M01 in Fig. 16. The dominant shapes can be seen in Fig. 14. Most of the shown eigenshapes belong to degenerate eigenfrequencies (or more precisely there are couples of modes with frequency difference below 1 Hz) due to workpiece axial symmetry, see 15. This degeneracy mathematically justifies naive expectation that direct FRFs in radial direction are practically the same around the circumference no matter where the modal testing is done (Fig. 16).

Fig. 14

Comparison of FEM simulated and measured FRF at the first machining position. Due to workpiece symmetry there are degenerate modes — there are couples of nearly identical eigenfrequencies and corresponding eigenshapes

Fig. 15

Example of (almost) degenerate modes: due to the symmetry of the workpiece, the set of eigenfrequencies contains pairs of very close eigenfrequencies. The actual shapes corresponding to these frequencies are very similar — similar shape but rotated, see (a), (b) for eigenfrequencies at ca 350 Hz and (a), (b) for ca 681 Hz

Fig. 16

Comparison of measured and FEA simulated FRF of the workpiece before the machining 10 mm below the upper edge of the cylinder

4.2 Machining stability experimental testing

The comparison of the experimentally identified stability and theoretically predicted one is in Table 2. The variable Z denotes axial distance of the machining test starting position from the upper edge of the workpiece. As amount of parameters considered in the analysis complicates graphically simple comparison of measured and calculated stability, the measured test stability is presented in Fig. 17 with respect to theoretically predicted process stiffness and damping. Stability limit based on dynamical properties of the workpiece in the middle of the experiment is presented as a reference. The figure gives idea how the process damping and stiffness affect the machining stability. The workpiece vibration measurements M1-M36 are presented in Fig. 18.

Fig. 17

Comparison of predicted and measured characteristic exponent (stability) as a function of predicted process stiffness and damping. The green field denotes theoretical stable and orange unstable conditions based on dynamical properties identified in the middle of the material removal during the experiment. The position of measurement points in the parametric space is also based on the model. The color of the points denotes experimentally identified stability red-unstable, green-stable

The cutting process described is not typical in the degree to which process damping is significantly more important than structural damping, but it does show that it should be considered in stability formulation and that it can be used in some types of machining to significantly improve machining efficiency or to simplify process stability modelling.

Fig. 18

Measured vibration velocity. Each graph title refers to the measurements listed in Table 2 and Fig. 16

Both experiment and theory show that low nose radius and high feed lead to more stable conditions (see Tab. 2) but these conditions are not suitable due to higher surface roughness — the average surface roughness is given by $Ra=\frac{f_e^2}{24\rho }$. The formula shows that roughness is more sensitive to feed than to radius and hence for given surface roughness it is preferable to use higher feed than lower radius. It is preferable to increase damping by using as low cutting speed as other technological constraints allow and as high depth of cut as possible. In the studied process, it follows from the formulas that if the depth of cut is higher than the tool nose radius, any further increase of the depth of cut stabilizes the process — the source of the destabilizing process stiffness is only at the insert nose but increase of the engagement of the straight part of the insert contributes to process damping.

One of the practical results is a demonstration of insignificance of modal damping for stability in the studied process. Due to the very low values of the modal damping the process damping plays crucial role in the machining stability.

The dominance of process damping over structural damping when machining thin-walled parts by a suitable cutting process can be advantageously used to predict the limits of machining stability. It is then sufficient to know the structural eigenfrequencies and undamped eigenvectors of the part, which are easily obtained using a standard FEM model.

5 Conclusion

The paper presents a detailed approach to the stability calculation in longitudinal turning of thin-walled workpieces for a method of calculating the force interaction of the cutting process based on the integration of the specific cutting force along the cutting edge, which allows to take into account the local behavior of the cutting geometry along the cutting edge. The novelty of the approach lies in two main points. Firstly, the effect of the change in tool-workpiece engagement due to vibration on the stiffness of the process was derived for cutting edge integration-based cutting force model. This effect was described by Eynian using a coarser Colwell model, but without the possibility of generalization to other models. Secondly, the process damping with respect to the orientation of cutting forces and the change in cutting geometry at the cutting edge due to the instantaneous mutual velocity of tool and workpiece at the cutting point was derived for the cutting force model. This approach allowed to determine the dependence of process stiffness and process damping on process parameters such as cutting speed, tool tip radius, feed and depth of cut. This, combined with a model of the workpiece dynamics, leads to the prediction of stable conditions.

An important observation arising from the application of the process model is that for a longitudinal workpiece finishing operation with low structural damping, process damping plays crucial role. In such a case, the dynamic behavior of the process-loaded workpiece can be reliably modelled using an undamped FE model without the need to perform time-consuming experimental modal analysis to obtain workpiece damping values. The proposed model and approach for stability assessment in thin-walled parts machining using process stiffness and damping was successfully validated on the case of vertical turning. A good agreement between the experimentally determined process states (stable/unstable) and the prediction using the developed model was shown. This makes the model very well suited for reliable design control and optimization of chatter-free cutting condition design using undamped FEA part models.

Appendix

The appendix contains a more detailed description of the calculations and additional information on the force models.

1.1 A1. Specific force model

The specific force model was built on measurements with different undeformed chip thickness ( 0.05 mm, 0.1 mm, 0.15 mm, 0.3 mm) cutting speed (80 m.min$^{-1}$,130 m.min$^{-1}$, 180 m.min$^{-1}$) rake angles (0$^\circ$, 4$^\circ$,8$^\circ$) and inclination angles (0$^\circ$, 25$^\circ$,45$^\circ$). Linear regression was used to fit measured data on turning with model (2). The identified specific cutting force model per chip width is given by the following formula

$$\begin{aligned} \begin{aligned} \mathrm {f}_t&=17-20\alpha +11\lambda ^2+3(v-2)+\\&+h(2230-1710\alpha +70\lambda ^2+20(v-2))+ \\&+h^2(-1370+1960\alpha -190\lambda ^2-410(v-2)) \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned} \begin{aligned} \mathrm {f}_n&=11-23\alpha +14\lambda ^2+9(v-2)+\\&+ h(1540-3230\alpha -850\lambda ^2+60(v-2))+\\&+h^2(-2200+4330\alpha +1010\lambda ^2-790(v-2))\\ \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned} \begin{aligned} \mathrm {f}_b&=h\lambda (+1070 -870\alpha +20(v-2))+\\&+h^2\lambda (-170 -180\alpha +110(v-2)) \end{aligned} \end{aligned}$$

(31)

where the dimensions are for simplicity omitted. The dimension of specific force per chip width is $\text {N} \text {mm}^{-1}$, both input angles $\alpha$ and $\lambda$ need to be in radians, cutting velocity v in $\text {m}\, \text {s}^{-1}$, undeformed chip thickness in mm.

1.2 A2. Integral limits for cutting force calculation

The calculation of the integral limits is based on conditions on engagement which state that the chip thickness must be positive and distance of the cutting edge element from the tool tip must be lower than the depth of cut, i.e., the lower limit condition is

$$\begin{aligned} 0&=f_e \sin s_1+(u (t)-u(t-\tau ))\cos s_1 \end{aligned}$$

(32)

which has the following solution

$$\begin{aligned} s_1&=-\arctan \frac{ u (t)-u(t-\tau )}{f_e} \end{aligned}$$

(33)

It is assumed that only the previous grove created by the circular tool tip is intersected by the cutting edge in actual position as the vibrations are assumed to be infinitesimally small.

In the calculation of the upper limit two cases must be distinguished due to piecewise character of the cutting edge

$$\begin{aligned} \begin{aligned} a_p+u&=\rho (1-\cos s_2)\ \\&\text {if}\ a_p\le \rho (1-\cos \kappa _0)\\ \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned} \begin{aligned} a_p+u&=\rho (1-\cos \kappa _0)+\rho \sin \kappa _0 \tan (s_2-\kappa _0)\\&\text {if}\ a_p>\rho (1-\cos \kappa _0) \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned} s_2&={\left\{ \begin{array}{ll} \arccos \left( 1-\frac{a_p-u}{\rho }\right) &{}a_p\le \rho (1-\cos \kappa _0) \\ \kappa +\arctan \left( \frac{a_p+u-\rho (1-\cos \kappa ))}{\rho \sin \kappa }\right) &{} a_p>\rho (1-\cos \kappa _0) \end{array}\right. } \end{aligned}$$

(36)

The first integration limit is inversely proportional to feed, which is a small quantity and thus this may have significant effect on stability. On the other hand it is not difficult to see that the effect of the second limit is negligible in comparison to other terms unless $a_p\ll \rho$ when

$$\begin{aligned} s_2\approx \sqrt{\frac{2a_p}{\rho }}+ \frac{u}{\sqrt{2\rho a_p}} \end{aligned}$$

(37)

The effect of the displacement-dependent integral limits on process stiffness (cutting force gradient with respect to displacement) is calculated using Leibniz integral rule.

1.3 A3. Linearization coefficients

The terms resulting from the linearization are as follows

$$\begin{aligned} \begin{aligned} F_{r0}&= \int _{s_{10}}^{s_{20}} \mathbf {e}_r\cdot \mathbf {T}(s)\, \mathbf {f}(s)\frac{dw}{ds}\, {\text {d}}\!{s} \\ A_r&=\int _{s_{10}}^{s_{20}} \mathbf {e}_r\cdot \mathbf {T}(s)\, \frac{\partial {\mathbf {f}}}{\partial {h}}\frac{\partial {h}}{\partial {\Delta }}\frac{dw}{ds}\, {\text {d}}\!{s}- \nonumber \\&-\mathbf {e}_r\cdot \mathbf {T}(s_{10})\, \mathbf {f}(s_{10})\frac{dw}{ds}(s_{10})\frac{\partial {s_1}}{\partial {\Delta }}\\ A_s&=\mathbf {e}_r\cdot \mathbf {T}(s_{20})\, \mathbf {f}(s_{20})\frac{dw}{ds}(s_{20})\frac{\partial {s_2}}{\partial {u}}\\ A_d&=\int _{s_{10}}^{s_{20}} \frac{\partial {(\mathbf {e}_r\cdot \mathbf {T}(s))}}{\partial {\dot{u}}}\, \frac{\partial {\mathbf {f}(s)}}{\partial {h}}\frac{\partial {h(s)}}{\partial {\Delta }}\frac{dw}{ds}(s)\, {\text {d}}\!{s}+\nonumber \\&+\int _{s_{10}}^{s_{20}} \mathbf {e}_r\cdot \mathbf {T}(s)\, \frac{\partial {\mathbf {f}(s)}}{\partial {\alpha }}\frac{\partial {\alpha (s)}}{\partial {\dot{u}}}\frac{dw}{ds}(s)\, {\text {d}}\!{s}+\nonumber \\&+\int _{s_{10}}^{s_{20}} \mathbf {e}_r\cdot \mathbf {T}(s)\, \frac{\partial {\mathbf {f}(s)}}{\partial {\lambda }}\frac{\partial {\lambda (s)}}{\partial {\dot{u}}}\frac{dw}{ds}(s)\, {\text {d}}\!{s}, \end{aligned} \end{aligned}$$

(38)

where the zero index denotes parameters without the perturbation of the tool-workpiece relative position and velocity, i.e., $\Delta =0,\ u=0,\ \dot{u}=0$

1.4 A4. Newton-based method for GEVP

In the Newton-based approach, the generalized eigenvalue problem $\mathbf{M}(\mu )\mathbf{u}(\mu )$ is replaced by more general problem

$$\begin{aligned} \mathbf{M} (\mu ) \mathbf{u} (\mu ) & =\beta (\mu ) \mathbf{B} \mathbf{x} \\ {\mathbf{s}^{*}} {\mathbf{B}} \mathbf{u} (\mu ) & = \kappa \end{aligned}$$

(39)

As $\mu$ approaches an eigenvalue, $\mathrm{\mathbf{M}} (\mu )$ becomes singular and the scaling condition (39) can be satisfied only if $\beta (\mu )\rightarrow 0$ as $\mu$ approaches an eigenvalue. The vectors $\mathbf {s}^*$ and $\mathbf {x}$ are chosen adaptively, the matrix $\mathbf{B}$ on the right side $\mathbf{B}=-\frac{d \mathbf{M}}{d\mu }$. The Newton-based iteration is based on the following formulas

$$\begin{aligned} \begin{aligned} \mu +\frac{\mathbf {s}^* \mathbf {B}\mathbf {x}}{\mathbf {s}^* \mathbf {x}}\rightarrow \mu \\ \frac{\mathbf {M}^{-1}{\mathbf {B}\mathbf {x}}}{\Vert {\mathbf {M}}^{-1} \mathrm {\mathbf {B}}\mathbf {x}\Vert }\rightarrow \mathbf {x}\\ \frac{\mathrm {\mathbf {M}}^{-T}\mathrm {\mathbf {B}}^T\mathbf {s}}{\Vert \mathrm {\mathbf {M}}^{-T} \mathrm {\mathbf {B}}^T\mathbf {s}\Vert }\rightarrow \mathbf {s} \end{aligned} \end{aligned}$$

(40)

which are applied until the norm $||\mathrm {\mathbf {M}}(\mu )\mathbf {u}(\mu )||$ is smaller than given threshold.