Skip to main content
SpringerLink
Log in

A novel approach to attain tooth flanks with variable pressure and helical angles utilizing the same cutter in the CNC gear skiving process

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

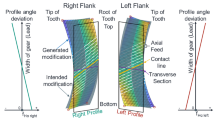
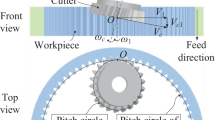
Abstract

To save manufacturing costs and enhance design flexibility in gear skiving, a dual closed loop, including inner and outer closed loops, is proposed to generate skived gear tooth flanks with different pressure angles and helix angles using the same cutter. The skiving cutter is firstly generated based on the suitable form of the corrected rack, which is defined according to the target tooth surface. The additional motions considering the motion limits of an electronic gearbox for the machining axis are added in the form of polynomials. The inner closed loop based on the Levenberg–Marquardt algorithm is developed to attain the coefficients of polynomials in fitting the skived gear tooth flanks to the target surface. After completing a cycle of the inner closed loop, the skived gear’s pressure/helix angle is changed in the outer closed loop to renew the target surface, and then a new cycle of the inner closed loop is restarted. The suitable range of the skived gear’s pressure/helix angle is satisfied when the dual closed loop is fully ended. The effectiveness and practicality of the proposed method are verified by the presented numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28

Similar content being viewed by others

Data availability

All data generated or analyzed during this study are included in the manuscript.

Code availability

Not applicable.

Abbreviations

\(a\) :

Polynomial coefficient

\(C\) :

Machine axes

\({\mathbf{k}}\) :

Unit normal vector in z-direction

\({\mathbf{L}}\) :

Upper-left 3 × 3 submatrix of \({\mathbf{M}}\)

\(m\) :

Gear module

\({\mathbf{M}}\) :

Transformation matrix

\({\mathbf{n}}\) :

Unit normal vector

\({\mathbf{r}}\) :

Position vector

\(s\) :

Grinding stock of work gear

\(S\) :

Coordinate system

\(t\) :

A half of gear pitch

\({\mathbf{t}}\) :

Tangent vector

\(u\) :

Profile parameter of normal rack

\(v\) :

Longitudinal parameter of inclined rack

\(\alpha\) :

Reference pressure angle

\(\beta\) :

Reference helix angle

\(\gamma\) :

Rake angle of skiving cutter

\(\eta\) :

Damping parameter

\(\lambda\) :

Relief angle of skiving cutter

\(\tau\) :

Side clearance angle

\(\varphi\) :

Rotation angle of cutter

\(b1\) :

Rotation axis of spindle assembly

\(c\) :

Skiving cutter

\(c1\) :

Rotation axis of cutter

\(c2\) :

Rotation axis of work gear

\(f\) :

Pitch point

\(n\) :

Normal section

\(oc\) :

Operation parameter of cutter

\(ow\) :

Operation parameter of work gear

\(p\) :

Reference pitch circle

References

  1. Seibicke F, Müller H (2013) Good things need some time. Gear Solutions 74–80

  2. Kreschel J (2012) Gleason power skiving: technology and basics. Gleason Company Publication

  3. Kobialka C (2013) Contemporary gear pre-machining solutions. Gear. Solutions 11(4):42–49

    Google Scholar 

  4. Radzevich SP (2010) Gear cutting tools fundamentals of design and computation. CRC Press, pp 705–712

  5. Litvin FL, Fuentes A (2004) Gear geometry and applied theory. Cambridge University Press

    Book  Google Scholar 

  6. Chen XC, Li J, Lou BC (2013) A study on the design of error-free spur slice cutter. Int J Adv Manuf Technol 68(1):727–738. https://doi.org/10.1007/s00170−013-4794-3

    Article  Google Scholar 

  7. Chen XC, Li J, Lou BC (2014) A study on the grinding of the major flank face of error-free spur slice cutter. Int J Adv Manuf Technol 72(1):425–438. https://doi.org/10.1007/s00170−014-5626-9

    Article  Google Scholar 

  8. Guo E, Hong R, Huang X, Fang C (2014) Research on the design of skiving tool for machining involute gears. J Mech Sci Technol 28(12):5107–5115. https://doi.org/10.1007/s12206-014-1133-z

    Article  Google Scholar 

  9. Guo E, Hong R, Huang X, Fang C (2015) A correction method for power skiving of cylindrical gears lead modification. J Mech Sci Technol 29(10):4379–4386. https://doi.org/10.1007/s12206-015-0936-x

    Article  Google Scholar 

  10. Guo Z, Mao SM, Li XE, Ren ZY (2016) Research on the theoretical tooth profile errors of gears machined by skiving. Mech Mach Theory 97:1–11. https://doi.org/10.1016/j.mechmachtheory.2015.11.001

    Article  Google Scholar 

  11. Moriwaki I, Osafune T, Nakamura M, Funamoto M, Uriu K, Murakami T, Nagata E, Kurita N, Tachikawa TYK (2017) Cutting tool parameters of cylindrical skiving cutter with sharpening angle for internal gears. J Mech Des 139(3):033301. https://doi.org/10.1115/1.4035432

    Article  Google Scholar 

  12. Shih YP, Li YJ (2018) A novel method for producing a conical skiving tool with error-free flank faces for internal gear manufacture. J Mech Des 140(4). https://doi.org/10.1115/1.4038567

    Article  Google Scholar 

  13. Tsai CY (2021) Power-skiving tool design method for interference-free involute internal gear cutting. Mech Mach Theory 164:1–19. https://doi.org/10.1016/j.mechmachtheory.2021.104396

    Article  Google Scholar 

  14. Shih YP, Li YJ, Lin YC, Tsao HY (2022) A novel cylindrical skiving tool with error-free flank faces for internal circular splines. Mech Mach Theory 170:1–19. https://doi.org/10.1016/j.mechmachtheory.2021.104662

    Article  Google Scholar 

  15. Luu TT, Wu YR (2022) A novel correction method to attain even grinding allowance in CNC gear skiving process. Mech Mach Theory 171:1–19. https://doi.org/10.1016/j.mechmachtheory.2022.104771

    Article  Google Scholar 

  16. Guo E, Hong R, Huang X, Fang C (2016) A novel power skiving method using the common shaper cutter. Int J Adv Manuf Technol 83(1):157–165. https://doi.org/10.1007/s00170−015-7559-3

    Article  Google Scholar 

  17. Zheng F, Zhang M, Zhang W, Guo X (2018) Research on the tooth modification in gear skiving. J Mech Des 140(8). https://doi.org/10.1115/1.4040268

    Article  Google Scholar 

  18. Fong ZH (2000) Mathematical model of universal hypoid generator with supplemental kinematic flank correction motions. J Mech Des 122:136–142. https://doi.org/10.1115/1.533552

    Article  Google Scholar 

  19. Shih YP, Fong ZH (2007) Flank modification methodology for face-hobbing hypoid gears based on ease-off topography. J Mech Des 129(12):1294–1302. https://doi.org/10.1115/1.2779889

    Article  Google Scholar 

  20. Shih YP, Chen SD (2012) A flank correction methodology for a five-axis CNC gear profile grinding machine. Mech Mach Theory 47:31–45. https://doi.org/10.1016/j.mechmachtheory.2011.08.009

    Article  Google Scholar 

  21. Tran VQ, Wu YR (2020) A novel method for closed-loop topology modification of helical gears using internal-meshing gear honing. Mech Mach Theory 145:1–15. https://doi.org/10.1016/j.mechmachtheory.2019.103691

    Article  Google Scholar 

  22. Shen YB, Liu X, Li DY, Li ZP (2018) A method for grinding face gear of double crowned tooth geometry on a multi-axis CNC machine. Mech Mach Theory 121:460–474. https://doi.org/10.1016/j.mechmachtheory.2017.11.007

    Article  Google Scholar 

  23. Jiang J, Fang ZD (2015) High-order tooth flank correction for a helical gear on a six-axis CNC hob machine. Mech Mach Theory 91:227–237. https://doi.org/10.1016/j.mechmachtheory.2015.04.012

    Article  Google Scholar 

  24. Boa P, Gonzalez H, Callejab A, Lacalle LNL, Barton M (2020) 5-axis double-flank CNC machining of spiral bevel gears via custom-shaped milling tools– Part I: modeling and simulation. Precis Eng 62:204–212. https://doi.org/10.1016/j.precisioneng.2019.11.015

    Article  Google Scholar 

  25. Escudero GG, Bob P, Gonzalez H, Callejaa A, Barton M, Lacalle LNL (2021) 5-axis double-flank CNC machining of spiral bevel gears via custom-shaped tools—Part II: physical validations and experiments. Int J Adv Manuf Technol 119:1647–1658. https://doi.org/10.21203/rs.3.rs-442857/v1

    Article  Google Scholar 

  26. Bizzarria M, Barto M (2021) Manufacturing of screw rotors via 5-axis double-flank CNC machining. Comput Aided Des 132:1–14. https://doi.org/10.1016/j.cagd.2022.102082

    Article  MathSciNet  Google Scholar 

  27. Rajain K, Sliusarenko O, Bizzarri M, Barton M (2022) Curve-guided 5-axis CNC flank milling of free-form surfaces using custom-shaped tools. Computer Aided Geometric Design 94:1–12. https://doi.org/10.1016/j.cad.2020.102960

    Article  MathSciNet  MATH  Google Scholar 

  28. Scherbarth S (2016) Tooth Cutter and method for cutting the teeth of gear tooth elements. US Patent 9352406B2

  29. Uriu K, Osafune T, Murakami T, Nakamura M, Iba D, Funamoto M, Moriwaki I (2018) Study on design of taper shaped skiving cutters for internal gears. Trans JSME (in Japanese) 84(861):17–00536. https://doi.org/10.1299/transjsme.17-00156

    Article  Google Scholar 

  30. Burney SM, Jilani TA, Ardil C (2004) Levenberg-Marquardt algorithm for Karachi Stock Exchange share rates forecasting. World Acad Sci Eng Technol 3:171–176

    Google Scholar 

  31. Lourakis MIA (2005) A brief description of the Levenberg–Marquardt algorithm implemented by levmar. Found Res Technol 1–6

    Google Scholar 

  32. German Institute for Standardization (1978) Tolerances for cylindrical gear teeth. DIN 3962-1

Download references

Acknowledgements

The authors are grateful to the Ministry of Science and Technology in Taiwan for its financial support under project number MOST 108-2628-E-008-007-MY3.

Funding

This research was supported by the Ministry of Science and Technology in Taiwan, project number MOST 108–2628-E-008–007-MY3.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Central University, No. 300, Zhongda Rd., Zhongli District, Taoyuan City, Taiwan, 320317, Republic of China

    Trong-Thuan Luu & Yu-Ren Wu

  2. School of Mechanical Engineering, Hanoi University of Science and Technology, 01 Dai Co Viet Rd., Hanoi City, Vietnam

    Trong-Thuan Luu

Authors
  1. Trong-Thuan Luu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu-Ren Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

TTL constructed the research design, accomplished the cutting simulation, and composed the manuscript, whereas YRW earned the funding and directed the research implementation. All authors worked concurrently to proofread and structure the submission.

Corresponding author

Correspondence to Yu-Ren Wu.

Ethics declarations

Ethics approval

Ethical standards are in place (no human participants or animals involved).

Consent to participate

Not applicable.

Consent for publication

All involved authors have read and consented to publish the manuscript.

Competing interests

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

In this paper, the corrected normal rack consists of seven segments, as shown in Fig. 29, proposed by Luu and Wu [15]. Each segment is presented in explicit equations in Table 8.

Fig. 29
figure 29

Definition of corrected rack (Rm1) [15]

Full size image
Table 8 Explicit equations of segments of the corrected normal rack [15]
Full size table

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luu, TT., Wu, YR. A novel approach to attain tooth flanks with variable pressure and helical angles utilizing the same cutter in the CNC gear skiving process. Int J Adv Manuf Technol 123, 875–902 (2022). https://doi.org/10.1007/s00170-022-10220-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-022-10220-4

Keywords

Search

Navigation