1 Introduction

The process of single point incremental sheet forming (SPIF) has been developed over a number of decades for the deformation of sheet materials using flexible methods for complicated prototypes. High geometric accuracy and surface quality have been achieved with respect to low-strength metal alloys. For instance, Dabwan et al. [1] has applied SPIF on AA1050-H14 aluminum alloy at room temperature which revealed excellent geometric accuracy and surface quality. However, the study commented that the step trainsition region indicated highly deformed region which increased the geometric inaccuracy and waviness error. Shrivastava and Tandon [2] has investigated the microstructure of AA1050 under room temperature SPIF and proposed that the grain refinement during the process increased the straining behaviour thus induced springback. Ambrogio et al. [3] has investigated SPIF on AZ31 magnesium alloy which revealed high performance in increase of formability and geometric accuracy, however, the risk of fracture was increased according the formability. Trzepiecinski et al. [4] have investigated room temperature SPIF on EN-2024-T3 and EN AW-7075-T6 aluminium alloys sheets. The results revealed that the efficient application of lubricant and reduction of step size significantly improved the surface quality. Room temperature SPIF indicated that high geometric accuracy and surface quality can be achieved for low-temperature materials as the maintenance of modest forming force and efficient lubrication. However, heat sources must be integrated for high-strength materials to reduce the forming force such as steel or titanium.

Sakhtemanian et al. [5] have studied pure titanium alloy SPIF using ultrasonic vibration at temperatures of up to 250 °C in order to synthesise a high-quality product. However, pronounced friction wear can be observed on the formed surface with detectable springback behaviour. Cheng et al. [6] and investigated the deformation behaviour and material flow during the SPIF process. The results commented that the dynamic effects from the ultrasonic vibration induced a noticeable reduction of the forming force and a significant increase of wear on deforming surface. The similar study by Li et al. [7] found that the inducing temperature for the high-temperature alloys should be maintained as constant to produce stable plastic deformation to the sheet materials where cannot be fulfilled using this mechanism. These limitations were overcome by integrating heat sources into the SPIF system in order to provide regional or localised heating to the workpiece, thus increasing ductility and assisting deformation. The electrical current system was integrated prior to carrying out the process on the Ti-6Al-4V sheets.

Honarpisheh et al. [8] have developed an electricity-assisted SPIF to support a flow flux through Ti-6Al-4V sheets with a temperature range of 400 to 500 °C. This enables the system to deform the Ti-6Al-4V sheets to various wall angles and designed shapes. Ao et al. [9] have used the same heat source to increase the deformation height of Ti-6Al-4V sheets by 417.9%. However, the high current flux caused severe electric sparks between the tool and the workpiece. The resulting dissipation of lubricant results in pronounced adherence of lubricant on surface which significantly affected the surface quality. Further, Chang et al. [10] have studied the stress state and corresponding forming load and proposed analytical models to predict forming force and relative components for ISF processes which provides a new method to calculate the contact area and through-thickness stress to reduce the error contribution from the friction fluctuation at contact area. However, the effects from lubricant dissipation should be reduced to further improve the surface quality for heat-assisted SIPF processes.

Göttmann et al. [11] applied a localised heating method during the SPIF process by integrating a laser heating system that, in advance of the tool, enabled a laser beam to generate a temperature of 500 °C to deform Ti-6Al-4V sheets. Springback was minimised owing to the localised nature of the heat and movement with the tool, factors which offered tight temperature control. Although the laser heating system improved geometric accuracy, the concentrated temperature exerted powerful effects, causing burn-offs on the outer surface of the workpiece. In addition, the high-cost laser heating system and external safety measurements meant that the process was complicated to set up.

To reduce the pronounced burns-off on the deforming surface for heat-assisted SPIF. Ambrogio et al. [12] developed an induction heating SPIF system which provided localised heating to the Ti-6Al-4V workpiece. This created a magnetic field from the eddy current between the heating coil and workpiece; the temperature was generated from the centre mass of the sheet metal to the edges. However, it was impossible to maintain the constant temperature during the high feed rate of the SPIF process. Additionally, tool movement caused uneven heating support which increased springback.

To further improve the geometric accuracy and surface quality, Li et al. [13] developed a high-frequency induction heating SPIF system which provided localised heating to deform Ti-6Al-4V sheets with a ball-roller tool, thus reducing friction at the tool-contact interface. The ball-roller tool design was proposed by Iseki and Naganawa [14] following tool path optimisation investigations. It was applied in relation to the electric heating SPIF of Ti-6Al-4V sheets by Liu et al. [15]. It was validated that this process led to the production of more optimal surface quality than conventional tools. Comparison with a common induction heater demonstrated that high-frequency induction heating could provide rapid eddy current transfer which was able to accelerate heat generation and to maintain a constant temperature. Ortiz et al. [16] observed that the microstructure evolution indicated a pronounced dynamic recrystallisation (DRX) at temperature of 700 °C, which successfully increased the deforming behaviour and reduced the forming force. This geometric accuracy was superior to that attained at lower temperatures. However, the rise in temperature also increased lubricant dissipation; this lubrication anomaly impacted surface quality. In order to minimise this effect, a ball-roller tool was designed which reduced the contact area between the surface and the tool, thus efficiently enhancing surface quality.

Lubricant is another factor affecting the surface quality in heat-assisted SPIF. Formisano et al. [17] have investigated lubricant application and its effects on surface roughness during the SPIF process on titanium alloys, observing that sustainable support of low viscosity lubricant is a key factor in enhancing lubricating functionality. Oleksik et al. [18] agreed the statement and suggested that localised heating is more efficient to maintain stability of lubricant. Further, Li et al. [19] have proposed a sustainable support of liquid MoS2 lubricant able to reduce the phenomenon of lubricant adherence on the surface during the induction heating SPIF of Ti-6Al-4V sheets up to 700 °C.

It can be observed from previous research that the application of a heat source is an effective method by which to deform Ti-6Al-4V sheets during the SPIF process. The temperature support for electric current and laser heating SPIF is normally maintained between 400 °C and 600 °C; induction heating is able to provide a constant localised temperature of up to 700 °C. Owing to the incremental movement of the SPIF process, it is not possible to sustain a constant temperature during further increases. However, it is essential to improve temperature conditions during the heating-assisted SPIF process of Ti-6Al-4V sheets so as to improve their formability, wear, corrosion and temperature oxidation resistance further.

Zhang et al. [20]investigated the mechanisms underlying deformation and fracture for Ti-6Al-4V alloys under different heat treatments and noted that excellent hardening and deforming behaviour can be achieved at the beta-transus temperature (980 °C). Further, Singh et al. [21] suggested that the increase of cooling rate may increase the hardening effects. This was principally ascribed to the maintenance of constant temperature and rapid cooling rate on surface which increased the volume of \(\alpha\)′-martensite and grain refinement within the microstructure. This proved that the above beta-transus temperature SPIF on Ti-6Al-4V could achieve favourable effects in straining behaviour to enhance the formability. However, the temperature must be controlled as a constant support with a sustainable cooling rate during the process to prevent the thermal expansion of tool and sheet metals to affect the geometric and surface quality.

In recent years, machine learning has been integrated into the SPIF system in order to predict temperature and springback behaviours. Jiang et al. [22] investigated the temperature prediction for an electric current SPIF process using an artificial neural network (ANN) framework. The model was trained using the temperature outputs from the finite element model (FEM) and validated with experimental data. The findings were useful for the prediction of parameters, such as temperature distribution and forming force, and facilitated estimation of microstructural evolution during the process. Wang et al. [23] developed an online adaptive shape predictive model for the purposes of predicting the forming geometry within each incremental step. The model was incorporated into a coupled constrained control algorithm so as to minimise geometric error and to optimise the potential step which could provide an accurate tool path to improve geometric accuracy.

It can be noticed from the above literature that there are issues in the field of heat-assisted SPIF processing that yet need to be addressed. These include uneven temperature distribution, thermal expansion-induced springback, unpredictable DRX and phase transition-induced straining behaviours. These factors significantly affect the geometric accuracy, surface quality as well as structure integrity. The aim of this study was to develop an induction heating SPIF system in order to deform Ti-6Al-4V sheets at a temperature above and in the region of beta-transus, and to apply a machine learning method in order to optimise tool path generation. The initial training experiments were designed with identical experimental parameters. Following their completion, the obtained geometric coordinates, temperature and forming force data were input into the machine learning system to develop an optimised tool path. The cooling lubricant and optimal tool path were then applied in order to validate the optimal results. Forming force, geometric accuracy, and surface roughness of the initial and machine learning optimisation samples were assessed using scanning electron microscopy (SEM) and electron backscatter diffraction in order to observe the mechanical behaviours and to document the relevant outputs, thus providing data on microstructural evolution.

Materials and set-up.

1.1 Sheet metals and lubricants

The workpieces used in the study were standard Ti-6Al-4V alloy thin sheets, 150 mm × 150 mm in dimension, and with a thickness of 1 mm. The chemical composition is presented in Table 1.

Table 1 Chemical composition of Ti-6Al-4V (wt.%)
Full size table

The cooling lubricant system in this study was following the research by Li et al. [19] on investigation of lubricants and ball-roller tool in the induction heating SPIF process of Ti-6Al-4V sheets. The authors proposed a lubricant system which enabled an apposite lubricating performance for temperatures of up to 700 °C. Since the target temperature in this study was in the region of the beta-transus temperature, the identical lubricant may not be able to provide sufficient functionality. A number of adjustments were therefore made in order to enhance lubrication performance. A layer of MoS2 paste lubricant was applied generally to the workpiece. According to the supplier’s information, this lubricant consisted of grease containing MoS2 particles, and offered a lubricative function in temperatures of up to 650 °C. In order to enhance the function at the beta-transus temperature, a liquid lubricant was designed by mixing MoS2 particles into high-temperature lubricating oil.

The MoS2 powder used in this study had a purity of 98.5% with a mean particle size of 1.5 μm. The lubricant oil could provide short-term lubrication in temperatures to a maximum of 600 \(^\circ{\rm C}\). The mixing process was in accordance with Diabb et al. [24]; 2% of MoS2 powder was shear-dissolved into lubricant oil for parameters of 600 rpm for 60 min. This percentage was chosen in keeping with the study on SPIF lubricants by Hussain et al. [25]; the authors proposed that a high percentage of MoS2 powder may decrease lubricating oil viscosity and result in adherence to the tool during the SPIF process. The liquid lubricant was designed in order to provide continuous support to the ball-roller tool through the cooling system, and to facilitate provision of enduring tool lubrication as shown in Fig. 1.

Fig. 1
figure 1

Schematic of the lubricating system

Full size image

1.2 Tool design

Tarín et al. [26] investigated alpha–beta transformation in Ti-6Al-4V alloys, and concluded that the beta-transus temperature was approximately 980 °C for 4 wt.% of vanadium. For the thin Ti-6Al-4V sheets used in this study, the beta-transus temperature could be estimated to be between 960 °C and 970 °C. In a localised heating-assisted SPIF process, deformation is based on the synchronisation of the constant temperature supply and the tool’s movement. Since the temperature was close to the beta-transus, a nickel ball-roller was selected for this study in order to improve the tool’s operational temperature.

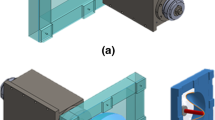
The ball-roller tool design in the SPIF process was first introduced by Iseki and Naganawa [14], who evaluated the function of a ball-roller with respect to reducing the friction area and optimising geometric accuracy. Liu et al. [15] improved the ball-roller design and innovated a cooling system within the tool so as to allow water to reduce the tool’s thermal expansion during the electric heating SPIF process. As shown in Fig. 2, there are two water valves on the tool which control the liquid lubricant inlet and outlet; a baffle plug has been designed to separate the liquid flow. The ball is 5 mm in diameter and made of IN 625 nickel alloy, which has a service temperature of 980 °C. The ball-roller is attached to the main tool body; lubricant balls are interposed between the ball-roller and the steel net of the cooling channel. The lubricant balls are also composed of IN 625 nickel alloy which has a diameter of 1 mm. The steel net, which has a grid length of 0.5 mm, keeps the lubricant balls in the lubricating slots. The purpose of the lubricant balls is to prevent any extrusion between the ball-roller and the slot wall. In the course of the process, potent thermal expansion may result in the strong adherence of the ball-roller to the tool wall and affect the rotation. Additionally, the lubricating balls can enhance liquid lubricant flow to the ball-roller.

Fig. 2
figure 2

Tool design: left, scheme draft of the tool design; right, the produced tool

Full size image

1.3 Experimental set-up

The induction heating SPIF system is illustrated in Fig. 3. The induction heater had a maximum power of 6.6 kW with a frequency that could be adjusted from 600 to 900 kHz. The heat was induced by an eddy current which could penetrate the workpiece to form an electromagnetic field between the workpiece and the heating coil. Since the eddy current was strengthened towards the material’s centre of mass, heat generation arose from within the workpiece to its surface. The heating coil diameter was optimised for heat generation, being designed with a dimension of 5 mm and three turns in an analogous manner to the ball-roller tool. The supplier’s information stated that the induction heater provided accurate and constant heating with an error of less than 2% for a minimum period of 20 h.

Fig. 3
figure 3

Induction heating SPIF system set-up

Full size image

Synchronised movement of the induction heater with the tool was achieved by designing a support fixture to connect these two components. A 50 kN load cell was mounted on the top of the tool so that, during the experiment, the reaction load from the tool could be measured. The temperature on the superior surface of the workpiece could be quantified using an infrared thermo-couple, with a temperature range of 400 to 1200 ℃ pointing the contact area.

A water tank was filled with 10 L liquid lubricant in order to provide an ongoing lubricating function to the tool. The flow rate could be controlled by a submersible pump, which operated within the range 1 to 50 L/h; this was connected to the inlet cooling valve. Another water tank included a submersible pump with similar parameters which was connected to the cooling channel’s outlet valve. During the experiment, the flow rate would be controlled according to the tool path’s locations in order to provide sufficient liquid lubricant to reduce ball-roller tool thermal expansion and friction.

1.4 Forming shape

The final shape took the form of a truncated cone with a main diameter, height, and wall angle of 100 mm, 30 mm, and 45°, respectively (Fig. 4a). MATLAB was used to form the tool path and to generate a G-code coordinates output file for application by the computer numerical control (CNC) machine. The tool path points are illustrated in Fig. 4b. It can be observed that the step tool path maintained the peak percentage of position coordinates which results in more tool movements. Such behaviour may increase the temperature variance at these positions and influence the geometric accuracy of the forming shape. Thus, the RBF networks were used to optimise the step tool path for superior geometric accuracy.

Fig. 4
figure 4

Designated forming shape: a dimensions; b tool path CNC forming points

Full size image

It is important to note that a contour tool path was applied in this study; a clear mark of a step tool path would be evident within the forming shape thus potentiating the likelihood of geometric, temperature and forming force instabilities. These factors can be enhanced by RBF network optimisation; the tool path is applicable for a wide range of SPIF processes. A helical tool path has the potential to diminish such behaviours as there is no step tool path. However, Malhotra et al. [27] stated that the algorithm is only limited to the axisymmetric movements. Behera et al. [28] further commented that the forming shape of helical tool path is not fully completed at the beginning and ending stage, and the output geometry is designed by wall angle not step size. Behera et al. [29] and Han et al. [30] suggested that a contour tool path provided a more complete forming shape as the step size can be defined in the CNC setting, whereas the helical tool path is only applicable to axisymmetric geometry and for the provision of high surface quality. The latter is complex to generate since the algorithm is specific for each forming shape and the process can only be controlled by the ramp angle in the CNC settings.

2 Methodology

2.1 Application of radial basis function networks and design of experiments

The main objective of machine learning is to improve geometric accuracy in complicated experimental environments. Thus, the main data to study include the tool path coordinates and the affected factors, i.e. temperature and forming force. As shown in Fig. 4b, it can be observed that the tool step path demonstrated the most position points. Owing to the rapid heating support from the high-frequency induction heater, the temperature variance for this particular path was higher than the rest of the tool path and thus increased the springback during the experiment. Thus, the coordinates associated with the corresponding temperature and forming force on this path could be collected for training by the machine learning algorithm.

In order to apply the RBF optimisation effectively, the experiments were designed in 3 phases, i.e. as initial, first RBF optimisation and second RBF optimisation sets, respectively. Each set consisted of 5 experiments with the same conditions. The machine learning studied the geometric coordinate output as the main data and related the behaviours to temperature and forming force in order to predict an optimised tool path and to improve geometric accuracy.

A RBF network was selected due to its universal approximation and rapid learning speed so that multiple factors could be evaluated and undergo analysis. RBF can be defined as a type of feedforward ANN network which has three layers (Fig. 5). The input layer consists of input data, such as geometric coordinates, temperature and forming force, on the corresponding tool path points. The hidden layer comprises a series of RBF non-linear activation units which facilitate study of the input layer. The final output is in the form of workout activation implemented in Gaussian functions. As illustrated in Fig. 5, the example analysis data set includes inputs from \({x}_{1}\) to \({x}_{n}\), together with hidden layer RBF calculating units from \({w}_{1}\) to \({w}_{n}\) and an output from \({y}_{1}\) to \({y}_{n}\). A RBF training model has numerous nodes in the hidden layer; the training is terminated when the calculation error meets the requirement of the desired volume or when a training iteration has been completed.

Fig. 5
figure 5

Example of RBF network

Full size image

The output of the ith radial basis activation function, \({\phi }_{i}\), in the hidden layer of the network can be calculated using Eq. (1) based on the Euclidean distance between the input pattern, \(x,\) and the centre, \(i\), where \(\parallel \cdot \parallel\) denotes the Euclidean distance between \(x\) and \({c}_{i}\), and \({c}_{j}\) and \({\sigma }_{j}\) are the centre and width of the hidden neuron, \(j\), respectively.

$${\phi }_{i}\left(x\right)=\mathrm{exp}\left(-\frac{{\Vert x-{c}_{i}\Vert }^{2}}{2{\sigma }_{j}^{2}}\right)$$
(1)

The output of the node, \(k,\) of the output layer of the network can then be calculated utilising Eq. (2):

$${y}_{k}=\sum_{j=1}^{n} {\omega }_{jk}{\phi }_{j}(x)$$
(2)

The majority of classical approaches deployed in the literature for training RBFs are performed in two stages. In the first stage, the centres and widths are determined using, for example, an unsupervised clustering algorithm, whilst in the second stage, the connection weights between the hidden and output layers are determined in such a way that the error criterion, e.g. the root mean squared error (RMSE), is minimised throughout the data set.

2.2 Accuracy analysis

Since the input in this study was based on the tool step path, the variant could be defined by the X and Z coordinates; the Y coordinates could be neglected. Thus, the model could be simplified to a 2-dimensional (2D) RBF paradigm which significantly reduced the calculation time in the RBF network. In this study, 130 tool path geometric coordinates with corresponding temperature and forming force data were considered as neurons in the RBF study. The output layer is 1 (tool path coordinates) and 3 input layers (tool path coordinates, temperature, forming force). A total of 12,000 input–output pairs were generated to respond the inputs. Please refer to the support document for the detailed calculation and explanation.

Fiorentino et al. [31] commented that the network training can be defined as a feedback loop which facilitates the study of the process parameters and Dittrich et al. [32] further classified machine learning of tool path generation in CNC processes which proposed that the model was contrasted against the experimental data; where five statistical parameters were compared, including the RMSE, the squared multiple correlation coefficient (\({R}^{2}\)), the bias or distortion (\(\beta\)), the Wilmott index (\({I}_{\mathrm{w}}\)) proposed by Willmott [33] to measure the prediction error for RMSE, and the error function (\(\varepsilon\)) proposed by Haller [34] to measure the standard normal cumulative probability.

$$RMSE={\left[\sum_{i=1}^{N} \frac{ {\left(\frac{{X}_{{c}_{i}}-{X}_{{m}_{i}}}{{X}_{{m}_{i}}}\right)}^{2}}{N}\right]}^{1/2}$$
(3)
$${R}^{2}=\frac{{\left(\sum_{i=1}^{N} \left({X}_{{m}_{i}}-{\overline{X} }_{m}\right)\left({X}_{{c}_{i}}-{\overline{X} }_{c}\right)\right)}^{2}}{\sum_{i=1}^{N} {\left({X}_{{m}_{i}}-{\overline{X} }_{m}\right)}^{2}\sum_{i=1}^{N} {\left({X}_{{c}_{i}}-{\overline{X} }_{c}\right)}^{2}}$$
(4)
$$\beta =\frac{\sum_{i=1}^{N} \left(\frac{{X}_{{c}_{i}}}{{X}_{{m}_{i}}}\right)}{N}$$
(5)
$${I}_{w}=1-\frac{\sum_{i=1}^{N} {\left({X}_{{c}_{i}}-{\overline{X} }_{{m}_{i}}\right)}^{2}}{\sum_{i=1}^{N} {\left(\left|{X}_{{c}_{i}}-{\overline{X} }_{m}\right|+\left|{X}_{{m}_{i}}-{\overline{X} }_{m}\right|\right)}^{2}}$$
(6)
$$\varepsilon ={\left[\frac{\sum_{i=1}^{N} {\left({X}_{{c}_{i}}-{\overline{X} }_{{m}_{i}}\right)}^{2}}{\sum_{i=1}^{N} {X}_{{m}_{i}}^{2}}\right]}^{1/2}$$
(7)

In the above equations, \(N\) represents the number of data in each group, and \({X}_{c}\) and \({X}_{m}\) indicate predicted and measured experimental data, e.g. geometric coordinates, temperature and forming force, respectively. The training was terminated when the values of \({R}^{2}\) and \({I}_{\mathrm{w}}\) were equivalent or lower than \(1.0,\) and \(\varepsilon\) was reduced to 2%, a strategy which revealed enhanced agreement with the results. The learning basis was recommended by Sharif Ahmadian [35], who investigated the use of RBF networks in numerical modelling; these were validated to give a precise output for 2D accuracy analysis.

2.3 Particle swarm algorithm

In this study, the platform, TensorFlow [36] was applied in order to run the RBF network training. The input layer of the RBF network consisted of the points on the step tool path, together with the corresponding data points including geometric coordinates, temperature and forming force from the experimental measurements. The output layer is the optimised tool which was predicted on the corresponding input layers.

In order to apply multi-level inputs, Han et al. [30] has investigated different ANN networks to predict the springback of SPIF and proposed that the particle swarm algorithm (PSO) can be integrated to the RBF network to study the random parameters. The PSO aims to search the potential solution (particle) in space. Each particle has independent space and velocity, the values on the direction and space can be determined by the optimisation function. Please see the attached supporting document for the step-by-step PSO integration.

2.4 Machine learning validation

The results of machine learning model test and training forming depth results are selected to validate the RBF model as illustrated in Fig. 6. It can be noticed that the test and training (predicted forming depth in log scale form) are consistent and converged after 1,500 epochs. The prediction accuracy is shown in Table 2. The results proved that the RBF model achieved excellent determination with low root mean squared error (R2) and distortion (\(\beta\)) which validated good agreement between test and training.

Fig. 6
figure 6

RBF learning curves. (RMSE values are in log scale)

Full size image
Table 2 Prediction accuracy of machine learning
Full size table

2.5 Experimental procedure and parameters

The experimental categories were described in Sect. 2.1. Since cooling is an external support to reduce the thermal effect on the tool, there was therefore no application of cooling lubricant in the initial experiment. For the first and second optimisations, cooling lubricant was assisted using modified cooling flow rate (Table 3). The experimental process is illustrated in Fig. 7. The first 5 experiments utilised the same process parameters; geometric coordinates, temperature and forming force data were collected after each experiment. The RBF framework then worked on the obtained data in order to compute the optimal tool path. It is important to note that the first RBF optimised tool path was based on initial group of experiments and second RBF optimised tool path was based on the first optimised group of experiments.

Table 3 Experimental parameters
Full size table
Fig. 7
figure 7

Working scheme of the machine learning-based networks

Full size image

3 Finite element model

ABAQUS/Explicit was used in order to establish an ideal model which has a constant temperature distribution to validate geometric accuracy, temperature and forming force from the initial and optimisation experiments. The simulation results will be compared with experiments to validate the improvements of RBF network tool path optimisation. By following the parameters from Li et al. [13] on investigation of induction heating SPIF for Ti-6Al-4V sheets at temperatures of 600 and 700 \(^\circ{\rm C}\). The tool in the simulation was considered to be an analytical rigid body, 5 mm in diameter. The dimensions of the workpiece comprised 150, 150 and 4 elements in x-, y-, and z- directions, respectively. A total of 90,000 coupled temperature and displacement (C3D8T) elements were assigned to the workpiece. The interaction was set as surface-to-surface contact of tangential behaviour with friction value of 0.1. This value was used in the previous study by Gatea et al. [37] in numerical modelling to study the fracture and damage behaviour based on Coulomb's friction law calculation which theoretically matched with the analytical model and experiments. And the value has been further validated by Gatea et al. [38] to study the forming parameters in SPIF process.

Since the beta-transus temperature is typically hard to utilise and to maintain in experiments, Oberwinkler et al. [39] proposed that 950 \(^\circ{\rm C}\) could be easier for the heating source to maintain which improved the agreement between experiments and simulations. Wang et al. [40] has validated the source and obtained better matched results. Thus, the temperature boundary condition was modified to 950 \(^\circ{\rm C}\) and then kept constant in order to reduce any effects from temperature variance. A BlueBEAR high performance computing system was employed in order to perform the simulation; the computing node included 36 Ice Lake Intel® Xeon® cores with 3.9 GHz per core and 120 GB memory.

In order to simulate the process accurately, stress and strain parameters were collected through the Instron 5500R uniaxial tensile test machine and thermal properties from THEMYS thermal analysis platform. The specimens were elongated up to the fracture. The test specimen geometry, with dimensions in alignment with ASTM E8 standards, is shown in Fig. 8a, b depicts the obtained stress–strain curves. The mechanical and thermal properties were tested accordingly and represented in Tables 4 and 5, respectively. Please note that the strain rate used in the uniaxial tensile test is following the experiment’s conditions and all uniaxial tensile and thermal tests were completed by authors’ mechanical testing centre.

Fig. 8
figure 8

Mechanical tensile test of Ti-6Al-4V alloy: a dimensions of the dog bone workpiece; b true stress–strain curves

Full size image
Table 4 Mechanical properties of Ti-6Al-4V
Full size table
Table 5 Thermal properties of Ti-6Al-4V
Full size table

4 Results and discussion

4.1 Geometric accuracy

The geometric profile of the formed shapes was measured using the FARO 3-dimensional (3D) scanning arm. All geometric coordinates were measured from the workpiece deforming surface centre path according to the step transition tool path. To reduce the unclamped springback from the workpiece, the sample edges was clamped prior to any geometric profile scanning. The CAD and simulation geometric profiles were used in the figures for experimental result validation. Each RBF optimised tool path was trained geometric coordinates, temperature and forming force distribution on the step transition tool path to compensate the thermal expansion from the workpiece and predict the correction for the displacement between theoretical and experimental profiles.

Figure 9a, c, e demonstrates the observable springback behaviour which occurred at the superior and inferior areas. The agreement between the experimental and simulation results was enhanced by the application of the first and second RBF optimisations and adjustment of cooling lubricant (Fig. 9b, d, f).

Fig. 9
figure 9

Observation of the formed shapes: a initial formed shape, c first RBF, e second RBF; measured geometric accuracy profiles: b initial, d first RBF, f second RBF

Full size image

This provided critical evidence that the predicted RBF tool path had a compensation effect on springback behaviour. The process ending stage at the lower area, revealed that the processing temperature above beta-transus (980 °C) induced unpredictable springback and pronounced adherence of lubricant. By applying RBF optimised tool path and cooling lubricant, the temperature had been reduced and the variance was dominated. The RBF optimised tool path thus compensated the deviation from the thermal expansion to reduce the springback. Further, the cooling lubricant system adjustment had noticeable effects on reducing the tool movement tracks as shown in Fig. 9f. The continuous and sustainable support enabled the tool to undergo sufficient lubrication thus reducing lubricant adherence to the workpiece. The detailed error percentage were presented in Table 6. It can be observed that the initial set of experiments deserved the peak error percentage and the values were decreased by each RBF networks optimisations. By introducing first and second RBF optimisation, the average error percentage reduced to 5.32% and 3.38% which shown a significant improvement in geometric accuracy. Please note that the error measurements from the experiments were averaged from the set experiments and compared with the simulation result.

Table 6 Error percentage of geometric accuracy between experiment groups
Full size table

4.2 Forming temperature

The experimental temperature profiles were measured using the infrared thermo-couple on the deforming surface, which corresponded to the contact area under the tool. The double-dotted line in Fig. 10 distinguishes the tool path from the truncated cone; the parameters in the region are virtual in order to connect the measured values.

Fig. 10
figure 10

Temperature measurements according to the step transition tool path: a initial, b first RBF optimisation, c second RBF optimisation

Full size image

It can be seen that the simulation temperature profile had a stable distribution with a small variation within the range 3 to 8 ℃. This could be presumed to be solid evidence of geometric accuracy. In the initial experiments, the temperature distribution at the step path appeared higher. There was a rapid increase in temperature; the temperature distribution at the common tool path demonstrated a relatively steady increase. It could be considered that the temperature control was insufficient for the step tool path relative to the common tool path due to its increased duration. Throughout, the temperature variance for the initial experiments was 120 ℃ (920–1040 ℃). Following the first and second RBF network optimisations, this parameter was reduced to 70 ℃ (910–980 ℃) and 45 ℃ (905–950 ℃), respectively. Thus, the introduction of the RBF network optimisations and cooling temperature control diminished the temperature variance to a constant level closer to the ideal simulation results.

4.3 Forming force

The forming forces presented in this study were measured according to the step tool path. The experimental results were compared with the simulation in order to validate the performance of the RBF network optimisations. Similarly to the forming temperature data, Fig. 11 illustrates the forming force according to the tool path along the step line. The double-dotted line distinguishes the tool path and the truncated cone; the values in the region are virtual in order to connect the measured parameters.

Fig. 11
figure 11

Forming force according to the step tool path: a initial, b first RBF optimisation, c second RBF optimisation

Full size image

A pronounced variance can be observed between the simulation and experimental results (Fig. 11a). The former became steady from the starting stage, i.e. 15 mm from the X direction, whilst the experimental data demonstrated an unstable increase. This could be accounted for as, according to the step tool path, the variance from the temperature distributions exerted a strong effect, impacting the forming force applied. The consequent unstable temperature and forming force distributions resulted in notable deflections in geometric accuracy.

When compared with the initial experimental data set, the experimental results following application of the first RBF network optimisation (Fig. 11b) were concentrated together and fitted the simulation result. After the second RBF network optimisation, improved fitting between experimental and simulation results was evidenced (Fig. 11c). This indicated that the temperature distribution according to this path was steady and able to provide superior geometric accuracy. Overall, the results from the experiment were lower than from the simulation as the temperature in the former was higher than in the latter. This increased workpiece material ductility, thus reducing the forming force distribution.

In summary, it can be observed that the forming force in the experiments revealed unstable distributions when compared with the temperature profiles. This effect could be attributed to the high temperature used in this study, which was greater than the beta-transus of Ti-6Al-4V. The strong DRX and beta transition have potent effects, affecting the material microstructure and therefore inducing unstable forming forces and increasing geometric inaccuracy. These observations matched the mechanical behaviour reported by Jha et al. [41], who documented the high-temperature deformation behaviour of a Ti-6Al-4V alloy. The RBF network optimisation, incorporating a cooling lubricant system, enhanced the steady performance of the temperature distribution which resulted in a stable forming force distribution according to the step tool path and thus, improved geometric accuracy.

4.4 Scanning electron microscopy (SEM) and energy-dispersive X-ray analysis (EDX)

Hitachi TM3030 SEM/EDX system was used to evaluate the surface quality on deforming surface and the diffusion of compound layer, microstructure evolution on thickness section. All samples (initial, first and second RBF) were prepared from the lower part of formed shapes. The first EDX analysis was applied to the samples’ deforming surfaces by first cleaned using 70% alcohol, followed by ultrasonic cleaning at 30 kHz for 30 min in order to remove any remaining contamination. Further SEM and EDX were applied to the thickness section by chemical polished with 0.04 μm Colloidal Silica (OP-S) suspension and etched using Kroll's reagent (2 mL HF, 10 mL HCl, 88 mL H2O).

As shown in Fig. 12a, the initial experiment illustrated a pronounced area of large micro-cracks, sizeable valleys and a notable amount of remaining lubricant adherence. Such phenomena resulted in a reaction between the material and lubricant elements which led to the formation of a compound mixture layer (Fig. 12d). The pronounced alpha-case and interlamellar \(\beta\) grains indicated a beta-transus. The formation of the compound layer and the alpha-case induced the geometric inaccuracy described in Sect. 4.1. The microstructure matched the findings of de Castro et al. [42] who assessed 1050 ℃ heat treatment on Ti-6Al-4V alloy for 30 min with heating and cooling rates of 20 °C/min and 6 °C/min. Where a Widmanstätten-type structure was obtained with a basket-weave microstructure. The alpha-case with basket-weave microstructure proved that the temperature has exceeded the beta-transus with a relatively slow cooling rate. The study proposed that the annealing of Ti-6Al-4V above beta-transus increased the DRX process significantly and induced notable thermal expansion during the process. Therefore, the microstructure formed in this study increased the micro-cracks due to the strong thermal expansion and resulted in deeper diffusion of compound layer and alpha-case.

Fig. 12
figure 12

EDX and SEM maps: EDX and micro-cracks on deforming surface: a initial, b first RBF, c second RBF; SEM maps on cross-section top surfaces: d initial, e first RBF, f second RBF; EDX maps on cross-section top surfaces: g initial, h first RBF, i second RBF; (Element map: titanium, red; molybdenum, green; oxygen, blue)

Full size image

By applying the first RBF optimisation and cooling lubricant, the incidence of micro-cracks was reduced and the cracks per se became smaller (Fig. 12b). Additionally, the compound layer was decreased (Fig. 12e). Lamella \(\alpha\) grains with nucleation of \(\beta\) grains were detected to initiate a slight \({\alpha }^{^{\prime}}\) martensite microstructure. The phenomenon can be attributed to the enhanced cooling rate from the cooling lubricant. Zhang et al. [43] have evaluated the oxidation behaviour of Ti–6Al–4 V during varied hot deformation processes, proposed that the activation energy at beta-transus temperature will exceed the formation and growth of critical nucleus grain boundaries and react with interfacial energy for nucleation of new phases and alpha-case formation. Seth et al. [44] agreed with statement and suggested that alpha-case is more pronounced at beta-transus temperature heat treatment with rapid cooling rate, and the structure exhibits brittle failure due to the numerous cracks in the alpha-case. In this study, it can be proven that the cooling lubricant only removed the compound layer and the reduced temperature decelerated the formation of \(\beta\) grains and alpha-case.

After the second RBF network optimisation (Fig. 12c), only small micro-cracks were observed owing to the reduced temperature and cooling lubricant. The obtained phenomenon indicated a complete removal of compound layer as shown in Fig. 12f. A bimodal microstructure which composed of primary \(\alpha\) grains and transformed \(\beta\) grains has been illustrated. According to Chong et al. [45] on the investigation of deformation mechanism and properties of Ti-6Al-4V alloy, the bimodal microstructure bearing balanced volume of \(\alpha\) – \(\beta\) grains and refined grain size which enhancing the straining behaviour. The microstructure will enhance the straining during the SPIF process where no alpha-case to increase the risk for brittle fracture and less compound layer to affect the surface quality.

The EDX maps in Fig. 12g–i indicated the removal of compound layer corresponding to initial, first and second optimisation experiment maps. It can be noticed that the compound layer has been removed according to the reduction of temperature and increase rate of cooling-lubricant. The results indicated a good cooperation between cooling lubricant system and RBF optimised tool path. The temperature initiation and friction at the contact area had been reduced after each RBF optimisation, which results in formation of bimodal microstructure that enhanced grain-boundary straining and promoted better surface quality with reduction of micro-cracks and diffusion of lubricant compound layer.

4.5 Surface roughness

The deforming surfaces from the SEM samples have been characterised using the Alicona Infinite Focus optical surface measurement system in order to obtain surface roughness measurements. The imaging capture area was 2.5 mm × 2.5 mm for all samples. A Gaussian filter was used so as to reduce the noise on inclined planar surfaces.

The surface roughness measurements were maximal following the initial experiment (Fig. 13a), results which could relate to the peak dissipation of lubricant seen at this stage. This phenomenon resolved following the first optimisation (Fig. 13b). Following the second RBF optimisation (Fig. 13c), a reduction in surface roughness peak value was achieved which implies that the dissipation of lubricant had decreased. This offered strong evidence that the temperature variance was controlled during the second RBF optimisation; the consequently reduced temperature and forming force resulted in a slow dissipation of lubricant.

Fig. 13
figure 13

Measurements of surface roughness: a initial, b first RBF optimisation, c second RBF optimisation

Full size image

The measurements of average surface roughness (\({S}_{a})\) for the samples are illustrated in Fig. 14. The first RBF optimisation revealed a decrease from the initial experiments to the second RBF network optimisation, which indicated that the unstable temperature and forming force resulted in an uneven surface. With the dissipation of the lubricant, the surface roughness was higher than in the second RBF network optimisation.

Fig. 14
figure 14

Average surface roughness for the selected area

Full size image

5 Conclusion

  • RBF network is a useful machine learning method to study the experimental parameters (geometric coordinates, temperature, forming force) based on abundant training groups. The results shown that the RBF optimised tool path can be gradually improved depends on two sets (each set 5 experiments) of training experiments and reduced the springback to 5% and below.

  • The ball-roller tool integration with cooling lubricant formed a functional way to reduce the thermal expansion on the tool. The sustainable support of liquid lubricant significantly improved the function of the lubricant and promoting geometric accuracy and surface quality.

  • The FEM analysis indicated ideal profiles (geometric, temperature, forming force) to compare with the measured results to indicate the improvements. It can be noticed that each RBF tool path optimisation with cooling lubricant induced a reduction in temperature which approached to the simulation and improved the geometric accuracy to the CAD profile.

  • The non-cooling lubricant experiments indicated rapid temperature increase at ending stage over the set temperature which accelerated the lamellar microstructure growth to form basket-weave structure. Such growth increased the springback with further enhancement of compound layer diffusion and alpha-case which increased the surface roughness.

  • The cooling lubricant indicated a pronounced temperature reduction which slow down the rapid growth of lamellar microstructure. The active lubricating service removed the formation of compound layer and balanced the temperature increase which improved the surface quality and enhanced the geometric accuracy.