1 Introduction

Ti–6Al–4 V alloy is a high-strength material that is widely applied in the aerospace and medical sectors. Ma et al. [1] have studied the crystal plasticity of titanium alloys and commented that the deformation of such material is usually performed at a high temperature to avoid the formation of deformed textures, which may result in an anisotropic mechanical behaviour due to the slip changes in the hexagonal closest-packed (HCP) structure of α-Ti. To deform such alloys to a designated shape with high geometric accuracy, the heat source electric heating has been proposed by Liu et al. [2] to induce a high-frequency current to induce heating to the entire workpiece, which is able to deform the workpiece at a maximum temperature of around 500 \(^\circ{\rm C}\). Göttmann et al. [3] first time-induced laser heating in single point incremental sheet forming (SPIF) to deform Ti–6Al–4 V alloy with excellent performance. However, the heating in electric SPIF is not localised and electric sparks have a significant impact on the surface quality. Laser heating is complicated in equipment set-up and high cost. To provide localised heating with low cost and simple set-up equipment, induction heating assistance has been developed recently by Ambrogio et al. [4], where the heat is supported localised underneath the workpiece and movement is synchronised with the tool. Li et al. [5] have improved the method by introducing a hollow tool with a ball-roller tooltip design, which can reduce the thermal expansion on the tool and enhance the surface quality. In induction heating SPIF, the localised temperature is generated only inside the material without affecting the surrounding area, which indicates high performance in reducing springback and avoiding the effects of electric sparks. Zhan et al. [6] have investigated the DRX of incremental sheet forming of aluminium alloy sheets under room temperature. The results indicate that the DRX is raised during the process and refined in the grains along the toolpath, which enhances higher strength and better plasticity of the material. For heat-assisted SPIF processes, the current challenges have remained on the shortage of studies on the thermomechanical behaviour and the relevant microstructural evolution throughout the process from stage to stage. Therefore, it is essential to study the relationship between thermomechanical behaviour and its effects on microstructural evolution and to establish a numerical model to complete the loop in this scientific field.

Yang et al. [7] found that the initiation of DRX and microstructural evolution of Ti–6Al–4 V are usually observed when the thermomechanical behaviour is above 700 \(^\circ{\rm C}\). A pronounced α-phase DRX can be detected, and the process influences the mechanical properties significantly. In recent years, CA models are generally studied to simulate the DRX process of alloys. For instance, Ding and Guo [8] investigated the microstructural evolution of a Ti–6Al–4 V titanium alloy during \(\beta\)-phase processing by using CA models. The simulated results successfully represented the microstructural evolution under experimental conditions. However, the stress–strain relevant parameters were obtained from experimentally observed results, which induced calculation errors on grain growth kinetics and dislocation density calculations in CA models. The results led to a further impact on the accuracy of DRXed calculation. To reveal precision grain level behaviour of hot compression of Ti–6Al–4 V alloy, Chuan et al. [9] and Said et al. [10] have investigated a novel approach involving combining the CPFEM method to provide crystal orientation and grain level strain distribution as CA model input. The simulated results revealed accurate grain growth and re-grain size by comparing them with experimental data. The calculated recrystallisation kinetics and flow stress successfully predicted the regime of the material microstructure evolution. Chen et al. [11] have proposed multiscale modelling to simulate discontinuous dynamic recrystallisation during hot works by coupling multilevel cellular automaton, which also proves the novelty of the study on multiscale modelling of hot deformation metal forming processes.

In this article, the DRX of \(\alpha\)-phase Ti–6Al–4 V alloy during hot SPIF will be simulated by combining CA and CPFEM. An experimental-scale finite element method (FEM) model was established by implementing the VUMAT subroutine in ABAQUS to simulate the SPIF experimental process. The grain level strain distribution will be obtained from the elements. Each localise element presents one grain. The received strain distribution will be used as an input to implement an EBSD-based RVE to obtain the crystallographic texture. Furthermore, the CPFEM grain level strain outputs can be used as inputs to simulate the microstructural evolution during the heat-assisted SPIF process. To validate the CA model, the simulation results, including grain size, dislocation density, and DRX fraction, were compared with experimental results. Finally, this article aims to study the relationship between the grain level parameters and the thermomechanical behaviours from experiments.

2 Materials and methods

2.1 Materials

All workpieces in this article are standard Ti–6Al–4 V alloy sheets with dimensions of \(150\mathrm{ mm}\times 150\mathrm{ mm}\times 0.8\mathrm{ mm}\). The chemical composition is displayed in Table 1.

Table 1 The chemical composition of Ti–6Al–4 V alloy sheet (wt %)
Full size table

2.2 Experimental parameters

For the hot sheet forming process of Ti–6Al–4 V, the common temperature used is around 400–500 \(\mathrm{^\circ{\rm C} }\), which is sufficient for plastic deformation behaviour [12, 13]. However, the obtained results did not reveal high geometric accuracy as the forming temperature is insufficient to produce DRX volume to reduce the forming force. The titanium α-phase HCP crystal plasticity model has been established in the previous study by Amouzou et al. [14], which validated that a pronounced phenomenon of DRX was achieved at hot deformation of 700 \(\mathrm{^\circ{\rm C} }\). The studies [5, 15] have investigated the microstructure of Ti–6Al–4 V under 700 \(\mathrm{^\circ{\rm C} }\) induction heating assisted SPIF, which indicated a pronounced DRX level at 700 \(\mathrm{^\circ{\rm C} }\). Thus, this study aims to develop the localised crystallographic texture and DRX behaviour of Ti–6Al–4 V thin sheets under the 700 \(\mathrm{^\circ{\rm C} }\) SPIF process. The feasible model will be able for users to apply in other metal forming processes with modification of materials properties. As the processing temperature is lower than the β-phase transition (980 \(\mathrm{^\circ{\rm C} }\)), only the α-phase HCP structure is considered for the crystallographic sliding to simplify the calculations. As the hot SPIF process combines thermomechanical deformation and dynamic straining behaviour, which contributes to the complexity of the microstructural level simulation. Sun et al. [16] have investigated the shear banding in titanium under deformation and dynamic compression and commented that the shear banding behaviour is pronounced at slip in basal and prism planes where the other planes can be neglected. Li et al. [17] have proposed a new method to combine CA and CPFEM to predict deformation-microstructure evolution-mechanical response for hot-working process of titanium alloys which proved the feasibility to treat DRX as one intrinsic part of constitutive behavior in coupling of CPFEM. Zhang et al. [18] have investigated the deformation and shear bands in the texture of α-phase HCP. The study commented that three families of the slip system: basal \(<a>\), prismatic \(<a>\), and pyramidal \(<c+a>\) are recommended to focus as main slip systems for deformation under phase transition temperature. By applying the same families of the slip system, 3 basal, 3 prismatic, and 6 pyramidal were considered in this article.

The induction heating SPIF system was shown in Fig. 1(a). The forming tool has a 10 mm nickel alloy ball-roller tooltip to reduce the friction on the workpiece. The tool was fixed with the induction heater, thus able to provide synchronised movements. The induction heater has a power of 6.6 kW with a high frequency of 900 kHz, which is able to provide a rapid and constant eddy current to penetrate the centre mass of the material to the edges. The geometric structure and the SPIF tool path were established using MATLAB 2016b. The designated shape has a diameter of 100 mm by 30 mm in height and a 45° wall angle, as illustrated in Fig. 1(b). The X, Y, and Z coordinates generated by MATLAB were used as a G-code tool path strategy, as displayed in Fig. 1(c). The detailed parameters are presented in Table 2. The applied lubricant was liquid MoS2, which was observed as efficient to reduce friction in the previous study by Li et al. [19] under similar experimental conditions of induction heating assisted SPIF of Ti–6Al–4 V sheets.

Table 2 Machine setting and experimental parameters
Full size table

2.3 CPFEM of experimental scale SPIF

For a thin sheet material in this study, the Voronoi tessellation method is not efficient as the Voronoi cells at the thin edge are unable to be fully demonstrated for an experimental scale. Thus, FEM was established to present an experimental scale CPFEM simulation. Each element in the CPFEM can be used to collect grain level strain variables for a specific area, and the elements at the edge can be accumulated to present the crystal plasticity behaviour through the thickness. The accumulative strain variable output will be used as input variables in an RVE model to simulate the results in detail. In the experimental scale CPFEM, coupled temperature-displacement implicit regime is selected. The tool is defined as a rigid body and assigned a temperature boundary condition of 700 \(\mathrm{^\circ{\rm C} }\) and the temperature is transformed to the workpiece by contact. Since the heat transfer is synchronised with the tool movement and the heating area is the same as the tooltip, therefore, contact behaviour is the best way to simulate heat transfer. The friction coefficient was set at 0.1. This value has been validated in the previous study by Li et al. [5] under similar experimental conditions of induction heating assisted SPIF of Ti–6Al–4 V sheets based on Coulomb's friction law calculation. The four sides of the workpiece are constraints (displacement to x, y, z = 0) as shown in Fig. 2(a). The orientation of elements is displayed in Fig. 2(b). A total of 90,000 elements (x-axis: 150 elements, y-axis: 150 elements, and z-axis: 4 elements) have been applied to the workpiece. The equivalent plastic strain of the deformed SPIF simulation is illustrated in Fig. 2(c).

The elastic constants in Table 3 were obtained from the study by Chatterjee et al. [20] on experimental tensile and CPFEM simulation of Ti–6Al–4 V, where the conditions are met with this article. The slip systems parameters in Table 4 were obtained from Thomas et al. [21] on hot deformation and CPFEM analysis of Ti–6Al–4 V under similar experimental temperature and strain conditions as in this article. The results are shown in Tables 3 and 4.

Table 3 Elastic constants (GPa) for the α phase of Ti–6Al–4 V
Full size table
Table 4 The parameters for slip systems in the α-Ti grains
Full size table

2.4 Representative volume elements (RVE)

The CPFEM of SPIF was used to provide the grain level mechanical behaviours approximately. To simulate the detailed microstructural development, the RVE model was established using the mechanical output from the CPFEM of SPIF.

The structure of RVE was generated by incorporating the EBSD output as input data into the DREAM.3D and extruding the result as an ABAQUS input file. This software was used to reconstruct the EBSD output and make segments and mesh the features of the dataset. The details of the software can be found in the documentation of DREAM.3D, which is induced by the previous study by Groeber and Jackson [22] on 3D materials microstructure modelling. As shown in Fig. 3(a), a sub-grain part from the EBSD data of the as-received sample was used to create the RVE model. This part is 100% α-phase with strong HCP texture and contains 356 grains, the orientation of these grains is then used as input data in DREAM.3D to create an RVE structure, presented in Fig. 3(b). The created RVE from DREAM.3D was saved as an ABAQUS input file to create a FEM for analysis as illustrated in Fig. 3(c). The FEM is \(23\mathrm{ \mu m }\times 23\mathrm{ \mu m }\times 23\mathrm{ \mu m}\) with 12,167 elements.

The same material properties and mechanical behaviours from the CPFEM of SPIF were used in this RVE model to simulate the detailed microstructural development.

2.5 Single-crystal constitutive model

The main objective kinematics of the single-crystal plasticity constitutive model is finalised on the dislocation mechanism, which has been investigated by Zhuang et al. [23]. The foundations of constitutive laws can be traced to the works by Hill and Rice [24] on the investigation of the constitutive laws of elastic–plastic crystals at arbitrary strain. Peirce et al. [25] have improved the constitutive laws and applied Kröner-Lee decomposition, which is induced by the calculation of deformation of gradient tensor F of a single crystal from Kröner-Lee decomposition Kröner [26] in the study of elastic–plastic behaviour of crystals. To simplify the constitutive calculations of single-crystal deformation, two independent atomic mechanisms are assumed: (1) general elastic lattice distortion, and (2) plastic deformation with no effect on lattice geometry. Under isothermal conditions, the intermediate configured lattice orientation can be assumed as the same as the initial state. The deformation of single-crystal is dominated by dislocation glide, which is under a deformation gradient tensor \(F\) and its derivatives as expressed as

$$F={F}^{e}\cdot {F}^{P}$$
(1a)
$$\mathrm{det}{F}^{p}=1$$
(1b)
$$J=\mathrm{det}F=\mathrm{det}{F}^{e}$$
(1c)

where \({F}^{P}\) is the plastic deformation gradient, which denotes the crystalline slip plane plastic shear deformation, and where the nonplastic component, \({F}^{e}\) is a nonplastic component, which denotes the lattice elastic stretch and rotation. \(J\) denotes the ratio of the deformed to the undeformed volume. By assuming no change in volume during plastic deformation, the macroscopic velocity gradient \(L\) can be expressed as

$$L=\dot{F}\cdot {F}^{-1}={L}^{e}+{L}^{p}$$
(2a)
$${L}^{e}={\dot{F}}^{e}\cdot {F}^{e-1}$$
(2b)
$${L}^{p}={F}^{e}\cdot {\dot{F}}^{p}\cdot {F}^{p-1}\cdot {F}^{e-1}$$
(2c)

where \({L}^{e}\) is the velocity gradient for the elastic part of the crystal, \({L}^{p}\) is the velocity gradient for the plastic part. \({\dot{\gamma }}^{\alpha }\) denotes the \(\alpha\) slip system shear rate. Asaro and Rice [27] on analysis of strain behaviour in single crystals have defined the plastic deformation for the crystal slip system using shear rate as

$${\dot{F}}^{p}\cdot {F}^{p-1}=\sum_{\alpha =1}^{n} {\dot{\gamma }}^{\alpha }{s}^{\alpha }\otimes {m}^{\alpha }$$
(3)

where \({s}^{\alpha }\) is the unit vector for slip direction and \({m}^{\alpha }\) is the unit vector for slip plane for \({\alpha }^{th}\) slip system. During single-crystal deformation, the lattice would be rotated and stretched. The normal vector \({\tilde{s}}^{\alpha }\) and \({\tilde{m}}^{\alpha }\) to the \({\alpha }^{th}\) slip system has been expressed by Nanson’s formula as displayed in Eq. (4a) and (4b).

$${\tilde{s}}^{\alpha }={F}^{e}\cdot {s}^{\alpha }$$
(4a)
$${\tilde{m}}^{\left(\alpha \right)}=\mathrm{det}{F}^{e}\cdot {m}^{\left(\alpha \right)}\cdot {F}^{e-1}$$
(4b)

By approximating the elastic deformation \(\mathrm{det}{F}^{e}=1\), which is made in Eq. (1b). Equations (4a) and (4b) can be transformed as

$${\tilde{s}}^{\left(\alpha \right)}={F}^{e}\cdot {s}^{\left(\alpha \right)}$$
(5a)
$${\tilde{m}}^{\left(\alpha \right)}={m}^{\left(\alpha \right)}\cdot {F}^{e-1}$$
(5b)

Furthermore, Eq. (5a) and (5b) can be rewritten as

$${\tilde{s}}^{\left(\alpha \right)}={L}^{e}\cdot {\tilde{s}}^{\left(\alpha \right)}$$
(6a)
$${\tilde{m}}^{\left(\alpha \right)}=-{\tilde{m}}^{\left(\alpha \right)}\cdot {L}^{e}$$
(6b)

By combining Eqs. (4a), (5a), and (6a), the final equation of plastic velocity gradient tensor \({L}^{P}\) can be expressed as shown in Eq. (7).

$${L}^{P}=\sum_{\alpha }\dot{\gamma }{S}_{0}^{\alpha }, {S}_{0}^{\alpha }\equiv {m}_{0}^{\alpha }\otimes {n}_{0}^{\alpha }$$
(7)

where \({m}_{0}^{\alpha }\) denotes the vectors of slip direction and \({n}_{0}^{\alpha }\) denotes the vectors of the slip plane normal in the slip systems with a variable of 0. \({\mathrm{\alpha }}^{th}\) denotes the sequence of slip system, \({S}_{0}^{\alpha }\) is the slip resistance in the unit of Schmid tensor. The elastic strain can be expressed as

$${E}^{*}=\frac{1}{2\left[{\left({F}^{*}\right)}^{T}{F}^{*}-I\right]}$$
(8)

where \({E}^{*}\) is the elastic strain, \(I\) denotes the 2nd order tensor of identity. The grain level stress of elastic constitutive laws can be expressed as

$${T}^{*}={\mathrm{CE}}^{*}$$
(9)

where \({T}^{*}\) in Eq. (9) denotes the crystalline Cauchy stress, \(C\) is a fourth-order elasticity tensor. The stress measure and the elastic work conjugate to the elastic strain can be expressed as

$${T}^{*}=\left({\mathrm{detF}}^{*}\right){F}^{*-1}{\mathrm{TF}}^{*-T}$$
(10)

where T is the grain level symmetrical Cauchy stress tensor, and the resolved shear stress is given by:

$${\tau }^{\alpha }={T}^{*}:{S}_{0}^{\alpha }$$
(11)

To investigate the grain level deformation, the movement of each grain is considered rigid rotation and orientation evolution. The shear strain rate and the shear stress must be integrated into the slip system. The equation of the deformation can be expressed as

$${F}^{*}={R}^{*}{U}^{*}$$
(12)

where \({F}^{*}\) denotes the nonplastic deformation gradient, \({R}^{*}\) is the lattice rigid rotation, \({U}^{*}\) is the stretch tensor, the following equation expressed the orientation of grains:

$$Q={R}^{*}Q{\left({R}^{*}\right)}^{T}$$
(13)

where \(Q\) denotes the grain orientation formed by the rotation tensor in terms of Euler angles. The following equation has expressed the strain rate using the power-law flow rule:

$${\dot{\gamma }}^{\alpha }={\dot{\gamma }}_{0}{\left(\frac{{\tau }^{\alpha }}{{s}^{\alpha }}\right)}^{\frac{1}{\chi }}\mathrm{sgn}\left({\tau }^{\alpha }\right)$$
(14)

where \({\dot{\gamma }}^{\alpha }\) and \({\dot{\gamma }}_{0}\) denote the shear rate and reference shear rate for \({\alpha }^{\mathrm{th}}\) slip system, \(\chi\) denotes the coefficient of material rate sensitivity,\({\tau }^{\alpha }\) denotes the \(\alpha\) slip system acting resolved shear stress, and \({s}^{\alpha }\) denotes the dislocation acted deformation resistance. The equations are given by

$$s^\alpha=s_{0}+\frac{1}{2}\mu\sqrt{\rho^\alpha}$$
(15a)

with

$${s}_{0}=\frac{1}{N}\left({u}_{1}\mathrm{exp}\left(-\frac{T}{{T}_{0}}\right)+\frac{{u}_{2}}{\sqrt{d}}\right)$$
(15b)

where \(\mu\) denotes the shear modulus, \(b\) represents the Burger’s vector, Eq. (15b) was proposed by Kocks and Mecking [28] in the study of work hardening, where \({s}_{0}\) is the slip resistance that is dependent on initial grain size, and \({\rho }^{\alpha }\) denotes the density of dislocation for \({\alpha }^{th}\) slip system. \(N\) represents the number of slip systems in total and the term \({u}_{1}\mathrm{exp}\left(-\frac{T}{{T}_{0}}\right)\) represents the slip resistance that is dependent on the temperature, where \({u}_{1}\) is a constant for fitting, \(T\) and \({T}_{0}\) represent the working temperature and the reference temperature. \(\frac{{u}_{2}}{\sqrt{d}}\) represents the slip resistance that depends on the size effect. \({u}_{2}\) denotes the coefficient of Hall–Petch and \(d\) represents the average grain size. To simplify the calculations, the initial slip resistance of each slip system was assumed as the same, which has been proposed by Hémery et al. [29] in the investigation of the slip behaviours with the degree of micro-texture in Ti–6Al–4 V. The development of dislocation density is governed by the annihilation and multiplication of dislocation movements. Mishra and Ma [30] on the analysis of dislocation evolution has induced the K–M model to express the multiplication term:

$$d{\dot{\rho }}^{+}={k}_{1}\sqrt{\rho }\dot{\varepsilon }$$
(16)

where \(d{\dot{\rho }}^{+}\) denotes the density of dislocation in increasing order, k1 represents the work hardening constant,\(\rho\) represents the density of dislocation, and ε̇ denotes the strain rate. To describe the term dislocation annihilation, the following equation has been proposed:

$$d{\dot{\rho }}^{-}=-{k}_{2}\rho \varepsilon$$
(17)

where \(d{\dot{\rho }}^{-}\) denotes the dislocation density in decreasing order, \({k}_{2}\) can be defined as a function that depends on the working strain rate and temperature. \({k}_{2}\) can be expressed as follows:

$${k}_{2}={k}_{20}{\left[\dot{\varepsilon }\;\mathrm{exp}\left(\frac{{Q}_{act}}{RT}\right)\right]}^{\frac{1}{\omega }}$$
(18)

Both \({k}_{20}\) and ω are constants for fitting, \({Q}_{act}\) denotes the deformation formed activation energy, and R represents the gas constant.

2.6 CA model

As the crystal plasticity behaviour is calculated by CPFEM, the output from the CPFEM is then used as input in the CA model to predict the DRX process. To address the recrystallisation nucleation and subsequent growth, two assumptions are proposed:

  1. 1.

    The dislocation density of primary grains is uniform and identical. DRX occurs as the value reaches the critical level. Each DRXed grain is depending on continued deformation with variation for each grain, and the mechanism is fully applied to the changes in dislocation density.

  2. 2.

    The occurrence of DRX nucleation on the grain boundaries is applied to all primary and DRXed grain boundaries.

The modelling nucleation rate has been proposed by Peczak [31] in the study of deformation temperature on dynamic recrystallisation, which can be described as

$$\dot{n}\left(T\right)=\dot{n}\left({T}_{\mathrm{m}}\right)\mathrm{exp}\left[-\frac{{Q}_{\mathrm{act}}}{{\mathrm{RT}}_{\mathrm{m}}}\left(\frac{{T}_{\mathrm{m}}}{T}-1\right)\right]$$
(19)

where \(\dot{n}\left(T\right)\) denotes the nucleation rate, \(\dot{n}\left({T}_{\mathrm{m}}\right)\) represents the nucleation rate at melting temperature \({T}_{\mathrm{m}}\), and \({Q}_{\text{act}}\) denotes the activation energy. The previous study by Derby and Ashby [32] on DRX analysis has proposed that the nucleation rate can be assumed as linearly proportional to the strain rate function \(\dot{n}=C{\dot{\varepsilon }}^{m}\). According to the study by Peczak and Luton [33], on the investigation of nucleation models of DRX, \(m\) can be assumed as 0.9. Another study by Peczak [31] proposed that the nucleation rate for DRX can be induced by the temperature and strain rate as follows:

$$\dot{n}\left(\dot{\varepsilon },T\right)=C{\dot{\varepsilon }}^{m}\;\mathrm{exp}\left(-\frac{{Q}_{\mathrm{act}}}{\mathrm{RT}}\right)$$
(20)

where C is a constant which can be determined from the nucleation rate \(\dot{n}\left({ \, \mathrm{s}}^{-1}{ \, \mathrm{m}}^{-3}\right)\) at a specific DRX level, the exponent m can be assumed as 1 to demonstrate the full plastic flow during DRX, which is suggested by the study of Ding and Guo [34] on DRX simulation. The DRX fraction can be expressed as

$$\eta =\dot{n}\frac{\varepsilon }{\dot{\varepsilon }}\cdot \frac{4}{3}\pi {r}_{\mathrm{d}}^{3}$$
(21)

where \(\eta\) denotes the DRX fraction, \(\varepsilon\) represents the true strain, \(\dot{\varepsilon }\) denotes the strain rate, and \({r}_{\mathrm{d}}\) is the mean radius of DRXed grain. Derby [35] has studied the steady state grain size under DRX and proposed that Eq. (21) can be relevant to flow stress as follows:

$$\frac{{\sigma }_{\mathrm{s}}}{\mu }{\left(\frac{2{r}_{\mathrm{d}}}{b}\right)}^{n}=K$$
(22)

where \({\sigma }_{\mathrm{s}}\) denotes the steady-state flow stress, \(\mu\) represents the shear modulus, \(b\) is Burger’s vector, and the exponent \(n\) can be considered \(\frac{2}{3}\) and \(K\) is a constant (range from 1 to 10) for titanium alloys. In this article, the nucleation of α-DRX occurs as a critical level of dislocation density or strain is initiated. The equation is given by

$${\rho }_{c}={\left(\frac{20\lambda \dot{\varepsilon }}{3{b}^{5}lM{\mu }^{2}}\right)}^\frac{1}{3}$$
(23)

where \({\rho }_{c}\) denotes the dislocation density at the critical level, \(\lambda\) represents the grain boundary energy,\(l\) denotes the average free path for dislocation, and \(M\) denotes the mobility at the grain boundary. The nucleation rate can be expressed as

$$\dot{n}={C}_{1}{\dot{\varepsilon }}^{\varphi }\mathrm{exp}\left(-\frac{{Q}_{\mathrm{act}}}{\mathrm{RT}}\right)$$
(24)

where \(\dot{n}\) is the nucleation rate, \({C}_{1}\) and φ are constants. The deformation of neighbouring grains is initiated by the stored energy and it is governed by the recrystallisation nucleation, which can be expressed as

$${Q}_{\text{deform }}=\frac{1}{2}{\rho }_{\mathrm{GND}}\mu {b}^{2}\psi$$
(25)

where \({Q}_{\text{deform}}\) is the stored energy under deformation, \(\psi\) denotes the material molar volume,\({\rho }_{\mathrm{GND}}\) represents the geometrically necessary dislocations (GND). According to the previous study, Hallberg and Ristinmaa [36] has investigated the influence of dislocation density in a reaction–diffusion system, the DRXed grain can be assumed as spherical and the driving force is given by:

$$P=\frac{{\mathrm{dE}}_{i}}{{\mathrm{dr}}_{i}}=\frac{{\mathrm{dE}}_{i}^{\mathrm{vol}}+{\mathrm{dE}}_{i}^{\mathrm{sur}}}{{\mathrm{dr}}_{i}}$$
(26)

where \(P\) denotes the driving force, \({\mathrm{dE}}_{i}^{\mathrm{vol}}\) represents the evolution in the volume energy, and \({\mathrm{dE}}_{i}^{sur}\) is the evolution in the energy of grain boundary. The above equation can be re-arranged as

$${\mathrm{dE}}_{i}^{\mathrm{vol}}=4\pi {r}^{2}\left({\rho }_{m}-{\rho }_{r}\right)\mu {b}^{2}$$
(27)

where \({\rho }_{m}\) is the matrix grain of dislocation densities and \({\rho }_{r}\) is the matrix grain of DRXed grains. The retarding force can be expressed as

$${\mathrm{dE}}_{i}^{sur}=-8\pi r\lambda dr$$
(28)

where \({\mathrm{dE}}_{i}^{sur}\) is the retarding force, r is the grain radius, Varshni [37] has defined the shear modulus under material temperature as Eq. (29):

$$\mu =49.02-\frac{5.821}{\mathrm{exp}\left(\frac{181}{T}\right)-1}\mathrm{GPa}$$
(29)

where \(\mu\) denotes the shear modulus. By applying the Read–Shockley equation, the grain boundary energy is given by

$$\lambda =\left\{\begin{array}{ll}{\lambda }_{m}&\theta {\ge 15}^{\circ }\\ {\lambda }_{m}\frac{\theta }{{\theta }_{m}}\left(1-\mathrm{ln}\frac{\theta }{{\theta }_{m}}\right)&\theta <{15}^{\circ }\end{array}\right.$$
(30)

where \(\lambda\) denotes the grain boundary energy, \({\lambda }_{m}\) corresponds to the boundary energy above \({15}^{\circ },\) and it is given by:

$${\lambda }_{m}=\frac{\mu b{\theta }_{m}}{4\pi \left(1-v\right)}$$
(31)

where \({\theta }_{m}\) denotes critical misorientation angle at 15° and \(v\) represents the Poisson ratio. The driving pressure can be calculated as

$$p=\frac{P}{4\pi {r}^{2}}$$
(32)

where \(p\) is the driving pressure, r is the radius of DRXed grains, the DRX growth is produced by the grain boundaries migration, and the migration rate can be expressed with the grain boundary mobility \(M\) as

$$M=\frac{b\delta {D}_{0b}}{{K}_{B}\theta }\mathrm{exp}\left(-\frac{{Q}_{\mathrm{diffu}}}{R\theta }\right)$$
(33)

where \(\delta\) denotes the characteristic grain boundary thickness, \({D}_{0b}\) represents the coefficient of diffusion at ideal 0 K, \({Q}_{\mathrm{diffu}}\) denotes the activation energy for self-diffusion activation energy, and the migration rate is given by

$$v=\mathrm{Mp}$$
(34)

where \(v\) is the migration rate that interacts with the isothermal macroscopic flow stress \(\sigma\) and the average dislocation density \(\sigma\) which can be expressed as

$$\sigma =0.5\mu b\sqrt{\overline{\rho }}$$
(35)

where \(\sigma\) is the isothermal macroscopic flow stress under hot deformation, \(\overline{\rho }\) denotes the average dislocation density. By assuming the \(\overline{\rho }\) is equivalent to the mean value of all the grains, the equation can be re-arranged as

$$\overline{\rho }=\frac{1}{{V}_{\text{total }}}\sum_{i=1}^{N} {\rho }_{i}{V}_{i}$$
(36)

where \({\rho }_{i}\) denotes the dislocation density, \({V}_{i}\) represents the volume at \({i}^{th}\) grain, and \({V}_{\text{total}}\) is the volume in total.

2.7 CA model and CPFEM model combination

In this article, the 2D CA model was produced by MATLAB using Moore’s neighbouring rule with periodic boundary conditions. The inputs are extracted from the CPFEM outputs to maintain the grain level variables. The CA is presented in 500 × 500 cells, with each cell simulating 2 μm. By referring to the study by Chen et al. [38] on the mesoscale simulation of the high-temperature DRX of steel, the process of CA and CPFEM consists of the following stages:

  1. 1.

    Generation of experimental scale CPFEM to obtain state variables of crystal orientation and grain level strain, strain rate, and temperature distribution.

  2. 2.

    Select a section from EBSD to get grains orientation, use DREAM.3D to build an ABAQUS RVE model, and apply the state variables from CPFEM.

  3. 3.

    Use the output crystal orientation to generate a pole figure to compare with EBSD results.

  4. 4.

    The CA model is established by applying state variables from CEPFEM as input.

  5. 5.

    By using the K–M equation, the dislocation density for the grains is calculated.

  6. 6.

    The nucleation of DRX occurs when the misorientation angle exceeds 15° in-between neighbouring cells.

A flowchart of the procedures of CPFEM and CA combination is shown in Fig. 4. The grain level strain and strain rate will be calculated from CPFEM and used as input in CA modelling to calculate the cell dislocation.

By obtaining the \({Q}_{\text{act}}\) values from the study by Li et al. [5] on the same experiments with similar conditions and another study by Xu et al. [39] on the investigation of hot deformation machining of Ti–6Al–4 V, the relevant parameters are presented in Table 5.

Table 5 Material parameters for CPFEM and CA model
Full size table

3 Results and discussion

3.1 CPFEM

To validate the CPFEM model, thickness distribution between simulation and experiment was performed to compare the difference. The experimental thickness was obtained from the FARO 3D scanner and the simulation thickness measurement was obtained from the thickness calculation of the upper and lower surface coordinates using the following equation:

$$t=\sqrt{{\left({x}_{1}-{x}_{2}\right)}^{2}+{\left({y}_{1}-{y}_{2}\right)}^{2}+{\left({z}_{1}-{z}_{2}\right)}^{2}}$$
(37)

where t is the sheet thickness, \({x}_{1}\), \({y}_{1}\), and \({z}_{1}\) are the coordinates of nodes on the top surface path, \({x}_{2}\), \({y}_{2}\), and \({z}_{2}\) are the coordinates of nodes on the lower surface path.

As shown in Fig. 5, it can be noticed that the simulation performed a close distribution as the experimental measurement, which indicated good validation.

As illustrated in Fig. 6(a), 3 specimens were cut off from the sample, and the transverse surface was used for EBSD investigation, as shown in Fig. 6(c). The corresponding elements on the CPFEM thickness side were used for data collection, as illustrated in Fig. 6(b). The node with 4 × 4 elements surrounding it was selected to calculate the strain distribution along with the thickness. Where a typical element is presented in Fig. 6(d).

The CPFEM outputs are based on calculations from "Single-crystal constitutive model" of temperature, plastic strain (\({\varepsilon }_{zz})\), and strain rate distribution data for Fig. 6(b) are illustrated in Fig. 7. Please note that these data were average data of the 4 × 4 elements, and the strain rate data were filtered by the Savitzky–Golay method, which is induced by the study by Press Teukolsky [40] on the study of high-frequency noise reduction in physical signals.

It can be noticed that a critical point (temperature, strain, and strain rate) is reached while the tool passes through the selected node. As shown in Fig. 7(a), the temperature distribution for the upper node is different from the centre and the lower node, since the temperature is rising at the experiment initiation stage, while the tool is passing through the centre and lower node, the temperature is slightly increased and the area at the end is fully heated. The temperature distributions result in differences in plastic strain (\({\varepsilon }_{zz})\) distributions. It can be seen in Fig. 7(b), that the lower temperature distribution results in lower strain distribution at the upper node, and the strain is increased as the strain rate is increased. It is noticed in Fig. 7(c) that the strain rate value reaches the peak value of 0.6, 0.7, and 0.8 s−1 for the upper, centre, and lower regions, while the tool passes through the unique node. Therefore, this is evidence that the strain rate is increased slightly for each increment, and the equivalent strain is increased accordingly. Nixon et al. [41] have investigated the experimental and constitutive modelling of \(\alpha\)-titanium and proposed that the strain of the workpiece is sensitive to the displacement rate of the indenter. In this work, the increment increase of strain rate has induced strong strain hardening effects on the workpiece. Due to the temperature supply from the induction heater, an initiation of DRX is achieved and the process is following the movement of forming tool from the upper to the lower region.

3.2 RVE and pole figures

The mesh of RVE is illustrated in Fig. 8(a). As stated in "Representative volume elements (RVE)", the RVE has 356 grains using 8-node thermally coupled brick, trilinear displacement, and temperature (C3D8T). A total of 12,167 elements were generated on the RVE model. The boundary conditions are illustrated in Fig. 8(b), the bottom surface is constrained with displacement \({U}_{x}={U}_{y}={U}_{z}=0\). A time-dependent temperature and strain rate (Fig. 7) was applied on the top surface of the RVE model. The grain orientation will be obtained from the simulation of RVE to form pole figures to compare with experimental pole figure results using MATLAB toolbox MTEX, which is produced by Niessen et al. [42] on the investigation of grain reconstruction and microstructure evolution of metals.

To validate the RVE and CA results, EBSD has been done on the transverse (thickness) direction of as-received, 700 \(\mathrm{^\circ{\rm C} }\) upper, centre, and lower samples and pole figures were obtained from EBSD investigation to compare with pole figure results from MTEX. The EBSD machine used was TESCAN MIRA3 FEG-SEM, and the data were analysed by AZtecCrystal. The following parameters were applied to EBSD characterisation, step size: 0.2 µm, pixel binning mode: 2 × 2, accelerating voltage: 30 kV, and electron beam current: 5 nA. The crystal coordinate system (CCS) and sample coordinate system (SCS) are in the following relationship, where normal direction (ND) = [0001] sample, rolling direction (RD) = [\(10\overline{1 }0\)] sample, transverse direction (TD) = [\(11\overline{2 }0\)] sample. To investigate the in-depth evolution in microstructure, the TD surface was selected for the EBSD investigation.

In this article, the basal \(\left\{0001\right\}\) and prismatic \(\left\{1010\right\}\) slip systems are the main objective to study, the common slip direction for these two systems is \(\langle 11\overline{2 }0\rangle\), which is parallel to basal poles. The pole figures of the as-received sample are shown in Fig. 9(a). The texture of the as-received sample illustrates a strong hot-rolled HCP basal feature which is more preferentially distributed along the TD direction and formed a fairly equiaxed basal/transverse texture.

As the experiment progressed to the 700 \(^\circ{\rm C}\) upper region, it can be noticed in Fig. 10 that the basal pole texture is gradually transformed from basal/transverse to the concentrated c-axis (parallel to the normal direction), and a prismatic slip \(\left\{1010\right\}\) is approximately formed. Since the DRX is time-consuming and sensitive to changes in temperature and strain rate, the prismatic slip texture at this stage is not substantial. However, it is still noticed that the nucleation of DRX towards the centre of basal oriented grain boundary, which indicates the rotation of grains angle leads to a pronounced increase of misorientation angles inside the basal pole to form a strong texture.

As the experiment processed to the 700 \(^\circ{\rm C}\) centre region in Fig. 11, the basal pole exhibits an expansion towards the rolling direction (RD) and a high-intensity prismatic pole is observed. This indicates that the growth of DRXed grains is formed at the initial basal pole grain boundary. The temperature at this stage is more steady-state and sufficient than the upper region, which enhances the DRX process and suppresses the twinning, thus resulting in an efficient basal slip and promoting a prismatic pole. The previous study by Warchomicka et al. [43] investigated the high-temperature deformation behaviour in Ti–5Al–5Mo–5 V–3Cr–1Zr and revealed that the dynamic strain-induced boundary migration (D-SIBM) is an important factor in DRX to form the deformation texture. As the temperature is sufficient, the nucleation of DRXed grains is usually formed at the grain boundaries with the D-SIBM due to the change of stored energies and dislocation densities between basal and prismatic-orientated grains. Li and Yang [44] studied the D-SIBM on hot compressed Ti-5Al-5Mo-5 V-1Cr-1Fe Alloy and proposed that the grains in the prismatic pole have a greater Taylor factor than the basal pole, which led to higher stored energy in the hot compression that initiated a driving force for D-SIBM from basal to prismatic oriented grains. This is good evidence that D-SIBM is combined with DRX at this stage to dominate the microstructure evolution.

For the 700 \(^\circ{\rm C}\) lower region in Fig. 12, the grains at the basal pole toward the RD axis form relatively higher intensity at the edge. The prismatic pole remains with a relatively lower intensity but clear texture, which shows that more sufficient DRX is achieved at this stage. The deformed grains are diffused from the basal to the prismatic pole. It can be observed that the strain and temperature from experiments exhibit a high impact on the crystal slip systems.

For the RVE-produced pole figures shown in part (b) from Figs. 9 to 12, it can be seen that the as-received samples have shown a great match for grains orientation with approximately 90% similar to the EBSD observed. The accuracy of modelling is slightly reduced to approximately 80% close to the EBSD measured from the upper to lower region, which is mainly attributed to pronounced temperature variance approaching the end of the process. Furthermore, the number of grains counted in RVE is only 356 grains obtained from the EBSD as-received sample. This number is sufficient for RVE to present a close pole figure; however, the inaccuracy will be increased in the calculation of the complex deformation system. It can be seen from Figs. 10(b) and 11(b), that the pole figures are still matched in an acceptable way which means the RVE is still able to predict the grain orientation at a relatively low DRX level, and the increase of temperature and strain rate at the lower region may cause further unpredictable DRXed grains. Furthermore, the twinning is suppressed in this study to reduce the complexity of transporting data between each system, thus it results in a relatively different pole figure in Fig. 12(b). It is still noticeable that the grain orientation in Fig. 12(b) has shown a tendency for grains to slip of HCP crystal in the hot deformation process, which can be assumed as accurate if a stable deformation and temperature distribution can be applied during the experiment. The tendency of grains to slip and the orientation of titanium HCP grains under stable deformation can be viewed in the study by Hama et al. [45] on the work-hardening and twinning behaviours of titanium sheet, where similar pole figures were obtained that represents the high critical resolved shear stress in the hot deformation of titanium sheet. Zhang et al. [46] on grain refinement of Ti–6Al–4 V in hot deformation has presented similar results and commented that the grain orientation has resulted from a grain refinement that implied significant improvement in the micro-hardness and tensile properties of the alloy.

3.3 CA and EBSD

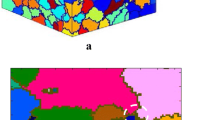
The EBSD IPF maps for 700 \(^\circ{\rm C}\) upper, centre, and lower stages are shown in Fig. 13. It is noted from Fig. 13(a) that the as-received sample consists of numbers of initial recrystallised grains which illustrates a typical hot-rolled Ti–6Al–4 V feature. As the experiment moved to the 700 \(^\circ{\rm C}\) upper region, the DRX is initiated, which tends to decrease the true stress. The initiation of DRX is more pronounced at the 700 \(^\circ{\rm C}\) centre region until the grains are recrystallised to coarser grains with a size of around 1 µm. The nucleation is increased incrementally, which limits the DRXed grain sizes and reduces the grain size. Detailed information on grain size can be found in Table 6.

The recrystallised percentage of the as-received and experimental samples is shown in Fig. 14. It can be noted that the recrystallised fraction is increasing according to the experimental process, from 19.7% for the as-received sample and process to 71% for the lower sample. The simulated CA microstructure is shown in Fig. 16. It is worth noting that the grain growth in the CA simulation is approximately 90% of the EBSD measurements. By investigating the CA simulated results, it can be seen that the nucleation of DRXed grains is more pronounced at grain boundaries, which indicates an increase in grains angle due to thermomechanical strain change throughout the process as shown in Fig. 15. The previous study by Shrivastava and Tandon [47] on microstructure analysis of SPIF commented that SPIF has strong work hardening behaviour that transfers the low-angle grains (< 15°) to high-angle grains (\(>\) 15°).

Please note, to simulate a microstructure close to the close-experimental as-received sample, the initial CA is first applied with a strain rate of 0.01 s−1 and a temperature of 700 \(^\circ{\rm C}\) to reach a recrystallisation level of 20%. The parameters follow the study by Paghandeh et al. [48] on investigations of the microstructural evolution of Ti–6Al–4 V alloy. This formed map is then set as the initial microstructure, the experimental parameters will be applied to this map to simulate the evolution.

By integrating the CPFEM grain orientation from the upper, centre, and lower nodes into the CA model to calculate the DRX fraction, the obtained simulating results are compared with the corresponding EBSD obtained results as shown in Fig. 17. As illustrated, the increase of DRX percentage is linear with the strain distribution. As the forming tool passes through the node (upper, centre, and lower) of the investigation, a critical value of temperature and strain is achieved and induced a peak DRX percentage. It can be noticed the increasing trend tends to reduce and maintain a steady-state level once the peak DRX percentage has passed and the results are agreed with the EBSD measured recrystallisation. It can be revealed that the temperature increases from the upper to lower node induce an increased trend of strain distribution according to these nodes. The reason can be correlated to the relatively constant strain rate. The temperature implies significant effects on the strain distribution. From the upper to lower stage, a 30 \(^\circ{\rm C}\) temperature variation is detected during the process, and it affects the increase of strain. At the upper stage, the induced temperature is not stable, thus resulting in lower strain distribution, which leads to the lowest DRX level. The temperature is at a steady state at the centre stage, and the highest temperature (730 \(^\circ{\rm C}\)) is obtained at the lower stage. The DRX is increasing accordingly to the temperature-induced strain. This proves that a small temperature variation may result in changes in strain distribution that significantly affects the DRX performance. By comparing with the EBSD examined recrystallised fraction, it can be observed that the EBSD values are slightly higher than the DRX results from CA. This is attributed to the calculation method in CA simulation that the continuous DRX only counts the evolution of low angle (\(<15^\circ\)) boundary grains to high angle (\(>15^\circ\)) grains. This may cause an error with the recrystallisation calculation in the AZtecCrystal software, where the DRX percentage includes the geometric DRX, continuous DRX, and discontinuous DRX. Regardless of the limited difference, both results still match well.

The CA simulated dislocation density results for the upper, centre, and lower regions are shown in Fig. 18. It is noted that the evolution of dislocation density is proportional to the DRX fraction, where the thermomechanical behaviours (strain rate and temperature) indicate significant effects in dislocation density development. The critical level on dislocation density also follows the zone of forming tool passing through the node area, and a steady-state region is reached once the critical level is passed.

It could be noted that the growth of dislocation density at the 700 \(\mathrm{^\circ{\rm C} }\) upper stage is more rapid than at the centre and lower stage, however, the peak point value is relatively low. The rapid increase of the growth can be attributed to the increase in strain rate at the centre and lower stage. As illustrated in Fig. 7, the peak value of the strain rate for the upper stage is around 0.6 s−1, and the value is increased to 0.7 s−1 at the centre stage and 0.8 s−1 at the lower stage. According to the previous study by Ding and Guo [34] on the hot deformation DRX analysis, the critical dislocation density can be reached more readily at a lower strain rate as it results in the initiation of DRX at a relatively small strain that leads to a rapid increase of DRX percentage. At a higher strain rate, the increase of critical strain and DRX percentage is more graduate, thus reducing the rapid growth of dislocation density, such as the phenomenon in this article.

Another study by Ding and Guo [8] on the experimental and simulation of microstructure evolution of Ti–6Al–4 V alloy suggested that strain rate and temperature have a significant effect on the dislocation density, as the critical value is increased with strain rate but decreased with temperature. In this article, it could be seen that the strain rate dominates the growth of dislocation density over the temperature, as the incremental increase of strain rate provides a noticeable increase in dislocation density even at the temperature at the centre and lower stage. Zhu et al. [49] on GND analysis in shear localisation of pure titanium commented that the work hardening is primarily contributed by active \(<a>\) slips that result in higher \(<a>\) type dislocation density. Another study by Sangid et al. [50] on the energetics of residual dislocations suggested that the local stress concentration in dislocations may generate residual dislocations on the energy barriers, thus resulting in higher dislocation density. The low-angle to high-angle transmission in this work is a role that increases the residual dislocations. Furthermore, a study by Guo et al. [51] on the investigation of the effects of stacking-fault energy (SFE) of \(\alpha\)-Ti stated that a change of slip mechanism could occur as temperature increases and the addition of Al elements. According to the study by Williams et al. [52] on the investigation of single-crystal Ti–Al alloys, the titanium alloys with an Al concentration of 5–6 wt % have shown identical critical resolved shear stress (CRSS) during temperatures from 400 to 1000 K. At this temperature range, the cross-slip is not pronounced and may results in dislocation entanglements in the alloy. Britton et al. [53] have commented that such a phenomenon may reduce the values of CRSS and increase the basal and prism slip. Thus, it can be assumed that the incremental induced deformation results in a slip in basal and prism planes (stated in "RVE and pole figures") increases the dislocation density, and results in substantial creep through the TD direction.

For a thermomechanical deformation with dynamic straining behaviour such as the experiments in this article, Hama et al. [54] have commented that the prismatic \(<a>\) type slip is more favoured for shear banding behaviour and in-plane anisotropy in work hardening. Thus, by using \(<a>\) type mode and Burger’s vector of 0.5 in the EBSD calculation of GND, the GND distribution maps and statistics results are displayed in Figs. 19 and 20. It can be clearly seen that the 700 \(\mathrm{^\circ{\rm C} }\) upper stage indicates an area of relatively low dislocation density (6.0 × 1014/m2) and it is increased to higher dislocation density at the centre (6.6 × 1014/m2) and lower stage (6.9 × 1014/m2). The measured GND results matched with the CA simulated results as 5.9 × 1014/m2 for the upper, 6.4 × 1014/m2 for the centre, and 6.8 × 1014/m2 for the lower stage.

The comparison of experimental mean grain size and CA simulated grain size regarding the upper, centre, and lower regions are shown in Fig. 21. It can be seen that the CA model indicated a trend of grain size reduction after straining work which is close to the EBSD results with a relative error of less than 5%. By comparing with Fig. 17, it can be noted that the mean grain size has been significantly refined with the incremental increase of strain and DRX percentage. For each stage (upper, centre, and lower) of the process, the incremental increase of temperature enhances the DRX initiation and results in a stress release in-between the subgrain, which accelerates the mobility of the grain boundaries misorientation. Zherebtsov et al. [55] investigated the microstructure and mechanical behaviour of Ti–6Al–4 V between 450 and 700 \(\mathrm{^\circ{\rm C} }\) with dynamic strain rate. The study reported that the hot deformation behaviour above 550 \(\mathrm{^\circ{\rm C} }\) indicates an ultrafine α and β subgrains, which is attributed to the enhancement of diffusion from the dynamic microstructural coarsening.

By referring to the EBSD measured data in Table 6, it is noticed that the low angle (\(<15^\circ\)) grains evolute to high angle (\(>15^\circ\)) grains according to the experiment process. By comparing with the experimental grain size data (obtained from EBSD), it can be seen that the experimental grain size is following the evolution of CA. Due to the small grain size measured from EBSD, the results from CA cannot provide a perfect match. However, the evolution between the CA and experimental results still agrees. The previous study by Orozco-Caballero et al. [56] has represented a similar behaviour and commented that the grains slip in α-Ti, which usually occurs while the temperature is above 650 \(\mathrm{^\circ{\rm C} }\), with a constant strain rate. In this article, the thermomechanical behaviour at 700 \(\mathrm{^\circ{\rm C} }\) upper is unable to accelerate the grains slip and dislocation for a full DRX, thus the result of 700 \(\mathrm{^\circ{\rm C} }\) upper is much lower than the centre and lower results. As the experiment is processed to the centre and lower region, enhanced DRX is achieved, which makes the results closer to each other.

Table 6 Grain data measured by EBSD
Full size table

The fraction of grain size for each experimental parameter is illustrated in Fig. 22. With assistance from Table 6, it is noted that the grain size is in a descending trend according to the experimental conditions. As the experiment initiates, the grain size is reduced to around 1 to 1.5 µm. There is no significant difference between the 700 \(^\circ{\rm C}\) upper to 700 \(^\circ{\rm C}\) lower samples. However, the maximum and minimum grain sizes distinguish the results. The maximum grain size of the upper sample is 10.4 to 6.3 µm, and the minimum grain size is reduced from 0.71 to 0.2 µm. The β-phase content and the sharp increase of grains angle from low to high also indicate that the thermomechanical behaviour from the SPIF is dynamic in the upper region and it is getting more steady at the centre and lower region, which balance the DRX process.

Wang et al. [57] have investigated the hot deformation and the microstructure evolution of Ti–6Al–4 V alloy. The study has detected a phenomenon that indicates a transformation of stable grain slip to active slip modes during 650 \(\mathrm{^\circ{\rm C} }\) deformation. Thus, it can be evident that the sustainable support temperature of 700 \(\mathrm{^\circ{\rm C} }\) in this work is sufficient to initiate the DRX process. With an increment increase of strain rate from the upper to lower region, the straining behaviour is also enhanced, thus leading to development in dislocation density.

4 Conclusion

  1. 1.

    The grain level strain, strain rate, and temperature distribution from the element-to-grain CPFEM are verified as useful to be used as input to establish the RVE model.

  2. 2.

    The pole figures obtained from the RVE reveal approximately 80–90% closed texture (grain orientation) as EBSD results and the changes in the pole figures at each stage indicate the microstructural evolution of the heat-assisted SPIF process.

  3. 3.

    The recrystallisation percentage is proportional to the incremental stage of the process, and the relationship is actively linked to the evolution of dislocation density. The temperature and strain rate distribution are key factors that dominate the distribution of dislocation density.

  4. 4.

    For an incremental increase in strain rate and temperature, the dislocation density is increased accordingly, which indicates that the strain rate shows higher domination in controlling the dislocation density, which overcomes the reduction of dislocation density from the temperature increase. Furthermore, it can be found that the dislocation entanglements and residual dislocations are secondary factors that increase the basal and prism slip, which increases dislocation density.

  5. 5.

    The grain size evolution is inversely proportional to the recrystallisation percentage and dislocation density where the slip of grains is increased with the increase of misorientation angles from a low angle (\(<15^\circ\)) grains to high angle (\(>15^\circ\)) grains homogenously. Such behaviour results in a reduction in grain size.

  6. 6.

    The critical point of the DRX percentage, dislocation density, and grain size corresponds to the contacting zone of forming tool passing through the node area. Once the peak value is reached, a steady-state region will be achieved.

This study has proposed a combination of CPFEM, RVE, and CA modelling of heat-assisted SPIF work of Ti–6Al–4 V sheets to provide the plasticity behaviour and microstructural evolution of the sheet materials under thermomechanical deformation. This study is only available for single crystal constitutive law based on HCP crystal structure. Therefore, there is no measurement of phase transition and no twin grain calculation. The current modelling can be improved in the future to apply polycrystalline inputs to simulate the plasticity behaviour above phase transition.

Fig. 1
figure 1

Induction heating SPIF system a working scheme, b CAD model, and c tool path

Full size image
Fig. 2
figure 2

CPFEM of heat-assisted SPIF a boundary conditions, b finite element mesh, and c equivalent plastic strain from deformed SPIF simulation

Full size image
Fig. 3
figure 3

The process of generation of RVE a EBSD IPF (inverse pole figure) map of the as-received sample, b RVE created by DREAM.3D, and c ABAQUS model

Full size image
Fig. 4
figure 4

The flowchart of the combination of CPFEM (ABAQUS VUMAT) and CA modelling

Full size image
Fig. 5
figure 5

Thickness distribution between experiment and simulation

Full size image
Fig. 6
figure 6

Represented specimen and model for a 3 cut-off investigation specimens from the experimental sample, b the correlated elements (upper, centre, and lower) on the CPFEM model, c EBSD investigation symmetry and scan surface, and d isotropic view of a typical element

Full size image
Fig. 7
figure 7

Grain level parameters a temperature, b plastic strain (\({\varepsilon }_{zz})\), and c strain rate

Full size image
Fig. 8
figure 8

The simulation of RVE a mesh of RVE and b boundary conditions of RVE

Full size image
Fig. 9
figure 9

Pole figures of as-received sample a experimental and b RVE

Full size image
Fig. 10
figure 10

Pole figures of 700 \(^\circ{\rm C}\) upper sample a experimental and b RVE

Full size image
Fig. 11
figure 11

Pole figures of 700 \(^\circ{\rm C}\) centre sample a experimental and b RVE

Full size image
Fig. 12
figure 12

Pole figures of 700 \(^\circ{\rm C}\) lower sample a experimental and b RVE

Full size image
Fig. 13
figure 13

EBSD IPF maps of a as-received, b 700 \(^\circ{\rm C}\) upper, c 700 \(^\circ{\rm C}\) centre, and d 700 \(^\circ{\rm C}\) lower

Full size image
Fig. 14
figure 14

Recrystallised level of as-received, 700 \(^\circ{\rm C}\) upper, 700 \(^\circ{\rm C}\) centre, and 700 \(^\circ{\rm C}\) lower

Full size image
Fig. 15
figure 15

EBSD band contrast-based grain boundary distribution maps a as-received, b 700 \(^\circ{\rm C}\) upper, c 700 \(^\circ{\rm C}\) centre, and d 700 \(^\circ{\rm C}\) lower

Full size image
Fig. 16
figure 16

CA simulated microstructure under dynamic strain rate and temperature a as-received, b 700 \(^\circ{\rm C}\) upper, c 700 \(^\circ{\rm C}\) centre, and d 700 \(^\circ{\rm C}\) lower

Full size image
Fig. 17
figure 17

Comparison of DRX fraction between experimental and CA simulated results

Full size image
Fig. 18
figure 18

Dislocation density from CA simulated results

Full size image
Fig. 19
figure 19

EBSD band contrast-based GND maps. a 700 \(^\circ{\rm C}\) upper, b 700 \(^\circ{\rm C}\) centre, and c 700 \(^\circ{\rm C}\) lower

Full size image
Fig. 20
figure 20

Statistics plots of GND results

Full size image
Fig. 21
figure 21

Comparison of simulated and experimental mean grain sizes as a function of deformation strain

Full size image
Fig. 22
figure 22

The area fraction of grain size for different experimental parameters

Full size image