1 Introduction

Current environmental regulations and policies, aimed at reducing carbon emissions, have accelerated the need to develop industry capabilities for a higher uptake of lightweight structures for e-mobility and fuel efficiency [1, 2]. In turn, these requirements have led to the development of joining processes with capabilities for (i) joining multi-material [3, 4]; (ii) high welding speed for high volume manufacturing of multiple product variants; and (iii) rapid development and deployment of new joining processes as required by shortened lead time and increased product variants [5]. Remote laser welding (RLW) is one of the joining processes which can potentially meet the aforementioned requirements due to several advantages such as imposing heat in a very controlled manner by modulating the power and location of the heat source, which define the welding thermal cycle. It offers a non-contact single-sided joining technology that allows high-speed welding for high-volume manufacturing [5, 6]. However, a key challenge is shortening the new process development time for the selection of key process parameters to meet welding thermal outputs pertaining to weld quality. Currently, the development of the RLW process is time-consuming due to the interactions between those factors that provide flexibility. Consequently, process development at present has relied on physical experiments (“weld trials”). Since modelling of weld thermal cycle is becoming more advanced, there is an opportunity to augment some of the physical experimentation through computer simulations.

The heat treatment induced during the welding thermal cycle causes significant metallurgical changes to the surroundings of the weld area (heat-affected zone (HAZ)) which determine the quality and mechanical properties of the weld. Beam oscillation leads to the inclusion of extra parameters which changes the weld thermal cycle and thus modify the mechanical behaviour of the weld [7]. Jiang et al. [7] found that beam oscillation leads to an increase in tensile strength by 20% and elongation by 45%. Hu et al. [8] investigated the effect of beam oscillation on the microstructure and mechanical properties of the laser welding of aluminium alloys. They found that the application of beam oscillation leads to an increase in ductility and tensile strength due to the formation of fine grains and modification of grain morphology. Therefore, the understanding and selection of the welding thermal cycle is a crucial task in obtaining the desired weld quality as described by microstructure and mechanical properties. To be able to do this, it is important to model the relations between the welding thermal cycle, welding process parameters (WPPs), and welding thermal outputs. It is worth noting that these relations are crucial not only to select WPPs but also to estimate welding process capability space (Cp-Space called in this paper), to understand process parameters allowable variation and then be able to control the process during the production phase. In the case of RLW, the key WPPs which govern the local temperature distribution during the weld thermal cycle are welding speed, heat source power modulation, and beam oscillation [9]. These WPPs are highly coupled with varying sensitivity to IPIs. For example, the adjustment of beam oscillation modifies the weld thermal cycle and results in changes in weld IPIs such as the peak temperature, HAZ volume, and cooling rate which affects the weld microstructure and the mechanical properties [10, 11].

Overall, there is a strong need for welding process parameter selection and for the understanding of their sensitivity to IPIs, which need to be determined during the process design phase. Physical experiments alone are not sufficient to survey the entire design space, as it takes weeks to run them. Efficient simulation of welding thermal cycle provides the option to be (i) run in the entire parameter space (high-fidelity simulations which replace physical experimentations), or (ii) integrated with physical experiments in such a way that simulations are run in un-tested settings of parameter space decreasing the number of experiments required (lower fidelity simulations which reduce the number of physical experiments). Additionally, experimental measurements of peak temperature and cooling rate are difficult due to very high peak temperature and small weld pool formed. However, they can be quantified by using simulation tools [12].

The local temperature distribution during the welding thermal cycle is important for process assessment. Moreover, with the advent of high computational advancements, numerical approaches such as finite element (FE) methods have gained importance as these can model different material combinations, heat source types, geometrical configuration, and boundary conditions for laser welding. The state of the art for numerical simulation of the welding processes can be found in [13,14,15]. To evaluate the welding thermal cycle, a precise elucidation of the heat source is crucial. Several heat transfer models have been developed for different dimensions and shapes of the heat source for the calculation of the welding thermal cycle. Rosenthal [16, 17] proposed a point heat source moving in an infinite material and Swift-Hook and Gick [18] approximated the solution to predict the power needed to cause melting. Different dimensions and shapes of the heat source models have been developed considering that the keyhole formed is circular and isothermal [19,20,21]. Heat transfer models with several designs of the heat source(s) from the very basic cylindrical to the most realistic conical/elliptical, double ellipsoidal, or a combination of them were developed [22,23,24]. Various numerical models using volumetric heat sources have been developed to calculate the temperature distribution for full and partial penetration during welding [25,26,27,28]. Bianco et al. [29] showed that a quasi-steady state of the temperature profile is reached, and Shanmugan et al. [30, 31] consider the heat source as a 3D conical Gaussian heat source to calculate the distribution of temperature in the laser-welded T-joint. The Gaussian distribution is one of the most frequent methods to describe the continuous heat distribution from the laser beam [32]. The newly developed RLW process with an oscillating beam improves strength, reduces spatter formation, and stabilises the process [33, 34]. It has also been found to improve the gap bridging ability for imperfect edges due to wider welds in tailored blanks [35] in addition to enhancing joint quality by increasing the bond area [36]. There is some evidence to suggest that the amplitude of oscillation can impact weld shape and tensile strength for the welding of dissimilar aluminium alloys [37]. Moreover, ductility has been shown to improve and shrinkage reduced during the second pass of the oscillating laser beam due to a lower cooling rate [7]. Most of the existing studies are based on the examination of post-welded microstructure and performance, but no studies have addressed the modelling of beam oscillation and its interactions on the welding thermal cycle during the welding of dissimilar Aluminium alloys; however, the interest is on the rise [8, 37].

In welding simulation, inputs are understood as welding process parameters (WPPs) and the quality performance is evaluated by using multiple outputs which are called intermediate performance indicators (IPIs) in this paper. It was observed that these process parameters not only affect the welding thermal cycle IPIs, but also the key performance indicators of other downstream processes. However, the current literature has focussed mainly on single or multiple inputs and single-output scenarios which are not sufficient for laser welding, since this process is characterised by multiple inputs and multiple output (MIMO) scenarios [38]. In this paper, a comprehensive and detailed process variation has been performed which addresses the MIMO scenario. To the best of our knowledge, there are not many conclusive studies reported in the literature so far which describe the interactions between the welding speed, heat source power, and beam oscillation.

In addition to the existing numerical models, it is a need to study the effect of beam oscillation on the weld thermal cycle. For this reason, this paper introduces a simulation methodology to develop (i) a numerical model for the welding process and design space refinement considering multiple inputs (i.e. key WPPs) and multiple-outputs (i.e. IPIs) system by conducting computer simulations; (ii) process capability space (Cp-Space) which is depicted by parametric contour maps based on the developed numerical model that allows the estimation of a desired process fallout rate in the case of violation of process tolerances; and (iii) a surrogate model to develop the relationship between the WPPs and IPIs and also for the quick estimation of IPIs without running time-consuming numerical simulations. The Cp-Space is the subset of the design space which includes all the selected WPPs producing all the accepted IPIs.

2 Modelling approach

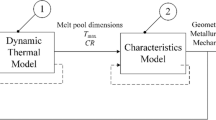
The approach proposed in this study addresses two main limitations of the current literature as mentioned in the introduction by taking into consideration (i) MIMO scenario for modelling welding thermal cycle, (ii) oscillating heat source as a process parameter, and (iii) process variation over the design space to reduce the number of physical experimentations required. The Cp-Space is defined to address the limitations by establishing a set of IPIs to extensively evaluate the laser welding process and refinement of the design space based on the given quality requirements. The flowchart of the three main objectives in this study are (i) weld thermal cycle estimation, (ii) Cp-Space definition and visualisation, and (iii) process parameter selection which are shown in Fig. 1 along with the necessary sub-steps.

Fig. 1
figure 1

Flowchart of the main objectives of this study along with necessary sub-steps

Full size image

2.1 Transient FEM heat transfer model for weld thermal cycle estimation

The first objective of this study is to estimate the welding thermal cycle using a transient heat transfer model to calculate the temperature distribution T(x,y,z,t) during welding. The geometry with the mesh element size and distribution is shown in Fig. 2. To decrease the computation time within the required accuracy, the following assumptions were considered: (i) No gap between the two metal plates were considered; (ii) material properties such as thermal conductivity (k), heat capacity (cp), and density (ρ) were assumed to be temperature-dependent; (iii) the latent heat of melting and solidification are included; (iv) no convection in the melt pool was considered in the model; (v) no vapour and plasma flow is simulated in the model. A Gaussian distributed volumetric heat source was considered which generates the heat inside the material such that fusion zone boundary lines are comparable to the experimental results [39]; and (vi) additional contributions to the calculated temperature profile from exothermal reactions (e.g. oxidation) as originating from oxidation (i.e. exothermal reactions) and local effects of the shielding gas were not considered in this research work.

2.1.1 Geometry

A 3D Cartesian coordinate system is used. In the 3D model, the size of the plate was 100 mm × 50 mm with a thickness of 3 mm. Each plate was divided into three domains: 100 mm × 49 mm × 3 mm (base metal), 100 mm × 1 mm × 3 mm (fusion region), and 100 mm × 1 mm × 3 mm (weld centerline) as shown in Fig. 2. This improves the distribution of tetrahedral mesh elements for the simulation having a total mesh consisting of about 1,169,117 domain elements as shown in Fig. 2. The validation of the model was done using the welding of titanium to aluminium alloys with material properties and coupon geometry as in D'Sonia et al. [40]. The material properties are shown in Tables 5 and 6 (Appendix). In this study, the validation of the FEM heat transfer model for weld thermal cycle estimation was done by conducting welding of Aluminium 6061 and Aluminium 5754 alloys for no oscillation conditions and from the literature for beam oscillation conditions. The thermal material properties of Aluminium 6061 and Aluminium 5754 used for the numerical simulation are obtained from the COMSOL material library [41]. Due to the unavailability of material properties beyond a certain temperature, the values are kept constant for the value known at the last temperature value. All these properties are defined locally using a piecewise function as the temperature is a local quantity.

2.1.2 Governing equations

The heat source is considered perpendicular to the workpiece surface along the z-axis, and moving with constant welding speed along the x-axis. The calculated temperature field is a function of space (x, y, z) and time (t) which is determined by the non-linear energy conservation Eq. (1) [42].

$$\rho {c}_{p}\left[\frac{\partial T}{\partial t}\right]=\overrightarrow{\nabla }\cdot\left(k\overrightarrow{\nabla }T\right)+{Q}_{\mathrm{laser}}$$
(1)

where ρ (kg m−3) is the material density, cp (J kg−1 K−1) is the specific heat capacity of the material, T (K) is the temperature, t (s) is the time, k (W m−1 K−1) is the thermal conductivity of the material, and Qlaser (J m−.3) is the energy input of the laser heat source per unit volume. The phase changes are considered by using the apparent heat capacity method which includes an additional term for latent heat as shown in Eq. (2) [43]

$${c}_{P}={c}_{P,\mathrm{solid}}.\left(1-{f}_{l}\right)+{c}_{P,\mathrm{liquid}}.{f}_{l}+{L}_{s\to l} \frac{{\Delta f}_{l}}{\Delta T}{H}_{m}$$
(2)

where cp,solid (J kg−1 K−1) is the heat capacity of the solid phase, cp,liquid (J kg−1 K−1) is the heat capacity of the liquid phase, Ls→l (J kg−1) is the latent heat, and fl is the phase transition function. For pure solid fl = 0, and for pure liquid fl = 1.

Fig. 2
figure 2

a Schematic illustrations of geometry and finite element mesh distribution across the three zones (base metal, fusion zone, and weld centerline), used for the simulations and b experimental setup for the welding

Full size image

2.1.3 Heat source design and boundary conditions

The most used heat source shapes for modelling thermal quantities during laser welding are 3D cylindrical and conical volumetric heat sources [21, 44]. They have a volumetric Gaussian-shaped energy distribution, with the nominal power of the heat source at the centre (x0,y0,z0) is defined as shown in Eq. (3). Note that this relationship represents the 3σ range (99.7% of total heat input) of a heat source [45].

$$Q\left(x,\;y,\;z\right)=\frac{3P}{\pi {r}^{2}d}\mathrm{exp}\left(-3\frac{({x-{x}_{0})}^{2}+ ({y-{y}_{0})}^{2}}{{r}^{2}}\right)\mathrm{exp}\left(-3\frac{({z-{z}_{0})}^{2}}{{d}^{2}}\right)$$
(3)

where P (W) is the power of the heat source beam, r (mm) is the heat source spot radius, and d (mm) is the thickness of the workpiece. In this design, the heat generated by the heat source is a simplified representation of the keyhole formation during the laser welding where the temperature is maximum at the top surface and minimum at the bottom. For a moving heat source, the position of its centre needs to change with time (x(t), y(t), z(t)). The position at the start of the simulation (t = 0) was chosen to be at the origin (x0, y0, z0). Circular oscillated heat sources in the xy-plane are used because it has been found that fewer welding defects were observed experimentally [12, 35, 36, 46]. The trajectory of the moving heat source is defined by Eq. (4)

$${(x}_{(t)},\; {y}_{\left(t\right)}, \;{z}_{(t)})=\left({x}_{0}+St-R\left(1-cos\left(2\pi ft\right)\right), \;{ y}_{0}+Rsin\left(2\pi ft\right),\; { z}_{0}\right)$$
(4)

where x(t), y(t), and z(t) are time-dependent heat source spot coordinates; x0, y0, and z0 mark the initial position of the heat source, S (mm min−1) is the welding speed, R (mm) is the radius of oscillation, f (Hz) is the oscillation frequency, and t is the time. The term St gives the displacement in the welding direction while (1 − Rcos(2πft)) and Rsin(2πft) produce the circular rotation for the oscillation of the beam. In Eq. (4) at R = 0 and f = 0 gives the equation of no oscillation condition. The term Qlaser (x, y, z, t) (J m−3) is the moving heat source term in the energy conservation equation (Eq. (1)). The expression for Qlaser (x, y, z, t) can be defined by inserting the coordinates of the spot centre from Eq. (4) into Eq. (3) leading to the relation as shown in Eq. (5), which represents heat generated by the volumetric heat source with and without oscillation [47].

$$\begin{aligned}{Q}_{\mathrm{laser}}\left(x,\;y,\;z,\;t\right)=\eta \frac{3P}{\pi {r}^{2}d}&\mathrm{exp}\left(-3\frac{{\left(x-{x}_{\left(t\right)}\right)}^{2}+{\left(y-{y}_{\left(t\right)}\right)}^{2}}{{r}^{2}}\right)\mathrm{exp}\left(-3\frac{{\left(z-{z}_{\left(t\right)}\right)}^{2}}{{d}^{2}}\right)\end{aligned}$$
(5)

where P is the nominal power of the heat source beam, r is the spot radius, and d is the penetration depth and x,y,z is the position of the point where the temperature is calculated, and η is the material’s optical absorption coefficient and defined by Eq. (6) [48]

$$\eta \left(T\right)=0.365{\left(\frac{\alpha }{\lambda }\right)}^{1/2}-0.0667\left(\frac{\alpha }{\lambda }\right)+0.06{\left(\frac{\alpha }{\lambda }\right)}^{3/2}$$
(6)

where α (Ω m) is the specific electrical resistivity of the workpiece and λ (m) is the wavelength of the laser. The initial temperature of the workpiece is assumed to be room temperature (T0). The heat loss due to the contact with the ambient atmosphere and by radiation during welding are governed by Newton’s law of cooling and the Stefan-Boltzmann relation [49]. Convective and radiative heat loss is considered for the top and bottom surfaces which follows Eq. (7) [49]

$$-k\nabla T=h\left(T-{T}_{0}\right)+\varepsilon \sigma \left({T}^{4}-{T}_{0}^{4}\right)$$
(7)

The input process parameters are welding speed, heat source power, radius of oscillation, frequency of oscillation, and heat source spot size as depicted in Eqs. (4) and (5). The output of the model is the temperature distribution which represents a function of position and time taken to complete the welding. Three outputs of interest have been derived from the transient temperature distribution which are (i) peak temperature (Tpeak), (ii) heat-affected zone volume (VHAZ), and (iii) cooling rate (Crate). The Tpeak is defined as the maximum temperature recorded during welding. The VHAZ is defined as a region bounded between the temperature to cause metallurgical transformation and grain growth but less than the melting point of the material as defined in Eq. (8).

$${V}_{\mathrm{HAZ}} = \frac{{\int }_{{t}_{1}}^{{t}_{2}}\iiint T(x,y,z,t)dxdydzdt}{{t}_{2}- {t}_{1}},\; T\;\in [470 K, 933 K]$$
(8)

The temperature range lies between solidus and where grain growth is not possible and is taken as 933–470 K temperature range. The Crate (dT/dt) is defined as the change in temperature from the melting point to the 470 K upon the time taken.

2.1.4 Formulation of surrogate model for regression relation between WPPs and IPIs

A surrogate model is developed to formulate an analytical relationship between the WPPs and the IPIs using second-order and third-order polynomials. The linear expression is not sufficient to model such a non-linear relationship whereas fourth-order polynomials (and higher orders) would lead to over-fitting. The general formulation of the second-order and third-order polynomial expressions is shown in Eq. (9).

$$y={\beta }_{0}+{\textstyle\sum }_{i=1}^{k}{\beta }_{i}{x}_{i}+{\textstyle\sum }_{i=1}^{k}\left({\textstyle\sum }_{j=1}^{i}{\beta }_{ij}{x}_{i}{x}_{j}\right)+ \textstyle\sum_{i=1}^{k}{\sum }_{j=1}^{i}\left({\sum }_{l=1}^{l}{\beta }_{ijl}{x}_{i}{x}_{j}{x}_{l}\right)$$
(9)

where x1, x2,…, xk are independent variables and β0, βi, βij, βijl … are the regression coefficients. The regression model is developed by writing codes in Python. The coefficient of determination (R-square) is calculated, and the t-test and p-value were evaluated to assess the goodness of fit. The difference between the predicted and simulation values was plotted to visualise the goodness of fit between the polynomial regression and the numerical model. A tenfold cross-validation has been performed to assess the predictive performance of the surrogate model and to judge the model performance to new data outside the model data set.

2.2 Process capability space (Cp-Space)

The input WPPs considered in this study are welding speed (S), heat source power (P), the radius of oscillation (R), and frequency of oscillation (f). The four WPPs (S, P, R, f) are defined in Eq. (10), where i represents the index of WPP, and n represents the total number of WPPs.

$$\mathrm{WPPs}=\{{\mathrm{WPP}}_{1}, \;{\mathrm{WPP}}_{2},\;\dots ,\;{\mathrm{WPP}}_{n}\}$$
(10)

The quality performance of laser welding is governed by the three IPIs which are Tpeak, VHAZ, and Crate and are formulated in Eqs. (11) and (12), where j represents the index of IPI, m represents the total number of IPIs, and f represents the MIMO-model.

$$\mathrm{IPI}=\{{\mathrm{IPI}}_{1},\;{\mathrm{IPI}}_{2},\;\dots ,\;{\mathrm{IPI}}_{m}\}$$
(11)
$${\mathrm{IPI}}_{j}=f({\mathrm{WPP}}_{1},\; {\mathrm{WPP}}_{2},\; {\mathrm{WPP}}_{3},\;\dots , {\mathrm{WPP}}_{n})$$
(12)

The upper limits (ULs) and lower limits (LLs) of WPPs have been determined by considering technological constraints based on the physical experimental studies present in the literature. The upper and lower limits of all the WPPs are given in Table 1. The combination of all possible WPPs within the permitted limits defines the design space (ω0). In this paper, the design space is represented in the form of parametric contour maps where the x- and y-axis show the variation of two different WPPs and the coloured contour surface shows the derived values of IPIs. The parametric contour maps are developed for three IPIs, Tpeak, VHAZ, and Crate. The temperature for the bottom surface can be used for predicting partial penetration to full penetration depending upon the requirements of the downstream processes. The upper and lower limits of the IPIs are given in Table 2. The upper limit of the Tpeak (TpeakUL) is 3500 K as at this temperature, the temperature at the bottom surface is at the melting point of the material which shows that it is full penetration welding. The lower limit of the Tpeak (TpeakLL) is the melting point of the material, as different combinations of process parameters yield the same Tpeak but have different Crate and VHAZ. To select the lower and upper limits of the Crate, the Crate is maximised for those combinations which yield the TpeakLL and TpeakUL respectively. So, the maximum value of Crate at the TpeakLL is the lower limit of cooling rate (CrateLL). Similarly, for the upper limit of cooling rate (CrateUL), maximum value of Crate is selected at TpeakUL This is because a higher cooling rate promotes fine-grain formation. In the case of selecting lower and upper limits of VHAZ, the minimum value of VHAZ is selected for the combinations which provide TpeakLL and TpeakUL respectively. So, the minimum value of VHAZ at the TpeakLL is the lower limit of cooling rate (VHAZLL) and similarly for the upper limit of VHAZ (VHAZUL). This is because VHAZ should be minimum for better welded joint performance.

Table 1 Welding process parameters and their allowance limits for defining design space
Full size table
Table 2 IPIs and their allowance limits for defining Cp-Space
Full size table

The second objective of the work is to develop Cp-Space. A numerical model is computed to estimate the IPI values over the design space. If the estimated IPI violates the allowance limits, WPPs are considered unfeasible. For the jth IPI, process capability space is defined as expressed in Eq. (13), where k is the index of the individual Cp-Space and m is the total number of IPIs

$${\alpha }_{j}=\{ {\mathrm{IPI}}_{j} \quad\mathrm{if} \;{\mathrm{IPI}}_{j}^{\mathrm{LL}}\le f\left({\mathrm{WPP}}_{1},.. . .,{\mathrm{WPP}}_{n}\right) \le {\mathrm{IPI}}_{j}^{\mathrm{UL}}$$
(13)

The final process capability space (ωm) is the intersection of process capability space of individual IPI (αj) and (ωj−1) as defined in Eqs. (14) and (15) and illustrated in Fig. 3, where the final image in the upper row (Fig. 3d) is the intersection of all individual process capability spaces (ωj) based on the allowance limits of all the IPIs. Figure 3 demonstrates the definition of the final process capability space from the design space (Fig. 3a) based on the intersection of the individual process capability space of each IPIs. The shaded area in yellow represents the feasible region and any process parameters inside this region satisfy all the requirements.

Fig. 3
figure 3

Conceptual representation of process capability space (Cp-Space) for no oscillation condition (where R = 0 mm and f = 0 Hz). The top row shows the process capability spaces (at each step with an intersection with IPIs) and the bottom row shows the parametric contour maps of each IPIs with the allowance limit

Full size image
$${\omega }_{j} = {\omega }_{j-1}\;\bigcap\; {\alpha }_{j}$$
(14)
$${\omega }_{m} = {\omega }_{m-1}\;\textstyle\bigcap_{j=1}^{m}\;{\alpha }_{j}$$
(15)

The final process capability space ωm envelops all the feasible WPP values inside the design space ω0. Clearly, the design space is limited by the technical feasibility of the process and therefore by the upper and lower limits of the WPPs.

2.3 Process capability space (Cp-Space) refinement

The last objective of this study is the refinement of Cp-Space depending on the requirements of the downstream processes to reduce the number of welding trials during early design phase. It is important to note down that the methodology for process parameter refinement provided in this study is for the early design phase and process assessment. The process parameter refinement is performed on the ωm. In this work, sequential refinement strategies are developed based on three requirements of welding manufacturers which are defined as boundary constraints. The first constraint set is related to the IPI constraints which address the proper coalescence of metals produced by heating to a suitable temperature such that enough molten metal is formed to have proper fusion. The second requirement set is related to the overall design objective function which addresses the functional and strength requirements to control weld defects and strength of the weld. Third constraints set is related to being able to address the key application requirements such as high production rate, low cost, and/or additional welding requirements, i.e. aesthetic requirements of welded joints. Sequential refinement strategies for a few of the downstream processes are given in Table 3 in the order of their hierarchy. Welding can be considered the combination of two processes: the first one is the melting and evaporation of the workpiece to have a fusion and the other is the heat treatment of the workpiece. Both processes are governed by the welding thermal cycle. Proper control over the welding thermal cycle can improve weld properties and reduce weld defects.

Table 3 Proposed multiple strategies for process capability space (Cp-Space) refinement for various downstream processes and requirements
Full size table

3 Experimental details

Dissimilar welding of Al-5754 with Al-6061 is performed in this study. The welded coupons are machined into the size of 100 mm (length) × 45 mm (width) × 3 mm (thickness) and cleaned with acetone to remove surface contaminations before welding. A butt joint configuration was employed. No shielding gas or filler wire was used during the experiments. A 10-KW Coherent ARM FL10000 laser system as shown in Fig. 2b, with a beam parameter product of 16 mm mrad with a core optical fibre of 100 μm diameter, was used. The laser system coupled with the WeldMaster remote welding head (Precitec GmbH, Germany) has a 150-mm collimating length, a focal length of 300 mm, and the resulting Rayleigh length of 5.3 mm. Beam oscillation is generated by the motorised mirror and collimator integrated with the WeldMaster Scan&Track remote welding head (YW52 Precitec GmbH, Germany). Only a core beam was used to carry out the experiments. The weld dimensions were measured using a Keyence VHX7000 optical microscope at five different points on the weld seam which is 20 mm away from the start and end of the welding position. The welding head is tilted at 4° from the vertical direction. Constant laser power of 4500 W is adopted throughout the welding experiments. The welding speed is increased from 4000 to 6000 mm/min in step size of 500 mm/min such that to generate enough data points to compare the experimental results with the numerical model and also to analyse the effect of welding speed in no oscillation condition.

4 Results and discussion

The transient heat transfer model is validated by the experimental results from the literature [40, 50]. A total number of around 800 numerical simulations were carried out which serve as a base for the discussed results. Each simulation took 25 min to solve for no oscillation conditions and 105 min for oscillation conditions. This is due to the increased complexity introduced with the heat source oscillation (Eq. (4)) and an increase in the number of mesh elements as the heat source traversing area has been increased. All outputs from the model have been calculated after it attains the quasi-steady state. The evolution of the temperature field at different times and time required to attain quasi-steady state for different outputs have been added in supplementary materials for both no oscillation and beam oscillation conditions. The effect of WPPs on the IPIs and the process capability space (ωj) has been discussed. The process capability space refinement is illustrated with the help of an example followed by establishing the regression relationship between the WPPs and the IPIs using a surrogate model for the quick estimation of IPIs.

4.1 Model validation

The model is validated in three steps: (i) validation of 3D temperature distribution, (ii) validation of the model for welding of Al-5754 to Al-6061 in butt joint configuration with no beam oscillation, and, finally, (iii) validation for the cases of welding with beam oscillation. The first step involves validating the temperature profile from the literature that describes the 3D temperature distribution for Al-5754 and Ti6Al4V welded joints using a single point temperature profile obtained by thermocouples [40]. The target is to estimate the error in 3D temperature measurement. The thermal cycle generated from the simulation and experiment using a thermocouple is shown in Fig. 4. The thermal cycle obtained from the simulated model showed a similar tendency to the experimentally obtained thermal cycle from the thermocouple which illustrates the rationality of the numerical model. The obtained values of the peak temperatures were within the acceptable range as the difference is less than 0.1% and is constant throughout the model. The calculated heating cycle in comparison with the experimental results show a less than 0.5% difference while the cooling cycle for both the metals was found to deviate by 8% for titanium alloy and 2% for aluminium alloy which is well within the acceptable range. This difference between titanium and aluminium is due to the high thermal conductivity of aluminium (158.7 W m−1 K−1) as compared to titanium (14.7 W m−1 K−1). This suggests that the heat transfer by conduction is dominant in aluminium as compared to titanium due to its higher thermal conductivity values. Also, the difference in the peak temperature in the thermal cycle for both alloys can be attributed to the combined effect of heat capacity and thermal conductivity of the alloys. The higher heat capacity of aluminium requires more energy to raise the temperature and higher thermal conductivity leads to a rapid loss in heat thus decreasing the temperature. In the second step, the model is validated for the welding of Al-5754 and Al-6061 in butt joint configuration with no beam oscillation. The intention is to estimate the accuracy of the model for the change of material used for welding and the geometry of the joint configuration. The goodness of the model is compared based on the weld width at the top surface obtained experimentally for varying welding speeds as shown in Fig. 5. The maximum error seems to be − 6%. Results show that an increase in welding speed at constant laser power can effectively decrease the weld width. This is due to a decrease in heat input to the workpiece. Due to the reduced heat input, less melting of the material occurs. Due to the smaller volume of the molten pool, weld beads with reduced widths are formed. In the third step, the model is translated from no oscillation to beam oscillation condition for a varying radius of oscillation using experimental data from the literature [50] which is shown in Fig. 5f. The model shows a good accuracy with an error of 4.5%, thus demonstrating that the model can be used for laser welding with and without oscillation. To analyse the effect of WPPs on the IPIs and the process capability space, the validated numerical model is solved for the butt welding of Al-5754 with Al-6061 as the results are based on steps 2 and 3 of the model validation. Variation of IPIs due to the variation in process parameters is studied for both no-oscillation and beam oscillation conditions.

Fig. 4
figure 4

Calculated temperature distribution of Al–Ti welded joint, investigated in this study (top). The position of the weld central line and the thermocouple (top) is indicated by the arrow (top). Comparison between experimental and simulated thermal cycle at the titanium (bottom left) and aluminium side (bottom right). Experimental data has been reproduced from [40]

Full size image
Fig. 5
figure 5

Comparison between the calculated weld morphology from the model and the experimented weld optical micrographs for Al-5754 and Al-6061 laser welded joint. a Calculated weld width, b optical micrograph at a heat source power of 4500 W and welding speed of 4500 mm min−1. c Calculated weld width, d optical micrograph at a heat source power of 4500 W and welding speed of 6000 mm min−1. e Comparison between the calculated and experimented value of weld widths for varying welding speeds at a constant power of 4500 W for welding of Al-5754–6061. f Comparison between the calculated and experimented value of weld widths for a varying radius of oscillation at a constant power of 3500 W, 1500 mm min−.1 and frequency of oscillation of 100 Hz for the welding of Al-6061 (experimental data taken from [50])

Full size image

4.2 Characterisation of peak temperature, HAZ volume, and cooling rate for no oscillation condition

For the no-oscillation condition, Fig. 3e shows the simulated peak temperature contours for different combinations of heat source power (P) and welding speed (S). For laser welding in conduction mode, the peak temperature must remain between the melting and the boiling point of the metal. For the keyhole mode, the peak temperature must be above the boiling point of the metal being welded. The upper limit of peak temperature is 3500 K and the lower limit is the melting point to define the process capability space for welding as illustrated in Fig. 3e. The space above the upper peak temperature limit will lead to the cutting of the workpiece and the space below the lower limit will lead to only heating of the workpiece without any melting.

It was observed that with the increase in power at constant speed, the peak temperature increases due to the local increase in net heat input per unit length to the workpiece defined as (ηP)/S, whereas when the welding speed is increased at constant power, the net heat input to the workpiece decreases, leading to a decrease in peak temperature. The simulated cooling rate and heat-affected zone volume profiles are shown in Fig. 3f, g, respectively, for different combinations of heat source power and welding speed. It was observed that at constant welding speed with the increase in power, HAZ volume increases due to the higher heat input to the workpiece while the cooling rate decreases, whereas when the welding speed is increased at constant power, the HAZ volume decreases as net heat input to the workpiece decreases, causing a decrease in peak temperature which leads to an increase in cooling rate.

An important characteristic of the results in Fig. 3 is that a particular weld attribute, such as the peak temperature or cooling rate or HAZ volume, can be achieved by multiple combinations of WPPs. The weld thermal cycle depends on heat input and heat distribution during welding as described by Eq. (1). The heat input due to a laser heat source is described by Eq. (3) which is a function of WPPs. If the quotient of process parameters is the same, then the same peak temperature can be attained. For example, from Eq. (3), heat input is a function of laser power and welding speed; the same peak temperature can be attained if the laser power is high at a very high welding speed and low laser power at a low welding speed. Thus, the same quotient of process parameters in both cases results in similar heat input resulting in a similar peak temperature. The heat distribution can be described by the heat capacity and thermal conductivity of the material as described by Eq. (1). For the similar quotient of thermal conductivity and heat capacity, heat transport is expected to be similar. Also, for an alloy system, the same heat transport can be generated due to the similar heat capacity and thermal conductivity. This existence of multiple paths to achieve the desired weld requirements exhibits the flexibility of the laser welding process. For the estimation of process capability space, the peak temperature is the most important IPI and is chosen first followed by either of the other two depending upon the requirements of the downstream processes as given in Table 3. The final process capability is the intersection of the individual process capability spaces for all the IPIs as shown in Fig. 3d and the shape of the final process capability space will remain constant irrespective of the order of IPIs considered.

4.3 Characterisation of peak temperature, HAZ volume, and cooling rate for beam oscillation condition

In the no oscillation welding, it was identified that laser power and welding speed are relevant, and this section focuses on the effect of radius of oscillation and frequency of oscillation because it has been established that laser power and welding speed are important factors affecting the weld thermal cycle. Process variables that correspond to the shape and overlapping of the heat source are the radii of oscillation, frequency of oscillation, and welding speed which is explained in detail in Appendix 2. Heat input per unit length in the case of oscillating heat source is defined as [(ηP)/(S + 2πRf)]. There are two possibilities during circular beam oscillation, with and without overlap of the path of the oscillating heat source as shown in Fig. 6. The onset of overlapping during oscillating heat source occurs when the position of the heat source is at a distance R in the y-direction and at a distance 2R in the x-direction which leads to the conditional relation as (4Rf/S) = 1 (detailed derivation is given in Appendix 2). The term 2πRf denotes the circumferential velocity of the oscillating heat source, and S denotes the welding speed of the heat source in the welding direction. A higher value of (2πRf/S) implies that the circular motion is more dominant compared to the linear forward motion, leading to more overlapping as shown in Fig. 6b, c. A lower value implies forward motion is dominant, leading to either no overlapping or few overlaps. The number of overlapping points as a function of welding speed, the radius of oscillation, and frequency of oscillation is estimated graphically due to the complexity of equations and the results are listed in Table 4.

Fig. 6
figure 6

Trajectory of the oscillating laser beam for no overlap S ≥ 4Rf (left), overlapping at a lower frequency of oscillation when S ≤ 4Rf (middle); and overlapping at a high frequency of oscillation when S ≪ 4Rf (right)

Full size image
Table 4 Number of overlapping points with the corresponding mathematical condition for the radius of oscillation (R), frequency of oscillation (f), and welding speed (S)
Full size table

4.3.1 Effect of frequency of oscillation

There are two opposing factors governing the heat uptake from an oscillating heat source: (i) decrease in heat input per unit length due to an increase in effective speed (S + 2πRf), i.e. linear plus circumferential speed, and (ii) increase in heat input due to increase in the number of overlapping points. Figure 7a shows the contour plot between the frequency of oscillation, the ratio of circumferential velocity to linear forward speed (2πRf/S), and the heat input per unit length considering overlapping points (calculated in Appendix 2). For constant ratio of circumferential velocity to linear forward speed, the heat input remains constant with the increase in the frequency of oscillation. It can be inferred from the plot that at a constant value of the ratio of circumferential velocity to linear forward speed, heat input remains constant with the increase in the frequency of oscillation. This illustrates that the range of WPPs investigated in this study shows that the frequency has a negligible effect on the heat uptake during welding. At a constant frequency of oscillation, with an increase in the value of the ratio of circumferential velocity to linear forward speed heat input increases. This is due to the increase in overlapping points as R increases or decreases in S which leads to an increase in heat input per unit length. This explicit solution is supported by the transient heat transfer simulations as shown in Fig. 7. Figure 7b, c show the simulated peak temperature for different combinations of frequency of oscillation, welding speed, and heat source power. It is evident that the effect of frequency of oscillation is negligible on the peak temperature in both cases as contour lines are parallel to the y-axis showing the frequency of oscillation. Similar trends are found for the cooling rate and HAZ volume. With an increase in oscillation frequency, the number of overlapping points for every rotation will increase which leads to re-heating and the effective speed of the heat source increases as it has to rotate more times in the same amount of time. This re-heating should lead to a rise in temperature, but it is compensated by a decrease in heat energy absorbed per unit length due to the increase in the actual speed of the heat source. The increase in the actual distance travelled by the heat source with an increase in f is demonstrated in Fig. 6.

Fig. 7
figure 7

Heat input per unit length with varying frequency and ratio of circular speed and linear forward speed (welding speed) (a). b parametric contour maps for peak temperature depending on the frequency of oscillation and welding speed at a constant power of 3500 W and c parametric contour maps for peak temperature depending on the frequency of oscillation and heat source power at a constant welding speed of 2500 mm min−1. The oscillation radius R was kept constant at 0.3 mm. The parametric contour maps are developed for the joining of Al-5754 with the Al-6061 alloy system for butt welding configuration

Full size image

4.3.2 Effect of the radius of oscillation

To examine the effect of radius of oscillation on the IPIs during laser welding, two types of parametric contour maps are generated as shown in Figs. 8 and 9. Figure 8 shows the simulated parametric contour maps of the peak temperature, HAZ volume, and the cooling rate for different combinations of the radius of oscillation and heat source power at a constant welding speed of 2500 mm min−1 and frequency of 200 Hz. As shown in Fig. 8a, at a constant power with an increase in the radius of oscillation, the peak temperature decreases as the effective heat source speed increases which results in a decrease in the heat input per unit length. However, for the HAZ volume, it depends on the relative length of the heat source spot radius (r), which is 0.2 mm in this study and the radius of oscillation. When R ≤ r, the HAZ volume remains constant with the increase in R as it is equivalent to the situation with a heat source having a larger spot radius. So, an increase in the width of HAZ is compensated by the decrease in depth leading to constant HAZ volume. When R > r, there is a sharp decrease in HAZ volume when R is just above r which is depicted in Fig. 8b at R = 0.3 mm. With an increase in R, HAZ volume increases until it reaches R = 3r. This is due to the delay in the cooling process due to repeated heating, though the maximum value of HAZ volume is still smaller than for R ≤ r. When R > 3r, the heat input rate decreases leading to quick removal of heat which decreases the HAZ volume. So, it can be concluded that HAZ volume decreases with the application of heat source oscillation as in practical cases R > 2r. Similarly, the cooling rate remains constant when R ≤ r; there is a sharp increment when R > r which is shown in Fig. 8c at R = 0.3 mm. It again decreases with an increase in R until R = 3r. When R is further increased, it decreases due to the decrease in heat input rate as the velocity of the heat source increases. At constant power, the lowest cooling rate is found when R ≤ r. So, the cooling rate increases when beam oscillation is applied (as for practical cases R > 2r). This is due to the decrease in the peak temperature due to the application of beam oscillation which reduces the net heat content and thus requires less time to cool the material which increases the cooling rate. In this study, the cooling rate is calculated as the difference of temperature from melting point to 470 K upon the time taken to the drop of temperature. At a constant welding speed and laser power, the heat accumulation decreases due to a decrease in heat input per unit length. This leads to a decrease in the cooling time required and hence increases the cooling rate. In some of the cases at a very large radius of oscillation, the peak temperature decreases below the melting point which leads to a decrease in temperature difference and also the cooling time which leads to a very high cooling rate. A resonance effect is found for the HAZ volume and cooling rate which is a function of oscillation radius and heat source spot size.

Fig. 8
figure 8

Parametric contour maps for heat source power vs radius of oscillation at a constant welding speed of 2500 mm min−1, frequency of oscillation of 200 Hz, and spot radius of 0.2 mm. a Contour maps for peak temperature, b contour maps for HAZ volume, and c contour maps for cooling rate. The parametric contour maps are developed for the joining of Al-5754 with Al-6061 alloy system for butt welding configuration

Full size image
Fig. 9
figure 9

Parametric contour map for the radius of oscillation vs welding speed at a constant power of 4000 W and frequency of oscillation of 200 Hz. a Contour map for peak temperature, b HAZ volume, and c cooling rate. The parametric contour maps are developed for the joining of Al-5754 with the Al-6061 alloy system for butt welding configuration

Full size image

Figure 9 shows the simulated parametric contour maps of the peak temperature, HAZ volume, and the cooling rate for different combinations of the radius of oscillation and welding speed at a constant heat source power of 4000 W and frequency of 200 Hz. The generated parametric contour maps (Fig. 9) show similar trends as in Fig. 8, but the maxima and minima are exchanged from right to left as both welding speed and heat source power are related to the heat uptake. An increase in heat source power is like a decrease in welding speed leading to an increase in heat input per unit length. This effect is also depicted in Fig. 7b, c.

4.3.3 Effect of beam oscillation on the process capability space

From Sect. 4.3.1, it was concluded that within the model assumption, the effect of the frequency of oscillation is negligible on the IPIs for the range of frequencies investigated in this study. So, the process capability space depends on only three WPPs yielding a 3D process capability space, where x, y, and z axes are the three WPPs which are heat source power, welding speed, and radius of oscillation. This 3D process capability space can be visualised by stacking up 2D contour plots in the xy plane with a constant value for the third process parameters, as shown in Fig. 10. The size of the process capability space increases and is applicable for broader process parameter ranges with an increasing radius of oscillation as depicted in Fig. 10. This demonstrates the increase in flexibility of the laser welding process due to the application of beam oscillation. The upper limit of the allowed peak temperature ceases to exist at the highest radius of oscillation as shown in Fig. 10f. For the same combination of welding speed and heat source power, the peak temperature decreases though the net heat input to the workpiece is the same when compared to the non-oscillating heat source. To attain the same peak temperature, an oscillating heat source requires more heat input as compared to a non-oscillating condition which is shown in Fig. 10a, b.

Fig. 10
figure 10

The process capability space for three process parameters to show 3D response surface as a stacked up 2D contour map. The z-axis for the 3D response surface is radius of oscillation which is varied at a R = 0 mm, b R = 0.15 mm, c R = 0.30 mm, d R = 0.45 mm, e R = 0.60 mm, and f R = 0.75 mm in the 2D contour maps at a constant frequency of 300 Hz

Full size image

4.4 Process capability space refinement

Process capability space refinement is illustrated by using the example of improving mechanical properties for the keyhole mode of welding for full penetration. In this example, the final process capability space is chosen for no oscillation condition which is illustrated in Fig. 11a. The region above the feasible region (marked yellow) corresponds to the cutting or over weld region. The region below the yellow-coloured region depicts the under-weld region where due to insufficient penetration leads to a poor coalition of the materials. The region at the bottom is no welding region/preheating as the peak temperature is below the melting point of the material. The first step for process capability space refinement is to select the proper peak temperature thus satisfying IPI constraints as given in Table 3. The peak temperature should be between the boiling point of the metal and 3500 K for the keyhole mode of welding as shown by the yellow-coloured region in Fig. 11b. The region just below the yellow-coloured region (in between the red and black lines) represents the region of conduction mode of welding. In the second step, the WPP combinations are narrowed down based on the objective functions (Table 5) which are minimising HAZ volume and maximising cooling rate. The narrowed down process capability space based on the objective function is shown in Fig. 11c. In the final step, those WPP combinations are selected from the refined space which has faster welding speed and lower heat source power (WPPs constraints as given in Table 3). For a special case of full penetration keyhole welding, the peak temperature should be 3500 K, so the refined process capability space will be just a line as shown in Fig. 11d. Therefore, the final refined process capability space has the full penetration welding with the lowest HAZ volume, highest cooling rate, highest welding speed, and lowest power. The robust process parameters can be selected from the refined process capability space having 2 estimates about the quality of the weld from the IPIs without prior experimental characterisation and mechanical testing. This approach reduces the number of experiments required.

Fig. 11
figure 11

a Final process capability space for welding having cutting/over-welding region, welding region, under-welding region, and no-welding/pre-heating region; b process capability space refinement based on IPI constraints, i.e. 3500 K ≥ Tpeak > Tbp having cutting/over-welding region, keyhole mode welding region, conduction mode welding region, and under-welding region; c process capability space refinement based on the objective functions, i.e. minimising HAZ volume and maximising cooling rate; and d final refined process capability space for full penetration welding. The temperature of 3500 K shows the estimated peak temperature for full penetration welding

Full size image

4.5 Surrogate for the quick estimation of IPIs

The frequency of oscillation has a negligible effect on the IPIs as concluded in Sect. 4.3.1 from the parametric contour maps. Therefore, regression analysis is only performed for welding speed (S), heat source power (P), and radius of oscillation (R) as independent variables and the peak temperature, cooling rate, and HAZ volume are evaluated as outcomes (IPIs). The adequacy of the surrogate model and the significance of the coefficients are analysed using the sequential analysis of variance (ANOVA). The R-square, adjusted R-square, and tenfold R-square for all the responses are greater than 90% which shows that the model is reasonable and effective which is presented in Table 7 in the Appendix.

The surrogate model for the thermal responses (Eqs. (16)–(18), used for the prediction within the process capability space and design space in terms of process parameters, is shown below:

$$\begin{aligned}{T}_{\mathrm{peak}}=&\;759.9-1695\times R+1.1\times P-0.4\times S\\&+1590\times {R}^{2}+1.5\times {10}^{-5}\times {P}^{2}\\&+5.1\times {10}^{-5}\times {S}^{2}-7.337 \times {10}^{-1}\times R\times P\\&+2.660\times {10}^{-1}\times R\times S-1.01\times {10}^{-4}\times P\times S\end{aligned}$$
(16)
$$\begin{aligned}{C}_{\mathrm{rate}}=&\;2949-816\times R-2.418\times P\\&+2.2035\times S-299\times {R}^{2}+3.55\times {10}^{-4}\times {P}^{2}\\&+9.9\times {10}^{-5}\times {S}^{2}+3.856\times {10}^{-1}\times R\times P\\&-7.81\times {10}^{-2}\times R\times S-4.60 \times {10}^{-4}\times P\times S\end{aligned}$$
(17)
$$\begin{aligned}{V}_{\mathrm{HAZ}}=&\;78-186\times R+6.6\times {10}^{-2}\times P\\&-1.788\times {10}^{-1}\times S+523\times {R}^{2}\\&+4.1\times {10}^{-5}\times {P}^{2}+1.02\times {10}^{-4}\times {S}^{2}\\&-1.970\times {10}^{-1}\times R\times P+2.989\times {10}^{-1}\\&\times R\times S-1.06\times {10}^{-4}\times P\times S-579\times {R}^{3}\\&+1.511\times {10}^{-1}\times {R}^{2}\times P-1.313\times {10}^{-1}\\&\times {R}^{2}\times S+3\times {10}^{-6}\times R\times {P}^{2}-2.2\times {10}^{-5}\times R\times {S}^{2}\end{aligned}$$
(18)

Figure 12a–c show the dispersion plots representing the relationship between the numerical (from the FEM model) and predicted values (from the surrogate model) of Tpeak, VHAZ, and Crate with a 95% confidence level. These dispersion plots indicate the accuracy and adequacy of the model developed and the predicted results are in good agreement with the measured data.

Fig. 12
figure 12

Value of the peak temperature, HAZ volume, and cooling rate from the FEM model vs predicted from the surrogate model with a 95% confidence interval to show the accuracy of the polynomial fit function. The dispersion plot was developed for the joining of Al-5754 with the Al-6061 alloy system for butt welding configuration using 740 data points extracted from the physics-based model

Full size image

4.5.1 Effect of input process parameters on responses

The response profiles for the effect of process parameters on the IPIs have been constructed according to the surrogate models (Eqs. (16)–(18)). Figure 13 shows the prediction profiler for the responses (IPIs) for oscillation and no oscillation condition with the variables within the working range. The surrogate model has similar trends as shown by the FEM simulations which are depicted in Fig. 13. Peak temperature and HAZ volume will always be lower in the case of beam oscillation for the same WPPs as shown in Fig. 13a, b, d, f. The peak temperature decreases with the increase in welding speed non-linearly as depicted in Fig. 13a due to the decrease in the interaction time between the heat source and the workpiece. Figure 13b shows the linear increment of the peak temperature with the increase in laser power as the laser power is the most dominant term in Eq. (18) affecting the peak temperature. With an increase in radius of oscillation, peak temperature decreases as shown in Fig. 13c, as heat is distributed to a larger area so the heat input per unit length decreases. An increase in welding speed leads to a decrease in the HAZ volume as depicted in Fig. 13d due to the decrease in the net heat input to the workpiece, while the opposite trend is found when the power is increased which increases HAZ volume as more energy is available to melt the materials, as shown in Fig. 13e. HAZ volume shows the cyclic effect as shown in Fig. 13f with the increase in radius of oscillation depending upon the two competing phenomena. The heat is distributed in a larger area, i.e. the heat input decreases leading to shallow penetration leading to a decrease in HAZ volume but on the other hand, a larger radius leads to a wider melt pool, thus increasing HAZ volume. The cooling rate will always be higher in the case of beam oscillation for varying welding speeds at a constant power as shown in Fig. 13g, while the cooling rate for beam oscillation conditions may be higher or lower for varying power at a constant welding speed as shown in Fig. 13h. Beam oscillation has a cyclic effect on the HAZ volume and cooling rate as shown in Fig. 13f, i.

Fig. 13
figure 13

Prediction profiler for the peak temperature (a–c), HAZ volume (d–f), and cooling rate (g–i) for both the no oscillation and beam oscillation conditions to depict the relationship between the welding process parameters and the thermal responses, and to depict the linear/non-linear dependency between them

Full size image

In the process capability space of peak temperature, the combination of the three main welding parameters (welding speed, heat source power, and radius of oscillation) will form a plane in the 3D design space which represents a specific peak temperature and each point on that plane will give the WPP combination to attain the required peak temperature as shown in Fig. 14. In Fig. 14, the peak temperature is set to 2500 K and the red line shows the solution for without oscillation. It provides ternary interactions (showing the interactions of all the process parameters at once, i.e. βijl in Eq. (8)) of WPPs for the development of process capability space as compared to the parametric contour maps which depend on the binary interactions of WPPs (showing interactions of two process parameters at a time and keeping the rest constant, i.e. βij in Eq. (8)). The process capability space depicted by contour maps shows the peak temperature for all possible ranges of WPPs. However, in the case of the surrogate model, the process capability space shows all the possible WPP combinations to achieve a particular peak temperature. Therefore, it provides a finer detail in the process capability space as compared to the parametric contour plots. The 3D graph generated will save time from running many simulations and shows the effect of the three process parameters at once.

Fig. 14
figure 14

Response surface generated from the regression model for the effect of welding speed, the radius of oscillation, and heat source power for a peak temperature of 2500 K. The red line shows the response surface for no oscillation conditions. The response surface is developed for the joining of Al-5754 with an Al-6061 alloy system for butt welding configuration

Full size image

5 Conclusions

This paper presents a novel methodology for the process capability space refinement for the laser welding process with and without beam oscillation. During this research, a FEM-based heat transfer model has been developed to simulate the intermediate performance indicators (IPIs) peak temperature, heat-affected zone volume, and cooling rate. The process capability space has been depicted by using parametric contour maps. The main conclusions are as follows:

  • There is a good agreement between the FEM model and the experiments in terms of both transient temperature profile and the weld width calculated on the top surface (a key performance indicator). The model is validated for both no oscillation conditions (having a maximum error of − 6%) and for beam oscillation (having a maximum error of 4.5%).

  • The process capability space refining strategy presented in the paper decreases the number of paths within the process capability space from the initial parameter settings to optimise process parameters. For example, the same peak temperature can be attained by various combinations of welding process parameters which, however, may lead to different values of HAZ volume and cooling rate. This non-linear relation of HAZ volume and cooling rate with the change in radius of oscillation can be handled by the process capability space.

  • Welding speed and laser power have a significant effect on the weld thermal cycle as established from the contour maps in case of no oscillation condition. In the case of beam oscillation, the significance of radius and frequency of oscillation has been developed on top of welding speed and laser power. From the parametric contour maps, it was found that the frequency of oscillation has no significant effect on the weld thermal cycle for the range it is investigated, and a significant effect was observed for the radius of oscillation. Thus, the main parameter affecting the weld thermal cycle during beam oscillation is the radius of oscillation in addition to laser power and welding speed which provides beam oscillation just one extra degree of freedom reducing the four parameters space to three parameters space. At a radius of oscillation greater than 0.65 mm, peak temperature drops below the threshold for full penetration welding. This shows that the radius of oscillation can be increased up to a critical limit, depending upon the peak temperature to achieve full penetration welding.

  • Application of beam oscillation leads to a decrease in the peak temperature and HAZ volume for the same net heat input to the workpiece due to the decrease in heat input per unit length.

  • The cooling rate and HAZ volume vary cyclically with the change in radius of oscillation and depend upon the ratio of the radius of oscillation (R) and heat source spot radius (r). For the practical range of use of beam oscillation (where R/r > 2), HAZ volume decreases and cooling rate increases.

  • The area of final process capability space increases with the application of beam oscillation. This increase in area exhibits the increase in flexibilities due to the application of beam oscillation as the process will be more robust due to larger acceptable regions and smaller fall out areas.

Finally, it should be stressed that the presented modelling approach focuses on the thermal aspect of the welding only and here the temperature is the only dependency which is considered in the input of the parameters for given materials. The model fits the experimental results with good accuracy for the IPIs studied [39]. Nevertheless, the FE model is based on assumptions, which warrant further in-depth studies and model improvements. The presented approach is general in its nature and can be applied to other welding techniques as it models heat source and heat transfer during welding which is fundamental for every welding technique. With some modifications to the physical model, this modelling approach may even be extended to wider applications of lasers, such as estimating the thermal accumulation during ultrafast laser welding and writing for semiconductors and photonic devices. The main parameters influencing the thermal accumulation can be estimated based on the energy deposition by laser and heat spread as described by Eq. (1) [51,52,53,54].