Novel analytical heat source model for cold rolling based on an energy method and unified yield criterion

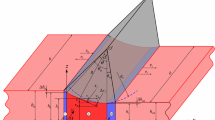
Abstract

Accurate calculation of the heat source in the roll gap during the cold rolling process is the basis for a well-designed coolant system, which is particularly important for reducing roll wear and improving the flatness quality of strip steel. Although many established numerical models have high precision when calculating the work roll temperature, complex modeling processes and large calculation times result in the inability to predict the work roll temperature quickly for the application of automatic control systems. Therefore, the authors developed a new analytical heat source model to calculate the axial temperature distribution of the work roll in the cold rolling process. First, according to the deformation characteristics of strip cold rolling, the deformation zone is divided into a plastic zone and two elastic zones, and the length of each deformation zone is calculated considering the effect of tension. Then, the friction heat generated in the elastic zone is calculated. Second, new exponential velocity and corresponding strain-rate fields satisfying kinematically admissible conditions are proposed to calculate the deformation heat and friction heat generated in the plastic zone. Finally, the work roll temperature prediction model is established by contemplating the heat source of the roll gap, emulsion heat transfer, air cooling, and contact heat transfer with the intermediate roll. By repeatedly optimizing the weighted coefficient d of intermediate principal shear stress on the yield criterion, the maximum error between the calculated results and the actual measured cold roll temperature data was reduced to 3.1%. The effects of the reduction ratio, rolling speed, and resistance to deformation on the deformation heat and friction heat are discussed, and the variation of temperature field of the work roll with time is analyzed quantitatively.

Appendix

According to the collinear vector inner product, the friction power $\dot{W}_{f}^{p}$ is

$$\begin{aligned} \dot{W}_{f} & = 4\int_{0}^{l} {\int_{0}^{w} {\tau_{f} |\Delta v_{f} |{\text{d}}F} } = 4\int_{0}^{l} {\int_{0}^{w} {{\varvec{\tau}}_{f} \Delta {\varvec{v}}_{f} {\text{d}}F} } = 4\int_{0}^{l} {\int_{0}^{w} {(\tau_{fx} \Delta v_{x} + \tau_{fy} \Delta v_{y} + \tau_{fz} \Delta v_{z} ){\text{d}}F} } \\ & = 4mk\int_{0}^{l} {\int_{0}^{w} {(\Delta v_{x} \cos \alpha + \Delta v_{y} \cos \beta + \Delta v_{z} \cos \gamma ){\text{d}}F} } \end{aligned}$$

(33)

where $\alpha$, $\beta$, and $\gamma$ are the angles between $\tau_{f}$ and the directions of the x, y, and z axes.

Since the tangential velocity discontinuity $\Delta v_{f}$ and the tangent of the roll surface have the same direction, the values of the direction cosines were determined by Eq. (1), and they are

$$\cos \alpha = \pm \frac{{\sqrt {R^{2} - (l - x)^{2} } }}{R}{, }\cos \gamma = \pm \frac{{\left( {l - x} \right)}}{R}{\text{ = sin}}\alpha , \, \cos \beta = 0$$

(34)

The differential element of the roll surface from Eq. (2) is

$${\text{d}}F = \sqrt {1 + (h_{x}^{{\prime}} )^{2} } {\text{d}}x{\text{d}}y = \sec \alpha {\text{d}}x{\text{d}}y$$

(35)

The components of tangential velocity discontinuity $\Delta v_{f}$ on roll surface from Eq. (16) are

$$\begin{array}{l} \Delta v_{x} = v_{R} \cos \alpha - v_{0} {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} \\ \Delta v_{y} = - v_{0} h_{x}^{{\prime}} \left( {\frac{1}{{h_{0} }} - \frac{1}{{h_{x} }}} \right){\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} y \\ \Delta v_{z} = v_{R} \sin \alpha - v_{0} \tan \alpha {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} \end{array}$$

(36)

By substituting Eqs. (34), (35) and (36) into Eq. (33) and integrating, we obtain

$$\begin{aligned} \dot{W}_{f} & = 4\mu kw\left[ {\int_{0}^{l} {\left( {v_{R} \cos \alpha - v_{0} {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right){\text{d}}x + \int_{0}^{l} {\left( {v_{R} \sin \alpha - v_{0} \tan \alpha {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right)\tan \alpha {\text{d}}x} } } \right] \\ & = 4\mu kw\left( {I_{1} + I_{2} } \right) \end{aligned}$$

(37)

$$\begin{aligned} I_{1} & = \int_{0}^{l} {\left( {v_{R} \cos \alpha - v_{0} {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right){\text{d}}x} = \int_{0}^{{x_{n} }} {\left( {v_{R} \cos \alpha - v_{0} {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right){\text{d}}x} - \int_{{x_{n} }}^{l} {\left( {v_{R} \cos \alpha - v_{0} {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right){\text{d}}x} \\ & = v_{R} R\left( {\frac{\theta }{2} - \alpha_{n} + \frac{\sin 2\theta }{4} - \frac{{\sin 2\alpha_{n} }}{2}} \right) + {\text{g}}_{f} v_{0} R\sin \alpha_{n} + {\text{g}}_{b} v_{0} R\left( {\sin \alpha_{n} - \sin \theta } \right) \end{aligned}$$

(38)

Similarly,

$$\begin{aligned} I_{2} & { = }\int_{0}^{l} {\left( {v_{R} \sin \alpha - v_{0} \tan \alpha {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right)\tan \alpha {\text{d}}x} \\ & { = }\int_{0}^{{x_{n} }} {\left( {v_{R} \sin \alpha \tan \alpha - v_{0} \tan^{2} \alpha {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right){\text{d}}x} - \int_{{x_{n} }}^{l} {\left( {v_{R} \sin \alpha \tan \alpha - v_{0} \tan^{2} \alpha {\text{e}}^{{1 - \frac{{h_{x} }}{{h_{0} }}}} } \right){\text{d}}x} \\ & { = } v_{R} R\left( {\frac{\theta }{2} - \alpha_{n} + \frac{{\sin 2\alpha_{n} }}{2} - \frac{\sin 2\theta }{4}} \right) + {\text{g}}_{f} v_{0} R\left[ {\ln \frac{{1 + \cos \alpha_{n} + \sin \alpha_{n} }}{{1 + \cos \alpha_{n} - \sin \alpha_{n} }} - \sin \alpha_{n} } \right] \\ & + {\text{g}}_{b} v_{0} R\left[ {\ln \frac{{\left( {1 + \cos \alpha_{n} + \sin \alpha_{n} } \right)\left( {1 + \cos \theta - \sin \theta } \right)}}{{\left( {1 + \cos \alpha_{n} - \sin \alpha_{n} } \right)\left( {1 + \cos \theta + \sin \theta } \right)}} + \sin \theta - \sin \alpha_{n} } \right] \end{aligned}$$

(39)

By substituting Eqs. (38) and (39) into Eq. (37) and integrating, Eq. (22) is given.