Skip to main content
SpringerLink
Log in

Optimization solution of vertical rolling force using unified yield criterion

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

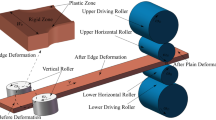
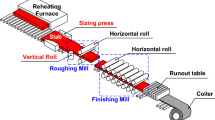
Vertical rolling is an important technique used to control the width of continuous casting slabs in the hot-rolling field. Accurate prediction of vertical rolling force is a core point maintaining rolling-mill equipment. Owing to the limitation of the algorithm in use, the prediction accuracy of most vertical rolling force models based on the energy method can only reach more than 10%. Therefore, it is challenging to optimize the rolling-force model to improve prediction accuracy. An innovative approach for optimizing the calculation of vertical rolling force with a unified yield criterion is presented in this paper. First, the maximal width of a dog-bone region is determined by the slip-line method, and the dog-bone shape is described using a sine-function model. Second, the velocity and corresponding strain-rate fields satisfying kinematically admissible conditions are proposed to calculate the total power of the vertical rolling process. Finally, the analytical solution of the rolling force and the dog-bone-shape model is obtained by repeatedly optimizing the weighted coefficient b of intermediate principal shear stress on the yield criterion. Moreover, the effectiveness of the proposed mechanical model is verified by measured data in the strip hot-rolling field and other models’ results. Results show that the prediction accuracy of the vertical rolling force model can be improved by optimizing the value of b. Then, the impacts of reduction rate, initial thickness, and friction factor on dog-bone shape size and vertical rolling force are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Availability of data and materials

The datasets used or analyzed during the current study are available from the corresponding author on reasonable request.

Abbreviations

W 0, W E :

Half of the initial and final slab width

W x :

Half of the slab width

ΔW :

Unilateral reduction,\(\Delta W{ = }{W_0} - {W_E}\)

ΔW x :

Unilateral reduction in deformation zone, \(\Delta {W_x}{ = }{W_0} - {W_x}\)

h 0 :

Half of the initial slab thickness

h Ι, h ΙΙ :

Half of the slab thickness in zones I and II

h p :

Peak height of deformation zone

h r :

Edge height of deformation zone

R :

Radius of edge roll

l :

Projected length of contact arc, \(l = \sqrt {2R\Delta W}\)

v 0 :

Entrance velocity

v R :

Peripheral velocity of edge roll

\(\theta\) :

Bite angle, \(\theta { = }{\sin^{ - 1}}\left( {{l \mathord{\left/ {\vphantom {l R}} \right. \kern-\nulldelimiterspace} R}} \right)\)

\(\varphi\) :

Contact angle

d 0 :

The maximum width of dog bone region

\({d}_{\varphi }\) :

Deformation zone’s width during edge rolling

d E :

Deformation zone’s width after edge rolling

β :

Undetermined parameters

b :

Yield criterion parameter

\({v}_{x},{v}_{y},{v}_{z}\) :

Components of velocity vector

J * :

Total power

\({\dot{W}}_{i}\) :

Internal plastic deformation power

\({\dot{W}}_{f}\) :

Friction power

\({\dot{W}}_{s}\) :

Shear power

\({\sigma }_{s}\) :

Material yield stress

k :

Yield shear stress, \(k = {{\sigma_s} \mathord{\left/ {\vphantom {{\sigma_s} {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}\)

m :

Friction factor

\({J}_{\mathrm{min}}^{*}\) :

Minimum value of total power

\({\tau }_{f}\) :

Friction stress

M :

Rolling torque

\(\omega\) :

Roll angular velocity

\(\overline{P }\) :

Rolling force

\({n}_{\sigma }\) :

Stress state coefficient

X :

Arm coefficient

x, y, z :

The directions of length, width, and thickness

References

  1. Ginzburg VB (1989) Steel-rolling technology: theory and practice. Marcel Dekker, New York

    Book  Google Scholar 

  2. Okado M, Ariizumi T, Noma Y, Yabuuchi K, Yamazaki Y (1981) Width behaviour of the head and tail of slabs in edge rolling in hot strip mills. Tetsu To Hagane 67:2516–2525. https://doi.org/10.2355/tetsutohagane1955.67.15_2516

    Article  Google Scholar 

  3. Tazoe N, Honjyo H, Takeuchi M (1984) New forms of hot strip mill width rolling installations. AISE Spring Conference. Dearborn, USA, pp 85–88

    Google Scholar 

  4. Shibahara T, Misaka Y, Kono T, Koriki M, Takemoto H (1981) Edger set-up model at roughing train in a hot strip mill. Tetsu To Hagane 67:2509–2151. https://doi.org/10.2355/tetsutohagane1955.67.15_2509

    Article  Google Scholar 

  5. Ginzburg VB, Kaplan N, Bakhtar F, Tabone CJ (1991) Width control in hot strip mills. Iron Steel Eng 68:25–39

    Google Scholar 

  6. Xiong SW, Zhu XL, Liu XH, Wang G, Zhang Q, Li H, Meng X, Han L (1997) Mathematical model of width reduction process of roughing trains of hot strip mills. Shanghai Metal 19(1):39–43

    Google Scholar 

  7. Xiong SW, Rodrigues JMC, Martins PAF (2003) Three-dimensional modelling of the vertical-horizontal rolling process. Finite Elem Anal Des 39:1023–1037. https://doi.org/10.1016/s0168-874x(02)00154-3

    Article  Google Scholar 

  8. Huisman HJ, Huetink J (1985) A combined Eulerian-Lagrangian three-dimensional finite-element analysis of edge-rolling. J Mech Work Technol 11:333–353. https://doi.org/10.1016/0378-3804(85)90005-1

    Article  Google Scholar 

  9. Chung WK, Choi SK, Thomson PF (1993) Three-dimensional simulation of the edge rolling process by the explicit finite-element method. J Mater Process Technol 38(1):85–101. https://doi.org/10.1016/0924-0136(93)90188-C

    Article  Google Scholar 

  10. Forouzan MR, Salehi I, Adibi-sedeh AH (2009) A comparative study of slab deformation under heavy width reduction by sizing press and vertical rolling using FE analysis. J Mater Process Technol 209(2):728–736. https://doi.org/10.1016/j.jmatprotec.2008.02.063

    Article  Google Scholar 

  11. Ruan JH, Zhang LW, Gu SD (2015) Finite element simulation based plate edging model for plan view pattern control during wide and heavy plate rolling. Ironmak Steelmak 41(3):199–205

    Article  Google Scholar 

  12. Yun D, Lee D, Kim J, Hwang S (2012) A new model for the prediction of the dog-bone shape in steel mills. ISIJ Int 52:1109–1117. https://doi.org/10.2355/isijinternational.52.1109

    Article  Google Scholar 

  13. Zhang YF, Di HS, Li X, Peng W, Zhao DW, Zhang DH (2020) A novel approach for the edge rolling force and dog-bone shape by combination of slip-line and exponent velocity field. SN Appl Sci 2:2055. https://doi.org/10.1007/s42452-020-03770-3

    Article  Google Scholar 

  14. Yu MH, He LN, Liu CY (1992) Generalized twin-shear stress yield criterion and its generalization. Chinese Sci Bull 37(24):2085–2089. CNKI:SUN:JXTW.0.1992-24-013

    Google Scholar 

  15. Zhao DW, Li J, Liu XH, Wang GD (2009) Deduction of plastic work rate per unit volume for unified yield criterion and its application. Trans Nonferrous Met Soc China 19:657–660. https://doi.org/10.1016/S1003-6326(08)60329-5

  16. Zhang YF, Zhang HY, Chen LJ, Zhao DW, Zhang DH (2018) Calculation of vertical rolling force through slip-line field. J Plast Eng 25:288–291. https://doi.org/10.3969/j.issn.1007-2012.2018.06.042

    Article  Google Scholar 

  17. Liu YM, Ma GS, Zhang DH, Zhao DW (2015) Upper bound analysis of rolling force and dog-bone shape via sine function model in vertical rolling. J Mater Process Technol 223:91–97. https://doi.org/10.1016/j.jmatprotec.2015.03.051

    Article  Google Scholar 

  18. Zhang SH, Wen HT, Lei D (2021) A novel yield criterion and its application to calculate the rolling force of a thick plate during hot rolling. J Braz Soc Mech Sci 43:12. https://doi.org/10.1007/s40430-020-02761-0

    Article  Google Scholar 

  19. Zhang DH, Liu YM, Sun J, Zhao DW (2016) A novel analytical approach to predict rolling force in hot strip finish rolling based on cosine velocity field and equal area criterion. Int J Adv Manuf Tech 84:843–850. https://doi.org/10.1007/s00170-015-7692-z

    Article  Google Scholar 

  20. Wang XH, Liu CY, Deng YC (2011) Model of deformation resistance of Q235 steel. Metall Inf Rev 1:25–30

    Google Scholar 

Download references

Funding

This study was funded by the National Natural Science Foundation of China (No. U20A20187) and the National Key R&D Program of China (No. 2017YFB0304100).

Author information

Authors and Affiliations

  1. The State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang, 110819, Liaoning, People’s Republic of China

    Yufeng Zhang, Li Xu, Hongshuang Di, Peng Wen, Dewen Zhao & Dianhua Zhang

  2. School of Materials Science and Engineering, Northeastern University, Shenyang, 110819, Liaoning, People’s Republic of China

    Yufeng Zhang, Meiying Zhao, Li Xu, Hongshuang Di, Peng Wen, Dewen Zhao & Dianhua Zhang

  3. Ordos Institute of Applied Technology, Ordos, 017000, Inner Mongolia, People’s Republic of China

    Xiaojuan Zhou

Authors
  1. Yufeng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Meiying Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hongshuang Di
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiaojuan Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Peng Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Dewen Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Dianhua Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Yufeng Zhang wrote the first draft of the paper. All authors revised and approved the final version of the manuscript.

Corresponding author

Correspondence to Hongshuang Di.

Ethics declarations

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent to publication

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Zhao, M., Xu, L. et al. Optimization solution of vertical rolling force using unified yield criterion. Int J Adv Manuf Technol 119, 1035–1045 (2022). https://doi.org/10.1007/s00170-021-08333-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-021-08333-3

Keywords

Search

Navigation