1 Introduction

Polymer extrusion is one of the most widely used plastic manufacturing processes. It is employed to obtain several products such as films, sheets, wire coatings, tubes, pipes, and many other profiles with complex shapes [1]. In plastic tube manufacturing, three main customer requirements need to be addressed: (i) the weight per unit length, (ii) the inner diameter, and (iii) the outer diameter of the tube. However, extrusion involves numerous interdependent input and output parameters (both process and system variables) [2]. Hence, tuning the process settings to meet the desired targets is often based on time-consuming trial and error procedures, leading to high process inefficiencies in scrap rates and lengthy setup phases, even when carried out by experienced machine operators. The mass flow rate of the extruder should be continuously measured to make a real-time estimation of the tube thickness and weight per unit length. Therefore, a soft sensor was developed to monitor tube thickness and its weight per unit length. Making use of a soft sensor, the extrusion line can be continuously monitored, and any deviation from the target outputs can be detected. Furthermore, a soft sensor can provide the machine operator with a useful tool to quickly evaluate the effect of any process parameter modification, allowing to speed up the extruder setup phase. This is especially relevant in a (relatively) small-batch production environment, where setup time can have a significant impact on the overall downtime. Moreover, direct measuring the flow rate or the tube thickness would require expensive gravimetric dosers or X-ray systems, respectively, which may not be feasible for a whole plant with many production lines.

A soft sensor is a technique employed to estimate process parameters (e.g., quality-based measures, variables indicating functionality, faults) in various applications when a hardware sensor is unavailable or unsuitable for making direct measurements [3]. It is also known as a virtual sensor or an inferential estimator. One of the soft sensors’ major purposes is to stabilize product quality via online estimation and reduce energy and material consumption via effective operation close to specifications [4]. Generally, soft sensors can be divided into “physical knowledge-based” and “data-driven” soft sensors.

Developing a “physical knowledge-based” soft sensor for the flow rate monitoring in extrusion requires the knowledge of the physical equations describing the material behavior and the boundary conditions. Materials like PVC, high-molecular polyethylene (HDPE), and polymer suspensions display wall slippage under certain conditions [5]. They violate the classic no-slip boundary condition used in Newtonian fluid mechanics and do slip over solid surfaces when the shear stress exceeds a critical value. Also, fillers inside the polymer’s matrix affect the material’s slip behavior. During the flow of a suspension of rigid particles, the particles cannot physically occupy the space adjacent to a wall as efficiently as they can away from the wall. This phenomenon leads to forming a generally relatively thin layer of fluid, the apparent slip layer, which has a significantly lower viscosity than the bulk, acting as a lubricant [6]. The mechanisms leading to the formation of the slip layer are extensively discussed in [7] and [8]. Inert fillers, defined as solid particulates, such as calcium carbonate (CaCO3), are often incorporated in large proportions in plastic compositions (including PVC) to reduce the material cost or modify the material properties. However, to predict the slip effect on the material flow as a function of the filler volume fraction (ϕ) is not a trivial problem. Investigating concentrated suspensions of polymethyl methacrylate (PMMA) particles in a viscous fluid, Jana et al. determined that the slip velocity increases with ϕ in 0.45 < ϕ < 0.52 [9]. Gulmus and Yilmazer studied a suspension of PMMA particles in hydroxyl-terminated polybutadiene and confirmed that for increasing ϕ the slip velocity also increases [10]. These results were contradicted by the work of Haworth and Khan [11], where the slip velocity increased for a lower concentration of talc particles in PP compounds, while Wilms et al. [12] obtained opposite results for limestone-filled suspensions made by different thickeners. The wall slip phenomenon in extrusion is complex and affected by numerous factors [13]. Recently, the single-screw extrusion of wood–plastic composites under wall slip conditions has been studied experimentally and theoretically by Wilczyński et al. [14]. They developed a global model of the extrusion process to predict the extrusion flow rate, pressure, temperature profiles, melting profile, and power consumption. Lewandowski and Wilczyński [15] performed fully 3D non-Newtonian finite element modeling to design the extruder and die characteristics into a global model for a comprehensive description of polymer extrusion in slip conditions. In further studies, Wilczyński et al. [16] validated the global model with experimental data, reporting that the predictions of the pressure gradient along the screw were slightly overestimated. However, the use of such a global model is computationally expensive since it requires a complex numerical simulation of both the extruder and the die [17].

An alternative approach consists of developing “data-driven” soft sensors based on physical quantities measured on the extrusion line.

Over the last few years, data-driven methods have received increasing attention in manufacturing (e.g., quality prediction), especially when complex processes and materials are involved and analytical approaches are unavailable. Román et al. [18] developed a neural network to predict the presence of surface defects in injection-molded plastic parts, obtaining a testing accuracy of 90.5% with a support vector machine (SVM) classifier. The possibility of using decision trees to predict the quality of injection-molded tensile specimens made of HDPE was investigated by Ogorodnyk et al. [19]. Ke and Huang [20] used multilayer perceptron neural networks to predict the geometrical dimensions of molded parts with an accuracy of 92%. Sun et al. [21] predicted multiple quality indexes of injection molding parts using multi-output support vector regressors (SVR), obtaining a good agreement with experimental results. SVR was also employed by Altarazi et al. [22] to predict the tensile strength of polymeric films made by compression molding and extrusion blow-molding, obtaining a high coefficient of determination (96%). Mulrennan et al. [23] developed a random forest-based soft sensor for the inline predictions of tensile properties of PLA sheets during twin-screw extrusion processing.

More specifically related to this research work, García et al. [24] used experimental data and regression models to predict extruded plastic tubes’ inner and outer diameter, observing good prediction performances. In their work, the estimation of the quality indexes (inner and outer diameter) was carried out through a purely data-driven approach where 15 extrusion and pulling process parameters were considered input features of the regression model. However, they used a high number of predictors, which can lead to high collinearity between variables. When a regression model has many correlated variables, their coefficients are poorly determined and exhibit high variance, i.e., the regression coefficients represent the noise rather than the genuine relationships in the population [25]. Regression models with many predictors are also more likely to overfit and less interpretable. Also, no variables related to the material properties were included in the prediction algorithms, even though they significantly affect the extrusion process.

In this work, two alternative approaches are proposed and compared to determine the extruder flow rate in slip conditions: the first relies on analytical models derived from physics and first principles. In contrast, the second is based on data-driven methods that use machine learning algorithms. In the first approach, a simplified analytical model was developed based on the well-known Tadmor and Klein (Tadmor, Z.; Klein, 1970) model. A velocity reduction term inspired by the generalized Navier slip law was introduced into the equation to consider the reduced drag flow due to the material slippage in the extruder. The extruder flow rate was estimated in the second approach after training, validating, and testing different machine learning algorithms. A feature selection phase was carried out before training the models. According to the analytical pressure-throughput models, the predictor variables were chosen among the physical quantities known to affect the flow rate the most. The amount of inert filler in the PVC compound was also included in the model’s input variables as a wall slip predictor. Once the volumetric throughput was known, the inner diameter of the tube was calculated through the mass continuity equation.

The novelty of this work mainly lies in the methodology adopted for the product quality prediction in the manufacturing of extruded tubes. First, regression algorithms (both analytical and data-driven) are used to estimate the extruder flow rate, while the weight and inner diameter of the tube are then determined using the continuity equation. Moreover, no pure “black-box” approach is deployed since predictor variables are chosen according to physics.

2 Materials and method

2.1 Material characterization

Four flexible PVC types were chosen among the most frequently used ones for tube manufacturing after a preliminary screening to include the materials exhibiting the maximum and minimum viscosity in the experimental campaign. The characteristics and compositions of these materials are reported in Table 1.

Table 1 Main characteristics of the four PVCs used during experiments
Full size table

The apparent shear viscosity curves for each material were obtained by capillary rheometry (Ceast, Rheologic 500) operating at three different temperatures: 145, 160, and 175 °C.

As shown in Fig. 1, the materials present a typical shear thinning behavior. Therefore, the viscosity was modeled using a power law equation [26]:

$$\eta =m(T){\dot{\gamma }}^{n-1}$$
(1)

where n is the flow behavior index of the material and m(T) is the flow consistency index which allows keeping into account the temperature dependence of viscosity, according to the WLF model:

$$m\left(T\right)=Dexp\left[\frac{{A}_{1}\left(T-{T}^{*}\right)}{{A}_{2}+\left(T-{T}^{*}\right)}\right]$$
(2)

where \({T}^{*}\) is a reference temperature and D, A1, and A2 are model coefficients.

Fig. 1
figure 1

Shear viscosity curves for the four flexible PVC types at the temperature of 145 °C

Full size image

The material’s density function ρ(p,T) is required to compute the mass flow rate. The pressure–volume–temperature curves (pvT) for each material were determined using the capillary rheometer in a temperature range of 50 to 180 °C. Experimental data were then fitted with the dual-domain Tait pvT model, and the zero-pressure curve was extrapolated.

2.2 Process equipment

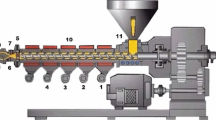
The experimental campaign was carried out on an industrial extrusion line equipped with a single-screw extruder having a 60-mm diameter barrier screw. The extruder was monitored using a temperature–pressure transducer (Gefran, ME) installed before the breaker plate. This melt transducer had a temperature–pressure operating range of 0–400 °C and 0–2000 bar, respectively, with an accuracy at the full-scale output of ± 0.25%. Once the polymer melt is pushed through the die and formed into a tube shape, a mechanism pulls the tube at a constant speed through two water-cooling tanks. After the first tank, the material shrinkage is almost complete, and a dual-axis laser device measures the tube’s outer diameter. A schematic representation of the process equipment is shown in Fig. 2.

Fig. 2
figure 2

Schematic of the tube extrusion line. Adapted from [27]

Full size image

2.3 Experiments

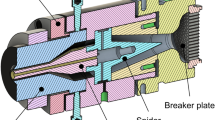
In order to determine the pumping characteristic of the extruder over a reasonable working range for the production practice, the experiments were carried out varying the following process variables: the material, the die diameter, and the screw speed. Eventually, two full factorial designs were adopted for the experimental campaign. In the first design of experiment, the material was changed among three levels (PVC A, B, and C); the die diameter was set to 17, 18, and 19 mm and the screw speed to 10, 20, 30, and 40 rpm. In the second design of experiment, only one material (PVC D) was considered; the die diameter was set to 20 and 21 mm and the screw speed to 12, 24, 36, and 48 rpm. Both the experimental factors’ levels and the materials were chosen in order to replicate the operating conditions of the extrusion lines in the industrial framework. The extruder temperatures were fixed for all the experiments: Tzone1 = 165 °C, Tzone2 = 170 °C, Tzone3 = 175 °C, Tzone4 = 175 °C, and Tdie = 165 °C, from the hopper to the die. The die dimensions were modified by replacing only the die, while the mandrel dimensions were fixed, keeping a mandrel diameter Dm = 15 mm. A schematic representation of the die is shown in Fig. 3.

Fig. 3
figure 3

Schematic configuration of the die and mandrel

Full size image

For each combination of material die dimensions, four runs were taken at four different levels of the screw speed N. Eventually, 56 experiments were carried out. The adopted experimental design is summarized in Table 2. For each experiment run, the die pressure drop ΔP, the melt temperature Tmelt, and the pulling speed vline, as well as the mass flow rate, were recorded. For each process condition combination, the mass flow rate measurement was recorded as follows: once the process reached the steady-state condition letting the extruder operate with the pulling mechanism off, the weight of a polymer melt sample extruded in 2 min was measured with a digital scale. Hence, the mass flow rate was obtained by dividing the measured weight by the sampling time. After reconnecting the extruded tube to the pulling mechanism, the melt temperature and die pressure drop were recorded for each run. The outer diameter and the imposed pulling speed were recorded, while the inner diameter of the tube was measured manually.

Table 2 Extrusion experimental design
Full size table

3 Modeling

3.1 Geometrical calculation of the inner diameter

The estimation of the inner diameter of the tube was performed using the mass continuity equation between two sections of the extruded pipeline, as illustrated in Fig. 4, where Sect. (0) refers to the cross-section of the tube right at the exit of the die.

Fig. 4
figure 4

Schematic representation of tube extrusion

Full size image

In contrast, Sect. (1) refers to the cross-section of the tube once the polymer has stopped shrinking after the water-cooling bath:

$${Q}_{m0}={Q}_{m1}$$
(3)

where Qm0, Qm1 are the mass flow rate at Sects. (0) and (1), respectively:

$${Q}_{m0}={Q}_{v0}{\rho }_{0}$$
(4)
$${Q}_{m1}={Q}_{v1}{\rho }_{1}={v}_{1}{S}_{1}{\rho }_{1}$$
(5)

where Qv0, Qv1, ρ0, and ρ1 are the volumetric flow rates and the material densities at Sects. (0) and (1), respectively. The material temperature is assumed to be equal to the melt temperature at Sect. (0) and the room temperature at Sect. (1). The pulling mechanism determines the tube speed at Sect. (1), v1. The cross-sectional area of the tube at Sect. (1) can be calculated as

$${S}_{1}=\frac{{Q}_{m0}}{{v}_{1}{\rho }_{1}}$$
(6)

Since the outer diameter at Sect. (1) is measured inline by a dual-axis laser device, the inner diameter of the tube can be calculated once S1 is known from Eq. (6):

$$d\left(1\right)=\sqrt{{D(1)}^{2}-\frac{4{S}_{1}}{\pi }}$$
(7)

The weight per unit length can also be calculated once Qm0 is known:

$${m}_{tube}=\frac{{Q}_{m0}}{{v}_{1}}$$
(8)

Hence, to estimate the weight and the inner diameter of the tube, the density and the volumetric flow rate of the extruded material (i.e. the extruder pumping characteristic) are needed. The development of a soft sensor for the inline estimation of the volumetric throughput of the extruder requires a predictive model capable of fitting the experimental data.

3.2 Model of the extruder characteristic

Since this work aims at developing a soft sensor for industrial purposes, the choice of the model (i.e., of its input parameters) must be based on the availability of measurable data during the tube extrusion process. For example, more advanced models allow keeping into account the leakage flow through the clearance between the flight and the barrel. However, it is not feasible to easily retrieve this data in the production framework. All of the analytical and data-driven models in this work do not require extra sensorization of the production lines. The single-screw extruder (SSE) can be considered a melt pump. The last zone of the extruder (metering zone) increases the polymer pressure to the level necessary for it to be pumped through the die at the desired rate. A model for the SSE pumping is given, for example, in [28] and was first proposed by Tadmor and Klein (1970). In these simple analyses, the polymer melt is considered a Newtonian isothermal fluid with constant viscosity. The effects of leakage phenomena over the flights and flight flanks are neglected, and the hydrodynamic boundary condition applies (i.e. no slip at the wall). Furthermore, it is assumed that the channel depth is very small compared to the screw diameter so that the flat plate model can be used [29]. According to the previous hypotheses, the SSE flow rate in the down-channel direction can be expressed as follows:

$${Q}_{v}=\frac{WH{v}_{bz}}{2}-\frac{W{H}^{3}}{12\mu }\frac{\Delta P}{{Z}_{p}}$$
(9)

where W is the channel width, H is the channel depth, vbz is the barrel velocity, µ is the Newtonian viscosity, and ΔP/Zp is the pressure gradient in the down-channel direction. ΔP is the pressure drop across the die, and Zp is the unwounded length of the metering zone. The first term in Eq. (9) represents the flow rate in pure drag flow, i.e., the flow rate as if no die was mounted at the end of the extruder, and is directly proportional to the screw speed, since

$${v}_{bz}=\pi DN\mathit{cos}\phi$$
(10)

where N is the screw speed and ϕ is the helix angle of the flight. A pressure-driven flow (the second term in Eq. (9)) decreases the overall output due to a positive pressure gradient in the down-channel direction. Equation (9) is the simplest throughput–pressure gradient model for the SSE. When the non-Newtonian behavior of the fluid is taken into account, Eq. (9) becomes

$${Q}_{v}=\left(\frac{4+n}{10}\right)WH{v}_{bz}-\left(\frac{1}{1+2n}\right)\frac{W{H}^{3}}{4\mu }\frac{\Delta P}{{Z}_{p}}$$
(11)

where n is the pseudo-plastic coefficient of the polymer. The viscosity, µ, is calculated with the power law equation as a function of the shear rate in the channel:

$$\mu ={m(T)\left(\frac{{v}_{bz}}{H}\right)}^{n-1}$$
(12)

Equation (11) can be written in a shorter form:

$${Q}_{v}=\left(\frac{4+n}{10}\right)\alpha N-\left(\frac{1}{1+2n}\right)\beta \frac{\Delta P}{\mu }$$
(13)

where α and β are model parameters that include the geometrical characteristics of the extruder. In this work, the first attempt to fit the experimental data was conducted using Eq. (13). The coefficients α and β were obtained minimizing the residual sum of squares:

$$RSS=\sum_{i}^{K}{\left({Q}_{v}-{\widehat{Q}}_{v}\right)}^{2}$$
(14)

where \({Q}_{v}\) and \({\widehat{Q}}_{v}\) are the experimental and predicted values (using Eq. (13)) of the flow rate, respectively, and K is the total number of samples (56).

The Tadmor and Klein model assumes that the polymer melt adheres to the screw and the barrel wall during extrusion. Even if this is generally accepted, several materials like filled polymers (e.g., wood plastics composites), elastomers, and pure polymers like PVC and HDPE display wall slippage under certain conditions.

For the slip analysis, a non-linear slip velocity law (generalized Navier slip law) is usually assumed to approximate the actual slip behavior of several fluids, including molten polymers [30]:

$${u}_{s}=-\beta {\tau }^{b}$$
(15)

where β is the slip coefficient, b is the slip law exponent, and τ is the wall shear stress. The nominal screw speed N in Eq. (10) was decreased by a slip velocity term, Nslip, to account for wall slippage in the extruder model. Its expression was derived by analogy to Eq. (15), leading to the following expression for the effective screw speed N':

$${N}^{^{\prime}}=N-{N}_{slip}=N-k{N}^{\delta }$$
(16)

Equation (9) thus becomes

$${Q}_{v}=\alpha {N}^{\prime}-\beta \frac{\Delta P}{m(T){N}^{{\prime}n-1}}$$
(17)

where α and β are model coefficients as in Eq. (13) and the viscosity was calculated with the power law equation, considering that \(\dot{\gamma }\propto\) vbz \(\propto\) N. Introducing Eq. (16) into Eq. (17), the full expression of the throughput is obtained:

$${Q}_{v}=\alpha \left(N-k{N}^{\delta }\right)-\beta \frac{\Delta P}{m(T){\left(N-k{N}^{y}\right)}^{n-1}}$$
(18)

Equation (18) contains four model parameters (α, β, k, and δ), determined by model fitting.

For what concerns the data-driven modeling, from the experimental data recorded for each process condition combination, a dataset of N = 56 observations (or instances) D = {(xi, yi),…,(xN,yN)} was created. Any input vector xi = (× 1, × 2,…, xd) (also called features vector) is associated with an output variable, yi. Polynomial regression, support vector regression, decision tree, and multi-layer perceptron neural network (MLPNN) models were trained to seek a function f that predicts a continuous output y given a new input x.

4 Data analysis methodology

The data acquired during the experimental campaign were processed using Python 3 from its distribution platform Anaconda, which includes the essential data science and machine learning packages. The code was edited and run through the Jupiter Notebook web application.

The input and output variables were defined as follows:

$$\begin{array}{l}{x}_{i}=\left(N, \Delta P,m\left(T\right),n, {C}_{filler}\right)\\{y}_{i}={Q}_{v}\end{array}$$
(19)

where Cfiller is the concentration of filler (CaCO3) in the PVC and it was included in the input features because it affects the slippage behavior of the material in the extruder. To ensure a good generalization error of a machine learning model, it is required to have at disposal a number of observations ten times greater than the number of features, i.e., 10 × 5 = 50 observations, as stated in [31]. As in this work, 56 experiments were conducted; the generalization heuristic was satisfied.

Prior to training the machine learning algorithms, data preprocessing needed to be applied to the raw data. Data normalization was applied to the input vectors with the minimum–maximum scaler method to map the original data into the uniform range [0,1]. Feature selection was carried out by choosing the input variables according to physical-based considerations. All the above-mentioned predictors are thus known to be informative, based on the evaluation of analytical extruder models from the literature. The dataset was then randomly split into a training set and a test set: 48 samples were used for model selection and hyperparameters tuning, while the remaining eight samples were held out to calculate an unbiased estimation of the generalization error (out-of-sample error). Model selection was based on k-fold cross-validation (CV) results to reduce bias and variance, ensuring that all the samples data were considered during the learning phase. The dataset was iteratively split into 12-folds (k = 12): 11-folds were used for model training and the one remaining for model testing. The average test error across all the 12-folds was then computed. k-fold CV was used simultaneously to find the optimal model hyperparameters, whose values control the learning process and are external to the model, which means they remain unchanged during the training phase. A schematization of the workflow for the model construction is given in Fig. 5.

Fig. 5
figure 5

Schematic of the machine learning model construction

Full size image

Both model selection and hyperparameters tuning must be based on specific evaluation metrics. The root mean square error RMSE was used as an evaluation metric:

$$RMSE=\sqrt{\frac{1}{N}\sum_{i=1}^{N}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}$$
(20)

This metric indicates how far from the regression line the target points are, and it has the advantage that it is expressed in the same units of the predicted variable. Moreover, it can be used for evaluating both linear and non-linear regression models. However, RMSE is not sufficient for a comprehensive assessment of a regression algorithm. In addition to the RMSE, two techniques for model diagnosing were considered: the residuals scatter plot and the learning curves.

5 Results and discussion

The experimental data are shown in the typical throughput-pressure plot in Fig. 6.

Fig. 6
figure 6

Throughput-pressure scatter plot of experimental data for a PVC A, b PVC B, c PVC C, and d PVC D

Full size image

The performances of different analytical and machine learning models are compared when predicting the extruder flow rate. The flow rate predicted values are then considered to estimate the tube’s weight and inner diameter.

5.1 Flow rate

In order to make a consistent comparison between the analytical and the data-driven regression methods, the performances of the analytical models were evaluated by carrying out a 12-fold CV.

In Table 3, the 12-fold CV errors for the analytical models and each of the proposed regression models are reported. The high discrepancy between the predicted and the experimental values is evident when calculating the flow rate with the classic Tadmor and Klein model. The root mean square error computed for all the considered materials was RMSE = 45 cm3/min. Figure 7 shows the comparison between the flow rate measured and calculated with Eq. (13) for the PVC A.

Table 3 Cross-validation error for different regression algorithms
Full size table
Fig. 7
figure 7

Flow rate prediction results with Tadmor–Klein isothermal non-Newtonian model for PVC A

Full size image

Observing Fig. 7, the following considerations can be deduced. First, the volumetric flow rate is not proportional to the screw speed at low pressure drops, as the Tadmor and Klein model would imply. As the screw speed increases, the flow rate increases less than proportionally so that the model systematically overestimates the flow rate since it does not consider the material slippage. Second, at constant screw speed, the model cannot describe the decrease of the flow rate when the pressure drop increases, especially at high pressure drops, which means that the behavior of the extruder is pressure-sensitive.

The introduction of a velocity reduction term in the Tadmor and Klein model allows considering the drag flow reduction due to the slip effects, especially at lower pressure drops. The prediction performances significantly increase from \(\mathrm{RMSE}=\pm 45 \frac{{\mathrm{cm}}^{3}}{\mathrm{min}}\) to \(\mathrm{RMSE}=\pm 29 \frac{{\mathrm{cm}}^{3}}{\mathrm{min}}\). The significant improvement of the slip model over the Tadmor and Klein model is mainly due to the ability of the slip model to capture the less than proportional increase of the flow rate with the screw speed while extruding materials that exhibit wall slip. Even if the novel analytical model exhibited a significant improvement over the Tadmor and Klein model, quality production standards require even higher prediction performance. As a result, data-driven techniques are being tested.

For what concerns the machine learning models, since CV was performed for each possible combination of the values of the considered hyperparameters, the reported results are relative to the learning algorithm whose hyperparameters allowed to obtain the best prediction performance (the smallest RMSE). For example, polynomial regression exhibited its best score when the degree of the polynomial features transformation was set equal to 2, predicting the volumetric flow rate with an accuracy of \(\pm \mathrm{13,80 }\frac{{\mathrm{cm}}^{3}}{\mathrm{min}}\).

Figure 8 represents the residuals scatter plot for the random forest regressor, which displays the predicted flow rate \({\widehat{Q}}_{v}\) on the x-axis and the difference between the observed and the predicted flow rate \({Q}_{v}-{\widehat{Q}}_{v}\) (residual) on the y-axis. Usually, the residuals are randomly scattered around zero, since the error committed by the model should be stochastic. However, a non-random pattern can be noticed in Fig. 8, which means that the deterministic part of the model is missing some explanatory information. On the other hand, learning curves are valuable tools to check if a training/testing dataset is suitably representative of a specific learning algorithm.

Fig. 8
figure 8

Flow rate residuals scatter plot Random Forest Regressor

Full size image

Figure 9 shows the learning curves for the MLP neural network regressor. The size of the training set and the training and testing performance is displayed on the x-axis and y-axis, respectively. The noisy movements of the curves suggest that the training/testing datasets are unrepresentative, i.e., they do not contain sufficient information to evaluate the ability of the model to generalize. Figure 10 depicts the residuals plot and the learning curves for the polynomial regression and the SVR. The residuals are randomly scattered around zero for both models, i.e., the models are not biased. The learning curves show how increasing the size of the training set the in-sample error and the out-of-sample error gradually increases and decreases, respectively. The results in Fig. 10 refer to a polynomial regression where the degree of the polynomial features transformation was set equal to 2, and the ridge regularization method (α = 0.01) was applied. The SVR used a polynomial kernel function (coeff = 1, degree = 3, γ = 1) and a regularization coefficient \(C=125\). These model hyperparameters were determined with the GridSearch method from the scikit-learn Pyhton package.

Fig. 9
figure 9

Learning curves of MLP regressor for flow rate prediction

Full size image
Fig. 10
figure 10

Flow rate a residuals plot and b learning curves for polynomial regression. Flow rate c residuals plot and d learning curves for SVR

Full size image

These results suggest that both the PR and SVR are suitable algorithms for predicting the extruder flow rate, where the SVR exhibits the best prediction performance, according to Table 3. Both models were then tested to estimate the out-of-sample error, using the data which had been left apart during the training phase. The prediction errors are \(\pm \mathrm{13,67}\) and \(\pm \mathrm{12,92}\frac{{\mathrm{cm}}^{3}}{\mathrm{min}}\) for the PR and SVR, respectively. Finally, the best algorithms were retrained on the entire dataset, and the mean absolute percentage error (MAPE) was calculated. The error committed by the polynomial regression is MAPE = 1.65% (accuracy = 98.35%), while the error committed by the SVR is MAPE = 1.17% (accuracy = 98.83%). In summary, both the PR and the SVR are unbiased models and exhibit a good fit of the experimental data, confirmed by the analysis of the residuals plots and the learning curves, respectively. Moreover, the error committed when predicting the extruder flow rate is small enough to be compatible with the required production quality standards. These regression models are thus suitable for predicting the extruder flow rate with acceptable accuracy.

5.2 Tube weight and inner diameter

Sensitivity analysis was performed to measure the effect of the estimated flow rate error on the tube inner diameter and weight error. Since an uncertainty of ± 5% on the flow rate leads to a tube weight error of ± 5% and an inner diameter error < 1%, which are acceptable to meet the industrial quality requirements, both the PR and the SVR are suitable to predict the extruder flow rate with sufficient accuracy.

The weight per unit length of the tube was calculated with Eq. (8) using the predicted volumetric flow rate. The inner diameter of the tube was calculated according to Eqs. (6) and (7). RMSE and accuracy results for the predicted inner diameter and weight of the tube are reported in Table 4, where the volumetric flow rate in Eq. (4) is estimated using the SVR algorithm.

Table 4 RMSE and accuracy results for the predicted inner diameter and weight of the tube
Full size table

The residuals for the two tube characteristics are shown in Fig. 11. The residuals are positive for almost all the samples, which means that the predicted weight of the tube is always greater than the corresponding experimental value. Since the residuals of the predicted flow rate are randomly scattered around zero, from Eq. (8), it can be deduced that the velocity of the line is systematically underestimated. This implies that the tube’s predicted inner diameter will also be underestimated, as seen in Fig. 11b. These results support the need for a more accurate real-time measurement of the line speed.

Fig. 11
figure 11

Residuals plot for a the inner diameter and b the weight per unit length

Full size image

6 Conclusions

The present work discussed the development of a soft sensor for the inline measurement of extruded PVC tubes’ weight and inner diameter. To achieve this goal, the flow rate of the extruder needs to be measured. Experimental data were used to compare both analytical and data-driven methods to predict the volumetric flow rate under slip conditions. First, regression algorithms (both analytical and data-driven) were used to estimate the extruder flow rate, with predictor variables chosen based on physical concerns. The weight and inner diameter of the tube were then determined using the continuity equation. This represents a novel approach for the product quality prediction in the manufacturing of extruded tubes. Moreover, no pure “black-box” approach were deployed. The novel analytical model proposed in this paper, which is based on physics principles, considers the wall slippage of the molten polymer exhibiting an accuracy of 95.5%. However, this model did not consider the influence of the filler concentration on the flow rate. More accurate results were obtained through machine learning regression algorithms, which allowed to include the percentage of filler (calcium carbonate) among the predictor variables, thus keeping into account the experimental evidence for which higher percentages of filler results in increased material slippage. The polynomial regression and the SVR exhibited the best performance among all the considered regression methods, with 98.35% and 98.83% accuracy, respectively, in predicting the extruder flow rate. The weight per unit length and the inner diameter of the tube were then calculated using the mass continuity equation. In particular, these calculations rely on the inline measurement of the velocity and the outer diameter of the tube. Since the estimated inner diameter and the weight resulted under- and overestimated, respectively, it was deduced that the line velocity was systematically underestimated. High accuracy of these measurements is thus mandatory to develop a reliable soft sensor for quality monitoring in tube extrusion.