1 Introduction

The pulling of wet reinforcing fibres through die may be simple; however, the dynamics and mechanisms of process parameters are very complex to fully comprehend due to continuous interaction between physical and chemical changes. In the literature, numerical and experimental investigations were attempted by several researchers to predict aspects of intrinsic pultrusion process to evaluate, e.g. pressure [1,2,3,4,5], cure mechanism [6, 7], pull force [8,9,10] and heat transfer mechanism. Phenomena involved are mainly heat transfer controlling viscosity of the resin, resin conversion and phase changes, die-material/surface in contact and stress–strain behaviour. To model pultrusion process focusing on pull forces, it is recommended that the material inside should be divided into separate regions such as taper region at wet material entry side, thermally active gel where process of curing is initiated, post gel region and region of separation region or part detached from die surface.

A statistical investigation on influence of process parameters like pull force and flexural strength of pultruded product was made by Lackey and Vaughan [11] and it was concluded that process parameters, influences pulling force, may vary significantly due to complex interaction change in cure kinetics [12, 13]. On the other hand, to have satisfactory experimental analysis, the elevated number of variables involved which are to consider is an undesirable time consuming and money spending operation. Even prediction of part properties from process intricacy is barely perceptible. For any explicit understanding of pultrusion operation, mathematical modelling should embrace fundamental laws for heat transfer, conservation of mass and momentum. For simplification, very few aspects have been studied in the literature when deriving numerical solution.

The process involves complex effect on cure kinetics resin, permeability, porosity and shape factor of roving of reinforcing materials. The permeability of any porous material was first investigated and proposed by Henry Darcy widely known as Darcy’s law. Change in pressure gradients during flow for hydraulic fluid depends on conductivity of the fluid involved wherein permeability and porosity controls pressure gradient for porous materials like resin impregnated fibres for thermoset and thermoplastics materials.

$$v=-K/\eta \nabla P$$
(1)

In the expression, v is the velocity of drag or pulling, \(K\) is permeability and ∇P is pressure difference and \(\eta\) is viscosity of resin. In Kozeny-Carman equation of permeability, where a model for ellipsoid material with granular beds was assumed to be valid for fibrous porous media [14, 15] is widely used.

$$K={R}^{2}/(4 {k}_{c}{)*[(1-{V}_{f})}^{3}/{{V}_{f}}^{2}]$$
(2)

where \({k}_{c}\) is the Kozeny constant, \(R\) the particle radius and \({V}_{f}\) the fibre volume fraction.

Gutowski et al. [16, 17] analysed compressibility and permeability of carbon fibre stack impregnated with oil as follows

$$P=\frac{3\pi B\left(\sqrt{{(V}_{f}}/{V}_{0})-1\right) }{[{\beta }^{4} {(\surd ({V}_{a}/{V}_{f)}-1)}^{4}]}$$
(3)

In the proposed mathematical expression, \(P\) is pressure normal to surface as given in Eq. (3). The transversal stiffness of fibres \(B\) and \(\beta\) is the constant representing ratio of span length to span height of the fibres involved. \(Vf\) final fibre volume fraction of the product wherein \({V}_{0}\) and \({V}_{a}\) initial fibre volume and maximum fibre volume fraction reconsidered in the model. This expression indicate that only pressure is being experienced by fibres packs.

In conventional pultrusion or in open bath pultrusion, compaction force or the pressure arises due to compaction is ignored due to low fibre volume fraction and short taper length. But with reasonable tape length in open bath pultrusion, increased fibre volume can be achieved without injection pressure [18,19,20,21]. Complexity of viscous region and compaction zone is profound for fast curing resin like polyester. Hence, to maintain higher tapping and viscous length die, specific design is required to be adopted.

The analytical model of Kim et al. [22, 23] proposes pressure inside pultrusion die as unidirectional flow in pulling direction and no permeability in z-direction. The expression is normally used for matrix continuity model.

$$dP/dx=U*\eta /{K}_{(x)}*[1-{V}_{fx}-(1-\Delta \nu /\nu ) *({V}_{fx}/{V}_{f}-{V}_{f(x)})]$$
(4)

In this Eq. (4), U is the pulling speed, (x) is the longitudinal permeability and \({V}_{fx}\) is the fibre volume fraction as functions of axial distance. Δν/ν represents the resin resultant volume change due to thermal expansion and overall shrinkage which can be ignored for simplification. Interactive pressure of respective regions can be calculated by integrating this expression with elemental respective axial distance is expressed in Eq. (5).

$$P(x)=U*\eta /K(x)* [1-{V}_{fx}/{V}_{f}] *x$$
(5)

However, many researchers proposed injection pultrusion, and total pulling force contribution is calculated as \({F}_{tot} = {F}_{com} + {F}_{vis}+ {F}_{fric} ,\) where \({F }_{tot}\) is total pulling force, \({F }_{com}\) is compaction force and \({F}_{fric}\) is frictional for after separation. These three different resistances are expressed separately by considering die width ‘w’ and axial distance:

$${F }_{com} = =\underline\int 2w(\dot{p}+\sigma ) tan \theta dx$$
(6)
$${F}_{vis}= =\underline\int 2w\tau dx$$
(7)

and

$${F}_{fric} = =\underline\int 2wf.\sigma dx$$
(8)

within \(0\le x\le {x}_{in}.\)

Pull-force modelling for other injection pultrusion indicates that several factors like sliding-induced shear and viscous adhesion force shrink-induced part-detached play’s important role are unaccounted on analytical models. In Eq. (5) for compaction, Eq. (6) for viscous drag force and Eq. (8) of friction coefficient have neither considered thin layer resin at die composite interface for zones separately for compaction zone, liquid zones and dry profile zones beyond curing nor the thermal expansion and shrinkage. Even bending angle of reinforcing fibres as function of axial length in taper section which plays a major role in controlling pull force is not conserved. Bending angle depends on the stiffness of the fibres and the length of the taper section die eventually compaction angle.

This work efforts are to capture complex variables like normal force, resin conversion, line speed and temperature by modifying many existing parameters during scale-up operation. Pressure-dependant variables are used in the proposed model to predict the experimental results at operation. In this study, experimental quantification on pull force in compaction die is performed on conventional pultrusion dies of two different tapping angles, wherein effect of temperature and fillers on straight die on friction is being testified by results received from inhouse made device. Along with polymer thin layer conversions separately for differ zones, flat straight die profile, thermal expansion and shrinkage, this mathematical model manifested the effects of die-compaction angle, fibre volume fraction, thickness and drag velocity on pull force. Therefore, the aim of this paper is to evaluate the effect of process parameters on pull force configuring materials and designing of die for the profile to be pultruded.

2 Experiments

2.1 Materials

A continuous random glass fibre mats with 450 and 300 g/m2 (gsm) were provided by Skaps Industries India PVT Ltd. Owens Corning supplied glass roving used was of 4800 tex (tex: the mass in gram per one kilometre of a fibre roving). A concoction of random glass mats and glass roving fibre package of 600 gsm were used. Organically modified montmorillonite (MMT) was obtained from SIGMA–ALDRICH. The OMMT contained 0.05–5 wt% aminopropyltriethoxysilane and 15–35 wt% of ocatadecylamine, appearance (colour) white to off-white appearance (form) powder, loss on drying ≤ 3.0%, size ≤ 20-micron and density 200–500 kg/m3 (bulk density). Precipitated calcium carbonate (CaCO3) powder from Gulshan Polyols Limited was employed as the conventional micron-filler of size ≤ 40-micron particle size. Orthphthalic acid-based unsaturated polyester resin (MECHSTER™ 9000P) tailored for the pultrusion process and supplied by Mechamco Resins Ltd was used in this study.

2.2 Characterisation

Differential scanning calorimetry (DSC) experiments were performed on a TA-60 Plus Shimadzu instrument, using hermetic pans and sample weights lower than 10 mg. The used materials in the experiments are formulated in resin paste and different low conversion as mentioned in Tables 1 and 2.

Table 1 Materials and formulation used for the friction measurement
Full size table

Isothermal scans were run at temperatures typically around 80 °C and kept it for 30 min to run out the residual Initiators. All curatives and additives are premixed separately before sampling. The sample preparation was done swiftly in order to avoid the loss of volatiles such as styrene that results in loss of data during the first stages of the reaction. DSC determines the conversion of resin by measuring residual heat by thermal initiation. Table 2 shows the final conversion and curatives like Paradox-C, MEKP, BPO and TBPB used in the experiment.

Table 2 Formulation and conversion in dead-end polymerization experiments
Full size table

2.3 Pultrusion line and experiment set up

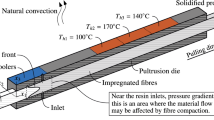
Working line schematic used in our work is shown in Fig. 1a. The line consists of creel stands for roving and racks for felts, veil fabrics and unwinding continuous filament-mat (CFM), a resin tank, a pre-forming assembly composed of perforated steel plates and other guide rollers, and a heated die, die with heating elements along its length, a pulling unit and a flying cut-off saw. Temperature profiles along the die, pulling force, pulling speed and pressure inside die are measured and recorded in data form. Hydraulic oil pressure exerted during pulling is monitored through PLC-controlled pulling unit. This pultrusion pulling unit can either be used for open bath or closed die pultrusion. In our regime, open bath pultrusion with 300-mm discontinued tapping section was used as shown on Fig. 1b.

Fig. 1
figure 1

a The schematic of the open bath pultrusion line. b The schematic of compaction zone in conventional pultrusion die

Full size image

Wetting of reinforcing fibres is very crucial for any composite part without dry patches. In open bath (Fig. 1b), impregnation technique used to wet fibres is achieved by pulling fibres through the resin tank. In order to ensure all fibres are sunk under resin, resin label is not allowed to go down below specified limit. Higher pulling speed and entangled fibres are avoided for better wettability. Impregnated fibres are guided through guide rollers and plate and finally through preforming assemble to have specified part cross section prior to entire into die. When pulled through the resin bath, excess of resin carried by roving at die entry will wet-out cloths like polyester veil or glass veil. Discontinued compaction tapper section assists in squeezing out excess resin and trapped air to get void free pultruded parts (typically between 1 and 5% vol.). Curing to solidification of profile is made by passing the squeezed material through heated die. Die temperature management is crucial in order to produce good quality components; hence, a gradual increase in resin temperature is achieved by placing more heating zones with different set temperatures along the length of the die time of mat entry during travelling though die and was recorded by the thermal sensors placed between the fibre pack. The fibre-package consisted of 10 layers of Bidirectional mats with 600 g/m2 and 60 roving with 4800 tex. The thickness of the produced composites was 8 mm of high-pressure tapper die (Fig. 1b).

Many variations on trials were conducted on adding additional mats, on the high-pressure conventional dies. Add-on reinforcing method in pultrusion is used to find pull force throughout the die used at different speed and filler loading; the temperature at surface and core during pulling is also recorded. To trace the magnitude of pull force change, additional mats, 200 mm wide and 254 mm long, were inserted in the centre prevailing fibre pack. The speed of pulling was set at 20–50 mm/min. Thermocouples were placed in between the mats to measure the temperatures of core and surface as well. The pulling speed was set at different speeds like 20 mm/min and 45 mm/min. As the mats travelled through the die, the time mat entered the die was recorded and based on speed; axial distance is calculated against pressure appeared. The experimental result for the high-pressure conventional die with extra tapping section is shown in Fig. 1b. It is planned such that pulling force magnitude positions front edge of the additional mats traveling along the die and y-axis, pulling force magnitude positions die-centre towards wall pulling is recorded separately for each driving forces which governs the ultimate pull forces.

The ‘add-on reinforcement’ in the pultrusion operation was conducted using the conventional die with discontinued specially designed 0.3-m tapper section as shown in Fig. 1b. As compaction zone is predominating on other frictional forces, separate experiment for downstream part of the die which undergoes resin drag and dynamic friction before gelling is required to conduct at room temperature. A short-length and long-length dies without tapper portion were used to comprehend contribution of friction of viscous zone and influence of its subsequent length. Furthermore, influence of die length on pulling force was investigated using different die lengths. A 1200-mm, 800-mm and 500-mm three conventional dies were employed in this experiment. The pulling speed and the fibre package remained unchanged as used in add-on reinforcing method. Schematic of the experiments in short die and long die is shown in Fig. 2a, b. All along ‘low fibre volume fraction’ were maintained in short and long dies.

Fig. 2
figure 2

a The schematic of short straight die length, b the schematic of side view of the mould used to predict the pull force in liquid zone

Full size image

Pull force arises from friction between composite and the die surface predicts the effect of temperature, resin conversion, pulling speed at gelling and post gelling region, anticipating shrinkage and thermal expansion of the product.

As shrinkage coefficient is governed by conversion of polymers and the filler loading in resin. Composites with different shrinkage factors were considered in conducting trials. The short 500-mm single cavity die as mould was used to find the compressive stress during compaction at different thickness and steel shim placed beforehand in the die was pulled to record pulling force against time for straight portion at different temperature, resin conversion and pulling speed. Compressive stress and pulling force required was recorded by an Instron universal testing machine (Model-Delta-C200-10 Tons). The side-view of the mould is also shown in Fig. 2a, b. Experiments were conducted on the same short die but keeping length of the steel plate long. Arrangement is made in such a way that the plate is three times longer than the mould to keep the contact area constant throughout the experiment. The experiment was conducted for three different filler loading in a resin of specific shrinkage factor, for two resins of different shrinkage factor at 105 °C constant temperature. In the experiment, the plate was wrapped with resin impregnated glass fibres at different % conversion.

The resin was formulated to have different % conversion and steel plate was pulled for a span of 6 min at speed of 10 mm/min. Formulated resin as listed in Table 1 is used in impregnating reinforcing materials and two layers of random mats with surface veils used for wrapping steel plate. Percentage conversion is controlled by placing reinforcing materials in a preheated 90 °C mould with specific thickness and maintained heating for 30 min. The heated plates for that period are long enough to run out the initiators from Parkadox-based formulated resin system. Different % conversion was confirmed by the DSC before keeping on the single cavity mould holding amid the steel shim. The mould was completely closed and pulling test was performed in three different stages. In the first stage, steel plate was pulled out by one-third of the total length at room temperature followed by 60 °C and 105 °C for remaining subsequent shim length. All along, 200 mm/min pulling speed was maintained and pulling force exerted due to friction recorded. Several impregnated partially cured fibre mats were first wrapped by surface veils as used in actual pultrusion process, then laid up evenly in both mould halves. A chromed steel shim of 2.0 mm in thickness and 90 mm in width and 300-mm length was placed between the fibre reinforcement materials, and the mould was then closed. The dimension of the mould cavity was 8 mm thick, 100 mm long and 100 mm wide – the initial contact length of the plate and the fibre mats was 100 mm, thus the initial contact area of 90 mm by 100 mm. To prevent fibres from moving up during pulling high-fibre volume, fraction was maintained thereby providing a high holding force.

Steel plate out of the mould at a constant speed was pulled gradually and force change versus time was recorded by Instron universal testing machine tester. From known cross-sectional area, pressure can be calculated wherein friction of coefficient obtained is pulling force divided by the contact area and the compaction stress. In investigating temperature effect on friction, heating tape was used on steel slim, wherein change in temperature was monitored. Liquid region friction experiments at different temperature were carried out by wrapping prepreg with different % conversion on steel plate placed into the mould as described in pultrusion operation. Similarly, material described in pultrusion method, resin with different filler contents like 10, 30 and 40 phr, was used.

3 Results and discussion

3.1 Pull force modelling

The pressure accounts force due to compaction at tapping zone, friction due to viscous drag and friction due to cured product with die surface. The modelling and simulation are strongly dependent on many physical process variables which need to be investigated. Many models are available in the literature such as the thermo-chemical modelling, fluid dynamics modelling, and thermo-mechanical modelling employed to investigate behaviour change in pressure experienced by the fibre pack during pulling through die. Three pressures that fibre pack being experienced mainly during drag are compaction resistance, viscous resistance and friction resistance (dry fibres and solid profiles with die surfaces).

Compaction resistance is mainly due to resistance of fibre bed to get squeezed during compaction depending on fibre volume fraction influenced by porosity of fibres and permeability of resin [23,24,25,26,27,28,29,30].

$$\delta =F*{L}^{3}/(192E*I)$$
(9)
$$L =\beta *({l}_{0}-{l}_{min})$$
(10)
$$\delta =({l}_{0}-l)$$
(11)

Assuming \({l}_{min}=d,\)

$$P=F/L*w = [({l}_{0}-l)192* E*I]/ \beta *{({l}_{0}-d)}^{3}\dot{w}$$
(12)
$$B\;\mathrm{is}\;\mathrm{bending\;stiffness}=192* E*I$$
(13)

considering, \(\dot{w}=L\),

$${V}_{f}=\pi {d}^{2}/4{l}^{2}$$
(14)
$${V}_{0}=\pi {d}^{2}/4{{l}_{0}}^{2}$$
(15)
$${V}_{a}=\pi /4$$
(16)

where ‘\(L\)’ is length of the fibre segment, ‘\(E\)’ is modulus of the fibres, ‘\(d\)’ is diameter of the fibre, ‘\(I\)’ is inertia of bending of the fibres, ‘\(F\)’ is contact force of the fibres, ‘\({l}_{0}\)’ is initial height of the prism, ‘\({l}_{min}\)’ is minimal height, ‘\(l\)’ is height, ‘\(\beta\)’ is constant by microscope span height to span length ration of fibres network, \(B\) is bending stiffness.

$$P=3\pi B [\surd ({V}_{f} (x)/ {V}_{0})-1]/ {\beta }^{4}{[\surd ({V}_{a} / {V}_{f} (x))-1]}^{4}$$
(17)

`This was modified by Carlone et al. formulation [25] for compaction zone with index \(\widehat{n}\) = 2. By principle of porosity in conical die,

$$\begin{array}{l}\{ {V}_{f} (x)\} = ({h}_{L}* {V}_{f} )/[ {h}_{L}+ ({L}_{m}-x)* tan \theta ]\\P =(3\pi B/\surd \varepsilon ) [\surd ({V}_{f} / {V}_{0})- \surd \varepsilon ]/ {\beta }^{4}{[\surd {(V}_{a} *\varepsilon /{V}_{f})-1]}^{2}\end{array}$$
(18)

where

$$\varepsilon =1+2({L}_{m }-x)/ {h}_{L} tan \theta$$
(19)

Fibre volume fraction can be calculated by deciding \({N}_{r}\) (no of roving in any particular volume). Where \({N}_{r}\) is the number of roving used in the specific volume and \({L}_{w}\) is the linear weight of fibre. Final volume fraction of um-reinforcing material [11, 14, 22] is a quantitative value of porosity(Φ), i.e. \((1-{V}_{f}) = \Phi\), and permeability (\(K\)) as proposed by Henry Darcy is

$${V}_{f}={N}_{r}\cdot * {L}_{w}/ (A*{\rho }_{f})$$
(20)

Theoretical values used in model fitting of \({V}_{0}= 0.350, {V}_{a}=0.785\) square and \(0.907\) for hexagonal, \(\beta = 2.54 *I=2.61*10(-7) , E=8.2*1010, {\rho }_{f} = 2620 kg/m2, {L}_{w}= 4800 [tex]\) for glass,

$$\int {dP}_{f}=\int (3\pi B/\surd \varepsilon ) [\surd ({V}_{f} / {V}_{0})- \surd \varepsilon ]/ {\beta }^{4}{[\surd ({V}_{a} * \varepsilon / {V}_{f})-1] }^{2}dx$$
(21)

This is the pressure experienced by fibre beds not by the resin or matrix. Hence, compaction pressure on matrix is evaluated.

$${U}_{x}= (K/ \eta ) * \delta P$$
(22)

where \({U}_{x}\) is the resin flow speed, \(K\) is the permeability and \(\eta\) is the resin viscosity, and \(\delta P\) is the pressure gradient and Permeability by Carlone et al. [27]:

$$K={d}^{2} {(1-{V}_{f})}^{3} /Kc*{{V}_{f}}^{2}$$
(23)

From fibre continuity,

$${V}_{f} (x)* h(x) = {V}_{f} * {h}_{L}$$
(24)

Since,

$$[{h}_{L}/ h(x)] = ({V}_{f} / {V}_{0}) +(1- {V}_{f}/ {V}_{0}) x/{L}_{m}$$
(25)
$${V}_{f} (x)= {V}_{f} /[ ({V}_{f} / {V}_{0}) +(1- {V}_{f} / {V}_{0}) x/{L}_{m}]$$
(26)

From matrix continuity [28, 29] on volumetric flux,

$$Q(x).h(x)= {U}_{x} (1- {V}_{f}) *{h}_{L}, Q(x) = {U}_{x} [({V}_{f} (x)/ {V}_{f})-{V}_{f} (x)]$$
(27)

Relative matrix flux

$${Q}_{R}(x)= [Q(x)- {U}_{x} (1- {V}_{f}(x))] = {U}_{x} [({V}_{f} (x)/ {V}_{f})-1]$$
(28)

Since apparent viscosity of the Carreau model may be written as follows:

$${\eta }_{a}= {\eta }_{0} {(1+ {(\lambda *\gamma )}^{2})}^{(n-1)/2}$$
(29)

From Darcy equation, \(P=\left({U}_{x}*\eta \right)/K,\)

$$(dP/dx) = [{Q}_{R}(x)* \eta ]/K$$
(30)
$$(dP/dx) = {Q}_{R}(x)* {\eta }_{0}{(1+ {(\lambda *\gamma )}^{2}) }^{(n-1)/2}]/K$$
(31)

\(\gamma\) = shear rate or velocity divided by layer distance,

$$dP/dx= \frac{{[Q}_{R}(x)* Kc* {{V}_{f}\left(x\right)}^{2}* {\eta }_{0}[1+ {{\left(\lambda *\gamma \right)}^{2}) }^{\left(n-1\right)/2} ] }{{d}^{2} {(1-{V}_{f} (x))}^{3}}$$
(32)

By principle of porosity in conical die,

$$\{{V}_{f} (x)\} = ({h}_{L}* {V}_{f} )/[ {h}_{L}+ ({L}_{m}-x) tan \theta ]$$
(33)

Now as per pressure gradient by Dong law [5, 8, 27],

$$\begin{array}{c}dP/dx=\int d{P}_{d}\\= \int \frac{G\cdot \eta \cdot U\cdot {{V}_{f}}^{2}\cdot {{h}_{L}}^{2} .({L}_{m}-x) tan \theta }{{d}^{2} * [(1-{V}_{f}) {h}_{L}+{2({L}_{m}-x) tan\theta ]}^{3}}dx\end{array}$$
(34)

where Gebart, defined shape factor G, as 57 for a quadratic fibre arrangement [31, 32]. Since Pd is pressure due to drag, it would be considered only because of matrix and for fibres bed reacting is the Pf. Hence, compaction pressure is a combined effect of matrix and the fibre bearing load. Compaction resistance is predominantly influenced by taping angle, fibre volume fraction speed of pulling and part thickness. In predicting resistance, initial taping angles θ radian is potentially considered for models but principally taping angle varies with axial distance which needs to be considered for fibre beds. Fibres close to core are experiencing less bending compared to fibres close to surface. Hence, in this study, ‘\({\theta }_{f}\)’ an average angle was calculated considering the gradient of change in taping angle depends on length of compaction zone and shape factor of reinforcement.

$$R=\int (\theta -1.47*{Z.}^{3}), 0.000<Z<0.25),\;{\theta }_{f} =(R./0.25)$$
(35)
$$\int d{P}_{c} = \int {P}_{f} Cos {\theta }_{f} * sin {\theta }_{f} dx + \int {P}_{d} sin {\theta }_{f} dx$$
(36)

Viscous resistance is believed to be drag resistance influenced by viscosity of resin and drag speed. Viscosity is a direct implication of the shear stress on composite surface before complete curing between gelling and post gelling phase [30,31,32,33,34,35].

$$\int d{P}_{v}= \int ({\eta }_{a}U/r Cos \widehat{\theta } dx$$
(37)
$$\int d{P}_{v}= \int ({({\eta }_{0} {(1+ (\lambda * \gamma )}^{2})}^{(n-1)/2}) U/r * Cos\;\dot{\widehat{\theta}}\;dx$$
(38)

r is the distance between the layers or fibres, varies with fibre arrangement [8, 31, 35] like

$$r=d (1-\surd ((\surd 3) (\pi {V}_{f} (x))/2)/2)$$
(39)

But in our study, adhesion of resin layer to the surface of die plays additional roles and is influenced by increase speed lessens heat effect on viscosity of resin (stress × gradient of speed). \(Cos \dot{\widehat{\theta }}\) was called liquid–solid affinity, where \(\dot{\widehat{\theta }}\) was contact angle of liquid–solid phase and σL was interfacial surface tension of solid-slurry. Infiltration and permeation ability of the liquid resin is directly influenced by affinity of the liquid and higher adhesion force. The monitored die surface decreases affinity between liquid resin and solid die surface. Since the viscosity changes with time influenced by heat, the average viscosity was considered in our study.

Considering the initial practical viscosity of the resin used as 0.4 Pa.s, the average viscosity can be calculated as follows,

$$\int d {\eta }_{v }=\int (0.4*exp(.0894*t) dt,$$
(40)
$$0<t <(x-L)/U$$

 while the adhesion load is,

$$\int d{A}_{d}= (520-(0.025* ( {\eta }_{v }/ (x-{L}_{\mathrm{m}})/U)) *2*3.14*h$$
(41)
$$\int d{P}_{v}= \int ({\eta }_{0} (1+{ (\lambda * U/r)}^{2})(n-1)/2U/r)* Cos \dot{\widehat{\theta }}dx$$
$$+\int (520-(0.025* {\eta }_{v } / (x-{L}_{\mathrm{m}})/U)) *2*3.14*{h}_{L} dx$$
(42)

Friction resistance arises from dry fibres and solid profile with die surface is presented as,

$$\int d{P}_{f} = \int Pd (x)*f*{Cos}^{2} \theta (x)) dx$$
(43)

where f is the friction coefficient. When the surface of the composite is solid, the expression is considered as normal stress between composite and die.

In our study, pull force model for friction resistance, shrinkage-induced part detached pressure which plays additional role to reduce friction is considered. Hence, the existing normal stress between die and solid profile gets reduced by \((\widehat{G} \delta R/r)\) helping to get part detached. Theoretical bulk modulus of the resin is \(\widehat{G}=4. *10^(8),\) and \(0.75<x,1.5)\), [4, 5, 28] wherein G-Bulk Modulus, \(\delta R\)-shrinkage of resin and \(\widehat{\lambda }\)- resin layer thickness. \(\delta R\) is the shrinkage of part which can be assumed as change in length since the radius parameters such as the shrinkage factor \((S)\) of the resin, layer thickness \((\widehat{\lambda })\) and extent of curing controls normal stress as modified to are as follows:

$$\int dP=\int (\widehat{G}).*(r)/(0.2*(x))dx$$
(44)
$$\int d{P}_{ef} =0.085*\int d{P}_{f} -\int dP$$
(45)

3.2 Start-up experiments and slip phenomenon

As shown on Fig. 3, during start-up stage, two different situations are analysed. One where reinforcing fibre saturated with only pristine resin and another wherein resin contains 30-phr filler and 5.5-phr nanofillers are pulled through the conventional ‘open bath’ discontinued tapper die, maintaining 50 mm/min pulling speed. The pulling force trajectory against times of Fig. 3 shows that dry fibre package pulling pressure reaches to maximum at 625 s and leads to 5398 N force but after about 650 s as pure resin began to run out, pressure drops and leads to 3429 N force for a specific area die profile. The shoulder of decrement observed faster for 30-phr filler loading in respect to 5-phr MMT-treated nano filler. This experiment indicates that friction is more for wet fibres with nano fillers but more vulnerable for dry fibres. The probable explanation could be due to interface layer thickness of resin which minimises the friction between fibres and die wall. The thicker the layer of resin as in case of higher viscosity due to higher filler content and less, as expected for pure resin and low-dosed nano fillers, the less would be the friction in between reinforcing fibres and die wall. Fillers are an essential component in the resin formulation which must be configured to have corrosion and heat resistance with good surface finish at low cost.

Fig. 3
figure 3

Effect of with and without filler during start up pulling

Full size image

3.3 Compaction effect by add-on reinforcement

Unlike the analytical and simulation model [36] in the literature, our study shows sudden rise in pressure rise from 0-bar to 160-bar and then gets to plateau initially as the add-on reinforcement travels through die as shown in Fig. 4. In fact, the pull force trajectory remained unchanged until 100 mm but follows sinusoidal pattern to reach maximum value (4680 N) and gets stabilised subsequent of gradual decrease in pressure. This sinusoidal trend of increasing of peak and resuming original value is noticed as fibre pack travel moves down axial distance. Indeed, peak gets broaden followed by gradual increase at initial compaction and drops insidiously until tapping angle gets flattened but hardly any change is observed in overall pulling force, for additional reinforcement.

Fig. 4
figure 4

Measured values for changes in temperature at core and surface and pull force during pulling along axial length

Full size image

Temperature change near the surface and inside the composite is recorded by thermocouples placed in the fibre package, one at just beneath the surface veil and another in the middle of fibre package. It is observed that rise in temperature is barely perceptible until the compaction zone ends, but interestingly, temperature change caused by the exothermic resin reaction just before 300 mm away of exist end reached its maximum value. This implies that the rest of the pulling force develops in late stream zone and is due to the gelling effect and solid friction post-curing. This implies composite cohesive force gets debilitated to die surface facilitating loose contact before the reaction peak temperature.

In the literature, the simulation model [36] shows the rise in pressure observed after traveling certain axial distance (300-mm) of die inlet. In contrary, our study observed (Fig. 5), decreasing compaction taping angle right from die entry while the magnitude of pull force increases and vice versa. The peak was observed at the entrance flat portion of die which experiences major compaction. Again, the late stream part of the die has less response to the additional mats, but a fliting response pattern was observed with decreasing tapping slope.

Fig. 5
figure 5

Measured values for changes in pull force during pulling at varying degree of compaction during pulling operation

Full size image

Figure 6 shows the similar trend in increases of pulling force with increasing pulling speed from 0.2 to 0.45 m/min. Response to pull force is higher and sensitive to higher speed similar to studies found in Ref. [36] wherein pressure increased from 0–80 and 0–68 bars for higher and lower speed with similar tapping angle. A possible explanation is that initial pull force is the existing pull forces and for any additional reinforcement at compaction experiences more pressure to accommodate the solid reinforcement into final die gap squishing out excess viscous resin. Viscous drag forces (mainly late stream) part of the die to contribute marginally unlike compaction forces of total pulling force [6, 8, 33, 37].

Fig. 6
figure 6

Measured values for changes in pull force at different experimental pulling speed along axial distance

Full size image

Hence, of a good understanding parameters in scale-up operation to get stable product (Fig. 7a) are crucial otherwise, one may encounter problems like over curing of the parts and eventually loss of heat, warpages of the product due to uneven curing, low productivity due to slow pulling speeds, scaling at part edge (Fig. 7b, c), seizure of dies and ultimately line/part failure (Fig. 7d), higher pulling force required leading to higher electrical (energy) consumption during manufacturing stage.

Fig. 7
figure 7

(a) Stable product in operation during pultrusion pulling. (b) and (c) Scaling of product in operation during pultrusion pulling. (d) Part failure in operation during pultrusion pulling

Full size image

In our study, MATLAB software was employed and influencing parameters including fibre volume factor, tapping angle of die, thickness of the profile and drag velocity were computed in model fitting and corelated to the experiments results. It was found that proposed model results were in good agreement with degree of compaction as recorded experimentally. It is worthy to mention that we are restricting axial length separately for compaction from 0 to 0.3 m and where in 0.3 to 1.5 m experienced flat portion for pressure due to viscous and friction. From model fitted 2D graphs (Fig. 8), paradigm of compaction pressure changes with sweeping fibre volume fraction, drag speed and profile thickness as appeared which are similar to recorded experimental results but rising trajectory is sharp, prominent and clear. In model fitting, variables like tapping angle ranges from 0.014 to 0.019° radian, fibre/volume fraction varied from 0.480 to 0.620, part thickness ranges from 0.004 to 014 Mt and drag speed varied from 0.0020 to 0.0032 m/s.

Using the governing Eq. (36) as derived from Eqs. (9)–(35), compaction pressure is plotted against many complex variables. It is found that tapping angle has negative influence on pressure which shows sensitive to higher values of variables when plotted in 2D graphs as shown in Fig. 8a, b. Pull force appeared sharp increase and lasts longer for thick profile but drops insidiously unlike thin profile, wherein sudden drops in pressure observed of parameters like fibre volume fraction and speed of pulling. With increasing speed and tapping angle, change in pulling pressure is plotted. Similarly, as shown in Fig. 9a, b, increased pull force is perceptible profoundly for increasing velocity, but difference is barely perceptible for dropping pressure, wherein for increased tapping angle shows long lasting pressure along axial distance (Table 3).

Fig. 8
figure 8

Experimental results showing the influence of (a) fibre volume fraction and (b) profile thickness on compaction pressure during pulling

Full size image
Fig. 9
figure 9

Experimental results on the influence of (a) pulling speed and (b) tapping angle on compaction pressure during pulling

Full size image

3D-surface plotting as shown in Fig. 10a depicts nature of pressure drops swiping thickness as functional parameters long axial distance. Spikes appeared prominently sharp and profound for ‘higher speed’ and ‘tapping angle’ deviating shifting harmony in axial distance. Similarly, Fig. 10b depicts paradigm of increased pressure swapping speed of pulling or drag velocity as function maintaining shifting harmony in axial distance. A comparison between measure values with model fitting is elicited in Table 2.

Fig. 10
figure 10

(a) 3D surface plot on influence of tapping angle on compaction pressure and (b) 3D surface plot on influence of profile thickness on compaction pressure

Full size image
Table 3 Comparison between model fitting and measured values
Full size table

3.4 Viscous force phenomena in liquid phase

To investigate the viscous force phenomena in liquid phase, experiment were conducted to investigate the contribution of viscous drag force to total pulling force. As shown in Fig. 11, pulling force at 80 mm/min speed, both dies (450 mm and 960 mm) show no significant change at liquid phase. Hence, increased length of straight portion in die makes no difference with shorten die length unless viscosity gets influenced by temperature, pulling speed and fibre volume faction. Before gelling as indicated in the add-on reinforcement method, the pultrusion die does not minor contribution to the pulling force; similarly predominantly in liquid phase, straight portion of longer die length cause no increase is pulling force. Pulling force in this region was only due to reaction and stimulated gelling and post gelling resin until the surface solidification.

Fig. 11
figure 11

Effect of speed and die length during pulling in liquid zone before solidification

Full size image

3.5 Viscous force verified by steel-shim

A thin liquid layer that exists between fibres and the die surface in the liquid zone has been assumed in the literature [38, 39] and it is the controlling factor of pull force and increases with increasing pulling speed or assumed proportional to overall pulling force. The phenomena are witnessed by compaction and viscous zone irrespective on influence of temperature.

The concoction behaviour of the resin gelling from liquid and subsequently to solid during operation through pultrusion die is very deceptive to comprehend. Viscosity gets burgeoned rapidly on gelling of resin, due to viscous friction at die surface. At die-composite interface, such mechanism of viscous friction could be influenced by resin conversion and temperature. Hence, it is intrigued to investigate the influences of processing parameters on friction force. A short-length die with steel plate was used to comprehend influence of temperature, conversion, filler loading of resin on friction of viscous zone. In experiments, heating tape wrapped around steel plate placed inside short die equipped with temperature controller, to facilitate to have different temperatures as described above. Process of controlling % conversion of resin and testifying the same by DSC was discussed above. In friction measurement process, different final conversion is achieved by adjusting reaction temperature, reaction time and amount of low temperature initiator (MEKP) [18,19,20,21, 42, 43]. Perkadox-C is also a low temperature promoter which synergise the influence of MEKP at a particular temperature. Benzol peroxide (BPO) an initiator is mixed with promoter tertiary butyl per-benzoate (TBBP) to have conversion at higher temperature.

The friction is the direct implication of pull force and can be measured as function of both parameters’ temperature and resin conversion. The stress normal to die surface is recorded by the pressure transducer. Pulling force required to pull thin plate is comparatively low but it is reasonable to compare pressure. There are initial drops in pressure due to drops in viscosity, but tension starts rising with passing secs. The most probable explanation would be due to shear thinning due to heat and shear effect of unreacted polymers and monomers facilitating pull force to decreased greatly [34, 35, 37], which may further be influenced by increasing speed. Further in the event of different % conversion at different temperatures, nature in changing friction and stress inside during viscous drag at gel and post-gelling region is shown in Fig. 12. Pull force for 30% conversion recorded at room temperature (25 °C) is higher compared that at 60 °C, wherein the difference is more profound at 50% conversion resin-impregnated fibres. This indicates that friction due to viscous drag becomes larger when resin is at ‘gel state’ and with increasing temperature at any given constant contact pressure situation gets more vulnerable for higher molecular weight resin. As the matrix starts crosslinking, affinity to die surface lessen and eventually reduced adhesion force is presumed but rising viscosity increase pulling force in viscous phase. Overall trend implies that higher temperature are more influential than the lower temperature regime in that it promotes crosslinking hence maximising the resin viscous condition.

Fig. 12
figure 12

Pull-force recorded using device for viscous drag during pulling

Full size image

Similarly, using governing Eq. (42) as derived from Eqs. (37)–(41) and subsequent model fitting by using MATLAB software considering simulations were computed to compare experiments results. The study accounted for a series of parameters including drag velocity, fibre volume fraction, thickness of the profile and tapping angle. In our study, adhesion force is considered which contributes significantly at low surface tension between solid and liquid surface interface. The surface tension directly varies with viscosity and that varies with speed. As drag speed increases, contribution of adhesion force to total viscous force is less significant. Hence, average viscosity was taken during fibre pack travel in the flat Sect. 2D-plot as shown in Fig. 13a, it was found out that viscous pressure responds promptly with increased drag velocity; wherein in Fig. 13b, similar behaviour as observed in compaction pressure, pressure shows decremental with increasing tapping angle. Figure 14a, b for change in profile thickness and fibre volume fraction shows similar paradigm as observed in compaction, but the overall contribution to total force is less. It is worthy to mention that axial length is restricted to 1.5 m for flat portion. From the model, it is evident that paradigm is incremental and reaches plateau due to increase in viscosity which inturn leads to gelling and subsequently to solidification. Gelation process is much faster and abrupt at higher temperatures and after gelation, and the curing continues with much slower pace because of the restricted movement of reactive groups. It is worthy to mention that gelation effect at faster heating rate causes the reaction rate, i.e. a controlled diffusion. This limited diffusion causes seldom failure to reach the complete conversion. Gelation time is accurately determined from half‐life and the time required to reach the maximum cure rate as normally calculated by isothermal cure kinetics of unsaturated polyester resin.

Fig. 13
figure 13

Influence of a fibre volume fraction and b profile thickness on viscous pressure during pulling

Full size image
Fig. 14
figure 14

Influence of (a) fibre volume fraction and (b) profile thickness on viscous pressure during pulling

Full size image

3.6 Dynamic friction force after cure

Separately, using governing Eq. (45) as modified of Eqs. (43) and (44) and subsequent model fitting by using MATLAB was made to investigate post curing solid surface friction of product. In the governing equation, shrinkage-induced part detached is considered. In order to rule-out uncured fibre pack core of thick manufactured part, a parallel experiment of steel shim pulling, was conducted in short die length. The results recorded were not be in line with exactly with 2D plotted model fitting for solid surface friction. Experiment using the same short die with heated steel shim was also conducted to predict the pulling force beyond curing at profile at die surface. The device which has better control on speeds of pulling and temperature plate can have better accuracy to understand behaviour of pull force beyond curing. For this long-cured zone, pulling is mostly generated due to dynamic friction of composite in contact with die surface.

Dynamic dry friction on different resins with specific shrinkage factor during pulling was recorded at 105 °C as shown in Fig. 15. During the period of dry pulling, with initial drops, friction gets stabilised with time. In addition, it is observed, with time a steady state appeared at marginally higher value of friction in the event of low shrinkage resin. Similarly, effect of filler and % conversion on friction during dry drag was studied as shown in Fig. 16, with initial drops, and friction embarks slow rising for all variants. The reason of initial drops is not clearly understood but increasing filler amount from 40% to the subsequent 30% and 10% shows incremental rising trend.

Fig. 15
figure 15

Pressure/pull-force recorded of polyester resin at different characteristic shrinkage

Full size image
Fig. 16
figure 16

Pull-force recorded using device during pulling post curing

Full size image

Beyond curing, comparatively higher cohesive force is expected between walls of the die and resin matrix at interface for low filler content resin which is an opposite condition for higher filler loading [38,39,40,41,42,43,44,45]. The initial drop may be explained as higher filler loading increase matrix morphology stiff and thereby reduces the dynamic frictional coefficient but with passing time, all variants get stabilised with higher friction at higher filler content [12, 13]. Further addition of filler makes the resin thicker, and rate of reaction slows down, and diffusion phenomena is more predominant and delayed conversion starts playing in due to heat on resin layer related to higher viscous resin-die interface ultimately decreasing stress compressibility.

Similarly, two different conversion of same resin was used to predict the behaviour of dynamic friction of the composite beyond curing. The reason of slightly higher pull force for resin at higher conversion at start is not clearly understood. But apparently, higher molecular network restricts to slip initially [46, 47] but stimulate sliding on curing faster than resin at low conversion, reducing contact stress with time. Pulling force gets stabiles with time and difference between low and higher conversion is barely perceptible.

Unlike experiments pulling force in 2D plot sweeping time, axial length is sweep against pulling pressure. However, drops in pull-pressure are evident in resin with higher shrinkage factor due to increasing negative pressure on total pressure of solid friction. The paradigm of pressure drop is very steady, almost similar pattern and consistent as is observed in 2D-plot shown in Figs. 17a, b and 18a. As found for compaction and vicious, increase in tapping angle has negative influence on frictional pressure wherein thickness and fibre volume fraction and positive influence. The gradual and steady drop pressure with increasing resin shrinkage factor is perceptible on minimising scale of pressure axis as plotted in Fig. 18b. It can be concluded that increasing part thickness and fibre volume fraction increase pressure resolving from frictional loads. Amount of pressure goes up exponentially with increasing thickness and fibre volume fraction and wherein pressure drops are noticeable severe for change in shrinkage factor.

Fig. 17
figure 17

Influence of (a) fibre volume fraction and (b) profile thickness on compaction pressure during pulling

Full size image
Fig. 18
figure 18

Influence of pulling speed and tapping angle on pressure due to friction during pulling

Full size image

4 Conclusion

This study shows that for the pulling in open bath pultrusion, the pulling pressure for any cross-section encounters associated frictional force which gets influenced by many crucial parameters. This parameters include the die tapping angle, die radius, thickness and length of die, die surface smoothness, guiders and resin tank used, heater position from die entry, die temperature, pulling speed, fibre volume fraction, configuration of material at die interface, resin viscosity, resin releasing rate from reinforced fibre, size and porosity of filler and its loading percentage. Eventhough it is difficult to develop model which predicts paradigm of burgeoning pull-force during large-scale operation, the proposed modified mathematical equation enables one to comprehend effect of intricate process parameters on pull force measured and its fitting in the model. Pressure arises at compaction zone is always predominant over pressures like viscous drags and dynamic friction.

This study results show that during viscous phase, higher resin conversion leads to a higher friction. Unlike speed of pulling, viscous friction is much more significant when the low temperature (e.g. room temperature) wherein friction drops at higher temperature and eventually debilitate at solidification. Again, it was found out that the die seizure/sloughing leads to fibre breakage. This is more prominent in case of smaller die due to surging adhesive force between die surface and resin, that can be mitigated by using mould releasing agents. Hence, sustainability of smooth operation during pulling relies on ultimate tensile strength of the part rather strength of the fibres being pulled in machine direction. On the other hand, gelling and post-curing solidification cause significant spikes in the pulling force on enlarging die length. However, longer dies in pultrusion benefits in maintaining good dimensional stability against heat distortion and therefore they should not be ruled out. Consequently, as observed in this study, it is worthwhile to mention that pull force measurement alone is not a satisfactory indicator of part curing at the exit and experimental verification on residence time, distribution heat and surface cure at the exit is required to substantiate at pulling operation.