1 Introduction

Among the several joining techniques, welding process has gained increasing importance in the industrial manufacture for getting increasing production volume of components with good requisite of welding quality as less distortions, deeper penetration and reduced HAZ [1, 2]. At the same time, consumption reducing and sustainability represent common objectives in the fight against climate change as well as indicator of any human activity [3,4,5]. For this reason, it is necessary to know and control the main process parameters influencing the welding zone and choose the right set, avoiding any trial (i.e. tools and machine cost, manpower, time, material, waste production and management), to get the component with the best performance. In this contest, developing predictive numerical models is the industrial and academic need to improve reliability, productivity and performant products. Moreover, numerical modelling is one of the pillars characterizing the fourth industrial revolution (also known as Industry 4.0 (I4.0)) improving industrial processes in terms of flexibility, efficient production, cost reduction and sustainability [6, 7]. The synergy, between the trending concept of the I4.0 and the manufacturers challenge in getting an excellent welded joint, induces to have an accurate awareness of the phenomena characterizing the joining procedure to achieve the desired and reliable outputs. This scenario proves the application of the numerical modelling as a valid tool for welding investigation and analysis as shown in [8]. Focusing on this concept, several researches were proposed, demonstrating the increasing interest in modelling the thermo-mechanical aspects of the welding process and their influence on the joined parts as deformations, residual stresses and microstructural changes [9,10,11]. Dancette et al. [12] developed a finite element (FE) model to investigate the deformation and the fracture behaviour of Usibor1500/DP600 dissimilar resistance spot welds. It was compared with 24 experiments at changing weld size, sheet thickness and loading type leading to a better understanding of the several aspects influencing the weld behaviour. The good numerical results showed the advantages of the design of optimized heterogeneous assemblies with reduced weight in the automotive industry. Mayghani [13] implemented a friction stir welding process by a Eulerian-based computational solid mechanic (CSM) model. Analysing the influence on the stresses, process temperatures, equivalent plastic strain and material flow and comparing the proposed model with the conventional Coulomb friction model, the author demonstrated the robustness of his procedure by comparison between experimental results and literature. Mondal et al. [14] proposed a new volumetric avocado shape heat source for welding processes. The model is an advanced version of the conventional ellipsoidal shape with non-symmetrical energy distribution and unequal axis length in the front and rear parts. The developed heat source model was validated by performing a FE-based heat transfer analysis for both gas tungsten arc welding (GTAW) and submerged arc welding (SAW). The good agreement with corresponding experimental results showed the accuracy of the new heat source model and its flexibility in analysing different fusion welding processes. Heyraud et al. [15] proposed a numerical two-scale approach, combining solid and shell finite elements, for non-local multiaxial equivalent stress at the weld toe and the weld root. The results and the comparison with other models from literature validated the potential of the innovative approach for the fatigue design of large welded structures. Shen et al. [16] developed and experimentally validated a series of FE models, by the commercial software ABAQUS/Explicit and SFTC DEFORM-3DTM, able to simulate the multilayer ultrasonic metal welding (UMW), with a vibration frequency of 20 kHz or higher, both for short welding duration (0.1–0.5 s) and long welding duration (1 s). The authors demonstrated the reliability of the proposed 3D FE models in simulating the several aspects characterizing the material response during UMW process and controlling the process during its evolution. The literature analysis shows as welding, both referring to HAZ and fusion zone, needs a detailed study to have a comprehensive knowledge of the thermo-mechanical phenomena occurring during the process, since they have a significant influence on the mechanical response and quality of the components. Moreover, the recent literature [17,18,19] highlights as developing robust numerical models is still attracting a relevant interest both for industrial and academic research. For this reason, with the aim to give a contribution in this direction, in the present work an uncoupled 3D thermo-mechanical analysis, by the commercial software codes SYSWELD and SFTC DEFORM-3DTM, was carried out to model single beads GMAW of AISI 441. The interest in arc welding process arises also for the several advantages of this welding technique when joining advanced materials: control of recovery, recrystallization and grain growth, increase of the tensile strength, improvement of the material ductility and fatigue resistance, significant incidence on weld cracking susceptibility [20,21,22,23]. By combining the strength of the two software in numerical modelling, the authors investigated the above-cited arc welding process. Two customized user sub-routines, to predict the grain growth and hardness variation, were developed and implemented in SFTC DEFORM-3DTM. The procedure for the heat source definition and calibration is also reported, and a comparison between the numerical results and the corresponding experimental data was carried out to validate the models. The effectiveness of the proposed procedure to measure and control residual stresses and strains, distortions, grain size evolution and hardness change is shown.

2 Experimental procedure

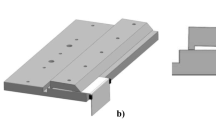
AISI 441 ferritic stainless steel (Table 1) was joined by GMAW procedure by a fully automated torch movement. The welds were performed on two plates of 1.5 mm of thickness and 248 HV0.01 of hardness, with the geometry, the clamping set-up and the coordinate system reported in Fig. 1. The welding process parameters were 220 A current, 11.9 V voltage, 800 mm/min weld speed and 12.2 m/min filler material speed deposition (AISI 307 with a diameter of ϕ = 1 mm, Table 2). Pure Argon was used as shielding gas with a flow rate of 15 l/min.

Table 1 Chemical composition of AISI 441
Full size table
Fig. 1
figure 1

Workpiece plates and experimental set-up: sample geometry (a), coordinate system and clamping set-up (b)

Full size image
Table 2 Chemical composition of AISI 307 filler material
Full size table

Considering the coordinate system reported in Fig. 1b, the influence of three factors on the quality of the weld bead was considered: Dx (torch position on x-axis), Gap (distance between the two plates) and S (overlap between the two plates), Fig. 2. In particular for Dx, two values 0 mm (torch on the contact line of the two plates) and 2 mm (torch shifted of 2 mm along x-axis) were considered, for Gap two values 0 mm and 2 mm were considered and for S three values 8 mm, 9 mm and 10 mm were considered.

Fig. 2
figure 2

Welding configuration of the plates and torch positioning: a–h

Full size image

Eight configurations were analysed (Fig. 2) with a repeatability of three, for a total of twenty-four tests. After welding, samples of 30 mm of length (y-direction, Fig. 1) were mounted into a resin holder for the microstructural investigation. The metallographic preparation consisted of mechanical polishing and etching by the use of Keller’s reagent (92 ml of distilled water, 6 ml of nitric acid, 2 ml of hydrochloric acid and 2 ml hydrofluoric acid). The cross sections of the welded components were analysed by an optical microscope to study the weld bead geometry, the HAZ extension and the grain size change, Fig. 3.

Fig. 3
figure 3

Test 7: cross-section metallographic analysis: welded zone, weld bead geometry, grain size and representation of the several zones characterizing this welding process

Full size image

Considering the weld bead geometry, it was noticed that test 2, 4, 5 and 6 didn’t reach a good quality requirement: a discontinuous weld bead was found as reported in Fig. 4. This result shows that the investigated gap represents a critical aspect, for the examined process parameters, since it doesn’t allow to correctly join the two plates.

Fig. 4
figure 4

Influence of the gap on welding quality: test 6 (a), (c) and test 5 (b), (d). A discontinuous weld bead was found along the cross section of the components

Full size image

Figure 5 shows the grain size change between the base material (unaffected zone) and the HAZ. Fig. 5a represents the base metal with an average grain size of 35 µm. Fig. 5b, c show the average grain size of the HAZ respectively for test 0 (grain growth to 65 µm) and test 3 (grain growth to 60 µm) both reporting a coarser grain, compared to base metal, due to the temperature increase that triggers the grain growth: an increase more than 70% was observed in grain size when comparing the base metal with the HAZ. In all the investigated samples, the grain maintained an equiaxial shape, featuring a dominant coarse grained HAZ [24, 25].

Fig. 5
figure 5

Cross section grain size analysis: base metal/unaffected zone (a), HAZ of test 0 (b), HAZ of test 3 (c)

Full size image

The micro-hardness was measured by an indentation matrix (22 × 3 points spaced 30 µm along the row and 50 µm along the column, Fig. 6a) showing a decreasing trend from base metal (unaffected zone) to HAZ (Fig. 6b) [26, 27]. This result agrees with the analysed grain growth (Fig. 5) according to the H-P relation that considers the hardness evolution as an inverse function of the grain size (Eq. (1)).

Fig. 6
figure 6

Hardness indentation matrix (a), hardness measurement from base metal to weld metal: test 0 (b)

Full size image
$${HV}_{ }={C}_{0}+\frac{{C}_{1}}{\sqrt{d}}$$
(1)

Where C0 and C1 are two material constants while d represents the average grain size.

In Fig. 7, the influence of the investigated factors Dx and S, on the welded samples, is shown. Fig. 7a reports the HAZ extension of the four welded samples, determined by measuring and comparing both the grain growth and the hardness variation. Comparing test 1, 0 and 3, in which the factor S (overlap between the two plates) is increased from 8 to 10 mm, an HAZ reduction is evident. The same behaviour is shown when comparing test 1 and 7, in which the factor Dx (torch position on x-axis) is shifted of 2 mm.

Fig. 7
figure 7

Cross section analysis of the welded components: HAZ extension (a), HAZ grain growth (b), and HAZ hardness change (c)

Full size image

In both cases, moving the heat source away from the welding zone (i.e. contact line of the two plates) results in reduced process temperatures leading to a different HAZ length. In fact, with the increase of Dx (torch change of position along x-axis) the heat source is moved away from the contact line zone of the two plates, shifting the heat flux distribution to an area characterized by a major heat dispersion with environment resulting in reduced reached temperatures. While, the increase of S leads to a reduced heat source penetration depth resulting, also in this case, in reduced process temperatures. According to the HAZ trend, the microstructure shows an average grain size reduction with the increase of the factors S and Dx. Also in this case, the lower reached temperatures lead to a decreasing tendency of the grain growth (Fig. 7b) resulting in an opposite trend of the hardness variation (Fig. 7c): coarser the grain size decreasing is the hardness (Eq. (1)).

The temperature history has been recorded by a FLIR A655sc Infra-Red Camera (IRC), allowing to store data related to thermal field over the entire weld surface of the specimens. Among the FLIR A655sc measurement configuration, the available temperature range acquisition of 100 °C to 650 °C was set, leading to analyse the cooling phase of the process that, for its long duration, is considered the main significant as cause of residual stresses and strains and geometrical distortion.

From the stored thermal data, it was possible to analyse the cooling temperature-trend from three points, positioned at the beginning, the centre and the end of the weld bead, Fig. 8. The temperature analysis will enable to calibrate, by an iterative trial and error procedure, the parameters featuring the heat source model of both the investigated FE software.

Fig. 8
figure 8

Thermal tracking point positioning along the welding line (a), and cooling temperature trend of the welded components (b)

Full size image

3 Numerical model

3.1 SYSWELD

Considering the experimental results, got by microscope and IRC, the numerical model of the commercial code SYSWELD for the prediction of the residual stresses and strains and the distortions was developed and calibrated. In particular, numerical modelling of the welding process by SYSWELD requires three main steps: material definition, geometry of the parts and heat source fitting. Material properties were implemented by the material definition tool available in the software. The geometry of the three parts (two plates and weld bead) was modelled in SYSWELD by a dedicated modulus, paying particular attention to the macrographs for the right weld bead shape, Fig. 9.

Fig. 9
figure 9

Test 3: comparison between weld bead and experimental macrograph (a), welded sample (b), and SYSWELD numerical model of the final component (c)

Full size image

The volumetric heat flux distribution was modelled as a three-dimensional Goldak’s double-ellipsoid defined by four parameters: the half width a, the depth of penetration b, the front length of molten pool c1 and the rear length of molten pool c2, Fig. 10a. These four parameters were experimentally determined and measured from the weld bead geometry and from the macrograph of the cross section of the welded component (Fig. 10b, c).

Fig. 10
figure 10

Goldak’s double-ellipsoid heat source model (a), experimental measurement of the Goldak’s double-ellipsoid parameters a, c1 and c2 (b), test 1: macrograph and Goldak’s heat source modelling (c)

Full size image

By the heat source fitting tool (HSFT), it is possible to adjust the Goldak’s double-ellipsoid (Fig. 10c) and to define the efficiency of the heat transfer from source into material ƞ. HSFT is a useful option existing in SYSWELD, which enables to calibrate the parameters of the heat source to obtain more accurate simulation results. The user is able to calibrate the heat source shape and efficiency by a combination of two procedures: (i) an iterative procedure of comparison between both the modelled fusion zone and HAZ with the macrograph of the analysed sample (Fig. 11a, b) and (ii) a cooling rate comparison between the data stored by IRC with those predicted by SYSWELD (Fig. 11c).

Fig. 11
figure 11

Test 1: calibrating heat source procedure - predicted fusion zone and HAZ (a), experimental macrograph near the welded zone (b), comparison between numerical and experimental cooling rate (c) - comparison between numerical and experimental results to evaluate the goodness of the calibration phase (d)

Full size image

The accuracy of the numerical thermo-mechanical analysis is related to the correctness of the heat source modelling and of the material properties data. Fig. 11d shows the comparison between the predicted HAZ and the macrograph at the end of the calibration phase. A good agreement was found between the numerical results and the corresponding experimental outcomes with a maximum difference of about 11% for test 1. Moreover, the experimentally registered temperatures by IRC were compared with the numerical thermal histories: the numerically predicted cooling rate agrees with the IRC data, Fig. 11c.

The good results obtained between predicted and measured data (i.e. fusion zone, HAZ and cooling rate, Fig. 11) confirm (i) the correctness of the heat source shape, size and efficiency, (ii) the accuracy of the material properties data and (iii) the robustness of the developed numerical model in predicting residual stresses and strains and distortions.

3.2 SFTC DEFORM-3D TM

Concerning the commercial FE software SFTC DEFORM-3DTM, the two plates were modelled as a plastic body meshed with 50,000 iso-parametric tetrahedral elements, while for the weld bead a plastic model with 32,000 elements was considered (Fig. 12).

Fig. 12
figure 12

Test 7: SFTC DEFORM-3DTM finite element modelling by welded component and cross section macrograph

Full size image

In this case, the Goldak’s double-ellipsoid heat source was modelled by a series of 3D heat exchange windows (Fig. 13) with a movement velocity of 800 mm/min as for the experimental welding speed. By the experimental weld bead geometry, cooling rate and HAZ were determined all the features characterizing the heat exchange windows: heat source parameters, convection coefficient and temperature.

Fig. 13
figure 13

Goldak’s double-ellipsoid (a), SFTC DEFORM-3DTM heat source modelling heat exchange windows (b), measurement of the ellipsoidal heat source parameters: the half width a, the front length of molten pool c1 and the rear length of molten pool c2 (c)

Full size image

In particular, the half width a, the front length of molten pool c1 and the rear length of molten pool c2 were measured on the welded plates (Fig. 13c), while the depth of penetration b, the temperature and the convection coefficient of the heat exchange windows were calibrated by an iterative trial and error procedure of comparison between the numerical and experimental HAZ extension and the cooling profile (Fig. 14).

Fig. 14
figure 14

Iterative trial and error procedure to calibrate the heat source depth penetration b (a), the temperature of the heat exchange window (b), the convection coefficient of the heat exchange window (c)

Full size image

The welding phenomena influencing the microstructure (i.e. grain size) of the HAZ were predicted by developing a customized user sub-routine involving the classic kinetic theory for grain growth [25, 28], Eq. (2).

$$D^m-D_0^m=t\cdot k$$
(2)

Where D is the current grain size, D0 is the initial grain size, m is the grain growth exponent, k is the kinetic constant and t is the soaking time. The grain growth kinetic constant k can be expressed by the Arrhenius form as function of the temperature, Eq. (3).

$$k={k}_{0}exp\left(-\frac{Q}{RT}\right)$$
(3)

Where k0 is a pre-exponential constant, Q is the activation energy for grain growth, R is the gas constant and T is the temperature. Combining Eqs. (2) and (3), it is possible to define the expression for the grain growth kinetics as in Eq. (4).

$$D=\sqrt[m]{{tk}_{0}exp\left(-\frac{Q}{RT}\right)+{D}_{0}^{m}}$$
(4)

The values of the numerical parameters of Eq. (4) are listed in Table 3.

Table 3 Parameters for the grain growth kinetics
Full size table

For t*k0 it was considered a constant value, validated during simulations and set equal to 105.

Finally, the hardness modification depending on the grain size evolution was calculated according to the H-P relation (Eq. (1)). The value of C0 and C1 was determined, for each test, through the previously measured values of the material hardness and grain size of both HAZ and base metal, Table 4.

Table 4 Constants for H-P hardness model
Full size table

Considering the average value of the four tests it was found 167.5 for C0 and 15.1 for C1 with an overall error less than 4% when recalculating the hardness for each single test.

4 FE analysis and results

4.1 SYSWELD analysis of residual stresses and strains and distortions

The calibration and validation phase completed, SYSWELD numerical model was used to analyse the effect of the investigated factors on residual stresses and strains and geometrical distortions. Fig. 15 shows the variation of the residual stresses and strains of the welded components: each curve represents the average value of the three repetitions made per each test.

Fig. 15
figure 15

Transverse section macrograph test 0 (a), SYSWELD analysed profile points test 0 (b), numerical analysis of the residual stresses (c), and maximum predicted residual strains (d)

Full size image

Analysing test 1, 0 and 3, in which the overlap between the two welded plates increased from 8 to 10 mm, a slight decreasing trend of the maximum peak of the residual stresses and strains is evident. This is mainly due to the reduced temperatures [30, 31] that result in a slow cooling rate leading to decreasing residual stresses and strains when higher overlaps were set. Also comparing test 1 and test 7, in which the torch position was shifted along x-axis, a residual stress and strain decrease for the reduced temperatures was shown.

Figure 16 reports the analysis of the distortions of the welded plates. According to the experimental set-up (Fig. 1), no displacements resulted in the clamped zone. Moreover, considering the components constrained only on one side, the final distortions were limited in a range of 0.10 to 0.25 mm, following the same behaviour of the previously analysed residual strains.

Fig. 16
figure 16

Numerical analysis of welding distortions: full-field analysis for test 0 (a), full-field analysis for test 1 (b), and maximum predicted value for all welded components (c)

Full size image

4.2 SFTC DEFORM-3DTManalysis of grain size change and hardness evolution

Concerning SFTC DEFORM-3DTM, Fig. 17a shows the numerical heat source moving along the contact line of the two plates, with a stable temperature profile (Fig. 17b). In Fig. 17c, the comparison between the predicted HAZ extension and the corresponding experimental value is reported. An overall average error of 10% was found (with a maximum of 14% when considering test 3) mainly due both to the numerical procedure (i.e. discretization, trial and error calibration procedure and number of numerical constants and equations) and to the experimental accuracy.

Fig. 17
figure 17

SFTC DEFORM-3DTM modelling of the heat source moving (a), numerical cross section temperature profile for test 7 (b), and comparison between numerical and experimental analysis of the HAZ extension (c)

Full size image

A greater number of tests allow to reduce the overall percentage error and the percentage error of each single test. In fact, the implementation of a statistical approach leads to build robust models able to predict the value of all the implemented empirical constants at varying of the process configuration and parameters. Nevertheless, the contained deviation between the predicted and measured data proves the robustness of the developed numerical technique, validating the accuracy of the proposed method in SFTC DEFORM-3DTM for Goldak’s heat source modelling by using heat exchange windows. Fig. 18 reports the predicted grain growth and hardness change in the HAZ, confirming the correctness of the worked-out FEM and user routine in predicting the thermal aspects of the GMAW process and the consequent microstructural (i.e. grain size) and mechanical (i.e. hardness) changes. In particular, Fig. 18a shows the stable and uniform cross section grain size prediction, representing a new microstructure featured by a coarser grain size, in the HAZ. According to experimental evidence, a decreasing hardness trend was observed in the HAZ (Fig. 18b) for the H-P relation (Eq. (1)).

Fig. 18
figure 18

Test 7-predicted grain size [mm] (a) and hardness variation [HV0.01] (b), comparison between experimental and numerical grain growth (c) and hardness evolution in the HAZ (d)

Full size image

In Fig. 18c, the comparison between numerical and experimental grain size variation in the HAZ is reported: an overall average error of 11% was ascertained, with a maximum error of 14% when considering test 7. While in Fig. 18d, the measured and predicted comparison of the hardness change in the HAZ with an overall average error less than 7% is shown. The numerical results, validated with the corresponding experimental cases, demonstrate that, although the GMAW is characterized by a relative simplicity of execution, the weld region undergoes a complex thermal cycle for the localized heating and consequent cooling steps. Thus, a microstructural change occurs resulting in an average grain size increase in the HAZ and a consequent hardness decrease particularly detrimental for the in-safety performance of the products. Finally, the main influence of the thermal phenomena on the mechanical material properties and good quality of welding was proved.

5 Discussion

As discussed in the previous sections, with the aim to have a greater control of the investigated process and to develop robust numerical models of relevant interest both for industrial and academic research, two numerical models were developed to have a deep knowledge of the influence of the configuration set-up on the mechanical properties of the welded components. The results highlighted the main importance of the correctness of the calibration phase related to modelling the heat source in terms of geometry, positioning, temperature, efficiency and movement: experimental macrograph of the weld bead, HAZ size and thermal history of the process are of fundamental importance for the success of the procedure. At the end of this approach, both in SYSWELD and in SFTC DEFORM-3DTM, the extension of the numerical HAZ corresponded with the experiments validating the accuracy of the numerical codes. An acceptable difference, with an overall average error of 10%, was found mainly due both to the numerical procedure and to the experimental accuracy: a greater number of tests allow to reduce this difference. The residual stresses and strains and the distortions of the components were analysed by SYSWELD, highlighting as each single configuration influences the process temperatures resulting in different cooling rate: reduced the cooling rate reduced residual stresses and strains and distortions. Hardness variation and grain size evolution were analysed by SFTC DEFORM-3DTM. Also in this case, the different temperatures, related to the different welding configurations, influenced the microstructure from base metal to weld metal. The results showed a new microstructure characterized by coarser grain size in the HAZ and, for the H-P relation, a consequent hardness decrease. The outcomes of the developed numerical model and customized user routines corresponded with the experimental data, showing an acceptable difference. Summarizing, thermal phenomena that occur during GMAW process, cause severe microstructural and mechanical property changes influencing the mechanical performances and the good quality of the final welded components.

6 Conclusions

In this work, two numerical models were developed to analyse the influence of some factors on the residual stresses and strains, the distortions, the grain growth and the hardness variation during GMAW process of AISI 441 plates. The commercial FE software SYSWELD was used for the numerical prediction of the residual stresses and strains and the distortions, while the commercial FE software SFTC DEFORM-3DTM was used for the numerical investigation of the grain size change and hardness evolution by developing two user sub-routines that implement the classic kinetic theory (i.e. grain growth) and the H-P equation (i.e. hardness decrease). Two software were implemented to have a wide knowledge of the several aspects characterizing the investigated process. The good agreement between the numerical and the experimental comparison of the HAZ extension validated the correctness of the modelled heat source parameters in SYSWELD and the robustness of the developed technique in SFTC DEFORM-3DTM to model the Goldak’s double-ellipsoid heat source by heat exchange windows. Furthermore, the validation of the numerical results with the experimental evidences demonstrated the reliability of the two developed numerical models and user sub-routines in predicting the thermal phenomena of GMAW process and the related metallurgical changes. Thus, the shown numerical procedure can be implemented for simulating the GMAW of AISI 441 steel plates, leading to analysing macro and microstructural aspects influencing the required quality outputs of the welded products. In this way, by the proposed approach, it is possible to predict, monitor and control the required microstructure and mechanical properties of the components and their final geometrical tolerances.