Abstract
We present a Computational Fluid Dynamics (CFD) framework for the numerical simulation of the Laser Metal Deposition (LMD) process in 3D printing. Such a framework, comprehensive of both numerical formulations and solvers, aims at providing a sufficiently exhaustive scenario of the process, where the carrier gas, modeled as an Eulerian incompressible fluid, transports metal powders, tracked as Lagrangian discrete particles, within the 3D printing chamber. On the basis of heat sources coming from the laser beam and the heated substrate, the particle model is developed to interact with the carrier gas also by heat transfer and to evolve in a melted phase according to a growth law of the particle liquid mass fraction. Enhanced numerical solvers, characterized by a modified Newton-Raphson scheme and a parallel algorithm for tracking particles, are employed to obtain both efficiency and accuracy of the numerical strategy. In the perspective of investigating optimal design of the whole LMD process, we propose a sensitivity analysis specifically addressed to assess the influence of inflow rates, laser beams intensity, and nozzle channel geometry. Such a numerical campaign is performed with an in-house C++ code developed with the deal.II open source Finite Element library, and publicly available online.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, Laser Metal Deposition (LMD) is increasingly proving its high potential as 3D printing Additive Manufacturing (AM) technology in new industrial scenarios [1]. In fact, LMD is producing great benefit for prototype fabrication thanks to its flexibility in terms of batch production and for manufacturing and repairing of new designed components characterized by complex—possibly highly optimized—geometries.
However, the complexity of the LMD process requires both model and numerical tools capable to cover a wide spectrum of physical phenomena that involve powder-particle transportation, interaction between particles and carrier gas, energy exchange with laser beam source, and then powder material phase-change (solid-liquid phase transition).
Many authors have published papers tackling such a process through Computational Fluid Dynamics (CFD) approaches, working with particle-tracking methods for predicting particle flow in a Lagrangian description, combined with Eulerian methods for describing the carrier gas flow. Zhang and Coddet developed three-dimensional CFD models in Ansys Fluent, solved using a Discrete Phase Modeling (DPM), i.e., a particle-tracking method that computes the particle dynamics, while Navier-Stokes equations have been considered to model the inert gas [2]. The same CFD numerical model is employed by Zeng et al. with the purpose of better understanding the powder deposition process and analyzing the influence of the geometrical and processing parameters, such as the standoff distance, the volumetric gas flow rate, and the powder mass flow rate, on the quality of the LMD printing technology [3].
Along the same perspective, similar approaches aiming at optimizing nozzle design and validating experimental measurements on the particle flow can be found in some early contributions [4, 5]. In particular, Tabernero et al. have used the particle tracking method implemented in the Ansys Fluent code to simulate the powder flux on a real continuous coaxial nozzle to predict the powder distribution shape, together with particle velocities and trajectories [4]. Arrizubieta et al. [5] have investigated optimal values of the carrier and shielding gases flow rates. Other works have employed numerical strategies based on DPM approaches to explore how nozzle geometry, powder properties, and feeding parameters can improve LMD process efficiency [6,7,8].
More recent contributions on gas/powder stream characteristics can be found in [9], where to perform the numerical modeling of a jet flow, Ferreira et al. have employed a 2D axisymmetric models of both the gas and powder streams, with a Reynolds Averaged Navier-Stokes (RANS) turbulent model implemented with the COMSOL Multiphysics software. The adopted Euler-Lagrange model revealed a good agreement between numerical and experimental results, pointing out the great impact of particle rebound conditions that should be linked to the particle concentration for a correct description of the powder stream structure, especially for nozzles with small exit diameters. Finally, the capability of fully Eulerian approaches and coupled Eulerian-Lagrangian approaches, both addressed to predict geometrical properties of the powder cone formed out from the nozzle, were investigated in [10]. By developing a customized OpenFOAM code and supported by experimental evidences, the authors proved how the Eulerian-Lagrangian approach, albeit more expensive than a fully Eulerian one, is able to accurately predict the experimented behavior, where the total flux divaricates in separate streams after the focal point.
The above-mentioned works neglect the thermal problem, i.e., the interaction between the particle flow and the laser beam source, aspects that play a crucial role in the entire LMD process. An interesting contribution in this direction is presented for instance in the work by Ibarra-Medina and Pinkerton [11], where a thermal coupling between powder flow and laser beam is proposed. In particular, in addition to various interactions that occur during the printing process, powder stream formation, powder heating and mass deposition into the melt pool are also considered and analyzed by using the commercial software CFD-ACE+. Numerical results have proved that mass concentration within the powder stream, overall powder stream heating, and mass deposition rate, are strongly dependent on the distance between the nozzle tip and the substrate. Wen et al. in [12] have also focused on laser-particle interaction process, which is treated through a model of particle temperature evolution: by considering particle morphology and size distribution based on real powder samples, they were able to predict the powder stream structure and the multi-particle phase change as liquid fraction evolution throughout the entire process.
A more recent contribution is provided in [13], where Guan and Zhao have developed a numerical model for powder stream dynamics and heating process to accurately describe the coaxial powder flow and its interaction with the laser beam. A RANS approach is proposed for turbulent continuum gas flows, while DPM describes the dynamic powder behavior. A two-way coupling approach is adopted to account for the momentum transfer between gas and powder, together with a thermal model for powder streams interacting with a Gaussian laser beam. The obtained results of powder stream are compared with the experimental results from published literature, showing a good agreement. Finally, in order to model complex free surface, fluid flow, thermal and laser interaction evolution, a novel multiphase thermo-fluid formulation based on a diffusive Level Set method coupled with the Navier-Stokes, energy conservation and radiative transport equations are implemented [14]. The reported results show that the penetration of the powder within the focal spot of the laser is favored by the large velocity of the particles, whereas the evaporation across the surface of the particles, due to laser absorption, drives powder motion either inside or outside the melt pool. Moreover, other features affecting the melt pool dimensions, such as the laser absorption, can be altered by a large amount of powder material that shields the melt pool from the energy source produced by the laser beam.
1.1 Contribution
The current literature shows that several numerical strategies have been implemented to aid the design of LMD set-ups, leading to possible optimal conditions of minimizing thermal gradients and speeding up the whole deposition process [15], but a comprehensive numerical tool, modeling the various multiphysics phenomena involved in fluid-particles interaction, still lacks.
From this perspective, the present work proposes a numerical strategy including both fluid-particles and particle-laser interactions, without relying on commercial softwares.
Within an Eulerian formulation we model the carrier gas as an advection-diffusion fluid problem combining Navier-Stokes with heat exchange equations; this is accompanied by a Lagrangian formulation for tracking powder particles that are modeled to exchange mass, momentum, and heat energy with the fluid and, at the same time, to evolve their liquid mass fraction according to laser beam source irradiation [16].
For this purpose, we developed a C++ code using the open source Finite Element library deal.II [17]. To accurately and efficiently represent the advection-diffusion problem [18], the Eulerian coupled problem is tackled through a fully nonlinear formulation of the Navier-Stokes equations, solved with a modified Newton-Raphson scheme. A stabilization method is introduced for heat equations in reason of high Péclet numbers (cf. [19,20,21,22]). In order to improve the performance of the Lagrangian problem, a parallel code is implemented for particles tracking.
Finally, a sensitivity analysis of the LMD process is proposed on the basis of the most meaningful parameters, describing both the configuration and the energy of the powder flow at different real working conditions. Such an analysis would pave the way to improvements of process parameters set up toward possible optimal design conditions. The source code of our software is publicly available at https://zenodo.org/record/5888175.
2 Modeling coupled problems of flow and heat transfer with particles
In the following we will denote with \({\varvec{u}}\) the vector field for fluid velocity, and with \(\mathbf{u}\) its discrete representation in the finite element formulation with the vector. Accordingly, T and p indicate the scalar fields of temperature and pressure respectively, while \({\mathbf {T}}\) and \({\mathbf {p}}\) their discrete vectorial representation. Finally, discrete values of each field associated with the n-th time step of the analysis will be denoted with subscript n.
2.1 General aspects on the governing equations
The phenomenon of convective heat transfer flows can be investigated through a multi-physics model consisting of a coupled system of nonlinear partial differential equations in terms of velocity, pressure and temperature. Such a phenomenon may be categorized in two different fluid-thermal coupling problems, depending on the forces that are responsible for the fluid motion: i) free or natural convection problems, where the fluid motion is produced by temperature-induced buoyancy forces that generate small Reynolds numbers within the flow, hence the nonlinear terms due to inertial effects can be neglected, resulting in a linear boundary value problem named Stokes flow; and ii) forced convection problems, where the application of pressure or viscous forces on the fluid boundary produces the fluid motion, with Reynolds number generally starting to grow and an advection-dominated problem characterizing the flow behavior, thus, requiring to employ the full Navier-Stokes equations.
We focus on this latter class of problems. By neglecting the effects of the temperature on the fluid flow (see [23]), we address the present study to the following advection-diffusion problem, composed by Navier-Stokes equations and thermal energy equation that describe the time-dependent heat transfer in a flow of a viscous incompressible fluid:
where t is the time, \(\nu\) the kinematic viscosity, \(\varvec{f}\) the force term, \(\kappa\) the diffusivity coefficient, and \(\gamma\) the heat source term. The system of Eqs. (1–3), supplemented with initial and boundary conditions, is a well-known multiphysics problem (see for instance [24,25,26]). The Navier-Stokes equations for incompressible fluid flow (1) and (2), consisting of the momentum conservation equation for a Newtonian fluid and of the mass-conservation (continuity) equation, allow us to model the carrier gas motions, delivering the powder particles. The thermal energy Eq. (3), accounting for the energy balance of the fluid, reproduces the temperature field in the LMD process, whose high gradients are generated by the laser beam source and the melt pool thermal features.
Additionally, the multiphase flow powder model is introduced, by describing the motion of particles in the fluids as dispersed phase, and their coupling with the pure fluid phase. The dispersed phase is not materially connected, such as gas-particle and liquid-particle flows. The particle-fluid interaction is instead modeled through mass, momentum, and energy information transfer [27]. In particular, the Newton second law applied on the particle dynamics leads to the following conservation equation
where \(m_p\) is the solid mass of the particle, \(\varvec{u}_p\) is the particle velocity, and \({\varvec{F}}_p\) is the resultant force acting on the particle. The energy coupling, i.e., the heat transfer between the two phases, is governed by
representing with \(c_p\) the specific heat capacity of the particle, \(T_p\) the particle temperature, and \(H_p\) the resulting power of heat source acting on the particle.
Note that the system of Eqs. (1–3), involving velocity, pressure, and temperature fluid fields, provides the Eulerian description of the LMD process, while particle motion and energy conservation, Eqs. 4 and 5, are described according to a Lagrangian approach.
2.2 Spatial discretization of the Eulerian coupled problem
Introducing the functional scalar space \(\mathcal {Q}\) and the vector spaces \(\varvec{\mathcal {S}}\) and \(\varvec{\mathcal {V}}\), the weak form problem statement for the Navier-Stokes equations in (1)–(2) can be formulated as follows: find \(\varvec{u}(\varvec{x},t) \in \varvec{\mathcal {S}}\) and \(p(\varvec{x},t) \in \mathcal {Q}\) such that
\(\forall \varvec{v} \in \varvec{\mathcal {V}}\) and \(\forall q \in \varvec{\mathcal {Q}}\), with the functional spaces being defined as
where \(\Gamma _D\) is the boundary involving prescribed Dirichlet conditions. Similarly for the heat Eq. (3), denoting the space of scalar functions with \(\mathcal {T}\), we may rewrite the problem in weak form: find \(T(\varvec{x},t) \in \mathcal {T}\) such that, \(\forall \tau \in \mathcal {T}\):
with \(\mathcal {T} := L_2\left( \Omega \right) .\) Once introduced the following bi- and trilinear forms
\(\forall \varvec{u}, \varvec{v} \in \varvec{\mathcal {H}}^1(\Omega )\) and \(q \in L_2(\Omega )\), we can finally write Eqs. (6), (7), and (8) as
This leads to the following discrete system of equations, complemented by corresponding boundary and initial conditions (cf. Eqs. (15) and (16)):
where \(\mathbf {u}\) and \(\mathbf {p}\) are the vectors collecting discrete values associated with \({\varvec{u}}\) and p, respectively, while matrices are assembled according to standard the Finite Element Method through the assembly operator \({\mathcal {A}}[\cdot ]\), i.e.,
Analogously, for heat transfer problem, the discrete form (17) is expressed as
with \(\mathbf {M}_{\mathrm {T}}\partial _t\mathbf {T} = {\mathcal{A}}\left[ m(\tau , \partial _t T) \right]\) and \(\mathbf {K}_\kappa \mathbf {T} = {\mathcal {A}}\left[ a_\kappa (\tau ,T) \right]\).
2.3 Particle modeling
As previously mentioned, the particle phase is handled according to a Lagrangian description where the single discrete particle is tracked though the Eulerian domain, and its properties (such as velocity, temperature and laser radiation energy) are determined through the point-wise values of the field.
Following [12, 13, 28], where the conservation equations for single particles yield the evolution of both motion and thermal properties, and assuming drag and gravity forces for \({\varvec{F}}_p\) as the key contributions of the fluid-particle interaction, the equations of motion (4) of the p-th particle is written as follows
where \(m_p\) is the mass of the particle, \(\varvec{u}_p\) is the particle velocity field, \(A_p\) is the area of the particle defined as \(A_p=\pi d^2_p/4\), being \(d_p\) the diameter of the particle, \(C_D\) the drag coefficient, \(\rho _p\) the particle density, and \(\varvec{g}\) the gravitational force.
The particles that form the powder stream interact through the energy balance Eq. (5) also with the temperature field, mainly generated by the laser source, and the melt pool temperatures. Exiting from the nozzle, they intersect the path of the laser beam and are then subjected to high energy radiation, causing a sudden increase of the powder temperature. Moreover, the energy reflected by both the melt pool and the substrate contributes to heating particles, concurrently exchanging heat with the surrounding fluid by convection. Notice that in the present study, we neglect the contribution of the particle internal conduction in the heat equation. As argued in [16], this assumption is valid when working with values of the Biot number \(\mathrm {Bi}\), lower than 0.1, being \(\mathrm {Bi}\) the ratio between convective and conductive heat transfer. In our case, where Stellite 6 powder and Argon gas are considered, the Biot number \(\mathrm {Bi}\) results \(\ll 0.01\).
Under these assumptions, we specify the energy conservation of a particle in terms of the heat source \(H_p\) that includes the absorbed laser power, the contribution of heat convection between the particle and the carrier gas, and the latent heat of melting of the particle, thus leading to rewrite the heat Eq. (5) as follows:
where \(c_p\) is the specific heat of powder particle, \(\eta _p\) is the particle material absorption coefficient, \(A_{p,p}\) is the effective projected area of the particle on laser beam, h is the convective heat transfer coefficient, \(A_{p}\) is surface area of the particle, \(T_p\) and T are the temperature of the powder particle and surrounding gas, respectively, \(L_f\) is the latent heat of fusion, that contributes to the heat transfer of powder particle due to phase change such as melting or partial melting, f is the liquid mass fraction. Finally, \(I_T\) is the total energy of the laser incident on the particle, defined as:
where P is the laser power and D(z) the effective laser beam diameter, that is obtained by the following expression
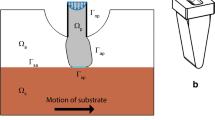
being \(\theta\) the divergence angle, \(z_0\) the focal point distance and \(D_0\) the laser beam diameter at the focal point (see Fig. 1).
Additionally, denoting with \(m_l\) the liquid mass, the following linear relationship is used for the liquid mass fraction f, and particle temperature between the solidus temperature \(T_{sol}\) and the liquidus temperature \(T_{liq}\):
and, consequently, its time derivative can be written as:
Therefore, the particles when reaching the solid temperature \(T_{sol}\) are assumed to melt partially and to exhibit a phase change from solid to liquid. The evolution of such a phase change is modeled in terms of liquid mass ratio \(m_l/m_p\), that starting from 0 in the initial solid phase tends to 1 in the liquid one.
Note that in the Eqs. (20) and (21) both the velocity \(\varvec{u}\) and the temperature T at the particle location are obtained by interpolating the approximated solution vectors \(\mathbf {u}\) and \(\mathbf {T}\), solving the Navier-Stokes Eqs. (1) and (2), and the heat Eq. (3), according to the shape functions of each finite element where the particle is located.
3 Numerical solvers for both time and spatial integrations
The following section introduces our modified Newton-Raphson algorithm, as proposed in [29], aimed at solving the coupled Navier-Stokes and heat transfer equations introduced in the previous section. We remark that the Eqs. (15)–(17) define a one-way coupled problem in velocity, pressure and temperature fields, meaning that for each time step we solve autonomously for both velocity and pressure vectors the Navier-Stokes Eqs. (15) and (16), and consequently, the temperature vector for the heat transfer conditions (17), where the velocity contributions are known. For this reason, we will describe the algorithms able to tackle the Navier-Stokes problem independently from that implemented for the heat transfer problem, rearranging each problem according to its time discretization.
3.1 Navier-Stokes solution
Time integration is here done applying a standard Forward Euler Method. The ensuing nonlinear field problem, discretized in time, is then approached through a Newton-Raphson numerical scheme solving for each time step the system of spatial-discrete equations.
In the Navier-Stokes equations the velocity field is then expressed as \(\partial _t\mathbf {u}=1/\Delta {t} (\mathbf {u}_{n+1} - \mathbf {u}_n)\), according to a standard Forward Euler Method for time integration, where \(\mathbf {u}\) is the velocity field at the time step \(n+1\), and \(\mathbf {u}_n\) is the velocity field at the previous time step n. Equations (1) and (2) can be then rearranged in the following form of residual vector \(\mathbf {r}\):
The Newton-Raphson approach applied to such a problem (see, for instance, [30]) solves for \(k=0,1,\ldots ,\bar{k}\), being \(\bar{k}\) the iteration where the convergenced solution \(\mathbf {x}^{\bar{k}} =\{ \mathbf {u}_{n+1},\mathbf {p}_{n+1} \}\) is reached, the following linearized system of equations:
where we indicate with \(\mathbf {x}^0=\{\mathbf {u}_{n},\mathbf {p}_{n}\}\) the initial guess vector for the iterative scheme, collecting both velocity and pressure discrete vectors at the time step n, and with \(\delta \mathbf {x} = \mathbf {x}^{k+1} - \mathbf {x}^{k}\) the correction vector at the kth iteration, \(\mathbf {x}^{k+1}\) and \(\mathbf {x}^{k}\) being solutions at \((k+1)\)th and kth iteration, respectively, and \(\mathbf {J}(\mathbf {x}^{k})\) is the Jacobian matrix evaluated at \(\mathbf {x}^{k}\), i.e., the directional gradient of \(\mathbf {r}(\mathbf {x})\) along \(\delta \mathbf {x}\) at \(\mathbf {x}^{k}\).
In order to save computational costs deriving from the most expensive routines of assembly and inversion of the Jacobian matrix \(\mathbf {J}(\mathbf {x}^{k})\), we implement a modified version of the scheme where the inverse of the Jacobian matrix \(\mathbf {J}^{0}\) assembled at \(\mathbf {x}^{0}\) is computed at the beginning of the loop solving for the iterative corrections. Also, we utilize a LU decomposition of the Jacobian matrix, whose factorization step is out of the iteration loop, allowing to save computational costs, as shown in [31]. Therefore, the linear system of iterative corrections (27) is substituted by the following ones
See [29] for further details.
3.2 Heat transfer solution
Based on the method commonly referred to as Streamline Diffusion, or SUPG (Streamline Upwind Petrov-Galerkin) [19,20,21,22], in which the equation is tested with functions \(\mu _K\varvec{u} \cdot \nabla \tau\) instead of \(\tau\) for the heat equation (cf. Eqs. (3), (8), and (17)), we can write the following stabilized form:
substituting the general Eq. (19). The SUPG terms, identified by superscripts, are defined as follows
where the sum is done over all elements K, and \(\mu _K\) is an element-wise constant stabilization parameter.
Regarding our assumptions for time discretization, we consider a backward differentiation of the second order to integrate in time the heat Eq. (3). This choice is made to limit further time-discretization errors, deriving from the bilinearity of the coupling term between temperature and velocity fields. Thus, the time discretization of heat equations is of one order greater than that of the velocity field in Navier-Stokes equations (see [18] for further details).
Note also that in the numerical strategy the fluid problem is solved before the heat problem, with the latter using the convergence solution \({\mathbf {x}}_{n+1}\) achieved in the former.
3.3 Lagrangian particle solution
Adopting a backward Euler method to perform time integration on the particle mechanical and thermal balance Eqs. (20)–(21), the particle temperature at the \((n+1)\)th time step is computed according to the following expression
the particle velocity is found solving the momentum equation
and finally the particle position can be updated according to the formula
The drag coefficient \(C_D\) in (31) is calculated in function of the particle’s Reynolds number \(\mathrm {Re}_p\) as follows [32]
The particle Reynolds number is defined as \(\mathrm {Re}_p = \rho /\nu d_p \left\| \varvec{u} - \varvec{u}_p \right\|\), where \(\nu\) and \(\rho\) are the kinematic viscosity and the density of the fluid, respectively, and \(d_p\) is the particle diameter. All other parameters in the above equations have been previously defined in Sect. 2.3. Note that the collision between the particles and the wall is taken into consideration assuming the following conditions
where \(\mathbf {u}_{p,n}\) and \(\mathbf {u}_{p,t}\) are the normal and tangential velocities, respectively, and e the coefficient of restitution, whereas f the coefficient of kinetic friction.
3.4 A fully coupled algorithm
The Lagrangian tracking algorithm of the particles, moving in the fluid domain, is combined with the Eulerian methods used to compute velocity, pressure and temperature fields. The resulting numerical scheme is represented in Algorithm 1, where the modified Newton-Raphson (mNR) scheme solving the Navier-Stokes discrete Eq. (26), and the Stabilized Temperature (ST) algorithm for heat discrete Eq. (29), are invoked as first steps within the time incremental loop. In particular, apart from an initialization phase out of the solving loop, for each time step \(t_{n+1}=t_n+dt\), with dt being the time-step size, we perform: i) the evaluation of the current velocity and pressure vectors \(\mathbf{u}_{n+1}\) and \(\mathbf{p}_{n+1}\) thorough the mNR iterative scheme; ii) the evaluation of the current temperature vector \(\mathbf{T}_{n+1}\) through the ST solver; iii) the particle evolution. The particle evolution is performed by calling two successive procedures, namely generate_particles and advect_particles functions. The former creates at each time step a collection of particles in the inlet portion of the domain, according to the prescribed mass flow rate, each characterized by known diameter, density, and initial values of both velocity and temperature. The latter function handles the dynamics of the particle, according to the Eqs. (30)–(32), which describe both the motion and the thermal evolution of the particle irradiated by the laser beam. The whole scheme terminates when a prescribed final time step \(t_\text {tot}\) is reached.

Note that several procedures in Algorithm 1, i.e., those in init computing both assembly and factorization of the iteration matrix and those in generate_particles and advect_particles, handling particle generation and motion, run in parallel on all CPU cores, by invoking standard C++ multithreading routines, allowing to be fully portable on any hardware architecture.
4 Numerical outcomes
This section reports both numerical set up and results of the simulated LMD manufacturing process, carried out with the numerical strategy discussed in the previous sections. The whole simulation is obtained by a custom C++ code using the deal.II open source library, public available at https://zenodo.org/record/5888175. The reported results are intended to provide a parametric study, by means of several numerical simulations performed varying the parameters that most influence the LMD process (see for instance [10, 33, 34]). Such parameters, although not being exhaustive, are of macroscopic nature and directly employable from an engineering viewpoint, specifically: i) nozzle geometry, i.e., the inclination of the channel through which particles and gas flow exit; ii) carrier gas flow rate imposed in the inlet; iii) powder mass flow rate entering the nozzle; iv) laser power used to melt the particles.
Diverse types of numerical outcomes are discussed, such as the evolution during the LMD process of both powder and carrier gas flows, and of their temperature distribution, as well as the interaction between particles and laser source. In particular, our simulations also provide the dynamics of the liquid mass ratio of the powders which models the amount of the melted material.
4.1 Simulations set up
Different combinations of the above-mentioned four parameters are explored, together with the influence that they have on the simulated multiphysics process. By changing five times the value of each parameter, a total amount of \(5^4 = 625\) simulations are performed, according to the values reported in Table 1. As for nozzle inclination \(\theta\) we intend the angle formed by the nozzle channel with respect to the vertical axis (see Fig. 2).
4.2 Geometry and physical settings
The 3D CAD model of a coaxial nozzle is created with the open-source software Salome [37], by means of a parametric generation of the geometry developed in an ad hoc Python code. This allows to reproduce different domains according to different angles of inclination of the coaxial channel.
In Fig. 2 we show the geometry for an inclination angle equal to 25 degrees.
The coaxial nozzle has an inlet face, for both particles and carrier gas, positioned in the upper part of the geometry and having the shape of a ring. The outer radius of this ring measures \(r_{out}=8.55 \text {mm}\) while the inner one measures \(r_{inn}=7.30 \text {mm}\), thus having a relative inner/outer distance of \(d_{ch}= 1.25 \text {mm}\) as channel thickness for both fluid and powder inlet flows. In the middle of the nozzle bottom, there is an additional channel with a radius of \(r_l = 3 \text {mm}\) for the laser beam. Finally, the cylinder is set to be large enough to ensure that the simulation of both powder and fluid stream are not affected by boundary effects. This part, located below the nozzle, represents the whole portion of the outlet whose height and radius are equal to \(h_{box} = 24.5 \text {mm}\) and \(r_{box} = 11.0 \text {mm}\), respectively.
We prescribe as boundary conditions an inlet gas velocity, constant over time, corresponding to one of the inlet gas flow rates reported in Table 1, i.e., {1.0, 1.5, 2.0, 2.5, 3.0} m/s. The dimensions of the inlet cross-section area are fixed in the analyses. The same velocities are also set for the initial velocity of the particles, which are assumed to be perfectly transported by the carrier fluid at the inlet; the associated powder flow rates are reported in Table 1. The inlet temperature is \(T_{in} = 350 \text {K}\). On the walls along the nozzle channel a no-slip condition is imposed for the fluid, whereas the involved particles have to perform a rebound with the coefficients of restitution and kinetic friction equal to \(e = 0.97\) and \(f_r = 0.09\) (see [38, 39]). Zero normal flux of temperature and pressure at the wall boundaries is also prescribed. Finally, in the outlet boundary both velocity and temperature are assumed to have a zero gradient, along with a prescription of zero pressure; the particles are allowed to cross such a boundary and exit the domain.
The initial values of both velocity and pressure fields are set to be zero, while the initial temperature field is equal to \(T_0 = 350 \text {K}\), according to the room temperature of the printing process [13]. Regarding the laser source, it has been modeled as an independent Eulerian field with the prescribed time law (22), which determines a Gaussian distribution in the transverse plane. The central axis of laser beam is set to be coincident with the Z-axis suggesting that the laser beam travels through the middle of the nozzle perpendicularly and then interacts with powder stream. The laser beam has an effective diameter \(D= 5.0 \text {mm}\), with power values reported in Table 1. Starting from the middle channel, the laser beam converges to the focal plane at \(z = -7.0 \text {mm}\) with a half angle of 3.7 degrees.
The considered gas is Argon, meanwhile Stellite 6 is used as powder; their properties are summarized in Table 2. The distribution of the size of powder particles diameter is Gaussian, with mean value equal to \(50 \mu m\) and variance equal to \(0.2 \cdot 10^{-3}\).
4.3 Discretization and numerical settings
The computational domain consists of a 3D structured hexahedral mesh generated by Salome with 518400 elements. This is shown on the right in Fig. 2, which includes the geometry of the nozzle. The mesh is fine enough to correctly represent the behavior of the fluid, with preliminary simulations—not reported here—showing a suitable independence on the mesh size for particles interpolation.
The time-step size used for all simulations is \(dt = 0.00005 \text {s}\). The solution of the Navier-Stokes equations within the employed mNR scheme uses a direct solver with a prescribed tolerance equal to \(10^{-10}\) with a maximum of 50 iterations. The heat equation is solved with a Conjugate Gradient method with tolerance equal to \(10^{-8}\) and maximum number of iterations equal to 20.
The model employs hexahedral Lagrange finite elements of degree 2 for the velocity, and 1 for both temperature and pressure. Simulations are conducted on an off-the-shelf desktop computer with eight-cores Intel(R) Xeon(R) W-2125 running at 4.00 GHz, with 256 GB of RAM, on a 64-bit Ubuntu Linux 20.04.1 LTS operating system.
Note that, as expected, computational costs, although they have been made affordable in reason of the parallelization of both particle generation and motion procedures, increases with the number of particles. In Fig. 3 the non-dimensional CPU times are reported against the number of particles at the inlet, corresponding to a certain value of inlet powder mass flow rates: the CPU time increases of about 70% as the particle number doubles.
4.4 Results and discussions
In this section we first show the results related to the particles distribution in the computational domain, describing the shape of the powder stream and the different configurations that are created along the vertical axis. Then, we present a study on the variation of the powder concentration at the focal plane, varying the flow rate of gas and powder, respectively. In the last part of this section, the interaction with the thermal field is shown, and, in particular, we analyze the evolution of the phase change of the particles that form the powder stream.
4.4.1 Distribution of powder stream
The shape of the powder stream has great impact on its thermal profile and it significantly affects the melting and solidification processes that characterize the quality of built parts. The distribution of the particles in the computational domain is shown in Fig. 4, showing that the use of a coaxial nozzle produces a powder stream with an annular pattern at the beginning of its path. Then, mainly owing to the drag of gas flow and inertia, particles start to merge into a main stream to form a waist, producing a concentrated region of powder below the nozzle. Below such a region, the powder stream diverges.
Particles velocity map for nozzle with a 25\(^\circ\) angle of inclination of the coaxial channel, powder mass and carrier gas flow rate equal to \(\dot{m}_p = 0.35 \text {g/s}\) and \(\dot{m}_g = 4 \text {l/s}\), respectively. Velocity magnitude of each individual particle passing through the nozzle (a), particles concentration projected on the Y-X plane cutting the central axis of the domain (b)
In order to investigate in depth the powder stream structure, the distribution of particles concentration on several transversal X-Y planes are reported in Figs. 5–7. Below the nozzle, the structure of particles concentration can be approximately categorized into three distinct stages: i) pre-waist, ii) waist, and iii) post-waist—see Fig. 5, 6 and 7, respectively. In addition, for every stage the values of the particles concentration at \(y = 0 \text {mm}\) are interpolated with a spline, in order to continuously display the trend of the powder distribution along the vertical axis. The curves are plotted next to the corresponding considered stages.
Particles concentration at pre-waist transversal X-Y plane, located at \(z = -4 \text {mm}\) (a), and relative spline interpolation at \(y = 0\) (b). The nozzle inclination angle is equal to \(\theta = 25^\circ\), the powder mass and carrier gas flow rate considered \(\dot{m}_p = 0.35 \text {g/s}\) and \(\dot{m}_g = 4 \text {l/s}\), respectively
Particles concentration at waist transversal X-Y plane located at \(z = -7 \text {mm}\) (a), and relative spline interpolation at \(y = 0\) (b). The nozzle inclination angle is equal to \(\theta = 25^\circ\), the powder mass and carrier gas flow rate considered \(\dot{m}_p = 0.35 \text {g/s}\) and \(\dot{m}_g = 4 \text {l/s}\), respectively
Particles concentration at post-waist transversal X-Y plane located at \(z = -10 \text {mm}\) (a), and relative spline interpolation at \(y = 0\) (b). The nozzle inclination angle is equal to \(\theta = 25^\circ\), the powder mass and carrier gas flow rate considered \(\dot{m}_p = 0.35 \text {g/s}\) and \(\dot{m}_g = 4 \text {l/s}\), respectively
The pre-waist profile located at \(z = -4 \text {mm}\) shows the typical annular powder stream structure formed at the nozzle exit, keeping such a form up to the focal plane, where the powder flux distribution exhibits a bimodal shape (Fig. 5). Then, the powder stream converges to form the waist stage at \(z = -7 \text {mm}\), revealing a typical Gaussian profile with the maximum concentration of a \(81.7 \text {kg/m}^3\) peak values (Fig. 6). At \(z = -10 \text {mm}\) the waist stage disappears and the powder stream goes through the post-waist stage: this can be seen from Fig. 7, where the maximum value of powder concentration drops to \(10.6 \text {kg/m}^3\) approximately, and the powder stream diverges. All the above results refer to a value of channel inclination angle of \(\theta = 25^\circ\), and powder and carrier gas flow rates \(\dot{m}_p = 0.35 \text {g/s}\) and \(\dot{m}_g = 4 \text {l/s}\), respectively. Figure 8 depicts the particle concentrations at focal planes for different carrier gas inlet velocities and powder mass inlet flow rate, according to Sect. 4.1. As expected, the particle concentration decreases as the powder mass flow rate decreases, but also as the inlet velocity of the carrier gas increases, due to a more diluted flow. In fact, considering a powder flow rate of \(0.35 \text {g/s}\) the concentration peaks tend to decrease, starting from a maximum value of \(81.7 \text {kg/m}^3\) for a carrier gas velocity \(u_g = 1 \text {m/s}\), up to a value of \(30.8 \text {kg/m}^3\) for \(u_g =3 \text {m/s}\).
Note finally that, in the perspective of designing optimal conditions for the LMD process, high values of particle concentration can be attained employing low amounts of both powder and carrier gas: a powder concentration of \(35.7 \text {kg/m}^3\) is reached in the simulations with powder and carrier gas flow rates \(\dot{m}_p = 0.15 \text {g/s}\) and to \(u_g = 1 \text {m/s}\), whereas we obtain \(30.8 \text {kg/m}^3\) for \(\dot{m}_p = 0.35 \text {g/s}\) and \(u_g = 3 \text {m/s}\).
4.4.2 Thermal profile of powder stream
On the basis of the intensity profile of the laser beam, we predict the temperature profile of powder stream as depicted in Fig. 9, where both laser intensity and particles temperature are reported. Starting from the nozzle exit, powder particles keep their initial temperature, around 350 K prescribed as the initial value, until they enter the laser interaction zone. Then, approaching the focal plane location, particles are quickly heated up by the laser beam and their temperature suddenly increases. Figure 9 shows the high gradient values that characterize the band in which the particles interact with the energy irradiated by the laser, leading to temperatures over 3000 K. Such values are consistent with those reported in several papers (e.g., [12, 13, 28]). Finally, after passing the focal zone, particles continue to exchange thermal energy exclusively with the external environment.
Another contribution to the heat exchange is given by the temperature field generated by the substrate. The substrate is simulated by placing a heated boundary in the neighborhood of the focal plane of the particles for a more realistic view of the LMD process (see, for instance, [40,41,42]). Figure 10 shows two temperature mappings, the one on the fluid, heated through the substrate, and the one present on the particles irradiated by the laser beam with a power of \(P=2200\text {W}\). The particles near to the substrate prove to have values of temperature higher than those of the fluid surrounding the substrate. This is an optimal condition for the printing stage: the metallic material when reaching the substrate is expected to be entirely in the liquid state in order to prevent non-homogenous track formations due to the presence of unmelted particles in the deposited layers [43].
Temperature field generated by the substrate together with the temperature of the particles considering a laser power equal to \(P=2200\text {W}\). The nozzle inclination angle and the powder mass and carrier gas flow rate considered are respectively equal to \(\theta = 25^\circ\), \(\dot{m}_p = 0.35 \text {g/s}\) and \(\dot{m}_g = 4 \text {l/s}\)
With the purpose of better highlighting where the particle flow may achieve the melted state, Fig. 10 gives us reasons to neglect in the following simulations the heated substrate [44, 45]. In particular, the phase transition from the solid to the liquid state of the single particle is tracked in terms of evolution of fraction of liquid mass \(m_l/m_p\), according to the simplified model of the liquid fraction evolution law (25).
Figure 11 reports the evolution of the \(m_l/m_p\) ratio, computed by averaging the liquid mass fraction of each particle occupying the x/y plane at a given z coordinate of the computational domain. As expected, the particles tend to melt at a slower rate as the laser power decreases, and therefore the distance from the nozzle at which the particles are completely melted increases.
Liquid mass fraction plotted against the vertical position of the particles and increasing laser power \(P=\{200,700,1200,1700,2200\}\text {W}\). The nozzle inclination angle and the powder mass and carrier gas flow rate considered are respectively equal to \(\theta = 25^\circ\), \(\dot{m}_p = 0.35 g/s\) and \(\dot{m}_g = 4 l/s\)
The laser heating effects are also affected by the time spent by the particles in the region with high laser intensity. As Fig. 11 shows, the value of \(m_l/m_p = 1\) is reached faster according to the laser power. This behavior is furthermore highlighted in Fig. 12, where the liquid mass fraction of each particle is mapped at the same time step of the analysis (in steady-state regime) by comparison between the process with 200 W laser power and that with 2200 W. In the first case, the complete fusion of the particles takes place after the focal plane, while, in the second case, it happens before.
Such a behavior is only qualitatively similar when changing the nozzle geometry. Figure 13 depicts several curves of the liquid mass fraction varying along the vertical axis for different inclination angles \(\theta\) of the nozzle channel, and for different laser powers P, according to the values reported in Table 1. For each level of P, the state of complete fusion is reached at distances from the nozzle as \(\theta\) decreases, in reason of the distance between the focal plane and the nozzle, increasing as the inclination of the coaxial channel becomes more collinear with respect to the vertical axis, i.e., with decreasing \(\theta\).
Liquid mass fraction plotted against the vertical position of the particles considering different values of inclination angle, and increasing laser power \(P=\{200,700,1200,1700,2200\}\text {W}\). Powder mass and carrier gas flow rate are equal to \(\dot{m}_p = 0.35 \text {g/s}\) and \(\dot{m}_g = 4 \text {l/s}\), respectively
Moreover, increasing the laser power leads to melting particles over the focal plane, with a flattening of the liquid mass curves, evident as the nozzle inclination angle increases. For \(\theta =15^\circ\) the point of complete melting is obtained at \(z = -14.0 \text {mm}\) when \(P=200\text {W}\), and at \(z = -11.8 \text {mm}\) when \(P=2200\text {W}\). On the other hand, for \(\theta =35^\circ\) a unit liquid mass fraction is reached at \(z = -4.1 \text {mm}\) for a laser power of 200 W, at a \(z = -3.0 \text {mm}\) for 2200 W. Such a trend indicates also that a similar melting process can be obtained with inclination angles from \(\theta =30^\circ\) to \(\theta =35^\circ\), significantly saving costs on the laser power, reduced from 1200–1700 W to 200 W.
The previous considerations are finally emphasized through Fig. 14, where the percentage of liquid mass fraction reached at the focal plane, associated with different inclination angle, is plotted versus the laser power. Such a percentage increases non linearly with the laser power, highlighting a sort of plateau for high laser powers, reached sooner as the inclination angle decreases. Considering high laser powers (1200, 1700, and 2200 W), values at least of 85% of the liquid mass fraction are reached at the focal plane for any inclination angles \(\theta \in [15,35]\) degrees. On the other hand, by increasing \(\theta\), a reduction of liquid mass fraction is observed for any value of laser power, three percentage points for \(P=2200\text {W}\), and about seven points for the other values of P. However, by accepting suboptimal percentages of molten material at the focal point, the laser power can be significantly diminished by suitably decreasing the inclination angle: about 97% of liquid fraction can be obtained either by laser powers \(P=2200\text {W}\) with \(\theta =35^\circ\), or by laser powers \(P=1200\text {W}\) with \(\theta =15^\circ\).
5 Conclusions
This work presented a comprehensive strategy for both modeling and simulating the LMD process as a coupled, multiphase, nonlinear flow problem, where a carrier gas fluid transports particle powder to be melted through a laser beam source. By means of a custom C++ code using the open source finite element library deal.II, we implemented a mixed description allowing to treat the fluid problem coupling Navier-Stokes with heat transfer equations with an Eulerian formulation and, at the same time, tracking the motion and temperature of the powder particles with a Lagrangian approach (see https://zenodo.org/record/5888175).
A phase change problem was also considered in the Lagrangian tracking particle algorithm. Particles are modeled to exchange mass, momentum, and energy with the Eulerian fluid according to interpolating functions, and also to evolve the initial powder solid mass into liquid mass by laser irradiation according to a linear dependency on the particle temperature.
An extensive sensitivity analysis was proposed by varying the meaningful parameters of the LMD process, i.e., inlet flow rate of both carrier gas and powder, inclination of the nozzle channel, and laser power. We discussed the distribution of the particles in the domain, investigating the configuration of powder and carrier gas flow rate, and the correlation between each other. In detail, the amount of particle concentration decreases as the powder mass inflow rate decreases, and as the flow rate of the carrier gas increases. This result translates into an optimization of the printing process, since the simulations proved that we can improve by 16% the particle concentration while reducing by 30% the inlet rates.
Then, by simulating the fully coupled problem, the obtained results showed that there is a strong influence of the nozzle geometry and laser beam power on the amount of molten powder. While the inflow rates do not affect the resulting liquid mass fraction, the nozzle inclination, and obviously the intensity of the laser source, remarkably influences both the distribution and the magnitude of the powder melting process. In particular, increasing the laser power particles tend to melt before reaching the focal plane, moving upward the complete melting point. This shift is more pronounced for nozzles with small inclination angles; on the other hand, strong inclinations lead to low amounts of molten material in the focal plane. Moreover, the limit state of complete melted particle configuration is reached in shorter times for higher laser powers, i.e., by spending low traveling times in the region with elevated laser intensity. The evolution of the particle liquid mass fraction along the vertical axis of the LMD chamber shows also that LMD systems designed with a sufficiently high nozzle inclination angle and low laser power can speed up the melting process with the same efficiency of lower inclinations. In the reported simulations, channel inclinations increasing from \(30^\circ\) to \(35^\circ\) can admit decreasing laser powers of about seven times.
This type of outcomes is therefore intended to pave the way to improvements in the set up of printing process, by predicting the stand-off distance, i.e., the nozzle base vs. substrate distance, necessary to reach the complete fusion of the particles. As recently argued in [15], such an information can lead to a considerable decrease of the thermal gradients that characterize the cooling of the molten pool and also to accelerate the deposition process of the metallic material, optimizing the whole printing process both in terms of time and costs.
Change history
20 July 2022
Missing Open Access funding information has been added in the Funding Note.
References
Rylands B, Böhme T, Gorkin R, Fan J, Birtchnell T (2016) The adoption process and impact of additive manufacturing on manufacturing systems. J Manuf Technol Manag
Zhang B, Coddet C (2016) Numerical study on the effect of pressure and nozzle dimension on particle distribution and velocity in laser cladding under vacuum base on CFD. J Manuf Process 23:54–60
Zeng Q, Tian Y, Xua Z, Qina Y (2017) Numerical modelling of the gas-powder flow during the laser metal deposition for additive manufacturing. 6:154
Tabernero I, Lamikiz A, Ukar E, de Lacalle LL, Angulo C, Urbikain G (2010) Numerical simulation and experimental validation of powder flux distribution in coaxial laser cladding. J Mater Process Technol 210(15):2125–2134
Arrizubieta J, Tabernero I, Ruiz JE, Lamikiz A, Martinez S, Ukar E (2014) Continuous coaxial nozzle design for LMD based on numerical simulation. Phys Procedia 56:429–438
Balu P, Leggett P, Kovacevic R (2012) Parametric study on a coaxial multi-material powder flow in laser-based powder deposition process. J Mater Process Technol 212(7):1598–1610
Grigoryants A, Tretyakov R, Shiganov I, Stavertiy A (2015) Optimization of the shape of nozzles for coaxial laser cladding. Weld Int 29(8):639–642
Liu S, Zhang Y, Kovacevic R (2015) Numerical simulation and experimental study of powder flow distribution in high power direct diode laser cladding process. Lasers in Manufacturing and Materials Processing 2(4):199–218
Ferreira E, Dal M, Colin C, Marion G, Gorny C, Courapied D, Guy J, Peyre P (2020) Experimental and numerical analysis of gas/powder flow for different LMD nozzles. Metals 10(5):667
Murer M, Furlan V, Formica G, Morganti S, Previtali B, Auricchio F (2021b) Numerical simulation of particles flow in Laser Metal Deposition technology comparing Eulerian-Eulerian and Lagrangian-Eulerian approaches. J Manuf Process 68:186–197
Ibarra-Medina J, Pinkerton AJ (2011) Numerical investigation of powder heating in coaxial laser metal deposition. Surf Eng 27(10):754–761
Wen S, Shin Y, Murthy J, Sojka P (2009) Modeling of coaxial powder flow for the laser direct deposition process. Int J Heat Mass Transf 52(25–26):5867–5877
Guan X, Zhao YF (2020) Numerical modeling of coaxial powder stream in laser-powder-based Directed Energy Deposition process. Addit Manuf 101226
Lin S, Gan Z, Yan J, Wagner GJ (2020) A conservative level set method on unstructured meshes for modeling multiphase thermo-fluid flow in additive manufacturing processes. Comput Methods Appl Mech Eng
Li T, Zhang L, Bultel GGP, Schopphoven T, Gasser A, Schleifenbaum JH, Poprawe R (2019) Extreme High-Speed Laser Material deposition (EHLA) of AISI 4340 steel. Coatings 9(12):778
Liu CY, Lin J (2003) Thermal processes of a powder particle in coaxial laser cladding. Opt Laser Technol 35(2):81–86
Bangerth W, Hartmann R, Kanschat G (2007) deal.II—a general purpose object oriented finite element library. ACM Trans Math Softw 33(4):24/1–24/27
Gresho PM, Lee RL, Chan ST, Sani RL (1980) Solution of the time-dependent incompressible Navier-stokes and Boussinesq equations using the Galerkin finite element method. Approximation methods for Navier-Stokes problems 203–222
Brooks AN, Hughes TJ (1982) Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput Methods Appl Mech Eng 32(1–3):199–259
Hughes TJ, Feijóo GR, Mazzei L, Quincy JB (1998) The variational multiscale method–a paradigm for computational mechanics. Comput Methods Appl Mech Eng 166(1):3–24
Bochev PB, Gunzburger MD, Shadid JN (2004) Stability of the SUPG finite element method for transient advection–diffusion problems. Comput Methods Appl Mech Eng 2301–2323
Burman E (2010) Consistent SUPG-method for transient transport problems: Stability and convergence. Computer Methods in Applied Mechanics and Engineering pp 1114–1123
Reddy JN (2014) An introduction to nonlinear finite element analysis: with applications to heat transfer, fluid mechanics, and solid mechanics
Temam R (2001) Navier-Stokes equations: theory and numerical analysis 343
Donea J, Huerta A (2003) Finite element methods for flow problems
Sochinskii A, Colombet D, Muñoz MM, Ayela F, Luchier N (2019) Flow and heat transfer around a diamond-shaped cylinder at moderate Reynolds number. Int J Heat Mass Transf 142:118435
Crowe CT, Schwarzkopf JD, Sommerfeld M, Tsuji Y (2011) Multiphase flows with droplets and particles
Tan H, Fang Y, Zhong C, Yuan Z, Fan W, Li Z, Chen J, Lin X (2020) Investigation of heating behavior of laser beam on powder stream in directed energy deposition. Surf Coat Technol 126061
Murer M, Formica G, Milicchio F, Morganti S, Auricchio F (2021a) An efficient and accurate numerical method for advection-diffusion coupled problems, submitted for publication in Computers & Fluids, # CAF-D-21-00232
Reddy JN, Gartling DK (2010) The finite element method in heat transfer and fluid dynamics
Demmel J, Grigori L, Hoemmen M, Langou J (2012) Communication-optimal parallel and sequential QR and LU factorizations. SIAM J Sci Comput 34(1):A206–A239
Yang H, Fan M, Liu A, Dong L (2015) General formulas for drag coefficient and settling velocity of sphere based on theoretical law. Int J Min Sci Technol 25(2):219–223
Donadello S, Furlan V, Demir AG, Previtali B (2022) Interplay between powder catchment efficiency and layer height in self-stabilized laser metal deposition. Opt Lasers Eng 149:106817
Gornushkin I, Pignatelli G (2021) Optical detection of defects during laser metal deposition: Simulations and experiment. Appl Surf Sci 570:151214
Jiazhu W, Liu T, Chen H, Li F, Wei H, Zhang Y (2019) Simulation of laser attenuation and heat transport during direct metal deposition considering beam profile. J Mater Process Technol 270:92–105
Lia F, Park J, Tressler J, Martukanitz R (2017) Partitioning of laser energy during directed energy deposition. Addit Manuf 18:31–39
SALOME Platform: The open source integration platform for numerical simulation
Gondret P, Lance M, Petit L (2002) Bouncing motion of spherical particles in fluids. Phys Fluids 14(2):643–652
Mabrouk R, Chaouki J, Guy C (2008) Wall surface effects on particle-wall friction factor in upward gas-solid flows. Powder Technol 186(1):80–88
Peyre P, Aubry P, Fabbro R, Neveu R, Longuet A (2008) Analytical and numerical modelling of the direct metal deposition laser process. J Phys D Appl Phys 41(2):025403
Kovalev O, Zaitsev A, Novichenko D, Smurov I (2011) Theoretical and experimental investigation of gas flows, powder transport and heating in coaxial laser direct metal deposition (DMD) process. J Therm Spray Technol 20(3):465–478
Donadello S, Motta M, Demir AG, Previtali B (2019) Monitoring of laser metal deposition height by means of coaxial laser triangulation. Opt Lasers Eng 112:136–144
Gibson I, Stucker B, Rosen DW (2010) Additive manufacturing technologies. Springer, Boston, MA.
Gao J, Wu C, Liang X, Hao Y, Zhao K (2020) Numerical simulation and experimental investigation of the influence of process parameters on gas-powder flow in laser metal deposition. Opt Laser Technol 125:106009
Jardon Z, Guillaume P, Ertveldt J, Hinderdael M, Arroud G (2020) Offline powder-gas nozzle jet characterization for coaxial laser-based directed energy deposition. Procedia CIRP 94:281–287
Acknowledgements
Authors wish also to thank Dr. Massimo Carraturo for his very useful comments and feedback on the paper draft.
Funding
Open access funding provided by Università degli Studi di Pavia within the CRUI-CARE Agreement. This work was partially supported by the Regione Lombardia through the project “MADE4LO – Metal ADditivE for LOmbardy” (No. 240963) within the POR FESR 2014-2020 program.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics approval and consent to participate
The article follows the guidelines of the Committee on Publication Ethics (COPE) and involves no studies on human or animal subjects.
Consent for publication
All authors have read and agreed to publish the manuscript.
Conflicts of interest
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Murer, M., Formica, G., Milicchio, F. et al. A coupled multiphase Lagrangian-Eulerian fluid-dynamics framework for numerical simulation of Laser Metal Deposition process. Int J Adv Manuf Technol 120, 3269–3286 (2022). https://doi.org/10.1007/s00170-022-08763-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-022-08763-7