1 Introduction

Driven by the revolutionary idea of a manufacturing process that can rapidly produce any individualized part of unlimited geometrical complexity, the primary focus of Additive Manufacturing (AM) was initially on its application for industrial prototyping [1, 2]. As a consequence of the continuous development and improvement of AM in terms of manufacturing techniques, machines and materials, its increased applicability nowadays enables the direct digital manufacturing of end use parts [2, 3]. A successful implementation of AM in (small-)series production, however, requires high performance and efficiency [4, 5].

The availability of quantitative, reliable information about the impact of the assigned tolerances on the resulting manufacturing costs is hereby a prerequisite for cost-efficient tolerancing [6]. The lack of current and accessible tolerance-cost data, serving as the basis to predict the effects of tolerance allocation on the resulting manufacturing costs by suitable cost models for AM, is critically recognized in literature  [6, 7]. A major obstacle in setting up reliable cost models for AM can be seen in the lack of structured approaches guiding the tolerance engineer through the various, interdisciplinary steps.

With the aim to close this gap and to enable a cost-efficient tolerance allocation for AM, this article presents a novel structured methodology for the development of tolerance-cost models for geometrical tolerancing for AM. After presenting the state of the art and the research question in Section 2, Section 3 discusses the systematic development of tolerance-cost models using Fused Layer Modeling (FLM) as an example to illustrate the different steps of the proposed workflow. This includes the identification and quantification of the main cost contributors in Section 3.1, the experimental acquisition of manufacturing information on the impact of process parameter selection on the resulting geometrical accuracy by design of experiment in Section 3.2 and finally the quantitative mapping of costs and tolerance values in Section 3.3. The exemplary application of the proposed methodology to an academic, simplified case study in Section 4 shows its practical applicability and serves as the basis to discuss its benefits and current limitations. Finally, a conclusion and an outlook are given in Section 5.

2 State of the art

The main aspects of cost-efficient tolerancing as well as of geometrical accuracy and cost modelling for AM are summarized in Sections 2.1–2.2 and subsequently discussed in Section 2.3.

2.1 Cost-efficient tolerancing

Geometrical part variations caused by manufacturing imprecisions are unavoidable but significantly affect the total product quality in terms of product functionality and aesthetics [8, 9]. The product developer is thus responsible to first specify the tolerance types and potentially required datums to all functional part features and second to allocate a specific value to limit the geometrical part variations [10]. Tolerance allocation is an essential part of detail design since the assigned tolerance values serve as a stringent constraint for process planning and thus indirectly predefine the manufacturing costs [11, 12].

Increasing cost awareness and pressure in series production, however, lead to a gradual replacement of traditional, rather qualitative and approximative approaches by quantitative methods of optimization-based tolerance allocation [6]. Tolerance-cost optimization turns the search for least cost tolerance values into a mathematical optimization problem which can efficiently be solved by powerful optimization algorithms. Its global aim is to minimize the total manufacturing costs as the objective by choosing the part tolerances as wide as possible and only as tight as necessary to statistically ensure the fulfilment of total product functionality [6]. The tolerance-cost model calculates or rather estimates the total costs by a function of the chosen tolerance values and is used as the objective [13]. Consequently, the validity of the optimization mainly depends on the quality of the tolerance-cost model [14, 15]. Associated research activities thus mainly focus on the efficient acquisition of reliable process and manufacturing information, the identification and quantification of the numerous single cost items and its joint consideration by individual tolerance-cost functions and total cost models.

In this context, any costs which are necessary to reach the assigned tolerances have to be described in one common model. This includes the quantification of a wide range of directly and indirectly measurable, fix and variable cost items [16], such as costs for material, tooling, fabrication, assembly, inspection, rework and rejection or service and maintenance [6]. The general cost models from literature must always be tailored to the given manufacturing situation [14] which implies their extension and adaption to either new or non-traditional machines and processes [17,18,19] and the consideration of specific aspects from series production [20, 21]. As the development of a reliable cost model requires the availability of detailed cost and manufacturing information, few alternative approaches, for example for the replacement of the cost model by a sensitivity curve based on the experience from design and manufacturing [22, 23] or the estimation of the global costs by an activity-based cost approach [24, 25], were presented in literature but have not established themselves in the context of tolerance-cost optimization.

Hence, empirical and analytically estimated manufacturing and cost information serve as the basis to mathematically describe the relationship between cost and tolerance together by so called tolerance-cost functions [6]. The most common, traditional approaches in literature are analytical, reciprocal and exponential functions with two up to four parameters [13, 14]. In comparison, non-traditional approaches, such as higher-order polynomial [26, 27], hybrid models [26, 28] or artificial and fuzzy neural networks [29, 30], are rarely taken into account [14, 21]. The selection of the model type and its fitting parameters, however, depends on the amount and type of data influenced by the given manufacturing process, machine and its settings, feature type, etc. [8, 14]. Besides, numerous research activities focus on the quantification and representation of further, hardly measurable or intangible cost impacts of tolerancing, such as the present worth of loss by product degradation influencing the satisfaction and loyalty of the customer [31, 32] or ecological and social costs [33, 34], as well as their consideration in the optimization process, mainly by specific quality loss functions [35].

The related works of the last decades have clearly emphasized that the definition of reliable cost models for tolerance allocation prerequisites an in-depth knowledge in manufacturing and cost accounting [6, 13, 14].

2.2 Investigation of geometrical accuracy and manufacturing costs in AM

The AM process in general is controlled by numerous process parameters, affecting build time and geometrical accuracy, achievable tolerances and consequently the total quality and costs of printed parts [36,37,38]. For this reason, the influence of process parameters on geometrical accuracy in AM has been studied extensively by many researchers in the past few years. It can hereby be concluded that part orientation, machine speed and layer height are the key factors influencing both geometrical accuracy and build time in most AM technologies due to the layered manufacturing principle [39,40,41,42,43,44,45,46]. In general, a small layer height results in higher geometrical accuracy, whereby the build time and thus the manufacturing costs are significantly increased [47]. Finding a satisfactory trade-off is therefore a tedious task for engineers. Regarding the results in related literature, it is obvious that the quantification of the influence of process parameters on part quality and manufacturing costs is quite difficult since it is mostly case- and technology-specific [2]. So, predicting manufacturing costs of additively manufactured parts is fairly sophisticated as different technologies have different factors influencing the resulting outcome of the process. In order to enable the use of AM in serial production, the calculation of manufacturing costs of additive products is a decisive but tedious task. Therefore, it is essential to gain insight knowledge of the specific process to precisely specify the manufacturing costs [11].

The determination of AM cost models has been in focus of research over the past years [48]. Current approaches primarily refer to single aspects of the respective AM technology, such as build time, energy consumption, the necessary handling steps or sensitivity analysis of specific process parameters of the cost model [49] and thereby either split the process [50, 51] or the overall costs itself [2, 52,53,54,55] in main categories and steps for calculating the manufacturing costs for single components.

Alexander et al. [50] were one of the first to develop a general cost model for calculating manufacturing costs in AM reviewing the FLM and the Stereolithography (SLA) method. Therefore, the process was divided into three main processes (preparation, manufacturing and post-treatment), whereby the manufacturing costs of a single component are thus the total of the costs of the three individual processes. Thereby, different activities and cost aspects concerning the respective process (labor costs, machine costs, costs of material and resulting build time) were considered in terms of mathematical equations [50]. As an adaption, Rickenbacker et al. [56] presented a cost model for the SLM process (Selective Laser Melting) in which all required pre- and post-processes were additionally considered [56]. Lindemann et al. [51] proposed another approach as they divide the process into four steps (preparatory activities, in-processing, manually removing the resulting parts and support structures and post-processing) in a time-driven cost model.

In contrast, Hopkinson and Dickens [52] developed a cost model in which the overall costs itself were divided into three main cost items (machine cost, personnel cost and material cost) to identify part costs for calculating the break-even point of different AM technologies (SLA, FLM, SLS) in order to compare them to conventional manufacturing technologies (injection molding). Ruffo et al. [53] further considered more cost-related activities for the Selective Laser Sintering (SLS) process [53]. Baumers et al. [54] developed a similar cost model, but hereby energy costs were considered as direct cost component. As a result, the estimation of the build time is considered to be of great importance since it bears a large part of the total costs. Gibson et al. [2] splits the overall costs for AM into four main categories (cost of the machine, production costs, material costs and labor costs), whereby their total represents the manufacturing costs of a single component. Herein, the build time is defined as the key factor and calculated more accurately compared to similar cost models. The authors claim that in this model, all types of AM technology can be considered [2]. Haghighi and Li [55] conducted a comprehensive study of three main cost elements (material consumption, energy consumption and time-dependent machine cost) in order to determine the relationship among different process parameters, geometrical performance and manufacturing cost elements for a single FLM machine. It was observed that methods for reducing geometrical variations are not necessarily associated with higher manufacturing cost, as opposed to conventional manufacturing processes.

As a different approach to the cost models presented above, Schröder et al. [57] developed a cost model which corresponds to a business model and serves for the evaluation of process costs of AM within the product development procedure. As with previous models, this model is activity-based; however, the number of cost-relevant activities is further increased as preceding (design phase, machine preparation, etc.) and downstream processes (administration, sales, testing phase, etc.) were considered. In accordance to the other models, the sum of the individual activities results in the total manufacturing costs [57]. Moreover, Laurejis et al. [58] proposed a process-based cost modelling (PBCM) for forecasting the production cost of future additive products prior to large-scale investment and thereby considered the redesign of parts for AM.

Although a multitude of works have been published on this topic, emphasizing the necessity and benefits of cost models in AM, only few take into account the relationship between the resulting costs and the achievable tolerances in relation to the geometric accuracy of additively manufactured components.

2.3 Discussion

Since the first applications of tolerance-cost optimization in the middle of the twentieth century, the lack of tolerance-cost data was continuously criticized [6]. The limited published data are either not up-to-date, too imprecise or does not fit the given use case and manufacturing environment. It is furthermore not known, if and to what extent, tolerance-cost data are accessible and available in industry since it is mostly not published for reasons of confidentiality [13, 14]. Consequently, the majority of academic research is based on either obsolete data from charts or textbooks or creates new tolerance-cost curves based on assumptions which cannot represent real manufacturing conditions leading to non-realistic optimization results [14]. In contrast to the continuous development of tolerance-cost optimization itself [6], only little progress was made to provide access to realistic and reliable tolerance-cost data. Whereas hardly any data and models are available for traditional manufacturing processes [14], there is a huge lack of processable and reliable information about the relationship between process parameters, achievable accuracies and the resulting costs for AM [7]. Its availability is, however, essential for a process-oriented tolerancing to support the basic idea of a seamless linkage between design and manufacturing [59]. Even though geometrical accuracy and cost estimation of additively manufactured parts receive increasing attention in research, a joint consideration of these two strongly interconnected issues is—except a few studies for only dimensional tolerances [7, 55, 60, 61]—still missing. A structured methodology is currently lacking which, on the one hand, transparently presents the relevant relationships between geometrical tolerances, process parameters and the resulting costs and, on the other hand, supports the tolerance engineer in the various interdisciplinary sub-activities as a step by step guideline.

Motivated to close this gap, this article addresses the research question how tolerance-cost data can systematically be acquired, processed and provided to the designer to enable a least cost allocation of geometrical tolerances for AM.

3 Methodology

A strong incorporation of manufacturing knowledge into the tolerancing activities is inevitable for a process-oriented and cost-efficient design. Especially in AM, the clear boundaries between design and manufacturing are becoming more and more blurred since the designer often additionally takes over the role of the process planner and the machine operator. In this context, a quantitative correlation between the assigned tolerances and the resulting manufacturing costs provides the basis for an early cost consideration when assigning tolerances [55]. However, since the total costs depend on the selected manufacturing technology and machine as well as on the part geometry and its functional relevant feature, they must be determined individually for the given conditions [14]. For this purpose, a step-wise methodology is proposed in the following to systematically develop tolerance-cost models for geometrical tolerances in AM (see Fig. 1).

Fig. 1
figure 1

General workflow for the development of tolerance-cost models for AM

Full size image

In the first step, all cost elements, which depend on the process parameters significantly influencing the achievable part tolerances, must be identified (see Section 3.1). For this purpose, a general activity-based cost model for AM from literature, covering all relevant fixed and variable costs from planning up to the deployment of the product, is presented and reduced to the essential elements for tolerance design. The highlighted contributions of the tolerances on the different activity-related costs help to tailor the tolerance-cost model to the given use case and AM technology.

Besides the machine-specific process parameters, the geometry of the part has a significant impact on the resulting part accuracy. Hence, the decomposition of the parts into its geometrical features and an identification of the functional-relevant ones is required in the next step. Both information is needed to define a benchmark artifact and a design of experiment (DoE) with respect to the given use case (see Section 3.2). Due to their strong interrelation, their mutual harmonization under the consideration of metrology and manufacturing restrictions is essential. With the aim to support the tolerance engineer in the interdisciplinary sub-activities, detailed information and advices are given in Sections 3.2.1–3.2.3.

The acquisition of experimental manufacturing information serves as the basis to study the relations between the process parameter settings and the resulting geometrical tolerances. In a further step, the total costs are mapped as a machine-specific tolerance-cost curve corresponding to a function of the achievable tolerances (see Section 3.3). This also includes the identification of the probability distribution of the resulting part tolerance since the general assumption of normality of data with respect to the central limit theorem is not a priori valid for AM parts [7]. In doing so, the proposed framework guides the tolerance engineer through the individual steps, which are discussed in detail in the following.

3.1 Identification and quantification of main cost items

In line with the state of the art in Section 2.2, time-driven and activity-based cost models have proven their applicability since they allow an individual allocation of the total costs on the different steps of the AM process with respect to their time effort [49]. Thus, it is possible to identify the individual cost-relevant process parameters to establish their relation to the total costs \(C=f(p)\). In line with the general cost model according to Alexander et al. and its further extensions [51, 56, 57], the total costs \(C_\mathrm {tot}\) can be expressed as the sum of costs for the following main activities of the AM process:

$$\begin{aligned} C_\mathrm {tot} =&~C_\mathrm {dat} + C_\mathrm {pre} + C_\mathrm {in} +C_\mathrm {post}+ C_\mathrm {rew} + C_\mathrm {insp}, \end{aligned}$$
(1)

where:

$$\begin{aligned}\begin{array}{lll}&C_\mathrm {dat}&\text {costs for an AM-compatible data preparation,}\\&C_\mathrm {pre}&\text {costs for pre-processing,}\\&C_\mathrm {in}&\text {costs for in-processing, i.e., the actual fabrication of the part,}\\&C_\mathrm {post}&\text {costs for post-processing,}\\&C_\mathrm {rew}&\text {costs for optional rework,}\\&C_\mathrm {insp}&\text {costs for inspection.} \end{array}\end{aligned}$$

For a general cost estimation and a cost-efficient design of the total process from planning up to the deployment of the product, further cost elements can be added for each involved activity. However, not all cost elements that can be covered by the general activity-based cost model in Eq. (1) are relevant for decisions in tolerance design and must not be considered in the tolerance-cost model. Therefore, the different cost aspects already presented in literature are in the following reduced to the activities and related costs that are significantly influenced by the assigned tolerances.

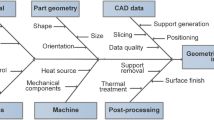
The problem, however, is that the impact of tolerance design on the resulting costs are not directly apparent. Rather, it must be taken into account that the tolerances indirectly determine the choice of the manufacturing process, machine and, above all, its process parameters influencing the various cost elements. To better illustrate these interrelations, Fig. 2 gives a comprehensive overview of the individual cost elements that are influenced by the choice of tolerances, indirectly via the process parameters. Additional activity-based costs exceeding Eq. (1), such as administrative or purchasing costs, are hereby neglected as they are not relevant in tolerance allocation. The individual cost elements are discussed activity by activity in the following, highlighting their indirect controllability by tolerance design.

Fig. 2
figure 2

Comprehensive overview of the interrelations between tolerances, process parameters and the individual cost elements

Full size image

The activity to check the designed part geometry for manufacturability and its transfer into an AM-compatible exchange format leads to the data preparation costs \(C_\mathrm {dat}\). However, it plays only a minor role in tolerance design since it is not influenced by the assigned tolerance values.

In the next step, geometry is translated into the machine code by slicing the part into a stack of layers and generating the tool paths for the layer-wise manufacturing including the steps of orientating and positioning of the parts in the build space, defining the process parameters and adding support structures if necessary. In addition, the machine has to be loaded with material leading to labor and machine down time costs. The data and machine pre-processing activities are summarily represented by \(C_\mathrm {pre}\) in Eq. (1). The required time and thus the resulting costs are nearly independent of the selected process parameters and thus the tolerance values.

In accordance to the VDI 3405 [62], the in-processing consists of three main sub-activities and its related costs to build the parts \(C_\mathrm {build}\), to remove them from the build chamber \(C_\mathrm {re}\) and to separate them from the build platform \(C_\mathrm {sep}\) forming the total in-processing costs:

$$\begin{aligned} C_\mathrm {in} = C_\mathrm {build} + C_\mathrm {re} + C_\mathrm {sep}. \end{aligned}$$
(2)

In AM, the entire part with its several features is built layer by layer and can be considered as one general activity. The resulting build costs \(C_\mathrm {build}\) are comprised as follows [63]:

$$\begin{aligned} C_\mathrm {build} =&\sum _{i=1}^{n}(V_{\mathrm {mat},i}\cdot C_{\mathrm {mat}, i}) + C_\mathrm {mach} \cdot \tau _\mathrm {build} + \\ {}&+ E_\mathrm {build}\cdot C_\mathrm {energy},\nonumber \end{aligned}$$
(3)

where:

$$\begin{aligned}\begin{array}{lll}&n&\text {total number of different materials in use,}\\&V_\mathrm {mat,i}&\text {volume of build or support material} \ i, \\&C_\mathrm {mat,i}&\text {costs for build or support material} \ i \ \text {per volume,}\\&C_\mathrm {mach}&\text {machine costs per hour,}\\&\tau _\mathrm {build}&\text {total build time in hours,}\\&E_\mathrm {build}&\text {energy consumption for AM of the part(s),}\\&C_\mathrm {energy}&\text {energy costs per unit.}\\ \end{array}\end{aligned}$$

The required material volume \(V_\mathrm {mat}\) for both part and support structures mainly depends on the average density of the used build and support material, the sum of the lengths of the single printing paths as well as their cross sections, which can be approximated to be constant over for the whole part in cost estimation [55]. The part material volume mainly depends on the part geometry and the infill, while further parameters, e.g., the layer height, do only have small influence on the material costs. In contrast, the support material volume additionally depends mainly on the part orientation, which has an direct impact on the achievable tolerances. Common pre-processing software provides in-built estimators to predict the material consumption for a given use case based on the virtually generated printing paths [64]. The total build time \(\tau _\mathrm {build}\) to manufacture a part by AM corresponds to “the sum of the forming time for each layer and the delay time between the subsequent layers’ manufacture” [65]. The build time \(\tau _\mathrm {build}\) is mainly influenced by the part geometry \(\Omega\) and the machine-specific process parameter settings p: \(\tau _\mathrm {build}=f(\Omega ,p)\) [65]. In general, analogical, parametric or analytical models can be used to predict or rather estimate the build time to support decisions in the different design and process planning steps. Since the accuracy of the build time prediction directly influences the cost model (see Eq. (3)), the build time estimator must be accurate enough to sensitively represent process parameter changes. Since analytical models are based on the virtually generated tool paths, they are more accurate and thus preferred in detailed design. [66] In line with the material quantity, pre-processing software can be used to achieve a sufficiently good approximation of the real build time [65, 67]. This allows the establishment of the relation between the choice of process parameters p and the required build time \(\tau _\mathrm {build}\) as an important, tolerance-dependent cost activity. Depending on the chosen process parameters, build times can differ between several hours for the same part geometry. Thus, it mainly influences the total manufacturing costs in combination with the hourly machine costs \(C_\mathrm {mach}\) including direct and indirect costs, such as machine purchase and production labor cost, machine depreciation and production overhead [51].

The total energy costs can be calculated as direct costs as follows [54, 55]:

$$\begin{aligned} E_\mathrm {build} = E_\mathrm {process} + E_\mathrm {standby} + E_\mathrm {heating}, \end{aligned}$$
(4)

where:

$$\begin{aligned}\begin{array}{lll}&E_\mathrm {process}&\text {required energy for part fabrication including movements of the nozzle and material extrusion,}\\&E_\mathrm {standby}&\text {required energy in machine standby,}\\&E_\mathrm {heating}&\text {required energy consumption for heating of nozzle, filament and bed,}\\\end{array} \end{aligned}$$

while \(E_\mathrm {build}\) mainly depends on the energy consumption of the utilized machine for part fabrication and the build time indirectly influenced by the assigned tolerances.

The time effort to finally take the parts out of the build chamber and to remove them from the build platform is negligible small for FLM in comparison to other AM processes such as Laser Powder Bed Fusion (LPBF). Hence, the in-processing costs are mainly dominated by the build costs \(C_\mathrm {build}\) (see Eq. (2)).

The subsequent AM technology-specific post-processing step is primarily necessary to manually or automatically remove the support structures leading to the costs \(C_\mathrm {post}\) including labor, material and machine costs (see Eq. (1)). Less support structures will hereby lead to less time effort and costs for the application of manual or automated dissolving procedures. Optional rework can be necessary to increase the part accuracy locally in individual areas or for functional critical features. The rework costs \(C_\mathrm {rew}\) correspond to the sum of the labor costs and machine costs for the required time and the material quantity for the individual rework operations. In a final step, the manufactured parts have to be inspected to prove the compliance with the specified tolerances leading to the inspection costs \(C_\mathrm {insp}\), which depend, among other things, on the size of the tolerance interval, the measurement method used and the working time required (see Eq. (1)). Wider tolerances will allow the choice of less accurate and expensive technologies for inspection and thus reduce \(C_\mathrm {insp}\).

In conclusion, the time-driven cost model of Eq. (1) is composed of various fixed and variable cost elements [14]. Although several cost drivers can be indirectly influenced by the design engineer (see Fig. 2), the build time is the main variable, process parameter-dependent factor which can indirectly be controlled by the tolerance engineer through a conscious tolerance selection. In traditional tolerance allocation for design, where just one single pre-selected machine is focused, cost elements which are tolerance-independent and thus constant, do not influence the choice of process parameters and consequently the tolerance allocation results, which is why they can be ignored [18]. However, if there is more than one alternative machine or process alternative, fixed costs have to be taken into account since the total cost model serves as the basis for the additional selection of a suitable machine [68, 69], process scheduling [70] or make-or-buy decisions [71].

3.2 Acquisition of manufacturing information

Since the individual cost-relevant process parameters p have a large impact on the resulting total individual manufacturing costs C of additively manufactured components (\(C=f(p)\)), it is essential for the development of suitable tolerance-cost models to obtain sufficient and relevant manufacturing information to quantify the relationship between the resulting tolerances and the cost-relevant process parameters (see Fig. 1). Due to the fact that achievable geometrical accuracy and tolerances in AM are highly dependent on the AM technology, the machine itself and the chosen process parameters, a general determination of the relationship between achievable tolerances and resulting costs is not feasible and needs to be done individually [72]. Therefore, it is inevitable that the method for acquiring manufacturing information regarding the relationship between achievable tolerances and resulting total costs is ideally adapted to the respective use case, the AM technology, the machine, the metrology and the associated restrictions in order to achieve the best compromise between resulting information and effort. The methodology proposed in this contribution for acquiring relevant manufacturing information consists of deducing a suitable benchmark artifact and defining a matching design of experiment under the consideration of aspects from metrology.

3.2.1 Benchmark artifact

Benchmark artifacts provide the possibility to systematically acquire specific manufacturing information for AM technologies and machines considering the influence of specific process parameters and the parts geometry and have therefore been extensively studied in the past [73]. Therefore, they are suitable to provide sufficient and reliable information about the geometrical capability of AM technologies and machines before printing the final part [74, 75]. Hence, by manufacturing and measuring the benchmark artifacts multi-times, conclusions about the relationship between machine-specific process parameters, the parts geometry and resulting tolerances and costs can be derived [76]. Nevertheless, due to the diversity of AM, one single artifact cannot be suitable for all applications [77]. Thus, a standardized benchmark artifact is not advisable. Rather the design must be adapted to the underlying research question and the restrictions associated to the AM technology, the machine and the metrology. For instance, depending on the chosen AM technology, it must be evaluated whether the positioning and the number of components in the build chamber have an impact on the resulting quality and must therefore be taken into account either while designing the benchmark artifact or in the specified design of experiment. Consequently, for designing benchmark artifacts, specific criteria must be met a priori in order to achieve representative results in combination with a reasonable testing effort. In this context, Rebaioli and Fassi [73] compared various benchmark artifacts and deduced process-independent guidelines for designing benchmark artifacts to evaluate the geometrical capabilities of AM technologies and machines in general. An excerpt of the guidelines according to Rebaioli and Fassi [73] in combination with ISO/ASTM 52902:2019 [78], which are most relevant for the development of tolerance-cost models, is listed below:

  • Minimal build volume of artifact for reducing material costs

  • Minimum manufacturing time

  • No need for support structures: avoidance of post-processing and thus time and costs and no influence on the geometrical accuracy of the artifacts features

  • Integration of all relevant basic geometrical features for determining dimensional and geometrical accuracy and form tolerances

  • Integration of as many as possible features in order to reduce testing effort

  • Features should be aligned along all Cartesian machine axes

  • Consideration of manufacturing and testing restrictions

  • Alignment of features under consideration of the measurement device for easy and quick measurement

  • Avoidance of complex and redundant features for reducing measurement time

The requirements listed here are partly in conflict with each other and can only serve as a general guideline for successfully designing a benchmark artifact which is suitable for the specific use case and the overall research objective. In order to determine the tolerance-cost relationship for real applications, the specific part can be decomposed into basic geometrical features which in turn can be combined in the benchmark artifact for reducing testing effort. Thus, for each feature, the relationship between geometrical accuracy and process parameters influencing both build time and quality of the 3D-printed parts can be derived. Rebaioli and Fassi [73] provide some examples of features which can be used for assessing specific geometrical tolerances. These features and the thereby derived geometrical tolerances can be seen in Table 1. Based on these features and the associated tolerances, specific benchmark artifacts, suitable for the respective research objective and the measurement and manufacturing restrictions, can be deduced.

Table 1 Geometrical features of test artifacts for assessing specific geometrical tolerances [73]
Full size table

Another aspect to be taken into account with regard to benchmark artifacts is the handling of datum references. For additively manufactured parts, respectively benchmark artifacts, one of the first steps is to define the build direction which will in turn determine the specification of the manufacturing datum of the resulting process [79]. Especially for the FLM technology, large surfaces are most commonly oriented planar on the build plate in order to maximize the adhesion and thus minimize warping, primarily for thin and tall parts. As a results it is advisable to choose these surfaces as primary datum [80].

3.2.2 Design of experiment

Another important step for acquiring sufficient and reliable manufacturing information for the development of tolerance-cost models for AM is the determination of relevant process parameters influencing the geometrical accuracy of 3D-printed parts and the quantification of their impact on resulting achievable tolerances. In order to investigate and quantify the influence of the mostly relevant process parameters on the geometrical accuracy of 3D-printed parts and thus on the resulting tolerances and costs, they need to be varied in a DoE. According to research results regarding the significance of process parameters on the geometrical accuracy of AM machines in general, it is useful to prioritize the three process-independent parameters, viz. the part orientation in the build space, the layer height and the machine speed (see Section 2.2), over the others, e.g., the infill or the number of contours. In contrast to the other parameters, the part orientation plays a major role in the design of the benchmark artifact. The positioning of the part is neglected due to the fact that all benchmark artifacts and the use case are printed one at a time allowing equal positioning. The use of a DoE therefore offers the advantage of gaining direct knowledge from cause-effect relationships. Especially for AM, the choice of a suitable DoE is crucial as nonlinear effects are often observed and redundant experiments can be prevented. In order to avoid obsolete prints and thus to save time and cost, it is essential to determine relevant process parameters and settings a priori based on findings of an initial pre-screening or literature research. For statistical validation, the DoE has to be repeated several times to generate a sufficiently large data basis for the assessment of achievable tolerances. Although repeat tests significantly increase the experimental efforts and the initial costs to set up the tolerance-cost model, they are inevitable to get reliable information on the achievable tolerances.

However, general statements on the suitability of a specific DoE and the required number of its repetition are difficult. Full-factorial designs serve as a good starting point for an initial screening determining the relevant influencing parameter as well as to investigate the total machine tolerance range. If initial findings and knowledge exist, designs with a reduced number of experiments, such as fractional factorial designs, can be applied to decrease the experimental effort.

3.2.3 Metrology

As a further step to develop tolerance-cost models for AM, the relationship between geometrical tolerances t and chosen process parameters p must be quantified. For this purpose, a metrology suitable for both the process and the benchmark artifact needs to be specified. The choice of the measurement device has in turn impact on the design of the benchmark artifact as already mentioned in Section 3.2.1 and thus must be fixed at an early stage in the process. In general, for the quantification of geometrical variations and thus tolerances, a distinction can be made between non-contact and contact measurement techniques. Using 3D-scanning as non-contact measurement technique, the measured parts are digitalized whereby the measurement method bases on the principles of optical triangulation, photometry and fringe projection method [81]. Especially for 3D-printed parts, the optical measurement technique is preferred, since complex shapes can be measured fast and with high data density. The quantitative assessment of the geometrical variations is subsequently performed using the virtual model obtained through digitization in comparison to the CAD model. If data are proven to be normally distributed, the achievable tolerances per settings can be calculated as the acceptance range of a multitude of its standard deviation  [18]. In case of non-normal distributed data, distribution-independent measures have to be used. As a result, the tolerance value t can be quantified as a function of the previously defined process parameters p as \(t=f(p)\) based on the obtained variations of the printed, digitalized and measured benchmark artifacts.

3.3 Data processing

In the last step, the relations between the process parameters p and the costs C as well as the achievable tolerances, respectively \(C=f(p)\) and \(t=f(p)\), are linked in a common tolerance-cost model to establish the relation \(C=f(t)\) between the individual manufacturing costs C and the assigned tolerance t (see Fig. 1). If process parameters, which mainly contribute to the total costs, only have a minor impact on the resulting part tolerances, there are numerous combinations of process parameters \(p_k\) which can lead to similar tolerance values [20]. Since least cost tolerance design primarily aims to identify the tolerances with the minimum total costs, the minimum cost points are taken into account to define the relevant cost curve [20] (see Fig. 3). However, an accurate tolerance-cost modelling prerequisites a data basis that sufficiently reflects the real manufacturing conditions. While measurement uncertainties or a too low sample size lead to scattering of the data points on the abscissa \(\Delta t_\mathrm {k}\) (see Section 3.2), simplifications and assumptions in cost estimation (see Section 3.1) contribute to a scattering on the ordinate \(\mathrm {\Delta } C_\mathrm {k}\) (see Fig. 3).

Fig. 3
figure 3

Fitting of tolerance-cost models to discrete tolerance and cost data

Full size image

The usage of fitting algorithms can then help to derive a mathematical function taking the discrete experimental gathered tolerance data \(t_k\) and the resulting manufacturing costs \(C_k\) into account [21] (see Fig. 3). As the data are highly dependent on numerous factors, such as the given manufacturing conditions, i.e., the chosen machine, the tools, the material, the manufactured feature types and sizes, a generally valid model cannot be defined a priori [25]. Thus, a number of different types of models and functions have been presented in literature over the years and have to be chosen individually fitting best for the given use case [14]. Although exponential and reciprocal functions are mostly used in literature and, alternative non-traditional approaches with a higher degree of free parameters as well as advanced approximative surrogate modelling techniques have been proposed to represent more sophisticated relations [6, 14], especially to model highly nonlinear effects occurring in AM. Besides the model type, the selection or rather the identification of the function-specific cost parameters is a crucial but an essential task to achieve a high model accuracy [14], although model type and coefficient uncertainties are inevitable [82] leading to superimposed fitting errors \(\delta _k\) [26] (see Fig. 3). Hence, the user must individually study which model can represent the real machine behavior most accurately. However, the merit of creating a continuous cost function is then limited as it is unclear how the interpolated tolerances between the real data points can be reached in manufacturing, especially if the scope of action is restricted by the number of optional settings for the relevant process parameters, e.g., the layer height. Hence, the usage of pure discrete tolerance-cost relations should be preferred, if data does not clearly indicate interrelations that can be properly mapped by a continuous function. As a result, an individual tolerance-cost relation \(f_\mathrm {C}\) as a function of one single tolerance t can be defined for each part contributing to the total product functionality and in sum to the total assembly costs.

In practical applications, however, multiple, mostly geometrical tolerances have to be assigned to individual part features. In traditional manufacturing technologies, such as milling or turning, the manufacturing process steps are feature-oriented and the part features are generated successively. Thus, the geometrical part tolerances can locally be controlled feature by feature by an individual choice of operations, tools and process parameters. In contrast, AM parts are generated layer by layer, so features with shared layers are created simultaneously by a set of tool paths with one equal set of process parameters. As a consequence, the tolerances generally cannot be assigned individually since they rather correlate with the global process parameter settings for the global part—except a layer-dependent adaption of the process parameters, hybrid manufacturing processes or feature-oriented post-processing treatments. Accordingly, the tolerance of the feature which consequences the most restrictive process parameters, and thus the usually higher manufacturing effort, primarily determines the choice of the global process parameters and simultaneously the achievable accuracy of the other features to assure the conformity of the total part. Although the designer primarily assigns part tolerances to assure the total product quality under variation, it is thus inevitable to jointly consider the AM-specific process parameters since they globally influence all part tolerance values and their distributions [7]. Finally, the acquired knowledge on the part tolerance distributions, the tolerance values and the resulting costs supports the design engineer in the manual or optimization-based definition of least cost tolerance values.

4 Application

In this academic case study, a cost-efficient tolerance design of a solenoid valve is focused, whereas the housing of the valve should be considered as the part of interest to be manufactured by FLM. It consists of several basic cylindrical and planar geometrical features, which are aligned in different axes. Figure 4 shows the CAD-model of the solenoid valve assembly as well as the tolerance specification of the housing and a printed and digitalized sample of it. The design was chosen in such a way that no support structures are necessary in the functional relevant part sections avoiding post-processing and, in turn, costs. The tolerances have been specified for a selection of functional relevant geometrical features exemplarily illustrating the applicability of the presented approach. For the given simplified use case, the tolerances \(t_1\), \(t_2\) and \(t_4\) are assigned to assure a proper fitting of further single parts, \(t_3\) is chosen to assure a constant flow of the fluid.

In the first step, the main process parameter- and thus tolerance-dependent cost items have to be identified with respect to the chosen FLM printer Raise3D Pro2 PlusFootnote 1. As discussed in Section 3.1, the in-processing costs according to Eq. (2) mainly contribute to the total manufacturing costs which can primarily be influenced by the tolerance design. Since the costs for the separation from the build platform and the removal from the build chamber can be neglected for FLM, there are no support structures needed for the functional relevant parts of the given design and the part should not additionally be reworked, the in-processing costs are equal to the build costs \(C_\mathrm {build}\).

The machine costs per hour for the given machine are determined as:

$$\begin{aligned} C_\mathrm {mach} = (5000/(2\cdot 100\cdot 4))\cdot 1,25~\EUR /\mathrm {h} = 7,8125~\EUR /\mathrm {h}, \end{aligned}$$
(5)

where:

$$\begin{aligned} \begin{array}{lll} &{}\text {Equipment costs} &{} 5000~\EUR ,\\ &{}\text {Amortization period} &{} 2 \text {years,}\\ &{}\text {Production days per year} &{} 100 \text {days,}\\ &{}\text {Hours of production per day}&{} 4 \text {hours,}\\ &{}\text {Overhead} &{} 25 \%.\\ \end{array} \end{aligned}$$
Fig. 4
figure 4

Assembly of the solenoid valve and tolerance specification of the housing

Full size image

The labor costs are considered as tolerance-independent and are thus neglected [55]. Acrylonitrile Butadiene Styrene (ABS) was preferred as build material over Polyactic Acid (PLA) due to its better geometrical accuracy and resulting surface roughness [83]. The material costs for the ABS filament is given by 50 €/kg. The energy costs per hour are approximated by an average electricity price of 0,235 €/kWh and an average energy consumption of \(P_\mathrm {avg}=0,65~\mathrm {kWh}\), while the build time is considered as the significant tolerance-dependent factor. The time efforts for standby and heating are assumed to be constant and are neglected in the following as they only contribute as a fixed cost term independent from the choice of the tolerance. They only become relevant if multiple AM machine alternatives are available and have to be considered in context of machine selection (see Section 3.1).

For the design of the benchmark artifact, firstly, the presented use case (see Fig. 4) has been decomposed into its functional features which are subsequently integrated in the benchmark artifact (see Fig. 5) according to the specified tolerances, whereby manufacturing and testing restriction have been considered under the consideration of the general design guidelines for benchmark artifacts for AM (see Section 3.2 and [73, 78]). The purpose of the resulting benchmark artifact is not to fully evaluate the geometrical capability of the regarded AM machine in general, but rather to derive the relationship between the tolerances and the resulting costs for the presented use case. For this reason, in contrast to other standardized artifacts, standard geometric elements such as, e.g., inclined surfaces are not integrated since the use case’s features are only mounted horizontally. Hence, the benchmark artifact is designed to verify each specified tolerance eight or nine times (for the perpendicular cylinders) to increase the number of data points (see Fig. 5).

Fig. 5
figure 5

Design and specified tolerances of the benchmark artifact

Full size image

As mentioned in Section 3.2.2, based on a literature review and experimental preliminary studies [72], the part orientation, layer height and machine speed are considered as significant parameters impacting the geometrical accuracy. As the influence of orientation is already considered in the benchmark artifact’s design by differently aligning the geometrical features (see Fig. 5), only the latter parameters need to be considered in the full-factorial DoE. All further process parameters were determined as fixed settings (see Table 2). In addition, it is defined that all process parameters are equal for the total additive manufacturing process and that only one part is manufactured in one print job. Table 3 summarizes the experiments and the estimated build times and material quantities as well as the individual cost elements and the total costs for the solenoid valve.

Table 2 Fixed process parameters
Full size table
Table 3 Full-factorial DoE and its resulting costs for the fabrication of the solenoid valve
Full size table
Fig. 6
figure 6

Digitalized sample with exemplarily highlighted features and measured part variations

Full size image

The artifacts are fabricated five times for each of the nine parameter combinations (see Table 3) for the purpose of statistical validation, leading to a total number of 45 physical specimens. In doing so, 40 or rather 45 data points, as a result of the five times printing of each artifact including 8 or 9 features, are used to determine the achievable tolerance per process parameter setting combination. The pre-processing and thus the definition of the process parameters according to the DoE was performed in the slicing software ideaMaker, whereby the material settings for ABS were adopted according to the manufacturer’s specifications for the choice of specific parameters (e.g., extrusion temperature) (see Table 2). In addition, the estimated build times and material quantities are used as the input for the tolerance-cost model (see Section 3.1). Subsequently, the specimens were digitalized using the optical 3D scanner ATOS Compact Scan 12M from GOM GmbHFootnote 2. According to a suitable inspection strategy (see Fig. 6), the tolerances have been quantified for each specimen.

4.1 Presentation of the results

Figure 7 shows the results of the experiments with its single measured variations \(\Delta _i\) for each setting and its resulting manufacturing costs \(C_\mathrm {tot}\). Since the part tolerance distributions do not correspond to a normal distribution and vary for the different process parameter settings, the 90%-quantile is exemplarily used to predict the achievable tolerances \(t_i\) from the single measurements. Though further statistical moments can be helpful to describe each tolerance part distribution, this aspect is not further discussed in this article.

Fig. 7
figure 7

Overview on the measurement results for features of interest of Fig. 4: feature variations from ideal (\(\Delta _i\)) and the achievable tolerances \(t_i\) in relation to the resulting manufacturing costs \(C_\mathrm {tot}\). The color intensity of the data points indicate their frequency

Full size image

Overall, it can be seen that the machine speed has a less significant influence on both manufacturing costs and resulting geometrical accuracy than the layer height for all geometrical features (see Fig. 7a–d). In accordance to the findings from literature  [55], the influence of the process parameters strongly depends on the selected orientation of the features. As expected, the layer height has a significant impact on the size tolerance of the cylindrical features perpendicular to the build direction (see Fig. 7a). In contrast, the layer height and the machine speed show less influence on the achievable tolerances for the vertically printed cylinders (see Fig. 7b). In line with [55], it can further be seen that actions to increase the geometrical accuracy do not necessarily consequence higher manufacturing costs. For the given use case, printing with a layer height of 0,3 mm and machine speed of 40 mm\(\backslash\)s \(\triangledown\) leads to higher build times and manufacturing costs than a layer height of 0.2 mm and a machine speed of 70 mm\(\backslash\)s \(\triangle\) or 100 mm\(\backslash\)s \(\bigcirc\) but also to larger geometrical variations (see Fig. 7a–d) and Table 3). Especially for small parts with complex shapes, the machine speed can have a more significant influence than the layer height, since elaborate travel paths for creating the parts complex contours lead to higher build times. Since the relations between tolerance and cost strongly depend on the individual part geometry and are highly nonlinear, the application of regression analysis to derive relationships that can represent the behavior in a realistic way becomes difficult as well as mostly non-useful since it remains unknown how the interpolated tolerances can be reached in reality.

4.2 Discussion

Finally, the potentials as well as the current limitations of the presented methodology are discussed in the following.

Potentials

In line with literature, the given case study has exemplarily emphasized that part quality and manufacturing costs depend on the chosen machine-specific process parameters. The direct mapping of the process parameters with the resulting build time and its combination with detailed-analysis build time estimation techniques enable a universal, problem-independent cost estimation and thus broad applicability of the presented methodology. In doing so, the design engineer can rely on valid tolerance-cost information in their decision-making in tolerance design. Especially for AM, the identification of the machine specific part tolerance distributions for the different unilateral geometrical tolerances is essential since they are often non-normal, asymmetrical distributed [7]. For a realistic tolerance analysis and thus tolerance-cost optimization, realistic part tolerance distributions are essential to ensure valid and reliable results [7]. Hence, the identification of tolerance-cost curves is an important activity of cost-efficient tolerance design. It helps to understand the effects of tolerances on both cost and part quality but also functions as quantitative model in manual or automatic tolerance-cost optimization approaches. Since process parameters and tolerances are strongly connected in AM, their interrelations have to be known a priori to ensure that the various allocated tolerances for one part can first be achieved at all and second at minimum cost.

Besides tolerance design, the feature-related cost and quality information should further be provided for concept and parameter design. The harmonization of the locations, orientations and also size of the different features within one part with respect to the given process-related correlations and restrictions helps to keep the build time and thus the total costs as low as possible. It is, for example, conceivable to consciously design parts where features of different quality are positioned in non-overlapping layers so that they can be manufactured with different process parameter settings tailored to the necessary local part quality.

Limitations

However, modifications of concept or parameter design are only effective if the total tolerance-cost model can represent varying process parameters in one single print activity. The presented methodology is aimed at universal tolerances for identical features on a part. However, the extension to a local adjustment of individual process parameters will allow the allocation of individual tolerances having a positive impact on the total build time. In contrast to the given example in the case study, where the most restrictive tolerance predominates the choice of process parameters defining the build time, the total costs will then be formed by largely independently allocated tolerances.

The crucial bottleneck of tolerance-cost modelling is the experimental effort. The case study has shown that even for a manageable number of standard features, tolerances and process parameters, a large number of experiments have to be carried out in advance. Sophisticated test artifact concepts and pre-screenings help to reduce the number of experiments and to increase the accuracy of tolerance-cost functions with respect to the relevant process parameter combinations. So it requires both cost-intensive time and resources [25]. However, a sufficiently large number of repetitions is inevitable to reduce model uncertainties and to reliably predict the resulting part distributions. The fact that tolerance-cost models must be tailored to the given use case requires the development of a case-specific benchmark artifact and further increases the initial costs to set up the cost model. In this regard, the development of a modular benchmark toolbox is useful to support the designer in a (semi-)automatic design of the benchmark artifacts. All these comparatively high initial efforts, however, are only profitable if the gained insights prevent the designer to choose tolerances unnecessarily tight. Thus, above a minimum lot size, it makes sense to put effort in gaining knowledge on the relations between costs and tolerances supporting a least cost tolerance design and thus amortizing these initial costs.

Nevertheless, different actions to decrease these initial costs are needed. On the one hand, sophisticated methods have thus to be developed commonly with industry to directly collect measurement and sensor data information inline in the actual manufacturing process [84, 85]. On the other hand, there is an urgent need for tools to predict the geometrical accuracy to reduce the number of experiments [86, 87].

5 Conclusion and outlook

Access and availability to up-to-date tolerance-cost data are essential for an optimization-based allocation of cost-efficient tolerance values. New manufacturing processes, such as AM, consequence the acquisition of tolerance-cost data and its transfer into tolerance-cost models enabling a conscious tolerance allocation with regard to cost and geometrical accuracy. This article focused on a methodology for the systematic development of tolerance-cost models as well as its exemplarily application for FLM.

Future research work should focus on the expansion and application of the methodology to further processes and materials of industrial relevance, such as LPBF or SLS. The obtained correlations between the process parameters and the resulting accuracy allow a concurrent optimal selection of process parameters and tolerances. In combination with methods for an individual adaption of process parameters for several layers to selectively control the geometrical accuracy of certain part sections, e.g., the variation of the machine speed or layer height over the part height by adaptive slicing, it can significantly improve the efficiency of AM. Intelligent approaches, collecting the information on resulting tolerances and distributions directly in manufacturing, are essential to significantly increase the amount of accessible up-to-date data and thus to improve the accuracy of tolerance-cost models.