1 Introduction

Nowadays, control charts have become an essential part of the quality control activities of most organizations to detect the presence of special causes of variation in a variety of manufacturing processes [1,2,3,4].

Traditional control charts require a preliminary set of experimental data related to the process to be constructed (phase I) [5]. However, there can be situations in which collecting this data set can be time-consuming, costly, and difficult to obtain. This is the typical case of low-volume productions, for which collecting a reasonable number of samples to set valid control limits may unacceptably delay monitoring [6,7,8].

The purpose of this paper is to propose a novel approach to statistically control the process of assembled products through the use of a control chart for nonconformities per unit (DPU-chart) based on defect prediction models.

In detail, if a defect prediction model based on a priori knowledge of the defectiveness occurring in the product is available, it can be used to construct a DPU-chart by avoiding the traditional implementation of phase I.

In this study, assembly processes are addressed in detail. In particular, a defect prediction model developed in a recent study by the authors [9] is used to set up a control chart to monitor DPU detected in each workstation of a manufacturing process. This model relies on the relationship between DPU and product structural complexity.

The DPU-chart, despite the conceptual similarity with traditional u-chart, totally differs in its design. This control chart does not require a process analysis and a preliminary experimental data collection (phase I). As a result, the methodology proposed could be of interest to researchers and practitioners that need to speed up the phase of construction of the chart. In particular, as mentioned, the proposed DPU-chart could be very attractive for low-volume productions.

The proposed method is applied to a real-world case study related to the production of wrapping machines assembly for the packaging of palletized load, whose total number of machines produced in a year generally reaches only a few dozen units.

The remainder of the paper is organized into five sections. “Sect. 2” reviews the prediction model for assembly defects. In “Sect. 3,” the DPU-chart is presented. “Sect. 4” presents a case study concerning the practical application of the proposed control chart in the low-volume production of wrapping machines. “Sect. 5” provides some guidelines for the practical application of the DPU-chart. “Sect. 6” summarizes the original contributions of this research, focusing on its implications, limitations, and possible future developments.

2 Conceptual background: defect prediction model for assembly processes

A large number of studies in the literature use assembly complexity to predict product defects [8, 10,11,12,13,14,15,16,17,18,19,20]. These models were developed for predictive and quality improvement purposes in several industrial fields, ranging from the electromechanical to the automotive sector. Most of them refer to mass productions, involving hundreds or thousands of pieces produced per month [10, 11, 13,14,15,16,17, 19]. Recently, the authors focused on identifying appropriate defect prediction models in assembly processes [9, 21,22,23,24] according to the product structural complexity paradigm proposed by Alkan [25] and Sinha [26]. The same model was also recently adopted to help inspection designers in the inspection process planning from the early design phases [9].

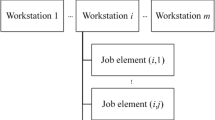
In detail, the product assembly process is decomposed into a series (m) of process steps, also called workstations, following specific operation standards. Each i-th workstation (i = 1, …, m) is made up of several elementary operations, defined as the minimum components of a specific task, as schematized in Fig. 1.

Fig. 1
figure 1

Schematic of the assembly process of a product [9, 24]

Full size image

It is assumed that errors made by operators in performing a certain elementary operation in a workstation may introduce at most one defect in the product that can be interpreted as a unique “macro-defect.” Accordingly, the totality of the possible defects within a certain workstation is at most equal to the total number of elementary operations in the same workstation. In practical applications, such assumption is reasonable when, for each i-th workstation, a refined segmentation of elementary operation is performed. Each sub-assembly coming from a workstation, i.e., a workstation-output, can be examined by inspectors using quality control activities appropriate according to the specific type of defects, e.g., dimensional verifications, visual checks, or mechanical tests.

To clarify these last concepts, a pedagogical example is proposed. Consider a simple assembly process composed by a single workstation, in which a bolt (with a nut) is manually tightened with a wrench. Table 1 shows the performed elementary operations with the defects that may be introduced. In this case, the number of elementary operations is 9 and, accordingly, the total number of possible defects that can occur in the workstation is at most 9.

Table 1 Subdivision of a workstation, i.e., the manually tightening of a bolt with a wrench in an apparatus, into elementary operations with indication of possible defects
Full size table

Verna et al. [9, 24] showed that the total number of defects detected in each i-th workstation divided by the number of produced units, i.e., the defects per unit related to the i-th workstation (\({DPU}_{i}\)), can be expressed as a function of product complexity, as follows:

$${DPU}_{i}=f{{(C}_{i})}$$
(1)

where \({DPU}_{i}\) is the defect per unit (DPU) in the i-th workstation and \({C}_{i}\) is the structural complexity associated to the i-th workstation, evaluated according to the approach proposed by Alkan [25] and Sinha [26], shown in Eq. (2).

$${C}_{i}={C}_{1,i}+{C}_{2,i}\cdot {C}_{3,i}$$
(2)

The three components of the structural complexity, \({C}_{1,i}\), \({C}_{2,i}\), and \({C}_{3,i}\), are described below.

\({C}_{1,i}\) is defined as the handling complexity of the i-th workstation and is the sum of complexities of individual product parts in each i-th workstation. It is calculated as shown in Eq. (3):

$${C}_{1,i}=\sum_{p=1}^{{N}_{i}}{\gamma }_{pi}$$
(3)

where, for each i-th workstation (i = 1, …, m), \({N}_{i}\) is the total number of product parts and \({\gamma }_{pi}\) is the handling complexity of part p, which can be approximated by the standard handling time [25].

\({C}_{2,i}\) represents the complexity of connections related to the i-th workstation. It is the sum of the complexities of pair-wise connections existing in the product structure assembled in the i-th workstation, as follows:

$${C}_{2,i}=\sum_{p=1}^{{N}_{i}-1}\sum_{r=p+1}^{{N}_{i}}{\varphi }_{pri}\cdot {A}_{pri}$$
(4)

where \({\varphi }_{pri}\) is the complexity in achieving a connection between parts p and r of the i-th workstation, and \({A}_{pri}\) defines the binary adjacency matrix of the i-th workstation. Note that the connection between parts is considered only once. In detail, \({\varphi }_{pri}\) can be approximated by the standard completion time of the connection between parts p and r in isolated conditions. Besides, \({A}_{pri}\) represents the connectivity structure of the system, as indicated in Eq. (5):

$$\mathrm{A}_{\mathrm{pri}}=\left\{\begin{array}{ccccccccccccccccc}1& \mathrm{if \ there \ is \ a \ connection \ between \ }p\mathrm{ \ and \ }r\mathrm{ \ in \ the \ }i-\mathrm{th \ workstation\ }\\ 0& \mathrm{otherwise}\end{array}\right.$$
(5)

Finally, \({C}_{3,i}\) is the topological complexity of the i-th workstation and represents the complexity related to the architectural pattern of the assembled product. It can be obtained from the matrix energy EAi of the adjacency matrix related to the i-th workstation, which is designated by the sum of the corresponding singular values \({\delta }_{qi}\) [26, 27], as follows:

$${C}_{3,i}=\frac{{E}_{Ai}}{{N}_{i}}=\frac{\sum_{q=1}^{{N}_{i}}{\delta }_{qi}}{{N}_{i}}$$
(6)

where EAi stands for graph energy (or matrix energy) related to i-th workstation and \({N}_{i}\) stands for the number of parts in the i-th workstation (i.e., the number of nodes). As the adjacency matrix of each i-th workstation is a symmetric matrix of size Ni with the diagonal elements being all zeros, the singular values corresponds to the absolute eigenvalues of the adjacency matrix [26, 28].

To clarify how the structural complexity associated to the i-th workstation can be obtained, a simple example is given. Consider an assembly process made up of a single workstation in which a simple product composed of N = 6 parts (w, j, k, x, y, and z) is assembled, as represented in Fig. 2. For the sake of simplicity, suppose that the 6 parts, as well as the connections between the parts, are identical. The standard handling time of each p-th part is \({\gamma }_{p}\) = 10 s (with p = 1, …, 6), while the standard completion time of the connection between parts p and r is \({\varphi }_{pr}\)= 20 s (with p = 1, …, 5 and r = p + 1, …, 6). According to Eq. (3), the handling complexity is \({C}_{1}=\sum_{p=1}^{6}{\gamma }_{p}\) = 60 s = 1 min. The complexity of connections is, by implementing Eq. (4), \({C}_{2}=\sum_{p=1}^{5}\sum_{r=p+1}^{6}{\varphi }_{pr}\cdot {A}_{pr}\) = 100 s = 1.67 min, since there are 5 connections between the parts. From the adjacency matrix A, shown in Fig. 2, the related graph energy is computed as the sum of its singular values that are the absolute eigenvalues of A in case of symmetric matrix. In detail, the eigenvalues of the adjacency matrix A are − 2.24, 2.24, and 0 with multiplicity 4. Thus, being the singular values the absolute eigenvalues of A, then \({E}_{A}=2.24\cdot 2+0\cdot 4=4.48\). According to Eq. (6), it is obtained that \({C}_{3}=\frac{{E}_{A}}{N}=\frac{4.48}{6}=0.75\). Finally, by applying Eq. (2), the structural complexity is \({C}={C}_{1}+{C}_{2}\cdot {C}_{3}=2.25\) min.

Fig. 2
figure 2

Connectivity structure of a simple product composed of six parts and its associated adjacency matrix A

Full size image

The defect prediction model shown in Eq. (1), depending solely on physical design information, is beneficial, especially in the early design stages, when real production data or the physical mockup of the product is not available. This model has been recently applied by the authors in the assembly of a low-volume production of wrapping machines, showing that the relationship between complexity and DPU follows a power-law relationship, as follows [9, 24]:

$${DPU}_{i}=a\cdot {{(C}_{i})}^{b}=a\cdot {({C}_{1,i}+{C}_{2,i}\cdot {C}_{3,i})}^{b}$$
(7)

where a and b are two regression coefficients estimated by nonlinear regression. For the assembly of wrapping machines, the coefficients obtained are \(a=3.05\cdot {10}^{-3}\) and \(b=1.58\), as will be described in “Sect. 4.”

3 DPU-chart

Considering the framework described in “Sect. 2,” the approach proposed in this study aims to statistically control the process by designing a control chart based on a defect prediction model. In detail, the proposed control chart is designed to monitor DPUi values, i.e., DPU occurring in each i-th workstation of the process (i = 1, …, m, see Fig. 1) in order to detect out of control situations. Accordingly, this chart can be categorized as a control chart for defects per unit (u-chart). Given \({x}_{i}\) total defects in a sample of \({n}_{i}\) inspected units in a certain i-th workstation, the average number of defects per inspection unit, \({DPU}_{i}\), can be defined as:

$${DPU}_{i}=\frac{{x}_{i}}{{n}_{i}}$$
(8)

where \({x}_{i}\) is the average number of defects (Poisson distributed random variable [5]).

In the proposed DPU-chart, the in-control mean value \({DPU}_{i}\) is set by a suitable defect prediction model. In the case of electromechanical products, the power-law relationship shown in Eq. (7) can be adopted to this aim. Therefore, for each i-th workstation of the process (i = 1, …, m), the parameters of the control chart for the average number of defects per unit (\({DPU}_{i}\)) may be derived as follows:

$${\mathrm{UCL}}_{{DPU}_{i}}={DPU}_{i}+3\cdot \sqrt{\frac{{DPU}_{i}}{{n}_{i}}}$$
(9a)
$${\mathrm{CL}}_{{DPU}_{i}}={DPU}_{i}$$
(9b)
$${\mathrm{LCL}}_{{DPU}_{i}}={DPU}_{i}-3\cdot \sqrt{\frac{{DPU}_{i}}{{n}_{i}}}$$
(9c)

where \({DPU}_{i}\), i.e., the in-control mean value of the DPU-chart, is modeled by the power-law relationship of Eq. (7).

An example of representation of the control chart for DPUi is provided in Fig. 3.

Fig. 3
figure 3

Example of representation of the DPU-chart

Full size image

In “Sect. 4,” the proposed methodology is applied to a real-life case study of a company specialized in the design and manufacture of wrapping machines. The case study will exemplify the application of the approach and will highlight its practical relevance.

4 Practical case study

The methodology proposed in “Sect. 3” is applied to the low-volume production of rotating ring wrapping machines for the packaging of palletized loads, produced by an Italian company (Tosa Group S.p.A.). Typically, each year, about 50 machines are assembled and each of them is highly customized. This study focuses in particular on the assembly of a single part of the rotating ring wrapping machine, i.e., the pre-stretch device, illustrated in Fig. 4. The main reason is that, although each machine differs from the others in some details, this device is common to all assembled machines [20]. The three functions performed by a pre-stretch device are as follows: (i) pulling/unwinding, (ii) pre-stretch and positioning of the plastic film, and (iii) performing the necessary number of windings.

Fig. 4
figure 4

Rotating ring wrapping machine produced by Tosa Group S.p.A. (Italy) with a focus on the pre-stretch device

Full size image

The assembly process of the pre-stretch device can be subdivided into m = 29 workstations, listed in Table 2. In this case study, a workstation is meant as an assembly step in which elementary operations are performed, whose output is a sub-assembly, i.e., the workstation-output. As shown in Table 2, in the first 9 workstations, the assembly is performed on the bench by the operator, while in the last 20 workstations the subassemblies are assembled on the frame plate. Each workstation is composed of elementary operations that have definite start and end points and are repeatable regularly throughout the working day [29]. The number of elementary operations in each workstation is also shown in Table 2. The latter, moreover, reports the nominal values of DPU occurring under stationary process conditions in each workstation (nominal DPUi) that were obtained by drawing on the company historical data [20, 23]. These data were considered the reference values of the average defectiveness rate of the assembly process in optimal working conditions and were used to develop a defect prediction model. In detail, according to the model described in “Sect. 2,” the structural complexity related to each i-th workstation, Ci, is calculated from the complexities \({C}_{1,i}\), \({C}_{2,i}\), and \({C}_{3,i}\), listed in Table 2, by applying Eq. (2). To better clarify this step, we propose the calculation of the complexity coefficients for the workstation no. 14 (one of the simplest workstation), related to the transmission system of motor no. 1 assembly. In such a workstation, two components are assembled: the driven wheel and the drive belt. The standard handling time of the two parts is 0.14 min and the time for connecting them is 0.44 min. Accordingly, by implementing Eqs. (3) and (4), respectively, it is obtained \({C}_{1}=\sum_{p=1}^{2}{\gamma }_{p}\) = 0.14 min and \({C}_{2}=\sum_{p=1}^{1}\sum_{r=p+1}^{2}{\varphi }_{pr}\cdot {A}_{pr}=\) 0.44 min, as reported Table 2. The adjacency matrix of the two components is A = \(\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\). The two different eigenvalues of A are 1 and − 1. Thus, the graph energy \({E}_{A}\) is computed as the sum of its singular values that are the absolute eigenvalues of A in case of symmetric matrix: \({E}_{A}=1+1=2\). According to Eq. (6), \({C}_{3}=\frac{{E}_{A}}{N}=\frac{2}{2}=1\). Finally, by Eq. (2), the structural complexity of this workstation is \({C}={C}_{1}+{C}_{2}\cdot {C}_{3}=\) 0.58 min.

Table 2 Subdivision of the assembly process of the pre-stretch device of wrapping machines into workstations (WS), defect prediction model’s variables (see Eq. (7)), nominal \({DPU}_{i}\) and \({DPU}_{i}\) predicted by Eq. (10)
Full size table

Different models were tested and compared to relate DPUi versus Ci. The adequacy of such models was assessed based on the analysis of regression residuals and of the S value as a measure of goodness-of-fit [30, 31]. A power-law curve was found to be the best model to define such a relationship, as discussed in “Sect. 2.” Accordingly, the defect prediction model, obtained according to Eq. (7), is the following [9, 24]:

$${DPU}_{i}=3.05\cdot {10}^{-3}\cdot {{(C}_{i})}^{1.58}$$
(10)

Table 2 finally reports the \({DPU}_{i}\) values predicted by Eq. (10).

The average number of defects per unit in each workstation, DPUi, is tracked by inspectors on a bimonthly basis. In detail, every 2 months, 9 devices are assembled by the company in each i-th workstation and, accordingly, the sample size is ni = 9. Each i-th workstation-output (i = 1, …, 29) is examined by inspectors that record the total number of defects occurring during each bimester. Inspectors perform various quality control activities to detect these defects, which may require specific equipment depending on the workstation-output [9]. The adopted inspection controls are listed in Table 3. Then, for all the workstations, the recorded defects are divided by the number of devices produced in each bimester to obtain the average defects per unit. The most recent DPUi values related to the last 12 bimesters (2 years) are reported in Table 4.

Table 3 Type and description of the controls performed in the workstations of the pre-stretch device to detect defects [9]
Full size table
Table 4 DPUi values related to each i-th workstation of the pre-stretch device tracked on a bimonthly basis. Out of control observations are written in bold type
Full size table

The DPU-chart developed in “Sect. 3” can be used to monitor the process. Adopting the DPU prediction model greatly speeds up the construction of the control chart. Indeed, since the preliminary collection of experimental data (phase I) is not necessary for the new approach, a time saving of several months is achieved (considering that data for 50 machines are obtained in one production year). In detail, according to Eqs. (9a), (9b), and (9c), the parameters of each DPU-chart are derived and are reported in Table 4. Since \({\mathrm{LCL}}_{{DPU}_{i}}\) < 0 for each i-th workstation, it is set \({\mathrm{LCL}}_{{DPU}_{i}}\)= 0 for the chart.

A DPU-chart is obtained for all the workstations. As an example, the DPU-chart for workstation no. 1 is provided in Fig. 5. As can be seen, the workstation 1 appears in statistical control.

Fig. 5
figure 5

DPU-chart for the i-th workstation (i = 1)

Full size image

When some points fall outside of the control limits and/or points behave in a systematic or nonrandom manner, there is evidence that the process is out of control, and investigation and corrective actions are required to find and eliminate the assignable causes responsible for this behavior. As an example, from the data in Table 4, a lack of statistical control is exhibited for workstations no. 10 and 26. In detail, the chart for workstation 10 highlights an increasing trend of the DPU values from the bimester no. 8, and two observation (i.e., corresponding to bimester no. 10 and 12) are signaled as out of control points, as shown in Fig. 6. On the other hand, for workstation no. 26, five out of control DPU values are detected by the chart, corresponding to bimester no. 4, 8, 9, 10, and 11 (see Fig. 7). In order to investigate the causes leading to the anomalous defectiveness found in the two workstations, specific and accurate checks were carried out. Regarding workstation 10, the critical assembly operation was the finishing of the frame plate holes, performed by the operator with a manual grinding machine. The inadequate training of the operator was identified as the variation cause. On the other side, the root cause of the workstation 26 behavior was a batch of an out-of-tolerance mechanical component purchased from an external supplier used for assembling the spindle release lever.

Fig. 6
figure 6

DPU-chart for the i-th workstation (i = 10)

Full size image
Fig. 7
figure 7

DPU-chart for the i-th workstation (i = 26)

Full size image

5 Application guidelines

The proposed DPU-chart could be very useful when a defect prediction model is available. Otherwise, some evaluations ought to be made. In detail, the following guidelines should be considered before designing a DPU-chart:

    • Case (i): a model for predicting DPU is available.

    • If a suitable model for predicting DPU is available, adopting a DPU-chart can be considered more convenient than a traditional u-chart, avoiding the implementation of phase I and directly deriving control limits from prior product knowledge. The prediction model is certainly closely linked to the specific manufacturing field. In the case of assembly processes, the prediction model framework described in “Section 2” can be adopted, and Eq. (7) can be considered a suitable equation to model DPUs in various applications. However, the regression coefficients a and b (see “Section 2”) may vary according to the specific industrial field. As aforementioned, in the case of wrapping machines, these coefficients are known from a previous study [24]. This model for wrapping machines can, to a certain extent, be preliminary extended to other similar applications in assembly production, particularly electromechanical products.

    • Otherwise, in sectors other than the electromechanical, alternative prediction models may be adopted, with settings based on literature data and/or previous experience (see, e.g., defect/fault prediction models for software applications [32, 33]).

    • Case (ii): a predictive model is not available.

    • In such a case, the interest in the proposed DPU-charts may be less evident, having to replace phase I with the construction of the defect model. As a consequence, it is necessary to evaluate case by case if it is more convenient to implement phase I or to build a new defect prediction model.

Referring to the case (i), to empirically validate the suitability of the prediction model developed for wrapping machines — see Eq. (10) — to other electromechanical products, a comparison is performed with a similar application related to the assembly of hardness testing machines. The new proposed case study concerns the assembly of the AFFRI® LD 3000 AF machine and, in particular, its machine head. As described in a previous paper [8], the assembly of machine head of hardness testing machines may be subdivided into 18 workstations. For each workstation, the DPUi are reported in Table 5. To build the prediction model, the structural complexity Ci is used as predictor, according to the Alkan [25] and Sinha [26] model (see “Sect. 2”). The obtained values are listed in Table 5. By applying Eq. (7), the regression model coefficients, denoted respectively a’ and b’, are: a’ = \(3.25\cdot {10}^{-3}\) and b’ = 1.52. Figure 8 compares the 95% confidence intervals of the regression coefficients of the two empirical models (i.e., that for the wrapping machines and that for hardness testing machines). The confidence intervals of both the regression coefficients are comparable as they overlap each other, thus indicating that the model developed for wrapping machines — Eq. (10) — may also be usable, as a first approximation, for different applications pertaining to the electromechanical field.

Table 5 Structural complexity and defects per unit relevant to the workstations of the machine head of hardness testing machines
Full size table
Fig. 8
figure 8

Comparison of 95% confidence intervals of regression coefficient estimates of Eq. (7) obtained for wrapping machines and hardness testing machines [8]

Full size image

6 Conclusions

Identifying suitable statistical process control (SPC) tools to control and monitor manufacturing processes is a key aspect of many industrial companies. In the modern industry, production volume continues to shrink due to the increasing customization and complexity of products. As a result, more and more small batches are produced (the so-called low-volume production). In this context, collecting experimental data to implement traditional SPC tools may be time-consuming, costly, and challenging. This paper proposes a novel DPU-chart based on the use of defect prediction models for assembled products.

In contrast to traditional monitoring charts, DPU-charts do not require preliminary experimental data in the phase of construction of the chart (phase I). Several prediction models have been developed in the scientific literature to predict defects per unit (DPU) occurring in the assembly workstations. In this research, the model developed by the authors in a previous study [9] in the electromechanical field is used to predict DPU occurring in each workstation from product structural complexity.

The proposed DPU-chart may be particularly beneficial when a defect prediction model is available, as it allows to avoid the construction of a conventional SPC chart (phase I) and to derive control limits directly from product assembly structure knowledge. In particular, through an empirical comparison with hardness testing machines assembly, it was obtained that the model developed for wrapping machines can also be preliminary suitable for other similar applications in the electromechanical field. Conversely, if a predictive model is not available, it is necessary to evaluate, on a case-by-case basis, whether it is more beneficial to adopt a conventional SPC chart or to build a new specific defect prediction model.

The novel approach to set up the DPU-chart can be of great help to improve process monitoring and control especially in a context of low-volume manufacturing, for which implementing phase I would typically take very long time to get enough data. As a result, the construction of the chart can be significantly accelerated, thus avoiding delaying the next monitoring phase. The relevance of this novel paradigm is supported by the findings obtained in a real production of wrapping machines, showing how the monitoring process can be successfully improved. Further research will be addressed to explore the use of artificial intelligence (AI) techniques to develop reliable defect prediction models that can be used as an alternative to the one proposed in this study.