Abstract
Remanufacturing automation must be designed to be flexible and robust enough to overcome the uncertainties, conditions of the products, and complexities in the planning and operation of the processes. Machine learning methods, in particular reinforcement learning, are presented as techniques to learn, improve, and generalise the automation of many robotic manipulation tasks (most of them related to grasping, picking, or assembly). However, not much has been exploited in remanufacturing, in particular in disassembly tasks. This work presents the state of the art of contact-rich disassembly using reinforcement learning algorithms and a study about the generalisation of object extraction skills when applied to contact-rich disassembly tasks. The generalisation capabilities of two state-of-the-art reinforcement learning agents (trained in simulation) are tested and evaluated in simulation, and real world while perform a disassembly task. Results show that at least one of the agents can generalise the contact-rich extraction skill. Besides, this work identifies key concepts and gaps for the reinforcement learning algorithms’ research and application on disassembly tasks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As the world’s population exponentially grows, consumption rates and the demand for new products also increase dramatically. Many end-of-life (EOL) products are continuously being disposed of, leading to several environmental problems. Responsible EOL treatment, which may include reusing, recycling, or remanufacturing [24] products or parts, is desirable in dealing with these products [9]. These processes can be beneficial both environmentally [6] and economically [28, 36]. Waste is minimised while valuable components and materials are recovered.
The disassembly of products is one of the EOL treatment processes’ primary steps and involves extracting and segregating the desired components, parts, or materials from the product [27]. The disassembly does not only input towards EOL treatment but also allow the repair and maintenance of products.
Automation has been successfully implemented for decades in traditional manufacturing processes, e.g. assembly, bin picking, and material handling. However, disassembly processes, where manual labour is preferred, introduce significant challenges in the handling of the takeback products. For example, the process of removing the refrigerator door’s gasket requires effective manipulation capabilities to handle the complex forces and frictions resulting from the joining technology (contact-rich manipulation), as shown in Fig. 1(b). Also, these products are often returned from the customers in used condition with many uncertainties in their physical appearance and condition that renders them difficult to handle and eventually successfully disassemble, like the refrigerators shown in Fig. 1(a).
Therefore, numerous (semi-)automated robotic disassembly cells have been introduced utilising more flexible approaches able to adapt to such uncertainties. Vongbunyong et al. [34] investigated a cognitive-based vision system that introduced reasoning, monitoring of execution, and learning abilities so it can disassemble products without prior product information. Bdiwi et al. [2] studied the disassembly process of electric motors based on image processing techniques for screw detection and classification, while Schneider et al. [29] proposed an algorithm to compute complex non-linear disassembly paths for objects that are in contact during the disassembly process.
The majority of these works proposed controllers based on classical control theory, which are widely used to control dynamic systems. However, they need a model of the system to compute the controller [13], which in our case, it is not easy due to the variety of conditions.
Machine learning (ML) techniques have been proposed to address problems where high flexibility and adaptability are required. ML, compared with humans, can identify more features in the signals [25]. Also, ML algorithms play an essential role in sustainable manufacturing in general, helping to optimise energy and material consumption [5].
Reinforcement Learning (RL) has been studied in several domains as an ML area, including control theory. These algorithms can learn and generalise skills [1] through interactions with the environment while detecting the features automatically, in contrast with supervised learning, where extensive human intervention is needed to label thousands or millions of data.
This work presents the state of the art of contact-rich disassembly operations using RL algorithms. Furthermore, to the best of our knowledge, it documents the first attempt to study the generalisation capabilities of two state-of-the-art RL algorithms to learn the object extraction skill when applied to the contact-rich disassembly task.
The rest of this article is organised as follows: Related works and critical analysis of the state of the art of contact-rich disassembly tasks in Section 2. The problem formulation and discussion of the RL approach and the selected algorithms in Section 3. The method and details of the experiments in Sections 4 and 5, respectively. A deeper discussion and comparison of the obtained results in Section 6. And a few concluding remarks in Section 7.
2 Related works
This section presents the state of the art of contact-rich disassembly tasks using RL. In addition, and due to the limited number of publications related to disassembly tasks, some related works using RL for contact-rich assembly are analysed. From the perspective of assembly operations, the aim is to find key concepts that could be used to perform disassembly tasks, understood in some scenarios as the reverse action of the former.
2.1 Assembly
Several works have applied deep RL algorithms in contact-rich assembly manipulation tasks. They are classified based on the taxonomyFootnote 1 described by OpenAI.
Model-based
algorithms learn a model of the environment that is used to predict the results of actions taken, allowing the agent to plan and act accordingly.
Luo et al. [22] used a model-based policy search incorporating a world dynamics model to learn the peg-in-hole task where the hole is made of deformable material. In another article, Luo et al. [23] combined a model-based algorithm with an operational space force controller for a high-precision peg-in-hole task. Both systems work when the peg is close to the hole, but they were not evaluated from arbitrary starting positions in free space to generalise the learned skill.
Thomas et al. [33] proposed a method that combines motion planning to generate collision-free trajectories to learn assembly skills. However, their approach relies on the geometric information from the object’s Computer-Aided Design (CAD) model to assemble, which is not generalisable. Ding et al. [7] propose a transferable force-torque dynamics model for the peg-in-hole task. They implement a multi-pose force-torque state representation to handle ambiguous feedback from sensors and an offline data generation method to reduce the number of real-world interactions. However, their approach relies on finetuning to be sample-efficient. Fan et al. [8] developed a framework that combines a model-based algorithm for computing optimal trajectories with positional and force/torque feedback and a model-free algorithm to learn manipulation skills for precision assembly tasks.
Value-based
algorithms compute the state-value function of each state (known as V ) or state-action pair (known as Q). Since V or Q represents the expected return of the state or state-action pair, the policy can take advantage of those values to select the action that increases the expected return. Both values can be learned by interacting with the environment.
Li et al. [18] used deep Q-Learning to adjust the robotic end-effector’s pose and orientation for the circuit breaker assembly. They developed a reward system based on the support vector machine (SVM) classification model to learn the manipulation skill. Despite this work shown generalisation across various random initial positions, the average success rate is not good enough, and learning a reward classifier is not feasible most times.
Oikawa et al. [26] used DQN to output the stiffness matrices as actions for admittance control. This approach maintains high control performance by outputting the position and force commands in short cycles for peg-in-hole and gear-insertion tasks. However, the admittance model requires higher sampling times to perform contact-rich tasks without unstable motion.
Policy optimisation
algorithms are model-free algorithms that improve the policy parameters directly without considering the Q value.
Levine et al. [31] employ a hybrid approach that combines the flexibility of mode-free algorithms with the efficiency of model-based algorithms to optimise a linear-gaussian controller to learn a range of motion skills. To generalise the learning, they located the targets in various initial positions.
Lee et al. [16] used TRPO to perform the peg-in-hole task. To enable efficient real robot training, they trained a model to encode heterogeneous sensory inputs, such as RGB images, force/torque data, and robot proprioceptive data, into a compact multimodal representation.
Actor-critic
algorithms integrate policy gradient (actor) algorithms and Q-Learning (critic), as it is the case of the DDPG or TD3 algorithm used in this paper (see Fig. 2).
Some authors combine RL algorithms with conventional feedback control (residual RL) to reduce the exploratory behaviour due to safety concerns and solve contact-rich manipulation tasks. Johannink et al. [12] use TD3 combined with a human-designed controller to insert a block in a hole. Although the proposed algorithm can learn a feedback controller that adapts to variations in the orientations, it requires a carefully crafted vision setup to infer the target blocks’ positions and angles in real-world scenarios. Schoettler et al. [30] used a P-controller to inject prior information into the RL algorithm to speed up the training process and minimise unsafe exploration behaviour. They learned a policy only from images (using those as state representation and goal specification) with Soft Actor-Critic (SAC) and TD3. Beltran et al. [3] used a PD controller to speed up the control policy’s learning for the peg-in-hole task given an uncertain goal position. Despite the improved generalisation capabilities, the framework is susceptible to the force control parameters, which may cause undesired behaviour during manipulation. Beltran et al. [4] combined SAC with a traditional force control algorithm to perform the peg insertion task. However, their implementation is highly dependent on the controller’s hyperparameters.
Li et al. [17] used DDPG, as distinct from previous work [18] where they used Q-Learning, to perform circuit breaker assembly. In this case, they limit the maximum commanded velocity, the joint position limits, the range of the end-effector, and the range of each joint’s torque parameters to guarantee safety constraints.
Luo and Li [20] developed a technique that allows a recurrent distributed DDPG algorithm to perform peg-in-hole and lap joint tasks by augmenting human demonstrations with successful episodes generated by the agents from replay buffers. Also, Luo and Li [21] introduced recurrency in a distributed DDPG to study partially observable assembly tasks, using as observation only the force/torque measurements from the sensor mounted on the robot end-effector.
Wu et al. [35] trained an encoder-decoder network to learn dense rewards from images and force/torque feedback. The SAC algorithm uses the learned dense reward function to perform peg-in-hole and object insertion tasks. The proposed algorithm reached better results on the evaluated tasks against other reward functions (sparse reward, handcrafted continuous reward), but it needs to be trained on the specific task.
2.2 Disassembly
Few works exploit RL to perform contact-rich disassembly tasks. Kristensen et al. [15] used a Q-learning algorithm to train and test agents into their own deployed framework for robotic unscrewing tasks.
Simonivc et al. [32] used the information obtained during disassembly tasks to perform assembly tasks. In this case, they implemented a hierarchical RL algorithm and a graph representation under the criteria that an assembly task is just a reverse execution of the corresponding multiple-stage disassembly task. The disassembly is complete when the motion is unconstrained in the desired degrees of freedom, and the built graph is used to perform the corresponding assembly task.
Strategies to allow the separation of a fixed component into a slot are presented by Herold et al. [11]. The authors identify that adjusting the robot’s position end-effector proportionally to the measured forces and including oscillating motion could be a good solution for the task. However, they execute the task performing predefined actions (the robot does not learn anything from the process), making it difficult to generalise to other scenarios.
2.3 Critic analysis
Unlike the assembly process, the information about the state of the product (physical and mechanical properties, for example) is often inaccurate or incomplete at the beginning of the process but is revealed during it. Then, even when the disassembly is not necessarily the reverse of assembly, it is possible to use the assembly’s advances in our favour to identify trends and relevant concepts. Table 1 shows how RL algorithms have been successfully applied to learn robotic manipulation skills, mostly related to the assembly of products.
The state of the art shows that actor-critic (that combines the best from policy optimisation algorithms and value-based algorithms) is the most widely used algorithm, followed by model-based algorithms, to learn manipulation skills. The most frequently learned skill is object insertion (widely applied to tasks similar to peg-in-hole tasks). Those publications consider that the robot’s end-effector already grasps the object to be manipulated.
Force/torque, vision, and pose are the primary information used to observe the system’s state and act according to it. Vision seems to be not extensively used. However, some of those publications suggest including the vision as a promising direction in future works.
Concerning disassembly, few works apply RL to perform tasks, particularly those that require contact-rich manipulation skills (and, as far as our knowledge, no one has exploited the extraction skill). This gap opens the door to a vast field in the research and application of RL algorithms for flexible remanufacturing processes in general and disassembly in particular.
3 Problem formulation
The nature of the disassembly process requires flexible and robust enough autonomous systems to overcome some issues such as the large variety and physical uncertainties associated with the EOL product condition and operation complexities. Driven by those issues, this work explores and evaluates two state-of-the-art RL algorithms’ generalisation capabilities to learn the extraction skill to perform a contact-rich disassembly task.
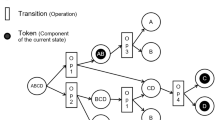
In this case, the problem was formulated as a Markov Decision Process (MDP), as shown in Fig. 2, modelled with a finite-horizon discounted return.
At every timestep of interaction with the environment, the agent sees an observation o of the complete description of the state s ∈ S of the environment. Then, it decides which action a ∈ A to take from the action space using, in our case, a parameterised policy π𝜃. The environment, which can change by itself or by the agent’s action, gives a reward signal rt = R(st,at,st+ 1) to the last one to measure how good or bad is the new state. The agent aims to maximise the cumulative reward discounted by a factor γ ∈ (0,1] by adjusting the policy’s behaviour via some optimisation algorithm.
3.1 Reinforcement learning algorithms
As indicated in Section 2.1, model-based RL algorithms need a model of the system. Since the disassembly process can be dealing with a large variety of products, this is not possible. Then, only model-free algorithms will be considered. Actor-critic algorithms were selected because they combine the best from both policy optimisation algorithms and value-based algorithms. They use the learned value function as a baseline to update the actor’s policy. These algorithms hold the promise of delivering faster convergence [14] while allowing us to learn from experience (off-policy). To learn the extraction skill for disassembly tasks, two model-free off-policy actor-critic RL algorithms for the continuous domain were selected: DDPG and TD3.
Deep Deterministic Policy Gradients (DDPG) is a model-free and deterministic off-policy actor-critic algorithm. It uses deep function approximators to learn the policy (and to estimate the action-value function) in high-dimensional, continuous action spaces [19].
Twin Delayed Deep Deterministic policy gradient algorithm (TD3) is an actor-critic algorithm based on DDPG. This algorithm relies on double Q-learning, target policy smoothing, and delayed policy updates to address the problems introduced by overestimation bias, leading to estimates and suboptimal policies in actor-critic algorithms [10].
4 Method
This initial research, about the extraction skill to perform contact-rich disassembly, uses a single-arm robotic manipulator and a target object to be disassembled on a table, as shown in Fig. 3. These elements form the prototype’s simplified version, as shown in Fig. 1(c).
Extraction task’s sequence using the best-learned policies for DDPG in real world and simulation (first and second rows respectively) and TD3 in real world and simulation (third and fourth rows respectively). Frames are taken every 3 timesteps for DDPG (object rotated at 70∘) and every timestep for TD3 (object rotated at 130∘)
The agents will learn how to move the robotic manipulator’s end-effector on the Cartesian plane parallel to the table to perform the contact-rich extraction of two rigid objects (object extraction skill). The configuration of the objects and the task to be performed represents, in simplified form, the disassembly process of the refrigerator door’s gaskets as shown in the referenced figure. The action taken, the received observation, and perceived reward shown in Fig. 2, together with other concepts related to the RL problem, are discussed below.
4.1 Setup to learn object extraction skill
Observations
To evaluate the agents’s generalisation capabilities, an observation based on the object or manipulator pose was designed. The observation space is composed by the normalised length of the episode, represented as the ratio between the current timestep and the maximum allowed timestep (max_steps); the relative position in the XY-plane of the TCP with respect to the initial grasping pose (posXY), and the rotation of the object (between 0 and 180∘ scaled to the [− 1,1] interval).
Actions
The action space is a 2-dimensional vector. Each component maps to the respective translation (in centimetres) of the robot’s end-effector in the [− 1,1] continuous interval on the XY-plane.
Reward
A deterministic sparse-reward function provides the reward at the end of the episodes. The environment gives the agent a positive reward equal to the maximum timestep (max_steps) for successful extractions. If the extraction fails because a critic force is detected or the maximum timestep is reached, the agent perceives a reward from the continuous function described by Eq. 1. This function heavily penalises short-displacement extractions. The instantaneous reward is empty (zero) during the execution of the task.
A sparse-reward function is used to identify how the agents learn and generalise the extraction skill. However, instead of guide the agents to the goal, the sparse reward makes the problem more challenging to solve.
Episode termination
The episodes end when the agent performs the corresponding disassembly task: extract the fixed object from the slotted one. Also, the episodes end when a critic force is detected or when the maximum timestep (max_steps) is reached regardless of whether the task was successfully executed or not.
Agents architectures
Both the policy and the Qϕ1 network for DDPG (also, the Qϕ2 network for TD3) have the same architecture. They receive as input the observation space’s components, concatenated as a flatten vector of 4 components (in the case of Q networks, the policy network’s action is included in the observation space, becoming six components), followed by two hidden dense layers of 32 neurons each one. The hidden layers use ReLU as the activation function. The policy has two output neurons that use the hyperbolic tangent function (tanh) to fit the action to the expected interval, and the Q networks use a linear activation function for their output neuron.
5 Experiments
The proposed RL experiments were trained and tested in simulation and validated in the real world. All components were connected and operated through a custom framework, developed in our lab, using Gym and Robot Operating System (ROS) Melodic. The simulated environment was developed on the novel Omniverse Isaac SimFootnote 2 (version 2020.2.2) robotics specific simulation platform from NVIDIA. In simulation and reality, the experiments were conducted using the highly sensitive, compliant and lightweight KUKA LBR Iiwa 14 R820 collaborative robot with a payload capacity of 14Kg.
The target to be disassembled contains two solid objects, as shown in Fig. 3: a slotted fixed base attached to the table and an embedded object (that fits inside the base) gripped by the robot’s end-effector. The dimensions are 0.1 × 0.1 × 0.03 m for the fixed base, 0.1 × 0.02 × 0.01 m for the slot, and 0.1 × 0.02 × 0.04 m for the embedded object with 1.5 ⋅ 10− 4 m clearance between the slot and the embedded object. The slot is centred by 0.01 m deep with respect to the base’s upper face.
In the real world, the Cartesian position of the end-effector (used to build the observation space and compute the reward) and the orientation of the embedded object (used to build the observation space) are obtained by reading the pose provided by the robot controller. The measurement of the external force acting on the end-effector while grasping the object to be extracted (used to calculate the reward) is obtained from the estimation of the Cartesian forces based on the measured values of the torque sensors at the joints. In the simulation, these values are published, in ROS, from the information retrieved through the API of the simulator’s physics engine.
The RL was implemented using the open-source library RLlib v1.0.0. The architectures for both agents were implemented using the Keras API from TensorFlow.
The neural network parameters were learned using the Adam optimiser with a learning rate of 10− 3 for both actor and critic. The training was done using an experience buffer replay of size 105 and batches of size 256. The discount factor was 0.99. The agents used the same exploration noise functions described in their original papers. Ornstein-Uhlenbeck noise with 𝜃 = 0.15, σ = 0.2 and a base scale of 0.1 for DDPG. Mean-zero Gaussian noise with a standard deviation of 0.1 for TD3. Both explorations were reduced linearly, from an initial scale of 1.0 to a final scale of 0.001, throughout training during 150 thousand timesteps. Also, for TD3 a mean-zero Gaussian noise with σ = 0.1 was used for target policy smoothing clipped to (− 0.5,0.5).
Ten training sessions were done for each algorithm to try to identify repetitive behaviours. They were performed using a computer with an Intel(R) Xeon(R) Silver 4114 CPU @ 2.20GHz, 125GiB of RAM, and a GPU GeForce RTX 2080 Ti. Each session was stopped at 375 thousand timesteps.
The best policies were selected for testing in simulation and real world, attending to the mean reward obtained during training. Figure 3 shows a typical extraction sequence, in simulation and real world, for DDPG and TD3.
6 Results and discussion
6.1 Training in simulation
Figure 4 shows the mean and standard deviation of the perceived reward (top plot) for both agents in the ten training sessions. Also, it shows the mean and standard deviation of the estimated Q-value returned by the Q-network (bottom plot) for both agents. In the case of the TD3 agent, the Q-value corresponds to the Qϕ1-network used to optimise the policy. This plot reveals that DDPG can better learn the extraction skill than TD3 for the setup described in previous sections.
DDPG achieved a great performance at the end of its exploration stage; then, it improved the performance during the exploitation stage very slowly. Even when its Q-function overestimated the Q-value during the exploitation stage, this value remained practically constant around the maximum expectation. On the other side, TD3 began to learn the skill, but at a certain point (at the end of its exploration stage), its learning performance decayed without recovering. This behaviour results from the poor Q-function estimation used as a baseline to update its actor’s policy, as shown in Fig. 4 (bottom plot).
Unexpectedly, there is a clear difference between how both policies act. The action space domain allows the manipulator to execute a maximum displacement of 0.1 m in any direction. The minimum amount of interaction with the environment (minimum episode length) required to perform a successful extraction is about ten timesteps, considering the initial object’s position and its physical dimension. Since the manipulator is configured to move with a maximum velocity of 0.01 m per second, the minimum extraction time is ten seconds.
TD3 learned the quickest way to perform the disassembly task as long as it can complete an episode successfully. The mean episode length supports this behaviour, as shown in Fig. 5. DDPG exhibits a trend to execute more timesteps than TD3 (in its better training’s performance interval around 100 thousand timesteps).
This behaviour is reflected in the mapping of the actions taken by both policies shown in Fig. 6. The graphical point cloud of the DDPG’s actions (left chart) is clustered around a median circumference. Because DDPG performs shorter displacements, its extraction speed (understood as the effective length of the episodes) is slower. On the other side, the TD3’s actions (right chart) are majorly mapped around the limits of the action space (extreme actions). This implies a maximum extraction speed but, at the same time, less robustness.
6.2 Testing in simulation
The learned skill’s generalisation capabilities were assessed with two tests: 1) different initial object’s rotations about its centre and 2) different initial object’s locations on the table. The agents ran 30 episodes for each particular case. Those tests were done with the exploration behaviour disabled.
In the first experiments, the target object’s rotation is sampled discretely between 0 and 180∘, spaced by 1∘. Figure 7 shows the mean and the standard deviation of the reward perceived by the best-trained policies and their mean episode length.
The DDPG policy can execute the task successfully (more than 15 successful episodes per angle) in 87.29% of the sampled rotations. The proportion of completed-task for DDPG could reach a higher value if the episode runs more timesteps than the maximum allowed for the rotation interval between 35 and 55∘. TD3 executed the task successfully (more than 15 successful episodes per angle) 35.35% of the sampled rotations. Consistent with the training process, DDPG has a much better performance than TD3 in executing the disassembly task, but TD3 is faster than DDPG.
In the second experiment, the initial position of the target object on the table was sampled to cover a rectangular region of 0.1 × 0.25 m with a step of 2.5 mm while keeping a fixed rotation. The region of interest is centred, in front of the robot, at 0.6 m. Two fixed rotations (50 and 130∘) were selected from the regions where the policies’ performance is quite diverse according to Fig. 7. The mean reward perceived by both agents at the end of the task is shown in Fig. 8.
The results show that the learned skill is generalisable for an extensive range of different initial positions. The minor variations are produced by the dynamic and precision of the manipulator’s motion during the simulation.
6.3 Transference to the real world
Also, the learned skill’s generalisation capabilities were evaluated in the real world. Different initial object’s rotations were introduced. In this case, the target object’s rotation was sampled discretely between 0 and 180∘, spaced by 10∘ to reduce the number of performed episodes. The agents ran five episodes for each particular case. Figure 9 shows the mean reward perceived by the best-trained policies and their mean episode length.
With a very similar behaviour to the simulation, the DDPG policy can execute the task successfully for at least all the sampled angles. TD3 maintains a poor performance, as seen in the simulation. In this case, the higher success rate on the task’s execution in the real world with respect to the simulation is because of the critic force threshold’s minor differences used in both environments. The training and tests carried out in the simulated environment were performed using a lower critic force threshold than the value used in reality (60 Newtons). Figure 10 shows the force measured during the execution of the episodes in the real world.
The simulated environment used a lower critical force value to ensure a safer execution of the task in the real world.
7 Conclusion and future work
Even when reinforcement learning algorithms have been successfully applied to learn robotics skills to perform many manipulation tasks, such as assembly, there are no sufficiently studied when applied on disassembly tasks.
Reinforcement learning algorithms can learn the object extraction skill interacting with the environment in an off-policy way. Also, they can generalise the learning through multiple initial conditions such as translations and rotations.
From their utilisation on assembly tasks, force/toque and vision sensors are exposed as a relevant information source to identify the environment’s state and act according to it. Their use would allow more complex tasks to be performed efficiently. Our future research will include more sensors as part of the observation space, particularly the force/toque, and perform disassembly of more complex geometric structures.
References
Andrychowicz M, Wolski F, Ray A, Schneider J, Fong R, Welinder P, McGrew B, Tobin J, Abbeel P, Zaremba W (2017) Hindsight experience replay. arXiv:1707.01495
Bdiwi M, Rashid A, Putz M (2016) Autonomous disassembly of electric vehicle motors based on robot cognition. In: 2016 IEEE international conference on robotics and automation (ICRA). https://doi.org/10.1109/ICRA.2016.7487404. IEEE, pp 2500–2505
Beltran-Hernandez CC, Petit D, Ramirez-Alpizar IG, Harada K (2020) Variable compliance control for robotic peg-in-hole assembly: A deep-reinforcement-learning approach. Appl Sci 10(19):6923. https://doi.org/10.3390/app10196923
Beltran-Hernandez CC, Petit D, Ramirez-Alpizar IG, Nishi T, Kikuchi S, Matsubara T, Harada K (2020) Learning force control for contact-rich manipulation tasks with rigid position-controlled robots. IEEE Robot Autom Lett 5(4):5709–5716. https://doi.org/10.1109/LRA.2020.3010739
Cioffi R, Travaglioni M, Piscitelli G, Petrillo A, De Felice F (2020) Artificial intelligence and machine learning applications in smart production: Progress, trends, and directions. Sustainability 12(2):492. https://doi.org/10.3390/su12020492
D’Adamo I, Rosa P (2016) Remanufacturing in industry: advices from the field. Int J Adv Manuf Technol 86(9):2575–2584. https://doi.org/10.1007/s00170-016-8346-5
Ding J, Wang C, Lu C (2019) Transferable force-torque dynamics model for peg-in-hole task. arXiv:1912.00260
Fan Y, Luo J, Tomizuka M (2019) A learning framework for high precision industrial assembly. In: 2019 international conference on robotics and automation (ICRA). https://doi.org/10.1109/ICRA.2019.8793659. IEEE, pp 811–817
Fellner J, Lederer J, Scharff C, Laner D et al (2017) Present potentials and limitations of a circular economy with respect to primary raw material demand. J Ind Ecol 21(3):494–496
Fujimoto S, Hoof H, Meger D (2018) Addressing function approximation error in actor-critic methods. In: International conference on machine learning. PMLR, pp 1587–1596
Herold R, Wang Y, Pham D, Huang J, Ji C, Su S (2020) Using active adjustment and compliance in robotic disassembly. In: Industry 4.0–shaping the future of the digital world: proceedings of the 2nd international conference on sustainable smart manufacturing (S2M 2019), 9–11 April 2019. https://doi.org/10.1201/9780367823085. CRC Press, Manchester, p 101
Johannink T, Bahl S, Nair A, Luo J, Kumar A, Loskyll M, Ojea JA, Solowjow E, Levine S (2019) Residual reinforcement learning for robot control. In: 2019 international conference on robotics and automation (ICRA). https://doi.org/10.1109/ICRA.2019.8794127. IEEE, pp 6023–6029
Kober J, Bagnell JA, Peters J (2013) Reinforcement learning in robotics: A survey. Int J Robot Res 32(11):1238–1274. https://doi.org/10.1177/0278364913495721
Konda VR, Tsitsiklis JN (1999) Actor-citic agorithms. In: Proceedings of the 12th international conference on neural information processing systems. MIT Press, pp 1008–1014
Kristensen CB, Sørensen FA, Nielsen HB, Andersen MS, Bendtsen SP, Bøgh S (2019) Towards a robot simulation framework for e-waste disassembly using reinforcement learning. Procedia Manuf 38:225–232. https://doi.org/10.1016/j.promfg.2020.01.030
Lee MA, Zhu Y, Srinivasan K, Shah P, Savarese S, Fei-Fei L, Garg A, Bohg J (2019) Making sense of vision and touch: Self-supervised learning of multimodal representations for contact-rich tasks. In: 2019 international conference on robotics and automation (ICRA). https://doi.org/10.1109/ICRA.2019.8793485. IEEE, pp 8943–8950
Li F, Jiang Q, Quan W, Song R, Li Y (2019) Manipulation skill acquisition for robotic assembly using deep reinforcement learning. In: 2019 IEEE/ASME international conference on advanced intelligent mechatronics (AIM). https://doi.org/10.1109/AIM.2019.8868579. IEEE, pp 13–18
Li F, Jiang Q, Zhang S, Wei M, Song R (2019) Robot skill acquisition in assembly process using deep reinforcement learning. Neurocomputing 345:92–102. https://doi.org/10.1016/j.neucom.2019.01.087
Lillicrap TP, Hunt JJ, Pritzel A, Heess N, Erez T, Tassa Y, Silver D, Wierstra D (2015) Continuous control with deep reinforcement learning. arXiv:1509.02971
Luo J, Li H (2020) Dynamic experience replay. In: Conference on robot learning. PMLR, pp 1191–1200
Luo J, Li H (2020) Recurrent distributed reinforcement learning for partially observable robotic assembly. arXiv:2010.08052
Luo J, Solowjow E, Wen C, Ojea JA, Agogino AM (2018) Deep reinforcement learning for robotic assembly of mixed deformable and rigid objects. In: 2018 IEEE/RSJ international conference on intelligent robots and systems (IROS). https://doi.org/10.1109/IROS.2018.8594353. IEEE, pp 2062–2069
Luo J, Solowjow E, Wen C, Ojea JA, Agogino AM, Tamar A, Abbeel P (2019) Reinforcement learning on variable impedance controller for high-precision robotic assembly. In: 2019 International conference on robotics and automation (ICRA). https://doi.org/10.1109/ICRA.2019.8793506. IEEE, pp 3080–3087
Matsumoto M, Ijomah W (2013) Remanufacturing. In: Handbook of sustainable engineering. https://doi.org/10.1007/978-1-4020-8939-8_93. Springer Netherlands, pp 389–408
Ni D, Xiao Z, Lim MK (2021) Machine learning in recycling business: an investigation of its practicality, benefits and future trends. Soft Comput 25(12):7907–7927. https://doi.org/10.1007/s00500-021-05579-7
Oikawa M, Kutsuzawa K, Sakaino S, Tsuji T (2020) Assembly robots with optimized control stiffness through reinforcement learning. arXiv:2002.12207
Parsa S, Saadat M (2019) Intelligent selective disassembly planning based on disassemblability characteristics of product components. Int J Adv Manuf Technol 104(5):1769–1783. https://doi.org/10.1007/s00170-019-03857-1
Ramírez FJ, Aledo JA, Gamez JA, Pham DT (2020) Economic modelling of robotic disassembly in end-of-life product recovery for remanufacturing. Comput Ind Eng 142:106339. https://doi.org/10.1016/j.cie.2020.106339
Schneider D, Schömer E, Wolpert N (2015) A motion planning algorithm for the invalid initial state disassembly problem. In: 2015 20th international conference on methods and models in automation and robotics (MMAR). https://doi.org/10.1109/MMAR.2015.7283702. IEEE, pp 35–40
Schoettler G, Nair A, Luo J, Bahl S, Aparicio Ojea J, Solowjow E, Levine S (2020) Deep reinforcement learning for industrial insertion tasks with visual inputs and natural rewards. In: 2020 IEEE/RSJ international conference on intelligent robots and systems (IROS). https://doi.org/10.1109/IROS45743.2020.9341714, pp 5548–5555
Sergey L, Wagener N, Abbeel P (2015) Learning contact-rich manipulation skills with guided policy search. In: 2015 IEEE international conference on robotics and automation (ICRA). https://doi.org/10.1109/ICRA.2015.7138994, pp 156–163
Simonič M, žlajpah L, Ude A, Nemec B (2019) Autonomous learning of assembly tasks from the corresponding disassembly tasks. In: 2019 IEEE-RAS 19th international conference on humanoid robots (Humanoids). https://doi.org/10.1109/Humanoids43949.2019.9035052. IEEE, pp 230–236
Thomas G, Chien M, Tamar A, Ojea JA, Abbeel P (2018) Learning robotic assembly from cad. In: 2018 IEEE international conference on robotics and automation (ICRA). https://doi.org/10.1109/ICRA.2018.8460696. IEEE, pp 3524–3531
Vongbunyong S, Kara S, Pagnucco M (2013) Basic behaviour control of the vision-based cognitive robotic disassembly automation. Assem Autom 33(1):38–56. https://doi.org/10.1108/01445151311294694
Wu Z, Lian W, Unhelkar V, Tomizuka M, Schaal S (2020) Learning dense rewards for contact-rich manipulation tasks. arXiv:2011.08458
Xia X, Zhu H, Zhang Z, Liu X, Wang L, Cao J (2020) 3d-based multi-objective cooperative disassembly sequence planning method for remanufacturing. Int J Adv Manuf Technol 106(9):4611–4622. https://doi.org/10.1007/s00170-020-04954-2
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature. This study was partially financed by European Union’s SMART EUREKA programme under grant agreement S0218-chARmER. Also, it is partially financed by H2020-WIDESPREAD project no. 857061 “Networking for Research and Development of Human Interactive and Sensitive Robotics Taking Advantage of Additive Manufacturing – R2P2”.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics approval
The authors understand and approve the ethical responsibilities of the authors.
Consent for publication
The authors consent to transfer the copyright of the article to publish.
Conflict of interest
The authors declare no competing interests.
Additional information
Author contribution
All the related authors contribute to the conceptualisation, data curation, investigation, methodology, writing—original draft, writing—review, and editing of the manuscript.
Availability of data and materials
Data used in this work have been properly cited within the article.
Consent to participate
The authors consent to participate.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Serrano-Muñoz, A., Arana-Arexolaleiba, N., Chrysostomou, D. et al. Learning and generalising object extraction skill for contact-rich disassembly tasks: an introductory study. Int J Adv Manuf Technol 124, 3171–3183 (2023). https://doi.org/10.1007/s00170-021-08086-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-08086-z