1 Introduction

Variation propagation modeling in multistage machining processes (MMP) considering punctual locators has been studied for more than two decades. The importance lies in the ability of the models to help in reducing variation by enabling a better understanding of the multistage machining processes, thereby making informed decisions in process planning, fault diagnosis, variation compensation, process-oriented tolerancing, and cost-quality optimization [1]. In this direction, the concept of stream of variation [2, 3] and the model of the manufactured part [4] have been proposed as means to mathematically model the relationship between the source of variation and the machined part.

The stream of variation approach was first introduced by Jin and Shi [2] two decades ago for part quality prediction in multistage assembly of processes, which was later refined in series of publications by Ding et al. [5]. The approach was extended to multistage machining process by Huang et al. [6] and its explicit equations derived by Djurdjanovic [7]. Zhou [3] improved the derivation by introducing differential motion vector to represent deviations of features of a workpiece while considering a 3-2-1 fixture layout. Loose et al. [8] extended the approach to include general fixture layout based on locators. Abellán-Nebot et al. [9] further extended the approach to include machining errors [9], fixtures with locating surfaces [10], and fixtures with bench vises [11].

Further, Huang et al. [12] proposed transformation of datum and machine tool errors to equivalent fixture errors using the techniques used in SoV. Recently, Wang et al. [13] applied Jacobian-Torsor model for part quality prediction considering generic fixture and generic shape workpieces with dimensional errors.

In the same direction, the model of the manufactured part based on small displacement torsor [4, 14,15,16,17] has been proposed for part quality prediction. The model treats the part-fixture interaction as a mechanism and often focuses on tolerance analysis. Both approaches consider three major sources of variation: machining-induced variation that is caused by cutting tool deviation from its nominal toolpath, datum-induced variation due to deviations induced in upstream, and fixture-induced variation caused by deviation of the locators.

However, these models do not consider form errors, as a single coordinate system is used to represent a feature of a part. Even though form errors are not critical to the quality of the part, there is a need to include them in the variation propagation modeling of MMP [1, 10, 18, 19]. Moreover, there is a need to include an N-2-1 fixture layout in models of part quality prediction [10, 18, 19]. To address this need, Loose et al. [8] extended SoV to include generic cases, for general fixture layouts (punctual) in using kinematic analysis. However, the matrices and the expression of these models tend to become tedious, especially when N-2-1 (N>3) fixture layout, locating surfaces, or generic cases are considered [8, 10, 13, 19,20,21]. These expressions require three Euler angles to obtain the 16 parameters of homogenous transformation matrices (HTM). In SDT-related approaches, the Jacobian matrix requires multiple matrices of 6 by 6.

These modeling tasks can be approached from two different directions. First, form errors along with position and orientation error can be captured by a Skin Model Shape (SMS) [22, 23]. The representation of parts by SMSs enables embedding comprehensive variation information within the model [23, 24], avoiding the need to express the part quality in an explicit mathematical model. The same SMS can be used for analyzing the machining processes and performing inspection processes. In addition, the techniques used in computational geometry, such as projection of points onto surfaces, further simplify the modeling approach. Second, dual quaternions can be used to mitigate the large matrices of the existing variation propagation models. Dual quaternions require only 8 parameters for the representation of an object. Further, only a set of an angle and an axis is required to generate a rotation operator in dual quaternions, as opposed to the 3 pairs of Euler angles and axes in HTM. These characteristics of dual quaternions provide relatively smaller matrix size and fewer steps for generating a transformation operator.

In this paper, a part is represented by multiple SMSs to enable separate operations on features. The convex hull of a difference surface between the primary feature and points of N-locators is then used to obtain encapsulating facets. The 3 points of a facet, through which the center of gravity passes, are selected and used to determine the magnitude of transformation required to assemble part to the primary locators. Following this step, the secondary and tertiary locators’ distances to their respective projected points are reduced, while maintaining contact with selected primary locators’ plane. Finally, the machining feature is replaced by a SMS that would be generated by a specific toolpath of a cutting tool. Using the approach, the variation propagation in MMP considering both generic fixture layout and form errors can be modeled.

This paper is organized as follows. In Section 2, the background on SMS, the algorithm for the projection of points, and dual quaternions are presented. In Section 3, the steps for representation of parts with form errors are discussed. In Section 4, the steps of setting up a part on an N-2-1 fixture layout are presented. In Sections 5, 6, and 7, the methods for performing virtual machining, conducing measurements, and multistage machining processes are explained. Finally, a case study, discussion, and conclusion are presented in Sections 8, 9, and 10.

2 Background

2.1 Skin Model Shapes

A Skin Model Shape is a discrete instance of the concept of Skin Model [23]. The concept of Skin Model is a non-ideal-continuous representation of a surface, which is regarded as an infinite model of the physical interface between a part and its environment [23, 25, 26]. Skin Model Shape was developed as a comprehensive geometric model for use in design, manufacturing, and inspection processes [23]. Since its inception, methods for generation of SMS [27], assembling of two SMSs [28], and assembling of multiple SMSs [29] have been added. Further, SMSs have been applied in a wide range of applications, including additive manufacturing [30], machining processes [31,32,33], tolerancing [34,35,36], digital twin [37], and over-constrained assemblies [38, 39].

Four main operations play a key role in the manipulation of Skin Model Shapes as defined in ISO 17450-1: (1) partitioning (division of extracted skin model corresponding to respective features), (2) extraction (representation of an object by point cloud), (3) filtration (separation of form defects from waviness and roughness), and (4) association (a mathematical operation to fit ideal features) [40]. Specifically, the partitioning and extraction operations help in representing and manipulating of parts and fixtures proposed in this paper.

2.2 Projection of points

The proposed approach uses projection of points onto surfaces to estimate the distance between a point and a target surface. Since surfaces with form errors can be captured by the points of SMSs, the triangulated points can be used to compute equations of planes. Using these equations, the position of the projected points on a surface can be obtained. Then, the point is checked if it falls within the vertices of a facet. Such steps are computationally inefficient. Instead, the algorithms, such as ray-triangle intersection [41], use an efficient way of finding the intersection points without the need to compute the equations of planes. The algorithm requires the origin of projection o, direction of projection \( \overline{U} \), and the three vertices of the facets on a target surface \( {\dot{\boldsymbol{p}}}^{1\dots B} \) as inputs. Thus, the projected point intersecting the surface \( \dot{I}\in {\mathbb{R}}^3 \) can be denoted as

$$ \dot{I}=\mathrm{I}\left(\dot{o},\overline{\mathrm{U}},{\dot{\boldsymbol{p}}}^{1\dots B}\right) $$
(1)

where \( \dot{I}\in {\mathbb{R}}^3 \) projected point intersecting the surface and B is the number of facets in the target surface.

2.3 Dual quaternions

Dual quaternions are 8-dimensional number system based on dual algebra and quaternions. Quaternions are 4-dimensional parameters that can be used to rotate objects in space [42]. A quaternion is obtained from an angle of rotation between two vectors and an axis of rotation. The quaternion \( \overset{\sim }{q} \) is expressed by its scalar part q0 and vector part \( \overline{q} \)

$$ \overset{\sim }{q}={q}_0+{q}_1i+{q}_2j+{q}_3k=\left({q}_0,\overline{q}\right) $$
(2)

where \( {q}_0=\cos \frac{\theta }{2} \) , \( \overline{q}=\overline{n}\sin \frac{\theta }{2} \) , i2 = j2 = k2 = ijk =  − 1, and \( \theta ={\cos}^{-1}\left(\frac{{\overline{n}}_1\cdotp {\overline{n}}_2}{\parallel {\overline{n}}_1\parallel \cdotp \parallel {\overline{n}}_2\parallel}\right)\in \left(0,\pi \right) \).

Dual quaternions can be used for both rotational and translational motion [43]. A dual quaternion \( \hat{q} \) is expressed as

$$ \hat{q}={\overset{\sim }{q}}_{\mathrm{r}}+\epsilon {\overset{\sim }{q}}_{\mathrm{d}} $$
(3)

where ϵ is a dual-operator such that ϵ ≠ 0 and ϵ2 = 0; \( {\overset{\sim }{q}}_{\mathrm{r}} \) is the real component and \( {\overset{\sim }{q}}_{\mathrm{d}} \) is dual component of the dual quaternion.

The rotation operator \( \hat{R} \), given two vectors \( {\overline{n}}_1 \) and \( {\overline{n}}_2 \) (as in Eq. (2)), is computed as

$$ \hat{R}\left({\overline{n}}_1,{\overline{n}}_2\right)=\left(\cos \frac{\theta }{2},\overline{n}\sin \frac{\theta }{2}\right)+\epsilon \left({0}_{1\times 4}\right) $$
(4)

The transitional operator, given distance between any two points \( \overline{t}\in {\mathbb{R}}^3 \), is obtained by

$$ \hat{T}=\left(1,\left(0,0,0\ \right)\right)+\epsilon \left(0,\overline{\frac{t}{2}}\right) $$
(5)

The two transformations can be combined to get the total transformation operator \( \hat{e} \) as

$$ \hat{e}={\overset{\sim }{R}}_{\mathrm{r}}+\epsilon \left(0,\frac{\overline{t}}{2}\right) $$
(6)

Then, for any object in space, \( \hat{A} \) is moved to a new position by

$$ {\hat{A}}^{\prime }=\hat{e}\hat{A}{\hat{e}}^{\ast } $$
(7)

where \( {\hat{e}}^{\ast }={\overset{\sim }{R}}_{\mathrm{r}}-\epsilon \frac{\overline{t}}{2}. \)

The above equations are used to transform an object represented by a set of planes and/or set of points. More detailed derivations of dual quaternions operations can be found in [44,45,46].

3 Representation of parts with form errors

In the context of variation propagation, a part is represented by a set of coordinate systems as in the case of stream of variation- and small displacement torsor-related approaches. The coordinate system representation treats a feature as a set of a single point and orthogonal axes, which cannot be used to capture part’s form errors. Form errors can, however, be captured by discretized models such as SMSs.

The effect of form error on the quality of the part is dependent on the size and position of the defect. Form errors are created from multiple sources in the machining processes, which are often difficult to attribute to. Often form errors are scattered randomly around surface. Due to the random nature of the position and size of form errors, the virtual representation is obtained using techniques such as Gaussian random fields [22]. Since a part with variation contains both systematic and random errors, the points generated by Gaussian random fields are added to the corresponding points that encode systematic errors [22]. Figure 1 shows an example whereby the Z values of the points of the systematic errors are added and the random errors while keeping the X and Y values the same. When there is no one-to-one correspondence of points on both surfaces, Eq. (1) can be utilized.

Fig. 1
figure 1

An example of an arbitrary planar surface. a Planar surface with systematic error (top) and random errors (bottom). b The sum of systematic and random errors

Full size image

Moreover, once the part is represented by SMS(s), multiple transformation operations are performed. For transformation, dual quaternions are selected for their mathematically compactness and simplicity. To transform a part, its point cloud has to be first expressed in terms of dual quaternions. Hence, for point cloud \( \dot{\boldsymbol{S}}=\left\{{\boldsymbol{X}}^{1\dots W},{\boldsymbol{Y}}^{1\dots W},{\boldsymbol{Z}}^{1\dots W}\right\} \), the corresponding dual quaternion is denoted by

$$ {\hat{\boldsymbol{S}}}^{1\dots W}=1+\epsilon \left(0,{\boldsymbol{X}}^{1\dots W}i,{\boldsymbol{Y}}^{1\dots W}j,{\boldsymbol{Z}}^{1\dots W}k\right) $$
(8)
$$ {\hat{\boldsymbol{S}}}^{1\dots W}=1+\epsilon {\dot{\boldsymbol{S}}}^{1\dots W} $$
(8a)

where W is the number of points.

When implementing Eq. 8a, the dual quaternions of the point cloud can be arranged in matrix of 8 by W as

$$ \hat{\boldsymbol{S}}=\left[1,0,0,0,0,{\boldsymbol{X}}^{1\dots W},{\boldsymbol{Y}}^{1\dots W},{\boldsymbol{Z}}^{1\dots W}\right] $$
(8b)

Since the number of points of a feature does not change in the subsequent operations, the 1…W can be dropped. Thus,

$$ \hat{\boldsymbol{S}}=1+\epsilon \dot{\boldsymbol{S}} $$
(8c)

In line with the ISO GPS standard operations, partitioning a part into its component features makes it convenient for performing operations related to the assembly, machining, and inspection of the part. For instance, a rectangular-shaped part is represented by 6 separate SMSs, as shown in Fig. 2. Each SMS of a feature can be indexed and referred accordingly. Hence, a part with M features can be represented as

$$ {\hat{\boldsymbol{S}}}_{1\dots M}=1+\epsilon {\dot{\boldsymbol{S}}}_{1\dots M} $$
(9)
Fig. 2
figure 2

Partitioned sides of a part (\( {\hat{\boldsymbol{S}}}_{1\dots M} \))

Full size image

4 Setting up a part on an N-2-1 fixture layout

An N-2-1 fixture layout, as opposed to a 3-2-1 fixture layout, has more than 3 primary locators. The locators are often treated as points in variation propagation models. Hence, the set of N locator points can be treated as a SMS. Such representation enables the direct use of the techniques developed for the assembly of SMSs.

The assembly operation is the underlying technique of variation propagation modeling and analysis thereon. Since form errors are found in different regions in different SMSs, it is difficult to accurately describe the assembly process of all SMSs in a single mathematical expression. Instead, the assembly of SMSs can be conducted using relative positioning algorithms. The relative positioning algorithms for the assembly of two dissimilar non-ideal surfaces shall respect three rules [28, 47]. These rules are (R1) the distance between two corresponding points of two features should be minimized, (R2) the points of a feature should not cross points of another feature, and (R3) when a part’s form errors are set to zero, the algorithm should converge to an assembly position when only orientation and position errors are considered. These requirements help in evaluating the robustness of the relative positioning algorithms [28].

In this direction, in assembling two features with form errors, two algorithms have been proposed by Schleich et al. [28]: the constrained registration and difference surface algorithms. The difference surface approach is recommended for predominantly planar surfaces. The approach has two main steps: finding the 3 contact points and reducing the distance between corresponding points. This paper reformulates the series of transformation operations performed using homogenous transformation matrix (e.g., [48]) and the strategy for reducing distance foot-points (e.g., [28]) by using dual quaternions. The steps of the proposed assembly approach along with the machining and inspections steps that follow are summarized in Fig. 3.

Fig. 3
figure 3

Summary of the steps of the proposed approach for a station. a Assembly of the primary datum feature to primary locators (green), b assembly of secondary datum feature to secondary locators (blue), c machining of part by non-ideal surface (black), and d inspection of the machined feature using projected points (red)

Full size image

4.1 Assembling to primary locators

To assemble the primary datum feature to primary locators, three main steps are required. First, the difference surface and corresponding perfect surface are obtained; second, stable contact points are computed; and finally, the part is moved by the magnitude of the computed transformation.

4.1.1 Computing difference surface

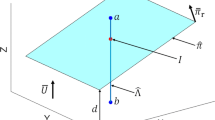
In assembling two non-ideal surfaces, the distance between the points of the two SMSs is computed first. Since the points of one SMS do not necessarily have corresponding points on the other, the points of one SMS are projected onto second SMS. To project points, an algorithm such as ray triangle intersection [41] can be used. Thus, a difference surface is generated using the signed distance between the projected points and the corresponding points. For two SMSs, \( {\dot{\boldsymbol{SMS}}}_1 \) and \( {\dot{\boldsymbol{SMS}}}_2 \), shown in Fig. 4a, the projection of the points of the first onto the second in the direction of \( \overline{U} \) can be expressed as

$$ {\dot{\boldsymbol{I}}}_{SMS_2}=\mathrm{I}\left({\dot{\boldsymbol{SMS}}}_1,\overline{U},{\dot{\boldsymbol{SMS}}}_2\right) $$
(10)
Fig. 4
figure 4

Representation of two SMSs by difference surface and perfect surface a relative position of two SMSs, b an equivalent position of a difference surface, and a perfect plane

Full size image

Then the difference surface between the two SMSs \( \dot{\boldsymbol{\varsigma}}\mathbf{\in}{\mathbb{R}}^3 \) is obtained by

$$ \dot{\boldsymbol{\varsigma}}=\left\{\boldsymbol{X},\boldsymbol{Y},{\boldsymbol{Z}}_{I_{SMS_2}}-{\boldsymbol{Z}}_{SMS_1}\right\} $$
(11)

The initial position of the two SMSs is now converted as a difference surface and a perfect surface. Figure 4b shows the pose of the difference surface along with perfect surface, both of which are equivalent to the pose of the two SMSs in Fig. 4a. The magnitude of the transformation required to assemble the difference and perfect surfaces is what is needed to transform either of the SMSs in a specific direction.

Similarly, in assembling the part to N primary locators at station h, the steps presented in Eqs. (10)–(11) can be used. Treating the N locators as a SMS enables applying the techniques used for assembling non-ideal surfaces. Thus, the N primary locators’ points \( {\dot{\boldsymbol{L}}}^{1\dots N}\in {\mathbb{R}}^3 \)can be projected onto the primary datum feature, assuming the initial configuration in space is as shown in Fig. 5a. The projected points \( {\dot{\boldsymbol{I}}}_{S_{\pi}}^{1\dots N,h} \) are obtained using

Fig. 5
figure 5

Illustration of the steps of the assembly to the primary locator. (a) N-locators (N = 15) and primary datum feature, (b) The difference surface and locator points without deviation, (c) Convex hull of difference surface, the stable facet and perfect facet and center of gravity

Full size image
$$ {\dot{\boldsymbol{I}}}_{S_{\pi}}^{1\dots N,h}=\mathrm{I}\left({\dot{\boldsymbol{L}}}^{1\dots N,h},{\overline{U}}_{\pi}^h,{\dot{\boldsymbol{S}}}_{\pi}^h\right) $$
(12)

where \( {\dot{\boldsymbol{S}}}_{\pi}^h \) is the primary datum surface and \( {\overline{U}}_{\pi}^h=\left(0,0,1\right) \), and π ∈ (1…M) the index of the primary datum feature.

Moreover, assuming all locator points will intersect the primary datum, the number of projected points will remain N. Hence, the difference surface\( {\dot{\boldsymbol{\varsigma}}}_{\pi}^{h,1\dots N}\in {\mathbb{R}}^3 \) becomes signed distance between the locators and the corresponding projected points,

$$ {\dot{\boldsymbol{\varsigma}}}_{\pi}^{h,1\dots N}={\left\{\boldsymbol{X},\boldsymbol{Y},{\boldsymbol{Z}}_{I_{\pi }}-{\boldsymbol{Z}}_L\right\}}^{h,1\dots N} $$
(13)

where ZL is the Z values of the primary locators’ points and the \( {\mathbf{Z}}_{I_{\pi }} \)Z value of the intersection points on the primary datum feature.

Figure 5b shows the difference surface between projected locator points on the primary datum feature and locator points with no deviations. These points are needed to determine the required transformation of the primary datum feature to be assembled to the primary locators.

4.1.2 Selecting a stable contact

Once the difference surface is obtained, the stable assembly position of the part is determined. First, the minimal volume that encapsulates the difference surface is extracted using a convex hull. For such purposes, algorithms such as the Quickhull algorithm [49] can be used. The output of the computation of the convex hull is sets of three vertices that can be triangulated to make a list of facets. These facets provide a list of all possible contact configurations [50]. Figure 5c shows facets obtained by computing convex hull. Mathematically, the convex hull of the difference surface \( {\dot{\boldsymbol{\varsigma}}}_{\uppi}^{h,1\dots N} \) can be depicted as

$$ {\dot{\boldsymbol{H}}}_{\varsigma_{\uppi}}^{h,1\dots B}=\mathrm{Hull}\left({\dot{\boldsymbol{\varsigma}}}_{\uppi}^{h,1\dots N}\right) $$
(14)

where \( {\dot{\boldsymbol{H}}}_{\varsigma_{\uppi}}^{h,1\dots B} \) is set of three vertices and B number of facets.

However, only a single facet can hold the part in a stable position. The stable facet is the one that intersects the line of resultant force passing through the center of gravity of the part, shown in Fig. 5c. The center of gravity point is projected onto the facets, such that when the line intersects the facet, it is considered as a stable facet, otherwise not a stable facet. Hence, for a list of convex hull facets \( {\dot{\boldsymbol{H}}}_{\varsigma_{\uppi}}^{h,1\dots B} \), the intersecting points \( {\dot{\boldsymbol{I}}}_{H_{\varsigma_{\uppi}}}^{h,1\dots B} \) are

$$ {\dot{\boldsymbol{I}}}_{H_{\varsigma_{\uppi}}}^{h,1\dots B}=\mathrm{I}\left({\dot{C}}_{S_{1\dots M}}^h,{\overline{U}}_{\pi}^h,{\dot{\boldsymbol{H}}}_{\varsigma_{\uppi}}^{1\dots B,h}\right) $$
(15)

where \( {\dot{C}}_{S_{1\dots M}}^h\in {\mathbb{R}}^3 \) is the center of mass of the part \( {\dot{\boldsymbol{S}}}_{1\dots M}^h \).

The index of the highest point in the direction of projection b⋆ is obtained using

$$ {b}^{\star }=\underset{b}{\mathrm{argmax}}{\dot{\boldsymbol{I}}}_{H_{\varsigma_{\uppi}}}^{h,1\dots B} $$
(16)

where b ∈ (1…B).

Following Eq. (16), the three vertices of the stable facet \( {\dot{\boldsymbol{F}}}_{\pi}^h \), corresponding to three primary locators, become

$$ {\dot{\boldsymbol{F}}}_{\pi}^h=\left\{{\dot{\boldsymbol{I}}}_{H_{\varsigma_{\pi }},1}^{b^{\star }},{\dot{\boldsymbol{I}}}_{H_{\varsigma_{\pi }},2}^{b^{\star }},{\dot{\boldsymbol{I}}}_{H_{\varsigma_{\pi }},3}^{b^{\star }}\right\} $$
(17)

4.1.3 Transforming a part by dual quaternions

The above steps reduce the assembly of part from an N-2-1 fixture layout to a 3-2-1 fixture layout. The plane of the stable facet, obtained from the three vertices, and that of the perfect surfaces can be represented by dual quaternions. The dual quaternion representation of the stable facet \( {\hat{F}}_{\pi}^h \) denoted as

$$ {\hat{F}}_{\pi}^h={\overline{F}}_{\pi, \mathrm{r}}^h+{\epsilon d}_{\pi, \mathrm{d}}^h $$
(18)

where \( {\overline{F}}_{\uppi}^h \) is the normal of the stable facet and \( {d}_{\uppi}^h \) is the shortest distance to the origin (obtained from the equation of a plane).

And the perfect horizontal plane \( {\hat{L}}_{\pi}^{0,h} \), corresponding to nominal position of the N locators, is denoted as

$$ {\hat{L}}_{\pi}^{0,h}=k $$
(19)

To assemble the stable facet to the perfect plane, rotation and translation operations are required. The rotation operator to make the two planes parallel is obtained using

$$ {\hat{R}}_{\uppi}^h=\hat{R}\left({\overline{L}}_{\pi, \mathrm{r}}^{0,h},{\overline{F}}_{\pi, \mathrm{r}}^h\ \right) $$
(20)

Moreover, the pure translation operator to bring the rotated stable facet \( {\hat{R}}_{\uppi}^h{\hat{F}}_{\pi}^h{\hat{R}}_{\uppi}^{h^{\ast }} \) and the primary locator is expressed as

$$ {\hat{T}}_{\uppi}^h\kern0.5em =\kern0.5em 1+\epsilon \frac{{\hat{F}}_{\uppi}^{0,h}-{\hat{R}}_{\uppi}^h{\hat{F}}_{\pi}^h{\hat{R}}_{\uppi}^{h,\ast }}{2}{\overset{\sim }{R}}_{\uppi, \mathrm{r}}^h $$
(21)

Equations (20) and (21) can be combined as total transformation operator \( {\hat{e}}_{\uppi}^h \) using

$$ {\hat{e}}_{\uppi}^h={\overset{\sim }{R}}_{\uppi, \mathrm{r}}^h+\epsilon \frac{{\hat{F}}_1^{0,h}-{\hat{R}}_{\uppi}^h{\hat{F}}_{\pi}^h{\hat{R}}_{\uppi}^{h,\ast }}{2}{\overset{\sim }{R}}_{\uppi, \mathrm{r}}^h $$
(22)

This operator can be used to assemble the two planes using \( {\hat{e}}_{\uppi}^h{\hat{F}}_{\pi}^{0,h}{\hat{e}}_{\uppi}^{h^{\ast }} \). More importantly, the part \( {\hat{\boldsymbol{S}}}_{1\dots M}^h \) can be moved by the same magnitude to get a new pose as

$$ {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime }={\hat{e}}_{\uppi}^h{\hat{\boldsymbol{S}}}_{1\dots M}^h{\hat{e}}_{\uppi}^{h,\ast } $$
(23)
$$ {\dot{\boldsymbol{S}}}_{1\dots M}^{h,\prime }={\overline{\boldsymbol{S}}}_{1\dots M,\mathrm{d}}^{h,\prime } $$
(23a)

The part \( {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime } \) (\( {\dot{\boldsymbol{S}}}_{1\dots M}^{h,\prime } \)) when expressed as point cloud) contains information about both the new position and representation of the part. Figure 6 shows the assembly of the primary datum feature \( {\hat{\boldsymbol{S}}}_{\pi}^{h,\prime } \) to the N primary locators. (The point cloud is excluded from the surface for better visualization.)

Fig. 6
figure 6

Stable position of primary datum feature after assembly (\( {\dot{\boldsymbol{S}}}_{\pi}^{h,\prime } \)) to selected primary locators

Full size image

4.2 Assembling to the secondary locators

Once the part is assembled to the primary locators, the secondary datum feature is assembled to the two secondary locators. The locators’ points are first projected on the secondary datum feature using the ray triangle algorithm [41]. The distance between the projected points and locators is then reduced while maintaining contact with the three primary locators’ plane. However, the distances between the locators and their projected points are not necessarily equal, as shown in Fig. 7. Thus, to make the distances equal, the part has to be rotated.

Fig. 7
figure 7

An illustration of the projection of secondary locator’s points onto secondary datum feature (top view)

Full size image

The part can be rotated using the angle between a vector connecting the two locators and a vector connecting the projected points. Since the part has to maintain contact with the primary locators’ plane, the axis of rotation should be perpendicular to the plane. Further, the direction of projection from secondary locators has to be parallel to the primary locators’ plane.

Mathematically, given the normal of the primary locators’ plane \( {\overline{n}}_{\uppi} \) and the normal of the nominal plane that would pass through the tertiary locator\( {\overline{n}}_{\uptau}^0 \), the direction of projection from the secondary locator \( {\overline{n}}_{\upsigma} \) is

$$ {\overline{n}}_{\upsigma}={\overline{n}}_{\uppi}\times {\overline{n}}_{\uptau}^0 $$
(24)

The projected points corresponding to the secondary locators \( {\dot{I}}_{P_1}^h \)and \( {\dot{I}}_{P_2}^h \) obtained by

$$ {\dot{I}}_{P_1}^h=\mathrm{I}\left({\dot{P}}_1^h,{\overline{n}}_{\upsigma}^h,{\dot{\boldsymbol{S}}}_{\upsigma}^h\right) $$
(25)
$$ {\dot{I}}_{P_2}^h=\mathrm{I}\left({\dot{P}}_2^h,{\overline{n}}_{\upsigma}^h,{\dot{\boldsymbol{S}}}_{\upsigma}^h\right) $$
(26)

where σ ∈ (1…M) the index of a secondary datum feature.

Since the points are projected parallel to a stable primary plane, the cross-product of the vectors \( \left({\dot{P}}_1^h-{\dot{P}}_2^h\right) \) and \( \left({\dot{I}}_{P_1}^h-{\dot{I}}_{P_2}^h\right) \) is perpendicular to the plane. Thus,

$$ {\overline{n}}_{\uppi}\sim \left({\dot{P}}_1^h-{\dot{P}}_2^h\right)\times \left({\dot{I}}_{P_1}^h-{\dot{I}}_{P_2}^h\right) $$
(27)

Therefore, the rotation around the axis \( {\overline{n}}_{\uppi} \) ensures contact of the primary datum feature with the stable locators’ plane. Using the two vectors, the rotation operator \( {\hat{R}}_{\upsigma}^h \) and intermediary position of the part \( {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime, \mathrm{R}} \) after rotation can be obtained as

$$ {\hat{R}}_{\upsigma}^h=\hat{R}\left(\left({\dot{P}}_1^h-{\dot{P}}_2^h\right),\left({\dot{I}}_{p_1}^h-{\dot{I}}_{p_2}^h\right)\right) $$
(28)
$$ {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime, \mathrm{R}}={\hat{R}}_{\upsigma}^h{\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime }\ {\hat{R}}_{\upsigma}^{h,\ast } $$
(29)

Once the secondary datum feature is rotated, the distance from either of the secondary locators to the intermediary position of the part \( {\dot{\boldsymbol{S}}}_{\upsigma}^{h,\prime \prime, \mathrm{R}} \) is obtained by \( {\dot{P}}_1^h-\mathrm{I}\left({\dot{P}}_1^h,{\overline{n}}_{\upsigma}^h,{\dot{\boldsymbol{S}}}_{\sigma}^{h,\kern0.5em \prime \prime, \mathrm{R}}\right) \). Thus, the translation operator \( {\hat{T}}_{\upsigma}^h \) and the resulting pose of the part \( {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime } \), after transformation by the same magnitude in the direction of the locators, become

$$ {\hat{T}}_{\upsigma}^h=1+\epsilon \frac{{\dot{P}}_1^h-\mathrm{I}\left({\dot{P}}_1^h,{\overline{\mathrm{n}}}_{\upsigma}^h,{\dot{\boldsymbol{S}}}_{\sigma}^{h,\kern0.5em \prime \prime, \mathrm{R}}\right)}{2} $$
(30)
$$ {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime }={\hat{T}}_{\upsigma}^h{\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime, \mathrm{R}}\ {\hat{T}}_{\upsigma}^{h,\ast } $$
(31)

Figure 8 shows the projected points onto the secondary datum feature while maintaining contact with a plane made by the selected primary locators. It should be noted that the projection direction is parallel to the stable primary locators’ plane.

Fig. 8
figure 8

Projection of secondary locators on secondary datum feature while the primary datum feature in contact with the plane of selected primary locators

Full size image

4.3 Assembling to the tertiary locators

The third step is to slide the part to the tertiary locator while maintaining contact with the selected primary locators’ plane and the secondary locators’ vector. The tertiary locator’s point is first projected onto the tertiary datum feature in the direction parallel to both the stable locators’ plane and the line connecting the secondary locators, as shown in Fig. 9. To get the direction of projection \( {\overline{n}}_{\uptau} \), the normals of the stable primary locators’ plane \( {\overline{n}}_{\uppi} \) and that of the secondary locators’ plane \( {\overline{n}}_{\upsigma} \)

$$ {\overline{n}}_{\uptau}={\overline{n}}_{\uppi}\times {\overline{n}}_{\upsigma} $$
(32)
Fig. 9
figure 9

Projection of a tertiary locator onto tertiary datum feature

Full size image

The part is then transformed by the distance from the tertiary locator to the projected points. Thus, the translational operator \( {\hat{T}}_{\uptau}^h \) and the transformed part \( {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime \prime } \) become

$$ {\hat{T}}_{\uptau}^h=1+\epsilon \frac{{\dot{P}}_3^h-\mathrm{I}\left({\dot{P}}_3^h,{\overline{n}}_{\uptau},{\dot{\boldsymbol{S}}}_{\tau}^{,h,\prime \prime}\right)}{2} $$
(33)
$$ {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime }={\hat{T}}_{\uptau}^h{\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime }{\hat{T}}_{\uptau}^{h,\ast } $$
(34)

where τ ∈ (1…M) is the index of the tertiary feature.

Equation (34) gives the final assembly of the part onto the fixture. Further, the non-interference rule R2 is respected at every step in the assembly process. This can be checked by computing the signed distance between the projected point and the origin of that point, which should not be less than zero. Furthermore, depending on the initial position of the part, however, each of the assembly steps cancels the previous step’s assembly. Thus, Eqs. (12)–(34) are repeated until a minimal distance error between part and fixture is reached [28]. Once the part is fully constrained, virtual machining is conducted.

5 Virtual machining using SMS

A SMS can be used to virtually machine a 3D representation of a part. The working principle is to cut the machining feature by a SMS formed by cutting tool edge that follows a toolpath. The actual toolpath creates orientation and position deviations for a constant tool deviation per operation [9]. Abellan-Nebot et al. [9] mathematically described the cumulative effect of the four main machining variation sources, i.e., cutting-tool wear induced, cutting-tool force-induced, geometric/kinematic error-induced, and thermal error-induced variations. These sources of variation are assumed constant per operation, thereby generating features with orientation and position errors.

The form errors are caused by both the quasi-static and dynamic behavior of the machine tool. It is out of the scope of this paper to include the specific causes of form errors in the model. Nonetheless, form errors can be generated using Gaussian random fields and added to the point cloud without form errors. This step captures the orientation and position errors as well as form errors.

Hence, the SMS of a feature created by a tool following a non-ideal toolpath can replace the machining feature, thereby creating a new machined feature, as shown in Fig. 10. Thus given a SMS created by following the actual toolpath \( \dot{\boldsymbol{\mu}}\mathbf{\in}{\mathbb{R}}^3 \) and machining feature while assembled to machine tool \( {\dot{\boldsymbol{S}}}_{\mu}^{h,\prime \prime \prime } \), using the dual quaternions representation becomes,

$$ {\hat{\boldsymbol{S}}}_{\mu}^{h,\prime \prime \prime }={\hat{\boldsymbol{\mu}}}^h $$
(35)

where subscript μ ∈ (1…M) is the index of the machining feature in a part \( {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime } \).

Fig. 10
figure 10

Virtual machining after assembling to N-2-1 fixture layout

Full size image

6 Virtual inspection

Once the virtual machining is completed, the part has to be inspected at an inspection station. Often, a part is set on a flat horizontal surface for inspection. To set the primary datum feature on a flat horizontal surface, three points of the feature are brought to contact, in a similar manner discussed in Section 4.1. Thus, to assemble the part, first the convex hull of the SMS \( {\dot{\boldsymbol{S}}}_{\pi}^{h,\prime \prime \prime } \)is used to get a set of encapsulating facets. To select the stable facet, the point of the center of mass \( {\dot{C}}_{S_{1\dots M}}^{h,\prime \prime \prime } \) is projected onto facets. Mathematically,

$$ {\dot{\boldsymbol{H}}}_{\pi}^{1\dots B,h,\prime \prime \prime }=\mathrm{Hull}\left({\dot{\boldsymbol{S}}}_{\pi}^{h,\prime \prime \prime}\right) $$
(36)
$$ {\dot{\boldsymbol{I}}}_{S_{\pi}}^{1\dots B,h,\prime \prime \prime }=\mathrm{I}\left({\dot{C}}_{S_{1\dots M}}^{h,\prime \prime \prime },{\overline{U}}_{\pi}^h,{\dot{\boldsymbol{H}}}_{\pi}^{1\dots B,h,\prime \prime \prime}\right) $$
(37)

where \( {\dot{\boldsymbol{I}}}_{S_{\pi}}^{1\dots B,h,\prime \prime \prime } \) the projected point corresponding to the center of mass and \( {\overline{U}}_{\pi}^h=\left(0,0,1\right) \).

The stable facet is then the one where the projected point intersects the plane and has the lowest value in the direction of projection. Since the point of projection in normal to the flat surface, only Z values of the intersecting points are used.

$$ {\dot{\boldsymbol{S}}}_{\pi}^{b^{\star },h,\prime \prime \prime }:{b}^{\star }=\underset{b}{\mathrm{argmin}}{\boldsymbol{Z}}_{{\mathrm{S}}_{\pi}}^{1\dots B,h,\prime \prime \prime } $$
(38)

where b ∈ (1…B).

Using the dual quaternion representation of the stable facet \( {\hat{S}}_{\pi}^{\star, h,\prime \prime \prime } \), obtained from the equation of a plane using the three points of \( {\dot{\boldsymbol{S}}}_{\pi}^{b^{\star },h,\prime \prime \prime } \), the required rotation \( {\hat{R}}_{\mathrm{g}}^h \) is

$$ {\hat{R}}_{\mathrm{g}}^h=\hat{R}\left({\hat{G}}^h,{\hat{S}}_{\pi}^{\star, h,\prime \prime \prime}\right) $$
(39)

where \( {\hat{G}}^h=k \), representing a flat surface.

The total transformation operator \( {\hat{e}}_{\mathrm{g}}^h \) and the transformed part \( {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime \prime } \) then become

$$ {\hat{e}}_{\mathrm{g}}^h=\kern0.5em {\overset{\sim }{R}}_{\mathrm{g},\mathrm{r}}^h+\epsilon \frac{{\hat{G}}^h-{\hat{R}}_{\mathrm{g}}^h{\hat{\boldsymbol{S}}}_{\pi}^{\star, h,\prime \prime \prime }{\hat{R}}_{\mathrm{g}}^{h,\ast }}{2}{\overset{\sim }{R}}_{\mathrm{g},\mathrm{r}}^h $$
(40)
$$ {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime \prime }={\hat{e}}_{\mathrm{g}}^h{\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime }{\hat{e}}_{\mathrm{g}}^{h,\ast } $$
(41)

Once assembled at the inspection station, the points of machining feature \( {\hat{\boldsymbol{S}}}_{\mu}^{h,\prime \prime \prime \prime } \)can directly be used for further analysis. However, when the exact points at pre-specified points, such as points collected using CMM are required, the points are projected onto a feature of interest using Eq. (1). The projected points are then used for further analysis such as tolerance analysis. This step decouples the inspection points from the main model of assembling the part to a fixture, as in the case of SoV. Figure 11 shows the projection of 4 points onto the machined surface. It should be noted that number points can be increased as deemed necessary.

Fig. 11
figure 11

An illustration of virtual inspection of a part (\( {\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime \prime}\Big) \) using 4 probe points

Full size image

7 Multistage machining processes

In multistage machining processes, the part may be required to be rotated in subsequent stations before assembling to the fixtures. For a part already assembled to a fixture at station h can be rotated by an angle δ (often by 1800) and around an axis \( \overline{n} \). Thus,

$$ {\hat{\boldsymbol{S}}}_{1\dots M}^{h+1}=\left(\cos \frac{\delta }{2},\overline{n}\sin \frac{\delta }{2}\right){\hat{\boldsymbol{S}}}_{1\dots M}^{h,\prime \prime \prime}\left(\cos \frac{\delta }{2},-\overline{n}\sin \frac{\delta }{2}\right) $$
(42)

The part \( {\hat{\boldsymbol{S}}}_{1\dots M}^{h+1} \) at station h + 1 is assembled to the fixture and virtually machined following the Eqs. (12)–(35), thereby applying the proposed method recursively to each station. Since datum features of the part change at each station, the indices of the datum features also change.

8 Case study

To validate the proposed method, a part machined in two stations, shown in Fig. 12a, was considered. Both stations have a 12-2-1 fixture layout, as shown in Fig. 12b, and the part has features with form errors whose flatness values ranging between 0.137 to 0.275 mm. The stock that was machined in the first station has the dimensions of 200 X 200 X 125 mm. The fixture and machining variations used as inputs are shown in Table 1. Figure 13 shows the two-stage machining process.

Fig. 12
figure 12

Dimensions of a part and a fixture. a Final part and b a 12-2-1 fixture layouts (P1 and P2 are set 80 mm above the primary locators)

Full size image
Table 1 Random deviations of locators and cutting tools in Stations 1 and 2
Full size table
Fig 13
figure 13

A two-station machining process. a Station 1 and b Station 2

Full size image

The case study aimed at satisfying the three rules used in evaluating positioning algorithms, described in Section 3. The three rules were R1 minimizing the distance between SMSs, R2 non-interference rule, and R3 convergence of the algorithm to nominal assembly position when the form errors (and orientation and translation errors) are equal to zero.

In this direction, the SMSs’ form errors were set to zero, in accordance with R3. To assemble the primary datum feature, multiple steps were taken. First, the stable facet of the difference surface between the 12 locators and the primary datum feature was obtained using Eqs. (12)–(17). The transformation magnitude required to move the perfect surface to the stable facet was used to transform the part by the same magnitude, using Eqs. (18)–(23). This transformation assembled the part to the primary locators.

Then, using Eqs. (24)–(31), the secondary locators were projected onto the secondary datum feature. The distance between the projected points and locators was then reduced while maintaining contact with the stable primary locators’ plane. To maintain contact, the rotation was conducted around the normal of the primary locators’ plane, followed by translation toward the secondary locators in the direction parallel to the stable plane. Finally, the tertiary datum feature was assembled in a similar manner by reducing the distance between the tertiary locator and its projected point, using Eqs. (32)–(34). These assembly steps satisfy the requirement of rule R1 as they reduce the distance between the part and the locator. Further, the non-interference rule R2 was satisfied at each step of assembling the datum features.

Moreover, the prediction rule R3 was evaluated by checking if the algorithm gives the same result as the one predicted by CAD/CAM machining simulation with induced locator and toolpath deviations. Virtual machining was performed by replacing the machining feature with a shape that would be made by the tool that follows a non-ideal toolpath. For this case study, only change in depth of cut per operation was considered. The same procedure was applied to Station 2. After Station 2, the part was moved to the inspection station using Eqs. (36)–(41). The test points whose origin set at [(40, 40, 120), (40, 160, 120), (160, 40, 120), (160, 160, 120)] for KPC1 and [(40, 200, 100), (40, 200, 120), (160, 200, 100), (160, 200, 120)] for KPC2 were projected onto their respective machined surface to obtain measurement points. Figure 14 shows the projected pointed after the part was assembled to a flat surface.

Fig. 14
figure 14

Point cloud of a part with its projected points after setting up on a flat surface. Red and blue points are used for computing KPC1 (a1, a2, a3, a4) and KPC2 ((b2-b1), (b4-b3), (b6-b5), (b8-b7)), respectively

Full size image

The projected points were used to compute the parallelism of features S3 and S8. The parallelism prediction made following the above approach was within 0.4% of the simulation result obtained using a commercial CAD/CAM simulation tool, as shown in Table 2. The CAD/CAM models had intentionally induced deviations of the locators and toolpath, as shown in Table 1.

Table 2 Comparison of the parallelism predictions using CAD/CAM and the proposed method
Full size table

Moreover, in predicting part quality considering form errors, multiple loops of the assembling steps (Eqs. (12)–(34)) were executed. In each iteration, the stable contact points on the part and the primary locators changed. However, at the end of the loops, the contacting locators converged to be the same as the locators when form errors were not considered (indicated in bold in Table 1). This is due to the relatively small flatness values and the profile of specific features—when larger flatness values and/or different profiles were used, the stable contact points changed.

9 Discussion

This paper presented a method for part quality prediction in MMP while considering both form errors and a generic fixture layout. When part form errors are considered the part relative to the fixture is no more orthogonal. However, it is challenging to perform experimental validation of machining on a part with randomly scattered form errors. Nonetheless, the parallelism prediction when form errors are set to zero was within 0.4% with respect to the prediction made using a commercial CAD/CAM tool. The CAM simulation setup is shown in Fig. 15. The position prediction errors made at the four corners of the features S3 and S8 are shown in Figs. 16 and 17, respectively. The prediction error is mainly from inaccurately selected test points on CAD/CAM models that correspond to the predicted points. The origin of the projected points can be adjusted to correspond to an actual CMM probe’s position. Further, the test points were selected to be close to the features’ edges for convenience of comparing with the points at the edges of CAD/CAM models; however, these points can be moved to any desired locations on the features.

Fig. 15
figure 15

CAD/CAM simulation setup with induced locator deviations used for validation. The cutting tool deviation (∆M) is not visible.

Full size image
Fig. 16
figure 16

Position prediction error at the 4 test points of Feature S3 relative to prediction obtained from CAD/CAM models with induced errors.

Full size image
Fig. 17
figure 17

Position prediction error at the 4 test points of Feature S8 relative to prediction obtained from CAD/CAM models with induced errors

Full size image

Moreover, this paper has presented how form errors can be considered in the variation propagation. The percentage of contribution of form errors was between −105.56% and 62.15%. As can be seen in Table 2, form errors can also have a corrective effect, thereby improving the result. For instance, the parallelism of KPC2 in experiments 2, 4, and 5 when form errors were considered was smaller than when form errors were not included.

These results are also dependent on inputs and point density. Five hundred sets of inputs, with random locator and tooltip deviations following a normal distribution N(0, 0.4), were later tested at 4 points of machined features while considering parts with and without form errors. When considering form errors, each feature of each part was generated using Gaussian random field (flatness ranging from 0.075 to 0.392 mm), resulting in 14406 points. After virtual machining in two stations, deviation from nominal was computed for cases with and without form errors. As shown in Fig. 18, even though there is a significant difference between the predictions with and without considering form error, form errors may contribute to a better prediction for specific SMS instances. When using CMM points at specific points, the same result is obtained when form errors are not considered, while different results are obtained when considering form errors. Similarly, the prediction made using high-density points gives results closer to reality, while low-density points may erroneously give values closer to nominal. Thus, care must be taken on the use of SMS instances.

Fig. 18
figure 18

Collective deviations at 4 test points of feature S3 given random inputs. The difference is between corresponding test points when considering form and no form errors

Full size image

Moreover, the computational efficiency of manipulating SMSs is highly dependent on the density of points per model [32]. Since multiple steps are required in assembling SMS, dual quaternions are likely to contribute to increasing computational efficiency. Better computational efficacy of dual quaternions relative homogenous transformation matrix has been reported in [51,52,53,54,55,56]. However, it is worth investigating the computational efficiency specifically in variation propagation models.

In the proposed approach, multiple conversions to and from dual quaternions and point clouds are needed. This is due to the projection algorithm works on point cloud, and transformation is performed on dual quaternion representation of a part. Nonetheless, converting to dual quaternions requires arranging points in the form of [1, 0, 0, 0, 0, X, Y, Z] and when converting to point cloud requires extracting the last 3 terms of the dual quaternion.

Furthermore, the proposed method applies only to rigid bodies. However, there is a need to include part deformation in variation propagation modeling of MMP [1, 19]. Adaptive meshing around locator along with FEA often used in sheet metal manufacturing can be explored.

10 Conclusion

The variation propagation models in MMP that consider both parts’ form errors and N-2-1 fixture layout have not been exhaustively studied. This paper derived mathematical models for predicting part quality by utilizing dual quaternions. The approach meets the three requirements of robust locating algorithms for the assembly of parts with form errors. According to the requirements, the assembly should be checked for non-interference and closeness to the assembly position of the nominal model when the part’s form errors are set to zero. To achieve this, a part was assembled to a 12-2-1 fixture layout by computing a convex hull of the difference surface corresponding to the primary locators and primary datum feature, followed by the displacement of the part by the magnitude required between the resulting stable facet and perfect plane. In assembling the secondary and tertiary datum features, the distance between the locators and their projected points were minimized. Once the part was assembled to the fixture, the machining feature was replaced by a point cloud that would be made by the machining process. The part was then inspected using points projected from specific test points. Following the approach, the parallelism prediction was within 0.4% of that of a commercial CAD/CAM simulation tool with induced errors. When a part with flatness values between 0.137 and 0.275 mm were considered, the contribution of form errors ranged between −105.56% and 62.15%. Yet, experimental validation techniques in MMP for parts with form errors need to be investigated.