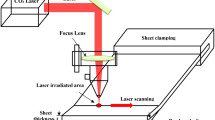
Abstract
Understanding the laser ablation mechanism is highly essential to find the effect of different laser parameters on the quality of the laser ablation. A mathematical model was developed in the current investigation to calculate the material removal rate and ablation depth. Laser cuts were created on the workpiece with different laser scan speeds from 1 to 10 mm s−1 by an ultrashort pulse laser with a wavelength of about 1000 nm. The calculated depths of laser cuts were validated via practical experiments. The variation of the laser power intensity on the workpiece’s surface during laser radiation was also calculated. The mathematical model has determined the laser-material interaction mechanism for different laser intensities. The practical sublimation temperature and ablated material temperature during laser processing are other data that the model calculates. The results show that in laser power intensities (IL) higher than 1.5 × 109 W cm−2, the laser-material interaction is multiphoton ionisation with no effects of thermal reaction, while in lower values of IL, there are effects of thermal damages and HAZ adjacent to the laser cut. The angle of incidence is an essential factor in altering incident IL on the surface of the workpiece during laser processing, which changes with increasing depth of the laser cut.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Laser ablation is highly popular for industrial applications. However, there are various research gaps in this field, especially for ultrashort pulse laser ablation of difficult-to-cut materials like ceramics. Controlling the laser ablation is performed by laser parameters. The laser parameters, which are related to the wavelength and laser power intensity, have influences on the laser-material interaction mechanism and the portion of transferred laser energy to the material. Because of the high sensitivity of ceramic materials against the thermal shocks and the considerable energy transmitted by the laser to the material, studying the effects of different laser types with different pulse duration on the thermal shocks and surface integrity is an interest of many researchers [1].
In an identical wavelength, a decrease of the pulse time leads to an improvement of the quality of the ablated surface. Oosterbeek et al. [2] investigated the influence of nano- and femtosecond lasers on alumina material with pulse times of 80 ns and 110 fs, respectively. They illustrated that material ablation without thermal degradation is possible when using the femtosecond laser. More molten material and thermal damages on the workpiece were observed with increasing pulse time from several hundred femtoseconds to several nanoseconds.
In addition to the pulse time, the amount of pulse energy affects the material ablation. Herrmann et al. [3] compared in an analytical work the ablation mechanisms of picosecond and femtosecond laser pulses in a range of 5 ps–10 fs with a maximum pulse energy of 1.0 × 10−15 J and a focus of 25 Å on a 100 Å × 100 Å × 50 Å silicon sample. However, the ablation strongly depends on the pulse length; the main material removal takes place on a time scale of a few picoseconds. While the damage initiation depends on the pulse energy, the beginning of the material removal shows a strong dependence on the pulse duration.
In the study of Jandeleit et al. [4], the laser ablations of Si3N4, SiC, and WC were compared. They utilised pico- and nanosecond lasers with laser power of 3–9 W. They investigated the material removal threshold as a limit, above which the material is removed. However, only the thermal effect without material removal is presented below this threshold. Accordingly, a pulse time reduction from 10 ns to 40 ps leads to a considerable increase (up to 20 times) in the material removal threshold. However, by increasing the pulse time beyond the mentioned threshold, the Material Removal Rate (MRR) was reduced up to 200%. For a single pulse, the average laser power intensity is introduced as below to simultaneously investigate the influence of pulse time and pulse energy [5]:
where El − pulseis the laser pulse energy (J), tpulse is the pulse duration (s), and Afoc is the laser irradiation area in the focus point (cm2).
According to Eq. (1), the average laser power intensity has a linear relation with the laser pulse energy and is reversely proportional to the pulse time and laser-irradiated area. Karnakis [6] studied the influence of a single laser pulse Nd:YAG with a wavelength of 355 nm, a maximum pulse duration of 44 ns, and maximum pulse energy of 0.5 mJ on a single crystal of silicon. Here, it was investigated how an increase of laser power intensity up to 20 × 109 W cm−2 affects the ablation depth and material removal mechanism. It was concluded that the removal mechanism is based on evaporation and melting. The ablation depth increased exponentially with laser power intensity, while the crater diameter varied linearly. As a result of growing laser power intensity, the crater shape changed from V-shape to a parabolic shape.
In ultrashort laser ablation, the material heating does not follow Fourier equations. However, the temperature of the surface increases with increasing irradiation time and the laser power density up to a maximum value (Tmax). The Tmax may exceed a phase transformation threshold within the pulse time (tpulse). Short and ultrashort pulsed lasers have pulse times in the range of 100 fs < tpulse < 100 ns. The laser pulses in the mentioned range usually induce laser power picks in orders of several mega- to terawatts [7]. A portion of laser energy is delivered on the surface within the thermal relaxation time and is localised in a skinny layer of material without any thermal diffusion, which causes electron excitation and electron heating [8]. In the case of ultrashort pulse lasers, the laser energy of a single pulse, which was radiated in less than 10 ps, leads to a material breakdown through a thin layer on the surface with ionisation of atoms, which converts a normal transparent material into absorbing plasma [9].
Ren et al. [10] modelled the interaction between an ultrafast laser and a gold layer using the electron warming model. In this model, the laser energy is first transferred to the free electrons and increases the electron temperature. The peak temperature of the free electrons, which was stimulated by the electron warming model, reached 40,000 K in about 100 fs. In contrast, the lattice temperature increased in a period of more than 5 ps. The lattice peak temperatures grew more extensive than the normal melting and the boiling points inside the film, and melting occurs from the surface exposed to the laser, followed by evaporation. At t = 20 ps, the liquid portion of the gold film was superheated up to 3880 K (the normal boiling point is 3127 K), and the solid part was superheated to 3840 K (the normal melting point is 1336 K).
In the study of Chen et al. [11], which was about the applicability of the electron warming model for a gold layer, the temperature of the workpiece surface increased up to 8000 K. The mentioned temperature was achieved after 1.0 ps. It is enough for material sublimation without melting. Moreover, it was reported that the increasing electron temperature in 0.3 ps after laser radiation results in a considerable acceleration of free electrons faster than the sound speed, and a repulsion pressure of electrons reach 1.24 GPa in the depth of 0.3 μm. The pressure caused by electrons and the thermal expansion of the material results in the workpiece destruction. Accordingly, so long as the laser power intensity (IL) value was less than 108 W cm−3, the irradiated material is molten and then evaporated. If IL is in the range of 108 to 1010 W cm−3, the substance is partially sublimated without melting. With higher IL, ionisation is a dominant mechanism of material ablation.
Brenk and Rethfeld [12] studied the electron warming model for silicon oxides. Here, the workpiece was an insulator without the free electrons in the conduction band. Multiphoton ionisation (MPI) was introduced as a crucial mechanism to generate free electrons with material ionisation. At the beginning of MPI, different critical parameters, such as the critical density of free electrons and lattice temperature, were determined. They showed that the laser absorption increases by increasing the density of electrons beyond a threshold that intensifies laser energy’s influence on the workpiece.
In insulators like structural ceramics, since there are no free electrons for direct excitation, if the incident photons provide enough energy to shift an electron from the valence into the conduction band, the electrons can detach from its atom [7]. No direct absorption can theoretically take place if the incoming photon energy level is lower than the bandgap. However, the density of low-energy photons becomes high enough, and they can simultaneously provide the required energy for a jump from a valance band to a higher conduction band. The excited electron by several photons participates in transferring the laser energy into the other valance electrons. The excitation of electrons by several low-energy photons is introduced as multiphoton absorption (MPA). The ionisation, which is attributed to the MPA, is the MPI. Ultrashort pulse lasers with frequencies lower than the UV range usually excite electrons with a multiphoton absorption mechanism, as shown in Fig. 1. This phenomenon leads to localised ionisation of material and transforms the material into plasma [9].
The generated conduction electrons by MPI absorb the laser energy during a pulse laser radiation, while the lattice remains cold. Therefore, the heat conduction should be described by two heat flow equations, for electrons and lattice. Here, the Drude model (or free electron model) provides the free electrons’ basic formulation in the material response to electromagnetic waves of a specific angular frequency. Accordingly, the free electrons’ heat capacity is linearly dependent on the electron temperature up to the fermi temperature [13].
In a MPA, transferring the energy to the electron depends on two factors: the energy level of the external field and the dissipated energy during collisions of the phonons with the atoms. The ratio of the energy lost by the electron in a collision is of the order of the ratio of the electron’s mass to the mass of the ion [14]. In a MPI mechanism, a valence electron absorbs enough photons to excite to a higher conduction band through the simultaneous absorption of several photons by an electron. Moreover, the conduction band’s excited electron can absorb several laser energy and act as a photon [15].
Sugioka et al. [16] summarised various investigations concerning the laser micro-fabrication allocated to the different interaction mechanisms between laser and material. In the ultrashort pulse lasers (USPL), IL may vary from 10 8 to 1014 W cm−2, contributing to the MPI mechanism, which is the considerably dominated material removal. Here, electron heating begins in a radiation time of fewer than 100 fs. In radiation times higher than 10 ps, thermal energy is transferred from free electrons to the atoms. Bäuerle [5] gathered the results of several studies in a graph, as shown in Fig. 2. It indicates the effect of IL on laser-material interaction for different metals, polymers, and dielectrics. In a range of IL = 10 8 – 1010 W cm−2, the small amount of the material is removed by melting and evaporation while the sublimation is dominant. In contrast, the material removal occurs through ionisation of the atoms without melting and evaporation for laser intensities more than 1010–1012 W cm−2.
Laser–material interactions vs. laser pulse intensity. (PLA/PLD, pulsed laser ablation/deposition; LA, laser annealing; LC, laser cleaning; LIS, laser-induced isotope separation; MPA, multiphoton absorption/ionisation; LSDW/LSCW, laser-supported detonation/combustion waves; LCVD, laser-induced CVD; LEC, laser-induced electrochemical plating/etching; RED/OX, long pulse or CW CO2 laser-induced reduction/oxidation) [5]
In the previous study, Soltani et al. [17] focused on a simulation of a laser ablation process on a silicon nitride workpiece by an ultrashort pulse laser, which predicted the depth of laser ablation. Despite a good correlation between the simulation and experimental results, there is a lack of finding the effects of different experimental parameters on the laser power intensity and the absorbed energy. In addition, the precise temperatures of the lattice and free electrons during laser processing were not calculated.
The laser-material interaction mechanism has an influence on the temperatures, which is affected by the laser parameters. It should be analysed how the experimental parameters affect the laser-material interaction mechanism. The main criterion of the ablation in different laser-material interaction mechanisms should also be studied in more details. Also, the effects of the laser parameters on the material removal rate were not considered in the previous work of Soltani et al. [17].
The goal of the current work is to develop a reliable simulation method to calculate the workpiece temperature, find the laser-material interaction mechanism during laser processing, and predict ablation depth. Following the previous work [17], it is aimed to investigate the interaction between an USPL and ceramic alloy Si3N4 (SL200-BG-Ceramtec Co), which is a gas-pressure-sintered Si3N4 (SL200-BG from Ceram Tec GmbH) with Y2O3 (~3 wt.%) and Al2O3 (~3 wt.%) as sintering aid additives [18]. The experimental tests were carried out by a USPL with a wavelength of λ = 1032 nm.
The applied model is a finite-difference numerical model. The effects of the angle of incidence and the Gaussian factors on the absorbed energy of the laser were considered. The two temperatures model (TTM) was applied to calculate the heat conductions in electrons and the lattice. The Drude model provided the basic formulation of energy transferring to the free electrons and their heat capacity. Here, the energy of the external fields and energy dissipation by the collision was considered. It was evaluated how the valence electrons absorb the incident energy in all contributed components. The absorbed energy by the valence electrons can initiate the ionisation and MPI mechanism.
Therefore, the chemical composition’s influence on the ablation mechanism and temperature was studied, and the minimum laser power intensity to remove material without thermal damage was computed. The ions and free electron densities were calculated to simulate the ablation of the material.
Finally, the precise temperature values of the lattice and free electrons were calculated considering the laser parameters. The effects of the laser parameters on the laser-material interaction mechanism and the main criterion of the ablation in different laser-material interaction mechanisms were determined. The sublimation temperature was computed as the ablation criterion in the thermal ablation mechanism. The critical density of ions and free electrons as the ablation criterion in the cold ablation mechanism was also calculated. Besides, the material removal rate affected by the laser parameters was analysed. The simulation data of the ablation depth and material removal rate were validated by comparison to the experimental results. The critical laser power intensity as a threshold of the cold and the thermal ablation mechanism was calculated in the simulation.
2 Experimental results
The experiments were conducted to investigate the experimental effects of a USPL on Si3N4 alloy (Ceram Tec - SL200 BG) as a high-performance ceramic material. Due to excellent chemical stability and mechanical strength, SL200-BG is utilised to produce welding components, gas nozzles, and forming tools. However, due to the high values of hardness and brittleness of the workpiece compared with the metals, a conventional machining process is still a challenge with dramatic tool wear and numerous surface defects. Therefore, the laser ablation is considered a non-contact machining process without any tool wear.
The laser process parameters and the applied alloy properties are provided in Tables 1 and 2, respectively.
As mentioned above, the value of IL influences the laser-material interaction mechanism. The amount of ablated material is highly dependent on the ratio of laser energy to the irradiated area, so-called total input energy density. An increase in total input energy density leads to a deeper ablation irrespective of the total laser radiation time. Equation (2) provides the calculation of laser input energy density (EL − input) [21]:
where EL − total is the total laser energy (J), wL is the width of laser ablation (mm), tL is the radiation time (s), and vL is the laser scan speed (mm s−1).
The laser input energy density has a very similar definition to laser fluency. However, a laser-ablated structure on a workpiece, for instance, a dash line structure, has several ablated elements with specific gaps. Here, the laser input energy density is applicable to connect the average delivered energy to the ablation depth and the gaps between them. It means that, despite the same laser parameters, the laser input energy density will decrease with an increase in the ablated elements’ gaps. Therefore, the effect of the ablated structure geometry is considered in the laser input energy density.
For a laser at a constant power and radiation area, the EL − input is a function of vL. Figure 3 illustrates the calculated EL − input according to Eq. (2) at various vL, which are in the range of practical experiments. The wL, according to the experimental measurements, is approximately equal to the laser spot diameter. The EL − total and the tL values were calculated for laser cuts with a length (LL) of 10 mm:
where EL − total is the total laser energy (J), tL is the radiation time (s), vL is the laser scan speed (mm s−1), PL is the laser power (W), and LL is the length of the laser cut (mm)
Accordingly, the EL − input has lower sensitivity at vL > 20 mm s−1 compared to vL = 0–20 mm s−1. Here, a growth of vL from 0 to 20 mm s−1 causes a dramatic drop of the EL − input from higher than 300 J mm−2 to less than 50 J mm−2. The current study, laser scan speed, ranging 2–100 mm s−1, results in a laser input energy density of 6.25–312.5 J mm−2. Furthermore, the influence of EL − input on the ablation depth (ae − L) and the width of thermal damages was examined.
According to Fig. 4, increasing laser input energy density from EL − input = 6.25 to 62.5 J mm−2 led to deeper laser ablations. No effect of thermal damage can be seen for the ablations with EL − input = 6.25 J mm−2, whereas increasing the EL − input to 62.5 J mm−2 resulted in thermal cracks, as shown in Fig. 4b. The majority of thermal cracks were initiated from the bottom of the laser ablation where it should have the maximum thermal gradient and temperature enhancement. The growth of cracks adjacent to the laser ablations toward the surface of the workpiece is a representation of a thermal tension field in the vicinity of the ablated zone. Therefore, it is expected that the laser energy on the wall of the laser cut results in a localised rise of temperature and thermal expansion. The wall surfaces absorb a noticeable portion of laser energy in deep laser cuts through several reflections of laser light. The laser beam reaches the bottom of the laser ablation, which has about > 100 μm depth, through several reflections. Therefore, the surface roughness, recast layer, trapped plasma cloud, and the increase of angle of incidence (AoI) affect the absorption and diffraction of the laser energy on the laser cut. Hence, the practical IL is reduced noticeably, which is a crucial factor determining the laser-material interaction mechanism.
As can be seen in Fig. 4, increasing laser input energy density from EL − input = 6.25 J mm−2 to EL − input = 62.5 J mm−2 led to a deeper laser cut. No effect of thermal damage can be seen for the ablations with EL − input= 6.25 J mm−2, whereas increasing the laser input energy density to 62.5 J mm−2 resulted in thermally induced cracks (Fig. 7b). The majority of thermal cracks were initiated from the bottom of the laser cut. It means that the maximum thermal gradient and temperature enhancement are at the bottom of the laser cut. Growing cracks adjacent to the laser cut toward the workpiece’s surface represent an increase in thermal tension or shear stresses in the laser cut’s vicinity. Therefore, the laser energy on the laser cut wall results in a localised rise of temperature and thermal expansion. The wall surfaces absorb a noticeable portion of laser energy in deep laser cuts through several laser light reflections. The laser beam reaches the bottom of the laser cut through the reflections, which is about > 100 μm deeper than the laser focal point. Therefore, the surface roughness, recast layer, trapped plasma cloud, and the increase of the AoI affect the absorption and diffraction of the laser energy on the laser cut. Hence, the practical IL is reduced noticeably, which is a crucial factor determining the laser-material interaction mechanism.
A plasma selective etch process was applied on a workpiece to investigate the physical changes in the laser cut’s vicinity. Figure 5 shows the etched surface of the workpiece. As illustrated in Fig. 8, the heat-affected zone (HAZ) and microstructural alternation can clearly be observed with the EL − input = 312.5 J mm−2. Moreover, a recast layer inside of the laser cut is detectable. The microstructural alternation occurs because of the elimination of silicon oxide, located between crystal grains [22, 23]. The presence of HAZ and thermal damages are indicators of high heat generated by laser beam energy.
According to the previous investigations, the recast layer on the laser cut wall is SiO2, which is formed due to the chemical reaction of silicon ions or molten material with Oxygen as described in Eq. (5) and (6) [24]:
The generated energy in this reaction is negligible compared to the laser energy and cannot be considered an influential factor in microstructural alternation and thermal damage.
After etching the cross-sections with H3PO4, the maximum width of thermal damages was measured on three different cross-sections for every laser cut, as shown in Fig. 6a. Figure 6b indicates how the HAZ changes with laser input energy density, EL − input. Accordingly, in EL − input < 40 J mm−2, the material has no thermal damages, whereas, for EL − input > 60 J mm−2, considerable thermal damages took place (see also Figs. 4 and 6). The range of laser input energy density, EL − input, between 40 and 60 J mm−2, is introduced as a transient area between ablation without and with thermal damages. Here, the laser energy is delivered to the workpiece's surface within the laser penetration depth. The laser penetration depth is about L = 19 nm, and it is assumed that 100% of the laser energy is absorbed through the laser penetration depth.
Therefore, it should be analysed how the applied laser parameters affect laser power intensity, the laser input energy density, the ablation geometry, irradiated surface temperature, and the mechanism of the laser-material interaction mechanism. An analytical model should be provided to predict the ablation depth, the effect of different parameters on the laser power intensity and absorbed energy, the exact temperature of free electrons and atoms during laser processing, and the mechanism of laser-material interaction.
3 Theoretical model
In the applied theoretical model, appropriate thermal conduction equations should be utilised to calculate the temperatures. Then, it should be possible to predict the depth of material ablation and temperature changes during the laser irradiation and the effect of laser parameters on it. Also, the reasons for the onset of thermal cracks and their growth parallel to the laser cutting wall can be studied by monitoring temperature gradients on cutting edges.
The developed simulation is based on the 2D analysis of laser-material interaction to calculate the depth of material ablation and the workpiece temperature in laser treatment of a silicon nitride sample. In this regard, the laser power intensity IL, which is delivered to the surface, is calculated by the following equation [7]:
where IL is the laser power intensity (W cm−2), Ipk is the maximum laser power intensity (W cm−2), Gspace is the Gaussian function for spatial laser beam shape, Gtime is the Gaussian function for temporal laser beam shape, and Gmod is the Gaussian function for beam motion.
The laser beam should be modelled in the first stage, considering that the laser power intensity varies over the whole laser radius and during each pulse time. In this context, the Gaussian distribution model is applied to define the laser power intensity in time and space with functions Gspace (Gaussian function for the spatial laser beam shape) and Gtime (Gaussian function for the temporal laser beam shape), respectively. Moreover, the laser beam’s motion should be considered by Gmod (Gaussian function for the beam motion), affecting the laser power intensity. Therefore, for a single pulse, Eq. (7) is reformulated without Gmod function, and with respect to Eq. (1), the energy of a pulse (El − pulse) can be extracted from the Gaussian factors in Eq. (7) as:
where \( {E}_{\mathsf{l}-\mathsf{pulse}} \) is the pulse energy (J), r0is the radius of the laser beam (cm), tp is the pulse time (s), Ipk is the maximum pulse intemsity (W cm−2), r is the radial component of the position vector (cm), θ is the angular component of the position vector (rad), and r0 and tp are respectively beam radius and laser pulse time, as specified by the manufacturer in the applied laser’s technical specifications.
Gspace means the Gaussian distribution that is as a function of the laser beam radius r0 and the distance from the laser beam centre, r [25]:
Figure 7 illustrates how the Gaussian distribution obtained from Eq. (9) changes as one moves away from the beam’s centre. As illustrated in Fig. 2, the Gaussian function for the spatial laser beam shape (Gspace) varies from 0 to 1 and increases as one approaches the beam centre, which is followed by an increase in laser power intensity. As can be seen in Fig. 7, the Gspace value reaches 10% of the maximum value at the edge of the laser beam. Therefore, in Eq. (9), the amount of laser power intensity at the edge of the laser beam reaches 10% of the intensity in the centre of the laser spot.
Since the applied laser in the current study is a Q-Switch pulse laser, in addition to the Gspace, the temporal laser beam energy is varied according to a Gaussian function of laser radiation time (Gtime). According to Paschotta [26], the temporal intensity of the laser increases up to a maximum value at t = tmax . The Gspace determines how the pulse energy is delivered to the workpiece at each laser radiation t concerning tmax and the pulse time (tp) [27]:
The values of Gspace throughout the radiation times during a single laser pulse is illustrated in Fig. 8. The applied laser is a Q-Switch pulse laser. In the utilised laser, the pulse energy vs. time is a Gaussian graph. The pulse duration was estimated considering the full-width half-maximum (FWHM) method. Here, pulse time is the with of the laser radiation with the Gaussian values greater than 0.5. Accordingly, the Gspace changes from 0.5 to 1 over the pulse duration, which results in a variation of the IL up to 50%.
By solving Eq. (8), the maximum laser power intensity (Ipk) can be determined that is approximately 2.5 times of average laser power intensity (IL − avg). The Ipk at the laser centre point is reachable at t = 0.5 tp.
The influence of the laser scan speed on the pulse overlapping and laser power intensity considered by Gaussian function for the motion of the laser beam (Gmod) is formulated in Eq. (11) [7]:
where Gmod is the Gaussian function for the motion of the laser beam, r0 is the laser beam radius (mm), vL is the laser scan speed (mm s−1), and t is time (s).
Figure 9 shows how the Gmod changes with the radiation time of the laser at different vL. Here, according to Eq. (11), the variation of Gmod versus the radiation time of the laser is illustrated in several vL in the range of 1–100 mm s−1. A more intense change in Gmod versus time occurs at a higher laser scan speed. In Eq. (11), the edge of the scanning laser beam reaches a certain location at the initial time t = 0. Since the value of the intensity of the laser power at the edge of the laser beam is 10% of the intensity at the centre of the laser spot, the value of the Gmod at t = 0 becomes nonzero. The Gmod value reaches its maximum when the laser beam travels a radius of the laser beam over a certain point. Therefore, as the laser scanning speed increases, the Gmod value is maximised in a shorter time. When the laser beam travels a laser beam diameter on the surface, the Gmod returns to the value as t = 0.
The laser’s AoI affects the radiation area, leading to variation of the laser power intensity. As the laser-cut deepens, not only does the shape of the V-shape laser-cut change but the angle of the laser beam on the surface also grows (Fig. 10). Accordingly, during the process, unlike the beginning of the laser radiation, the laser beam is not perpendicular to the ablated surface. The effect of changing the AoI of the laser could be introduced by a coefficient (CAoI), based on the geometry of the laser-cut. It is mathematically calculated as below in the current study:
where CAoI is the coefficient of AoI, AoI0 is the initial AoI (ae–L = 0 μm) (rad), ae − L is the depth of the laser cut (μm), and wL is the width of laser ablation (μm).
Eventually, the laser power intensity, IL, corresponding the angle of the incident at each time increment can be calculated as follows:
After calculation of the IL the amount of the volumetric energy which is absorbed by the surface is calculated by Eq. (14) [16]:
where Eabs is the volumetric absorbed laser energy by the material (J cm−3), R is the reflection coefficient, L is the maximum depth of laser diffusion (cm), and z is the subsurface depth through the material (cm).
Fresnel’s refraction formulas calculate the reflected coefficient (R) at the sample surface [5]. The amount of reflected energy depends on the frequency of the incident energy, the angle of incidence, the quality of the sample surface, and the material properties. Here, the sample’s refractivity index, which is equal to (n − ik), has a real part and an imaginary part, k. n varies slowly with temperature and k is related to the absorption coefficient, α = 4πk/λ, where λ is the wavelength. The density of the lattice dislocation, the free electron temperature, and free electron density increase with an enhancement of temperature. Hence, the absorption coefficient grows with a temperature elevation. The α is related to T by an exponential function, α = α0 exp(T/T0). Here, T0 changes with the wavelength [16, 30]. Additionally, the evaporation and heterogeneous melting of the target leads to the formation of a plasma plume and molten droplets, which attenuate the radiated energy intensity [31]. Not only, the reflection coefficient values, R, depend on the material properties, the laser wavelength, and surface quality, but the maximum depth of laser diffusion (L) changes with them.
The refractivity and absorption coefficients also depend on the microstructure of the material. Silicon nitride contains a layer of an intergranular amorphous phase, which mainly holds a higher concentration of impurities and free electrons than Si3N4 grains. Due to the high concentration of impurities relative to the grains, this amorphous layer has a principal effect on the reflection and absorption of radiated energy. In β-Si3N4, the grains are elongated rod-shaped, the α-Si3N4 grains have oval shapes. The concentration of the intergranular amorphous phase is the lowest in the direction of the grain axis. Therefore, the amount of energy absorbed in this direction is the least [28]. As the wavelength of incident energy grows from the UV to the near IR, the samples with β− and α-Si3N4 show a monotonic decrease in the absorption coefficient as well as reflectivity [29].
In the steady state, Si3N4 is chemically stable up to a temperature of about 2170 K [28]. With a single pulse of the laser, since the temperature locally changes within 10 ps, the reactions, which directly depend on the diffusion of atoms, such as phase transformation or chemical oxidation, do not launch. However, during the ablation with several laser pulses, the chemical oxidation affected the reflectivity as well as melting and plasma formation.
The absorbed energy is initially allocated for heating free electrons, which results in the generation of photons. An atom ionises if a photon, which collides with the atom, has enough energy to excite a valence electron to the conduction energy layer. The photon energy (Ephoton) can be calculated as follows:
where Ephoton is the photon energy (J), h is the Planck constant (6.626 × 10−34 Js), λ is the laser wavelength (m), and c is the speed of light (m s−1).
As indicated in Eq.(15), the photon energy is inversely proportional to the laser wavelength. In other words, atomic ionisation occurs when the laser wavelength (λ) is shorter than a threshold value. However, if the photon density is high enough, atomic ionisation due to MPI can occur even when the laser wavelength is longer than the threshold value.
In the case of activation of the MPI mechanism, some part of energy leads to the generation of free electrons [12]. Free electrons are supplied by elements in the material. To provide free electrons, the energy needed to jump the valence electrons to the conduction band must be provided. Therefore, according to the density of free electrons, the amount of volumetric energy required to generate free electrons, which is supplied by laser radiation on the surface, must be calculated:
where Nfree is the density of free electrons (cm−3), Eg is the energy for generating 1 mol of the free electrons (J mol−1), and NA is the Avogadro constant (6.02 × 1023 1 mol−1).
Eg is the required energy to jump 1 mol of valence electrons to the conduction band. If the material includes several chemical compounds, the corresponding breaking energy should also be considered for the weakest chemical bonds. In this study, the material is a ceramic alloy with a base material of silicon nitride. The additives are ~3 wt% Al2O3 and ~3wt% Y2O3 (SL200-BG). Therefore, it should also be taken into account the bandgap energy of the valence electrons and the corresponding energy of chemical bonds of Al–O, Si–O, Y–O, and Si–N. Consequently, It is expected that the component with a minimum required energy to create 1 mol free electrons should be ionised before the others.
On the other side, an amorphous oxynitride phase is mainly concentrated in the grain boundaries between the β-Si3N4 grains. Thus, in the amorphous phase, metallic impurities more easily diffuse into the grain boundaries than inside the grains [22]. According to Kasap’s study [32], the electrical breakdown is initiated by structural imperfections, metallic impurity concentration, and local tension fields. Lombardo et al. [33] studied the electrical breakdown on Si components. As concluded, in an insulator, the metallic or semiconductor components as well as defected zones in the lattice in the first step are locally ionised and provided the free electrons for electrical conductivity. The free electrons or valence electrons, which have no contribution in a chemical bond, are concentrated in the defected zones. Therefore, those electrons cause an electrical breakdown in lower potentials rather than a flawless zone. Besides, the tensile stresses facilitate the breakage of chemical bonds. Accordingly, in the current laser process, the electron warming and MPI mechanism should locally be initiated in the defect zones at the grain boundaries. It is expected that owing to the laser radiation, the destruction and ionisation of the material propagate through the β-Si3N4 grains succeeding in the grain boundaries. According to the material specifications, the grain sizes are in the range of 1–5 μm, and the grain boundary width is about 1–200 nm. It means that the total volumetric concentration of the impurities and additive components in grain boundaries is < 10 vol.%. So, the free electron density locally increases at material imperfections such as grain boundaries, and through the diffusion of free electrons from the grain boundary through the grains, the ionisation inside the grain also takes place.
According to the study of Brenk et al. [12], the plasma frequency is a function of the density of free electrons (Nfree):
where fp is the plasma frequency (rad s−1), Nfree is the free electron density (m−3), e is the electron charge (−1.6 × 10−19°C), me is the electron mass (9.11 × 10−31 kg), and ϵ0 is the dielectric constant of vacuum (8.85 × 10−12 F·m−1).
When the laser frequency equals the plasma frequency, the density of free electrons reaches the critical value (Ncrt) in which the material can absorb the maximum laser energy and electron warming and MPI mechanism are dominant. Based on laser specifications, this value, Nfree, would be around 1.12 × 10−21 cm−3. Since the laser-free electron interaction is available locally in the grain boundaries, the Nfree should reach the critical value at the grain boundary. The material ablation requires the repulsive force among free electrons which is higher than the mechanical strength of the material. The repulsive tension (σ) by free electrons can be calculated as follows [11]:
where ce0 is the initial electron-specific heat capacity (7 × 10−4 J mol−1 K−2) [34], ρ is the electron density (mol cm−3), Te is the electron temperature (K), and σ is the repulsive tension (N cm−2).
Early efforts in the simulation showed that the maximum free electron temperature should be in the range of 1000–10,000 K. Also, as the density of free electrons reaches 4.5 × 1021 cm−3, the calculated repulsive tension in Eq. (18) is enough to damage the amorphous silicon (with mechanical strength 7 MPa [35]) located in the grain boundaries. Therefore, the Ncrt in this study equals to 4.5 × 1021 cm−3.
Otherwise, if the density of photons is not enough, and the laser wavelength is longer than the threshold value, the heating of the lattice structure takes place rather than activation of the MPI mechanism. In this case, electron-phonon coupling volumetric energy (Eeph) is transferred to the material as a result of a collision between heated free electrons and atomic structure. Equation (19) provides the mathematical calculation of Eeph [12]:
where Eeph is the electron-phonon coupling volumetric energy (J cm−3), αK is the electron-phonon coupling coefficient (J (cm3 K1)−1), Te is the electron temperature (K), and Tl is the lattice temperature (K).
The Eeph is the amount of energy that is ultimately used to heat the lattice at the laser penetration depth. Equation (20) provides the calculation regarding increasing the lattice temperature [36]:
where cp is the material-specific heat capacity (J (g K)−1), ρ is the material density (g cm−3), K is the material heat conductivity (W (cm K)−1), and Tl is the lattice temperature (K).
Finally, the volumetric amount of energy leading to heating of the electrons (Ehe) is obtained by subtraction of heating lattice structure, Eeph, and generation of free electrons (EeGen) from the volumetric-absorbed laser energy by the material (Eabs) [7]:
Equation (22) provides the electron warming based on the volumetric energy leading to Ehe [36]:
where ce0 is the initial electron-specific heat capacity (7 × 10−4 J mol−1 K−2) [34], ρe is the electron density (mol cm−3), Ke is the electron heat conductivity (1.05 W (m K)−1) [34], and Te is the electron temperature (K).
The material ionisation with the maximum depth of laser diffusion (L) depends on the magnitude of the Eabs. The material ionisation causes local damages in the lattice and ablates the workpiece material. Hence, a new workpiece surface is generated. For each pulse, the volumetric absorbed laser energy reduces after material ionisation. The new value of the Eabs again leads to ionisation until the value of Eabs becomes less than the EeGen. Due to the Gaussian distribution of the laser energy in the spot area, the V-form ablation occurs, which in turn causes the variation of the AoI. Hence, the IL reduces with the ablation depth.
4 Simulation
The laser ablation process should be divided into discrete time steps. In every time step, the practical laser power intensity and the absorbed energy of the laser were calculated according to Eqs. (13) and (14). The electron warming model calculated the absorbed energy, according to Eqs. (21) and (22). Also, Eqs. (16)–(18) were pplied to analyse the atomic ionisation, the repulsive stresses, and activation of the MPI mechanism. If the density of free electrons becomes higher than a specific threshold value, the MPI mechanism should be activated as described. The amount of energy that ensures the minimum density of free electrons in the absorption layer was the threshold value required to activate the MPI mechanism. Otherwise, the energy should only be used to heat up the electrons. The MPI mechanism causes the density of the free electrons to change. Therefore, at each time step with the MPI, the free electron density should be updated along with the temperature of the free electrons and other physical properties. Then Eqs. (19) and (20) was used to transfer the energy of the electrons to the atoms.
The finite-difference model and its numerical equation were used to calculate the thermal gradient and temperature values in the free electrons and atoms after laser energy absorption. In the model, the finite difference method was applied with Du Fort-Frankel formulation to calculate the temperature of electrons and the material:
where cp is the material-specific heat capacity, ρ is the material density, K is the material heat conductivity, \( {T}_{i\ j}^n \)is the temperature in node with row number i, column number j, and in time step n, ∆x is the width of every element on the workpiece surface, ∆y is the depth of every element through the workpiece material.
Each pulse includes the radiation time of tp = 10 ps. Since the repetition frequency of the utilised laser is 400 kHz, the cooling time that is the rest time between two consecutive pulses would be 2.5 μs.
It is essential to select the appropriate time step ∆t in order to obtain the convergence for Eq. (23) [37]. If the material ablation for each node is expected, its corresponding cp and K values should be rewritten so that the absorbed energy does not lead to the increasing temperature of this node and is entirely transferred to the nodes in underlying layers.
According to Fig. 11, the 2D simulation was carried out for the beam radius instead of the full beam. Therefore, the total time of the simulation is determined considering beam radius and velocity. The workpiece was discretised in elements with width and length of ∆x = 2 μm and ∆y = 20 μm, respectively, as shown in Fig. 11. The simulation was performed on the A-A cross-section parallel to the central laser beam axis. The data of the elements, including temperature values and the material properties, is stored in the corresponding matrixes. The absorbed energy of the pulse is calculated, considering the Gaussian and AoI factors, according to Eq. (13). The time increments for the radiation phase, and the cooling sections are not the same to maintain the stability of Eq. (23). Material state and its physical properties, like cp and K change with temperature. Hence, at each time step, the absorbed energy of the laser and mechanism of laser-material interaction is determined. Then, the elements data should be updated, including the temperatures of lattice and electrons, thermal properties of the material and free electrons, the density of ions, and free electrons. Finally, regarding the volume of ablated material, the geometry of the model is refreshed. A significant portion of absorbed energy is dissipated through thermal conduction in the material in the cooling section. In this regard, thermal conduction follows classical equations like Fourier conduction equations.
As shown in Fig. 12, in every time increment, the updated properties of the material and the applied laser, the Gaussian equations, laser incident angle, and the practical laser power intensity were calculated. A comparison of the computed laser power intensity with a critical value has clarified the laser-material interaction mechanism. The ablation depths in the interacted nodes were calculated through the laser-material interaction mechanism. The necessary laser power intensity, a threshold to switch the laser-material interaction mechanism from a thermal interaction to MPI, should be calculated in the simulation. Besides, in the thermal laser-material interaction mechanism, the practical sublimation temperature should be determined. Hence, for two different ablation tests, the mentioned values should be obtained by comparing the depth of ablations in the simulations with the corresponding experimental values. The maximum depth of ablation in the simulation validates with the corresponding experimental results.
5 Validation of simulation results
In this section, the ablation depth values, calculated by the simulation, were compared with the corresponding experimental results. Besides, the material removal rate, computed by the simulation, is also compared with the experimental values. The comparison showed a good agreement between the calculated values and the test results.
The next section describes the temperatures obtained from the simulation. The temperature values are compared with the HAZ in the practical results. The variables affecting temperature values and laser-material interaction mechanism can also be calculated in the simulation, such as laser absorption and power intensity during the laser process.
In the final part, determining factors such as the critical power intensity and the sublimation temperature were obtained by the simulation. The correct calculation of these values is crucial in the accurate and valid estimate of the cutting depth.
5.1 Depth of laser cuts
The simulated values of depth of laser cuts and material removal rate were validated with the corresponding experimental results. Figure 13 provides a comparison between simulation and experimental results. Accordingly, the simulation and experimental results are in good agreement. The error regarding the prediction of the laser cutting depth, ae − L was a maximum 10%. The source of the error may be attributed to the laser energy dissipation due to its collision with plasma and exchange energy of chemical reactions mentioned in Eqs. (5) and (6) as well as absorption of the laser energy in several reflections on the wall of deep laser cuts. The mentioned laser dissipation factors were not considered in the simulation model. As can be seen in Fig. 13, there is a logarithmic relation between the EL − input and ae − L:
where A = 4.81 J mm−2 and B = 217 μm.
According to Eq. (24), if EL − input is equal or less than A, the value of ae − L is equal to zero. Therefore, the A value is considered an ablation threshold.
The dimensions of V-shaped laser cuts in terms of ae − L and the wL were measured, and further, the total volume of the removed material by the laser was calculated. The relation between QL and EL − input is logarithmic with a negative coefficient and described as follows:
where C = 780.03 J mm−2 and D = 0.091 mm3 s−1.
The constant C is another threshold in Eq.. Until the QL is a negative value, Eq. is a valid equation for EL − input ≤ C. In EL − input = C, the QL should be zero. In the EL − input = C =780.03 J mm−2 and the PL = 50 W, the laser scan speed is 8.1 × 10−3 mm s−1. Hence, with an almost zero laser scan speed, the depth of laser cut cannot exceed a threshold value. It means that all the laser energy at a threshold ablation depth should be dissipated through the laser cut.
5.2 Temperature variations
Except for the depth of cut, the sample temperature can be calculated by the simulation during the laser process. The temperature values can indicate which part of the workpiece is most vulnerable to thermal shock. Here, it is essential to know the laser-material interaction’s exact mechanism to compute the temperature values. Therefore, the parameters affecting the mechanism, such as the laser power intensity, should initially be investigated.
The laser energy is distributed with the effects of several Gaussian factors, as shown in Eq. (13). The maximum radiation intensity of each pulse is calculated as Ipk = 1.83 × 1011 W cm−2 by Eq. (8). Since the repetition frequency and the power of the utilised laser are respectively 400 kHz and 50 W, the EL − pulse should be 125 μJ. Replacing the EL − pulse, the tp, and the r0 into Eq. (8) and considering Eqs. (9) and (10), the Ipk was calculated.
Another crucial factor is the angle of incidence. As explained before, the AoI can be changed by increasing the ae − L. In Fig. 10 and Eq. (12), effects of the ae − L on the AoI are illustrated. According to Eq. (13), the laser power intensity in the different AoI values would be changed with coefficient of AoI (CAoI). Figure 14 indicates calculated IL based on Eq. (13) throughout the laser beam radius in different AoI. As the maximum concentration of laser energy is on the centre of the beam (Fig. 14a), AoI highly influences the total laser power intensity in the centre of the laser beam where the maximum laser power intensity dramatically decreases from 1.1 × 1010 W cm−2 to 5 × 108 W cm−2 by increasing the AoI from 0° to 88° (Fig. 14b).
There is a IL − crt that differentiates the laser-material interaction mechanism and a principal factor in finding the temperature values. In IL > IL − crt, due to the considerable laser energy transferred to the material surface at about 100 fs, the free electrons temperature values become much higher than the material temperature in the radiation time [12]. The raise of the electrons temperature and free electron density due to ionisation of material leads to repulsive forces, destroying the whole irradiated surface.
In IL < IL − crt, the repulsive forces of free electrons are not enough to ablate the workpiece surface. Here, the laser energy transfers to the lattice in the workpiece and causes a thermal interaction in the material. As explained in Fig. 6, when the laser input energy density is in the range of 40 J mm−2 < EL − input< 60 J mm−2, the first indication of a HAZ and thermal damages is in the edges where laser cuts appear.
In thermal interaction, at the sublimation temperature (Tsep) a large portion of ablated material is directly transferred from the solid to the gas phase. Here, the lattice temperature during laser radiation is high enough in which the material evaporation takes place with the maximum speed (the sound speed) [12].
The Tsep as the ablation temperature in thermal interaction must be calculated in the non-equilibrium state of the experiments. For this purpose, after finding the IL − crt, the mathematical model was solved for given EL − input = 20 J mm−2, and 62.5 J mm−2. The effect of the chosen laser parameters on the ae − L and AoI indicated their indirect effect on IL since the IL decreases about 80% with increasing AoI from zero to 80°, which can change the laser-material interaction from thermal to ionisation mode. In EL − input = 20 J mm−2, the measured depth of laser cut from the experimental results was replaced in the mathematical model. If the material temperature in any node reached the sublimation temperature, the node supposed as ablated material. The Tsep was calculated. With the calculated sublimation temperature, depth of laser cut was obtained in EL − input = 62.5 J mm−2 and was validated with the corresponding experimental result.
According to Fig. 15, the percentage of absorption energy, considering Eq. (14), dramatically decreases by increasing EL − input up to 40 J mm−2. With comparison to the experimental results, it was found that the thermal influence of laser on the laser cuts increased in EL − input > 40 J mm−2, as indicated in Fig. 6, which is evidence of laser energy dissipation in the workpiece that is followed by increasing temperature instead of material ablation. Therefore, thermal interaction between laser and material at EL − input > 40 J mm−2 is dominant. To find out the IL − crt, the maximum EL − input in which no thermal damage presents, is detected in the first step. Then, AoI is calculated with respect to ae-L as a result by EL − input. Finally, the IL − crt is calculated according to Eq. (13). Accordingly, the minimum laser power intensity to avoid thermal damages is 1.5 × 109 W cm−2. Therefore, the laser-material interaction mechanism changes from MPI to thermal interaction by a reduction of laser power intensity to IL − crt = 1.5 × 109 W cm−2. The change of AoI, as shown in Fig. 14, higher than 70° results in a reduction in the laser power intensity to the value lower than the IL − crt. Consequently, the thermal interaction mechanism predominates over MPI.
Changing the laser-material interaction to the thermal mechanism leads to a dramatic increase in temperature in the working area. Figure 16 illustrates how free electron and ablated material temperature changes with the radiation time. Accordingly, the AoI has a remarkable influence on the temperature of free electrons. The free electron energy is transferred to the atomic lattice as thermal energy with relaxation time in the range of several picoseconds for ceramic materials [10]. Thus, the difference between the material temperature and free electrons reaches around 3000–8000 K. The IL becomes smaller, with an increase of the AoI, as mentioned before. Consequently, the absorbed energy by electrons and Te reduces. As shown in Fig. 16, the decrease of IL has a stronger effect on Te, rather than lattice T since the lattice absorbs energy from the free electrons first after several picoseconds (the relaxation time). Therefore, during single pulse radiation, according to the comparison of free electrons (dash lines) and material (full lines) temperatures in Fig. 16, it is found that the difference between the material and the free electron temperatures becomes smaller (~3000 K) when AoI increases to 70°.
To ablate material, the Nfree should exceed the Ncrt, as explained in Eq. (17). According to the simulation results, up to 70% of Si is ionised by the laser up to the depth of 19 nm (laser penetration depth) to provide free electrons with the density of Ncrt with dominance of MPI as laser-material interaction. The high density of ions in the laser penetration depth with the same charge causes a high level of the repulsive force between the free electrons based on Eq. (18). Due to the repulsive forces between the free electrons, it is expected that the whole material containing heated atoms and ions in this thin layer is distracted and removed from the surface. Therefore, the thermal energy of the removed material is not transferred to the underlying layers.
It is expected that the change of interaction mechanism from MPI to melt expulsion results in the formation of a thin molten layer in contact with the underlying surface, which remains even after the ending of the laser pulse time. The molten material has enough time to increase the workpiece temperature with the transfer of thermal energy during the solidification process.
In the case of thermal interaction, the material is removed once the workpiece temperatures reach the Tsep. In steady-state conditions, the chemical destruction of Si3N4 takes place at 2200 K, and the melting temperature is 3000 K (see Table 2). However, during laser irradiation, the rate of temperature increase is much higher than steady-state condition, and temperature can rise without any melting or chemical distraction. The determination of the corresponding temperature for removing material was a big challenge. According to the simulation and experimental results, the material temperature should exceed 4500 K with higher than 1500 K superheat (Fig. 17). In this condition, most material transforms into a gas state and enormously expand due to the laser energy. So, the material removal occurs through the melt expulsion as a result of local evaporation and the shock wave of the laser pulses.
The simulation results indicate that through increasing laser input energy density, EL − input, from 30 to 312 J mm−2, temperatures even higher than 4000 K might be obtained in the depth of 400 μm. The rapid temperature rise contributes to thermal shock throughout the workpiece depth. From the comparison between obtained simulation results and Fig. 6, it can be assumed that the thermal shock in EL − input > 40 J mm−2 has led to the material destruction up to the depth of 110 μm (Fig. 6a). It is in good agreement with the provided results in Fig. 6b.
Figure 18 indicates the simulated temperature distribution and the ablation topographies for different laser input energy densities. For EL − input = 6.25 J mm−2, no thermal effect can be detected, and the cold ablation is dominant. In the case of EL − input = 7.8 J mm−2 and 15.6 J mm−2, the increasing temperature mostly takes place in the peripheral of the laser cut where the laser power intensity is considerably lower than that in the laser beam centre. It leads to a shallow HAZ area near the laser cuts on the surface of the workpiece, which agrees with the experimental evidence mentioned in the other work by Soltani et al. [21]. To investigate the maximum depth of HAZ on the surface of the workpiece, microscopic images from the top of a laser cut, which was produced with the laser scan speed, vL = 2 mm s−1 (EL − input= 312.5 J mm−2), were taken (Fig. 19). Then the surface of the sample was polished to remove the recast layer. As shown in Fig. 19, under the recast layer, the HAZ was detected on the surface, which is an indicator of a thermal reaction on the surface of the workpiece (Fig. 19a). Afterwards, the samples were polished to a depth of 5 μm. By polishing up to a depth of 5 μm, the HAZ on the surface was removed (Fig. 19b), while some fsed SiO2 particles still remained in the laser cut. Therefore, the depth of HAZ next to the laser cuts could be less than 5 μm. The same results were investigated in all the laser cuts with EL − input > 40 J mm−2. Based on the results, the depth of HAZ in the laser cuts’ vicinity was a maximum of 5 μm on the surface. Besides, the exothermic oxidation of Si+ to recast SiO2 enhances the HAZ development near the laser cuts on the workpiece surface [21].
Laser HAZ and thermal damages of cuts with the picosecond laser (average pulse intensity, IL = 2.49 × 1011 W cm−2 and laser input energy density, EL-input = 312.5 J mm−2). a Top view after removing surface debris. b Top view polished to 5 μm [21]
According to previous results, thermal laser-material interaction for EL − input = 62.5 J mm−2 is expected to lead to a significant temperature rise, as shown in Fig. 18. Because of the high concentration of laser energy in the laser beam centre, a remarkable thermal effect is observed that is followed by more thermal damage.
According to the obtained results, the IL − crt is a principal factor in determining the laser-material interaction mechanism. In the non-thermal ablation, a severe increase in electron temperature and free electron density leads to the ablation of the whole material containing heated electrons before transferring the laser energy to the workpiece surface. However, in IL < IL − crt, the rise of temperature in the workpiece surface causes thermal damages as well as material ablation.
6 Conclusion
In the current investigation, the interaction mechanism between USPL with the wavelength of about 1000 nm and silicon nitride was studied. The minimum laser power intensity (IL − crt) for material ionisation as well as the Tsep as the ablation temperature in thermal interaction were calculated.
The ae − L in a mathematical model is found and compared with the practical results for EL − input = 6.25, 20 and 62.5 J mm−2. With appropriate values for IL − crt and Tsep, the mathematical model precisely predicted the laser ablation depths for the given EL − input. Next, the mathematical model was validated by the experiments with respect to laser ablation depth for different EL − input = 6–12.5 J mm−2. The model predicted the laser ablation depth with about 10% error in comparison to the corresponding experimental results. The amount of absorbed laser energy and the temperature of material ablation are other outputs of the mathematical model. The obtained results from this study are summarised below:
-
Decreasing laser power intensity to less than 1.5 × 109 W cm−2 leads to the change of interaction mechanism from MPI to melt expulsion. The reduction of IL is attributed to the changes in the AoI. It contributes to the reduction of QL temperature rise, an increase of HAZ, and in following thermal damage.
-
The minimum EL − inputto remove material is 4.81 J mm−2. In the beginning, the QL is maximum and gradually decreases with increasing EL − input. For EL − input > 20 J mm−2, the laser power intensity is less than 1.5 × 109 W cm−2. In this range, MPI is not the interaction mechanism, and workpiece temperature is higher than 4500 K due to rapid material heating. In this range of EL − input, the temperature of adjacent to the laser cut rise to 4000 K during laser radiation, which causes thermal damages with a maximum width of 100 μm.
In the peripheral of the laser cut, since the intensity of the laser was considerably lower than in the beam centre, the temperature enhances. It results in a shallow HAZ area near the laser cuts on the surface with a depth of <5 μm.
Data availability
The mentioned data in the current study are available from the corresponding author on reasonable request.
References
Samant AN, Dahotre NB (2010) Three-dimensional laser machining of structural ceramics. J Manuf Process 12(1):1–7
Oosterbeek RN, Ward T, Ashforth S, Bodley O, Rodda AE, Simpson MC (2016) Fast femtosecond laser ablation for efficient cutting of sintered alumina substrates. Opt Lasers Eng 84:105–110
Herrmann RFW, Gerlach J, Campbell EEB (1998) Ultrashort pulse laser ablation of silicon: An MD simulation study. Appl Phys A Mater Sci Process 66(1):35–42
Jandeleit J, Horn A, Weichenhain R, Kreutz EW, Poprawe R (1998) Fundamental investigations of micromachining by nano- and picosecond laser radiation. Appl Surf Sci 127-129:885–891
Bäuerle D (2011) Laser Processing and Chemistry. Springer, Berlin
Karnakis DM (2006) High power single-shot laser ablation of silicon with nanosecond 355nm. Appl Surf Sci 252(22):7823–7825
Dold CA (2013) Picosecond laser processing of diamond cutting edges. VDI-Verlag, Düsseldorf
Nolte S, Schrempel F, Dausinger F (eds) (2016) Ultrashort Pulse Laser Technology. Springer International Publishing, Cham
Liu X, Du D, Mourou G (1997) Laser ablation and micromachining with ultrashort laser pulses. IEEE J Quantum Electron 33(10):1706–1716
Ren Y, Chen JK, Zhang Y (2012) Modeling of ultrafast phase changes in metal films induced by an ultrashort laser pulse using a semi-classical two-temperature model. Int J Heat Mass Transf 55(5-6):1620–1627
Chen JK, Tzou DY, Beraun JE (2006) A semiclassical two-temperature model for ultrafast laser heating. Int J Heat Mass Transf 49(1-2):307–316
Brenk O, Rethfeld B (2012) Electron dynamics in transparent materials under high-intensity laser irradiation. Opt Eng 51(12):121810–121811
Ossi PM (ed) (2018) Advances in the application of lasers in materials science. Springer, Cham
Keldysh LV (1965) Concerning the theory of impact ionization in semiconductors. Sov Phys JETP 21(6):1135
Tan D, Sharafudeen KN, Yue Y, Qiu J (2016) Femtosecond laser induced phenomena in transparent solid materials: fundamentals and applications. Prog Mater Sci 76:154–228
Sugioka K, Meunier M, Piqué A (eds) (2010) Laser Precision Microfabrication. Springer-Verlag, Berlin
Soltani B, Hojati F, Daneshi A, Azarhoushang B (2019) Simulation of laser ablation mechanism of silicon nitride by ultrashort pulse laser. Procedia CIRP 82:208–213
Wippler J, Fünfschilling S, Fritzen F, Böhlke T, Hoffmann MJ (2011) Homogenization of the thermoelastic properties of silicon nitride. Acta Mater 59(15):6029–6038
Ceramtec MAD. Ceramic materials: advanced ceramics for mechanical engineering. https://www.ceramtec.com/files/ca_from_the_experts_en.pdf. Accessed Oct 2015
Khader I, Kailer A (2010) Damage mechanisms in silicon nitride wire-rolling tools: lab-scale experiments and correlation with finite element modeling. J Mater Process Technol 210(10):1314–1325
Soltani B, Azarhoushang B, Zahedi A (2019) Laser ablation mechanism of silicon nitride with nanosecond and picosecond lasers. Opt Laser Technol 119:105644
Sōmiya S (2013) Handbook of advanced ceramics: materials, applications, processing, and properties. Academic Press, Amsterdam
Kim J-D, Lee S-J, Suh J (2011) Characteristics of laser assisted machining for silicon nitride ceramic according to machining parameters. J Mech Sci Technol 25(4):995–1001
Dahotre NB, Harimkar SP (2008) Laser fabrication and machining of materials. Springer, New York
Eichler J, Eichler HJ (2006) Laser Bauformen, Strahlführung, Anwendungen. Springer, Berlin
Paschotta R (2008) Encyclopedia of laser physics and technology. Wiley-VCH, Weinheim
TRUMPF Tech. Doc. Dep (2007) Technical information: Laser machining, solid-state laser. Dokumentation, Technische
Rihakova L, Chmelickova H (2015) Laser micromachining of glass, silicon, and ceramics. Adv Mater Sci Eng 2015(2):1–6
Flaherty T, Kelly PV, Lynch S, Cundill RT, O’Keeffe M, Crean GM (1994) Determination of the optical reflectivity and absorption coefficients of silicon nitride ceramics. Adv Mater 93. https://doi.org/10.1016/b978-0-444-81991-8.50224-7
Heller J, Bartha JW, Poon CC, Tam AC (1999) Temperature dependence of the reflectivity of silicon with surface oxide at wavelengths of 633 and 1047 nm. Appl Phys Lett 75(1):43–45
Nedialkov NN, Atanasov PA, Sawczak M, Sliwinski G (2003) Ablation of ceramics with ultraviolet, visible, and infrared nanosecond laser pulses. Proc. SPIE 5120, XIV International Symposium on Gas Flow, Chemical Lasers, and High-Power Lasers, (10 November 2003). https://doi.org/10.1117/12.515847
Kasap S (ed) (2006) Springer handbook of electronic and photonic materials. Springer Science+Business Media Inc, Boston
Lombardo S, Stathis JH, Linder BP, Pey KL, Palumbo F, Tung CH (2005) Dielectric breakdown mechanisms in gate oxides. J Appl Phys 98(12):121301
Koroleva O, Mazhukin A (2017) Determination of thermal conductivity and heat capacity of silicon electron gas. Mathematica Montisnigri 40:99–109
Kasunic KJ (2015) Optomechanical systems engineering. Wiley, Hoboken
Itina TE, Utéza O, Sanner N, Sentis M (2008) Ultrashort laser interaction with metals and optical multi-layer materials: transport phenomena and damage thresholds. In: Phipps CR (ed). SPIE, 70050N
Hoffman JD (2001) Numerical methods for engineers and scientists, 2nd edn. CRC Press, Boca Raton
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was financially supported by the “Ministerium für Wissenschaft, Forschung und Kunst Baden Württemberg” who provided the financial support of the graduate school “Generierungsmechanismen von Mikrostrukturen” (GenMik).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics approval
All used materials and applied devices included in the manuscript belong to the authors and do not require any third party permission.
Consent to participate
The mentioned authors participated in all steps of the manuscript preparation.
Consent for publication
All authors have read and agreed to publish the manuscript if accepted.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Soltani, B., Hojati, F., Daneshi, A. et al. Simulation of the laser-material interaction of ultrashort pulse laser processing of silicon nitride workpieces and the key factors in the ablation process. Int J Adv Manuf Technol 114, 3719–3738 (2021). https://doi.org/10.1007/s00170-021-07111-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-07111-5