1 Introduction

The parts of a mechanical assembly are manufactured with random deviations from their nominal geometry. Once the parts are connected, the geometric errors stack up through the contact features between them. As a result, an assembly dimension (i.e., the relative position between features of different parts) may also deviate so that the function of the product could be negatively affected.

Such issues are commonly avoided by specifying tighter tolerances on part features. This requires that the parts are manufactured with more accurate processes, which are usually slower and more expensive. To get a good compromise between quality and cost, the designer should find out which tolerances have the most influence on the variation of the assembly dimension, and reduce them more than others with less influence. These decisions can be optimized by solving a problem of tolerance allocation: given the allowable variation on the assembly dimension, determine the set of tolerances that minimizes the total manufacturing cost.

In its traditional formulation, tolerance allocation regards the tolerances as the only variables to be optimized. However, the error stackup depends on the nominal dimensions of the features as well. In principle, these could be optimized together with the tolerances, so that the specified assembly variation could be met with wider tolerances on the individual parts.

The optimization of nominal dimensions is a special case of robust parameter design, a problem aimed to reducing output variation in any type of system. In literature, the problem has been tackled using two main approaches. The first one is based on experimental or simulation plans, which are suitable for complex systems that cannot be described by simple mathematical models. The second one is based on analytical or numerical optimization, which allows an easier search for solutions in continuous spaces of many variables, with possible constraints and multiple objectives. Robust optimization seems to have more applications in tolerancing, probably due to the availability of mathematical methods for stackup analysis. In few cases, however, dimensions and tolerances have been treated jointly in the same optimization problem.

Integrating dimension and tolerance optimization is the main goal of this paper. Although in principle the robust allocation problem would make sense for any type of assembly, the study will focus on planar linkages for applications in structures and mechanisms. These are interesting for tolerancing problems as their complex layout may involve some difficulties in stackup calculations; moreover, they lend themselves to a simple, standard definition of the optimization problem. The proposed method treats the dimensions as direct optimization variables, while the tolerances are set in background using conditions for optimal allocation. These are found using an analytical optimization method (Lagrange multipliers), a cost-tolerance function including the effect of dimensions, and a method for stackup analysis based on a static analogy.

The paper is structured as follows. Section 2 reviews available studies on parameter and tolerance design for generic systems, mechanical assemblies and linkages. Section 3 defines the optimization problem and the assumptions underlying the proposed method, which is described in Section 4 and demonstrated on two examples in Section 5. The conclusions in Section 6 discuss the benefits and limitations of the method.

2 Background

The work is related to several research topics as discussed below.

2.1 Robust parameter design

A system is designed with the goal of improving its outputs through an optimal setting of its inputs. However, this may not guarantee a consistent behavior of the system because of variation sources (noise factors and errors in the input values), which may cause excessive output variation. Taguchi introduced the concept of robust design, which aims to reduce the effect of variation sources on outputs [1, 2]. He also proposed methods based on design of experiments (DOE) to achieve this goal [3, 4]. The core of Taguchi methods is parameter design, which uses an experimental plan based on orthogonal arrays to select the settings of system inputs (control factors) that are less sensitive to noise factors. Applications of the methodology to the design of manufactured products are reported in [5,6,7]. Attempts were also made to translate the Taguchi concepts into either practical design principles [8], or metrics to evaluate the robustness of a design [9].

Alternative DOE approaches to parameter design are mostly based on the response surface methodology (RSM). Its advantages on Taguchi methods include more efficient plans and the estimation of interaction effects between control factors, which can drive the search for optimal solutions [10,11,12,13]. Extensions of Taguchi and RSM approaches have been proposed to treat cases with multiple outputs or multi-objective decisions [14,15,16], and to improve the estimation of interaction effects [17]. Other studies adopt different experimental strategies and criteria for parameter selection [18, 19].

Robust optimization methods have been proposed as an alternative to DOE when dealing with complex cases involving many variables, constraints, unknown output functions, or statistical distributions [20,21,22,23]. The selection of parameter settings is modeled as an optimization problem in a continuous domain; the proposed objective functions include the output range for a given input setting [24,25,26], and the effect of the uncertainty in the model used for output calculation [27].

2.2 Tolerance allocation

The problem of tolerance allocation for a mechanical assembly has been studied extensively in literature. Given the allowable variation on the output (the assembly dimension), the goal is to determine the tolerances on the part dimensions that are linked to the output through a chain of assembly relationships (tolerance chain). This is described by an exact or approximate stackup function, which can be found by either geometric inspection or one of the available methods of tolerance analysis [28]. The optimal allocation is usually the one that minimizes a cost function while satisfying the constraint on output variation.

Introductions to tolerance allocation and classic application examples are given in [29, 30]. A recent review on allocation methods [31] cites about 250 studies, classifying them in a detailed taxonomy. This includes the definition of the optimization problem (objective functions, constraints), the cost-tolerance models, and the assumptions on assembly requirements, tolerances (dimensional or geometric), and stackup criteria (worst-case, statistical). Other reviews [32, 33] are also recommended for a full account of available approaches.

Most methods use search algorithms to find optimal tolerance allocations. In this work, an analytical solution is preferred for an easier integration with parameter optimization. In literature, analytical methods have been proposed under simplified yet realistic assumptions (dimensional errors with normal distributions, linear or first-order Taylor stackup functions). The most widely known is the method of Lagrange multipliers [34], which is also the basis for many numerical solutions.

Robust design concepts have been applied to tolerance allocation, in the attempt to balance the conflicting criteria of reducing cost and output variation. As in generic design problems, DOE and optimization are the two main routes to robust allocation.

In Taguchi methods, tolerance design is carried out after parameter design [35]. It is based on the quality loss function, which expresses the economic impact of deviations from the target output value. The concept is used to allocate tolerances on the control factors of the system, once an experiment has allowed to estimate the contribution of each factor to the overall quality loss. Modifications of Taguchi’s tolerance design have been proposed in [36,37,38]. Other DOE approaches replace the quality loss with alternative selection criteria including the output variance [39] and various formulations of a cost function [40,41,42,43].

In optimization methods, quality measures are introduced into the objective functions or the constraints of the problem. Two common choices for the quality measure are the quality loss and the nonconforming rate. In the first approach (design for quality), the objective function is a sum of the manufacturing cost and the quality loss; this defines an unconstrained optimization problem, which has been solved with several search algorithms (see again [31,32,33] for reviews) and applied to some special formulations of the tolerancing problem [44,45,46,47,48,49,50,51,52]. In the second approach (design for reliability), several formulations have been proposed: minimize cost with a constraint on the nonconforming rate [53,54,55,56,57], maximize a process capability index [58], or optimize a function of cost and various indices related to the nonconforming rate [59,60,61]. Other formulations and choices of the objective function are discussed in [62,63,64,65,66].

2.3 Optimal selection of dimensions and tolerances

A few studies have dealt with the optimization of both dimensions and tolerances. This usually involves extending tolerance allocation problems by adding one or more dimensions as optimization variables, with constraints on the allowable design ranges. The sum of cost and quality loss (or a function of nonconforming rate) is minimized with several methods in problems involving single dimensions [67,68,69] or tolerance chains [70,71,72,73,74]. In [75], the cost is evaluated as the sum of separate elements depending on parameters and tolerances, while the output range is treated as a constraint. In [76, 77], a multi-objective genetic algorithm is used to optimize regression functions of cost. In [78], a Pareto frontier is generated to balance cost optimization with application-dependent performance metrics. In the RSM-based method of [79], a modified process capability index is defined to balance the conflicting objectives of minimum cost and maximum process capability.

An additional requirement with respect to plain tolerance allocation is that the solution space must also satisfy the geometric closure of the assembly as well as possible structural or functional requirements. These issues are usually overcome by solving two sequential optimization problems. In [80], the dimensions are found by minimizing the output variance for a tentative tolerance setting; then, the tolerances are allocated by minimizing a linear combination of cost and output variance. In [81], the dimensions are selected by minimizing quality loss using RSM on a plan of simulations; then, the tolerances are refined by minimizing an objective function including quality loss and cost of scrap or rework. In the single-variable problem of [82], the two stages optimize process means and variances with respect to cost and quality loss by closed formulas.

In the attempt to avoid two separate optimization stages, [83] minimizes the total cost with a constraint on the assembly dimension by Lagrange multipliers with numerical solution; unlike other cases, the optimal dimensions are selected in narrow ranges around reference values satisfying geometric and functional constraints. Other methods join the two stages by excluding cost from the objective function. [84] minimizes the variance of an overall performance measure given by the weighted sum of the variances of the functional requirements. In [85], process means and tolerances are selected with a geometric procedure that finds the points furthest from the boundaries of the allowable ranges in the space of nominal dimensions.

2.4 Tolerance allocation on linkages

The above problems have also been studied for some types of linkages. The design of parameters is usually done by extending classical design problems in order to comply with specific structural or kinematic requirements. For structures, robust design optimization is an extension of deterministic structural optimization with random uncertainty sources including dimensional errors [86,87,88,89]. For mechanisms, the kinematic synthesis problem has been extended to a stochastic formulation to consider the effects of dimensional errors on the desired kinematic function [90,91,92,93,94,95,96].

Tolerance allocation on mechanisms is often addressed by minimizing output variation over a set of different poses; the output is usually defined as the position of a point of interest. In [97], Lagrange multipliers are used in two optimization stages, which optimize output variation and cost. In [98], Lagrange multipliers are combined with a penalty function to minimize the cost with stackup constraints. In [99, 100], the output variation is minimized with a cost constraint. Taguchi-like methods have been proposed with different experimental designs to take into account kinematic and dynamic parameters [101, 102], joint clearances and additional errors from assembly and operating conditions [103], and sets of poses of the mechanism with reduction to a single performance index [104]. Both experimental and optimization methods have been attempted for specific types of mechanisms such as robotic manipulators [105, 106]. A related problem has also been addressed for machine tools through the statistical analysis of multibody models [107].

In the above studies, dimensions and tolerances are usually optimized in distinct phases of mechanism design, namely kinematic synthesis (with given tolerances) and tolerance allocation (with given dimensions). In one case, however, the two phases are joined into a single problem. It consists in a robust optimization based on a graphical model, an ellipsoid in the space of variables, whose semi-axes are in inverse relationship with the sensitivity of the output to the corresponding variables [108]. This allows to express the objective of robust design by geometric conditions on the ellipsoid (size, aspect ratio, and orientation); the conformance is checked by comparing the ellipsoid with a tolerance box representing the tolerances specified on the variables [109].

2.5 Overview

The hypothesis of this work is that the dimensional parameters of an assembly can be optimized together with the tolerances in order to reduce the output variation due to manufacturing errors. It is apparent that this objective has been recognized in a diversity of design problems well beyond the field of tolerancing. Robust parameter design as a DOE methodology allows to treat complex systems whose outputs can only be evaluated by physical testing or computer simulation. However, it is not suitable to problems with many variables, constraints, and interaction effects; the parameters are selected from discrete values, and optimal settings can only be found by iterations of the experiments. These limits are overcome by robust optimization methods, which require continuous and possibly differentiable output functions. In both approaches, parameters and tolerances are usually selected in distinct phases rather than in a single optimization problem.

The same dichotomy between DOE-based and optimization approaches applies to tolerance allocation. The availability of methods for tolerance stackup calculations justifies a relative preference for optimization methods, which incorporate robustness by adding the quality loss or the nonconforming rate to either the objective functions or the constraints. However, the allocation problem is usually defined with given dimensions. The separate optimization of dimensions and tolerances has been attempted with DOE approaches or multi-objective problems, where the two usual objectives (output variance and cost) are combined with weighting functions or kept separate for a final selection of Pareto-optimal solutions. The effective integration of the two problems seems to be restricted to special formulations, which include single-dimension problems, selection of parameters in narrow ranges, or optimization problems without cost functions.

Tolerance allocation on linkages has been mostly studied for applications on path-generating mechanisms, where the optimization spans a set of positions of the tracing point. The robust optimization of dimensions and tolerances has been perceived as a useful extension of the allocation problem with given dimensions, with promising theoretical contributions (such as the sensitivity ellipsoid) that could pave the way for the treatment of increasingly complex design cases.

The literature review seems to justify the goal of a seamless optimization of dimensions and tolerances. An aspect that has been relatively neglected, and which will be discussed below, is that treating dimensions as additional optimization variables emphasizes the need of cost models including the influence of dimensions as well as tolerances. Such a model has been proposed in a recent study [110] as an extended formulation of one of the available cost-tolerance functions, and will be used in this study.

3 Problem and assumptions

This work will consider planar linkages with rigid links connected by revolute and prismatic joints. They are assumed to be exactly constrained; this condition applies to isostatic structures such as trusses, but also to mechanisms with a degree of freedom locked in a reference pose. These assumptions cover a wide diversity of function-generating and path-generating mechanisms; the proposed method does not place limits on the number of links and joints, although particularly complex mechanisms may require the analysis of many poses as well as a greater amount of calculations for each pose. The extension to mechanisms with higher kinematic pairs may require further developments for the necessary extensions of the calculation procedures.

The output Y defined on the linkage is a linear or angular dimension defined at assembly level, such as the absolute position of a point along a certain direction, the distance between two joints, or the orientation of a link. The output is to be controlled within a tolerance TY from a nominal value Y0 to ensure the desired function of the linkage.

The output depends on n dimensions Xi of individual parts; they include the lengths of links, and the diameters of holes and pins. The relationship between the output and the dimensions is assumed to be a linear (or linearized) stackup equation:

$$ Y=\sum \limits_{i=1}^n{S}_i{X}_i $$

where Si is the sensitivity of the output to dimension Xi.

Each dimension has a nominal value X0i and a tolerance Ti, which can be controlled through the manufacturing process of the part. In statistical tolerancing, the dimensions Xi are assumed to be independent and normally distributed. Their means are equal to the X0i, and their standard deviations σi are in a constant proportion with the Ti. The nonconforming rate is assumed to be low, e.g., ≤ 0.27% if Ti ≥ 3σi. Under these assumptions, Y is also normally distributed with mean Y0 and standard deviation in the same proportion with T0; the output tolerance is calculated from part tolerances through the root-sum-square (RSS) equation:

$$ {T}_Y=\sqrt{\sum \limits_{i=1}^n{S}_i^2{T}_i^2} $$

If any of the above assumptions is violated, the stackup of the input tolerances results in a higher output error due to various reasons (covariance terms, linear accumulation of systematic errors, etc.). These effects are accounted for by a correction factor c ≥ 1 in the RSS equation [29]:

$$ {T}_Y=c\sqrt{\sum \limits_{i=1}^n{S}_i^2{T}_i^2} $$

A 50% increase of the output tolerance is often assumed (c = 1.5), although more accurate statistical expressions of the correction factor are available [111].

In tolerance allocation, the X0i are given and the Ti are the variables of the following optimization problem:

$$ {\displaystyle \begin{array}{l}\min \sum \limits_{i=1}^n{f}_i\left({T}_i\right)\\ {}\mathrm{s}.\mathrm{t}.\kern0.5em {T}_Y^2={c}^2\sum \limits_{i=1}^n{S}_i^2{T}_i^2\end{array}} $$
(1)

where fi(Ti) is the cost-tolerance function for Xi. Further constraints on the values of the individual Ti can be avoided assuming that the minimum cost is always reached within the allowable tolerance ranges.

The proposed extension considers the X0i as optimization variables in addition to the Ti. That is, in addition to the optimal tolerances, the optimal values of the nominal dimensions are also searched for in the domain of possible configurations of the linkage. Just like the tolerances, the dimensions must also meet some conditions, which include the following:

  • Constant values possibly set for some dimensions in order to control the overall size of the linkage;

  • The nominal value of the output dimension:

$$ {Y}_0=\sum \limits_{i=1}^n{S}_i{X}_{0i} $$

  • Relationships that must occur between the dimensions in order to ensure the geometric closure of the assembly; as a simple example, in a rectangular truss the lengths of two links (one horizontal and one vertical side) determine the lengths of all the other links (the opposite sides and the diagonal).

The optimization problem could be formally defined by adding constraints for these conditions to (1). However, this choice would lead to different constraint equations for each different case, and would lose the chance of a solution in common form for all possible linkages. For the purposes of this work, it is rather suggested that the designer identifies a set of independent dimensions, i.e., those that can be freely optimized without violating the above conditions. These will be treated as the optimization variables, while the other non-constant dimensions will be expressed as functions of the independent ones.

The independent dimensions may even be chosen outside the set of X0i; in some cases, it might be better to optimize auxiliary geometric variables, such as an angle (e.g., to determine two sides of a right triangle) or a ratio between two dimensions (to allow their choice in a wide range while controlling the aspect ratio of the linkage). Any possible set of independent dimensions is likely to lead to the same optimal set of X0i; the choice should generally be guided by the need for simplicity and clarity of the geometric relationships. When dealing with mechanisms, however, explicit constraints may need to be added to the optimization problem in order to avoid solutions that are technically not feasible, e.g., causing the jamming of a mechanism. In this paper, such possibility will not be considered, and any kinematic and static verification of the linkage will be assumed to have been carried out according to the type and function of the mechanism being designed. General criteria for these tasks are currently dealt with in kinematic synthesis, where the parameters of a mechanism are optimized either deterministically or including the effects of random errors with given tolerances [90,91,92,93,94,95,96].

The above defined optimization problem has two more difficulties than plain tolerance allocation:

  • The cost-tolerance functions depend on the nominal dimensions: a given tolerance is more expensive to satisfy on a larger dimension due to some variation sources in the manufacturing process (e.g., deformations of workpieces and fixtures);

  • The sensitivities Si depend on the nominal dimensions: these determine the layout of the linkage, and therefore the geometric relationships among the different links and joints.

4 Method

The proposed solution is based on a known method for tolerance allocation, which is used to establish analytical conditions on the optimal tolerances. These are expressed as a function of the dimensions using a suitable cost-tolerance function. An optimization problem is then defined for a set of independent dimensions. Its solution requires the calculation of sensitivities, which is done through a tolerance analysis method based on a static analogy.

4.1 Optimal allocation

For any choice of dimensions, the optimal tolerances are the solution of the allocation problem (1). The Lagrange multiplier method [34] finds them by solving the following unconstrained optimization problem:

$$ \min C=\sum \limits_{i=1}^n{f}_i\left({T}_i\right)+\lambda \left({T}_Y^2-{c}^2\sum \limits_{i=1}^n{S}_i^2{T}_i^2\right) $$

The multiplier λ is calculated by equating the derivatives ∂C/∂Ti to zero:

$$ \lambda =\frac{\partial {f}_i/\partial {T}_i}{2{c}^2{S}_i^2{T}_i} $$

The above expression can be made explicit by choosing a relatively simple form for fi(Ti), such as the reciprocal power function:

$$ {f}_i={a}_i+\frac{b_i}{T_i^k} $$
(2)

where ai is a fixed cost with respect to tolerance, while bi and k are the factor and the exponent of the variable cost with respect to tolerance (the only parameters that appear in ∂C/∂Ti). As λ is constant for i = 1, ... n, the following analytical relationship among the optimal tolerances is found:

$$ {\left({T}_i\right)}_{\mathrm{opt}}\propto {\left(\frac{b_i}{S_i^2}\right)}^{\frac{1}{k+2}} $$
(3)

These known results will be the starting point to build a method for the simultaneous optimization of dimensions and tolerances. The method of Lagrange multipliers with RSS equation and reciprocal power cost-tolerance function could seem a limiting choice: in fact the allocation problem is treated in literature with less restrictive assumptions on the distributions of dimensions (not normal), on the stackup functions (not linear, or even not known a priori), and on the very nature of the optimization problem (with discrete variables in the presence of alternative choices on processes and equipment). The proposed approach may be justified by the objective of verifying the feasibility of extending the problem considering the various types of constraints (geometric, functional, structural) that may occur on part dimensions. Based on existing approaches, it is not obvious that the improvements over classical tolerance allocation outweigh possible complications in defining and solving the problem. It is believed that the answer to these questions should be sought in the simplest formulation of tolerancing problems, where an assembly dimension is determined by the linearized stackup of part dimensions satisfying basic statistical assumptions (independence, normal distributions, limited nonconforming rate). This will allow a sufficiently simple analytical formulation, on which the possible benefits of the extension can be more easily evaluated.

4.2 Cost-tolerance function

As mentioned, the cost parameters in (2) depend on the dimensions. The reciprocal power function has been widely used in literature assuming values for bi and k from application-dependent cost data. In an expanded form of the same function proposed in [110], the exponent is constant and the factor is empirically related to the nominal dimension:

$$ {b}_i={\beta}_i{X}_{0i}^{k/3} $$
(4)

Therefore, the variable cost of a feature depends on its nominal dimension through a power-law relationship with an exponent equal to one-third of that of its tolerance. This result was obtained in [110] through the regression of data from several sources on the costs of machining processes as a function of the tolerance grades on the machined features. The same analysis led to the estimate of a value k = 0.55 for the exponent of the cost-tolerance function, which should be verified on real cost data in specific production contexts.

The coefficient βi depends on the properties of the part feature associated to the dimension:

$$ {\beta}_i={f}_{\mathrm{A}i}\cdotp {f}_{\mathrm{F}i}\cdotp {f}_{\mathrm{M}i}\cdotp {b}_0 $$
(5)

where:

  • fAi is the area of the feature in cm2;

  • fFi depends on the shape of the feature; possible values on rotational parts are 0.75 and 1.25 respectively for external and internal features; on prismatic parts, 1.5 for cylindrical features, 1–1.5 for non-cylindrical features, and 0.5–1 for planar features (higher values for smaller features);

  • fMi is inversely related to the machinability of the material, with base 1 for mild steel, in a range from about 0.3 for aluminum alloys to about 2 for stainless steels;

  • b0 is a constant that does not influence the allocation results (b0 = 1.0 · 10−3 from [110]).

Compared to the basic reciprocal power function, the expanded form makes explicit the influence of the nominal dimension in the cost of a feature. As discussed in [110], this should improve the consistency of the results of tolerance allocation, as the costs of all features involved in a tolerance chain are more easily estimated on a common scale. The function is even more useful in the present work, where the nominal dimensions are treated as additional variables of the optimization problem.

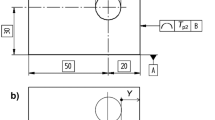
Equation (4) was obtained for linear dimensions, but can be extended to angular dimensions. However, the cost of an angular dimension is likely to depend not so much on the nominal angle as on the adjacent linear dimensions. In a general situation of the type illustrated in Fig. 1, an angle θ in radians is limited by two linear features (e.g., edges of a part) with lengths l1 and l2. If one of the two elements is subject to tolerance (T1 or T2), the resulting variation on θ is

$$ {T}_{\theta }=\frac{T_1\sin \theta }{l_2}\kern0.75em \mathrm{or}\kern0.75em {T}_{\theta }=\frac{T_2\sin \theta }{l_1} $$
Fig. 1
figure 1

Tolerance on an angular dimension

Full size image

For simplicity, it can be assumed that Tθ is related to the geometric mean l of the two lengths:

$$ {T}_{\theta }=\frac{T_l\sin \theta }{l}\kern0.5em ,\kern0.75em l=\sqrt{l_1{l}_2} $$
(6)

In (4), the angle must be associated to an equivalent nominal dimension Xθ, which has the same cost as l for the same variation. Considering only the variable cost, (2) and (4) give the condition

$$ \frac{X_{\theta}^{k/3}}{T_{\theta}^k}=\frac{l^{k/3}}{T_l^k} $$

which combined with (6) becomes

$$ \frac{X_{\theta}^{k/3}}{T_{\theta}^k}=\frac{\sin^k\theta }{T_{\theta}^k{l}^{2k/3}}\kern0.75em \to \kern0.75em {X}_{\theta }=\frac{\sin^3\theta }{l^2}=\frac{\sin^3\theta }{l_1{l}_2} $$
(7)

Therefore, the expanded form (4) of the variable cost factor can also be used for an angular dimension in radians by replacing the nominal angle with an appropriate function of the angle and of the adjacent linear dimensions.

Substituting (4) into (3) gives a new condition on optimal tolerances, which explicitly takes into account the nominal dimension and the properties of the feature:

$$ {\left({T}_i\right)}_{\mathrm{opt}}\propto {\left(\frac{\beta_i{X}_{0i}^{k/3}}{S_i^2}\right)}^{\frac{1}{k+2}} $$
(8)

Without loss of generality, it is now assumed that all the links are similar for material, shape, section size, and hole diameters. This implies that the coefficients βi have the same values for all the Xi. This can be justified by considering the product (fAi · fFi) that appears in the expression (5) of βi. The features are either the holes (for the link lengths and the hole diameters) or the cylindrical surfaces of the pins (for the pin diameters). The pin surfaces have double area fAi with respect to the holes (assuming that each pin connects two links), but a shape coefficient fFi half that of the holes (0.75 vs 1.5), and thus equal value of their product. As a result, the condition (8) on optimal tolerances for the linkage simplifies to

$$ {\left({T}_i\right)}_{\mathrm{opt}}\propto {\left(\frac{X_{0i}^{k/3}}{S_i^2}\right)}^{\frac{1}{k+2}} $$
(9)

4.3 Objective function for nominal dimensions

The optimal dimensions can be found by solving another optimization problem whose only variables are the X0i. The objective function is the stackup of the optimal tolerances

$$ \sigma =c\sqrt{\sum \limits_{i=1}^n{S}_i^2{T}_i^2} $$

where the Ti satisfy the condition (9) for each possible set of Xi. To optimize the output variance σ2, the problem can be defined as

$$ \min \sum \limits_{i=1}^n{S}_i^2{\left(\frac{X_{0i}^{k/3}}{S_i^2}\right)}^{\frac{2}{k+2}}=\sum \limits_{i=1}^n{X}_{0i}^a{\left|{S}_i\right|}^{3a}\kern0.5em ,\kern1.25em a=\frac{2k}{3\left(k+2\right)} $$
(10)

with a = 0.14 for k = 0.55. The overall problem is therefore solved concurrently by two nested optimizations: minimum-variance dimensions are found by assuming minimum-cost conditions for the tolerances. Once the optimal dimensions are known, the optimal tolerances are scaled to the specified output tolerance TY:

$$ {T}_i=\frac{T_Y}{c}\frac{\left({T}_i/{T}_1\right)}{\sqrt{\sum \limits_{i=1}^n{S}_i^2{\left({T}_i/{T}_1\right)}^2}}\kern0.5em ,\kern1em \frac{T_i}{T_1}={\left(\frac{X_{0i}^{k/3}}{X_{01}^{k/3}}\frac{S_1^2}{S_i^2}\right)}^{\frac{1}{k+2}} $$
(11)

This last step should not be considered a second optimization phase, as the proportions between the tolerances are already included in condition (9) and therefore incorporated by (10). The underlying assumption is that the optimality condition does not depend on the tolerance specification on the output dimension. This is not guaranteed, however, because cost-tolerance functions are not linear; a proportional increase of all tolerances would thus change the relationships between the corresponding costs, which may yield a total cost that is no longer optimal. To verify if the nested optimizations are able to approximate the solution of the original optimization problem (1), the solution space must be explored in the search of the minimum cost over the acceptable combinations of independent dimensions. In the following, such a verification will be made on two simple examples by enumerative search; in more complex cases, different constrained or unconstrained search algorithms may be required.

4.4 Calculation of sensitivities

In the objective function (10), the sensitivities Si = ∂Y/∂Xi depend on the dimensions. Given the layout of the linkage, the Si can be calculated with one of the tolerance analysis methods available in literature. The method that will be used here was previously proposed for rigid and exactly constrained assemblies [112] and later demonstrated on planar linkages [113].

The method is based on a static analogy, which converts the tolerance analysis problem into an equivalent problem of force analysis. In the linkage of Fig. 2a, the output Y is the position of a point along a given direction and has unknown sensitivities to the dimensions of the parts (lengths of links, diameters of holes and pins). As shown in Fig. 2b, the problem is solved by considering an equivalent static model, where an external force F is applied to the output point along the output direction. The analysis of the forces on the static model requires a free-body diagram to show the support reactions and the forces between the links; these are calculated from the equilibrium equations, which are equal in number to the unknown force components as the linkage is exactly constrained. The solution of the static model gives the axial internal forces Fi in the links. The sensitivities of the output to link lengths are then found dividing the internal forces by the external force:

$$ {S}_i=\frac{F_i}{F} $$
(12)
Fig. 2
figure 2

Static analogy: (a) output and dimensions; (b) equivalent static model

Full size image

Other types of dimensions and outputs can be treated similarly. If the output is the distance between two points of the linkage, opposite forces are applied to the two points in the direction of their distance. For angular dimensions or outputs, the internal or external force is replaced by a torque. A mechanism can be analyzed in one of its poses by locking its degrees of freedom with additional constraints; the internal force or torque corresponding to each constraint gives the sensitivity of the locked linear or angular displacement.

Due to joint clearances, the output also depends on diameters D and d of holes and pins. Their sensitivities are calculated as

$$ {S}_D=\frac{1}{2}\frac{F_i}{F} $$
(13)
$$ {S}_d=-\frac{1}{2}\sum \limits_j\frac{F_j}{F} $$
(14)

where Fi is the axial force of the same link of a hole and the Fj are the radial forces on a pin by adjacent links or supports (Fig. 2b).

As discussed in [113], the static analogy derives from the application of the principle of virtual work to the equilibrium condition on an assembly or linkage. Although it has only been demonstrated on planar systems, the analogy could therefore be extended to three-dimensional problems. This would require further developments to deal with new cases of geometric errors (e.g., angular errors in different directions), and to establish their correspondences with new types of internal forces (e.g., twisting moments or bending moments in different directions). In the treatment of spatial mechanisms, further types of joints would have to be considered (e.g., helical or spherical joints); moreover, it is likely that the solution of some 3D static models is so complex to require a dedicated software implementation.

5 Examples

The method will now be demonstrated on two examples: a structure with one independent dimension, and a mechanism with two independent dimensions.

5.1 Structure

Figure 3 shows a truss with three members, simply supported at points A and B. The upper member has nominal length L1 and nominal angle δ to the horizontal. All the joints include pins with nominal diameter d and holes with nominal diameter D = d, connected with a line fit. The optimization variables include the nominal dimensions L2 and L3, and the tolerances on all dimensions (L1, L2, L3, D, d). The output is the vertical position Y of point C with respect to A (nominally equal to L1 sinδ), for which a tolerance TY is specified.

Fig. 3
figure 3

Truss structure

Full size image

From Eqs. (1), (2), and (4), the cost associated to dimension i can be expressed as

$$ {f}_i\left({T}_i\right)={a}_i+\frac{\beta_i{X}_{0i}^{k/3}}{T_i^k} $$
(15)

The cost function can be simplified by excluding the fixed cost ai and considering that, under the assumptions discussed in the comment to Eq. (8), the coefficient βi is equal for all the dimensions of a planar linkage. A suitable objective function fC is thus the sum of the variable costs divided by the common coefficient β. From (15), such function has the following expression:

$$ {f}_C=\sum \limits_{i=1}^n\frac{X_{0i}^{k/3}}{T_i^k} $$
(16)

Therefore, the optimization problem (1) can be stated as follows:

$$ {\displaystyle \begin{array}{l}\min {f}_C=\frac{L_1^{k/3}}{T_1^k}+\frac{L_2^{k/3}}{T_2^k}+\frac{L_3^{k/3}}{T_3^k}+\frac{D^{k/3}}{T_D^k}+\frac{d^{k/3}}{T_d^k}\\ {}\mathrm{s}.\mathrm{t}.\kern0.75em {T}_Y^2={c}^2\left({S}_1^2{T}_1^2+{S}_2^2{T}_2^2+{S}_3^2{T}_3^2+{S}_4^2{T}_D^2+{S}_5^2{T}_d^2\right)\end{array}} $$
(17)

As discussed in subsection 4.2, the solution to (17) will be found by solving the equivalent problem (10), where the sensitivities Si have now to be evaluated.

As the unknown dimensions L2 and L3 are dependent on each other, the angle γ between the two members is taken as the optimization variable, so that

$$ {L}_2=\frac{\cos \left(\delta +\gamma \right)}{\sin \gamma }{L}_1,\kern0.75em {L}_3=\frac{\cos \delta }{\sin \gamma }{L}_1 $$

The equivalent static model is defined as shown in Fig. 4a: a vertical force F is applied to C and causes support reactions in A and B for the equilibrium of the structure. The analysis of the free-body diagram in Fig. 4b gives the forces acting on the links and pins.

Fig. 4
figure 4

Equivalent static model for the truss: (a) external force and support reactions; (b) free-body diagram

Full size image

The sensitivities of Y to the lengths X1, X2, and X3 of the links are calculated from (12):

$$ {\displaystyle \begin{array}{l}{S}_1=-\frac{L_1}{L_2}\\ {}{S}_2=-1-\frac{L_1}{L_2}\sin \delta \\ {}{S}_3=\frac{L_1}{L_2}\frac{\cos \delta }{\sin \gamma}\end{array}} $$

For the diameters D1, D2, and D3 of the holes, the sensitivities are calculated from (13):

$$ {\displaystyle \begin{array}{l}{S}_{D1}=\frac{1}{2}\frac{L_1}{L_2}\\ {}{S}_{D2}=\frac{1}{2}\left(1+\frac{L_1}{L_2}\sin \delta \right)\\ {}{S}_{D3}=\frac{1}{2}\frac{L_1}{L_2}\frac{\cos \delta }{\sin \gamma}\end{array}} $$

Similarly, the sensitivities related to the pin diameters dA, dB, and dC are calculated from (14):

$$ {\displaystyle \begin{array}{l}{S}_{d\mathrm{A}}=-\frac{1}{2}\left[1+\frac{L_1}{L_2}+1+\frac{L_1}{L_2}\sin \delta +\sqrt{1+{\left(\frac{L_1}{L_2}\cos \delta \right)}^2}\right]\\ {}{S}_{d\mathrm{B}}=-\frac{1}{2}\left(\frac{L_1}{L_2}\cos \delta +1+\frac{L_1}{L_2}\sin \delta +\frac{L_1}{L_2}\frac{\cos \delta }{\sin \gamma}\right)\\ {}{S}_{d\mathrm{C}}=-\frac{1}{2}\left(1+\frac{L_1}{L_2}+\frac{L_1}{L_2}\frac{\cos \delta }{\sin \gamma}\right)\end{array}} $$

Although the tolerances on individual diameters could be optimized separately, a common specification is assumed for all the holes (X4, with nominal diameter D) and for all the pins (X5, with nominal diameter d). Considering that there are two equal holes on each link, the sensitivities of Y to these two variables are obtained as a function of γ from the following equations:

$$ {\displaystyle \begin{array}{l}{S}_4=\sqrt{2{S}_{D1}^2+2{S}_{D2}^2+2{S}_{D3}^2}\\ {}{S}_5=-\sqrt{S_{d\mathrm{A}}^2+{S}_{d\mathrm{B}}^2+{S}_{d\mathrm{C}}^2}\end{array}} $$

From (10), the objective function for the dimensions is therefore

$$ \varphi \left(\gamma \right)={L}_1^a{\left|{S}_1\right|}^{3a}+{L}_2^a{\left|{S}_2\right|}^{3a}+{L}_3^a{\left|{S}_3\right|}^{3a}+{D}^a{\left|{S}_4\right|}^{3a}+{d}^a{\left|{S}_5\right|}^{3a} $$

where L1, D, and d are constant, while L2, L3, and the sensitivities Si (i = 1, ... 5) are functions of γ.

Figure 5 shows the graph of ϕ for L1 = 100 mm, D = d = 5 mm, and δ = − 30°; within the range 0° < γ ≤ 90°, the function has a minimum for γ = 32.9°, which determines the optimal dimensions L2 = 183.9 mm and L3 = 159.4 mm. The figure also shows the graph of the function ϕ1 limited to the first three terms, which would have been used if the joint clearances were neglected. The difference between the two graphs suggests that such simplification would lead to underestimating the output variance by over 30%, and to a different optimal solution (γ = 90°).

Fig. 5
figure 5

Output variance for the truss

Full size image

The optimal tolerances Ti (i = 1, ... 5) can be calculated from (11), where n = 5 and the nominal dimensions X0i are L1, L2, L3, D, and d. Assuming TY = 0.2 mm and c = 1.5, this gives the optimal tolerances listed in Table 1 along with the nominal dimensions and sensitivities. Figure 6 shows a drawing of the optimized structure.

Table 1 Optimization results for the truss
Full size table
Fig. 6
figure 6

Optimal dimensions and tolerances for the truss

Full size image

Figure 7 shows the graph of total cost fC, the objective function in (17), obtained by finding the optimal tolerance allocation for the different configurations of the structure with the same values of L1, D, d, and δ. It is apparent that the variation of cost with the optimization variable follows a similar pattern to that of the output variance. The minimum cost differs by just 0.2% to that of the solution found with the proposed method (indicated on the graph), and corresponds to a very close value of the variable (γ = 27.4°). When γ increases beyond the optimal value, the cost increases significantly: in comparison to a solution with γ = 30° (truss shaped as a right triangle in C, very similar to the one illustrated in Fig. 6), the cost would increase by about 6% for γ = 60° (truss shaped as an equilateral triangle), and by 25% for γ = 90° (truss shaped as a right triangle in B).

Fig. 7
figure 7

Total cost for the truss

Full size image

5.2 Mechanism

Figure 8 shows a mechanism for the transmission of motion between two linear axes [114]. As the slider A moves along direction OA, the tracing point B translates along direction OB at an angle δ with the perpendicular to OA. The lever AEC with dimensions rA and h is connected to the lever CDB with dimensions l and rB; they have equal internal angles (90° - δ) and proportional dimensions (rA/h = l/rB). The followers OD and OE with lengths h and l are connected to levers AEC and CDB, so as to form a parallelogram ODCE with an inside angle γ in O and angles α and β to the paths of A and B, where

$$ {\displaystyle \begin{array}{l}\tan \alpha =\frac{r_A\cos \left(\gamma +\delta \right)}{l+{r}_A\sin \left(\gamma +\delta \right)}\\ {}\beta =90{}^{\circ}-\left(\alpha +\gamma +\delta \right)\end{array}} $$
Fig. 8
figure 8

Mechanism for transmission of linear displacement

Full size image

As a result of the movements of the four links, the slider and the tracing point are both approaching or moving away from O; their travel is limited by two extreme poses where the parallelogram is folded (γ = 0) or completely unfolded (γ = 90° - δ). The output Y is the position of B along its path OB for a given position of A, corresponding to γ = 45° - δ/2 (halfway from the extreme poses). A tolerance TY must be satisfied at minimum cost by selecting both dimensions and tolerances. Given the nominal lengths of the outermost bars (rA = 150 mm, rB = 200 mm) and the nominal diameters of the joints (D = d = 10 mm), the problem boils down to two independent dimensions: angle δ and length l.

The dimensions influencing the output include six lengths (X1, ... X6), two diameters (X7, X8), and two angles (X9, X10). Table 2 explains the meaning of the Xi and lists the nominal dimensions X0i, some of which depend on the unknown independent dimensions δ and l. For the two angles, the nominal dimensions are set at equivalent values according to (7).

Table 2 Dimensions related to the output for the mechanism
Full size table

With the above notation, the optimization problem has the following definition:

$$ {\displaystyle \begin{array}{l}\min {f}_C=\sum \limits_{i=1}^{10}\frac{X_{0i}^{k/3}}{T_i^k}\\ {}\mathrm{s}.\mathrm{t}.\kern0.75em {T}_Y^2={c}^2\sum \limits_{i=1}^{10}{S}_i^2{T}_i^2\end{array}} $$
(18)

with the same meaning of fC as in the previous example.

The mechanism can be treated as an exactly constrained linkage by locking slider A in the given pose. Consequently, the equivalent static model in Fig. 9a has fixed supports in O and A. The external force F is applied to B along direction OB. The free-body diagram in Fig. 9b shows the forces acting on all links and pins. The equilibrium equations to each part give the following expressions for the unknown forces:

$$ {\displaystyle \begin{array}{c}{F}_D=F\frac{l\cos \left(\alpha +\delta \right)+{r}_B\sin \alpha }{l\cos \left(\alpha +\beta +\delta \right)}\\ {}{F}_{CH}={F}_D\sin \left(\beta +\delta \right)-F\sin \delta \\ {}\begin{array}{c}{F}_{CV}={F}_D\cos \left(\beta +\delta \right)-F\cos \delta \\ {}{F}_E=\frac{F_{CH}\left[{r}_A\sin \beta +h\cos \left(\beta +\delta \right)\right]+{F}_{CV}\left[{r}_A\cos \beta +h\cos \left(\beta +\delta \right)\right]}{r_A\sin \left(\alpha +\beta +\delta \right)}\\ {}\begin{array}{c}{F}_{AH}={F}_E\cos \alpha -{F}_{CH}\\ {}{F}_{AV}=-{F}_E\sin \alpha +{F}_{CV}\\ {}\begin{array}{c}{F}_{OH}=-{F}_D\sin \left(\beta +\delta \right)+{F}_E\cos \alpha \\ {}{F}_{OV}={F}_D\cos \left(\beta +\delta \right)-{F}_E\sin \alpha \end{array}\end{array}\end{array}\end{array}} $$
Fig. 9
figure 9

Equivalent static model for the mechanism: (a) constraints and external force; (b) free-body diagram

Full size image

Then, the resultants FC, FE, FA, and FO are calculated as the vector sums of the respective components.

According to the static analogy, the sensitivities of Y to the lengths are calculated from (12):

$$ {\displaystyle \begin{array}{l}{S}_1=\frac{F}{F}\cos \alpha =\cos \alpha \\ {}{S}_2=\frac{F_{CH}}{F}\cos \alpha +\frac{F_{CV}}{F}\sin \alpha \\ {}{S}_3=\frac{F_D}{F}\\ {}\begin{array}{l}{S}_4=-\frac{F_E}{F}\\ {}{S}_5=-\frac{F_{CH}}{F}\sin \left(\beta +\delta \right)-\frac{F_{CV}}{F}\cos \left(\beta +\delta \right)\\ {}{S}_6=-\frac{F_{AH}}{F}\cos \beta -\frac{F_{AV}}{F}\sin \beta \end{array}\end{array}} $$

The sensitivities of Y to the diameters are calculated by adding the contributions of the corresponding forces from (13) and (14):

$$ {\displaystyle \begin{array}{l}{S}_7=\frac{1}{2}\sqrt{{\left(\frac{F_A}{F}\right)}^2+2{\left(\frac{F_C}{F}\right)}^2+3{\left(\frac{F_D}{F}\right)}^2+3{\left(\frac{F_E}{F}\right)}^2}\\ {}{S}_8=-\sqrt{{\left(\frac{F_A}{F}\right)}^2+{\left(\frac{F_C}{F}\right)}^2+{\left(\frac{F_D}{F}\right)}^2+{\left(\frac{F_E}{F}\right)}^2+{\left(\frac{F_O+{F}_D+{F}_E}{F}\right)}^2}\end{array}} $$

The sensitivities of Y with respect to the angles in radians are given by the bending moments at the vertices D and E of the levers, divided by the external force:

$$ {\displaystyle \begin{array}{l}{S}_9=-{r}_B\sin \alpha \\ {}{S}_{10}=-{r}_A\left(\frac{F_{AH}}{F}\sin \beta -\frac{F_{AV}}{F}\cos \beta \right)\end{array}} $$

The output variance

$$ \phi \left(\delta, l\right)=\sum \limits_{i=1}^{10}{X}_{0i}^a{\left|{S}_i\right|}^{3a} $$

varies with the two independent dimensions as shown in the graph of Fig. 10. The function is decreasing with length l: for any δ the optimal length is the maximum of the predefined range (from 50 to 150% of length rB). The function is influenced only marginally by δ, with minimum values at the extremes of its range (from 30° to − 30°). The point of minimum indicated in the graph corresponds to δ = − 30° and l = 250 mm, which give h = 120 mm, α = 21.8°, β = 37.8°, and γ = 60° in the given pose of the mechanism.

Fig. 10
figure 10

Output variance for the mechanism

Full size image

Again, the optimal allocation of the tolerances Ti (i = 1, ... 10) is given by (11), where the nominal dimensions X0i and the sensitivities Si have now been evaluated from the dimensions of the mechanism as listed in Table 3. The optimal tolerances are calculated assuming TY = 0.4 mm and c = 1.5. Figure 11 shows a drawing of the optimized structure.

Table 3 Optimization results for the mechanism
Full size table
Fig. 11
figure 11

Optimal solution for the mechanism

Full size image

Figure 12 shows the graph of the total cost fC defined in (18) with the same values of rA, rB, D, and d. Again, the cost varies in the solution domain very similarly to the output variance. The solution found with the proposed method is actually optimal with respect to cost (fC = 190.5). Within the allowable ranges for the two independent dimensions, the cost varies in a range of about 20%.

Fig. 12
figure 12

Total cost for the mechanism

Full size image

6 Conclusions

The paper has dealt with an extended version of tolerance allocation on planar linkages. In addition to choosing a set of minimum-cost dimensional tolerances, it seeks optimal values for the nominal dimensions in order to reduce the variation on an assembly-level dimension of interest. A linkage with optimal dimensional parameters will need wider tolerances on the parts, allowing a further cost reduction.

The concept has its roots in the robust design methodology, which aims to make the output of a system insensitive to internal or external noise factors. While most existing methods are based on experimental design, the proposed method adopts a robust optimization approach as it finds an optimal solution using mathematical models of the objective and constraints. This is feasible for mechanical assemblies (including the structures and mechanisms covered in the paper) provided that the cost and the output variance have simple analytical expressions. To meet this condition, the method integrates two previous results: a static analogy for stackup calculations, and an expanded formulation of the reciprocal power cost-tolerance function.

The approach has potential advantages over existing methods for optimizing both dimensions and tolerances:

  • Being based on optimization rather than on DOE, it is suitable to cases with many dimensions varying within wide ranges; it can easily take into account geometric closure constraints, and allows a continuous search for the optimum without the need to choose among discrete alternatives (as in Taguchi methods) or to iterate the experiment (as in RSM approaches);

  • It minimizes both output variance and cost without the need to tackle the two optimization problems sequentially (with the risk of obtaining suboptimal solutions) or to balance the two objectives (with the risk of arbitrariness in the weighting coefficients).

The application of the method to two simple examples confirms that the proposed optimization strategy is able to find optimal solutions with respect to cost. It also shows that further cost reductions in the order of 10–20% can be achieved compared to tolerance allocation with given parameters. It is expected that the simultaneous optimization of dimensions and tolerances can be even more advantageous for more complex design cases.

On the other hand, the method in its current state has some limitations, which will have to be overcome in future developments:

  • The assumptions are realistic but do not cover all possible applications; further extensions may consider cases of interrelated tolerance chains, non-normal distributions of dimensions, minimization of quality loss, and geometric tolerances according to ISO and ASME standards;

  • Setting up the optimization problem requires a preliminary study to reduce the solution space to a subset of independent dimensions; it remains to be seen whether general criteria can be developed to take into account geometric closure as well as additional design constraints (kinematic, structural);

  • The robust optimization of a linkage is bound to a given layout of the links and joints; further cost reductions could be obtained by extending the optimization to alternative layouts, where the number and the connections of the links are also optimized along with dimensions and tolerances.

  • Some calculation details are linked to the specific application context of this work (planar linkages with lower kinematic pairs); these should be generalized in order to allow the treatment of spatial linkages and generic mechanical assemblies.