1 Introduction

Today, modeling and simulation play an imperative role in metal cutting research and development. Simulations of chip formation, cutting forces, and tool wear progression as well as the robust design of the micro-geometry of the cutting edge are among the few applications being currently unutilized for warranting improved tool performance. However, a reliable simulation of the cutting process has, in most cases, remained a challenging task due to the complex interactions between the tool and workpiece material. The workpiece material in the vicinity of the cutting edge is subjected to extreme conditions with strain rates in the order of 105 s− 1 while the temperature in the shear zones can exceed 1200 °C. Identification of the material behavior under such extreme conditions has proved to be cumbersome using the conventional mechanical testing methods. To this end, a number of tailored experimental methods, namely, the Taylor’s impact test, Split Hopkinson Pressure Bar (SHPB) test, or high-speed compression tests incorporating the cylindrical or the so-called Top-Hat samples have been utilized to attain the dynamic response of material under the deformation rates and temperature range encountered in metal cutting. The flow stress data obtained from these tests are typically used to calibrate proper constitutive models for metal cutting simulation [1,2,3,4,5]. Nevertheless, these methods are subjected to some limitations. Except for Taylor’s tests or when Top-Hat samples are used in SHPB tests, the measured strain rates are far below the common values encountered within the shear zones (i.e., 104–105 s− 1). Furthermore, the maximum attainable strains are often below 1 mm/mm, whereas the strain values can exceed values above 5 mm/mm on the shear zones for metal cutting. The other limitation of these methods is the amount of experimental effort required to generate the flow stress data at a wide range of strain, strain rate, and temperature for proper calibration of constitutive models.

To avoid the limitations of conventional dynamic testing, various inverse approaches directly focusing on metal cutting have been developed for the identification of the workpiece material behavior. The OXCUT computer program of Shatla et al. [6] was among the earliest attempts. This program uses the Oxley’s slip-line theory [7] for prediction of the cutting force, average stresses, and temperatures on the shear plane. Oxley et al. [8, 9] assumed that the shear zones are parallel-sided, and the shear plane is located at the center of the primary shear zone. Sartkulvanich et al. [10] extended the original OXCUT platform; an effort which led to unique estimations of material parameters by measuring the relative thickness of the primary and secondary shear zones on the chip segments after the quick-stop test. Özel and Zeren [11] determined flow stress and the distribution of the frictional stress at the tool-chip interface based on an extension of Oxley’s machining theory. The authors combined predictions of the extended model with the SHPB test results for improved estimation of JC parameters for AISI 1045, Al 6082-T6, and Ti6Al4V. A number of studies focused on the implementation of more robust optimization algorithms for inverse identification of JC parameters have been made. For instance, Filho [12] used the particle swarm optimization algorithm, and Shrot and Bäker [13] utilized a re-identification process of the JC parameters based on Levenberg-Marquardt optimization algorithm. Malakizadi et al. [14] combined response surface methodology with Oxley’s machining theory for inverse identification of JC parameters. The authors later extended this approach by a re-evaluation of the JC parameters and friction coefficients using finite element (FE) simulations [15]. In a more recent investigation, Fernandez-Zelaia and Melkote [16] proposed a Bayesian inference framework, which benefits from a nonstationary Gaussian process surrogate model, to reproduce the FE simulation of cutting simulation for calibration of JC material parameters.

Tounsi et al. [17] developed a primary shear zone (PSZ) model based on an unequal thickness of material deformation across the shear plane. The authors used the distribution of the state variables (i.e., stress, strain, strain rate, and temperature) across the primary shear zone to estimate the Johnson-Cook (JC) material parameters for different steels. The stress distribution obtained from the model in [17] was later improved by Shi et al. [18], referred to as the distributed primary zone deformation (DPZD) model. The authors combined the DPZD model with the quasi-static indentation results to obtain the JC material parameters for Inconel 718 [19]. This approach led to a unique estimation of the JC parameters independent of an initial guess. Zhou et al. [20] proposed an unequal division parallel-sided shear zone model and implemented a particle swarm optimization algorithm to determine JC parameters for Inconel 718. Aside from PSZ, Pujana et al. [21] presented a new approach for material’s behavior on the secondary shear zone (SSZ) by including temperature measurement. In addition, they revised the inverse algorithms applied to PSZ.

In this study, the DPZD model of Shi et al. [18] is extended to include temperature dependence of the mechanical and thermal properties of the workpiece material (i.e., density, yield stress, and specific heat). The JC material parameters for C38, 42CrMo4, and AA6082 are obtained using the estimated state variables (i.e., stress, strain, strain rate, and temperature). The performance of the identified JC parameters is evaluated using FE simulations, machining experiments, and available data in the literature. To see the overall performance of the identification process presented in this study, the JC parameters obtained for C38 from both original and enhanced DPZD models are compared with experimental data, and identified JC parameters for 42CrMo4 and AA6082 are compared with the JC parameters available in the literature. By doing so, the performance of the enhanced approach is observed for different materials that are obtained using different methods.

The paper is organized as follows; the orthogonal cutting test for the C38 steel is described in Section 2 along with cutting conditions and necessary material properties of C38, 42CrMo4, and AA6082. In Section 3, the proposed enhanced DPZD model is described based on [18] including the temperature dependencies in the considered workpiece materials. The process of identification of JC parameters is explained in the first part of Section 4. The second part is dedicated to the identified JC parameters for C38, 42CrMo4, and AA6082. By using the JC parameters identified in Section 4, FE simulations are performed, and the results are compared with experiments and available data in the literature. The FE simulation details, results, and comparison are given in Section 5. Lastly, the conclusions are stated in Section 6.

2 Experimental details and materials

Orthogonal machining experiments are performed for C38 steel with 5 different cutting conditions. Data gathered from these experiments are used to compare the performance of the original and enhanced DPZD models. Table 1 shows the chemical composition of the mentioned workpiece.

Table 1 The chemical composition of C38
Full size table

The Sandvik Coromant H13A uncoated cemented carbide TCMW16T304 inserts without chip-breaker—giving 0° rake and 7° clearance angles when mounted on the tool holder—were used for all machining experiments. The cutting edges were measured prior to the machining tests, and those with narrow variations (25 ± 3 μm) were selected for the experiments. This was necessary to minimize the effects of the cutting edge geometrical variations on the measured responses. Initially, several flanges of a given dimension (about 2 mm) were fabricated, and they were machined in the radial direction to meet the orthogonal condition, as shown in Fig. 1. The workpiece material was taken directly from the crankshaft to include the deformation and microstructural history of the workpiece material during the identification of JC parameters. The experiments are performed under dry conditions in an EMCO 365 CNC lathe equipped with a Kistler 9275A three-component dynamometer to measure cutting forces (see Fig. 1). To measure the chip thickness, a Leitz DMRX light optical microscope equipped with AxioVision digital image processing software is used.

Fig. 1
figure 1

Experimental setup for orthogonal machining of C38

Full size image

For further investigation, we used the experimental data for 42CrMo4 and AA6082 reported in [21] and [22], respectively. By doing so, we investigated the performance of our calibrated JC parameters for different materials. Table 2 shows the cutting conditions for the experiments.

Table 2 The cutting conditions for C38, 42CrMo4, and AA6082 experiments
Full size table

For FE simulations and the enhanced version of the DPZD model, temperature-dependent material properties (i.e., yield strength, heat capacity, and thermal conductivity) are required. These properties are obtained from [22, 23] for AA6082. For C38 and 42CrMo4, the temperature-dependent yield strength data from [24] is used while temperature-dependent heat capacity is obtained from JMatPro [25]. The temperature-dependent properties of the insert H13A are taken from [15] (see Table 3).

Table 3 Temperature-dependent material properties for AA6082, C38, 42CrMo4, and H13A
Full size table

3 A thermomechancially enhanced DPZD model

It is of significant importance to make fast assessments of the cutting parameters in terms of stress, strain, strain rate, and temperature distributions in the cutting zone. This is particularly true when calibrating the material parameters with inverse analysis. Based on assumed distributions of the stress and strain rate fields in the PSZ, the DPZD model can be used to provide estimations close to the ones from FE analyses in an extremely short time. In this paper, a thermal enhanced DPZD model is developed based on [18] to include the effect of temperature on the stress distribution. The enhanced model is used in the calibration and validation processes of JC material parameters for machining process.

3.1 DPZD model

The DPZD model shown in Fig. 2 assumes two parallel lines defining the workpiece side (CD) and the chip side (EF) of the PSZ region ΩPSZ. The maximum shear strain rate is assumed to occur along shear line (AB), which subdivides the region ΩPSZ into two equal portions. In the PSZ, the stress, strain, strain rate, and temperature fields are assumed to be dependent only on the x-direction pointing from the chip side to the workpiece side of ΩPSZ. The model also assumes continuous chip formation, perfectly sharp cutting edge, plane-strain conditions, and isotropic material properties for the flow stress. In Fig. 2, the considered PSZ and the necessary parameters are shown, such as cutting speed V, chip speed Vc, uncut chip thickness tu, chip thickness tc, rake angle α, shear angle φ, PSZ thickness h, and the local x- and y-directions of the PSZ. Moreover, based on standard kinematics of the PSZ, the normal and shear velocities, Vn and \({V}_{s}^{+},{V}_{s}^{-}\), are given. The force balance between the shear stress along shear line \(\tau _{\max \limits }\), normal pressure P, cutting force Fc, and feed force Ft is also shown in Fig. 2.

Fig. 2
figure 2

Illustration of the parallel-sided shear zone model: (left) Tool-workpiece interaction of the gray-shaded PSZ region, (middle) a close-up of the region ΩPSZ with local unit bases n and t, (right) assumed force balance along shear line AB

Full size image

3.2 Strain rate and strain distributions in the PSZ

Under the assumptions of plane-strain and pure shear in the PSZ, the rate of deformation tensor d ∈ΩPSZ is defined as:

$$ \boldsymbol{d} := \frac{\dot{\gamma}}{2} \boldsymbol{a}_{d} $$
(1)

where \(\dot {\gamma }\) is the pure shear strain rate and ad := 2(n ⊗t)sym is the second-order pure shear basis in the unit basis vectors t and n shown in Fig. 2. In order to match the assumptions in Section 3.1, the shear strain rate field \(\dot {\gamma } \in {\varOmega }_{PSZ}\) is assumed to vary solely in the x-direction. In addition, the shear strain rate is assumed to have a piecewise distribution [18] defined as:

$$ \dot{\gamma}= \begin{cases} \dot{\gamma}_{AB}\left( 1+2\frac{x}{h}\right)^{r} & -\frac{h}{2}\leq x\leq 0 \\ \dot{\gamma}_{AB}\left( 1-2\frac{x}{h}\right)^{r} & 0\leq x\leq \frac{h}{2} \end{cases} $$
(2)

where \(\dot {\gamma }_{AB}\) represents the shear rate at the shear plane (AB) and r is an exponent controlling the shape of the strain rate distribution. It may be remarked that the assumed shear strain rate distribution is similar to Oxley’s distribution [7]. As to \(\dot {\gamma }_{AB}\) in Eq. 2, from the kinematic relation \(\dot {\gamma }=V_{s,x}\), we can integrate the distribution of the consequent shear velocity field Vs. By including the shear velocities \({V}_{s}^{+}\) and \({V}_{s}^{-}\) in Fig. 2 as boundary conditions in the integration, it turns out that \(\dot {\gamma }_{AB}\) is obtained as:

$$ \dot{\gamma}_{AB} = \frac{V(r+1)}{h} \frac{\cos (\alpha )}{\cos (\varphi -\alpha )} $$
(3)

Moreover, since the region ΩPSZ is a Eulerian frame for the material flow, the shear strain field takes on the arguments γ = γ[x[t],t] whereby the γ-field is given from the material time derivative:

(4)

where Vn is the constant material flow velocity along the x-axis as shown in Fig. 2b. As alluded in Eq. 4, stationary material flow is assumed leading to γ → γ[x]. Hence, in view of Eq. 2, the shear strain distribution is integrated from Eq. 4 to yield the piecewise continuous expression:

$$ \begin{array}{@{}rcl@{}} \gamma &=& \frac{1}{V_{n}} {\int}_{-\frac h 2}^{x} \dot{\gamma} [x^{\prime}] dx^{\prime} \leadsto \gamma \\&=& \begin{cases} \gamma_{AB} \left( 2- \left( 1+2\frac{x}{h}\right)^{r+1} \right) & -\frac{h}{2}\leq x\leq 0 \\ \gamma_{AB} \left( 1-2\frac{x}{h}\right)^{r+1} & 0\leq x\leq \frac{h}{2} \end{cases} \end{array} $$
(5)

where

$$ \gamma_{AB} = \frac{\cos (\alpha )}{2\sin (\varphi) \cos (\varphi -\alpha )} $$
(6)

It follows from Eq. 5 that the maximum value of the shear strain is 2γAB occurring on the chip side. It depends solely on the shear and rake angles, and it is thus formally independent on the cutting velocity and the width of the shear zone. It is also noted that the shear strain and strain rate distributions are independent of the temperature in the DPZD model. Hence, these distributions are identical for the original and the enhanced versions of the model.

3.3 Stress distribution in the PSZ

In the DPZD model, the stress field of the PSZ is presented as:

$$ \boldsymbol{\sigma} = \boldsymbol{\sigma}_{d} + p \boldsymbol{1} \text{ with } \boldsymbol{\sigma}_{d} := \tau \boldsymbol{a}_{d} $$
(7)

where p is the pressure corresponding to the volumetric deformation constraint 1 : d = 0, 1 is the 2nd-order identity tensor and τ = τesign[τ] is the pure shear stress associated with the shear flow in ΩPSZ. Moreover, the effective pure shear stress is τe = |τ|. Based on the assumption that the shear strain rate \(\dot {\gamma } = \dot {\gamma } [x]\), the shear stress field τ ∈ΩPSZ is assumed to be a piecewise linear function of x as:

$$ \tau_{e} = \begin{cases} -(\tau_{0}(T)-\tau_{\max})2\frac{x}{h}+\tau_{\max} & -\frac{h}{2}\leq x\leq 0 \\ (\tau_{0}(T)-\tau_{\max})2\frac{x}{h}+\tau_{\max} & 0\leq x\leq \frac{h}{2} \end{cases} $$
(8)

where \(\tau _{\max \limits }\) is the maximum shear flow stress, and τ0 is the shear strength of the material. At the beginning of the shear zone (CD), the shear stress is equal to the initial shear strength of the material, i.e., τe(h/2) = τ0(T). The maximum shear stress \(\tau _{\max \limits }\) occurs at the shear plane (AB) due to strain and strain rate hardening effects, even though there is a temperature increase. At the end of the shear zone (EF), the shear stress is the thermally degraded shear strength of the material, i.e., τe(−h/2) = τ0(T). Considering the maximum shear flow stress \(\tau _{\max \limits }\) along the shear line (AB) in Fig. 2, the balance formulation is given as:

$$ \tau_{\max}=\frac{(-F_{c} \cos \varphi+F_{t} \sin \varphi) \sin \varphi}{t_{u}w} $$
(9)

where Fc is cutting force, Ft is feed force, φ is shear angle, tu is undeformed chip thickness, and w is depth of cut, as in Fig. 2.

Hence, the enhanced DPZD model includes the effect of thermal softening in the assumed stress distribution, where the shear flow stress τ0(T) is considered temperature-dependent from given experimental evidence. Since the temperature field is strongly linked to the model response, there is a thermomechanical coupling between the experimental input and the thermal part of the model response. The basic challenge is to link the temperature-dependent experimental (experienced based) distribution τe(T) in Eq. 8 to the temperature distribution of the model. To this end, a specific algorithm is developed as described in Section 3.5. We also remark that the thermally uncoupled model in [18] is obtained when the effective shear stress is assumed to be equal to the initial shear strength along both the EF and the CD lines.

3.4 Temperature distribution in the PSZ

The temperature distribution is obtained from the energy equation formulated as:

(10)

where K is the thermal conductivity, ρ is the density, Cp is the coefficient of specific heat of the workpiece, \(\dot {T}\) is the material time derivative of the temperature, and \(\dot {W}^{p}\) is the plastic work rate providing input heat to the temperature generation. Due to the high strain rates in the cutting process, the shearing in ΩPSZ is assumed adiabatic. Thus, the conduction term in Eq. 10 is neglected. With the assumption of only x-direction dependency, the steady-state temperature distribution in ΩPSZ can be obtained in view of Eqs. 1 and 7 as:

(11)

In the enhanced thermomechanical DPZD model, we emphasize that the material properties are temperature-dependent, such as the density ρ(T) and specific heat Cp(T). This contributes to a more realistic temperature distribution. Combining this modification with temperature-dependent shear stress distribution, the plastic work rate in Eq. 11 becomes:

$$ \dot{W}^{p}=\tau(T) \dot{\gamma}=\rho(T) C_{p}(T) V_{n} \frac{dT}{dx} $$
(12)

3.5 Algorithm resolving the coupled stress and temperature distributions

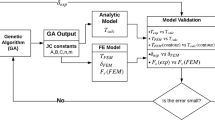
In the enhanced DPZD model, a thermomechanically coupled relation between stress and temperature is established to update the distributions according to temperature-dependent properties. By using Eq. 12, the temperature distribution is calculated, and temperature-dependent parameters are updated accordingly. The update process of stress and temperature distributions is shown as a flowchart in Fig. 3. According to Fig. 3, the update process follows these steps; initially, assumed temperature T∗ is equal to room temperature, implement τ0(T∗) into Eq. 8 and calculate τ(T∗), choose r and calculate \(\dot {\gamma }\), integrate γ, calculate T using Eq. 12, check the convergence between T∗ implemented in and T, update T∗ to T, jump to , and repeat the steps until convergence.

Fig. 3
figure 3

Flowchart describing the two-way coupling between the temperature and flow stress distributions of the DPZD model

Full size image

3.6 Comparison between original and enhanced DPZD models

As mentioned in the previous sections, in contrast to the original DPZD model, the enhanced version establishes a two-way relation between stress and temperature distributions while updating the involved material properties (see Fig. 3) so that they are equilibrated in terms of energy (12). The addition of temperature dependence makes a significant difference in the stress distribution due to the thermal softening effect. Also, the temperature dependence in ρ(T) and Cp(T) affects the temperature distribution. The distributions of stress and temperature of the enhanced and the original DPZD models are given in Fig. 4 for C38 test no. 3 (see Table 2). The comparison shows that the stress at the chip side (EF) is much lower in the enhanced DPZD model which is more realistic when the thermal softening effect is considered. Moreover, as a result of temperature-dependent properties, the temperature at the chip side (EF) is lower for the enhanced model compared with the original DPZD model.

Fig. 4
figure 4

Distributions of effective stress and temperature for C38 test no. 3 obtained from original and enhanced DPZD models

Full size image

4 Inverse identification of material parameters

It is possible to calibrate the JC material parameters for machining simulations by connecting the DPZD and JC models. In this section of the paper, the process is explained, and the identified parameters are given.

4.1 Identification process

The identification process follows the developments in [26] to consider the JC flow rule in Perzyna format written as:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{d} &=& \frac{\dot{\gamma}}{2} \boldsymbol{a}_{d} = \dot{\epsilon}_{e} \frac 3 2 \frac{\boldsymbol{\sigma}_{d}}{\sigma_{e}} \text{ with } \dot{\epsilon}_{e} \\&:=& \dot{\epsilon}_{0} \exp \left[ \frac{\phi }{C g[T] \left( A+B {\epsilon_{e}^{n}}\right)} \right]>0 \end{array} $$
(13)

where yield function is defined as \(\phi := \sigma _{e}-g[T]\left (A+B {\epsilon _{e}^{n}}\right )>0\), \(\sigma _{e}=\sqrt {3/2}\left |\boldsymbol {\sigma }_{d}\right | = \sqrt {3} \tau _{e}\) is the effective von Mises stress (pertinent to a uniaxial test), and \(\dot {\epsilon }_{e}\) is the associated effective strain rate. In view of Eq. 13, we also find that the effective pure shear rate is \(\dot {\gamma }_{e} = \sqrt {3}\dot {\epsilon }_{e}\), where \(\dot {\gamma }_{e}=\dot {\gamma } \text {sign} [\tau ]\). Moreover, in Eq. 13, A, B, C, and n are the standard JC parameters, and \(\dot {\epsilon }_{0}\) is the reference strain rate parameter. Completely in line with the original JC model, g[T] is the degradation function representing thermal softening defined as:

$$ g[T]=1-\left( \frac{T-T_{\text{r}}}{T_{\text{m}}-T_{\text{r}}}\right)^{m} $$
(14)

where Tr and Tm are room and melting temperatures, respectively, and m is an exponent of the thermal degradation. To calibrate the parameters, an objective function is defined as follows:

$$ \min_{x} \sqrt{\sum\limits_{i=1}^{N} |F_{i}-f_{i}(x)|^{2}} \quad \text{ and } \quad x_{lb} \leq x \leq x_{ub} $$
(15)

where \(x = \left \{ A, B, C, n, m\right \}\) is the vector that contains JC material parameters to be calibrated, \(F = \sqrt {3}\tau _{e}\) from Eq. 8 is the effective stress calculated from DPZD model and f = σe is the consistent JC flow stress computed from the assumed shear strain rate (2), shear strain (5), and temperature distributions (12). For the effective strain rate in Eq. 13, we immediately obtain the effective flow stress f = σe in the standard format:

$$ \sigma_{e} = (A+B {\epsilon_{e}^{n}} )(1+C \log \left[ \dot{\epsilon}_{e}/\dot{\epsilon}_{0} \right]) g[T] $$
(16)

As stated in Eq. 15, the objective function minimizes the difference between the effective stress of the DPZD and the consistent JC flow stress distributions within given upper and lower boundaries. In the minimization process the MultiStart algorithm is used to create different starting points for the objective function which reduces the dependence of the initial guess. This algorithm also prevents the objective function to get stuck at a local minimum point due to the bad starting point selection. To ensure that the function is approaching a global minimum, different numbers of starting points are used in the MultiStart algorithm. Also, it must be noted that the JC parameters n and m are restricted within the lower and upper boundaries, which are selected based on available data in the literature, and values of these boundaries as well as references are given in the following sections.

4.2 Identified material parameters

As mentioned in Section 1, to see the overall performance of the identification process and identified parameters, the JC parameters are obtained for C38 from both original and enhanced DPZD models which are used in FE simulations, and the results are compared with experimental data in the Section 5. In this regard, both original and enhanced DPZD models are used in the identification process, and it is observed that the difference shown in Fig. 4 has a significant effect on the identified material parameters. To show this effect, the JC material parameters A, B, C, n, and m, which are identified based on C38 test no. 3, are given in Table 4.

Table 4 Identified Johnson-Cook material parameters for C38 test no. 3
Full size table

To see the overall performance for different materials, JC material parameters are identified for C38, 42CrMo4, and AA6082 by using the enhanced DPZD model. For the estimations, different cutting conditions are selected. For C38, test no. 3 is used for estimation while test no. 2 is selected for 42CrMo4 and AA6082 (see Table 2). The reasoning behind this is to make the estimation based on an average cutting condition that can represent the material’s behavior also in other cutting conditions. The calibrated parameters are given in Table 5 with the parameters from the references to compare.

Table 5 The Johnson-Cook material parameters for C38, 42CrMo4, and AA6082
Full size table

It is worth to mention that the exponent r in Eq. 2 is selected based on the effective strain rate distribution obtained from the FE simulations. From the simulation results, it is found that r = 4 shows a good agreement for C38 and 42CrMo4 while r = 2 satisfies the distribution for AA6082. Moreover, the JC parameters n and m are restricted to be in between 0.2–0.7 and 0.7–1.3, respectively for AA6082. The limits for n and m are 0–0.25 and 0.9–1.1, respectively, for both C38 and 42CrMo4. These range of restrictions are selected based on available data in the literature [11, 15, 21, 27,28,29,30,31,32,33,34,35,36,37,38,39,40,41].

5 Finite element simulation

The identified JC parameters are validated by FE simulations and available data in the literature. By doing so, the performance of the identification process and the parameters are observed in terms of robustness and efficiency. In this section, the simulation details are given, and results are discussed for C38, 42CrMo4, and AA6082.

5.1 Simulation details

The cutting simulations are performed in 2D by using the commercial finite element program SFTC DEFORM 2DTM. In the simulations, plane strain conditions are assumed, and an 8-mm cut is considered. It is observed that the system reaches steady state thermal and mechanical conditions during the 8-mm cut. Quadrilateral elements are used for meshing both workpiece material and insert with minimum element size of 0.005 mm. The minimum element size is used for the regions of importance such as shear zones and contact areas as shown in Fig. 5. Applied mechanical and thermal boundary conditions can also be seen in Fig. 5.

Fig. 5
figure 5

Boundary conditions for two-dimensional (2D) FE model

Full size image

The insert is assumed to be rigid, and the material properties are given in Table 3. The workpiece material is assumed to be rigid viscoplastic material, and the JC material model as outlined in Section 4 is used to describe the flow stress. The calibrated JC material parameters for C38, 42CrMo4, and AA6082 obtained from the enhanced DPZD model are given in Table 5 with parameters used in the references. Machining simulations are performed for both our calibrated JC parameters and referenced ones to compare the performance of the parameters.

The heat transfer between the insert and workpiece material is assumed to be 105 kW/m2 which is a common value for machining simulations [15, 42, 43]. The friction coefficient between the insert and the workpiece material is selected according to the references. For 42CrMo4, the Coulomb friction model (τ = μσ) with the friction coefficient μ = 0.23 is used as in [21]. For C38 and AA6082, a pressure-dependent shear friction model is used as follows:

$$ \tau_{f}=m_{0}(1- \exp (-\beta P))k $$
(17)

where τf is shear stress at the insert-workpiece interface, k is the shear strength of the workpiece, P is pressure at the chip-insert interface, and m0 and β are the coefficients of the friction model. m0 is selected as 1 for both materials while β is taken from [15] as 0.0045 and 0.012 for steel (i.e., C38) and aluminum (i.e., AA6082), respectively. The reason of using different friction models for different workpiece materials (i.e., AA6082 and 42CrMo4) is to make a valid comparison to observe the performance of different JC material parameters. For that purpose, we tried to repeat the same simulations performed in the references by using the same parameters and boundary conditions with the only difference being the JC parameters. Also, the pressure-dependent shear friction model is a good representative for the complex frictional behavior at the chip-insert contact [37]. Because of these reasons and to represent nonlinear frictional behavior in machining, the pressure-dependent shear friction model is implemented for simulations of C38 workpiece material.

5.2 Simulation results and discussion

5.2.1 Comparison of original and enhanced DPZD models

By using calibrated sets of material parameters for C38 given in Table 4, FE simulations are performed, and results (i.e., forces, chip thickness, and percentage difference based on experimental data in parentheses) are shown in Table 6. A comparison between two simulations and the experimental results shows that the JC parameters calibrated based on the enhanced model give closer results to the experimental measurements in terms of cutting force (9% difference) and chip thickness (34% difference) compared with the original version (47% and 92% difference, respectively). However, in terms of feed force, the parameters calibrated by using the original DPZD model yield closer results to the experiment (2% difference) compared with the enhanced version (32% difference).

Table 6 Experiment and FE simulation results for C38 test no 3
Full size table

Moreover, in Figs. 6 and 7, snapshots from the simulations mentioned in Table 6 are shown to observe the differences in distributions of state variables such as stress, strain, strain rate, and temperature as well as contact length and shear angle. From Fig. 6, it can be seen that the contact length (CL) obtained from the parameters of the original model is higher than from the parameters of the enhanced model, which indicates higher cutting and feed forces as well as thicker chips. In terms of the shear angle measured from the assumed shear line, it is observed that the shear angle from FE simulations using parameters of the original model (φO) is smaller than that from the corresponding simulation of the enhanced version (φE). The calculated shear angle in the DPZD model for C38 test no. 3 is 25.48°, while φE and φO are 25° and 21°, respectively, according to the machining simulations. This shows that the calculated shear angle and the shear angle obtained from FE simulation can correlate quite well if JC parameters are calibrated by using the enhanced version of the DPZD model.

Fig. 6
figure 6

Effective strain and strain rate distributions from the simulations of C38 test no 3 with (a) JC from original DPZD and (b) JC from enhanced DPZD

Full size image
Fig. 7
figure 7

Effective stress and temperature distributions from the simulations of C38 test no. 3 with (a) JC from original DPZD and (b) JC from enhanced DPZD

Full size image

Based on Figs. 6 and 7, the difference of distributions of state variables can be observed. For instance, due to higher CL, the material deforms more in the tool-chip contact area which results in increased strain value for simulations with JC obtained from original DPZD. The same reason also causes the temperature to reach higher values as shown in Fig. 7 (a4 and b4). As another aspect, from the stress distribution shown, it can be seen that the stress is distributed in a larger area, and the maximum value is higher for the parameters obtained from the original DPZD, which indicates higher forces and thickness of PSZ. Overall, the parameters obtained from the enhanced DPZD model seem favorable.

5.2.2 Performance of calibrated material parameters

To observe the performance of the identified JC parameters (given in Table 5) for different materials, simulation results are compared with experiments and referenced data. The comparison between experiments and simulations for C38 yields the results given in Fig. 8. According to the results, the cutting forces are in good agreement with the experimental results (6–9% difference). In terms of feed force, the difference is higher (i.e., 23–30%) compared with the difference in the cutting force. However, there is no extreme difference for different cutting conditions, and the trends for experimental data and simulation results are similar. This suggests that test no. 3 is suitable for estimating JC parameters for this range of cutting conditions.

Fig. 8
figure 8

Measured cutting force (Fc), feed force (Ff), and chip thickness (tc) values from experiment (Exp) and simulation (Sim) of machining of C38 (see Table 2 for cutting conditions)

Full size image

In Fig. 8, experimental chip morphology and thickness values for both experiments and simulations are shown. Based on the results, the difference in chip thickness values is in the range of 28–40%. Further investigation shows a relation between cutting conditions and the differences in chip thickness. Considering test nos. 1, 3, and 5, an increase in cutting speed decreases the difference between simulation and experimental values from 40% (i.e., test no. 1) to 28% (i.e., test no. 5). Moreover, for increasing feed (test nos. 2, 3, and 4), the difference is increasing (i.e., from 28 to 36%). However, an in-depth investigation is needed for the understanding of the combination of these two effects on the difference between simulations and experiments in terms of chip thickness.

In Fig. 9, the experiments and simulation results are compared for 42CrMo4. The simulations Sim1 and Sim2 are performed by using referenced JC parameters and the ones obtained in this study, respectively (see Table 5). From the results, it can be seen that our calibrated JC parameters yield lower forces and chip thickness compared with JC in [21]. Even though Sim2 estimates a chip thickness closer to the experiment, Sim1 gives better results overall with maximum differences of 4%, 45%, and 50% for cutting force, feed force, and chip thickness, respectively.

Fig. 9
figure 9

Measured cutting force (Fc), feed force (Ff), and chip thickness (tc) values from experiment (Exp), simulation with referenced JC parameters [21] (Sim1) and simulation with the JC parameters obtained in this study (Sim2) of machining of 42CrMo4 (see Table 2 for cutting conditions)

Full size image

However, it is worth to mention that current simulation results are quite different from the results given in [21] for the referenced JC parameters (see Table 7). For instance, there are 15% and 42% differences between the cutting and feed forces, respectively, even though the JC parameters, friction, and heat transfer coefficient are taken the same. This suggests that the differences in predictions are associated with the differences in FE software, here DEFORM 2D with Lagrangian and ABAQUS with ALE formulations in [21]. In addition, other differences such as the contact formulation and element type (e.g., number of integration points) can cause different results. This should be considered when evaluating the performance of JC parameters reported in the literature. A similar observation was made by Malakizadi et al. [37] by comparing the simulation results obtained from DEFFORM, AdvantEdge, and ABAQUS for machining AISI1045 and AISI 1080 plain carbon steels.

Table 7 FE simulation results for 42CrMo4 test no. 2
Full size table

The results for AA6082 are shown in Fig. 10. A comparison between the experiments and the simulations based on our proposed JC parameters indicates a maximum of 16% difference in cutting forces, while the JC parameters from [15] give closer results to experiments (maximum 14% difference). In terms of the feed force, the difference is quite low (2%) for test nos. 2 and 3; however, the difference is 15% for test no. 1. The difference in chip thickness is higher compared with the difference in forces (maximum 37%) for our calibrated parameters. On the other hand, the JC parameters from [15] yield a better result for the chip thickness with a maximum 4% difference. Overall, the simulations performed by using JC parameters from [15] give better results for AA6082. However, the method proposed in [15] requires a high number of simulations (27 simulations to be precise) to optimize the material parameters, and it is computationally very costly. In contrast, the estimation of the parameters through the enhanced DPZD model is very fast after the exponent r in Eq. 2 is calibrated which requires only a few simulations.

Fig. 10
figure 10

Measured cutting force (Fc), feed force (Ff), and chip thickness (tc) values from the experiment (Exp), simulation with referenced JC parameters [15] (Sim1) and simulation with our JC parameters (Sim2) of machining of AA6082 (see Table 2 for cutting conditions)

Full size image

6 Conclusion

In this study, an enhanced DPZD model is developed to describe the thermomechanically coupled stress and temperature fields in the PSZ. Thus, the JC parameters obtained from the thermomechanically coupled calibration process have a better performance overall than the uncoupled approach and the other methods referenced in this study. The advantages of the enhanced DPZD method of estimating material parameters can be summed up as:

  • More realistic stress field and estimation of the material parameters compared with original DPZD model due to coupled stress and temperature fields

  • Very fast and robust estimation process for obtaining material parameters for machining process

  • Process does not require high number of machining experiments and/or simulations

  • Based on C38 results, the difference between experiment and simulations varies between 6 and 9% for cutting force, 23 and 32% for feed force, and 28 and 40% for chip thickness

  • 42CrMo4 results show the difference varies between 10 and 13% for cutting force, 49 and 53% for feed force, and 14 and 35% for chip thickness

  • The difference for AA6082 is between 13 and 16% for cutting force, 1 and 14% for feed force, and 24 and 37% for chip thickness

However, there is still room for improvement for the enhanced DPZD model. For instance, the model can be improved by including the unequal division of the shear zone. The assumptions used in the model can be modified in a way that also includes the changes in the y-direction. Moreover, in the DPZD model, secondary shear zone (SSZ) effects are neglected which should be incorporated in the future.