1 Introduction

Technological developments in the global supply chain have increased the requirements for physical storage technology. The reasons why warehouses are needed include the following: (i) an imbalance in the inflow and outflow of goods due to the mismatched dynamics of production and consumption, (ii) the combining of goods from numerous producers in single shipments, (iii) the realization of the daily supply of goods in their production and distribution, (iv) the realization of additional activities, such as packaging and final assembly [1]. An important part of meeting these requirements of automated warehouses is the autonomous vehicle storage and retrieval system (AVS/RS). The type of AVS/RS treated in this paper is a tier-captive system. In these systems, the shuttle is confined to a tier that it cannot leave. The main movement of the shuttle is in the horizontal direction, with limited mobility in the vertical direction. The shuttle vehicles are like short single-lane stacker cranes of AVS/RS. Furthermore, the lifts, positioned at the end of every storage aisle, transport totes only in the vertical direction. The common system treated in this paper has two lifts, one for input and one for output. Between these two transportation devices, buffer slots are located in each main tier. This leads to the independence of shuttle movements and lift movements. These systems are also called shuttle-based storage and retrieval systems (SBS/RS) [25]. At present, these systems are also used for pallets as can be seen in Fig. 1. In the present investigation, the shuttle serves not just a single tier, but a main tier plus a number (e.g., 4) of sub-tiers. Due to the fact that space is not an unlimited resource, racks with multiple-deep storage are rising in popularity [20]. Because of the less needed space for the ride of the shuttle with an increase of the storage depth, multiple-deep storage saves ground space. This leads to shuttle carriers of greater complexity because of the high payload for pallets, which leads in turn to higher cost. Cost-containment measures aim to reduce the number of shuttles. To meet these requirements, a calculation method is needed to effectively describe these systems.

Fig. 1
figure 1

LTW shuttle system for pallets. Source: LTW Intralogistics GmbH

Full size image

The aim of this paper is to provide a decision tool that accurately and quickly evaluates the throughput of SBS/RS with shuttles serving multiple tiers of multiple-deep storage. The presented approach can then be used in the design process of new storage systems. This approach is not limited to a certain number of tiers per shuttle, and it is not limited to a fixed storage depth; the material handling provider can determine the throughput of the SBS/RS regardless of the number of tiers per shuttle and the storage depth. The presented approach is also valid for the simplest single-deep storage system to model, in which every tier has its own shuttle up to a theoretically unlimited number of tiers per shuttle and infinite storage depth. For reasons of space and costs, the leading manufacturers of such SBS/RS are developing systems with up to sixfold-deep storage or even deeper, with up to 5 sub-tiers served by a single shuttle depending on the size of the goods.

The usage of the approach is mainly for material handling providers who design new systems at given requirements such as storage capacity, throughput, length, and height. Using this calculation, it is possible to define a system that meets the requirements.

This paper is organized as follows. Table 1 lists the abbreviations used in this paper. The first part, Section 2, is a literature review of all papers relevant to SBS/RS. The treated shuttle system and the underlying assumptions are presented in Section 3. In Section 4, the performance calculation is outlined, focusing in particular on interarrival time, shuttle service time for various rack storage depths, and the number of tiers per shuttle. The open-queueing model with limited capacity is used. This approach takes into account the interactions between lifts and shuttles. The numerical study presented in Section 5 demonstrates the accuracy of the developed calculation model by comparison to a discrete-event simulation (DES). The parameters for this numerical study are based on a system provided by a European material handling provider. A comparison of different numbers of tiers per shuttle and different rack depths follows, with a performance measurement of each such configuration. Finally, in Section 6, the paper is summarized, and an outlook on future research is provided.

Table 1 Abbreviations
Full size table

2 Literature review

There are two ways to obtain accurate performance measures for SBS/RS. One way is to use a discrete-event simulation (DES) to evaluate the performance of the systems. Various publications take this approach (e.g., Ekren et al. [8, 11], Marchet et al. [32], Trummer et al. [36], Lerher et al. [21, 23, 24, 26,27,28] , Kriehn et al. [17], Ha et al. [14] and Ekren [9]). This literature is not treated in this paper in further detail because of the diverging aims of those studies and the present investigation.

The second way to treat a SBS/RS is an analytical approach to evaluate potential performance. There are three widely different types of analytical approaches in the literature to analyze a SBS/RS.

The first type is a cycle-time model of the system. These approaches are concerned solely with the subsystems: lifts and shuttles. The interactions between these two subsystems are not captured. These cycle-time approaches are of two kinds. One approach validate analytical results through simulation (e.g., Sari et al. [33], Lerher [20, 22]); the other approach does not (e.g., Lerher [18, 19], Lerher et al. [25, 29], Borovinšek et al. [2], Ekren et al. [10] and Manzini et al. [30]). These publications are also not treated in further detail here, with the exception of Lerher [19], who discusses a system with multiple tiers per shuttle. The other papers fail to capture interactions between the lift and shuttle subsystems.

The second analytical approach is an approximation approach using an open-queueing network. The interarrival times and service times within this queueing network are determined by cycle-time models. The open-queueing network is used to take account of the interactions between lifts and shuttles. Again, some such studies are not validated through simulation (e.g., Heragu et al. [15], Wang et al. [38]), while others are (e.g., Marchet et al. [31], Ekren et al. [12], Epp et al. [13], Tappia et al. [35]). The shortcoming of these approaches is that they evaluate waiting times between lifts and shuttles. On the basis of that approach, the time to retrieve one tote from the system can be calculated, but it is not possible to evaluate the throughput of the whole system [4].

The third approach is a single-queueing model, as exemplified by Kartnig et al. [16] using a single Markov queue M|G|1 to treat SBS/RS. Their approach is validated through simulation. One point that must be mentioned is in their approach, the maximum waiting time must be obtained from a simulation model. In three publications [5,6,7], Eder et al. developed an approach relying on a single-queueing model with limited capacity (M|M|1|K and M|G|1|K). Their analyses use a space-continuous cycle-time model to evaluate the interarrival times and service times of the queueing model in accordance with the VDI3653 [37] reference point method. This causes an estimation error due to distance-dependent differences in speed profiles; such effects are not captured in their approach. In Eder [3], the transition to a time-continuous and spatially discrete approach is effectuated. The latest publication of Eder [4] uses also this open-queueing model with limited capacity and extends the model to multiple-deep storage systems.

With the exceptions of Lerher [20], Eder et al. [5], Manzini et al. [30], Tappia et al. [35], and Eder [4], all publications mentioned in this paper only discuss single-deep racks. These papers use a probability-based approach to take storage depth into account. The approaches of Lerher [20] and Eder et al. [5] are limited to a storage depth of 2. Lerher [20] assumes that the rear storage locations are filled first and that front storage locations are filled with a filling degree of 50%. Eder et al. [5] do not make such assumptions. Instead, the selection of storage slots is random, resulting in different probabilities and times within the service-time approach. Manzini et al. [30] develop a cycle-time model that is continuous in space but does not capture the distance-dependent differences in speed profiles. Tappia et al. [35] assume that a shuttle transports a satellite, which transports the totes from a storage slot onto a shuttle. The movement of these two vehicles is decoupled in the investigated system. Because this is different from the discussed system in the present paper, that publication is not treated in further detail. Another publication that must be mentioned is Lerher [19], which discusses a SBS/RS with shuttles serving multiple tiers. His presented approach is a cycle-time model that is continuous in space. Table 2 gives an overview of the publications on SBS/RS.

Table 2 Literature overview
Full size table

This literature overview shows that there are a number of publications with different queueing approaches discussing single- and multiple-deep SBS/RS. Eder [3, 4] approaches the system closest to its real behavior. The queueing system presented in that investigation is time-continuous, with a spatially discrete evaluation of lift interarrival times and shuttle service times, corresponding well to reality. What also can be seen is that there is no literature addressing the field of a sorting factor to optimize the cycles within the system. In the present paper, the main idea of Eder et al.’s [4] approach is used and advanced. The main changes are (1) an extension of the single-tier serving shuttle to a shuttle that serves multiple tiers and (2) the inclusion of a sorting factor to account for the fact that the pallets can be sorted into retrieval batches to avoid re-storage processes.

3 System description

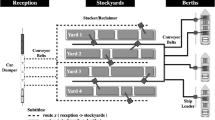
The system investigated in this paper is a tier-captive, single-aisle SBS/RS with multiple-deep storage and shuttles serving multiple tiers. As an example, a SBS/RS with double-deep storage and shuttles serving three tiers is shown in Fig. 2. A vertical lift transports the pallets from the I/O point to the main tiers and back is positioned in front of each rack. Each I/O point is located on the first main tier in front of a lift. Buffers are placed between lifts and shuttles in each main tier. Each shuttle is assigned to one main tier in one aisle, meaning that for each rack, the number of vehicles is equal to the number of main tiers. Moreover, each vehicle can handle one pallet at a time and serve some number of sub-tiers. The racks are multiple-deep and double-sided, and each storage location is capable of holding one pallet.

Fig. 2
figure 2

Shuttle system

Full size image

The main assumptions and notations are listed below. The assumptions made here are based on a SBS/RS produced by a European material handling provider. These assumptions have also been made in other publications (Eder et al. [3,4,5,6,7]).

  • Both lifts serve the transactions in single command cycles under a FCFS rule, one lift for the input cycle and one for the output cycle.

  • The shuttles serve the transactions in single and double cycles under a FCFS rule.

  • The dwell point of the input lift is the I/O.

  • The dwell point of the output lift is the point of service completion.

  • The dwell point of the shuttle is the point of service completion.

  • The lifts and shuttles accelerate/decelerate in a constant manner. If not, an acceleration/deceleration rate has to be calculated that exhibits the same behavior as the real, variable acceleration/deceleration.

  • The lifts and shuttles velocity is constant. If not, a velocity rate has to be calculated that exhibits the same behavior as the real, variable velocity.

  • There are different transfer times from and to the shuttle depending on the depth of the rack.

  • There is no difference in time between the transfer of a tote to and from the lift. If there is a difference in the real system, there is no influence on the calculation, because only the sum of times for loading and unloading is used.

  • There are always totes waiting on the I/O point to be stored. This assumption is necessary to achieve maximum throughput. Otherwise, the input lift would have to wait for incoming totes, which would affect the potential performance of the SBS/RS under consideration.

  • The totes are stored in an evenly distributed manner throughout the entire storage rack.

  • The order in which totes should be re-stored is evenly distributed among all stored totes.

  • The tote to be re-stored is re-stored to the next free storage location.

  • The filling degree is limited to a known value to enable a relocation cycle.

4 Analytical approach

To determine the performance of a SBS/RS system, one aisle is modeled. Following Epp et al. [13], Marchet et at. [31], and Heragu et al. [15], the performance of the system can be evaluated by modeling a single aisle because the storage and retrieval transactions are evenly distributed among all aisles and tiers.

The analytical approach for multiple-deep storage presented in this paper is based on the analytical approach in Eder [3, 4]. This approach uses an open-queueing model with limited capacity (M | G | 1 | K). This model has three main parts to determine the throughput: the interarrival time to a single tier, the shuttle service time, and the open-queueing model M | G | 1 | K. To adopt this approach, several changes must be made to the assumptions, and new relations must be established.

The procedure of the approach used herein therefore is as follows [4]:

  • Determine the lift interarrival time of a pallet at each storage level.

  • Determine the shuttle service time within a single storage level.

    • Determine the shuttle ride time within a single storage level.

    • Determine the mean time needed to transfer the pallet to and from the shuttle.

    • Determine the probability that a relocation of a pallet is needed.

    • Determine the ride time required in the relocation cycle.

    • Determine the mean time needed to transfer the pallet to and from the shuttle in the relocation cycle.

    • Determine the mean time required for the relocation cycle.

  • Determine the throughput using the open-queueing model M | G | 1 | K.

The notations used in this analytical approach are listed in Table 3.

Table 3 Notation of the tier-captive, single-aisle AVS/RS
Full size table

4.1 Interarrival time

The first part in the calculation of the throughput of one tier is the determination of the lift interarrival time. Therefore, we need the ride time and the time for transferring the pallet to and from the lift [3].

$$ t_{lift}=2\cdot t_{R_{L}}+t_{t_{L}} $$
(1)

The mean time needed for the ride is

$$ t_{R_{L}}=\frac{1}{n_{t_{main}}}\sum\limits_{k=1}^{n_{t_{main}}} \mathbf{t}(|l_{I/O}+(k-1)\cdot {\varDelta} y_{main} |) $$
(2)

Taking into account that the lifts do not reach their maximum speed over short distances, the function t(l) must be split into two sections: one part for distances below \( l <\frac {v^ 2}{a} \), viz.,

$$ \mathbf{t}(l)=2\sqrt{\frac{l}{a_{li}}} $$
(3)

, and another part for larger distances, viz.,

$$ \mathbf{t}(l)=\frac{l}{v_{li}}+\frac{v_{li}}{a_{li}} $$
(4)

.

Equation 1 gives the lift’s cycle time for one single command lift cycle. The interarrival time is this cycle time multiplied by the number of main tiers.

$$ t_{A}=t_{lift} \cdot n_{t_{main}} $$
(5)

This equation accounts for the fact that one lift serves all tiers of an aisle.

4.2 Service time

The second part needed to determine throughput is the shuttle service time. To discuss the different aims of the throughput calculation, as described in the Introduction, different shuttle service times are investigated.

  1. 1.

    Determination of the throughput for the process of storing into the SBS/RS (one lift acting in a single command cycle, shuttles performing single command cycles) [3]

    $$ t_{S_{SC_{storage}}}=2 \cdot t_{R_{S\_SC}} + t_{t_{S}} $$
    (6)
  2. 2.

    Determination of the throughput for the process of retrieving out of the SBS/RS (one lift acting in a single command cycle, shuttles performing single command cycles)

    $$ t_{S_{SC_{retrieval}}}=2 \cdot t_{R_{S\_SC}} + t_{t_{S}} + w_{rel} \cdot t_{rel} $$
    (7)
  3. 3.

    Determination of the throughput for a symmetrical storage/retrieval process of the SBS/RS (two lifts acting in a single command cycle, shuttles performing single command cycles) [4]

    $$ t_{S_{SC{storage + retrieval}}}=4 \cdot t_{R_{S\_SC}} + 2 \cdot t_{t_{S}} + w_{rel} \cdot t_{rel} $$
    (8)
  4. 4.

    Determination of the throughput for a symmetrical storage/retrieval process of the SBS/RS (two lifts acting in a single command cycle, shuttles performing dual command cycles) [4]

    $$ t_{S_{DC{storage + retrieval}}}=2 \cdot t_{R_{S\_SC}} + t_{R_{S\_DC}}+ t_{t_{S}} + w_{rel} \cdot t_{rel} $$
    (9)

The determination of the service time contains the same arguments as the determination of the cycle times of the lifts. A distinction must be made between the ride time from A to B and the time required to transfer the pallet to and from the shuttle.

The mean time for the ride can be expressed as

$$ \begin{array}{@{}rcl@{}} t_{R_{S\_SC}}&=& \\ &&\frac{1}{n_{sl}}\frac{1}{n_{t_{sub}}}\sum\limits_{k=1}^{n_{sl}}\sum\limits_{l=1}^{n_{t_{sub}}} \\ &&MAX[\mathbf{t}(k \cdot {\varDelta} x );\mathbf{t}(l \cdot {\varDelta} y_{sub} )] \end{array} $$
(10)

Equations 3 and 4 must be used depending on the distance. This equation addresses the contributions of vertical and horizontal movements within a main tier. In this equation, the maximum time needed for horizontal or vertical movement determines the total time.

The first term is the same as for a single cycle. The second term represents the ride to the slot where the pallet to be retrieved is located.

The mean time for this is as follows:

$$ \begin{array}{@{}rcl@{}} t_{R_{S\_DC}}&=& \\ &&\frac{1}{n_{sl}^{2}}\frac{1}{n_{t_{sub}}^{2}}\sum\limits_{k=1}^{n_{sl}} \ \sum\limits_{l=1}^{n_{sl}} \sum\limits_{m=1}^{n_{t_{sub}}} \sum\limits_{n=1}^{n_{t_{sub}}} \\ &&MAX \left[ \mathbf{t}\left( |(k-l)\cdot {\varDelta} x|\right);\mathbf{t}\left( |(m-n)\cdot {\varDelta} y_{sub}|\right)\right] \end{array} $$
(11)

To calculate the influence of multiple-deep storage, the following points must first be determined:

  • Adaptations of the shuttles’ cycle times without any relocation cycle

    • Mean time to transfer the pallet to and from the shuttle (\(t_{t_{S}}\)) (see Section 4.2.1).

  • Adaptations concerning the relocation cycle

    • Probability that a relocation cycle is needed (wrel) (see Section 4.2.2).

    • Mean ride time needed for relocation (\(t_{R\_rel}\)) (see Section 4.2.3).

    • Mean time necessary to transfer the pallet to and from the shuttle in the relocation cycle (\(t_{t_{S\_rel}}\)) (see Section 4.2.4).

    • Mean time for the relocation cycle (trel) (see Section 4.2.5).

4.2.1 Mean time needed to transfer the pallet to and from the shuttle

For double-deep racks, the mean time can be calculated as follows [4]:

$$ t_{t_{S}}=t_{tb}+\frac{1}{2}f\cdot t_{t1}+[ \frac{1}{2}f+(1-f) ] t_{t2} $$
(12)

The first term (ttb) in this equation is the time required to transfer the tote to/from the shuttle and to/from the buffer. The second term (\(\frac {1}{2} f\cdot t_{t1}\)) represents the mean transfer time to/from the shuttle and to/from the storage location next to the aisle. The factor (f ) represents the filling degree of the storage system and the probability that a storage location is occupied. The factor \(\frac {1}{2}\) in this term represents the fact that, in double-deep storage, totes that are not located next to the aisle are ordered with the same probability as totes located next to the aisle. The third term (\([ \frac {1}{2}f+(1-f) ] t_{t2}\)) describes the time needed for the transfer to/from the shuttle out of and to the storage location that is not situated next to the aisle. This term covers two possibilities: (1) in the retrieval process, the storage location next to the aisle is occupied and the tote in this storage location is not ordered (\(\frac {1}{2}f\)) and (2) the transfer to/from a storage location that is not next to the aisle. The probability of a transfer to/from this storage location is (1 − f). These two probabilities are multiplied by the time requires to transfer a tote from a storage location not situated next to the aisle [4].

For multiple-deep storage of depth (sd), the mean transfer time is as follows [4]:

$$ \begin{array}{@{}rcl@{}} t_{t_{S}}&=&t_{tb}+ \\ &&\sum\limits_{n=1}^{sd} \ \sum\limits_{i=0}^{n-1} \frac{1}{sd-i} \binom{sd-1}{i} f^{sd-1-i}\cdot \left( 1-f \right)^{i} t_{tn} \end{array} $$
(13)

This equation is the same for any number of tiers served by one shuttle.

4.2.2 Probability of relocation

The probability of relocation hangs upon the fact that a given ordered pallet is not directly retrievable. The equation describing this probability for double-deep storage is the following:

$$ w_{rel}=\left( 1-w_{sort} \right)\frac{1}{2}f^{2} $$
(14)

Factor f2 in this equation describes the fact that both storage locations have one slot occupied. Factor \(\frac {1}{2}\) represents the fact that a relocation is necessary if the tote that is located further from the aisle is ordered. Factor \(\left (1-w_{sort} \right )\) describes the fact that the relocation cycle is not necessary owing to sorting during the storage process.

For different storage depths, the probability of a relocation cycle is based on the equation from Eder [4] and advances with the coefficient of sorting. This coefficient describes the fact that the ordered pallets are sorted during the storage process, so that there are fewer relocation cycles necessary:

$$ \begin{array}{@{}rcl@{}} w_{rel}&=&\left( 1-w_{sort} \right) \\ && \cdot \sum\limits_{n=0}^{sd-2} \ \sum\limits_{i=1}^{sd-1-n} \frac{i}{sd-n} \binom{sd}{n} f^{sd-n}\cdot(1-f)^{n} \end{array} $$
(15)

This equation again shows no dependence on the number of tiers per shuttle.

4.2.3 Mean ride time necessary in the relocation cycle

The distances in the relocation cycle depend on the free storage locations next to a storage slot in which the ordered pallet is placed. Here, there is a difference with Eder [4]. He assumed that the ordered pallet was in the middle of an aisle. In the present paper, on the other hand, the ordered pallet is assumed to be at the end of the aisle in the bottom sub-tier of the considered main tier. This means that the ride route is in only one direction in the two-dimensional framework (vertical and horizontal); this is the worst case for the relocation cycle. That means this approach underestimates the performance of the system, but the error can be neglected. In Figs. 3 and 4, the possible relocation locations are shown. This cycle sequence can also be described in the following equation, which is also valid for greater storage depths.

$$ \begin{array}{@{}rcl@{}} t_{R\_rel}&=& \\ &&\sum\limits_{i=0}^{n_{sl}-1} \ \sum\limits_{j=0}^{n_{t_{sub}}-1} \frac{(f^{sd})^{X} \cdot \left( 1-\left( f^{sd} \right)^{2 \cdot Y} \right)}{Y} \\ &&\cdot 2 \cdot MAX\left[ \mathbf{t}(i\cdot {\varDelta} x);\mathbf{t}(j\cdot {\varDelta} y_{sub}) \right] \end{array} $$
(16)

The first term \(f^{sd^{X}}\) in this equation describes the probability that the slot on the opposite side of the slot of interest is fully occupied and that the slots on either side the slot of interest are fully occupied. The exponent in this term refers to the number of occupied slots to one side and two dimensions of the considered slot. The term \((1-f^{sd^{2 \cdot Y}})\) describes the status that at least one storage location among the next-closest slots is free to store a pallet. The denominator Y is due to the fact that all slots of the next relocation distance are taken into account. The last term in this equation describes the maximum time for movement in the vertical and horizontal directions. The time functions t(i ⋅Δx) and t(j ⋅Δy) equally depend on the distance, as do those in Eqs. 3 and 4.

Fig. 3
figure 3

Relocation distance for fn = 1

Full size image
Fig. 4
figure 4

Relocation distance for fn = 2

Full size image

The probability of the further slots in the relocation distance is due to the two fixed dimensions: vertical and horizontal. This can be seen in Figs. 3 and 4. Figure 3 describes the further consideration of the slots in entire rows and columns. This is the first possible way to determine the distance of the relocation cycle. For certain parameter configurations, this would be the best way, but if the parameters of a SBS/RS are too different in vertical and horizontal directions, other strategies of relocation are faster. To describe this in mathematical form, the following equation is developed:

$$ f_{n}= round \left( \frac{\frac{{\varDelta} y}{a_{sh_{y}}}}{\frac{{\varDelta} x}{a_{sh_{x}}} } \right) $$
(17)

This ratio of the time needed to ride the same distance according to Eq. 3 provides the decision whether the relocation strategy is to proceed according to Fig. 3 or whether another strategy is better, such as can be seen in Fig. 4.

If the acceleration of the shuttle is relatively high and the distances between the slots and the tier are also high, then the expected distance exceeds those at which Eq. 3 is valid. Then, the ratio must be calculated according to the following equation, which refers to Eq. 4.

$$ f_{n}= round \left( \frac{v_{sh_{x}} \cdot \left[ {\varDelta} y - \left( \frac{v_{sh_{x}}}{a_{sh_{x}}}-\frac{v_{sh_{y}}}{a_{sh_{y}}} \right) \cdot v_{sh_{y}} \right]}{{\varDelta} x \cdot v_{sh_{y}}} \right) $$
(18)

The following equation calculates a factor necessary in the determination of the factors X and Y. It represents the actual relocation area in the rack, and it is illustrated in Fig. 3 by the different colors and hatching:

$$ n_{m}=MAX(i,f_{n} \cdot j) $$
(19)

To calculate (16), the factors X and Y are necessary in order to describe the probability of the ride to the different storage slots.

The equations for the ratio fn = 1 are as follows:

$$ X\left( n_{m}\right)=\left\{\begin{array}{ll} 2 \cdot {n_{m}^{2}}-1, & n_{m} < n_{t_{sub}} \\ 2 \cdot n_{t_{sub}} \cdot n_{m} -1, & n_{m}\geq n_{t_{sub}} \end{array}\right. . $$
(20)
$$ Y\left( n_{m}\right)=\left\{\begin{array}{ll} 2 \cdot n_{m}+1, & n_{m} < n_{t_{sub}} \\ n_{m}, & n_{m}\geq n_{t_{sub}} \end{array}\right. . $$
(21)

As can be seen, these equations for X and Y have two regions of validity. As written, the first line of each equation describes the case that a further taking into account of the storage slots is in two dimensions. This is the case until the factor nm reaches the number of sub-tiers. At that point, further calculation expands only in the horizontal direction, which is calculated in the second line of each equation. The factor X describes the number of occupied slots below the storage slot of interest. In Figs. 3 and 4, for the green slots the factor X describes the number of red and blue slots. The factor Y describes the number of storage slots in the same relocation region; in Figs. 3 and 4 these are marked with a uniform color.

For higher ratios of fn the equations transform into the following:

$$ X\left( n_{m}\right)=\left\{\begin{array}{ll} & n_{m} < f_{n} \cdot n_{t_{sub}} \\ \frac{2}{f_{n}} {n_{m}^{2}}+ 2\frac{f_{n}-1}{f_{n}} n_{m}-1, & \& \\ & \frac{n_{m}+(f_{n}-1)}{f_{n}} \in \mathbf Z.\\ & \\ \ldots& \\ & \\ & n_{m} < f_{n} \cdot n_{t_{sub}} \\ \frac{2}{f_{n}} {n_{m}^{2}}+\frac{2}{f_{n}} n_{m}-1, & \& \\ & \frac{n_{m}+1}{f_{n}} \in \mathbf Z.\\ \\ & n_{m} < f_{n} \cdot n_{t_{sub}} \\ \frac{2}{f_{n}} {n_{m}^{2}}-1, & \& \\ & \frac{n_{m}}{f_{n}} \in \mathbf Z.\\ \\ 2 \cdot n_{t_{sub}} \cdot n_{m} -1, & n_{m}\geq f_{n} \cdot n_{t_{sub}} \end{array}\right. . $$
(22)
$$ Y\left( n_{m}\right)=\left\{\begin{array}{ll} & n_{m} < f_{n} \cdot n_{t_{sub}}\\ \frac{1}{f_{n}} n_{m}+\frac{f_{n}-1}{f_{n}}, & \& \\ & \frac{n_{m}+(f_{n}-1)}{f_{n}} \in \mathbf Z.\\ & \\ \ldots& \\ & \\ & n_{m} < f_{n} \cdot n_{t_{sub}}\\ \frac{1}{f_{n}} n_{m}+\frac{1}{f_{n}}, & \& \\ & \frac{n_{m}+1}{f_{n}} \in \mathbf Z.\\ \\ & n_{m} < f_{n} \cdot n_{t_{sub}}\\ \frac{f_{n}+1}{f_{n}} n_{m}+1, & \& \\ & \frac{n_{m}}{f_{n}} \in \mathbf Z.\\ \\ n_{m}, & n_{m}\geq n_{t_{sub}} \end{array}\right. . $$
(23)

4.2.4 Mean time needed to transfer the pallet to and from the shuttle in the relocation cycle

The mean time needed to transfer the pallet from and to the shuttle in the relocation cycle is similar to the mean time necessary to transfer the pallet from and to the shuttle (13).

For all storage depths, the following equation holds [4]:

$$ t_{t_{S\_rel}}= \sum\limits_{n=1}^{sd} \ \sum\limits_{i=0}^{n-1} \frac{1}{sd-i} \binom{sd-1}{i} f^{sd-1-i} \left( 1-f \right)^{i} t_{tn} $$
(24)

4.2.5 Mean time needed in the relocation cycle

The mean time needed in the relocation cycle is the summation of the mean ride time necessary \(t_{R\_rel}\) (Section 4.2.3) and the mean time needed to transfer the pallet to and from the shuttle during the relocation cycle \(t_{t_{S\_rel}} \) (Section 4.2.4) [4].

$$ t_{rel}=t_{R\_rel}+t_{t_{S\_rel}} $$
(25)

4.3 Open-queueing model M | G | 1 | K

To evaluate the influence of the buffers and the influence of the interactions between lifts and shuttles, a time-continuous open-queueing model with limited capacity is used. With the help of this model, the throughput 𝜗tier of one single tier can be calculated [3]:

$$ \vartheta_{t_{main}}=\frac{1}{t_{A}}\cdot(1-p_{k}) $$
(26)
$$ \vartheta_{t_{main}}=\frac{1}{t_{S}} \cdot (1-p_{0}) $$
(27)

There are two methods to determine the throughput. The first method is based on the interarrival time and the blocking probability (26). The second is the use of the service time and the probability of emptiness of the queuing system (27). The term “blocking probability” means that the entire system is filled and lacking space for more pallets to enter it. Applied to a shuttle system, this means that the lift must wait for an empty space in the input buffer. The probability of emptiness means that the server must wait because there is no pallet in the queuing system. In a SBS/RS, this means that the shuttle has to wait for a pallet.

The throughput of an aisle is equal to the throughput of one tier multiplied by the number of tiers [3]:

$$ \vartheta=\vartheta_{t_{main}} \cdot n_{t_{main}} $$
(28)

The blocking probability of a queueing system is calculated as follows [34]:

$$ p_{k}=\frac{\rho^{\frac{\sqrt{\rho \cdot e^{-s^{2}}}\cdot s^{2} -\sqrt{\rho \cdot e^{-s^{2}}}+2K}{2+\sqrt{\rho \cdot e^{-s^{2}}}\cdot s^{2} -\sqrt{\rho \cdot e^{-s^{2}}}}} \cdot (\rho-1)}{\rho^{2\cdot\frac{\sqrt{\rho \cdot e^{-s^{2}}} \cdot s^{2}-\sqrt{\rho \cdot e^{-s^{2}}} +K+1}{2+\sqrt{\rho \cdot e^{-s^{2}}}\cdot s^{2}-\sqrt{\rho \cdot e^{-s^{2}}}}}-1} $$
(29)

Despite the relatively complex appearance of this equation, it contains only three arguments. The main argument is the utilization of the service station (=shuttle). This rate is provided by the subsequent equation, which is composed of the lift interarrival time and the shuttle service time [3]:

$$ \rho=\frac{t_{S}}{t_{A}} $$
(30)

K is the capacity of the queueing system. It is the sum of the number of buffer spaces and the capacity of the shuttles; the latter is always one pallet in the discussed SBS/RS [3].

$$ K=n_{buf} + 1 $$
(31)

The third argument is s, the coefficient of variation of the service process time. This coefficient can be calculated similarly for a single-tier serving shuttle and single-deep racks [3]. The coefficient of variation for shuttles performing single handling cycles can be calculated as follows [3]:

$$ s=\frac{\sqrt{\frac{\left( 2\cdot \frac{n_{sl} \cdot {\varDelta} x}{v_{sh}}\right)^{2}}{12}}}{t_{S}} $$
(32)

The formula for double handling cycles is [3]:

$$ s=\frac{\sqrt{\frac{\left( 2\cdot \frac{n_{sl} \cdot {\varDelta} x}{v_{sh}}\right)^{2}}{18}}}{t_{S}} $$
(33)

These simple equations can be used because the coefficient of variation for a single-tier serving shuttle and single-deep storage is always higher than for multiple-deep storage, so that the resulting error is less than 10%. This causes a difference in the throughput that is less than 2%, and the resulting error can be neglected [4].

The probability of emptiness of the queueing system contains the same arguments as the blocking probability and can be calculated as follows [34]:

$$ p_{0}=\frac{\rho-1}{\rho^{2\cdot\frac{\sqrt{\rho \cdot e^{-s^{2}}} \cdot s^{2}-\sqrt{\rho \cdot e^{-s^{2}}} +K+1}{2+\sqrt{\rho \cdot e^{-s^{2}}} \cdot s^{2}-\sqrt{\rho \cdot e^{-s^{2}}}}}-1} $$
(34)

5 Numerical study

Section 5.1 offers a validation of the approach of the whole aisle with shuttles serving multiple tiers of multiple-deep storage by comparing the analytical model to a DES. Subsequently, in Section 5.2, an outline of how the model should be used to improve SBS/RS is presented. An example demonstrates the impact of the number of tiers served by a shuttle and the storage depth of the rack.

5.1 Numerical evaluation of approximation quality

The performance of a SBS/RS is of key importance during the design process of such systems. Understanding the various impacts of the number of tiers served per shuttle and of the storage depth helps to determine an economically and ecologically ideal SBS/RS design. Thus, certain parameter configurations, shown in Table 4, were selected in order to present a variety of different settings. The system of interest had up to 15 main tiers and up to three sub-tiers per main tier. The length was up to 70 storage slots per tier on each side of the aisle. The parameters in Table 4 are based on data from a European material handling provider of SBS/RS.

Table 4 Tested parameter configurations of the tier-captive, single-aisle SBS/RS
Full size table

For the validation, the results of the analytical model were compared to an ensemble of 30 independent replications of the simulation model. The simulation runs were performed by DES software SIMIO (version 10). The simulation model simulated the real SBS/RS with all of its processes. The order list of pallets for retrieval was created evenly across all stored pallets. The control of the shuttles and the lifts was modeled on the real system and attempted to avoid the waiting times between these two subsystems. The storage of the pallets was evenly distributed over all tiers and over all storage locations.

In Fig. 5, the curve of DES results lies between the two curves of analytical model results. In the DES, the shuttles execute a combination of single command cycle and dual command cycle, so the curve of the DES is expected to lie between the two analytical calculation curves. This plot illustrates the closeness with which the open-queueing system approaches the real system. This figure shows the throughput for a single-deep rack with shuttles serving two tiers. The amount of double cycles for the simulation model varied from 50 to 75% and depended on the control policy of the shuttles. The reason for the mixture of single and dual command in the simulation models is that the input to the various tiers must be controlled so that the waiting times for the shuttles are kept to a minimum. A complex control policy is required to solve this, and it is not the aim of the present paper to provide such a control policy.

Fig. 5
figure 5

Throughput of a rack of length 105 m of single-deep storage with shuttles serving two tiers and a filling degree of 90%

Full size image

Figure 6 shows a comparison between the analytical calculation and the simulation concerning the throughput of shuttles with multiple-deep storage. The mean squared error of 10% and 98% is 3.15% for fivefold-deep storage. Thus, precise results are to be expected from this analytical approach. This comparison is performed to validate the approach to the cycle times of the shuttle for multiple-deep storage.

Fig. 6
figure 6

Throughput of one single tier of length 105 m of fivefold-deep storage with shuttles serving single tiers

Full size image

Figure 7 shows the influence of the number of tiers served by a shuttle and of the storage depth on the throughput of tiers with different numbers of sub-tiers and different storage depths at a filling degree of 90%. For this example, the number of tiers was set to four to maintain a consistent number of available storage slots with respect to the number of sub-tiers. Thus, the first configuration had four main tiers. Therefore, every shuttle had only one tier to serve, and there were four shuttles working in the represented example. The second discussed system included two main tiers, with each shuttle serving two tiers. The last system in this figure has only one main tier, so the shuttle has to serve all four tiers. In the figure, each system is illustrated by a curve of its own. The influence of the storage depth can also be seen in this figure. The decrease in throughput with increasing storage depth is relatively high on a single tier. This effect loses strength at the scale of a whole aisle, as shown in the next subsection. The reason for this is that when switching from single- to double-deep, aisle length contracts by fully half in order to provide the same number of storage spaces. The following subsection discusses this effect of the storage depth on a whole aisle in greater detail and discusses the influence on throughput as well.

Fig. 7
figure 7

Throughput of four tier of length 105 m with different storage depths and shuttles serving 1, 2, or 4 tiers each

Full size image

5.2 Optimization example

The optimization example is based on the requirements listed in Table 5. The aim of this optimization example is to find a geometrical parameter which delivers the highest throughput at the given requirements from Table 5 with the given parameters of the system from Table 4.

Table 5 Requirements for the tier-captive SBS/RS
Full size table

The system requires a storage capacity of 2000 spaces per aisle, with no height or length restrictions. The maximum storage depth of a rack is five. The width of an aisle is given by W = 1.5 m + 2 m⋅sd. For the footprint, the space required for buffers, lifts, and I/O points in front of the aisle is ignored. Following [13, 15, 31], the throughput of a multiple-aisle SBS/RS can be calculated by calculating the performance of a single aisle.

The lift and shuttle parameters take the same values as in Section 5.1.

The procedure of this optimization is as follows:

  • Determine the length of an aisle by a given storage depth, given the number of tiers served by a shuttle as well as a different number of tiers

  • Determine the throughput according to the procedure in Section 4 with a filling degree of 90%

  • Determine the maximum throughput of each configuration determined in the first step

The results of these calculations are displayed in Table 6. The results for a single aisle with different numbers of tiers served by a shuttle and different storage depths are visualized in Fig. 8. The requirement of 2000 storage locations led to a decrease in rack length with increasing storage depth, with an increasing number of tiers served by a shuttle, and with an increasing number of aisles. Due to the fact that the ratio of height and length is always nearly the same, the length decreases with an increase in the number of aisles. The reason why an aisle is getting shorter with an increase of the number of tiers served by a shuttle is that the performance of the shuttle decreases; thus, the length has to become shorter to compensate for this. The number of tiers for maximum throughput decreased with an increasing number of aisles. Additionally, the storage depth influenced the number of tiers. Here, the number of tiers decreased with increasing storage depth. The number of tiers served by a shuttle showed the strongest influence on the number of tiers per aisle, with tiers per aisle increasing with an increasing number of tiers served by a shuttle. The required ground space for the SBS/RS can be seen as a measure of the cost. For the investigated configurations, the footprint decreased with an increasing number of tiers served by a shuttle and with increasing storage depth. Generally, the cost would be expected to decrease proportionally, with particular respect to the number of aisles. However, the cost for each shuttle increased with increasing shuttle complexity. So the real optimum cannot be determined in general for this the real costs of the different configurations had to be known. Table 6 provides performance measures for these configurations in terms of the three main requirements of a SBS/RS:

  • The maximum number of pallets that can be stored in an hour 𝜗storage

  • The maximum number of pallets that can be retrieved in an hour 𝜗retrieval

  • The maximum number of pallets that can be stored and retrieved at the same time in an hour 𝜗storage+retrieval

Fig. 8
figure 8

Optimization example

Full size image
Table 6 Optimization example
Full size table

In general, throughput behaved as expected, declining with an increasing number of tiers. Another interesting aspect of multiple-deep storage is that the maximum throughput of the pure storage process is higher than the maximum throughput of the pure retrieval process. This obviates the need for a re-store in the storage process, since it can happen during the retrieval process. The coefficient of sorting wsort was set to zero in this example. If this coefficient is set to one, the storage process would have throughput equal to that of the retrieval process. The maximum throughput of a SBS/RS for the combined storage/retrieval process is always less than the total throughput of both pure processes. This leads to the dual command cycles for the shuttle work in the combined process. However, this result is falsified by the fact that in the combined process not all storages and retrievals are counted together; only some of them are counted. This means, for example, that throughput for a combined process of 𝜗storage+retrieval = 148/h stores 148 pallets stored and retrieves 148 pallets, which is in total 296 pallets per hour.

6 Conclusion

The strong system performance of tier-captive SBS/RS has been increasingly sought by industries. In the last years, these systems have also come to be used for the storage of pallets rather than just small totes. For this reason, development has proceeded in the direction of shuttles serving multiple tiers, combined with multiple-deep storage. Nevertheless, there are few available decision tools for evaluating performance. Existing methods discuss SBS/RS with either shuttle serving multiple tiers or multiple-deep storage but not both. Thus, this study presented a fair, accurate method for the calculation of the performance of tier-captive, single-aisle SBS/RS with shuttles serving multiple tiers of multiple-deep storage. Another feature investigated was the influence of sorting into retrieval batches, i.e., a coefficient of sorting. The system was modeled as a continuous-time, open-queueing system with limited capacity. Subsequently, the interarrival and service times were evaluated using a cycle-time model of lifts and shuttles with discrete spatial values. The distinctive feature of this approach is that it can treat shuttles serving multiple tiers of multiple-deep storage using a probability-based approach that takes into account the relocation process and the time needed for this process. It also takes into account the different speed parameters of the shuttle in vertical and horizontal directions. This helps improve the relocation process to find the least time needed. The accuracy of the analytical model in comparison to a DES was validated by a numerical study.

Finally, the present study outlined how the presented queueing model can be used to design tier-captive SBS/RS for given requirements, such as storage capacity, storage throughput, retrieval throughput, and throughput for symmetrical storage/retrieval. The resulting ground space for each design was also calculated, to show the expected cost to build such a system. The depicted example showed the influence of the number of tiers served by a shuttle as well as of the storage depth. Also shown in this example were the differences in throughput for storage, retrieval, and the symmetrical combination of storage and retrieval, this last being a very strict design requirement. Also depicted were the different storage and retrieval throughputs as functions of storage depth. Here, the reachable throughput increases with an increase of the storage depth and decreases with an increase in the number of tiers served by a shuttle. Another intriguing coefficient introduced in this paper was the coefficient of sorting. This coefficient describes the storing of pallets in batches of the same order to avoid a relocation cycle. This storage strategy is often used in real storage systems, increasing the retrieval throughput and the symmetrical storage/retrieval throughput. This approach can be used to design a storage system for any predefined requirements, presenting an advantage for any provider of SBS/RS. For example, when designing a new storage system, this approach can be used to calculate the key data for building such a system in a simple and accurate manner. The presented assumptions were based on a SBS/RS of a European material handling provider.

Further work will be dedicated to SBS/RS with alternative system configurations. Such a system may have a varying number of lifts with alternative handling cycles. Like four lifts and each lift operates in dual command cycles or lifts with more storage place on the handling tablet. This will lead into complex handling cycles. Also of interest is the storage of different pallet heights within the same main tier, as well as size variation of the pallets within the same tier, resulting in a variety of storage depths. All these points will be incorporated into future work.