Skip to main content
SpringerLink
Log in

Experimental and numerical investigation of deformation characteristics during tube spinning

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

A Correction to this article was published on 10 October 2020

This article has been updated

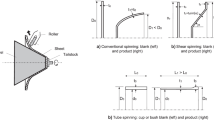
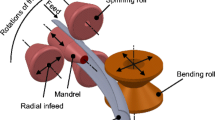
Abstract

The primary objective of this study is to predict the geometric shape and thickness change during multi-pass tube spinning to a hemispherical shape. A computationally efficient, axisymmetric finite element model of the tube-spinning experiments is described. Uniaxial tensile tests are conducted for the development of the material model. The post-necking hardening curve is identified using a hybrid experimental-numerical method and represented by a combined Swift-Voce model. For validation of the finite element model, spinning experiments are performed at room temperature on thin-walled cylinders of 6061-O aluminum alloy. The experiments are interrupted after spinning passes 2, 4, 6, and 8 and the shape and thickness are measured. Also, local strain measurements on the final spun tube (pass 8) are accomplished by a scribed grid. By comparing the predictions to the experiments, good agreement is obtained on the shape, thickness, and strain evolution in multi-pass spinning. The deformation mechanism of this process is described by analyzing the history of plastic strain on an element of the numerical model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Change history

  • 10 October 2020

    The original published article contained a mistake.

Abbreviations

β :

material parameter (Voce law)

ε 0 :

material parameter (Swift law)

ε θ :

hoop strain

\( \overline{\varepsilon_t^p} \) :

logarithmic plastic strain

η :

constant

λ :

constant

μ :

friction coefficient

σ t :

true stress

σ s :

true stress (Swift law)

σ v :

true stress (Voce law)

a :

weight ratio of hybrid Swift and Voce law

k 0 :

material parameters (Swift law)

l 0 :

material parameter (Voce law)

n :

material parameter (Swift law)

q :

material parameter (Voce law)

O :

annealing heat treatment condition

w 0 :

initial width of the 1/8th tensile specimen

w(y):

variation of width along axial direction

y :

axial (Cartesian coordinate system)

z :

axial (cylindrical coordinate system)

References

  1. Kalpakjian S, Rajagopal S (1982) Spinning of tubes: a review. J Appl Metalwork 2(3):211–223. https://doi.org/10.1007/BF02834039

    Article  Google Scholar 

  2. Music O, Allwood JM, Kawai K (2010) A review of the mechanics of metal spinning. J Mater Process Technol 210(1):3–23. https://doi.org/10.1016/j.jmatprotec.2009.08.021

    Article  Google Scholar 

  3. Wong CC, Dean TA, Lin J (2003) A review of spinning, shear forming and flow forming processes. Int J Mach Tool Manu 43(14):1419–1435. https://doi.org/10.1016/S0890-6955(03)00172-X

    Article  Google Scholar 

  4. Jiang SY, Zheng YF, Ren ZY, Li CF (2009) Multi-pass spinning of thin-walled tubular part with longitudinal inner ribs. T Nonferr Metal Soc 19(1):215–221. https://doi.org/10.1016/S1003-6326(08)60255-1

    Article  Google Scholar 

  5. Liu CH (2007) The simulation of the multi-pass and die-less spinning process. J Mater Process Technol 192:518–524. https://doi.org/10.1016/j.jmatprotec.2007.04.021

    Article  Google Scholar 

  6. Wang L, Long H (2011) Investigation of material deformation in multi-pass conventional metal spinning. Mater Des 32(5):2891–2899. https://doi.org/10.1016/j.matdes.2010.12.021

    Article  Google Scholar 

  7. Ram Mohan T, Mishra R (1972) Studies on power spinning of tubes. Int J Prod Res 10(4):351–364. https://doi.org/10.1080/00207547208929937

    Article  Google Scholar 

  8. Roy MJ, Klassen RJ, Wood JT (2009) Evolution of plastic strain during a flow forming process. J Mater Process Technol 209(2):1018–1025. https://doi.org/10.1016/j.jmatprotec.2008.03.030

    Article  Google Scholar 

  9. Hayama M, Kudo H (1979) Analysis of diametral growth and working forces in tube spinning. Bulletin of JSME 22(167):776–784. https://doi.org/10.1299/jsme1958.22.776

    Article  Google Scholar 

  10. Chang SC, Huang CA, Yu SY, Chang Y, Han WC, Shieh TS, Chunga HC, Yao HT, Shyua GD, Hou HY, Wang CC, Wang WS (1998) Tube spinnability of AA 2024 and 7075 aluminum alloys. J Mater Process Technol 80:676–682. https://doi.org/10.1016/S0924-0136(98)00174-5

    Article  Google Scholar 

  11. Davidson MJ, Balasubramanian K, Tagore GRN (2008) An experimental study on the quality of flow-formed AA6061 tubes. J Mater Process Technol 203(1-3):321–325. https://doi.org/10.1016/j.jmatprotec.2007.10.021

    Article  Google Scholar 

  12. Srinivasulu M, Komaraiah M, Rao CKP (2012) Experimental studies on the characteristics of AA6082 flow formed tubes. J Mech Eng Res 4(6):192–198. https://doi.org/10.5897/JMER11.063

    Article  Google Scholar 

  13. Yao J, Murata M (2005) An experimental study on spinning of taper shape on tube end. J Mater Process Technol 166(3):405–410. https://doi.org/10.1016/j.jmatprotec.2004.08.025

    Article  Google Scholar 

  14. Yao J, Murata M (2002) Effects of indented feed of roller tool on parallel spinning of circular aluminum tube. J Mater Process Technol 128(1-3):274–279. https://doi.org/10.1016/S0924-0136(02)00465-X

    Article  Google Scholar 

  15. Akkus N, Kawahara M (2006) An experimental and analytical study on dome forming of seamless Al tube by spinning process. J Mater Process Technol 173(2):145–150. https://doi.org/10.1016/j.jmatprotec.2005.11.011

    Article  Google Scholar 

  16. Zoghi H, Arezoodar AF, Sayeaftabi M (2013) Enhanced finite element analysis of material deformation and strain distribution in spinning of 42CrMo steel tubes at elevated temperature. Mater Des 47:234–242. https://doi.org/10.1016/j.matdes.2012.11.049

    Article  Google Scholar 

  17. Huang CC, Hung JC, Hung C, Lin CR (2011) Finite element analysis on neck-spinning process of tube at elevated temperature. Int J Adv Manuf Technol 56(9-12):1039–1048. https://doi.org/10.1007/s00170-011-3247-0

    Article  Google Scholar 

  18. Wong CC, Lin J, Dean TA (2005) Effects of roller path and geometry on the flow forming of solid cylindrical components. J Mater Process Technol 167(2-3):344–353. https://doi.org/10.1016/j.jmatprotec.2005.05.039

    Article  Google Scholar 

  19. Kezhi L, Nanhai H, Yan L, Kemin X (1998) Research on the distribution of the displacement in backward tube spinning. J Mater Process Technol 79(1-3):185–188. https://doi.org/10.1016/S0924-0136(98)00009-0

    Article  Google Scholar 

  20. Hua FA, Yang YS, Zhang YN, Guo MH, Guo DY, Tong WH, Hu ZQ (2005) Three-dimensional finite element analysis of tube spinning. J Mater Process Technol 168(1):68–74. https://doi.org/10.1016/j.jmatprotec.2004.10.014

    Article  Google Scholar 

  21. Parsa MH, Pazooki AMA, Ahmadabadi MN (2009) Flow-forming and flow formability simulation. Int J Adv Manuf Technol 42(5-6):463–473. https://doi.org/10.1007/s00170-008-1624-0

    Article  Google Scholar 

  22. Zhan M, Zhou Q, Yang H, Zhang J (2007) Establishment of 3D FEM model of multi-pass spinning. Chin J Mech Eng 20(4):19–23. https://doi.org/10.3901/CJME.2007.04.019

    Article  Google Scholar 

  23. Alberti N, Cannizzaro L, Valvo EL, Micari F (1989) Analysis of metal spinning processes by the Adina code. Comput Struct 32(3-4):517–525. https://doi.org/10.1016/0045-7949(89)90343-X

    Article  Google Scholar 

  24. Liu JH, Yang H, Li YQ (2002) Study of the stress and strain distributions of first-pass conventional spinning under different roller-traces. J Mater Process Technol 129(1-3):326–329. https://doi.org/10.1016/S0924-0136(02)00682-9

    Article  Google Scholar 

  25. Mori KI, Nonaka T (2005) Simplified three-dimensional finite element simulation of shear spinning process based on axisymmetric modeling. J Manuf Process 7(1):51–56. https://doi.org/10.1016/S1526-6125(05)70081-5

    Article  Google Scholar 

  26. Raujol-Veillé J, Toussaint F, Tabourot L, Vautrot M, Balland P (2015) Experimental and numerical investigation of a short, thin-walled steel tube incremental forming process. J Manuf Process 19:59–66. https://doi.org/10.1016/j.jmapro.2015.03.008

  27. ASTM E8 / E8M-16, 2016, “Standard test methods for tension testing of metallic materials,” ASTM international, West Conshohocken, PA, https://doi.org/10.1520/E0008_E0008M-16, www.astm.org.

  28. Korkolis YP, Kyriakides S (2008) Inflation and burst of anisotropic aluminum tubes for hydroforming applications. Int J Plast 24(3):509–543. https://doi.org/10.1016/j.ijplas.2007.07.010

    Article  MATH  Google Scholar 

  29. Knysh P, Korkolis YP (2017) Identification of the post-necking hardening response of rate-and temperature-dependent metals. Int J Solids Struct 115:149–160. https://doi.org/10.1016/j.ijsolstr.2017.03.012

    Article  Google Scholar 

  30. Ha J, Baral M, Korkolis YP (2018) Plastic anisotropy and ductile fracture of bake-hardened AA6013 aluminum sheet. Int J Solids Struct 155:123–139. https://doi.org/10.1016/j.ijsolstr.2018.07.015

    Article  Google Scholar 

  31. Baral M, Ha J, Korkolis YP (2019) Plasticity and ductile fracture modeling of an Al–Si–Mg die-cast alloy. Int J Fract 216(1):101–121. https://doi.org/10.1007/s10704-019-00345-1

    Article  Google Scholar 

  32. Swift H (1952) Plastic instability under plane stress. J Mech Phys Solids 1(1):1–18. https://doi.org/10.1016/0022-5096(52)90002-1

    Article  MathSciNet  Google Scholar 

  33. Voce E (1948) The relationship between stress and strain for homogeneous deformation. J Inst Met 74:537–562

    Google Scholar 

  34. Chen WH (1971) Necking of a bar. Int J Solids Struct 7(7):685–717. https://doi.org/10.1016/0020-7683(71)90088-6

    Article  MATH  Google Scholar 

  35. Hoge KG (1966) Influence of strain rate on mechanical properties of 6061-T6 aluminum under uniaxial and biaxial states of stress. Exp Mech 6(4):204–211. https://doi.org/10.1007/BF02326150

  36. Manes A, Peroni L, Scapin M, Giglio M (2011) Analysis of strain rate behavior of an Al 6061 T6 alloy. Procedia Eng 10:3477–3482. https://doi.org/10.1016/j.proeng.2011.04.573

  37. Roy, B. K., Korkolis, Y. P., Arai, Y., Araki, W., Iijima, T., & Kouyama, J., 2019, “Experimental and finite element investigation of wrinkling during spinning of a thin-walled tube,” Proceedings of the NUMIFORM Conference, pp. 547–550.Belytschko, T., Liu, W.K., Moran, B. and Elkhodary, K., 2013, “Nonlinear finite elements for continua and structures,” John Wiley & sons.

  38. Zienkiewicz, O.C., and Taylor, R.L., 2000, “The finite element method: solid mechanics,” Vol. 2, Butterworth-Heinemann.

  39. Bathe KJ (2002) Finite element methods. Springer-Verlag, Berlin, Heidelberg

  40. Belytschko, T., Liu, W.K., Moran, B. and Elkhodary, K., 2013, “Nonlinear finite elements for continua and structures,” John Wiley & sons.Roy, B. K., Korkolis, Y. P., Arai, Y., Araki, W., Iijima, T., & Kouyama, J., 2019, “Experimental and finite element investigation of wrinkling during spinning of a thin-walled tube,” Proceedings of the NUMIFORM Conference, pp. 547–550.

  41. Banabic, D., 2010, “Sheet metal forming processes: constitutive modelling and numerical simulation,” Springer Science & Business Media.Hoge KG (1966) Influence of strain rate on mechanical properties of 6061-T6 aluminum under uniaxial and biaxial states of stress. Exp Mech 6(4):204–211. https://doi.org/10.1007/BF02326150

  42. ABAQUS, 2014, “Theory Manual,” Version 6.14, Simulia, Inc.

Download references

Funding

This study received financial support from the Ministry of Education, Science, Sports, and Culture, of the Government of Japan.

Author information

Authors and Affiliations

  1. Graduate School of Science and Engineering, Saitama University, 255 Shimo-ohkubo, Sakura-ku, Saitama, 338-8570, Japan

    Biplov Kumar Roy

  2. Department of Integrated Systems Engineering, The Ohio State University, 234 Baker Systems, 1971 Neil Avenue, Columbus, OH, 43210-1271, USA

    Yannis P. Korkolis

  3. Division of Mechanical Engineering and Science, Graduate School of Science and Engineering, Saitama University, 255 Shimo-ohkubo, Sakura-ku, Saitama, 338-8570, Japan

    Yoshio Arai & Wakako Araki

  4. Asahi Seisakusho Co., Ltd., 7915 Kake, Iwatsuki-ku, Saitama City, Saitama, 339-0078, Japan

    Takafumi Iijima & Jin Kouyama

Authors
  1. Biplov Kumar Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yannis P. Korkolis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yoshio Arai
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wakako Araki
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Takafumi Iijima
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Jin Kouyama
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yannis P. Korkolis.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1

This Appendix tabulates the coordinates of the roller during spinning (see Table 2).

Table 2 Roller position coordinate with spinning pass
Full size table

Appendix 2

This Appendix describes the comparison of results from the axisymmetric and a 3D shell element model. Due to the high computational time, only part of the first spinning pass was considered. A monitoring element at 50 mm from the free end (see Fig. 17) was selected in both models. Figure 18 compares the evolution of the hoop and meridional plastic strains during spinning. The models predict similar tendencies for the evolution of the strains, as well as a similar reduction in radius. On the other hand, the computational cost of the two models is vastly different: the corresponding solution times are listed in Table 3: the shell element model took approximately 500 times more to run than the axisymmetric one (i.e., approx. 10 days vs. 30 min). This is the reason why only the beginning of the spinning was simulated for this comparison. Furthermore, attempts to use the explicit solver for this problem were thwarted by numerical instabilities, at least for this high radius-to-thickness ratio of about 71. Therefore, in this work, the implicit axisymmetric model is used.

Fig. 17
figure 17

Spinning toolpath and monitoring element position

Full size image
Fig. 18
figure 18

History of hoop and meridional plastic strain changes with the roller axial position

Full size image
Table 3 FEA solution time
Full size table

Appendix 3

The simulation procedure that is executed by the commercial FE package ABAQUS is presented here. For simulation purposes, tube spinning is considered a quasi-static non-linear contact problem. Figure 19 presents the flow chart of the non-linear FE computational solution algorithm (Chapter 2, Section 2.2 in [39]). Figure 20 displays in more detail the flow chart of Coulomb friction algorithm, as used in ABAQUS (Chapter 5, Section 5.2.3 in [39]). Lastly, Fig. 21 shows the schematic that explains the geometric parameters associated with a contact pair involving a master (here, roller) and a slave (here, tube) surface.

Fig. 19
figure 19

Flow chart of non-linear FE solution algorithm for tube spinning simulation

Full size image
Fig. 20
figure 20

Flow chart of Coulomb friction algorithm for tube spinning simulation

Full size image
Fig. 21
figure 21

Schematic of tube spinning simulation contact (gap and penetration)

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Roy, B.K., Korkolis, Y.P., Arai, Y. et al. Experimental and numerical investigation of deformation characteristics during tube spinning. Int J Adv Manuf Technol 110, 1851–1867 (2020). https://doi.org/10.1007/s00170-020-05864-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-020-05864-z

Keywords

Search

Navigation