A joint Bayesian spatiotemporal risk prediction model of COVID-19 incidence, IC admission, and death with application to Sweden

Abstract

The three closely related COVID-19 outcomes of incidence, intensive care (IC) admission and death, are commonly modelled separately leading to biased estimation of the parameters and relatively poor forecasts. This paper presents a joint spatiotemporal model of the three outcomes based on weekly data that is used for risk prediction and identification of hotspots. The paper applies a pure spatiotemporal model consisting of structured and unstructured spatial and temporal effects and their interaction capturing the effects of the unobserved covariates. The pure spatiotemporal model limits the data requirements to the three outcomes and the population at risk per spatiotemporal unit. The empirical study for the 21 Swedish regions for the period 1 January 2020–4 May 2021 confirms that the joint model predictions outperform the separate model predictions. The fifteen-week-ahead spatiotemporal forecasts (5 May–11 August 2021) show a significant decline in the relative risk of COVID-19 incidence, IC admission, death and number of hotspots.

1 Introduction

Most people who have become ill with COVID-19 can recover at home. However, infected patients with severe symptoms need hospital care (Varghese et al. 2020). Clinical treatments include the administering of antiviral drugs (e.g. hydroxychloroquine or lopinavir/ritonavir) or the handling of complications including advanced organ support (e.g. supplemental oxygen and ventilatory support) (WHO 2020). A substantial proportion of the COVID-19 infected individuals deceases (Elezkurtaj et al. 2021).

Most of the literature on COVID-19 has focused on one of its outcomes separately, i.e. the number of incidences, or the number of IC admissions or the number of deaths. These outcomes are the three most important factors for the authorities to control as well as pieces of information for the public at large (Sahu and Böhning 2021). However, several studies on COVID-19 have suggested that the incidence, IC admission, and mortality curves parallel each other, although with lags and with unknown proportionality (IHME 2021; Ma et al. 2020; Onder et al. 2020). Nevertheless, so far, most studies have not taken into account the interplay between the outcomes by means of multivariate models (Congdon 2021). The aim of this paper is to (partly) fill this gap in that it jointly predicts and maps the three outcomes.

The joint prediction of the three outcomes taking into account their interplay has major advantages compared with separate modeling and prediction (Congdon 2021; Martins and Andreozzi 2016; Sahu and Böhning 2021). First, each equation in the joint model is affected by common socioeconomic and environmental factors, although usually with different impacts on the outcomes. In addition, there is a natural chronological order between the outcomes. Considering the simultaneity of the outcomes contributes to a more comprehensive understanding and prediction of the ongoing disease dynamics. Second, the three outcomes complement each other. For instance, the number of incidences is commonly associated with measurement error¹ while the other two outcomes tend to be more accurately reported. By accounting for the associations between the outcomes, joint modeling reduces biased estimation of the parameters of the constituting separate equations, thus improving forecasting and mapping of each outcome (Chu 2021; Newalla et al. 2020; Scobie et al. 2021). Third, joint analysis is important from a policy and planning point of view. When the number of incidences increases, the numbers of hospitalizations and IC admissions and deaths follow suit, although with spatial and temporal lags with unknown proportionality (Borchering et al. 2021). Insight into the dependencies between the outcomes is basic information for the health authorities, hospitals and funeral enterprises to adequately manage their facilities and resources. The number of incidences is needed for the health autorities to issue warnings and implement behavioural restictions, for instance, distancing or lockdowns.² Hospitals need predictions of the numbers of incidences as input for their predictions of hospitalizations, notably IC admissions, because COVID-19 patients require additional resources while the capacity is not easily adjusted in the short and medium term to meet higher demand. In a similar vein, funeral enterprises need predictions on the number of incidences, hospitalizations and IC admissions as inputs for their predictions of the number of deaths.

To capture similar patterns in the three disease outcomes, models with shared effects accounting for the interdependencies between the disease outcomes caused by common factors are required (Downing et al. 2008; Gomez-Rubio et al. 2019; Mahaki et al. 2018; Vicente et al. 2020; Serhiyenko et al. 2016). Deviations from the shared patterns due to outcome-specific factors are captured by specific effects (Knorr-Held and Best 2001).

The spread of COVID-19 varies both in time and space (Briz-Redón and Serrano-Aroca, 2020; Liu et al. 2020) making spatiotemporal modelling and mapping a necessity for adequate policy responses (Brett et al. 2018; Southall et al. 2020; Jaya and Folmer 2021a). The numbers of incidences, hospitalizations, IC admissions, and deaths per spatiotemporal unit are monitored on a daily or weekly basis in most countries. However, this does not apply to the main risk factors, notably demographic characteristics (Arani et al. 2021; Mutair et al. 2021), human behaviour (Chan et al. 2020; Nature 2020), socioeconomic conditions (Aleman et al. 2020; Cerqua and Letta 2022; Hawkins et al. 2020; Karmakar et al. 2021; Naylor-Wardle et al. 2021) and environmental variables (Azuma et al. 2020; Eslami and Jalili 2020; Lim et al. 2021; Poirier et al. 2020). The risk factors are commonly monitored for much larger time intervals than the three COVID-19 outcomes. However, for prediction purposes observations on the risk factors are not needed as their impacts can be inferred from the numbers of the COVID-19 outcomes, as reflected by their spatiotemporal trends and patterns which can be captured by hierarchical random effects models (Jaya and Folmer 2020, 2021a; Lopez-Qulez and Munoz 2009; Balamchi 2021; Choo and Walker 2008). The type of model based on spatiotemporal trends and patterns but without the risk factors is denoted as the pure model (Jaya and Folmer 2020; Lopez-Quılez and Munoz 2009).³ Particularly, if spatial and temporal autocorrelation and their interaction account for the majority of the space–time variation of the COVID-19 outcomes, one cannot expect a significant improvement in forecasting performance from an extension of the pure model by including covariates in the model (Lawson and Lee 2017; Lesaffre and Lawson 2012; Jaya and Folmer 2022a, under review; Turner and Witt 2001).⁴ Even more so, latent correlation between the random effects and the covariates frequently result in erroneous interpretations of the coefficients of the risk factors and deterioration of the prediction performance of the extended model.⁵ This applies especially to count data, as in the case of the COVID-19 outcomes (Jaya and Folmer 2022a, under review). On the other hand, if the research goal is to explicitly estimate the effects of the risk factors, then the covariates should be included in the model while the random effects capture residual spatiotemporal autocorrelation or heterogeneity. The model is denoted as the causal model (Jaya and Folmer 2022a, under review).⁶ Both the pure model and the causal model can be applied to identify spatiotemporal high-risk clusters (hotspots) (Jaya and Folmer 2020, 2021a, b; Lawson and Lee 2017; Lesaffre and Lawson 2012).

A spatiotemporal pure model consists of structured and unstructured spatial and temporal random effects and their interaction. The structured spatial and temporal random effects capture spatial and temporal correlation, respectively, the unstructured spatial and temporal random effects capture spatial and temporal heterogeneity, respectively. The four kinds of interaction between the spatial and temporal random effects (structured spatial effect × structured or unstructured temporal effect; unstructured spatial effect × structured or unstructured temporal effect) are captured by the interaction term (Knorr-Held 2000).

Pure spatiotemporal disease models can be adequately estimated using Bayesian statistics. Particularly, the Bayesian framework provides a convenient setting for hierarchical random effects models and forecasting. See amongst other Jaya and Folmer (2020, 2021b) and the references therein for details.

The objective of this paper is to jointly predict the relative risk of COVID-19 incidence, IC admission and death for Sweden based on regional weekly observations for the period 1 January 2020 – 4 May 2021. Because accurate data on hospitalization was not available, the prediction of the risk of the second outcome is restricted to IC admission. The use of regional data is motivated by policy considerations as the Swedish health care system is organized at the regional level. Joint out-of-sample spatiotemporal predictions will be compared to single equation predictions. In addition, we generate forecasts for the out-of sample period 5 May 2020 – 11 August 2021.

The paper is organized as follows. Section 2 discusses the joint spatiotemporal model, its Bayesian estimation and the prediction framework. Section 3 presents the data, descriptive statistics and the estimation results while Sect. 4 contains the predictions, including the exceedance probabilities and hotspots. Section 5 concludes.

2 The joint Bayesian spatiotemporal COVID-19 risk model

Let ${y}_{it}$, ${o}_{it}$, and ${z}_{it}$ denote the numbers of confirmed COVID-19 incidences, IC admissions and deaths in region $i$ at time $t$, respectively, for $i = 1,\dots ,n$ and $t = 1,\dots , T$. We model ${y}_{it}$ marginally, ${o}_{it}$ conditionally on ${y}_{it}$ and q of its time lags and ${z}_{it}$ conditionally on ${y}_{it}$ and $r$ of its time lags.

We assume that the numbers of COVID-19 incidences, IC admissions, and deaths in region i in period t, follow Poisson distributions or, in the case of overdispersion, when the data contain large numbers of zeros, negative binomial (NB) distributions (Berk and MacDonald 2008; Payne et al. 2017), or zero-inflated Poisson (ZIP) distributions (Lewsey and Thomson 2004), or zero-inflated negative binomial (ZINB) distributions (Agarwal et al. 2002). For now, we assume that ${y}_{it}$, ${o}_{it}$, and ${z}_{it}$ follow Poisson distributions with means and variances equal to $\lambda_{it}^{y} = E_{it}^{y} \theta_{it}^{y}$, $\lambda_{it}^{o} = E_{it}^{o} \theta_{it}^{o}$, and $\lambda_{it}^{z} = E_{it}^{z} \theta_{it}^{z}$, respectively. Hence:

$$y_{it} \sim {\text{Poisson}}\left( {E_{it}^{y} \theta_{it}^{y} } \right){ }$$

(1a)

$$o_{it} |y_{ik} \sim {\text{Poisson}}\left( {E_{it}^{o} \theta_{it}^{o} } \right)$$

(1b)

$$z_{it} |y_{il} \sim {\text{Poisson}}\left( {E_{it}^{z} \theta_{it}^{z} } \right)$$

(1c)

where $E_{it}^{h}$ and $\theta_{it}^{h}$ are the expected count and the relative risk of COVID-19 outcome $h$, respectively. (To avoid repetition, we use $h$ to collectively refer to the three outcomes. Hence, unless stated otherwise, $h= y,o,z$). The expected number of confirmed COVID-19 outcomes h is defined as:

$$E_{it}^{h} = N_{it}^{h} p^{h}$$

(2)

with $N_{{{\text{it}}}}^{h}$ denoting the number of persons at risk for outcome h and ${p}^{h}$ the constant probability of outcome h across all regions, respectively (Last 2001). ${N}_{\mathrm{it}}^{h}$ may be the entire population or a subset of the population, depending on susceptibility (Sellon and Long 2014).⁷ According to the WHO (2021), the entire population is susceptible to COVID-19 infection, IC admission, and death as a result of the coronavirus infection. Hence, we take the constant probability $p^{h}$ as (Abente et al. 2018; Jaya and Folmer 2020):

$$p^{h} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \mathop \sum \nolimits_{t = 1}^{T} h_{it} }}{{\mathop \sum \nolimits_{i = 1}^{n} \mathop \sum \nolimits_{t = 1}^{T} N_{it} }}{ }$$

(3)

A common definition of the relative risk is the standardized event ratio (${\text{SER}}^{h}$) defined as the ratio of the number of a confirmed cases $h$ and the corresponding expected count (Yin et al. 2014):

$${\text{SER}}_{{{\text{it}}}}^{h} = \frac{{h_{{{\text{it}}}} }}{{E_{{{\text{it}}}}^{h} }}$$

(4)

The standardized event ratio can be unreliable for sparse count data. Particularly, a spatiotemporal unit with a small number of observed outcomes and a small population at risk may be incorrectly classified as a high-risk unit (Jaya and Folmer 2017, 2020; Yin et al. 2014). To improve the relative risk estimate, we reduce spatiotemporal variation via smoothing by introducing spatiotemporal dependence and heterogeneity into the Poisson regression model, i.e. by borrowing strength across spatiotemporal units (Yin et al. 2014). Taking the logarithmic link function of the average number of events $\lambda_{{{\text{it}}}}^{h}$ yields:

$$\log \left( {\lambda_{it}^{h} } \right) = \log \left( {E_{it}^{h} } \right) + \log \left( {\theta_{it}^{h} } \right)$$

(5)

with $E_{it}^{h}$ the offset which is taken to have a regression coefficient fixed at 1. Using the offset as the denominator of the rate, the log relative risk reads (Blangiardo and Cameletti 2015):

$$\log \left( {\theta_{it}^{h} } \right) = \log \left( {\frac{{\lambda_{it}^{h} }}{{E_{it}^{h} }}} \right)$$

(6)

Accounting for spatiotemporal dependence and heterogeneity, the log relative risk for each outcome in Eq. (1) takes the form of a generalized linear mixed model as follows:

$$\eta_{it}^{y} = \log \theta_{it}^{y} = \alpha^{y} + \omega_{i}^{y} + \upsilon_{i}^{y} + \phi_{t}^{y} + \varsigma_{t}^{y} + \delta_{it}^{y}$$

(7a)

$$\eta_{it}^{o} = \log \theta_{it}^{o} = \alpha^{o} + \mathop \sum \limits_{k = 0}^{q} \gamma_{1,\,\,\,\,k + 1} \log \left( {\frac{{y_{i,t - k} }}{{E_{i,\,\,\,\,t - k}^{y} }}} \right) + \omega_{i}^{o} + \upsilon_{i}^{o} + \phi_{t}^{o} + \varsigma_{t}^{o} + \delta_{it}^{o}$$

(7b)

$$\eta_{it}^{z} = \log \theta_{it}^{z} = \alpha^{z} + \mathop \sum \limits_{l = 0}^{r} \gamma_{2,\,\,\,\,l + 1} \log \left( {\frac{{y_{i,\,\,\,\,t - l} }}{{E_{i,t - l}^{y} }}} \right) + \omega_{i}^{z} + \upsilon_{i}^{z} + \phi_{t}^{z} + \varsigma_{t}^{z} + \delta_{it}^{z}$$

(7c)

where ${\alpha }^{h}$ is the intercept, ${\omega }_{i}^{h} \mathrm{and} {\upsilon }_{i}^{h}$ are the structured and unstructured spatial random effects, respectively,${\phi }_{t}^{h} \mathrm{and} {\varsigma }_{t}^{h}$ the structured and unstructured temporal random effects, respectively, and ${\delta }_{it}^{h}$ the interaction effect capturing the interaction between a pair of structured or unstructured spatial and temporal random effects (Knorr-Held 2000). The random effects capture the effects of the unobserved risk factors (Jaya and Folmer 2020; Kazembe 2007) while the lagged variables $\mathrm{log}\left(\frac{{y}_{i,t-k}}{{E}_{i,t-k}^{y}}\right) \mathrm{and} \mathrm{log}\left(\frac{{y}_{i,t-l}}{{E}_{i,t-l}^{y}}\right)$ account for the time lags of incidence risk for IC admission $({o}_{it}$) and death (${z}_{it}$), respectively.⁸

Models (7a)–(7c) can be combined into a single model by stacking the outcomes as $\varvec{g} = \left( {\varvec{y}^{\prime } ,\varvec{o}^{\prime } ,\varvec{z}^{\prime } } \right)^{\prime } = \left( {g_{{11}}^{y} , \ldots ,g_{{nT}}^{y} ,g_{{11}}^{o} , \ldots ,g_{{nT}}^{o} ,g_{{11}}^{z} \ldots ,g_{{nT}}^{z} } \right)^{\prime }$, the population at risk as $\varvec{E} = \left( {\varvec{E}^{{\varvec{y}^{\prime } }} ,\varvec{E}^{{\varvec{o}^{\prime } }} ,\varvec{E}^{{\varvec{z}^{\prime } }} } \right)^{\prime } = \left( {E_{{11}}^{y} , \ldots ,E_{{nT}}^{y} ,E_{{11}}^{o} , \ldots ,E_{{nT}}^{o} ,E_{{11}}^{z} , \ldots ,E_{{nT}}^{z} } \right)^{\prime }$ and the log relative risk as ${\varvec{\eta}} = \left( {\log \left( {\theta_{11}^{y} } \right), \ldots ,\log \left( {\theta_{nT}^{y} } \right),\log \left( {\theta_{11}^{o} } \right), \ldots ,\log \left( {\theta_{nT}^{o} } \right),\log \left( {\theta_{11}^{z} } \right), \ldots ,\log \left( {\theta_{nT}^{z} } \right)} \right)^{\prime}.$ According to Gomez-Rubio et al. (2019) and Knorr-Held and Best (2001), many disease outcomes share common risk factors and thus have similar spatiotemporal patterns of variation. To capture similar spatiotemporal patterns (clusters) in the outcomes, structured spatial variation and structured temporal variation are decomposed into specific and shared effects (Gomez-Rubio et al. 2019; Knorr-Held and Best 2001). Specifically, the structured spatial effect is defined as $\omega_{i}^{h} = \ddot{\omega }_{i}^{h} + \varphi^{h} \tilde{\omega }_{i}$ and the structured temporal effect as $\phi_{i}^{h} = \ddot{\phi }_{i}^{h} + \varrho^{h} \tilde{\phi }_{i}$ with $\ddot{\omega }_{i}^{h}$ and $\ddot{\phi }_{i}^{h}$ denoting the structured spatial and structured temporal specific effect, respectively, and $\tilde{\omega }_{i}$ and ${\widetilde{\phi }}_{t}$ the structured spatial and structured temporal shared effect, respectively, with coefficients ${\varphi }^{h}$ and${\varrho }^{h}$, respectively, representing their impacts on outcome $h,$ respectively. Including the structured spatial and structured temporal specific ($\ddot{\omega }_{i}^{h}$ and $\ddot{\phi }_{t}^{h}$) and shared effects ($\tilde{\omega }_{i}$ and $\tilde{\phi }_{t}$) with weights $\varphi^{h}$ and $\varrho^{h}$ in $\eta_{it}^{h}$, Eqs. (7a–c) can be jointly written as: ⁹

$$\begin{aligned} \eta _{{it}}^{h} = & \alpha ^{h} + I_{o} \left( {\mathop \sum \limits_{{k = 0}}^{q} \gamma _{{1,k + 1}} \log \left( {\frac{{y_{{i,t - k}} }}{{E_{{i,t - k}}^{y} }}} \right)} \right) + ~I_{z} \left( {\mathop \sum \limits_{{l = 0}}^{r} \gamma _{{2,l + 1}} \log \left( {\frac{{y_{{i,t - l}} }}{{E_{{i,t - l}}^{y} }}} \right)} \right) \\ ~~~~~~~~~~~~~~~~~~~~~~ & + \;~\left( {~\ddot{\omega }_{i}^{h} + \varphi ^{h} \tilde{\omega }_{i} } \right) + \upsilon _{i}^{h} + \left( {\ddot{\phi }_{t}^{h} + \rangle ^{h} \tilde{\phi }_{t} } \right) + \varsigma _{t}^{h} + \delta _{{it}}^{h} \\ \end{aligned}$$

(8)

with $\left\{ {\alpha^{h} , \upsilon_{i}^{h} ,\varsigma_{t}^{h} ,\delta_{it}^{h} } \right\}$ defined in Eqs. (7a–7c), $I_{o}$ and $I_{z}$ the indicator functions for IC admission and death, respectively. We take model (8) as a hierarchical Bayesian latent Gaussian model (LGM) consisting of fixed and random effects (Rue et al. 2017). The coefficients of the fixed effects ($\gamma_{1,\,\,\,\,k + 1}$ and $\gamma_{2,\,\,\,\,l + 1} )$ present the impacts of the time lags of incidence on the IC admission and death, respectively. The random effects (i.e., $\ddot{\omega }_{i}^{h} ,\tilde{\omega }_{i} ,\upsilon_{i}^{h} ,\ddot{\phi }_{t}^{h} ,\tilde{\phi }_{t} ,\varsigma_{t}^{h} , {\text{and }}\delta_{it}^{h}$) account for the structured spatial specific and shared effects, unstructured spatial effects, structured temporal specific and shared effects, unstructured temporal effects, and spatiotemporal interaction effect, respectively.

For estimation of model (8), we consider (i) the likelihood of the data, (ii) the prior distributions for the parameters which are assumed to follow Gaussian distributions (iii) the hyperprior distributions for the hyperparameters which are also assumed to follow Gaussian distributions. Regarding (i), the observations of outcome $h$ in region $i$ at time $t$, ${g}_{it}^{h}$, are conditionally independent¹⁰ of the observations of the other outcomes given the linear predictors $\eta_{it}^{h}$. Hence, from Eqs. (1a–1c) and (8), we have:

$$g_{it}^{h} |\eta_{it}^{h} \sim iid\,\,\,\,{\text{Poisson}}\left( {E_{it}^{h} \exp \left( {\eta_{it}^{h} } \right)} \right)$$

(9)

with ${\eta }_{it}^{h}$ defined in Eq. (8).

Regarding (ii), we assign vague Gaussian prior distributions to the parameters $\alpha^{y}$, $\alpha^{o}$, $\alpha^{z}$, $\gamma_{1,1} , \ldots ,\gamma_{1,q + 1}$, $\gamma_{2,1} , \ldots ,\gamma_{2,r + 1}$, $\varphi^{y} ,\varphi^{o} ,\varphi^{z} ,$ $\varrho^{y}$, $\varrho^{o}$ and $\varrho^{z}$ (Jaya and Folmer 2021a; Martinez-Beneito and Botella-Rocamora 2019). For the structured spatial specific effects the intrinsic conditional autoregressive model (iCAR) (Besag et al. 1991) and the more general Leroux CAR (LCAR)¹¹ model (Leroux et al. 2000) are common prior distributions.¹² The LCAR is an extension of the iCAR and is applicable to a wider variety of spatial correlation scenarios (Lee 2011). The iCAR prior for $\ddot{\omega }_{i}^{h}$ is (Besag et al. 1991):

$$\ddot{\omega }_{i}^{h} |\ddot{\omega }_{ - i}^{h} ,\sigma_{{\ddot{\omega }^{h} }}^{2} ,{\mathbf{W}}\sim {{\mathcal{N}}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} w_{ij} \ddot{\omega }_{j}^{h} }}{{\mathop \sum \nolimits_{i = 1}^{n} w_{ij} }},\frac{{\sigma_{{\ddot{\omega }^{h} }}^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} w_{ij} }}} \right)$$

(10)

where $w_{ij}$ is an element of the spatial weights matrix W defined as:

$$w_{ij} = \left\{ {\begin{array}{*{20}c} {1\,\,\,\,{\text{if}}\,\,\,\,i\,\,\,\,{\text{and }}j\,\,\,\,{\text{are adjacent neighbors}}} \\ {0 \,\,\,\,{\text{otherwise}} } \\ \end{array} } \right.$$

and $\sigma_{{\ddot{\omega }^{h} }}^{2}$ is the variance parameter of $\ddot{\omega }_{i}^{h}$. The LCAR prior reads (Leroux et al. 2000):

$$\ddot{\omega }_{i}^{h} |\ddot{\omega }_{ - i}^{h} ,\sigma_{{\ddot{\omega }^{h} }}^{2} ,{\mathbf{W}}\sim {{\mathcal{N}}}\left( {\frac{{\rho^{h} \mathop \sum \nolimits_{j = 1}^{n} w_{ij} \ddot{\omega }_{j}^{h} }}{{\rho^{h} \mathop \sum \nolimits_{j = 1}^{n} w_{ij} + 1 - \rho^{h} }},\frac{{\sigma_{{\ddot{\omega }^{h} }}^{2} }}{{\left( {\rho^{h} \mathop \sum \nolimits_{j = 1}^{n} w_{ij} + 1 - \rho^{h} } \right)}}} \right)$$

(11)

where ${\rho }^{h}$ denotes the spatial autoregressive parameter. (The iCAR prior is the limiting case of the Leroux prior when ${\rho }^{h}$ equals 1). The structured spatial shared effect ${\widetilde{\omega }}_{i}$ is also assigned a CAR (iCAR or LCAR)) prior. The unstructured spatial effects ${v}_{i}$ are assigned exchangeable Normal priors (Osei and Stein 2019)¹³:

$$\upsilon_{i}^{h} |\sigma_{{\upsilon^{h} }}^{2} \sim {{\mathcal{N}}}\left( {0,\sigma_{{\upsilon^{h} }}^{2} } \right)$$

(12)

where $\sigma_{{\upsilon^{h} }}^{2}$ is the variance parameter of $\upsilon_{i}^{h}$. A common prior for the structured temporal specific effects $\ddot{\phi }_{t}^{h}$ is a random walk of order one (RW1) (Schrödle and Held 2011):

$$\ddot{\phi }_{t + 1}^{h} - \ddot{\phi }_{t}^{h} |\sigma_{{\ddot{\phi }^{h} }}^{2} \sim {{\mathcal{N}}}\left( {0,\sigma_{{\ddot{\phi }^{h} }}^{2} } \right){ }$$

(13)

with $\sigma_{{\ddot{\phi }^{h} }}^{2}$ the variance parameter of $\ddot{\phi }_{t}^{h}$. An alternative to the RW1 prior when the data has a pronounced linear trend is the random walk of order two (RW2). It reads as:

$$\ddot{\phi }_{t}^{h} - 2\ddot{\phi }_{t + 1}^{h} + \ddot{\phi }_{t + 2}^{h} |\sigma_{{\ddot{\phi }^{h} }}^{2} \sim {{\mathcal{N}}}\left( {0,\sigma_{{\ddot{\phi }}}^{2} } \right)$$

(14)

Note that both RW priors are cyclic accounting for irregular patterns of fluctuation in the data (Gómez-Rubio 2020; Riebler et al. 2011). The structured temporal shared effects $\tilde{\phi }_{t}$ are also assigned RW (i.e. RW1 or RW2) priors. For the unstructured temporal ${\varsigma }_{t}^{h}$ we assume exchangeable Normal priors (Schrödle and Held 2010):

$$\varsigma_{t}^{h} |\sigma_{{\varsigma^{h} }}^{2} \sim {{\mathcal{N}}}\left( {0,\sigma_{{\varsigma^{h} }}^{2} } \right)$$

(15)

where ${\sigma }_{{\varsigma }^{h}}^{2}$ is the variance parameter of ${\varsigma }_{t}^{h}$. For spatiotemporal interaction we choose the interaction structured spatial random effect × structured temporal random effect with corresponding priors. The interaction captures deviations from the shared spatial and temporal trend (Iddrisu et al. 2018; Knorr-Held 2000).

Regarding (iii), the spatial autoregressive hyperparameter $\rho^{h}$ of the LCAR prior and the variances $\sigma_{{\ddot{\omega }^{h} }}^{2} ,\sigma_{{\tilde{\omega }}}^{2} , \sigma_{{\upsilon^{h} }}^{2} ,\sigma_{{\ddot{\phi }^{h} }}^{2} ,\sigma_{{\tilde{\phi }}}^{2} ,\sigma_{{\varsigma^{h} }}^{2}$ and $\sigma_{{\delta^{h} }}^{2}$ require prior distributions, called hyperpriors. As hyperprior for $\rho^{h}$ in Eq. (11), we select $\log \left( {\rho^{h} /\left( {1 - } \right)} \right)\sim {{\mathcal{N}}}\left( {0,0.450} \right)$ (Blangiardo and Cameletti 2015). (The transformation is used to ensure that $\rho^{h}$ takes values between 0 and 1 (Bivand et al. 2015; Martinez-Beneito and Botella-Rocamora 2019)). The weakly informative half-Cauchy distribution with scale parameter 25 is assigned to the square roots of the variances $\{ \sigma_{{\ddot{\omega }^{h} }}^{2} ,\sigma_{{\tilde{\omega }}}^{2} , \sigma_{{\upsilon^{h} }}^{2} ,\sigma_{{\ddot{\phi }^{h} }}^{2} ,\sigma_{{\tilde{\phi }}}^{2} ,\sigma_{{\varsigma^{h} }}^{2}$, $\sigma_{{\delta^{h} }}^{2} \}$ (Gelman 2006).

$\begin{aligned} {\text{Let}}\,\,\,\,\Omega & = (\eta _{{11}}^{y} , \ldots ,\eta _{{nT}}^{y} ,\eta _{{11}}^{o} , \ldots ,\eta _{{nT}}^{o} ,\eta _{{11}}^{z} , \ldots ,\eta _{{nT}}^{z} ,\alpha ^{y} ,\alpha ^{z} ,\gamma _{{1,1}} , \ldots ,\gamma _{{1,q + 1}} ,\gamma _{{1,1}} , \ldots ,\gamma _{{1,r + 1}} , \\ \ddot{\omega }_{1}^{o} , \ldots ,\ddot{\omega }_{n}^{o} ,\ddot{\omega }_{1}^{z} , \ldots ,\ddot{\omega }_{n}^{z} ,\tilde{\omega }_{1} , \ldots ,\tilde{\omega }_{N} ,\upsilon _{1}^{y} , \ldots ,\upsilon _{n}^{y} ,\upsilon _{1}^{o} , \ldots ,\upsilon _{n}^{o} ,\upsilon _{1}^{z} , \ldots ,\upsilon _{n}^{z} ,\ddot{\phi }_{1}^{y} , \ldots ,\ddot{\phi }_{T}^{y} ,\ddot{\phi }_{1}^{o} , \ldots ,\ddot{\phi }_{T}^{o} ,\ddot{\phi }_{1}^{z} , \ldots ,\ddot{\phi }_{T}^{z} ,\tilde{\phi }_{1} , \ldots ,\tilde{\phi }_{T} , \\ \varsigma _{1}^{y} , \ldots ,\varsigma _{T}^{y} ,\varsigma _{1}^{o} , \ldots ,\varsigma _{T}^{o} ,\varsigma _{1}^{z} , \ldots ,\varsigma _{T}^{z} ,\delta _{{11}}^{y} , \ldots ,\delta _{{nT}}^{y} ,\delta _{{11}}^{o} , \ldots ,\delta _{{nT}}^{o} ,\delta _{{11}}^{z} , \ldots ,\delta _{{nT}}^{z} ,\varphi ^{y} ,\varphi ^{o} ,\varphi ^{z} ,\rangle ^{y} ,\rangle ^{o} ,\rangle ^{z} )^{\prime } \\ \Psi & = \sigma _{{\ddot{\omega }^{y} }}^{2} ,\sigma _{{\ddot{\omega }^{o} }}^{2} ,\sigma _{{\ddot{\omega }^{z} }}^{2} ,\sigma _{{\tilde{\omega }}}^{2} ,\sigma _{{\upsilon ^{y} }}^{2} ,\sigma _{{\upsilon ^{o} }}^{2} ,\sigma _{{\upsilon ^{z} }}^{2} ,\sigma _{{\ddot{\phi }^{y} }}^{2} ,\sigma _{{\ddot{\phi }^{o} }}^{2} ,\sigma _{{\ddot{\phi }^{z} }}^{2} ,\sigma _{{\tilde{\phi }}}^{2} ,\sigma _{{\varsigma ^{y} }}^{2} ,\sigma _{{\varsigma ^{o} }}^{2} ,\sigma _{{\varsigma ^{z} }}^{2} ,\sigma _{{\delta ^{y} }}^{2} ,\sigma _{{\delta ^{o} }}^{2} ,\sigma _{{\delta ^{z} }}^{2} ,\rho ^{y} ,\rho ^{o} ,\rho ^{z} )^{\prime } \\ \end{aligned}$ be the vectors of the parameters and hyperparameters, respectively. The joint posterior distribution of the joint Bayesian spatiotemporal model in Eq. (8) is then given by:

$$p\left( {{{\varvec{\Omega}}},{{\varvec{\Psi}}}|{\mathbf{g}}} \right) = \frac{{p\left( {{\mathbf{g}}|{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{{\varvec{\Omega}}}|{{\varvec{\Psi}}}} \right)p\left( {{\varvec{\Psi}}} \right)}}{{p\left( {{\mathbf{g}}|{{\varvec{\Psi}}}} \right)}} \propto p\left( {{\mathbf{g}}|{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{{\varvec{\Omega}}}|{{\varvec{\Psi}}}} \right)p\left( {{\varvec{\Psi}}} \right)$$

(16)

where $p\left(\mathbf{g}|{\varvec{\Omega}},{\varvec{\Psi}}\right)$ denotes the conditionally independent likelihood function given the linear predictors and ${\varvec{\Omega}}\mathrm{and }{\varvec{\Psi}},$ $p\left({\varvec{\Omega}}|{\varvec{\Psi}}\right)$ is the prior distribution of ${\varvec{\Omega}}$ given ${\varvec{\Psi}},$ and $p({\varvec{\Psi}})$ is the hyperprior distributions $\mathrm{and} p(\mathbf{g}|{\varvec{\Psi}})$ the marginal likelihood. The latter is a normalizing constant and can be ignored as it does not include the parameter vector ${\varvec{\Omega}}$.

For the joint likelihood function $p\left(\mathbf{g}|{\varvec{\Omega}},{\varvec{\Psi}}\right)$, the vector of observed disease outcomes, ${\varvec{g}},$ is conditionally independent given ${\varvec{\Omega}}$ and ${\varvec{\Psi}}$ (see note 10). Hence, the likelihood can be expressed as:

$$p\left( {{\mathbf{g}}|{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right) = \mathop \prod \limits_{l = 1}^{n} \mathop \prod \limits_{t = 1}^{T} p\left( {{\mathbf{g}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right) = \mathop \prod \limits_{l = 1}^{n} \mathop \prod \limits_{t = 1}^{T} p\left( {{\text{y}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{\text{o}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{\text{z}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)$$

(17)

For the second component of the joint posterior distribution in Eq. (16), $p\left( {{{\varvec{\Omega}}}|{{\varvec{\Psi}}}} \right)$, we assume a multivariate Normal prior for ${{\varvec{\Omega}}}$ with mean $0$ and precision¹⁴ matrix Q(${{\varvec{\Psi}}}$). Hence:

$$p\left( {{{\varvec{\Omega}}}|{{\varvec{\Psi}}}} \right) \propto \left| {{\mathbf{Q}}\left( {{\varvec{\Psi}}} \right)} \right|^{\frac{1}{2}} \exp \left( { - \frac{1}{2}{\mathbf{\Omega^{\prime}Q}}\left( {{\varvec{\Psi}}} \right){{\varvec{\Omega}}}} \right),$$

(18)

where $\left| . \right|$ denotes the determinant. The latent Gaussian field ${{\varvec{\Omega}}}$ is taken as a Gaussian Markov random field (GMRF) (Rue and Leonhard-Held 2005; Sidén et al. 2018). Thus ${\mathbf{Q}}_{{uu^{\prime}}} \ne 0$ only if $u\prime$ = $u$ or ${u}^{^{\prime}}$ is an immediate neighbour of $u, \mathrm{for} u=1,..U\mathrm{ with }U$ the number of elements of${\varvec{\Omega}}$. Finally, the hyperparameters controlling the variability of the parameters are assumed to be independent of each other implying that the joint hyperprior $p\left({\varvec{\Psi}}\right)$ $=\prod_{s=1}^{S}p\left({\Psi }_{s}\right)$ with $S$ the number of elements of ${\varvec{\Psi}}$. Combining Eqs. (16–18) and the multiplicative joint hyperprior $p\left({\varvec{\Psi}}\right)$ gives:

$$\begin{gathered} p\left( {{{\varvec{\Omega}}},{{\varvec{\Psi}}}|{\mathbf{g}}} \right) \propto \mathop \prod \limits_{l = 1}^{n} \mathop \prod \limits_{t = 1}^{T} p\left( {{\text{y}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{\text{o}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{\text{z}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right) \hfill \\ \times \left| {{\mathbf{Q}}\left( {{\varvec{\Psi}}} \right)} \right|^{\frac{1}{2}} \exp \left( { - \frac{1}{2}{\mathbf{\Omega^{\prime}Q}}\left( {{\varvec{\Psi}}} \right){{\varvec{\Omega}}}} \right) \times \mathop \prod \limits_{s = 1}^{S} p\left( {{\Psi }_{s} } \right) \hfill \\ \propto \exp \left( {\mathop \sum \limits_{i = t}^{n} \mathop \sum \limits_{t = 1}^{T} \log \left( {p\left( {{\text{y}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{\text{o}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)p\left( {{\text{z}}_{it} |{{\varvec{\Omega}}},{{\varvec{\Psi}}}} \right)} \right) - \frac{1}{2}{\mathbf{\Omega^{\prime}Q}}\left( {{\varvec{\Psi}}} \right){{\varvec{\Omega}}}} \right) \hfill \\ \times \left| {{\mathbf{Q}}\left( {{\varvec{\Psi}}} \right)} \right|^{\frac{1}{2}} \mathop \prod \limits_{s = 1}^{S} p\left( {{\Psi }_{s} } \right) \hfill \\ \end{gathered}$$

(19)

The posterior density in Eq. (19) can be calculated applying integrated nested Laplace approximation (INLA) using the R-INLA package (Rue et al. 2009; Jaya and Folmer 2020, 2021a).¹⁵ Instead of considering the full posterior distributions of ${\varvec{\Omega}}$ and ${\varvec{\Psi}}$, INLA proceeds on the basis of approximations to the marginal posterior distributions $p\left({\Omega }_{u}|\mathbf{g}\right)$ and $p\left({\Psi }_{s}|\mathbf{g}\right)$. The marginal posterior distribution of ${\Omega }_{u}$ is:

$$p\left( {{\Omega }_{u} |{\mathbf{g}}} \right) = \smallint p\left( {{\Omega }_{u} |{{\varvec{\Psi}}},{\mathbf{g}}} \right)p\left( {{{\varvec{\Psi}}}|{\mathbf{g}}} \right)d{{\varvec{\Psi}}}$$

(20)

and the marginal posterior distribution of ${\Psi }_{s}$ is:

$$p\left( {{\Psi }_{s} |{\mathbf{g}}} \right) = \smallint p\left( {{{\varvec{\Psi}}}|{\mathbf{g}}} \right)d{{\varvec{\Psi}}}_{{ - {\varvec{s}}}}$$

(21)

The following tasks must be performed to obtain Eqs. (20) and (21): (i) compute $p\left({\varvec{\Psi}}|\mathbf{g}\right)$ from which all the marginal posteriors $p\left({\Psi }_{s}|\mathbf{g}\right)$ can be calculated, and (ii) compute $p\left({\Omega }_{u}|{\varvec{\Psi}},\mathbf{g}\right)$ from which the marginal posteriors of $p\left({\Omega }_{u}|\mathbf{g}\right)$ are calculated. Hence, the posterior means, standard deviations, forecasts, and other statistics are obtained from their marginal posterior distributions $p\left({\Omega }_{u}|\mathbf{g}\right)$.

The R-INLA package also provides goodness-of-fit statistics, notably the deviance information criterion (DIC) (Spiegelhalter et al. 2002) and the Watanabe Akaike information criterion (WAIC) (Watanabe 2010). It also yields the marginal predictive likelihood (MPL) (Dey et al. 1997), mean absolute error (MAE), root mean square error (RMSE) (Pal 2017), and Pearson correlation coefficient (r) (Santa et al. 2019), which are appropriate statistics for prediction performance evaluation.

Forecasts of the relative risk of incidence, IC admission and death in a joint Bayesian setting are based on the posterior predictive distributions $p\left({\widehat{\theta }}_{it}^{h}|\mathbf{g}\right)$ (Wang et al. 2018). Forecasting in R-INLA can be handled by fitting a model with missing observations. Specifically, one combines observed values with missing or unavailable (NA) observations for the forecast periods (see amongst others Jaya and Folmer 2020, 2021b). For the prediction of a variable at $t=1$, the most recent information (at time $t=0$) and previous information ($t<0$) is used. For the prediction for $t>1$, say $t=s$, the information for the prediction at $t=1$ is used, plus the predictions at $t=1, 2,\dots ,s-1$ (recursive updating).

As mentioned in the Introduction, hotspots are of special interest from a policy point of view. They can be identified using the exceedance probability (Jaya and Folmer 2021a; Lawson 2010) which is defined as the probability that the estimated posterior mean of the relative risk of outcome $h$ in region $i$ at time $t$ is greater than a threshold value $c$, that is, $\mathrm{Pr}\left({\widehat{\theta }}_{it}^{h}>c|\mathbf{g}\right)$. It is calculated as:

$${\text{Pr}}\left( {\hat{\theta }_{{it}}^{h} {\text{ < }}c|{\mathbf{g}}} \right) = 1 - \int\limits_{{\hat{\theta }_{{it}}^{h} \le c}} {p\left( {\hat{\theta }_{{it}}^{h} |{\mathbf{g}}} \right)d\theta _{{it}}^{h} }$$

(22)

where $\int\limits_{{\hat{\theta }_{{it}}^{h} \le c}} {p(\hat{\theta }_{{it}}^{h} \left| \varvec{g} \right.){\text{d}}\hat{\theta }_{{it}}^{h} }$ is the cumulative probability of $\hat{\theta }_{it}^{h}$ given ${\mathbf{g}} = \left( {\varvec{y^{\prime}},\varvec{o^{\prime}},\varvec{z^{\prime}}} \right)^{\prime}$ and the threshold value $c.$ To identify spatiotemporal hotspot we also need the cut-off value of the exceedance probability, denoted $\gamma .$ Hence, a spatiotemporal unit is classified as a hotspot if ${\text{Pr}}\left( {\hat{\theta }_{it}^{h} > c|{\mathbf{g}}} \right)$ > $\gamma$. Common values for $c$ are $1$–3, for $\gamma$ $0.90$ and 0.95 (Lawson and Rotejanaprasert 2014). For further details, see Jaya and Folmer (2021a).

3 The joint COVID-19 prediction model for the Swedish regions, 1 January 2020–4 May 2021

The empirical analysis is based on weekly COVID-19 data provided by the Public Health Agency of Sweden (PHAS), covering all 21 Swedish regions ($n=21$) from 1 January 2020 until 4 May 2021 ($T=70$). COVID-19 incidences, $\left(y\right)$, are the confirmed weekly numbers of new cases with COVID-19 infection according to the Swedish case definition (PHAS, 2021) and reported in accordance with the Infection Control Act of COVID-19. IC admissions, $\left(o\right),$ are the weekly numbers of new patients with a laboratory-confirmed COVID-19 infection admitted to intensive care. Deaths $\left(z\right)$ are the weekly numbers of deceased persons with a laboratory-confirmed COVID-19 diagnosis and reported as deceased in the database SmiNet. The weekly numbers and rates per 100,000 inhabitants of incidences, IC admissions, and deaths are presented in Fig. 5, Appendix 1. A summary of the data is presented in Table 1 .

Table 1 Accumulated numbers and rates of COVID-19 incidences, IC admissions and deaths per region from 1 January 2020 to 4 May 2021

Fig. 1

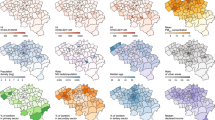
Posterior means of the relative risk for (a) incidence, (b) IC admission, and (c) Death for selected weeks for W11-15 (11 Mar 2020–8 Apr 2020), W17 (22 Apr 2020), W18 (29 Apr 2020), W21 (20 May 2020), W24 (10 Jun 2020), W26 (24 Jun 2020), W27 (1 Jul 2020), W43 (21 Oct 2020), W44 (28 Oct 2020), W45 (4 Nov 2020), W47 (18 Nov 2020), W48 (25 Nov 2020), W57 (27 Jan 2021), W58 (3 Feb 2021), W59 (10 Feb 2021), W60 (17 Feb 2021), W68 (14 Apr 2021), W70 (28 Apr 2021). W refers to the week and the date to the beginning of the week

Fig. 2

Observed and out-of-sample predicted relative risk using individual and joint modelling for a incidence, b IC admission, and c death for selected weeks (see note 24)

Fig. 3

Observed and predicted relative risk hotspots for individual and joint modelling a incidence, b IC admission, and c death for selected weeks (given in note 24)

Fig. 4

Predicted weekly relative COVID-19 risk of a incidence, b IC admission, and c death for W71-85 (5 May 2021—11 August 2021)

Figure 5 shows that in most regions there are three waves of incidences and IC admissions and two waves of deaths. The first wave of the three outcomes started in March 2020 and peaked in April 2020, especially in the Stockholm region (Owen 2021). The second wave started in September 2020 and peaked in December 2020. It had a rapid increase in the number of incidences, followed by an increase in IC admissions and deaths (Claeson and Hanson 2020). The third wave began in February 2020 and peaked in April 2021 .

Fig. 5

Weekly numbers of new incidences, IC admissions, and deaths per region. Note: The primary axis on the left-hand side denotes the weekly number of incidences, the secondary axis on the right-hand side the numbers of IC admissions and deaths

Table 2 Posterior means of the fixed and random effects, their 95% credible intervals, the fractions of the variances, the impacts of the temporal shared effects, and the LCAR coefficients^a

Table 3 Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), and Pearson correlation coefficient (r) for joint and individual out-of-sample prediction for selected weeks^a

Table 4 Misclassification rates of hotspot for incidence, (b) IC admission, and (c) death for selected weeks (given in note 24) for individual and joint modelling ^a

Table 5 Deviance information criterion (DIC), Watanabe–Akaike information criterion (WAIC), marginal predictive likelihood (MPL), Pearson correlation ($r)$, mean absolute error (MAE) and root mean square error (RMSE)${\widetilde{\mathrm{R}}}^{2})$ ${\widetilde{\mathrm{R}}}^{2})$ for 32 sub-models of the model in Eq. (8)^a

Several circumstances contributed to the high numbers of IC admissions and deaths during the first wave, notwithstanding the relatively low numbers of incidences. Despite the Swedish Public Health Agency's recommendations, testing was low or non-existent during the first wave (Folkhälsomyndigheten 2020; Froberg et al. 2021). In addition, mainly individuals admitted to hospitals were tested. Furthermore, there were frequent local outbreaks of asymptomatic healthcare workers in primary care institutions, home healthcare institutions, and palliative care institutions contributing to transmission, IC admission and death (Dillner et al. 2021; Froberg et al. 2021). Rapid local transmission was most pronounced in Stockholm where the bulk of COVID-19 deaths occurred during the initial outbreak (Folkhälsomyndigheten 2020).

The first step in the estimation procedure was model selection. Eight variants of model (8) were estimated and tested applying stepwise forward selection. The model variants differed by likelihood (Poisson and Negative Binomial), number of time lags of incidence ($y$) for IC admission ($o$) and death ($z$),¹⁶ structured spatial and structured temporal specific effects and structured spatiotemporal interaction.¹⁷ Structured spatial and structured temporal shared effects were included in all variants.

The base variant is V1 with the shared effects and the current and lagged incidences for IC admission and death. Variant V2 is V1 extended with the structured temporal specific effect while V3 and V4 are V1 extended with the structured spatial specific effect and the structured spatiotemporal interaction effect, respectively. (As we only consider structured effects (note 17). structured will be deleted below. In a similar vein, we just speak of spatiotemporal interaction or merely interaction as we only consider shared interaction). V5 is V1 plus the temporal and spatial specific effects. V6 and V7 are V2 and V3 extended with spatiotemporal interaction effect, respectively. V8 is V1 extended with temporal and spatial specific effects and spatiotemporal interaction effects. For each variant we considered sub-models by alternating the Poisson and the negative binomial likelihood and RW1 and RW2 trends. In total, we estimated 32 sub-models.¹⁸

We compared the fit of the 32 sub-models using the DIC and WAIC, and evaluated their predictive performance using the MPL, r, MAE, and RMSE, using leave-one-out¹⁹ cross-validation. The results are presented in Table 5, Appendix 2. As a rule of thumb, the best model is the one with the smallest DIC, WAIC, MAE, RMSE and the largest MPL and r. Table 5 shows that variant V6 with Poisson likelihood and RW1 trend performed best. It was selected for further analysis. The variant is denoted M6 below. Further analysis of M6 showed that the second time lag (${\gamma }_{23}$) of incidence had no significant effect on IC admission and was deleted (result available upon request). Furthermore, the precision of the spatial shared effect was infinite ($\infty$), corresponding to zero variance (result available upon request) indicating that it does not contribute to explaining the variation in the outcomes across space. We re-estimated the model without the spatial shared effect and the second time lag of incidence for IC admission. We assessed the performance of the revised M6 by examining the goodness of fit between the observed and predicted values. The correlation between the observed and predicted values of the three outcomes is above 0.90 (result available upon request) indicating that the model fits the data well (Bradley 2020). The estimation results are summarized in Table 2.

Below, we focus the discussion on the posterior means rather than on the credible intervals. Table 2 shows that the intercepts of incidence, IC admission, and death are ${\alpha }^{y}=-2.47;{\alpha }^{o}=-2.45, {\alpha }^{z}=-3.27$, respectively, giving the following mean relative risks: $\mathrm{exp}(-2.471)= 0.08$, $\mathrm{exp}\left(-2.45\right)=0.09$, and $\mathrm{exp}(-3.27)=0.04$, respectively. The means are close to zero, indicating that they do not explain much of the spatiotemporal risk variation. Consequently, the variation is mainly due to the other model components.

The regression slopes of lagged $\mathrm{log}\left(\frac{{y}_{it}}{{E}_{it}^{y}}\right)$ for all time lags have positive effects on the relative risk of IC admission and death. Specifically, the elasticities of lagged $\mathrm{log}\left(\frac{{y}_{it}}{{E}_{it}^{y}}\right)$ in the current and previous week for IC admission are 14.80% and 23.00%, respectively. For death the elasticities are 13.90%, 22.20%, and 13.30% for the current, previous and penultimate week, respectively. The elasticities for IC admission and death risk for the current and one-week lagged incidence are approximately the same with the strongest effects occurring for one-week lagged.

The posterior mean of the variance of a random effect represents its contribution to the variation of the risk estimate; the fraction its share in the total variation of the three estimates jointly. Table 2 shows that the posterior means of the variances of the random effects vary greatly, from 0.02 of the temporal effect for IC admission to 1.62 of the interaction effect for incidence risk. Table 2 furthermore shows that the variance of the temporal shared effect ($\widetilde{\phi }$) accounts for 13.75% of the joint random variation which is substantially smaller than the contribution of the joint spatiotemporal interaction effects ($54.03\%+11.47\%+17.14\%=82.63\%)$ but substantially larger than the contribution of the joint temporal effects (1.56% + 0.73% + 1.33% = 3.62%). The posterior means of the weights of the temporal shared effects of incidence, IC admission, and death are 1.00, 1.06, and 1.12, respectively, indicating that the temporal shared effect contributes similarly to the spatiotemporal variation of each disease outcome.

The correlations²⁰ between the temporal shared effect and the temporal specific effect for incidence, IC admission, and death are 0.344, − 0.578, and 0.568, respectively. For incidence and death, the temporal shared effect and the specific temporal effect strengthen each other while for IC admission they work in opposite directions. The negative correlation for IC admission indicates that there were possibly different factors at work, notably intensive care capacity limitations necessitating that patients were transferred to hospitals in nearby regions to temporally free up space (Berger et al. 2022; Paterlini 2020; Winkelmann et al. 2022). The spatial autoregressive coefficients of the LCAR prior for IC admission, incidence, and death of 0.43, 0.23, and 0.05, respectively, are in line with this assumption. They indicate that for IC admission there was more spatial interaction than for the other outcomes.²¹

Figure 1 presents the estimated posterior means of the relative risk per outcome for 21 regions for selected weeks based on M6 with parameters listed in Table 2.²² The weeks are chosen to highlight the shifts in the posterior means of three outcomes. A relative risk greater than one means that the corresponding posterior mean is larger than the overall average across space and time.

Figure 1(a) shows that the estimated relative risk of COVID-19 incidence in all regions was low during the first 13 weeks W1-W13 (1 January 2020–25 March 2020) (estimated relative risk < 0.50, in green). From W14 (1 April 2020) onward, it began to increase, starting at medium intensity (estimated relative risk 0.5–1.0, yellow) in two southern regions, and subsequently spreading to several western and northern regions. The increase in incidence coincided with an increase in testing, although with local variation (Florida and Mellander 2021; Folkhalsomyndigheten 2020; Pashakhanlou 2021). For instance, in Stockholm, substantial upscaling of testing capacity happened during the second half of the first wave (Fredriksson and Hallberg 2021; Roden 2020). During the weeks W24-W26 (10 June 2020 24 June 2020), there were two high-risk regions (estimated relative risk 1–2, orange) in the southwest and medium risk regions (estimated relative 0.5–1.0, yellow) in the north and the east. During the next week the high-risk regions disappeared and the number of medium risk regions declined. Between W27-W43 (1 July 2020–21 October 2020) there were no high-risk regions and the number of medium risk regions declined further. During W43 (21 October 2020) the next outbreak started in two regions in the south with relatively high intensity (orange). Next, the outbreak began spreading to the majority of the regions. Between W45–W70 (4 November 2020–28 April 2021), more than 80% of Sweden's regions were high risk regions. Some regions in the north had extremely high risk (relative risk > 3).

Figure 1(b) shows that the estimated relative risk of IC admission was low (green) in all regions during the first 10 weeks. It began to rise in W11 (11 March 2020), with moderate intensity (yellow) in the south-east. Next, it started quickly to spread to more than 80% of the regions until W17 (22 April 2020). Between W18-W43 (29 April 2020–21 October 2020), the estimated IC admission risk gradually started decreasing. From W44 (28 October 2020) onwards, the estimated risk of IC admission began to rise again until W70 (28 April 2021). Over 80% of the regions were high risk regions during that period, several of them extremely high-risk regions, particularly in the north.

Figure 1(c) presents the estimated spatiotemporal distribution of the relative risk of COVID-19 death. During the first 11 weeks W1–W11 (1 January 2020–11 March 2020) it was low in all regions (green) but began to turn moderate (yellow) in the south-east and Stockholm followed by a quick proliferation (orange) to more than 80% of the regions until W21 (20 May 2020. From W22-W43 (27 May 2020–21 October 2020), the estimated death risk gradually decreased everywhere but started to rise again in W43 (21 October 2020) to reach a peak in W53 (30 December 2020) with over 80% of the regions high risk regions, and several of them extremely high risk regions, particularly in the southeast and north. With the exception of the north, the estimated death risk continuously decreased from W68 (14 April 2021) until the end of W70 (April 2021).

The estimated relative risks for the three outcomes show similarities but also differences (see also Fig. 3 in Online Resource (1). The relative IC admission risk and relative death risk are strongly correlated across space and time, with correlation greater than 0.70. The correlations between the relative incidence risk on the one hand and the relative IC admission risk and the relative death risk on the other are greater than 0.50 but smaller than the correlation between the relative IC admission risk and death risk, notably during the early stages of the pandemic. We hypothesize that this is related to the slow start of testing and recording of the three outcomes. As mentioned above, testing was low or non-existent during the first wave depressing the number of incidences (Folkhalsomyndigheten 2021; Froberg et al. 2021). Particularly, persons with only mild symptoms were recommended not to seek medical care or visit hospitals and thus forewent testing leading to underestimation of incidence. Another factor contributing to the relatively low correlation between the relative incidence risk and the relative IC admission risk is that during the initial stages, a large proportion of the infection occurred at nursing homes where many infected elderly died before they were admitted to IC (Nordström et al. 2021).²³

4 Prediction of the joint COVID-19 outcomes using M6, 5 May 2021–11 August 2021

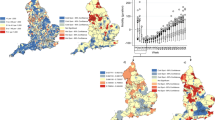
The estimated M6 is used to generate weekly forecasts for the three relative risks for 15 weeks ahead from W71-W85 (5 May 2021–11 August 2021). Before doing so, we analysed the predictive performance of M6 by out-of-sample prediction for selected weeks.²⁴ At the same time, we compared joint modelling with individual modelling. Individual models for three relative risks have the same model specification as M6 but without the temporal shared component. In addition, they are estimated individually. The observed and joint and individual model relative risks predictions are presented in Fig. 2.

Figure 2 shows that the joint model quite accurately predicts the three kinds of relative risk and outperforms the individual approach, except for IC admission. This also follows from the Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Mean Square Error (MSE), and the Pearson correlation coefficient (r) in Table 3.²⁵ The table shows that compared to the individual approach the joint approach has smaller MAE, MAPE, and RMSE and larger $r$ for incidence and death relative risk $.$ For IC admission relative risk the MAE, MAPE and RMSE are larger for the joint approach than for the individual models.

Individual and joint prediction are further evaluated by considering the identification of spatiotemporal hotspots, (discussed in Sect. 2) with threshold $c=1$ and the cut-off value $\gamma =0.90.$ The spatiotemporal pattern of observed ($\mathrm{Pr}\left({\mathrm{SER}}_{it}^{h}>1|\mathbf{g}\right)>.90)$ versus predicted ($\mathrm{Pr}\left({\widehat{\theta }}_{it}^{h}>1|\mathbf{g}\right)>.90$) hotspots is presented in Fig. 3 while the misclassification rates are presented in Table 4.

Table 4 shows that the misclassification rates of both approaches are lower than 30% indicating a good performance (Limam et al. 2004). The joint approach clearly outperforms the individual approach, except for IC admission which is probably related to the intensive care capacity problems and recording issues discussed in see Sect. 3.

The misclassifications for joint modelling concern especially incidence and IC admission risk and to a less extent death risk. In the case of incidence risk, 59 observed hotspots are incorrectly predicted to be non-hotspots while 235 spatiotemporal units were correctly classified (i.e. 181 observed hotspots and 54 observed non-hotspots were correctly predicted). For IC admission 9 observed non-hotspots were incorrectly classified as hotspots and 24 observed hotspots were predicted as non-hotspots. For death 1 observed non-hotspot was incorrectly classified as hotspot and 30 observed hotspots were incorrectly classified as non-hotspot. Hence, the problem is the misclassification of hotspots as non-hotspots. Note that misclassification increases for increasing cut-off values $\gamma$ for fixed threshold $c$ or, alternatively, for increasing $c$ for fixed $\gamma$ (Jaya and Folmer 2021a). As a consequence, if for policy reasons the emphasis is on the correct identification of hotspots, $c$ or $\gamma$ could be lowered to reduce the misclassification rate of hotspots.

Finally, we present the spatiotemporal predictions of the relative risks of the three outcomes in Fig. 4 for W71–W85 (5 May 2021–11 August 2021) using M6.

Figure 4 shows that in W71 (5 May 2021) the predicted relative risk for incidence is high (> 1) for the entire country and extremely high (> 2) in some regions in the south-east and middle-east. The following week the regions with extremely high relative incidence risk have disappeared while a substantial number of high risk regions have become moderately risky. In W73 (19 May 2021) the entire country has become moderately risky while for some regions the relative risk has dropped below 0.5. In W74 (26 May 2021) the relative incidence risk has dropped below 0.5 almost everywhere except for some regions in the southeast and the middle east with a relative risk between 0.5 and 1. For the remainder of the prediction period, the relative incidence risk is less than 0.5 everywhere.

For IC admission the relative risk is high in the north, in mid-Sweden and in a region in the southeast in W71 (5 May 2021). It is moderately risky for the remainder of the country while for some regions it is below 0.5. For the remainder of the prediction period W73-W85 (19 May 2021–11 Augustus 2021). IC admission is predicted to be below 0.5 everywhere. The relative death risk for the entire country for the entire prediction period is predicted to be below 0.5. Finally, no hotpots are predicted for the three outcomes for the entire country for the entire prediction period for $c$ = 1 and $\gamma = 0.90$.²⁶

5 Conclusions

This paper presents a spatiotemporal Bayesian hierarchical model for the joint prediction of the relative risk of the COVID-19 outcomes incidence, intensive care admission and death. The model takes into account common and specific temporal patterns of the outcomes, thus capturing similarities and differences in the spatiotemporal prediction distribution of the relative risk associated with each outcome. Following Chu (2021), Newalla et al. (2020) and Scobie et al. (2021), we argued that joint prediction reduces biased estimation of the parameters of the constituting individual equations, thus improving forecasting and mapping. The application is in line with this proposition. It showed that for incidence risk and death risk the prediction of hotspots by the joint approach outperforms the predictions by the individual approaches.

The joint approach presented here applies a pure model that captures the spatiotemporal developments of the dependent variables in terms of structured and unstructured spatial and temporal random effects and their interaction. It thus accounts for the impacts of the covariates on the dependent variables indirectly, namely in terms of spatiotemporal trends. The pure model is “data scarce” because it only requires observations on the population at risk and the dependent variable per spatiotemporal unit. In the application, the spatial unit for both variables is the region, the timeframe for the population at risk is 15 months and for the 3 outcomes a week. The data configuration allows frequent updating and makes it suitable for weekly prediction. For COVID-19, but also for other infectious diseases, this is a basic requirement for the health authorities, hospitals and funeral enterprises to take suitable action, such regional or national coordination of hospitalization and IC admission, particularly for the short term.

In the application, we predicted the relative risk of COVID-19 incidence, IC admission, and death in Sweden from January 1, 2020 to May 4, 2021. The analysis revealed a common temporal pattern between the three COVID-19 risks. The finding is consistent with Scobie et al. (2021). The joint model was applied to forecast the incidence risk, IC admission risk and death risk for the period after the sample period, i.e. from 5 May 2021 to 11 August 2021. The model forecasted a significant decline in the relative risk of all three outcomes and no hotspots.

To conclude this section, we briefly discuss a causal model containing covariates as an alternative model to the pure model to generate COVID-19 predictions, viz. Olmo and Sanso-Navarro (2021). This paper uses a conventional econometric approach to predict the number of COVID-19 incidences while applying a Bayesian averaging framework to accommodate the large set of potential covariates. The model is instrumental to evaluating the critical covariates of COVID-19 incidence and explaining differences in the number of new confirmed cases across neighbourhoods for a given time period. However, because the model is based on static (time-invariant) covariates, forecasting spatiotemporal variation in COVID-19 outcomes is not possible, as shown by Lim et al. (2021) and Wen et al. (2018). A shortcoming of our model on the other hand is that it does not explicitly identify the socioeconomic and environmental factors driving the spatiotemporal variation of the disease outcomes. However, if the covariates are measured for the same space–time units as the outcomes, extension of the pure model to a causal model can be achieved straightforwardly (Jaya and Folmer 2021b, 2022a under review, 2022b).

Our approach furthermore complements the Olmo and Sanso-Navarro (2021) approach in that it explicitly considers spatiotemporal interaction. The inclusion of this variable in a prediction model for an infectious disease such as COVID-19 is basic as the intensity of infectious diseases tends to move in space and time. The case study presented in the Sects. 3 and 4 showed that for incidence and death the variance of the interaction effect is by far the most important component of the total variance and for IC capacity the next largest (see Table 2). The spatiotemporal interaction effect of COVID-19 transmission among regions is critical to formulating pandemic policies (Liu et al. 2021; Wang et al. 2021; Wu et al. 2021).

Finally, we note that the paper is limited in scope in that it presents spatiotemporal predictions of the overall relative risks of incidence, IC admission and death. Although this is an interesting and policy relevant objective, disaggregation by sub-populations according to inter alia age, sex, profession, health status, travel behaviour are highly policy relevant as the three kinds of relative risk have been found to vary across sub-populations (Newalla et al. 2020). In addition, spatial disaggregation is desirable as the Swedish regions are very heterogeneous.

Appendices

Appendix 1

Spatiotemporal distribution of the disease outcomes

See Fig. 5

Appendix 2

Model comparison

See Table 5