Bayesian inference in multivariate spatio-temporal areal models using INLA: analysis of gender-based violence in small areas

Abstract

Multivariate models for spatial count data are currently receiving attention in disease mapping to model two or more diseases jointly. They have been thoroughly studied from a theoretical point of view, but their use in practice is still limited because they are computationally expensive and, in general, they are not implemented in standard software to be used routinely. Here, a new multivariate proposal, based on the recently derived M models for spatial data, is developed for spatio-temporal areal data. The model takes account of the correlation between the spatial and temporal patterns of the phenomena being studied, and it also includes spatio-temporal interactions. Though multivariate models have been traditionally fitted using Markov chain Monte Carlo techniques, here we propose to adopt integrated nested Laplace approximations to speed up computations as results obtained using both fitting techniques were nearly identical. The techniques are used to analyse two forms of crimes against women in India. In particular, we focus on the joint analysis of rapes and dowry deaths in Uttar Pradesh, the most populated Indian state, during the years 2001–2014.

1 Introduction

Crimes against women (CAW) have become a major issue in many countries due to the social concern about this form of violence that keeps women from a dignified and full life. In this context, statistical techniques in general and spatio-temporal areal models in particular can be a valuable tool to look into the spatial and temporal distribution of such form of violence. Although spatio-temporal models have been mainly applied in epidemiology to analyze chronic diseases such us cancer, some research uses these models to look for clusters of certain crimes such as burglary (see, for example Li et al. 2014). Very recently, Vicente et al. (2018, 2020) study CAW in India using univariate spatio-temporal areal data. However, the complex and multifaceted nature of the problem makes it difficult to establish relationships between certain crimes, something crucial to understand the phenomenon and to develop prevention or intervention policies. To gain knowledge about CAW, establishing relationships between different forms of crimes can set the way forward. These relationships may be expressed in terms of similar or completely different spatial and temporal patterns, that is, in terms of correlations between spatial and temporal patterns of different crimes. This would indicate whether or not the high incidence of a particular type of crime in one specific region goes in hand with another one, or if the temporal trends of two different crimes increase or decrease in parallel. The joint analysis of different forms of crimes can be carried out using multivariate spatio-temporal models. Not only could multivariate models account for the correlations between crimes, but they would also improve estimates by borrowing information from nearby areas and time points related to the different crimes or phenomena under study.

There is a considerable amount of research about multivariate spatial models for count data. Joint modelling has mainly relied on multivariate conditional autoregressive models (MCAR) within a fully Bayesian perspective. Mardia (1988) extends the work of Besag (1974) and develops a theoretical framework based on multivariate conditionals. This multivariate approach considers separable models in which the covariance structure is the Kronecker product of a matrix to model spatial dependence and a matrix to deal with dependence between the studied univariate responses. These models assume the same spatial smoothing for all responses, but other authors (see, for example Gelfand and Vounatsou 2003) propose a non-separable multivariate proper CAR (pCAR) model with different smoothing parameters for each univariate response. Some other approaches (Jin et al. 2005) induce dependence between responses conditionally, but this has the inconvenience of ordering them arbitrarily, since different marginal distributions arise according to the order of responses when the sequence of conditional probabilities is defined. Jin et al. (2007) solve this problem by formulating a linear model of coregionalization that avoids undesired dependence on the order of the responses. Generally, this proposal does not allow the incorporation of univariate spatial dependency structures beyond conditional autoregressive distributions, which turns out to be a limitation of this methodology. A multivariate generalization of spatial structures beyond conditional autoregressive distributions was proposed by MacNab (2011).

A general coregionalization framework for multivariate areal models that covers many of the proposals in the literature was derived by Martinez-Beneito (2013). However, this procedure may be computationally expensive and unapproachable for a moderate to large number of responses. To overcome this problem, Botella-Rocamora et al. (2015) present the so called M-based models, a reformulation of the Martinez-Beneito framework developing a simpler and computationally efficient technique. Also within the framework of linear coregionalization models, MacNab (2016a, b) presents a class of coregionalized multivariate conditional autoregressive models that allow flexible modeling of multivariate spatial interactions. For a thorough review of the topic the reader is referred to the work of MacNab (2018) in which the three main lines in the construction of multivariate proposals are discussed. Namely, the approach based on multivariate conditionals (Mardia 1988), an approach based on univariate conditionals (Sain et al. 2011), and a coregionalization framework (Jin et al. 2007).

In this work we extend the M-based proposal of Botella-Rocamora et al. (2015) to the spatio-temporal setting, and besides the correlation between spatial patterns of different responses, correlation between temporal trends are also included. Additionally, a space-time interaction term with different variance parameters for each crime is considered. Though multivariate models have been traditionally fitted using MCMC, here we also propose to fit these models using integrated nested Laplace approximations and numerical integration, a technique known as INLA (Rue et al. 2009), that can be implemented using R (see Lindgren and Rue 2015).

Our proposal can be a valuable tool to study CAW, a phenomenon that has awaken social concern in the last decades as it affects millions of women. In 1996, the World Health Assembly declared violence against women as a serious public health problem, and as a result, the World Health Organization (WHO) published the first World Report on Violence and Health (World Health Organization (WHO) 2002). The WHO subsequently stated that violence against women is a public health problem of epidemic proportions (Ellsberg and Heise 2005) that takes the lives of more than 1.6 million women due to domestic violence. Though crimes against women are found all over the world, there are countries where the issue is particularly worrying for three main reasons: the large number of affected women, the nature of certain forms of crimes, and the social acceptability of violence against women. Embedded in religious, cultural and social practices, gender-based violence spreads in these countries. One such country is India, where gender-based violence is deeply entrenched in society with very specific forms of crimes against women. Similar to many regions in South Asia, patriarchal concepts legitimize violence against women, generate gender inequality (Russo and Pirlott 2006), and place women at the base of the social hierarchy, contributing to the increase of violence against them, especially sexual violence (Kohli 2012; Solotaroff and Pande 2014; Gupta et al. 2004; Rahman and Rao 2004). Sexual violence in India affects 27.5 million women, and the reported number of rapes is increasing every year becoming a major issue (Raj and McDougal 2014). International attention was focused on sexual violence in India during 2012, when a student was gang raped and beaten on a bus and died from the injuries. The same year, two girls were raped and hanged by gangs (Mullan 2014). These cases made society focus on India’s rape crisis, demanding urgent action. However, few attempts have been made to discover spatio-temporal patterns of crimes against women in India, which may help to shed light on the problem. In this work, we focus on rapes and dowry deaths, two forms of violence against women deeply-rooted in India. In particular we put the attention on the state of Uttar Pradesh, the most populated state and one accounting for the highest percentage of crimes against women. As far as we know, there are still no multivariate spatio-temporal analyses of crimes against women in India, so we believe that this research can help to identify similarities between spatial patterns of different crimes and their evolution over time. This in turn may help social researchers to reveal common risk factors and to better understand and disentangle the complicated and worrying issue of CAW.

The rest of the paper is structured as follows: Sect. 2 reviews the M-model proposals and presents a spatio-temporal extension. Identifiability issues as well as prior specifications are also discussed in this section. Section 3 brings to light the problem of rapes and dowry deaths in India and gives the results of a joint analysis of rapes and dowry deaths during the period 2001–2014 in the districts of Uttar Pradesh. A comparison of the results obtained when implementing alternative models using WinBUGS (Lunn et al. 2000) and INLA is also discussed in this section. The paper closes with a discussion.

2 M-models for multivariate spatio-temporal modelling

Let $O_ {itj}$ and $E_ {itj}$ be the number of observed and expected cases, respectively, in the ith geographic unit ($i=1, \ldots , I$), the tth period ($t=1, \ldots , T$), and the jth crime ($j=1, \ldots , J$). We assume that conditional on the relative risk, $R_{itj}$, the number of observed cases in each area-time-crime stratum follows a Poisson distribution

$$\begin{aligned}&O_{itj}| R_{itj} \sim Poisson(\mu _{itj}=E_{itj} \cdot R_{itj}), \\&\quad \log \mu _{itj}=\log E_{itj}+\log R_{itj}, \end{aligned}$$

where, the log-risk is modelled as

$$\begin{aligned} \log (R_{itj})= \alpha _j + \theta _{ij} + \gamma _{tj} + \delta _{itj}. \end{aligned}$$

Here $\alpha _j$ is an intercept for the jth crime, $\theta _{ij}$ and $\gamma _{tj}$ are the spatial and temporal main effects for the jth crime, and $\delta _{itj}$ is the spatio-temporal interaction within the jth crime. Denoting by ${\varvec{\Theta }}=\lbrace \theta _{ij}: i=1, \ldots , I; j=1, \ldots , J \rbrace$ and ${\varvec{\Gamma }}=\lbrace \gamma _{tj}: t=1, \ldots , T; j=1, \ldots , J \rbrace$ two matrices whose columns are the spatial and temporal random effects respectively, and by ${\varvec{\Delta }}_j=\lbrace \delta _{itj}: i=1, \ldots , I; t=1, \ldots , T \rbrace$ a matrix capturing the spatio-temporal interaction within each crime, the advantage of multivariate modelling is that dependency between the spatial and temporal patterns of the different crimes can be included in the model so that a latent association between crimes can help to improve the estimates and to discover risk factors related to the phenomena being studied.

Below, we address how to incorporate into the model spatial and temporal dependencies within crimes and correlation between the spatial and temporal patterns of the crimes. Firstly, dependence between spatial patterns of the crimes is addressed through the use of M-models (Botella-Rocamora et al. 2015), and the same idea is used to deal with temporal dependence between crimes. Secondly, a disease-specific spatio-temporal interaction is included, and finally, some identifiability issues are raised.

2.1 Inducing spatial and temporal dependence within and between crimes

To understand how dependence between the spatial risks and between the global temporal trends of the different crimes are included in the model, let us express the matrices ${{\varvec{\Theta }}}$ and ${\varvec{\Gamma }}$ as

$$\begin{aligned} \begin{matrix} {\varvec{\Theta }}={\varvec{\Phi }}_{\theta } {\mathbf {M}}_{\theta }, \\ {\varvec{\Gamma }}={\varvec{\Phi }}_{\gamma } {\mathbf {M}}_{\gamma }, \end{matrix} \end{aligned}$$

(1)

where ${\varvec{\Phi }}_{\theta }$ and ${\varvec{\Phi }}_{\gamma }$ are random effects matrices of order $I \times K_{\theta }$ and $T \times K_{\gamma }$ whose columns are distributed independently following a spatially correlated distribution and a temporally correlated distribution respectively. Usually $K_{\theta }$ and $K_{\gamma }$ are considered equal to J, i.e., as many spatial/temporal effects as crimes, although they may be different. For example, $K_{\theta }=2J$ for the multivariate formulation of the Besag et al. (1991) model, BYM hereafter in the paper, that includes two random effects to incorporate spatially structured and unstructured variability respectively. On the other hand, the dimension of the model can be reduced ($K_{\theta }<J$, $K_{\gamma }<J$ ) in situations where it is believed that several crimes share a common spatial/temporal pattern, obtaining computationally more efficient models (see Corpas-Burgos et al. 2019, for a discussion). The matrices ${\mathbf {M}}_{\theta }$ and ${\mathbf {M}}_{\gamma }$, of orders $K_{\theta } \times J$ and $K_{\gamma } \times J$, are responsible for inducing dependence between the different columns of ${\varvec{\Theta }}$ and ${\varvec{\Gamma }}$. More precisely, dependence between the columns of ${\varvec{\Theta }}$ means correlation between spatial patterns of the crimes under study, whereas the dependence between their rows indicates spatial correlation within crimes. Similarly, dependence between columns of ${\varvec{\Gamma }}$ means correlation between the temporal patterns of the crimes, and dependence between rows leads to temporal correlation within crimes. We refer to (1) as the M-model where ${\mathbf {M}}_{\theta }$ and ${\mathbf {M}}_{\gamma }$ are nonsingular but arbitrary matrices.

Different spatial priors have been considered in the literature to deal with spatial dependence. In the field of multivariate models, Botella-Rocamora et al. (2015) use a proper conditional autoregressive (pCAR) prior and Corpas-Burgos et al. (2019) consider an M-based version of the BYM. In this paper we take into consideration both the pCAR and the BYM models. In addition, we also examine the intrinsic conditional autoregressive prior (iCAR) and the Leroux et al. (1999) prior (LCAR) for the columns of ${\varvec{\Phi }}_{\theta }$. In the Corpas-Burgos et al.’s proposal they consider ${\varvec{\Phi }}_{\theta }=[ {\varvec{\Phi }}_{s}: {\varvec{\Phi }}_{h}]$, where ${\varvec{\Phi }}_{s}$ is the $(I \times J)$ matrix of spatially correlated random effects following an iCAR distribution, and ${\varvec{\Phi }}_{h}$ is the $(I \times J)$ matrix of spatially unstructured terms. As previously mentioned $K_{\theta }=2J$ with this formulation. In synthesis, the columns of ${\varvec{\Phi }}_{\theta }$ follow a multivariate normal distribution with mean ${\mathbf {0}}$ and covariance matrix ${\varvec{\Omega }}$ whose expression depends on the spatial prior. Namely,

• iCAR

  $$\begin{aligned} {\varvec{\Omega }}_{iCAR}= \sigma ^2_s ({\mathbf {D}}_w - {\mathbf {W}})^{-}=\sigma ^2_s{\mathbf {Q}}_{\theta }^{-}, \end{aligned}$$

  where ${\mathbf {W}}=(w_{il})$ is the spatial proximity matrix defined as $w_{ii}=0$, $w_{il}=1$ if the ith and the lth areas are neighbours and 0 otherwise, ${\mathbf {D}}_w= diag(w_{1+}, \cdots , w_{I+})$, with the diagonal elements $w_{i+}$ being the number of neighbours of the ith area, and $\sigma ^2_s$ is the variance parameter. The symbol $^{-}$ refers to the Moore-Penrose generalized inverse.

• pCAR

  $$\begin{aligned} {\varvec{\Omega }}_{pCAR}= \sigma ^2_s({\mathbf {D}}_w - \rho {\mathbf {W}})^{-1}, \end{aligned}$$

  which defines a proper distribution if and only if $1/d_{min}< \rho < 1/d_{max}$ (see for example Jin et al. 2007), where $d_{min}$ and $d_{max}$ are the minimum and maximum eigenvalues of ${\mathbf {D}}_w^{-1/2}{\mathbf {W}}{\mathbf {D}}_w^{-1/2}$.

• LCAR

  $$\begin{aligned} {\varvec{\Omega }}_{LCAR}= & {} \sigma ^2_s \left[ \lambda ({\mathbf {D}}_w - {\mathbf {W}}) + (1-\lambda ) {\mathbf {I}}_I \right] ^{-1} \\= & {} \sigma ^2_s\left[ \lambda {\mathbf {Q}}_{\theta } + (1-\lambda ) {\mathbf {I}}_I\right] ^{-1}, \end{aligned}$$

  where ${\mathbf {I}}_I$ is the $I\times I$ identity matrix. The covariance matrix ${\varvec{\Omega }}_{LCAR}$ is of full rank if $\lambda \in [0,1)$.

Note that the pCAR and the LCAR priors become the iCAR prior if $\rho =1$ and $\lambda =1$.

Regarding the temporal component, random walk priors of first order (RW1) are assumed for the columns of ${\varvec{\Phi }}_{\gamma }$ i.e., each column follows a multivariate normal distribution with mean ${\mathbf {0}}$ and covariance matrix given by $\sigma ^{2}_t {\mathbf {Q}}^{-}_{\gamma }$, where ${\mathbf {Q}}_{\gamma }$ is the structure matrix (see Rue and Held 2005, p. 95). This matrix is similarly defined as the spatial structure matrix ${\mathbf {Q}}_{\theta }$ but in time, that is two contiguous time points are neighbours. The variance parameters for the columns of ${\varvec{\Phi }}_{\theta }$ and ${\varvec{\Phi }}_{\gamma }$ are fixed at one, so the degree of spatial and temporal smoothing relies on the matrices ${\mathbf {M}}_{\theta }$ and ${\mathbf {M}}_{\gamma }$. Otherwise, these variance parameters and the cells of the ${\mathbf {M}}$-matrices would not be identifiable (Martinez-Beneito 2013).

The multivariate approach allows the estimation of the correlation between the spatial patterns of the crimes, an interesting and useful feature, as a high positive correlation would support the hypotheses of common risk factors. As shown in Botella-Rocamora et al. (2015), for models with a separable structure, this covariance matrix between the spatial patterns can be estimated as $\mathbf {M^{\prime }_{\theta }} {\mathbf {M}}_{\theta }$. However, for BYM M-models this condition is not satisfied, as the spatial component is split into two terms with two M-matrices, so it is not reasonable to use $\mathbf {M^{\prime }_{\theta }} {\mathbf {M}}_{\theta }$ to estimate the covariance matrix between spatial patterns of the different crimes. For this reason, Corpas-Burgos et al. (2019) recommend using the covariance matrix of the $\log ({\varvec{\Theta }})$ columns as the covariance matrix between the spatial patterns. On the other hand, a high positive correlation between the temporal patterns would indicate that risk factors intrinsically related to the time dimension, such as certain policies, affect both crimes rather similarly and hence provide valuable information to deal with the phenomena being studied. Employing RW1 prior distributions ensures that the ${\varvec{\Phi }}_{\gamma }$ columns share a common distribution which guarantees that the covariance matrix between the temporal patterns can be estimated using $\mathbf {M^{\prime }_{\gamma }} {\mathbf {M}}_{\gamma }$. As suggested by one reviewer, the temporal trend could be modelled as the sum of a fixed linear term and a non linear term (random effect), similar to the work by Lombardo et al. (2018) in a different context. In such a case, one could assess if there is a significant slope. However, the final temporal trend would be the sum of the linear and the non-linear part and a positive slope might not result in a clear increase or decrease in the trend. Moreover, the matrix $\mathbf {M^{\prime }_{\gamma }} {\mathbf {M}}_{\gamma }$ would no longer represent the covariance matrix of the temporal trends, but the covariance matrix of the non linear part. An alternative proposal would be to consider a random walk prior of second order (RW2) for time, which implicitly includes a linear term. However, for the application considered here, DIC and other selection criteria point towards a RW1.

2.2 Spatio-temporal interaction

Multivariate spatio-temporal models including the effects of area and time additively can be very restrictive in practice as the same temporal evolution is assumed for all areas within the same crime. The incorporation of a random effect for the spatio-temporal interaction models the specific behaviour of a geographical unit at a given year, thus allowing each area to have its own, specific temporal evolution. Consequently, the assumption of equal time evolution for all areas is relaxed, obtaining more flexible models. Martinez-Beneito et al. (2017) propose a multidimensional framework where different dependence structures can be considered for multiple factors (space, time, and crime here). However, this procedure is computationally expensive and it is not clear how to approach this situation using M models. Given that our model already includes crime-specific spatial and temporal patterns with induced dependence between crimes, the spatio-temporal interaction within crimes is a residual term and simpler models capturing the space-time dependence can be more convenient. Here we contemplate independent spatio-temporal interactions for each crime. These spatio-temporal interactions only consider dependence in space and time and may have the same or different amount of smoothing for each crime.

Recalling that ${\varvec{\Delta }}_j$, $j=1, \ldots , J$, is a ($I \times T$) matrix with the interaction random effects for the jth crime, it is assumed that its vectorization follows a multivariate normal distribution with mean ${\mathbf {0}}$ and covariance matrix ${\varvec{\Sigma }}_{\delta _j}=\sigma ^{2}_{\delta _j} {\mathbf {Q}}^{-}_{\delta }$, i.e.,

$$\begin{aligned} \text {vec}({\varvec{\Delta }}_j) \sim N({\mathbf {0}}, \sigma ^{2}_{\delta _j} {\mathbf {Q}}^{-}_{\delta }). \end{aligned}$$

Four types of interaction will be defined depending on the covariance matrix (Knorr-Held 2000). In Type I interactions all cells of ${\varvec{\Delta }}_j$ are independent without any structure in space and time, that is ${\mathbf {Q}}_{\delta }={\mathbf {I}}_{IT}$, where ${\mathbf {I}}_{IT}$ is the $IT\times IT$ identity matrix. In Type II interactions, ${\mathbf {Q}}_{\delta }={\mathbf {Q}}_{\gamma } \otimes {\mathbf {I}}_{I}$, and the rows of ${\varvec{\Delta }}_j$ are independent with a RW1 distribution. In other words, area-specific temporal trends are not spatially correlated. An independent iCAR prior is assumed for each column of ${\varvec{\Delta }}_j$ in Type III interactions, that is, time-specific spatial patterns are not temporally correlated. Therefore, the structure matrix is ${\mathbf {Q}}_{\delta }={\mathbf {I}}_{T} \otimes {\mathbf {Q}}_{\theta }$, where ${\mathbf {I}}_{T}$ is the $T\times T$ identity matrix. Finally in Type IV interactions, the structure matrix is defined as ${\mathbf {Q}}_{\delta }={\mathbf {Q}}_{\gamma } \otimes {\mathbf {Q}}_{\theta }$, giving rise to area-specific temporal trends spatially correlated (or spatial patterns temporally correlated). The interactions considered here are separable as they are defined in terms of Kronecker products of covariance/precision matrices. The difference between them is whether or not the elements of the interaction terms have any correlation structure in space, time or both. Regardless the correlation structure, the interaction term allows different temporal trends for each area (or different spatial pattern for each year). Other non-separable models, such as P-splines interaction models, have been proposed in the literature. Adin et al. (2017) compare the Type IV interaction with P-splines models and show that the area-specific trends are similar.

2.3 Identifiability issues and hyperprior specification

Univariate spatio-temporal models present some identifiability issues that can be overcome for example using constraints. These problems also arise in the multivariate setting, and to achieve identifiability between the crime-specific intercept and the corresponding main spatial and temporal random effects, sum to zero constraints are considered over these components of the model. In addition, because the main spatial and temporal effects are also included in the spatio-temporal interaction random effects, sum to zero constraints are also considered for this latter term. For more details about the required constraints for the different type of interactions (Type I, II, III, and IV), see Goicoa et al. (2018). In the multivariate setting, additional identifiability concerns emerge. As pointed out in Botella-Rocamora et al. (2015), any orthogonal transformation of the columns of ${\varvec{\Phi }}_{\theta }$ (and ${\varvec{\Phi }}_{\gamma }$) and the equivalent orthogonal transformation of the rows of ${\mathbf {M}}_{\theta }$ (and ${\mathbf {M}}_{\gamma }$), causes an alternative decomposition of ${\varvec{\Theta }}$ (and ${\varvec{\Gamma }}$), and therefore these quantities are not identifiable. However, ${\varvec{\Theta }}$, ${\varvec{\Gamma }}$, and the covariance matrices ${\mathbf {M}}_{\theta }^{\prime }{\mathbf {M}}_{\theta }$ and ${\mathbf {M}}_{\gamma }^{\prime }{\mathbf {M}}_{\gamma }$ are perfectly identifiable. Consequently, inference is confined to those quantities.

The cells of the ${\mathbf {M}}$-matrices act as coefficients (weights) in the decomposition of ${\varvec{\Theta }}$ and ${\varvec{\Gamma }}$ in Eq. (1), so they can be seen as regression coefficients and treated as fixed effects with a normal prior with mean 0 and a large fixed variance leading to what is call fixed effects M-models (FE). Note that, assigning $N(0,\sigma ^2)$ priors to the cells of the ${\mathbf {M}}$-matrices is equivalent to assigning a Wishart prior to ${\mathbf {M}}^{\prime }{\mathbf {M}}$, i.e., ${\mathbf {M}}_{\theta }^{\prime }{\mathbf {M}}_{\theta } \sim Wishart(J, \sigma ^2_{\theta } {\mathbf {I}}_J)$ and ${\mathbf {M}}_{\gamma }^{\prime }{\mathbf {M}}_{\gamma } \sim Wishart(J, \sigma ^2_{\gamma } {\mathbf {I}}_J)$ (see Botella-Rocamora et al. 2015, for further details). Alternatively, random effects M-models (RE) can be considered in which the entries of the ${\mathbf {M}}$-matrices are treated as independent normal random variables with mean 0 and standard deviation $\sigma$. In this case, a uniform prior between 0 and a large number is considered for $\sigma$. In our analysis, for RE M-models, Gaussian distributions with mean 0 and standard deviations $\sigma _{\theta _s}$ (for the spatially structured part), $\sigma _{\theta _h}$ (for the spatially unstructured part in the BYM model), and $\sigma _{\gamma }$ (for the temporally structured part) are considered for the cells of the ${\mathbf {M}}$-matrices with uniform priors between 0 and 100 for the standard deviations. The same vague uniform priors are considered for the standard deviation $\sigma _{\delta _j}$ of the spatio-temporal interaction. For FE M-models, and following Corpas-Burgos et al. (2019), improper $M_{ij}\propto 1$ distributions (this means that $\sigma$ is set to $\infty$) are used for the cells of the ${\mathbf {M}}$-matrices with WinBUGS. When fitting the models using INLA, a Wishart prior for ${\mathbf {M}}^{\prime }{\mathbf {M}}$ is considered.

3 Joint analysis of crimes against women in Uttar Pradesh

3.1 Descriptive analysis

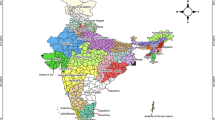
Uttar Pradesh (see Fig. 1 for its location in India and its administrative division into districts, and Table 4 in the “Appendix” to label the districts) is the most populated state in India, and it accounts for the highest percentage of overall crimes against women in India, which has being increasing in the last years [11.4% in 2014; 10.9% in 2015; 14.5% in 2016 and 15.6% in 2017 according to National Crime Records Bureau (2015, 2016, 2017, 2019)].

Fig. 1

Map of the administrative division of Uttar Pradesh into districts and its location in India (top right corner). The name of the districts matching the numbers can be found in Table 4 in the “Appendix”

In this work we focus on the joint analysis of rapes’ incidence and dowry deaths in the 70 districts of Uttar Pradesh during the period 2001–2014. Figures of rapes in India are seriously worrying even though they are believed to be underreported (Vogelman and Eagle 1991; Koss 1992). On the other hand, dowry death is a form of crime related to the dowry system, a social practice ingrained in the Indian marriage process. In general, the subordinate role that is assigned to women turns them into merchandise, and disputes over the dowry are a clear example of this. Unfortunately, the Dowry Prohibition Act (1961) has not been able to stop this practice. Any death related to dowry disputes is considered a dowry death, and a suicide committed by a woman who has suffered mental or physical violence in relation to the dowry is also a dowry death.

Data on the number of CAW in Uttar Pradesh during the period 2001–2014 have been obtained from the National Crime Record Bureau (NCRB). During this period, the number of rapes increased by 77% in Uttar Pradesh (1956 in 2001, 3462 in 2014), and this growth was even higher in the country as a whole, 138%. The increase is particularly remarkable in the last two years of the period, probably due to an improvement in the victim support system (Raj and McDougal 2014). According to the NCRB (National Crime Records Bureau 2015), India is the country with the highest number of dowry deaths in the world. During 2014, more than eight thousand cases of dowry deaths, 8455, were registered in the country, and 2469 occurred in Uttar Pradesh, nearly a 30% of all dowry deaths in India. Some descriptive statistics about the number of rapes and dowry deaths in the districts of Uttar Pradesh by year are provided in Table 1. The number of rapes registered per district is highly variable, with minimum values ranging from 0 to 5 cases and maximum values between 51 and 164 cases. Figures for dowry deaths are somewhat more stable, but still coefficients of variation per year are very high. Crude rates (per 100,000 women) of rapes and dowry deaths in Uttar Pradesh during the studied period are shown in Fig. 2. An increase in rates, particularly noticeable for rapes, is observed from 2003 onward. In 2008, dowry deaths rates seem to stabilize.

Table 1 Descriptive statistics

Fig. 2

Evolution of the crude rates (per 100,000 women) of rapes and dowry deaths in Uttar Pradesh in the period 2001–2014

The similarities between the temporal rate trends of rapes and dowry deaths during the study period leads us to hypothesize the existence of a relationship between the risk of rapes and dowry deaths. This apparent relationship may indicate that certain facts in time (public policies, intervention programs, laws to protect women) may be exerting some influence on these phenomena. For this reason we have calculated the correlation between the standardized incidence ratio (SIR) of rapes and dowry deaths. On one hand, the SIR for rapes and dowry deaths in all districts has been obtained for each year of the period, and the correlation between the SIR vectors for rapes and dowry deaths (correlation between crude spatial patterns) has been computed. On the other hand, for each district, we have obtained the SIR vector of rapes and dowry deaths between 2001 and 2014, and the correlation between crude temporal trends has been calculated. Some summary statistics are displayed in Table 2. The correlations between the crude spatial patterns range between 0.32 and 0.62. We have also computed the global crude spatial patterns of rapes and dowry deaths in the whole period and the correlation is 0.53. This would indicate that certain districts are more prone to the occurrence of both crimes. The correlations between the crude temporal patterns range between $-\,0.37$ and 0.87 indicating that, depending on the district, both crimes evolve in the same or the opposite direction. We have also calculated the crude temporal trends of rapes and dowry deaths in all of Uttar Pradesh and the correlation between them is 0.59, indicating that the correlation between overall temporal patterns may be high. The correlations observed between both crimes indicate that it might be advantageous to analyse these crimes jointly.

Table 2 Correlations between spatial (by year) and temporal patterns (by district) of rapes and dowry deaths based on crude standardized incidence ratios (SIR)

3.2 Model fitting using WinBUGS and INLA

3.2.1 Model fitting

The multivariate M-based proposal presented in Sect. 2 has been implemented to study the joint spatio-temporal distribution of rapes and dowry deaths in Uttar Pradesh between 2001 and 2014. Both specifications of M models are contemplated for the spatial and temporal effects, the fixed effects (FE) and the random effects (RE) M-models. We use BYM, iCAR, LCAR, and pCAR priors to model the spatial patterns and a RW1 prior to model the temporal effects. The four types of interactions have been considered for the spatio-temporal interaction random effect. A vague normal distribution with a precision close to zero was used for the intercepts ($\alpha _j$), and uniform vague prior distributions for the standard deviations.

Initially, the models were implemented in WinBUGS. Three chains were run for each model with 30,000 iterations each and a burn-in period of 5000 iterations. One out of every 75 iterations has been saved, leading to a final sample size of 1002 iterations. The Brooks-Gelman-Rubin statistic, the effective sample size, and an examination of the simulated chains were used to evaluate the convergence of the identifiable variables in the model. Convergence was checked for the standard deviations, the crime-specific intercepts, and the elements of matrices ${\varvec{\Theta }}$, ${\varvec{\Gamma }}$ and ${\varvec{\Delta }}$. We require that the Brooks-Gelman-Rubin statistic is less than 1.1, and that the effective sample size is at least 100 for each variable. The simulated chains produced practically independent posterior draws with first order autocorrelations close to 0. Corpas-Burgos et al. (2019) present the R-code to implement spatial FE M-models and RE M-models in WinBUGS, when BYM is used to model the spatial pattern. We have extended this code to spatio-temporal M-models, and we have also considered the pCAR, LCAR, and iCAR distributions for the spatial effects.

As it is widely acknowledged that MCMC techniques can be computationally very demanding in certain cases, particularly in multivariate spatio-temporal models when the number of areas and time periods increase, the well-known INLA technique has been also considered here (Rue et al. 2009). Recently, Palmí-Perales et al. (2019) have developed the R package ‘INLAMSM’ (https://CRAN.R-project.org/package=INLAMSM) to implement multivariate spatial models for lattice data using INLA. In particular these authors consider two versions of an improper multivariate CAR and a proper multivariate CAR priors: the first version assumes a diagonal matrix for the covariance between diseases (that would indicate independence between diseases), and the second version considers more general multivariate priors with a dense symmetric matrix to model the covariance between diseases. In addition, this package includes the FE M-model (Botella-Rocamora et al. 2015) with different proper CAR priors for each disease. In this paper, we have modified the INLA function for the pCAR, so that FE M-models and RE M-models with BYM, iCAR and LCAR priors for the spatial effects can be conveniently fitted. So most of the spatial priors used in the literature are extended to the multivariate setting and can be conveniently used within INLA. Moreover, these authors use a Wishart distribution for ${\mathbf {M}}^{\prime }{\mathbf {M}}$ and here we also consider a $N(0,\sigma ^2)$ distribution for each cell of the ${\mathbf {M}}$-matrices. While both alternatives are equivalent, the assignment of normal priors to each cell of the ${\mathbf {M}}$-matrices allows to fit more flexible models, such as those specified in Corpas-Burgos et al. (2019), relaxing the assumption of a common scale parameter for the cells of the ${\mathbf {M}}$-matrices. Though the advantages of INLA are clear, it may have some inconveniences in this particular setting. The computational convenience of M-models is based on the reformulation of Kronecker products of the covariance matrices as simple matrix products. However, to implement the FE M-models in INLA, INLAMSM uses a class of generic models that define the latent component moving away from the original philosophy of M-models as they do not replace Kronecker products by simple matrix products. In our case, with two crimes, the computational time is substantially reduced with certain spatial priors.

In what follows, a succinct comparison of the results obtained in the joint analysis of rapes and dowry deaths in Uttar Pradesh using INLA and WinBUGS is presented. The WinBUGS and INLA code to fit all models is available at https://github.com/spatialstatisticsupna/Mmodels_SERRA_article.

3.2.2 Comparing results using WinBUGS and INLA

We begin by comparing the estimated relative risks (posterior means) obtained with INLA (simplified Laplace strategy) and WinBUGS using the library pbugs to run the models in parallel (Martinez-Beneito and Vergara-Hernández 2019). Figure 3 displays dispersion plots of posterior means of rapes and dowry deaths relative risks obtained with INLA vs. those obtained with WinBUGS. The estimated relative risks correspond to a FE M-model with an iCAR prior for space, a RW1 prior for time, and a Type II spatio-temporal interaction. Clearly, the relative risk estimates obtained with INLA and WinBUGS are identical. As it will be detailed later, models with a Type II spatio-temporal interaction are the most suitable candidates in terms of model selection criteria. Similar findings were obtained for the spatial ($\exp {(\theta _{ij})}$), temporal ($\exp {(\gamma _{tj})}$), and spatio-temporal pattern estimates ($\exp {(\delta _{itj})}$). Identical fits with INLA and WinBUGS were also observed for additive models and models with Type I, Type III, and Type IV interactions (not shown here to save space).

Fig. 3

Dispersion plots of the final relative risks for rapes and dowry deaths obtained with the type II interaction RE M-model with in INLA (y-axis) versus WinBUGS (x-axis), using the iCAR (first row), pCAR (second row), LCAR (third row) and the BYM (last row) spatial priors

Regarding computing times for the models presented in Sect. 2, models with Type II and Type IV interactions are the slowest regardless the fitting technique, INLA or WinBUGS. One reason for this may be that the number of constraints is much higher for Type II and Type IV spatio-temporal interactions than for the Type I and Type III counterparts. The number of constraints on the spatio-temporal interaction random effect for Type II and Type IV are 70 (number of regions) and 84 (number of regions+number of time periods) respectively, whereas for Type I and Type III interactions the number of constraints are 1 and 14 respectively (see Goicoa et al. 2018). Given that adding restrictions entails computational cost, models with Type II and Type IV interactions are expected to run more slowly. In general, models in INLA run faster, particularly with pCAR, LCAR, and BYM priors. For these models, the computing time ranges between 15 min (additive models) and 69 min (Type IV interaction) with INLA and between 400 min (additive) and 620 min (Type IV interaction) with WinBUGS. This indicates that the fit with INLA is between 9 and about 25 times faster than the fit with WinBUGS. Here, we would like to clarify that the pCAR and LCAR spatial priors are proper and hence WinBUGS does not place sum-to-zero constraints. However, as pointed out by Goicoa et al. (2018) a milder confounding issue still remains between the intercept and the spatial term. Consequently, sum-to-zero constraints are required. Though this is rather simple in INLA, it is not so straightforward in WinBUGS, and we have centered the spatial random effects in each iteration of the MCMC algorithm, which in turn produces an increase in computing time. This does not happen with the iCAR (where in general WinBUGS is slightly faster than INLA) because WinBUGS internally places sum-to-zero constraints in this prior. The reason why INLA seems to be slightly slower in this case may be that constraints in this case are well handled in WinBUGS and INLA uses Kronecker instead of simple matrix products. The exception is the Type IV interaction, where the constraints slow down the computations in WinBUGS as they have to be defined manually. In summary, INLA seems to be a more efficient tool regarding computing time for the implementation of M-models.

Posterior means and 95% credible intervals for the crime-specific intercepts have been obtained and are displayed in Table 5 in the “Appendix”. Pretty similar results are obtained with all the models and fitting techniques. We also fitted the models with the LCAR and BYM priors in WinBUGS without centering, and the final relative risk estimates were identical to the ones obtained with INLA, but differences were observed in the crime specific intercepts and the spatial patterns. Regarding the hyperparameters of the models with a spatio-temporal Type II interaction term, Table 6 in the “Appendix” provides the posterior mean, the posterior standard deviation, and 95% credible intervals. It is very clear that crime-specific standard deviations of the interaction term ($\sigma _{\delta _j}$) do not practically change when using INLA and WinBUGS. Small differences are observed in the estimates of $\sigma _{\theta }$ and $\sigma _{\gamma }$.

In summary, results obtained with INLA and WinBUGS are practically identical, and given that INLA is, in general, much faster than WinBUGS, and constraints are easily handled in INLA, we consider that fitting multivariate models using INLA is an interesting alternative to WinBUGS. In the next section, we provide all the results of the real data analysis using INLA.

3.3 Joint analysis of rapes and dowry deaths using M-models in INLA

Multivariate models presented in Sect. 2, including the different spatial priors and space-time interaction types, have been fitted to study rapes and dowry deaths in Uttar Pradesh during the period 2001–2014. The models are compared in terms of the Deviance Information Criterion (DIC) (Spiegelhalter et al. 2002), the Watanabe-Akaike information criterion (WAIC) (Watanabe 2010), and the logarithmic score (LS) (Gneiting and Raftery 2007), a measure of model prediction performance. The values are displayed in Table 3. The lower the value of the criterion, the better the model.

Table 3 Model selection criteria, DIC, WAIC and LS, for the proposed models

The same multivariate models with the same standard deviation for the spatio-temporal interaction of both crimes have been fitted, but poorer results were obtained and results have been omitted to save space. Additive models exhibit the highest values of all the criteria, indicating that they are not flexible enough to model the data. Models with Type II spatio-temporal interaction are the most suitable candidates with notable differences in terms of DIC, WAIC, and LS with the rest of models including other interaction types. Overall, and according to all criteria, the differences between distinct models with the same Type II interaction are not very large, and it is very difficult to select the best one in terms of goodness of fit (DIC and WAIC) or prediction ability (LS). However, we notice that estimates of spatial correlation parameters $\rho _j$ ($j=1,2$) within crimes in models with a pCAR prior, and estimates of the spatial tuning parameter within crimes $\lambda _j$ ($j=1,2$) with a LCAR prior, are close to 1 (see Table 6 in the “Appendix”). This means that the differences between these models and the model with an iCAR prior tend to vanish completely. That is, the pCAR and the LCAR are essentially the iCAR, but the latter is a simpler model with a substantial reduction in computing time (about two times faster). On the other hand, estimated incidence risks using all models with Type II interaction are practically identical. Then, M-models (FE and RE) with an iCAR prior for the spatial random effect present the best tradeoff between complexity and goodness of fit. Moreover, FE M-models are in general faster than RE M-models, and consequently, we have finally selected a FE-M model with an iCAR spatial prior and a Type II spatio-temporal interaction to display the results.

The spatio-temporal multivariate model proposed in this paper also permits to split the final risk for each crime into the spatial, temporal, and spatio-temporal component, each providing information that may be related to different issues. The crime-specific intercepts $\exp (\alpha _{j})$ can be interpreted as an overall risk for each crime; the district-specific spatial risk for each crime, $\exp (\theta _{ij})$, can be related to the idiosyncrasy of the districts and may be reflecting the effect of certain traditions, demographic and socio-economic characteristics, or religious practices. The crime-specific temporal component $\exp (\gamma _{tj})$ indicates a global evolution of the crime in the state and may reflect the effect of factors that change over time such as policies, women supportive plans, or laws to protect women. Finally, the spatio-temporal risk $\exp (\delta _{itj})$ is a residual term that may be modelling heterogeneity related to differences in the effect of certain actions in time in each area. In general, similar spatial and temporal patterns would indicate a relationship between the crimes being studied.

Fig. 4

Posterior mean of the district-specific spatial risk, $\exp (\theta _{ij})$ (left column), and the exceedence probabilities, i.e., $P (\exp (\theta _{ij})>1|{\mathbf {O}})$ (right column), for rapes (top) and dowry deaths (bottom)

Figure 4 displays the posterior mean of the district-specific spatial risk, $\exp (\theta _{ij})$ (left column), and the exceedence probabilities, i.e., $P (\exp (\theta _{ij})>1|{\mathbf {O}})$ (right column), for rapes (top) and dowry deaths (bottom). A clear Northwest-Southeast gradient (the largest diagonal axis of the map) is observed in the relative risk estimates for both crimes, although the spatial patterns present some differences. Whereas most of the areas in the Northwest part of the state exhibit a high risk of rapes, districts with high risk of dowry deaths are mainly located in the central part of the map. In fact, a Southwest-Northeast gradient is observed for dowry deaths in the central part of the map, something that is not clear for rapes. However, the maps reveal an interesting fact: most eastern districts present a small district-specific risk for both crimes, and this would require further insight to understand why the risk of both crimes is lower in these districts than in Uttar Pradesh as a whole. INLA allows to produce samples from the approximated joint posterior for the hyperparameters. From them, we have been able to obtain samples of the estimated correlation matrices (between spatial and between temporal patterns). The estimated posterior mean of the correlation between the spatial patterns is 0.30, with a 95% credible interval (0.08, 0.50). Similar results were obtained using WinBUGS. This positive correlation would indicate that certain districts are more prone to the occurrence of both crimes. However, finding common spatial risk factors is a challenge.

Fig. 5

Temporal pattern of incidence risks (posterior means of $\exp {(\gamma _{tj})}$) for rapes and dowry deaths in Uttar Pradesh

Figure 5 displays the global temporal trends common to all districts (posterior means of $\exp {(\gamma _{tj})}$) for each crime. Both trends exhibit a marked decrease from 2001 to 2003, and a constant increase until 2008. From then on, a remarkable increase is observed for rapes, whereas the trend remains stable for dowry deaths. The positive correlation here is evident, when one crime increases (decreases), the other one also increases (decreases). This is confirmed with the estimated posterior mean of the correlation between the temporal trends: 0.82 with a 95% credible interval (0.38, 1.00). This estimated high correlation indicates that rape risks keep pace with dowry death risks, indicating that some events in time may have affected the two crimes similarly. It is suspected that changes in government (and consequently in policies) may have had some influence on both crimes. During the study period, three different parties held government in India, and another three different parties ruled the state of Uttar Pradesh. A tentative hypothesis is that female protection policies (Protection of Women from Domestic Violence Act 2005) may have encouraged women to report rapes, a well known underreported crime (Vogelman and Eagle 1991; Koss 1992), and hence led to an increase in rape risk in the last years of the study period. It may also be responsible for the stabilization of dowry deaths, a crime where underreported cases are not expected (Mukherjee et al. 2001). However, these are mere hypotheses as evaluating the effects of certain policies requires a longer time period, and it is even more complicated to include such information in the model unless covariates about investment on plans to protect women and give them support are available.

Figure 6 shows the geographical risk patterns (posterior mean of the relative risk) of rapes (top) and posterior probabilities of risk exceedance, $P(R_{itj}>1|\mathbf{O})$ (bottom) in the study period. The same information for dowry deaths is displayed in Fig. 7. The increase in risk in rapes is clearly observed in the maps, which become darker from 2003 to 2014. The increase is particularly remarkable from 2010 onwards. The maps for dowry deaths also reveal a stable pattern in the last years of the period. Both figures show that most eastern districts exhibit a low risk for both crimes. The pattern of high risk areas (those with $P(R_{itj}>1|\mathbf{O})>0.9$) of rapes is more irregular. In some years of the period (2003 and 2010 mainly), most of the areas do not exhibit high risk. However, at the end of the period, nearly all the areas do have a high risk with the exception of some districts in the eastern part of Uttar Pradesh. Regarding dowry deaths, most of the high risk areas are located in the central-western part of the state and the pattern remains fairly stable during the study period.

Fig. 6

Map of estimated incidence risks for rapes (top) and posterior probabilities that the relative risk is greater than one ($P(R_{itj}>1|\mathbf{O})$) (bottom) in Uttar Pradesh

Fig. 7

Map of estimated incidence risks for dowry deaths (top) and posterior probabilities that the relative risk is greater than one ($P(R_{itj}>1|\mathbf{O})$) (bottom) in Uttar Pradesh

Finally, the temporal evolution of the final risk (posterior means of $R_{itj}$) and 95% credible intervals for several districts, Aligarh, Ghazlabad, Kheri, Mainpuri, Sant Kabir Nagar, and Varanasi are shown in Fig. 8. These districts are interesting because the risk evolution is very different. Aligarh exhibits high relative risks for both crimes. In particular, the risk of rapes does not stabilize and continues growing, standing about three times higher than the overall risk in Uttar Pradesh at the end of the period. Regarding dowry deaths, the risk is significantly high, but it stabilizes over time around twice the risk of whole Uttar Pradesh. Kheri shows a decreasing evolution of risks for both crimes that stabilizes around one at the end of the period. In Mainpuri, the risk of dowry deaths is significantly high during the whole period in contrast to rapes. Sant Kabir Nagar has a significant low risk of both crimes until 2009 approximately. From then on, the trends start to diverge due to a significant increase of the risk of rapes. Varanasi has significant low risks with a fairly stable evolution for both crimes, though they tend to one at the end of the period.

Fig. 8

Temporal evolution of final risk estimates for rapes and dowry deaths in some districts in Uttar Pradesh: Ghazlabad, Kheri, Mainpuri, Sant Kabir Nagar, and Varanasi

4 Discussion

Spatio-temporal areal models have been widely used in epidemiology, but the use of these models to analyze crimes against women has been the exception rather than the rule. Multivariate models are powerful techniques that provide valuable information to locate hot spots and may help social researchers to make hypotheses about potential risk factors related to certain forms of violence against women. Given the multifaceted dimension of crimes against women and the difficulty to determine relationships between crimes and socio-economic, demographic, religious factors, and other transitory or circumstantial elements, a multivariate approach may help to reveal relationships between different crimes that can shed light on this complex phenomenon. Moreover, if it is believed that different crimes against women could share risk factors, a rather sensible approach, the use of multivariate spatio-temporal models will make it possible to estimate these dependencies and improve understanding of the problem.

In this paper, we consider an extension of the spatial M-models proposed by Botella-Rocamora et al. (2015). In addition to the spatial M-model, we introduce a temporal M-model and a spatio-temporal interaction. The model makes it possible to estimate correlations between spatial and temporal patterns which would respectively indicate potential geographical factors and transitory events related to both crimes. As the interaction term is a residual term, we do not consider inter-crime dependence for this term because variability is mainly captured by the main effects. Instead, we use different variance parameters for both crimes leading to a different amount of spatio-temporal smoothing. This model provides better results than a model with the same variance parameter. This seems sensible as the standard deviation of the spatio-temporal random effects for rapes is about twice the standard deviation for dowry deaths. Different models have been considered to analyse the data, but those that achieve the best tradeoff between complexity and goodness of fit (measured in terms of DIC and WAIC), and prediction ability (measured with the LS) are the so called M-models with an iCAR prior for space, a RW1 prior for time, and a Type II interaction. In fact, the crime-specific spatial parameters of the pCAR and LCAR model are very close to one pointing towards the iCAR prior for space.

The analysis of rapes and dowry deaths in Uttar Pradesh reveals interesting findings. On one hand, the correlation between the estimated spatial patterns is positive and significant, though not very strong (0.30). This indicates that certain districts tend to present high risks of both crimes, but the underlying spatial patterns are not similar. The estimated pattern reveals that the risks of rapes and dowry deaths in the most eastern districts of Uttar Pradesh are significantly low, and consequently further insight is needed to study the characteristics of these regions which could bring light to the understanding of the phenomena being studied. On the other hand, the estimated correlation between temporal patterns is 0.82, indicating a strong, positive association and that the two crimes evolve in line. We could hypothesize that certain policies or laws, such as the Protection of Women from Domestic Violence Act 2005, has had some influence on both crimes, but it is rather complex to validate such hypothesis.

The methodology developed in this paper is a first attempt to disentangle the intricate phenomenon of crimes against women. As suggested by one reviewer, including covariates in the model would be of great interest. However, this is not an easy task as there are some delicate issues to tackle first. The first one is that given that the spatial correlation is not very strong, it seems sensible to consider different covariates for each crime, and, even if both crimes share a common risk factor, they might be unequally affected. The second, and possibly the most important issue, is confounding fixed effects by random effects. It is well known that in spatial disease mapping, the effect of a covariate may be confounded with the spatial random effect leading to biased estimates of the fixed effects and to variance inflation (Reich et al. 2006; Hodges and Reich 2010). Consequently, if a risk factor is included in the model, the estimation may not be valid (see for example Kelling et al. 2020). This is even worse in the spatio-temporal setting where confounding may be present due to the spatial, temporal, and the interaction random effects. We are currently working on how to deal with this relevant issue in univariate spatio-temporal models, where a reparameterization is proposed (see Adin et al. 2020). However, including this reparameterization to deal with confounding in the multivariate setting is not straightforward, as the spatial and temporal main effects become time and spatially varying random effects, and it is not clear how correlations between crimes should be incorporated and, more importantly, interpreted. Further research is needed to deal with all these issues before incorporating covariates in the models proposed in this paper.

Finally, model fitting has been implemented using WinBUGS and INLA. In particular, we have implemented the LCAR and BYM M-models in INLA. Our study indicates that there are practically no differences between WinBUGS and INLA in the data analysis considered in this paper in terms of relative risk estimates, and the derived spatial and temporal patterns. Small differences were only observed in the model hyperparameter estimates. In addition, we have seen that in the cases analyzed here, INLA is, in general, a computationally more efficient alternative than WinBUGS. However, further research is needed when the number of areas, time periods, and crimes increases as INLA does not replace Kronecker products by simple matrix products. We are currently investigating this issue.

Appendix

See Tables 4, 5, and 6.

Table 4 District identifiers (ID) of Uttar Pradesh

Table 5 Posterior means, standard deviations, and 95% credible intervals for the crime-specific intercepts ($\alpha _j,\, j=1,2$) of the models with a spatio-temporal type II interaction term

Table 6 Posterior means, standard deviations, and 95% credible intervals for the hyperparameters of the models with a spatio-temporal type II interaction term