Flow dynamics in a model of a dilated thoracic aorta prior to and following prosthetic replacement

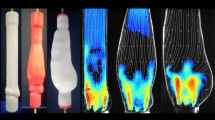
Abstract

We numerically investigate the flow dynamics in a model of a dilated thoracic aorta, and compare the flow features with the case of a prosthetic replacement in its ascending part. The flow is characterized by an inlet jet which impacts the aortic walls and sweeps toward the aortic arch. Secondary flows generated by the transvalvular jet evolve downstream into a helical flow. The small curvature radius at the end of the aortic arch induces flow separation and vortex shedding in the initial part of the descending aorta, during the systole. The implantation of a prosthesis determines several modifications in the global and local flow patterns. An increase of the pulse wave velocity in the aorta leads to larger pressures inside the vessel, due to the geometrical and rigidity modifications. The sweeping jet is more aligned along the axial direction and propagates faster along the aortic arch. Consequently, a stronger separation of the flow downstream of the aortic arch is observed. By also exploiting manifold analysis, we identify regions characterized by near-wall disordered flows which may present intense accumulation and drop of concentration of biochemicals. These regions are localized downstream of the prosthetic replacement, in the aortic arch, and may be more prone to a new emergence of vessel dilation.

Graphical Abstract

1 Introduction

Prosthetic replacement of aortic sections is a common surgical procedure. Needless to say, grafts are crucial in the mitigation of diseases, such as coarctations and aneurysms. First documented cases of ascending aorta [1, 2], and aortic arch [3] replacement were mostly focused on aneurysms treatment. These pioneering surgery operations paved the way for a plethora of studies in the field of prosthetic replacements of the aorta, aimed at properly understanding the best treatment for diverse diseases (cf. [4] for a review). As an example, the Bentall procedure [5] is a reference choice in the diseases involving the aortic valve and ascending aorta. Alternatively, valve-sparing operations such as the David and Yacoub procedures are minimally-invasive operations, with positive long-term outcomes [6, 7].

A significant fraction of the total cases of aneurysms in the thoracic aorta indeed occurs in its ascending part [8]. Thoracic aorta aneurysms together with possible associated serious consequences such as aortic dissection and rupture present a high mortality rate [9]. Also, aortic dilations are common in patients with Bicuspid Aortic Valve (BAV), a congenital disease which affects around 1–2% of the population [10]. In BAV patients, two of the three leaflets composing the aortic valve are fused. This disease is associated with a 50% probability of developing aneurysms in the ascending aorta [11, 12]. Approximately half of the cases also present stenotic behaviors, i.e. abnormal peak jet velocities resulting from reduced cross-sections of the aortic valve [13]. Bicuspid aortic valve and complications stem from positive feedback between modifications of mechanical properties and altered flow patterns. Almost one-third of BAV interventions are associated with ascending aorta replacement [14,15,16]. Typical surgical guidelines suggest ascending aorta resection when the diameter exceeds 50–55 mm, even if this threshold is extremely dependent on the medical history of the single patient [4, 17]. The surgical extent and technique of the ascending aorta replacement is also extremely case-sensitive [18], although a cut in a beveled fashion is preferred to preserve the aortic curvature [19, 20].

The understanding of the flow modifications resulting from prosthetic replacements is crucial in overcoming uncertainties and in the development of effective surgical strategies. In this perspective, fluid dynamics tools are a suitable candidate to shed light on these aspects [21,22,23]. Patient-specific modelling (PSM) shows great potential in the understanding of practical implications of interventions for a specific case [24]. Rapid prototyping techniques allow reproducing realistic geometries and material properties, in order to capture specific flow features in a short time, compatible with the requirements of producing relevant data for diagnostics [25]. In-vitro analyses have the remarkable advantage to provide guidelines for the choice of the most appropriate surgical intervention and/or prosthesis, as well as further interpretation of the in-vivo diagnostic images such as 4D Cardiovascular Magnetic Resonance [26,27,28].

Along with experimental techniques, numerical methods are able to reproduce the flow features in the thoracic aorta [29]. Typically, geometries are based on anatomic data extracted from CT Angiography or Magnetic Resonance Imaging (MRI) [30,31,32]. A significant effort has been made to understand shear stresses acting on the vessel walls, since they have been linked to the degradation of aortic walls mechanical properties (see e.g. [33] among others). The large amount of data generated by a PSM-based approach can help in formulating an efficient diagnosis and therapy for a specific patient. However, computational tools may also be a powerful means to gain statistically significant information from the so-called digital twins [34].

At each heartbeat, blood is injected inside the aorta through the aortic valve during the systole. The valve jet propagates into the aorta, which can be seen as a compliant vessel curved and twisted. As the vessel bends, the jet shifts and a helical flow is generated during the mid-systole [35]. In the distal arch, the flow may recirculate and, in the descending aorta, the helical flow may decay [35]. After the closure of the aortic valve, secondary rotational and recirculating flows dominate, leading to coherent helical patterns. At the same time, the strong deceleration induces instability and disorganization of the flow field at smaller scales [36].

Helical flows and recirculation influence wall shear stresses variability in time and space which, in turn, may affect stenosis and plaque formation [33]. It is not surprising that several numerical studies have been dedicated to the understanding of flow modifications under pathological conditions and the effect of prosthetic replacements in the thoracic aorta, see for instance Ong et al. [37] for an extensive review. Most of the studies are focused on prosthetic replacements in the distal aortic arch or descending aorta due to aneurysms. Ong et al. [38] studied an endovascular repair in an aneurysmatic descending aorta, showing a positive effect on flow features in the descending aorta. A similar configuration was studied in Filipovic et al. [39], with analogous conclusions. Lei et al. [40] and Nauta et al. [41] investigated the effect of geometry variations induced by prosthetic replacement in the aortic arch, under the assumption of rigid vessel walls, with a focus on atherogenesis. While the first showed significant variations of near-wall quantities, the latter highlighted that the surgical procedure lead to a more organized flow. Scharfschwerdt et al. [42] performed an in-vitro study of a thoracic aorta prior to and following a prosthetic replacement in its ascending part, showing an increase in the peak pressure and pulse-wave velocity in the prosthetic case, and a marked increase in wall tension downstream of the prosthesis. Similar conclusions were obtained in vivo by Palumbo et al. [43]. The same authors also observed modifications of shear stresses distal to the prosthesis.

While features of prosthetic replacements in the aortic arch and downstreams have been widely studied through computational fluid dynamics [37], the large-scale flow modifications and near-wall transport induced by a prosthesis in the ascending aorta still need to be systematically assessed. However, they are known to be related to tissue disorganization, phlogosis and other pathologic events, and a relevant question concerns the emergence of new regions where the disease may propagate after prosthetic replacement [44]. In this work, we numerically characterize the flow modifications induced by the implantation of a prosthesis in the ascending aorta through the replacement of the dilated part of the aorta with an idealized prosthetic geometry of a correct sizing. We aim at characterizing the large-scale structures of the flow and correlate them to the near-wall transport and to their clinical significance so as to assess regions of concern after prosthetic replacement. Numerical models typically include the coupling between fluid dynamics and deformations of the solid structures, possibly including also the coupling with the electrical stimuli [45,46,47]. Being focused on the fluid dynamics, we employ a Coupled Momentum Method approach to describe realistic vessel deformations [48,49,50] and the effect of a prosthetic replacement, with an idealized inlet condition given by a top-hat profile mimicking the transvalvular jet originating from the vena contracta just downstream of the valvular orifice [51]. We aim at unveiling the primary role of geometry and deformability modifications on flow patterns and stresses acting on the vessel walls, while keeping the flow boundary conditions unchanged.

To this purpose, we employ a realistic geometry obtained through contrast-enhanced computed tomography angiography, characterized by dilation of the ascending part, combined with realistic boundary conditions, and vessel and fluid properties. We then perform a virtual prosthetic replacement by substituting the ascending part of the aorta and compare the resulting flow against the presurgical case. The paper is organized as follows. Section 2 presents the problem formulation and numerical tools. Section 3 is devoted to the presentation of the results and the comparison between the pre- and post-surgical cases, by first focusing on the transvulvar jet impact in the ascending aorta during systole and then describing the flow propagation in the aortic arch and diastole with relevant integral quantities. Section 3.4 is focused on the near-wall flow and transport and their clinical relevance. Finally, Sect. 3.5 gives an insight into the observed aortic vessel deformations.

2 Problem formulation and numerical methods

The hemodynamic flow in the thoracic aorta is considered. The geometry is based on diagnostic images acquired through contrast-enhanced tomography (CT) scan, as shown in Fig. 1a. The considered case is characterized by dilation up to $\approx 50$ mm of the ascending aorta, i.e. a case in which surgical intervention is suggested. The numerical study is performed by employing the open-source tool SimVascular (version 2021.06) [48, 52], which provides a complete pipeline from image analysis to hemodynamic simulations. A segmentation procedure is performed to identify the vessels lumen, through the definition of a series of sections orthogonal to the vessel axis. Specifically, the aortic lumen was selected and a series of sections orthogonal to the vessel axis were traced. The resulting geometry is shown in Fig. 1b. The numerical domain includes the ascending part of the aorta right after the Valsalva sinuses, a relatively long segment of the descending aorta (whose outlet will be denoted hereafter as AbAo), and the three primary bifurcations of the aortic arc, (moving downstreams: brachio-cefalic trunk (BCT), left common carotid (LCC) and subclavian artery (LSA)). The prosthetic geometry was mimicked by substituting the ascending part of the aorta with a vessel of fixed, circular, cross- section, whose area is coincident with the inlet one, which smoothly joins to the native vessel in the vicinity of the brachiocephalic trunk bifurcation (see Fig. 1b). At the re-connection with the aortic walls, a discontinuity in the mechanical properties is present. The joining between the prosthesis and the original aorta is not orthogonal to the vessel axis, since, typically, the junction involves vessels of different diameters. The virtual surgery was performed following the advice of the medical expert included in the research team.

The blood flow inside a large vessel such as the aorta can be assumed Newtonian [53,54,55]. We thus study the incompressible flow of a viscous Newtonian fluid of viscosity $\mu =3.5$ mPa s and density $\rho _f=1060$ kg/$\hbox {m}^3$. The Navier–Stokes and continuity equations within the vessel read:

$$\begin{aligned} \rho _f \left( \partial _t\varvec{u}+\varvec{u}\nabla \varvec{u}\right) = - \nabla p +\mu \nabla ^2 \varvec{u}, \quad \nabla \cdot \varvec{u}=0. \end{aligned}$$

(1)

Fig. 1

a Result of the segmentation procedure: the aorta inlet is located right downstream of the Valsalva sinuses, and the three bifurcations in the aortic arch are included in the model as outlets. Another outlet is located downstream in the descending aorta. b Virtual ascending aorta resection: the ascending part of the aorta model is replaced with a cylindrical vessel whose cross section is constant up to the aortic arch, in the close vicinity of the first bifurcation, beyond which the original geometry is preserved

SimVascular employs the coupled momentum method (CMM) [48], which stems from the Galerkin formulation of the following bulk equations for the solid vessel displacement $\varvec{v}$ for a linear elastic and isotropic material:

$$\begin{aligned} \rho _s \partial _{tt}\varvec{v}=\nabla \cdot \varvec{\sigma }_s + \varvec{b}, \quad \varvec{\sigma }_s=\textbf{C}:\varvec{\varepsilon }, \quad \varvec{\varepsilon }=\nabla _s \varvec{v}=\frac{1}{2}\left( \nabla \varvec{v}+\nabla \varvec{v}^T\right) \end{aligned}$$

(2)

where $\rho _s$ is the solid density, $\varvec{\sigma }_s$ is the stress tensor, $\varvec{b}$ is the body force and $\varvec{C}$ is the fourth-order elasticity tensor. By employing the thin wall approximation, i.e. assuming the thickness to be much smaller than the vessel deformations, the continuity of stresses at the fluid-solid interface $\Gamma _i$ of the vessel, results in the body force $\varvec{b}=-{\varvec{\sigma }_f \varvec{n}}/{h},$ where $\varvec{n}$ is the surface normal, h is the local thickness of the thin solid vessel and $\varvec{\sigma }_f$ is the stress tensor of the fluid. Owing to the small thickness, quantities are assumed constant inside the domain and thus the weak form of Eq. (2) applies only on the solid domain boundaries, without the need to discretize the bulk of the vessel.

The problem is completed with the inlet and outlet conditions as follows.

At the inlet boundary, located just downstream of the aortic valve, a flow rate waveform is imposed [50], with an inlet condition given by a top-hat profile which fairly reproduces the jet originating just upstream. A periodic flow rate of period $T=1$ s is imposed at the inlet (see Fig. 2a), extracted from Alastruey et al. [50]. To mimic a pathological aortic valve jet right downstream of the Valsalva sinuses associated with the aorta dilation, we consider a top-hat velocity profile in a circular area of size $A_i=1.7\,\hbox {cm}^2$ ($A_{tot}/A_i\approx 5.4$, where $A_{tot}$ is the total inlet area), a typical value of effective orifice area [56] which, combined with the considered inlet flow rate, gives a peak velocity of approximately 3–4 m/s, i.e. a moderate stenosis [13]. In particular, the circular inlet jet is a reasonable approximation of the flow observed in patients with bicuspid aortic valve with minimal retrograde flow [57]. At each outlet (see Fig. 2b) a three-element windkessel model is imposed [58]:

$$\begin{aligned} \begin{aligned} P(t)=&{\left[ P(0)-R_p Q(0)\right] \textrm{e}^{-t / \tau }+R_p Q } +\int _0^t \frac{\textrm{e}^{-(t-{t}') / \tau }}{C} Q({t}') \textrm{d} {t}', \quad \tau =R_{\textrm{d}} C, \end{aligned} \end{aligned}$$

(3)

which mimics the behavior of the cardiovascular system not included in the model as a zero-dimensional circuit for the unknown volumetric flow rate Q and pressure P at the considered boundary. The quantities $R_p$ and $R_d$ defined a proximal and distal resistance of the peripheral cardiovascular system while C represents its compliance. The employed physiological values, extracted from Stokes et al. [59], are reported in Table 1. We also consider a viscoelastic external tissue support on the lateral boundaries of the vessel by fixing its stiffness and damping as $k_s=0.01$ Pa/mm and $c_s=0.15$ Pa s/mm, respectively [50, 60].

Fig. 2

a Inlet flow rate, non-dimensionalized with $UL^2$, as a function of time. b Sketch of the inlet and outlets together with their labeling

Table 1 Values of the windkessel parameters for the brachiocephalic trunk (BCT), left common carotid (LCC), subclavian artery (LSA) and outlet at the abdominal aorta (AbAo)

The employed CMM model allows for the definition of the vessel wall thickness as well as the Young modulus and the Poisson ratio. We consider a typical value of the vessel wall thickness, i.e. $h=2$ mm [61,62,63,64]. The Young modulus of the aortic walls is set so as to guarantee typical deformations, in the case of patients with dilated thoracic aorta, between systole (s) and diastole (d). With a variation of pressure of $\approx 5000$ Pa between systole and diastole with the considered parameters [59], an estimate of the deformation is given by $\Delta d\approx (1-\nu /2)(p_s-p_d)R^2/(Eh)$, with $R\approx 0.01$ m. A variation of diameter $\Delta d= d_s-d_d \approx 7\%$, in the typical range for patients with aortic dilation and with BAV [65,66,67,68], is obtained with a value of the Young Modulus $E=0.3$ MPa. This value is in line with measured elastic moduli, see e.g. Choudhury et al. [62]. We note also that the considered aortic walls are slightly stiffer compared to healthy patients. We thus expect slightly larger values of peak pressure and flow rates, due to the decreased vessel compliance. The Poisson’s ratio for the aortic walls and prosthesis is assumed to be $\nu =0.499$. The prosthetic part presents thickness $h=0.36$ mm and Young modulus $E=12$ MPa, typical values of a Dacron® graft, in line with previous studies [69, 70]. Therefore, the graft is approximately ten times stiffer than the aortic walls. It is worth noting that Dacron grafts are typically given in discrete diameters. In the present study we assume that the prosthetic diameter matches the inlet section, which presents a diameter of 34 mm, a commercially available size [71]. To ensure a constant diameter throughout the whole ascending aorta and the match with the diameter in the aortic arch, a cut in a beveled fashion at the reconnection is performed, mimicking a typical surgical procedure.

The choices for the parameters define a physiologically relevant flow configuration. Quantities are non-dimensionalized with the mean velocity through the inlet during one period $U\approx 1$ m/s, the diameter of the inlet jet $L=0.015$ m, and the period $T=1$ s. With these choices, the Reynolds number results $\hbox {Re}=UL/\nu =5000$ while its peak value is $\hbox {Re}_p \approx 15,000$. The Wormesley number reads $\hbox {Wo}=L(\omega /\nu )^{1/2}=21.7$. Note that, despite the large Reynolds number, high values of velocity are sustained for a very short time during the cycle, and the heartbeat frequency does not allow the energy cascade to go down to small scales. Therefore, turbulence does not fully develop and a classical grid convergence analysis ensures realistic results [72]. In the following, for the sake of clarity, we will refer to non-dimensional variables.

The resulting mesh, obtained through the open-source package TetGen, embedded in SimVascular, is composed of approximately $1.2\times 10^{6}$ tetrahedral elements. SimVascular relies on a finite-element formulation based on PHASTA [73] for the implementation of the Navier–Stokes equations, of the Coupled Momentum Method as well as of the boundary conditions and of the external tissue support. The finite-element solver PHASTA employs stabilized Lagrange polynomials P1–P1. The nonlinear problem at each time step is set with a tolerance of $10^{-6}$. We employ a second-order generalized Alpha method, with $\alpha =0.5$ for the time marching, with a time step $\delta t=0.001$. The simulation is initialized with a solution of the case with rigid walls, and stopped when the peak pressure difference between two consecutive periods becomes lower than 0.1%. Convergence of the rigid solution is achieved in 8–10 periods, while the deformable wall case converges after 2 periods. The mesh detail as well as the detailed numerical grid independence analysis is reported in “Appendix A”.

3 Results

In this section, we present the numerical results of our analysis for the vessel geometry before and after the implantation of the prosthesis (Fig. 1), so as to give a general characterization of the reference flow.

Fig. 3

a Sketch of prosthetic case with outlets labels. b Flow rate (non-dimensionalized with $U L^2$) and c average pressure (non-dimensionalized with $\rho U^2$) as functions of time for the last period, (blue) Inlet, (orange) BCT, (yellow) LCC, (purple) LSA, (green) AbAo, for the presurgical (solid lines) and the postsurgical case (dashed lines) (color figure online)

Figure 3 shows the (a) flow rate and (b) average pressure as functions of time, at each inlet and outlet. The flow rate waveforms at each outlet mimic the inlet one, with a peak value reached slightly after the one of the inlet waveform. In particular, the peak values at the three bifurcations of the aortic arch are significantly lower than the one occurring in the descending aorta outlet AbAo. Conversely, similar waveform are observed for the average pressure at each outlet, with a clear increase in the pressure growth observed at the AbAo outlet.

The peak flow-rate in the descending aorta is about half of the value found in the ascending aorta. In dimensional variables, the inlet pressure, probed just downstream of the Valsalva sinuses, increases from $\approx 100$ mmHg to $\approx 135$ mmHg, giving a pressure difference between systole and diastole of 35 mmHg. Similar results were numerically obtained by Viola et al. [74], in terms of pressure at the aortic valve in the case of a moderate stenosis. The delay in the peak observed in Fig. 3 underlies the presence of a pulse wave, whose velocity (PWV) is defined as the ratio between the arc length of the aorta centerline ($=392$ mm) and the time delay between the peak of the flow rate at the inlet and at the outlet ($\approx 0.06$ s) and reads PWV$\approx 6.5$ m/s. A similar value is obtained by considering the delay in the pressure waves. This value is in line with previous experimental measurements in the ascending aorta [75,76,77].

In the prosthetic case, the flow rate and pressure waveforms are similar to the presurgical case; however, higher flow rates at the outlets are observed, in particular at AbAo. Additionally, the peak flow rate at AbAo is anticipated and, overall, the measured mean pressures after the prosthesis implantation are higher compared to the presurgical values. The increase of pressure is also anticipated. Since the prosthetic ascending aorta is less compliant and its cross-sectional area is smaller, the peak pressures increase. The reduced compliance of the ascending aorta also induces anticipation of the peak flow rate and pressure at the outlets.

3.1 Inlet jet flow dynamics

We now describe the local flow features associated with these pulse waves and the considered geometry and inlet conditions. Figure 4 shows the the initial stage of development of the flow in the presurgical case through a streamline plot overposed to a volume rendering of the velocity magnitude in the instants marked in panel (c). During the early systole, the inlet jet propagates into the ascending aorta. At $t=0.08$ (panel a), the jet generates a strong entrainment of fluid, with the subsequent formation of a recirculation region which dominates the proximal ascending aorta. Increasing time (panel b), the jet propagates further and deviates from its straight trajectory. The jet impacts the aortic walls at $t=0.12$. The following phase of development is shown in Fig. 5 in comparison with the presurgical case. Then the jet sweeps on the aortic walls and accelerates, following the external curvature. At the same time, the recirculating region expands and deflects according to the boundary constraint imposed by the wall.

Fig. 4

Presurgical case. Streamline plot of the velocity field at different instants in the vicinity of the peak systole, overposed to a volume rendering of the velocity magnitude. Panel c indicates the considered instants

The largest velocities are observed just downstream of the impact region. The jet thus follows the outer vessel curvature, while the recirculating region has now invaded the whole ascending aorta. The streamlines also depict an increasing secondary flow, transverse to the sweeping flow direction.

Fig. 5

Flow at two different instants around peak systole, for the post- (top) and pre-presurgical (bottom) cases, a $t=0.12$, b $t=0.14$. Volume rendering of the velocity magnitude and velocity streamlines

In the prosthetic case, the highest velocity is localized right downstream of the impact region, and the jet propagation mostly occurs along the axial direction. Conversely, the flow configuration of the presurgical case (bottom figure of panel a) denotes a more isotropic propagation, with the trace of the sweeping jet more spread and less oriented along the axial direction. These considerations are confirmed by panel (b), which shows the flow at $t=0.14$. The flow in the prosthesis follows more closely the outer curvature region of the aortic walls and propagates toward the aortic arch differently from the presurgical case that instead presents a relevant flow orthogonal to the axial direction. Owing to the different confinement of the inlet jet, the size of the recirculating regions significantly differs between the two cases. Non surprisingly, larger velocities are attained in the prosthetic case. Also, the region of recirculating flow in the vicinity of the aortic root is drastically reduced by the presence of the prosthesis. As a consequence, the impacting jet is more inclined in the postsurgical case, compared to the presurgical one, and the flow is more aligned toward the vessel axis, after prosthetic implantation.

Fig. 6

Volume rendering of the vorticity magnitude at different instants around peak systole, for the presurgical (top) and prosthetic (bottom) cases, a $t=0.1$, b $t=0.12$, c $t=0.14$, d $t=0.16$

The vortex dynamics in the peak systole can be appreciated in Fig. 6, which displays a volume rendering of the vorticity magnitude right after peak systole. The annular region of large vorticity (visible in panel a) associated with the propagating jet bends toward the outer wall, in panel (b). At the impact, the annular vortex deforms (panel c) and then elongates while transported toward the aortic arch. In panel (d), the vortex ring breaks into smaller vortices while propagating downstream. More in detail, at $t=0.1$, the vortex ring in the prosthetic case is already inclined due to the earlier interaction with the aortic wall, compared to the presurgical case. Correspondingly, the presence of the prosthesis reduces the jet propagation: at $t=0.12$, the jet of the prosthetic case starts to propagate toward the aortic arch while the presurgical case is still bending towards the wall. In the following development of the flow, the two cases exhibit a similar flow pattern. However, the vortical structures of the prosthetic case propagate farther, due to the reduced lumen of the prosthesis.

Further details on the flow configuration in the ascending aorta are provided in Fig. 7, which shows the velocity and normal vorticity field at the section of the ascending aorta of panel (c), for the preoperative case. The streamlines are obtained only from the inplane velocity components, in order to highlight the secondary flows. Right before the peak systole, the streamlines in the considered plane are aligned toward the aortic arch. The axial vorticity is negligible, at the considered instant. Nevertheless, the axial velocity is positive in the outer curvature region, while it is slightly negative in the inner arch region. At $t=0.12$, we observe the presence of two large recirculations, associated with two normal vortex cores of opposite sign. These recirculations are a trace of the annular vorticity region observed in Fig. 6. Associated with this flow structure, the normal velocity sweeping on the outer curvature wall increases. Similarly, a stronger negative normal velocity is observed in the inner arch region, of intensity comparable to the reference one. At late systole ($t=0.18$), four vortex cores, each one associated with another one of opposite sign, aligned with an angle of approximately $30^\circ$ with the y direction, are observed. These two cores are the trace of two different vortex tubes, which can be observed also in Fig. 6c. At the same time, the axial velocity which sweeps on the outer curvature region decreases, and there is no more a clear distinction between regions of positive and negative normal velocity.

Fig. 7

Presurgical case. Color maps of a the velocity along the vessel axis and b of the axial vorticity (right), overposed to the streamlines obtained from the inplane velocity, at four different instants. c Sketch of the position of the section and internal/external curvature regions (color figure online)

The inlet jet dynamics dominates the early and peak systole, in the ascending aorta. The transvalvular jet impacts obliquely on the wall similarly to the transmitral jet in the left ventricle [21, 78,79,80,81], where a large-scale vortex in the left ventricle is observed. In that case, the inclined impact of the mitral jet on the walls leads to an upward flow which ensures a smooth outflow from the left ventricle. At the same time, the vortex ring survives and is inclined because of the outflow. Similarly, the inclined impact in the ascending aorta leads to a flow directed toward the inner aortic arch (see Fig. 7). However, the confinement effect exerted on the impacting vortex ring is much stronger in the dilated case, which leads to the rupture of these rings and the formation of vortex filaments, aligning with the vessel axis. At the same time, the jet entrainment is not symmetric and induces a strong secondary flow which sweeps along the lateral directions. This fluid transport leads to an initial breaking of the vortex ring in its upstream part, see Fig. 6c. These secondary flows evolve into a helical coherent motion. The helicity of the flow destroys the coherent vortex filaments advected downstream in the aortic arch, whose flow is described in the following.

The differences in the observed waveforms between pre- and post- operative cases can be correlated to the different jet dynamics in the ascending aorta during systole. The jet impact is anticipated, in the prosthetic case, because of the larger confinement given by the prosthesis. The resulting sweeping jet is more aligned toward the aortic arch, also thanks to the reduced compliance of the prosthesis, which allows smaller velocities along the normal-to-the-wall direction and therefore gives a stronger confinement to the flow. The different confinement also induces a much smaller recirculation in the presence of the prosthesis. As a consequence, less fluid is trapped in the ascending aorta and propagates toward the aortic arch and to the outlets, giving a rationale to the observed waveforms.

3.2 Flow propagation in the aortic arch and diastole

Figure 8 shows the streamlines at late systole, overposed to a volume rendering of the velocity magnitude. The streamlines in panel (a) are twisted in a helical motion, and present large values of velocity in the region where the inlet jet sweeps on the aortic walls. This helical motion originates from the superposition of the secondary flow to the main flow of the sweeping jet. As time increases, the rotating component of the velocity field becomes stronger, and a region of large velocity magnitude originating from the jet is transported in the aortic arch following a helical motion. Then, the high-momentum flow propagates into the descending aorta. Here, a recirculating flow is observed in the inner curvature region, just downstream of the aortic arch. At $t=0.28$, after the systolic peak, the streamlines are more disorganized due to the instability promoted by the flow deceleration, although an overall vortex motion can be observed. The flow still sweeps along the outer curvature region.

Fig. 8

Presurgical case. Streamline plot of the velocity field at different instants in the late systole, overposed to a volume rendering of the velocity magnitude. Panel e indicates the different considered instants

Compared to the presurgical case, the streamlines of the prosthetic case are more aligned toward the axial direction (Fig. 9). However, a significant helical flow component can be inferred from the helical twisting of the large velocity filaments. As the flow reaches the descending aorta, a more intense recirculating flow is localized in the region of large curvature downstream of the aortic arch.

Fig. 9

Volume rendering of the velocity magnitude and velocity streamlines for the prosthetic (left) and presurgical (right) cases, a $t=0.2$, b $t=0.28$

Figure 10 shows the comparison between the two cases of the velocity field in a planar section aligned with the z direction, which includes the vessel axis along most of the aortic arch and descending aorta. Color indicates the normal (x) component of the velocity, that can be employed to infer the presence of recirculations in the planes orthogonal to the axis of the vessel. The streamlines instead visualize the velocity components which lie in the considered plane. In panel (b), $t=0.16$, the streamlines well align with the vessel axis, although there are localized regions characterized by a more intricate pattern. In the same regions, the color map depicts an elongated region of large and opposite velocity in the initial part of the aortic arch, which can be associated with the presence of a rotating flow whose vorticity axis cuts the plane where the velocity changes sign. In panel (c), $t=0.2$, the rotating flow propagates downstreams. At the inlet of the descending aorta, the streamlines show the presence of a recirculating flow, in the inner arch region. Eventually, the observed recirculation becomes larger, detaches and is advected downstream (panel d, $t=0.24$), while the helical flow propagates up to the end of the aortic arch.

In the prosthetic case (lower panels of Fig. 10), comparison of the flows presented at $t=0.16$ provides evidence that the presence of the prosthesis promotes and anticipates the onset of a recirculating zone just at the beginning of the descending part of the vessel. Also, the recirculating flow has propagated slightly more distally, as shown by the color map of the normal velocity. As time increases, the above-described recirculation region increases in size and, at $t=0.24$ (panel d) a vortex is shed downstreams. The presurgical case presents a smaller recirculation region and, as a consequence, the vortex shed is smaller.

Figure 11 shows the presurgical flow during the diastole, on the same section of Fig. 10. The coherent axial motion is no more present, and the flow is disorganized due to the instability caused by the flow deceleration. However, in addition to the several recirculations in the plane, a rotating motion that involves most of the section and a counterflow in the descending aorta are observed. As time increases (panels c, d, $t=0.6$ and $t=0.8$, respectively), the flow velocities decrease and the streamlines recover the alignment with the tube.

Fig. 10

Color maps of the velocity along the x direction, overposed to the streamlines obtained from the in-plane velocity, in a section orthogonal to the x direction (panel a), at different instants (panels b–d) prosthetic (bottom) and presurgical (top) cases (color figure online)

Fig. 11

Color maps of the velocity along the x direction, overposed to the streamlines obtained from the inplane velocity, in a section orthogonal to the x direction (panel a), at different instants (panels b–d), in the presurgical case (color figure online)

In summary, the flow propagation in the aortic arch is dominated by the presence of a persistent helical flow which twists the streamlines and breaks coherent vortex tubes, during the systole. This helical motion is given by the superposition of a sweeping jet toward the axial direction and a secondary flow which transports fluid toward the inner curvature region. The asymmetry in this transport leads to the dominance of one rotating component over the other, which is progressively dissipated on the walls while moving downstream (see Fig. 7c). The surviving vortex transports in an overall circular motion the downstream propagating fluid, as shown by the elongated vortex filaments observable in Fig. 10. The strong curvature at the end of the aortic arch leads to a localized adverse pressure gradient, which drives the flow separation at the inner portion of the arch, in analogy with observations in the case of elbow tubes [82]. The recirculating flow also presents a rotating component, which propagates downstream with time. The strong deceleration during diastole destabilizes the flow (Fig. 11). However, the progressive dissipation during diastole shows the re-emergence of an overall circulatory motion in the aorta.

3.3 Enstrophy and kinetic energy evolution during the cardiac cycle

The considerations of the previous section are quantified by analyzing the kinetic energy E and the enstrophy $\mathcal {E}$ (rescaled with the volume of the considered vessel), which respectively read:

$$\begin{aligned} E=\frac{\int _\Omega \frac{1}{2}\mid \varvec{u}\mid ^2d\Omega }{\int _\Omega d\Omega }, \quad \mathcal {E}=\frac{\int _\Omega \mid \varvec{\omega }\mid ^2 d\Omega }{\int _\Omega d \Omega }, \end{aligned}$$

(4)

where $\omega$ denotes the vorticity and $\Omega$ the whole domain. While the former gives a quantitative indication of the energy and its time evolution, the latter provides an estimate of the recirculating flow in the aorta. Figure 12 shows these quantities as a function of time. In both cases, the systolic ejection generates an initial abrupt increase that is followed by a slow decay. The prosthetic case (orange lines) reaches slightly larger values of the kinetic energy. However, a stronger decay is also observed, during diastole. The minimum value reached (right before the beginning of the systole) is significantly smaller than the value observed in the presurgical case. The enstrophy presents a similar behavior with time. Slightly larger values of the enstrophy are observed in the prosthetic case during systole and the initial stage of diastole. For $t>0.5$, the enstrophy associated with the prosthetic case decreases more than the one associated with the presurgical case.

Fig. 12

Kinetic energy E (a) and enstrophy $\mathcal {E}$ (b), rescaled with the volume of the fluid domain, as functions of time, for the presurgical (blue lines) and prosthetic (orange lines) cases (color figure online)

The increase of kinetic energy in the prosthetic case is correlated to the better sweep of the inlet jet on the aortic walls observed in the initial dynamics. The faster diastole decay can instead be related to the stronger confinement and increased rigidity of the ascending aorta which, once the dominant effect of the inlet jet is damped, leads to an increase of the stresses acting on the fluid and thus to an increase of the energy dissipation. As a consequence, also the rotating component of the flow decays faster than in the presurgical case, even though during late systole it presents slightly larger values, due to the decreased lumen of the vessel.

In summary, a prosthetic replacement in a dilated ascending aorta inevitably introduces (i) a geometrical and (ii) a rigidity constraint. The geometrical constraint initially induces a better sweep in the ascending aorta, compared to the presurgical case, which induces a slightly larger peak in the kinetic energy and an increased flow at the outlets. However, associated with it, larger pressures are attained inside the vessel, due to the increased confinement of the inlet jet. The increased velocity also leads to the presence of a larger flow recirculation downstream of the aortic arch. These differences also induce a different propagation of the pulse wave inside the aorta and lead to a faster decay of the rotational component of the flow and of the kinetic energy, in the prosthetic case, indicating that the prosthesis induces an earlier and more effective regularization of the flow during late systole. These differences in the flow features change the picture of shear stresses acting on the vessel walls.

Fig. 13

Color maps of the time-averaged wall shear stress (TAWSS), non-dimensionalized by $\rho U^2$, for the a presurgical and b prosthetic cases. c Maximum value of the WSS as a function of time, for the presurgical (blue) and prosthetic (orange) cases (color figure online)

3.4 Shear stresses and near-wall flow

The healthy and pathological nature of the aortic walls is deeply linked to the shear stresses acting on the vessel walls [33]:

$$\begin{aligned} \varvec{\tau }= \varvec{\sigma }_f \varvec{n} - \left( \left( \varvec{\sigma }_f \varvec{n}\right) \cdot \varvec{n}\right) \varvec{n}. \end{aligned}$$

(5)

As a matter of fact, shear stresses can be correlated to the near-wall processes. Endothelial cells are essential in ensuring vessel homeostasis in response to wall stresses and/or accumulation of biochemicals. These cells are sensitive to forces and mass transport of chemical species and are actively involved through release of substances in a plethora of functions, e.g. anti-coagulation and anti-atherogenesis, modulation of the immune response, vascular tone [83, 84]. Several pathologies, such as atherosclerosis, are induced by endothelial remodeling, which in turn is associated to the history of shear stresses acting on the same regions at each heartbeat [83]. Any alteration in the shear-stress spatiotemporal pattern has potentially negative effects on the vessel health: regions of low shear stresses with large orientation variations (e.g. recirculation regions) induce inflammatory response and disorganization of the endothelial cells, with several consequences such as aneurysm growth; similar effects have been inferred when large gradients of shear stresses are present [85]. Besides, wall shear stresses are related to the near-wall velocity field (and thus to the mass transport) since $\varvec{u}=Re\varvec{\tau }\delta n+\mathcal {O}(\delta n^2)$, where $\delta n$ is the (small) distance normal to the wall. In the context of our study, the main question concerns the emergence of regions where the alteration of shear-stress pattern may promote the disease propagation after the prosthetic replacement.

Fig. 14

Color maps of the Oscillatory Shear Index (OSI), for the a presurgical and b prosthetic cases (color figure online)

The near-wall flow behavior can be inferred by considering indices such as time-averaged wall shear stresses, or more refined topological analyses based on manifold theory [86, 87]. We begin by introducing the average of the wall shear stresses in one period (TAWSS) and the Oscillatory Shear Index (OSI):

$$\begin{aligned} \hbox {TAWSS}=\frac{1}{T}\int _0^T \mid \varvec{\tau } \mid dt, \quad \hbox {OSI}=\frac{1}{2}\left( 1-\frac{\mid \int _0^T\varvec{\tau }dt\mid }{\int _0^T\mid \varvec{\tau }\mid dt}\right) , \end{aligned}$$

(6)

where T is the heartbeat period. While the former represents the time-average over a heartbeat, the latter is an indicator of the oscillatory behavior of the wall shear stress, and can assume values ranging from 0 (no variations in the WSS vector direction) to 0.5 (zero average of the WSS vector). Figure 13 shows the color maps of the TAWSS in the pre- and post-surgical aortas. In both cases, largest values are attained in the external part of the ascending aorta, although a small region of low stress is localized where the transvalvular jet impacts the wall. Moreover, large values are observed also in the epi-aortic branches. The distribution of shear stresses in the ascending aorta is reminiscent of the large velocity region induced by the jet-wall interaction (Fig. 5). Intermediate values are localized at the inner region of the aortic arch and in the external region of the descending aorta. However, the highest TAWSS ($\hbox {TAWSS}=6.3\times 10^{-3}$ for the dilated case and $\hbox {TAWSS}=7.3\times 10^{-3}$ for the prosthetic one) are located in the ascending aorta. We observe the formation of regions of low shear stresses, compared to the presurgical case, in a region of the aortic arch right downstream of the prosthesis, and right after the epi-aortic branches. In the external curvature region just downstream of the aortic arch, larger values of shear stresses are observed in the prosthetic case, together with a larger region of low shear in the internal part. These differences are related to the larger separated flow localized in this region, for the prosthetic case.

Figure 14 shows the oscillatory shear index. Large values (OSI $\approx 0.5$) are observed in the jet impact region, in the external curvature region of the aortic arch, just distally of the epi-aortic branches, and in the inner curvature region of the descending aorta. These regions roughly correspond to the ones characterized by low TAWSS. Conversely, the external curvature region, where the inlet jet sweeps, is characterized by very low values of OSI, i.e. the flow is predominantly oriented along one direction.

Fig. 15

Color maps of $\nabla \cdot \bar{\varvec{\tau }}_u$, overposed to a visualization through Line Integral Convolution technique of $\bar{\tau }_u$, for the a presurgical and b prosthetic cases (color figure online)

Further detail on the near-wall transport can be inferred by studying WSS coherent structures through manifold theory [86,87,88,89,90]. Relevant informations are obtained from the divergence of the normalized shear stress vector $\varvec{\tau }_u=\varvec{\tau }/\mid \varvec{\tau }\mid$. Regions with positive/negative values of divergence of the average value in one period $\bar{\varvec{\tau }}_u$ depict repelling/attracting manifolds, which are associated with regions of drop/accumulation of transported biochemicals at the near-wall [90]. Figure 15 presents the colormaps of $\bar{\varvec{\tau }}_u$, in the presurgical and prosthetic cases. In both cases, we note the presence of a repelling (red) localized region where the jet impacts on the wall, whereas an attracting manifold (blue) develops around this region clearly delimiting the region involved in the transvalvular jet impingement. The extent of this region is not observed to change after the implant. Irrespective of the considered case, multiple intersecting attracting and repelling manifolds are observed i) at the level of the brachiocefalic trunk (BCT), ii) downstream of the subclavian artery (LSA), iii) on the external curvature region of the aortic arch (see view from above) downstream of the epi-aortic branches, and iv) in the internal curvature region of the descending aorta, where a recirculating flow is present. Interestingly, the overall pattern of the repelling and attractive lines is quite similar, in the two cases, whereas their intensity is always increased after the surgery. In these regions, we observe the emergence of more intricate structures absent in the dilated case. Also, attracting and repelling manifolds are localized at the juncture between prosthesis and aortic arch, with several intersecting structures absent in the dilated case. A complete description of the near-wall transport requires also describing the time variation of $\nabla \cdot \varvec{\tau }_u$ during one heartbeat. To this aim, we report two instants in Fig. 16a, together with the standard deviation of $\nabla \cdot \varvec{\tau }_u$ over one period (i.e. the so-called Topological Shear Variation Index, TVSI), which gives a measure of the contraction/expansion variability (Fig. 16b, c). A large variability has been correlated to tissue disorganization and potential injury of the vessel walls [90]. The prosthetic case presents larger values of TVSI, compared to the presurgical one, in the same regions where the largest contraction/expansion values were observed.

Fig. 16

a Colormap of $\nabla \cdot {\varvec{\tau }}_u$ for two instants, in the presurgical case. b, c Colormaps of the TVSI for the b presurgical and c prosthetic case (color figure online)

The analysis of both classical indices and manifold theory converges indicating the differences induced by the prosthetic replacement and their clinical implications. The presence of regions (i-iv) with low shear stresses associated with orientation variations of the WSS, as well as regions with large gradients of WSS, is correlated to intersecting attracting and repelling manifolds of large variability, confirming that these are zones of disordered flows which, in turn, may be correlated to an increased probability of aneurysm growth [90].

3.5 On the compliance of the aortic vessels

To evaluate the effect of the compliance of the aortic walls, Fig. 17a presents the deformed aortic walls, for the post- (left) and pre-surgical (right) cases. Non-surprisingly, in the region where the prosthesis is localized, displacements are very small. Downstream of the prosthesis, displacements increase, and a “balloon-like” effect of the aortic vessel is observed. Panels (c, d) show the relative variation of the area with time, for different sections sketched in panel (b). All sections present the same qualitative variation, characterized by a plateau of the maximum value of area, approximately for $0.1<t<0.4$. In the presurgical case, area variations are similar and of the order of 15%, with slightly larger values attained in the ascending aorta. The presence of the prosthesis strongly modifies this picture. The two sections in the ascending aorta barely change (at most 5% of area variation), while deformations increase downstream of the prosthesis, suggesting that the presence of a prosthesis not only modifies the flow features and the stresses acting on the wall, but also the deformations of the aortic walls. These deformations, although obtained in a simplified framework where the aortic walls are modeled as an isotropic material, give an indication of the regions which are more subject to large solicitations. In this case, the large curvature region downstream of the aortic arch presents stronger flow separations, larger stresses and deformations, compared to the presurgical case.

Fig. 17

a Deformed aortic walls according to the displacement field. c, d Area, rescaled with its value at the beginning of the cardiac cycle, as a function of time, for the sections reported in panel b, presurgical (c) and prosthetic (d) cases

The considered aortic geometry and parameters present some peculiarities, compared to a healthy aorta, which are worth mentioning here. First, the aortic valve jet reaches a velocity of $\approx 3.5$ m/s. As a consequence, the jet propagation is more intense than in a healthy case. Also, the dilation of the ascending aorta induces a more inclined impact of the jet compared to a healthy case (see e.g. [51]). In the considered prosthetic case, the stenotic jet impacts on the wall with a large angle, although it presents a better sweep compared to the dilated case. In the dilated case, the helical flow, as well as the intensity of the vortex rings, increases, because of the delayed impact with the vessel walls.

4 Conclusion and perspectives

We investigated the flow modifications induced by an idealized prosthetic replacement in a model of a dilated thoracic aorta. We focused on the primary modifications induced by a variation of the geometry and mechanical properties of the ascending aorta, in a simplified framework. We described the persistent flow features both in the dilated and the prosthetic case. The early and peak systole dynamics are dominated by the development of the inlet jet and its impact on the aortic walls. Associated with the jet-wall interaction, the jet sweeps toward the aortic arch, while the flow propagation generates secondary flows of recirculating nature. The superposition of these two flows leads to a progressively more intense helical flow that propagates in the aortic arch. The vortex ring associated with the development of the inlet jet becomes unstable while it is advected downstream through the aortic arch. The helical flow contributes to the breakdown of the resulting vortex tubes into smaller structures. During late systole, helical flow becomes important and, during the diastole, the flow is dominated by the swirling constantly sweeping the aortic walls. A persistent flow separation is observed just downstream of the aortic arch because of the sudden bending of the vessel axis. The prosthetic replacement causes the jet to be more aligned with the axial direction, towards the arch. This results in larger peak flow-rates and increased peak pressures at the outlets. Additionally, the decreased lumen and increased rigidity of the prosthesis lead to a higher and faster decay of the kinetic energy and of the enstrophy (associated with the recirculating flow) during the diastole. This behavior is in agreement with the smaller structures found just after the systolic peak in the prosthetic case compared to the dilated one (Fig. 6) and with the increased stresses at the vessel walls, in particular in the ascending aorta. Figure 9 shows a region of relative hemostasis in the aortic bulb during the systole. However, this region is more extended in the prosthetic case, possibly leading to a higher thromboembolism potential. Also, we observed that the flow separation occurring just downstream of the most curved section of the aortic arch, develops earlier and is more extended in the prosthetic case (Fig. 10). The phenomenon is in agreement with the higher energy dissipation and suggests the local alteration of wall-shear-stresses pathologies [88,89,90]. In summary, we identified several regions of disordered flow highlighted by the considered near-wall indices, which may be more prone to a propagation of the disease toward the aortic arch after the surgical procedure: i) at the level of the anonymous artery, ii) downstream of the subclavian artery, iii) on the external curvature region of the aortic arch (see view from above) downstream of the epi-aortic branches, and iv) in the internal curvature region of the descending aorta, where the flow separates. These regions may be of particular interest in a hypothetical follow up of this idealized surgical procedure. These considerations are correlated to the observed vessel deformations. In the presurgical case, the largest relative deformation is observed in the proximal section and decreases moving downstreams (Fig. 17c). After the implantation, the vessel can deform only distally to the prosthesis and the relative deformations are significantly increased compared to the presurgery irrespective of the considered section (yellow and purple lines in Fig. 17d). This result is coherent with an increased probability of the progression of the vessel dilation distal to the prosthesis after the implantation [43].

This work aims at giving an insight into the flow modifications induced by a prosthetic replacement in the thoracic aorta. Despite the simplified framework, results showed how dominant flow features are modified by the prosthetic replacement, even without performing the replacement of the aortic valve, which inevitably modifies the inlet jet. The present results are limited by the employed model (e.g. the deformability of the mesh and the constitutive model for the aortic walls) and boundary conditions (the idealized inlet jet). A more refined modeling of the aortic valve opening and closing requires Fluid–Structure-Interaction models, in particular when interested in the flow field in the near vicinity of the Valsalva sinuses (see e.g. [69, 91]). Nevertheless, results captured some relevant flow and near-wall transport features which would be persistent also employing more detailed models. These results may be improved and expanded by employing more refined models for the deformations and by including also the aortic valve, and need to be extended also to different geometries and inlet/outlet conditions.

Appendix A: Grid independence analysis

In this section, we report the mesh detail as well as the sensitivity of the results to the employed mesh. Figure 18 shows the detail of the employed mesh, labelled here Mesh A, for (a) the presurgical and (b) the prosthetic case. At the lateral wall boundaries, we employ three boundary layers with increasing ratio of 1.25. Both meshes present a local refinement at the inlet and outlets of half the global characteristic size. Besides, the mesh associated with the prosthetic case presents a local refinement of half the global characteristic size, in the vicinity of the Young modulus discontinuity.

The grid independence study is performed in the prosthetic case. Three meshes are obtained by progressively and uniformly decreasing the characteristic element size, whose characteristic dimensions are reported in Table 2. We initially compare the flow rate and average pressure waveforms at the inlet and outlets (Fig. 19). Results show a good agreement between the waveforms obtained by different meshes. Therefore, spatially integrated quantities are weakly impacted by the mesh refinement. We then investigate the local flow patterns dependence on the considered mesh. Figure 20 shows the average and standard deviation of the velocity magnitude, sampled on two lines that lie on a horizontal section in the ascending aorta. The velocity profiles agree with each other. In particular, the profiles of Mesh B better agree with those of Mesh A, compared to the ones of Mesh C (the coarsest mesh). These local differences are at most 3% of the peak velocity, between Mesh A and Mesh B. In a similar fashion, Fig. 21 shows the velocity magnitude in a line belonging to one section in the descending aorta. The profiles are similar, and local differences are at most 1% of the peak velocity, between Mesh A and Mesh B. Therefore, the results weakly depend in terms of spatially-averaged quantities, and local quantities present variations of few percents compared to coarser meshes. We thus employed mesh A for all calculations reported in this work. A mesh with the same characteristic size and local refinements is employed for the presurgical case.

Fig. 18

Numerical grids employed in this work, for the a presurgical and b prosthetic cases

Table 2 Overview of the characteristic dimensions of the three meshes employed in the grid independence study

Fig. 19

Comparison of a flow rate and b pressure waveforms at the inlet and each outlet (according to panel c), for the three considered meshes of the prosthetic case, i.e. Mesh A (solid lines), Mesh B (dashed lines), Mesh C (dot-dashed lines)

Fig. 20

Grid independence study. Distribution of the a average (on the top) and of the b standard deviation (on the bottom) of the velocity magnitude in one period, plotted across two lines on a two-dimensional section of the aorta, reported in panel c. Colours denote Mesh A (blue), Mesh B (orange), Mesh C (yellow) (color figure online)

Fig. 21

Grid independence study. Distribution of the a average and of the b standard deviation of the velocity magnitude in one period, plotted across one line on a two-dimensional section of the aorta, reported in panel c. Colours denote Mesh A (blue), Mesh B (orange), Mesh C (yellow) (color figure online)