1 Introduction

Brazing is a common choice for joining and repairing parts made of nickel-based superalloys. To achieve a joint suitable for high temperatures the brazing metal is based on nickel with melting point lowering elements like, e.g., silicon or boron. During brazing the melting point lowering elements diffuse fast into the base material causing the brazing metal to solidify isothermally. This process is known as transient liquid phase bonding or diffusion brazing [1, 2] and aims for a smooth transition of mechanical properties between the base metal and the brazing layer. However, isothermal solidification needs sufficient time to be completed to prevent the formation of brittle intermetallic phases. This poses strict requirements to the parameters of the brazing like duration and temperature which are hard to meet in reality especially for wide gaps between the joining partners [3, 4].

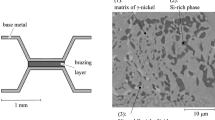
An example for the formation of detrimental intermetallic phases is the abradable labyrinth sealing systems of a turbomachinery. Such sealing systems are commonly used to minimize leakage flows in the secondary air system of a turbomachinery. They are composed of a rotor that rubs into a static liner structure. A common liner is a honeycomb structure which is brazed onto a carrying plate. During brazing the braze metal can rise up to the later rubbing surface and forms a layered composite with the base metal as schematically shown on the left side of Fig. 1. A typical microstructure of the brazing layer is shown on the right side of Fig. 1. The identified phases are \(\gamma \)-nickel solid solution (1), a silicon-rich phase that is potentially NiSi (2) and several silicides that are rich of nickel and chromium (3). Apart from the ductile \(\gamma \)-nickel solid solution, the identified phases exhibit both high hardness and brittle behavior [5, 6].

Fig. 1
figure 1

Left: schematic top view of a honeycomb double-foiled segment with capillary braze, right: exemplary microstructure (contrast of back-scattered electrons) of the brazing layer in a honeycomb double-foiled segment as a composition of brittle and ductile phases, figure taken from [7]

Full size image

Further examples of brittle–ductile microstructures have been studied by Li and Schulson [8]. They experimentally studied fracture mechanisms in brittle nickel silicides which were toughened by the addition of a ductile phase of \(\gamma \)-nickel solid solution. The potential of improving the fracture toughness of high-temperature-resistant alloys as well as the existence of brittle phases in an abradable liner structure motivates an assessment of microcracking as a critical damage mechanism that is controlled by the heterogeneous microstructure. As the production of samples with a controlled variation of microstructural parameters is cumbersome, in this work, a computational model capable of predicting mechanical damage in various microstructures is proposed instead. Preliminary crystal elastic–plastic micromechanical simulations indicate the initiation of damage inside of the brittle phases that potentially induces the failure of the whole material. Only for dominantly ductile microstructures one can expect a shift from brittle to ductile failure [7].

So far, to the best of our knowledge, no explicit modeling of the evolution of microdamage in brazed nickel-based alloys has been done. The modeling of cracks as discontinuities can be divided into discrete and smeared/diffused methods. Among discrete methods there is the extended finite element method (XFEM) [9,10,11,12], the element-free Galerkin method [13, 14], the discontinuous Petrov-Galerkin method [15], the extended isogeometric analysis (XIGA) [16, 17] and the cracking particle method [18, 19]. Major challenges in discrete methods are the necessary remeshing to reduce mesh dependency of crack paths and the need of enriched shape functions near crack tips (see, e.g., [20]).

The diffused phase field approach for damage in comparison is a straightforward and universal method that is based on a multi-field solution in which the deformation and damage field variables are coupled in a bidirectional manner [21]. The phase field approach for damage is especially promising for modeling damage on the microscale. Complex crack patterns due to heterogeneous microstress and strain fields as well as multiple crack initiation sites and coalescence of cracks can be considered without any restrictions. A phase field approach can also depict partial damage in a microstructure which potentially leads to a stress redistribution and should therefore be incorporated in the microdamage simulation. Furthermore, strict discontinuities as modeled in discrete approaches are not necessarily the optimal description of cracks unless one is looking at an ideal crack based on the debonding of atomic layers. On scales larger than the atomic scale one has to deal with a composition of several cracks and pores forming on a smaller scale in the process zone of the crack that is to be modeled. The phase field approach for damage as a diffused method is able to account for such a damage process zone in the vicinity of a crack in a homogenized manner.

Li and Zhou [22] used an embedded cell approach to calculate a microstructure-based fracture toughness by calculating the J-Integral around a microstructurally resolved crack tip. This is a reasonable approach if the heterogeneities of the microstructure are large and therefore on the same scale as the macroscopic crack. In this contribution the focus lies on the case where the heterogeneities of the microstructure are much smaller than the macroscopic crack to facilitate a clear separation of scales. This case was also studied by Chakraborty et al. [23, 24] for fracture of nuclear grade materials by means of phase field damage simulations. They focused on the influence of multi-axial loading conditions on the fracture behavior of microstructures which were porous on different scales. In our contribution the promising phase field approach for damage will be transferred to polycrystalline and dual-phase microstructures.

The goal of the present work is threefold. First, the applicability of a phase field approach for microdamage in a brittle single-phase polycrystalline microstructure will be assessed together with a comparison of two common formulations of the surface density functional. Second, the feasibility of calculating effective values for the critical strain energy density and the critical energy release rate based on averaging over a volume element (VE) representing the microstructure will be studied. Third, we aim at a better understanding of the role of microstructural parameters in the initiation and propagation of microcracks in dual-phase microstructures.

2 Constitutive modeling of the brittle and ductile phases

In this section the constitutive models used to describe the material behavior of the individual phases are presented. All possible phases are represented by one brittle and one ductile phase. In both phases an anisotropic elastic behavior with cubic crystal symmetry is considered. Plastic deformation in the ductile phase is depicted along the crystallographic slip systems. Damage is restricted to the brittle phase as the focus lies on the risk of quasi-brittle failure behavior as a critical damage mechanism in brazed joints of nickel-based alloys. The employed constitutive laws are implemented in the simulation toolkit DAMASK [25] provided by the MPIE in Düsseldorf.

2.1 Phenomenological crystal elasto-plasticity for the individual grains

For the mechanical behavior of the ductile phase of nickel solid solution (phase 1 in Fig. 1), a phenomenological elastic–viscoplastic material law is used which considers the face-centered cubic (fcc) crystal structure of an individual grain. The elastic deformation \(\textbf{F}_{\textrm{e}}\) depicted by the Green-Lagrange strain tensor \(\textbf{E}_{\textrm{e}} = 1/2 (\textbf{F}_{\textrm{e}}^{\textrm{T}}\textbf{F}_{\textrm{e}}-\textbf{I})\) causes a stress following the generalized Hooke’s law. Here, \(\textbf{I}\) is the second rank identity tensor. In the employed framework the second Piola-Kirchhoff stress tensor in the plastic configuration \(\textbf{S}_{\textrm{p}}\) is calculated as

$$\begin{aligned} \textbf{S}_{\textrm{p}} = \mathbb {C} : \textbf{E}_{\textrm{e}}. \end{aligned}$$
(1)

The 4th-order elastic stiffness tensor \(\mathbb {C}\) in Eq. (1) inherits the symmetries of the cubic crystal lattice for which three independent elastic constants are required (\(C_{\textrm{11}}\), \(C_{\textrm{12}}\) and \(C_{\textrm{44}}\)) [26]. A multiplicative decomposition divides the total deformation gradient \(\textbf{F}\) into a lattice preserving plastic deformation step followed by a lattice distorting elastic deformation step, \(\textbf{F} = \textbf{F}_{\textrm{e}}\textbf{F}_{\textrm{p}}\). The plastic velocity gradient \(\textbf{L}_{\textrm{p}}\) is needed to calculate the rate of the plastic deformation gradient as \(\dot{\textbf{F}}_{\textrm{p}} = \textbf{L}_{\textrm{p}}\textbf{F}_{\textrm{p}}\). The plastic deformation is assumed to follow the slip systems of the underlying crystal lattice. For a fcc crystal lattice, a flow rule can be formulated as

$$\begin{aligned} \textbf{L}_{\textrm{p}} = \sum ^{12}_{\alpha =1} \dot{\gamma }^{\alpha } \textbf{m}^{\alpha } \otimes \textbf{n}^{\alpha }, \end{aligned}$$
(2)

which is composed of the slip direction \(\textbf{m}^{\alpha }\) and the normal of the slip plane \(\textbf{n}^{\alpha }\) defining the slip system \(\alpha \) [25]. According to the phenomenological power law of Rice, Hutchinson and Peirce [27,28,29], the shear rate of plastic deformation \(\dot{\gamma }^{\alpha }\) in the slip system \(\alpha \) can be calculated as

$$\begin{aligned} \dot{\gamma }^{\alpha } = \dot{\gamma }^{\alpha }_{\textrm{0}} \left| \frac{\tau ^{\alpha }}{\tau ^{\alpha }_{\textrm{c}}}\right| ^n \, \textrm{sgn}\left( \tau ^{\alpha }\right) . \end{aligned}$$
(3)

Here, the Schmid shear stress \(\tau ^{\alpha } = \mathbf {S_{\textrm{p}}}: \textbf{m}^{\alpha } \otimes \textbf{n}^{\alpha }\) acts as a driving force for dislocation movement and is compared to the material-dependent critical resolved shear stress \(\tau ^{\alpha }_{\textrm{c}}\) in the slip system \(\alpha \). The reference shear rate \(\dot{\gamma }^{\alpha }_{\textrm{0}}\) serves as a proportional factor in the corresponding slip system. The stress exponent n controls the dependency of the strain rate and the shear stress. Decreasing values of n account for increasingly viscoplastic material behavior. For strain-hardening materials, the critical resolved shear stress increases during plastic deformation according to

$$\begin{aligned} \dot{\tau }^{\alpha }_{\textrm{c}} = \sum ^{12}_{\alpha '=1} h_{\alpha \alpha '} \left| \dot{\gamma }^{\alpha '}\right| . \end{aligned}$$
(4)

The hardening matrix \(h_{\alpha \alpha '}\) represents the interaction of dislocations in the same slip system (\(\alpha ' = \alpha \)) as well as between distinct slip systems (\(\alpha ' \ne \alpha \)), thereby accounting for active and latent hardening. It can be described as

$$\begin{aligned} h_{\alpha \alpha '} = q_{\alpha \alpha '} h_{\textrm{0}} \left| 1-\frac{\tau ^{\alpha '}_{\textrm{c}}}{\tau _{\mathrm {\infty }}}\right| ^{a} \textrm{sgn}\left( 1-\frac{\tau ^{\alpha '}_{\textrm{c}}}{\tau _{\mathrm {\infty }}}\right) . \end{aligned}$$
(5)

The resistance against dislocation slip is limited by a saturation value \(\tau _{\mathrm {\infty }}\) which is assumed to be equal for all slip systems. \(h_{\textrm{0}}\) and a are used to fit the relation between the critical resolved shear stress and the corresponding element of the hardening matrix \(h_{\alpha \alpha '}\). In all 12 slip systems the hardening parameters are assumed to be the same for the case of the fcc crystal structure [25]. The matrix \(q_{\alpha \alpha '}\) assigns a factor of 1.0 for coplanar slip systems and 1.4 for systems with distinct slip planes.

Fischer et al. [30] identified the corresponding material parameters for Haynes 214 by comparing experimental tensile tests with virtual tensile tests on a polycrystalline representative volume element (RVE) at different strain rates. Jamaloei et al. [31] found Ni\(_{\textrm{3}}\)Si precipitates in the ductile phase of a brazed nickel-based alloy. Due to an identical crystal structure and a similar size of the Ni\(_{\textrm{3}}\)Si and the \(\gamma '\) precipitates in Haynes 214 the already identified material parameters of Haynes 214 should be suitable for the ductile phase found in a brazed nickel-based alloy. The crystal elastic constants for the individual grains of the ductile phase were chosen so that they match the effective Young’s modulus E and Poisson’s ratio \(\nu \) of a quasi-isotropic polycrystalline tensile sample while retaining a single-crystal anisotropy factor typical for a nickel-based alloy (Zener ratio of \(A = 2.4\)) [32].

The hard phases in the microstructure (phases 2 and 3 in Fig. 1) are regarded as purely brittle. They are collectively given a linear crystal elastic material behavior according to Eq. (1) that matches the elastic properties of \(\textrm{Ni}_{\textrm{3}}\textrm{Si}\) as a representative of the brittle phases. The crystal elastic constants of \(\textrm{Ni}_{\textrm{3}}\textrm{Si}\) are taken from first principle calculations done by [33]. When doing so, the brittle phase has a moderate single-crystal anisotropy factor with a Zener ratio of \(A = 1.6\). Any minor amount of plastic deformation in the brittle phase is neglected as the expensive determination of the material parameters of crystal plasticity would not be reasonable in this case. Additionally, the damage in the brittle phase is explicitly modeled which already accounts for crack blunting mechanisms (cf. Sect. 2.2). The constitutive parameters used for the crystal elastic behavior of the brittle phase as well as for the crystal elastic–plastic behavior of the ductile phase are listed in table 1.

Table 1 Parameters of the crystal elastic–plastic constitutive laws used in the individual grains on the microscale for both phases [30, 32, 33]
Full size table

2.2 Modeling of damage in the brittle phase

For the continuous process of microdamage in the brittle phase a phase field-based approach for brittle fracture based on that proposed by Miehe et al. [21] is employed. It is a variational formulation of damage in which the sum of the stored elastic energy and the surface energy of cracks in a body build up the total energy functional. The principal variables are the deformation expressed as the elastic Green-Lagrange strain tensor \(\textbf{E}_{\textrm{e}}\) and the phase field expressed by the order variable \(\varphi \). The order variable is defined as the complement of a classical damage variable d and describes a decrease of order at a point in the material during an increase of damage

$$\begin{aligned} \varphi = 1 - d \,\,\, \textrm{with} \,\,\, 0 \le \varphi \le 1, \, \dot{\varphi } \le 0. \end{aligned}$$
(6)

A regularization of the crack topology based on an exponential function is employed to avoid discontinuities in the displacement field which is visualized in one dimension in Fig. 2. The regularized crack topology consists of a core zone of complete damage where the damage variable d is equal to one and a process zone of partial damage which surrounds the core zone.

Fig. 2
figure 2

Spatial distribution of the damage variable d(x) for a sharp crack (left) and a regularized crack topology (right)

Full size image

In terms of the damage variable d, the regularized crack topology in one dimension can be written as

$$\begin{aligned} d\left( x\right) = \textrm{exp}\left( -\frac{\left| x\right| }{l_{\textrm{c}}} \right) . \end{aligned}$$
(7)

Here, the length scale parameter \(l_{\textrm{c}}\) controls the size of the process zone of partial damage surrounding the core zone. An ideally sharp crack would be found in the center of the core zone. Exponential approach (7) solves the differential equation

$$\begin{aligned} d\left( x\right) - l^2_{\textrm{c}}d''\left( x\right) = 0. \end{aligned}$$
(8)

The weak form of this differential equation is obtained by multiplication with a test function \(\tilde{d}\) and partial integration

$$\begin{aligned} \int _{-\infty }^{\infty } \left( \tilde{d}d + l^2_{\textrm{c}} \tilde{d}'d' \right) \textrm{d}x = 0. \end{aligned}$$
(9)

From the weak form, one can derive the functional

$$\begin{aligned} I\left( d\right) = \int _{\Omega } \left( d^2 + l^2_{\textrm{c}} d'^2 \right) \textrm{d}V. \end{aligned}$$
(10)

If one inserts regularized crack topology (7) into this functional and uses \(\textrm{d}V = \Gamma _{\mathrm {l_{\textrm{c}}}} \textrm{d}x\), the value of the regularized crack surface \(\Gamma _{\mathrm {l_{\textrm{c}}}}\) is

$$\begin{aligned} \Gamma _{\mathrm {l_{\textrm{c}}}} = \frac{1}{2l_{\textrm{c}}} I\left( d= e^{-\left| x\right| /l_{\textrm{c}}}\right) . \end{aligned}$$
(11)

The regularized crack surface \(\Gamma _{\mathrm {l_{\textrm{c}}}}\) converges toward the surface area \(\Gamma \) of the ideally sharp crack for \(l_{\textrm{c}} \rightarrow 0\). Based on (10) and (11), a crack surface density \(a_{\textrm{surface}}\) can be calculated. In three dimensions, it is composed of a non-local part containing the spatial gradient of the order variable and a local part containing the order variable itself

$$\begin{aligned} a_{\textrm{surface}} = \frac{1}{2} l_{\textrm{c}} \left| \nabla \varphi \right| ^2 + \frac{1}{2l_{\textrm{c}}} \left( 1-\varphi \right) ^2. \end{aligned}$$
(12)

Two different formulations of the crack surface density functional are considered. The first one is original formulation (12) with a quadratic local part. The second formulation differs from the original one by a modification of the local part from a quadratic to a linear function in order to achieve a compact support of the crack as pointed out in [21, 34]

$$\begin{aligned} a_{\textrm{surface}} = \frac{1}{2} l_{\textrm{c}} \left| \nabla \varphi \right| ^2 + \frac{1}{l_{\textrm{c}}} \left( 1-\varphi \right) . \end{aligned}$$
(13)

This compactness of the crack is related to the amount of neighboring material that takes part in the damage process and is further discussed in the results section. Despite its benefits in depicting a sharp crack, no consistent mathematical foundation for this modified formulation of the crack surface density functional is known to the authors.

In rate form, one obtains the principle of virtual power comprising the rate of stored elastic energy \(\dot{E}\) and the rate of dissipation D due to the growth of fracture surface and the external power P

$$\begin{aligned} \dot{E} + D - P = 0. \end{aligned}$$
(14)

Two contributions to the evolution of the stored elastic energy are distinguished that are associated with the change of the order variable and the change of the elastic deformation

$$\begin{aligned} \dot{E} = \int _{\Omega } \dot{W}_{\textrm{e}} \textrm{d}V = \int _{\Omega } \left( \left( \delta _{\varphi } W_{\textrm{e}}\right) \dot{\varphi } + \left( \delta _{\textbf{E}_{\textrm{e}}} W_{\textrm{e}}\right) \dot{\textbf{E}}_{\textrm{e}} \right) \textrm{d}V. \end{aligned}$$
(15)

The elastic energy stored in the body is degraded during damage. As the degradation function, a quadratic approach \(g(\varphi ) = \varphi ^2\) is chosen to account for a saturation of degradation as the state of complete damage is approached. For the degraded elastic energy density one obtains

$$\begin{aligned} W_{\textrm{e}} = \frac{1}{2} \varphi ^2 \, \textbf{S}_{\textrm{p}} :\textbf{E}_{\textrm{e}}. \end{aligned}$$
(16)

For the second term in the power balance one has to calculate the work that is dissipated during the growth of crack surface. The crack surface density \(a_{\textrm{surface}}\) can be calculated from the field of the order variable representing the regularized crack topology using (12) or (13). The dissipation is then calculated as the rate of the crack surface density multiplied by a material-dependent surface energy density \(g_{\textrm{c}}\) integrated over the whole domain of the body

$$\begin{aligned} D = g_{\textrm{c}} \int _{\Omega } \dot{a}_{\textrm{surface}} \textrm{d}V = \int _{\Omega } \dot{W}_{\textrm{surface}} \textrm{d}V = \int _{\Omega } \left( \delta _{\varphi } W_{\textrm{surface}}\right) \dot{\varphi } \, \textrm{d}V. \end{aligned}$$
(17)

Based on the principle of virtual power (14) one can derive the balance equations of the coupled problem. The balance equation for the elastic body can be written as

$$\begin{aligned} \textrm{Div}\left( \textbf{S}_{\textrm{p}} \right) + \textbf{b} = 0, \end{aligned}$$
(18)

where the stress is calculated from Hooke’s law in which the constitutive tensor \(\mathbb {C}\) is degraded by the above-introduced quadratic function \(g(\varphi ) = \varphi ^2\)

$$\begin{aligned} \textbf{S}_{\textrm{p}} = \delta _{\textbf{E}_{\textrm{e}}} W_{\textrm{e}} = \varphi ^2 \mathbb {C} :\textbf{E}_{\textrm{e}}. \end{aligned}$$
(19)

For the evolution of the order variable, one obtains in the standard formulation

$$\begin{aligned} \mu \left\langle \dot{\varphi } \right\rangle _+ = \left( 1-\varphi \right) \frac{g_{\textrm{c}}}{l_{\textrm{c}}} - \varphi \left( \mathbb {C} :\textbf{E}_{\textrm{e}} \right) :\textbf{E}_{\textrm{e}} + g_{\textrm{c}} l_{\textrm{c}} \Delta \varphi . \end{aligned}$$
(20)

If one uses the linear model with compact support instead, one gets

$$\begin{aligned} \mu \left\langle \dot{\varphi } \right\rangle _+ = \frac{g_{\textrm{c}}}{l_{\textrm{c}}} - \varphi \left( \mathbb {C} :\textbf{E}_{\textrm{e}} \right) :\textbf{E}_{\textrm{e}} + g_{\textrm{c}} l_{\textrm{c}} \Delta \varphi \end{aligned}$$
(21)

as an evolution equation for the order variable. The left-hand sides of Eqs. (20) and (21) are penalty terms that enforce a monotonous decrease of the order variable to depict an irreversible damage process. Any positive rate of \(\varphi \) will add artificial energy to the system. The sensitivity of this penalization is controlled by the numerical parameter \(\mu \). From (21), one can extract directly the local critical strain energy density \(W_{\textrm{c}}\) which defines the point of damage initiation as the ratio of the model parameters \(g_{\textrm{c}}\) and \(l_{\textrm{c}}\)

$$\begin{aligned} W_{\textrm{c}} = \frac{1}{2} \frac{g_{\textrm{c}}}{l_{\textrm{c}}}. \end{aligned}$$
(22)

For standard formulation (20), one cannot determine the local critical strain energy density a priori as the resistance against the accumulation of damage depends on the current state of the order variable. In other words, there is no purely elastic regime as damage will start as soon as the deformation begins. Therefore, one is restricted to an explicit phase field simulation of the specific damage field to determine the local critical strain energy density that leads to an unstable damage behavior of the material. Following Pham et al. [35], schematic stress–strain curves for a homogeneous, one-dimensional damage field for the quadratic and linear formulations of the surface energy density are shown in Fig. 3. At this point we look at the pointwise stress–strain behavior and do not consider possible localization of damage as will be discussed later for heterogeneous microstructures. The quadratic formulation shows no purely elastic regime. A stage of gradually increasing damage is followed by a softening regime with a smooth transition between both stages of deformation. The linear formulation shows a purely elastic regime that is followed by softening with an abrupt transition between the two stages of deformation. Mathematical consistency in the calculation of the crack surface area can only be shown in the standard formulation with a quadratic local part of surface energy density (12) but not for modified version (13). This should be kept in mind when comparing results of the standard and the modified version in Sect. 4.3.

Fig. 3
figure 3

Schematic pointwise stress–strain curves for a homogeneous damage field for the quadratic (left) and linear (right) formulation of the surface energy density

Full size image

3 Micromechanical simulation setup for calculation of fracture energy quantities

3.1 Geometry and boundary conditions

The field of the deformation gradient \(\textbf{F}\) and the order variable \(\varphi \) are concurrently coupled and solved in a staggered scheme using a spectral solver provided in the computational framework DAMASK [25]. The spectral solver is based on a fast Fourier transform which is restricted to a regular solution grid and periodic solutions but is significantly faster than a FEM-based solution scheme if one is interested in periodic fields like for example an RVE. For time integration a fixed point iteration (implicit Euler scheme) is used. The computational domain considered is a microstructural VE consisting of an artificially generated aggregate of convex grains. The generated geometry is periodic, which corresponds to the periodic solution field of the spectral solver. A modified Voronoï tessellation is employed in which the sphericity of the grains is iteratively increased to avoid small angles in the polyhedrons representing the grains. An example of an artificial polycrystalline microstructure is given in Fig. 4. The focus of this study lies on the effect of microstructural heterogeneity on the microdamage behavior. The heterogeneities of interest are the crystallographic mismatch between grains and the mechanical contrast between phases. Therefore, the morphology of the grains is not studied in further detail.

Fig. 4
figure 4

Two-dimensional artificial polycrystalline microstructure under uni-axial tensile loading in x-direction with periodicity of geometry in x- and y-directions

Full size image

A random crystallographic orientation is assigned to each grain as no texture was observed in the experiments used for calibration and validation. For the modeling of a dual-phase microstructure the polycrystalline grain structure is colored according to the desired volume fraction of the brittle and the ductile phases. Grain and phase boundaries are not explicitly resolved. They are implicitly considered by a jump in crystallographic orientation or phase specific constitutive behavior at the intersection of two grains or phases. Uni-axial tensile tests in the x-direction are performed to analyze the stress–strain response of the aggregate. A convergence study regarding the resolution of microcracks revealed that a resolution as high as 512 voxels in each direction is needed for reliable simulation results based on an two-dimensional RVE with 15 grains per edge. However, preliminary simulations showed that a model with enough microstructural heterogeneities and sufficiently resolved cracks is not yet computationally feasible in three dimensions. For this reason, the computational domain is reduced to two dimensions. This is a simplification which leads to the modeling of prismatic grains, neglecting three-dimensional pathways of the cracks. In Sect. 5.3 the limits of the two-dimensional approach will be discussed in more detail.

3.2 Calculation of effective energy quantities

Two energy quantities are of interest for which effective values are to be calculated based on an RVE. This means they should serve for the information transport of the material behavior from the microscale to the macroscale. Here, these quantities are the critical strain energy density and the critical energy release rate.

The critical strain energy density is a local criterion for damage initiation that can be defined on multiple scales. We define the component scale as the macroscale and the scale of the microstructural heterogeneities as the microscale, see Fig. 5.

Fig. 5
figure 5

Critical strain energy density \(W_{\textrm{c}}\) as a local damage criterion on multiple scales. Effective values for \(W^{\textrm{macro}}_{\textrm{c}}\) can be calculated as the volume average of the strain energy density on the microscale at critical state of the deformation. Due to different heterogeneities such as grains and phases the critical value for the strain energy on the microscale is in general higher than on the macroscale

Full size image

The critical strain energy density on the macroscale, \(W^{\textrm{macro}}_{\textrm{c}}\), is calculated as the volume average of the strain energy density in the RVE when a critical state of deformation is reached

$$\begin{aligned} W^{\textrm{macro}}_{\textrm{c}} = \left. \overline{W} \right| _{\textrm{crit}} = \frac{1}{V_{\textrm{RVE}}} \left. \int W^{\textrm{micro}} \textrm{d}V \right| _{\textrm{crit}}. \end{aligned}$$
(23)

Due to peaks of the stress and strain fields in a heterogeneous brittle microstructure the critical value for the strain energy density on the microscale \(W^{\textrm{micro}}_{\textrm{c}}\) will be in general higher than the macroscopic value. Only for a perfectly homogeneous microstructure they will be the same on both scales, hence

$$\begin{aligned} W^{\textrm{macro}}_{\textrm{c}} \le W^{\textrm{micro}}_{\textrm{c}}. \end{aligned}$$
(24)

As outlined in Fig. 6, scale coupling assumes that the edge length of the RVE, \(l_{\textrm{RVE}}\), gives approximately two times the dimension \(l^{\textrm{macro}}_{\textrm{c}}\) of the process zone accompanying a crack on the macroscale

$$\begin{aligned} l_{\textrm{RVE}} \approx 2l^{\textrm{macro}}_{\textrm{c}}. \end{aligned}$$
(25)

The factor of two stems from the definition of \(l_{\textrm{c}}\) as approximately half of the smeared crack width (see Fig. 2).

Furthermore, the dimension of the heterogeneities \(l_{\textrm{h}}\) needs to be small relative to the RVE and large relative to the dimension \(l^{\textrm{micro}}_{\textrm{c}}\) of the process zone of a microcrack (see Sect. 4 for the corresponding studies). The scale separation can be formulated as the inequality

$$\begin{aligned} l_{\textrm{component}}>> l_{\textrm{RVE}}>> l_{\textrm{h}}>> l^{\textrm{micro}}_{\textrm{c}}. \end{aligned}$$
(26)

For the calculation of the critical energy release rate, the local critical energy release rate \(g_{\textrm{c}}\) of the phase field damage framework is distinguished from the effective critical energy release rate \(G_{\textrm{c}}\) that can be measured for the whole specimen (globally) in fracture mechanical experiments, which then is calculated on the macroscale as

$$\begin{aligned} G^{\textrm{macro}}_{\textrm{c}} = \left. - \frac{\textrm{d}\Pi _{\textrm{sample}}}{\textrm{d}A_{\textrm{proj}}} \right| _{\textrm{crit}}, \end{aligned}$$
(27)

where \(\textrm{d}\Pi \) is the increment of the total potential as the balance of external \(\textrm{d} W_{\textrm{ext}}\) and internal work \(\textrm{d} W_{\textrm{int}}\) and \(\textrm{d}A_{\textrm{proj}}\) is the increment of the projected crack surface measured on the macroscale. Additionally, energy release rates on the macroscale and the microscale are distinguished as it is done for the critical strain energy density. The effective critical energy release rate \(G^{\textrm{micro}}_{\textrm{c}}\) in a VE representing the microstructure is calculated as

$$\begin{aligned} G^{\textrm{micro}}_{\textrm{c}} = \left. - \frac{\textrm{d}\Pi _{\textrm{RVE}}}{\textrm{d}A_{\textrm{micro}}} \right| _{\textrm{crit}}. \end{aligned}$$
(28)

Due to branching and deflection of cracks on the microscale the cumulative crack surface \(A_{\textrm{micro}}\) will be in general larger than the projected crack surface \(A_{\textrm{proj}}\) that can be measured on the macroscale. Only for a crack that is ideally sharp the increments in crack surface of the two scales are expected to be the same. If the volume element is representative not only for the microstructure but also for the process zone of a macroscopic crack, the increment in the total potential \(\textrm{d}\Pi \) should also be the same for both scales, hence

$$\begin{aligned} \textrm{d}A_{\textrm{micro}} \ge \textrm{d}A_{\textrm{proj}} \, \rightarrow \, G^{\textrm{micro}}_{\textrm{c}} \le G^{\textrm{macro}}_{\textrm{c}}. \end{aligned}$$
(29)

According to the results of Chakraborty et al. [23] the local and global value of the critical energy release rate for a SENT specimen are not the same but show similar values. It is assumed that the local critical energy release rate \(g^{\textrm{macro}}_{\textrm{c}}\) on the macroscale can be calculated as

$$\begin{aligned} g^{\textrm{macro}}_{\textrm{c}} = 2 W^{\textrm{macro}}_{\textrm{c}}l^{\textrm{macro}}_{\textrm{c}}. \end{aligned}$$
(30)

Based on this assumption and \(G^{\textrm{macro}}_{\textrm{c}} \approx g^{\textrm{macro}}_{\textrm{c}}\), inequality (29) serves to check the plausibility of the results. The energy release rates on different scales are visualized in Fig. 6.

Fig. 6
figure 6

Critical energy release rates on multiple scales. Global values for the energy release rate are given a capital letter G, while local values are given a small g. The difference between the geometries of a crack on the macroscale and cracks on the microscale is highlighted

Full size image

In case of a purely brittle microstructure, one can calculate the effective value of the critical energy release rate from

$$\begin{aligned} G^{\textrm{micro}}_{\textrm{c}} = \left. - \frac{\textrm{d}\Pi _{\textrm{RVE}}}{\textrm{d}A_{\textrm{micro}}} \right| _{\textrm{crit}} = \left. \frac{\textrm{d} W_{\textrm{ext}} - \textrm{d}\left( \overline{W}V_{\textrm{RVE}}\right) }{\textrm{d}A_{\textrm{micro}}} \right| _{\textrm{crit}}. \end{aligned}$$
(31)

If the microstructure also contains a ductile phase, one must incorporate the plastic work \(W_{\textrm{p}}\) in the ductile phase in the calculation of the effective critical energy release rate. For linear elastic fracture mechanics to be applicable the plastic deformation of the ductile phase has to be small. The effective critical energy release rate can then be expressed as

$$\begin{aligned} G^{\textrm{micro}}_{\textrm{c}} = \left. - \frac{\textrm{d}\Pi _{\textrm{RVE}}}{\textrm{d}A_{\textrm{micro}}} \right| _{\textrm{crit}} = \left. \frac{\textrm{d} W_{\textrm{ext}} - \textrm{d}\left( \overline{W}V_{\textrm{RVE}}\right) - \textrm{d}W_{\textrm{p}}}{\textrm{d}A_{\textrm{micro}}} \right| _{\textrm{crit}}. \end{aligned}$$
(32)

It is assumed that the deformation becomes critical when the Considère point in the volume-averaged engineering stress–strain curve is passed

$$\begin{aligned} \frac{\textrm{d} \, \overline{\sigma }_{\textrm{eng}}}{\textrm{d} \, \overline{\varepsilon }} = 0. \end{aligned}$$
(33)

For the calculation of the effective critical energy release rate, it has to be ensured that the phase field has already localized to form pronounced cracks. First microcracks appeared visually when the order the minimum value of the order variable reached \(\varphi _{\textrm{min}} < 0.01\); hence, we demanded this as an additional requirement for the minimal value of the order variable. This happens shortly after the Considère point in the volume-averaged stress–strain curve. An exemplary volume-averaged stress–strain curve together with the microdamage patterns at different levels of deformation is given in Fig. 7.

Fig. 7
figure 7

Exemplary volume-averaged stress–strain curve of a single-phase brittle microstructure with patterns of microdamage corresponding to the Considère point (left), initial softening (middle) and severe softening leading to numerical instability (right)

Full size image

It should be noted that the RVE-based approach gradually loses its validity in the softening regime of the volume-averaged stress–strain curve as the crack lengths approach the cell size of the RVE. Figure 8 shows exemplary the evolution of the effective energy release rate \(G_{\textrm{micro}}\) and the effective strain energy density \(W_{\textrm{macro}}\) in the vicinity of instability of deformation. After the appearance of the first microcracks, one can find a plateau during which \(G_{\textrm{micro}}\) shows very little fluctuation. If one follows the deformation further into the softening regime, which is not depicted in Fig. 8, the values for \(G_{\textrm{micro}}\) will start to fluctuate strongly as the microcracks approach a fragmentation of the volume element.

Regarding the calculation of the cumulative crack surface \(A_{\textrm{micro}}\) it should be noted that we conduct a volume integration of the crack surface density given by (12) and (13). This leads to larger values of \(A_{\textrm{micro}}\) as one would estimate based on the microcrack patterns as shown exemplary in Fig. 7. Hence, the corresponding values of \(G_{\textrm{micro}}\) are smaller. The reason for this is the incorporation of partial damage over the whole microstructure in the case of a quadratic local part of crack surface density (12). In the case of a linear local part of crack surface density (13) the lack of mathematical consistency is a possible reason for the overestimation of the cumulative crack surface \(A_{\textrm{micro}}\).

The horizontal white line in the second and third pattern of microdamage in Fig. 7 is associated with a small numerical error caused by the steep transition in material behavior in the core zone of a crack. When trying to reconstruct a jump function with a discrete Fourier transform, one encounters spurious Fourier modes known as Gibb’s phenomenon. Fortunately, this spatial oscillation does not affect the results noticeably; particularly, the volume averaged energy quantities are negligibly influenced by this error.

Fig. 8
figure 8

Evolution of the energy release rate and the strain energy density in the vicinity of instability of deformation (quadratic surface energy density). The effective energy quantities are evaluated shortly after the Considère point when first microcracks appear

Full size image

4 Calibration and validation of the damage model in a single-phase brittle microstructure

The following sections evaluate the independence of the effective energy quantities with respect to the dimension \(l^{\textrm{micro}}_{\textrm{c}}\) of the process zone accompanying a microcrack and the validity of an RVE-based approach.

4.1 Convergence of effective energy quantities regarding the dimension parameter \(l^{\textrm{micro}}_{\textrm{c}}\)

First, the dimension \(l^{\textrm{micro}}_{\textrm{c}}\) of the microcrack process zone is decreased relatively to the grain diameter \(d_{\textrm{grain}}\). This means that the damage field transitions from a strongly diffusive pattern of partially damaged areas to an increasingly stronger localization of damage that finally results in sharp cracks. During this transition, the cracks do not only become more pronounced but are also increasingly deflected by the heterogeneities and tend to follow the boundaries between the heterogeneities due to the peaks in stress and strain that are present there. When varying \(l^{\textrm{micro}}_{\textrm{c}}\), one can keep either \(W^{\textrm{micro}}_{\textrm{c}}\) or \(g^{\textrm{micro}}_{\textrm{c}}\) constant. One of the two local energy quantities on the microscale will also vary according to (22). Figure 9 shows a clear convergence of the effective critical strain energy density \(W^{\textrm{macro}}_{\textrm{c}}\) but no convergence of the effective critical energy release rate \(G^{\textrm{micro}}_{\textrm{c}}\) if one keeps \(W^{\textrm{micro}}_{\textrm{c}}\) fixed. For a fixed \(g^{\textrm{micro}}_{\textrm{c}}\) in contrast, Fig. 10 shows convergence of the effective critical energy release rate \(G^{\textrm{micro}}_{\textrm{c}}\) but no convergence of the effective critical strain energy density \(W^{\textrm{macro}}_{\textrm{c}}\). In fact, the effective counterpart to the varying local energy quantity shows a dependence of \(l^{\textrm{micro}}_{\textrm{c}}\) according to (22) in both cases. These studies show that a threshold for the maximum value of \(l^{\textrm{micro}}_{\textrm{c}}\) can be determined by the condition of the separation of scales between a heterogeneity and a microcrack. Here, the separation of scales allows for a clear distinction of the macroscopic and microscopic damage process zone, which leads to \(l^{\textrm{micro}}_{\textrm{c}}\) no longer coupling the macroscopic values of the strain energy density and the energy release rate.

Fig. 9
figure 9

Evolution of effective values of critical strain energy density and critical energy release rate regarding \(l^{\textrm{micro}}_{\textrm{c}}\) with a fixed local critical strain energy density \(W^{\textrm{micro}}_{\textrm{c}}\) as model input (linear surface energy density)

Full size image
Fig. 10
figure 10

Evolution of effective values of critical strain energy density and critical energy release rate regarding \(l^{\textrm{micro}}_{\textrm{c}}\) with a fixed local critical energy release rate \(g^{\textrm{micro}}_{\textrm{c}}\) as model input (quadratic surface energy density)

Full size image

4.2 Representativeness of microstructural volume element regarding effective energy quantities

Next, the validity of calculating effective energy quantities to transport information of the material behavior from the microscale to macroscale is assessed. This is done by successively increasing the section of the virtual microstructure while checking if the corresponding effective energy quantities converge to a saturation value. This means the average number of grains inside of the VE is successively increased. Three different numbers of grains with five different random realizations of the microstructure are evaluated in terms of the mean value and the standard deviation of the effective energy quantities. The trend of the effective critical strain energy density \(W^{\textrm{macro}}_{\textrm{c}}\) and the effective critical energy release rate \(G^{\textrm{micro}}_{\textrm{c}}\) with respect to the number of grains is given in Fig. 11. Clear convergence with a remaining variation of the mean value of 1% is observed for \(W^{\textrm{macro}}_{\textrm{c}}\), but no convergence is observed for \(G^{\textrm{micro}}_{\textrm{c}}\). The standard deviation due to micro-morphological variations can be reduced for both quantities, but there is a positive trend of \(G^{\textrm{micro}}_{\textrm{c}}\) with an increasing amount of grains in the VE.

This is similar to what Gitman et al. [36] call a deterministic size effect.Footnote 1 In this study the value of the effective critical energy release rate depends linearly on the absolute edge length of the volume element \(l_{\textrm{VE}}\). A dimensional analysis of the energy release rate can make the origin of this size effect clear. The increment in energy is scaling with the volume (\(l^3_{\textrm{VE}}\)), whereas the increment in fracture surface scales with the area (\(l^2_{\textrm{VE}}\)). [36] observed an inverse size effect of the slope in the softening phase of a material stress strain response. The question arises, why the two size effects show inverse behavior. An important difference to the size effect observed in this study is the following. In contrast to a VE with one dominant localization zone, we evaluate the effective critical energy release rate shortly after the point of instability, where the assumption of statistic homogeneity of the material on the macroscale is still true in good approximation. Therefore, an increasing number of grains in the VE also leads to an increasing area of localized damage as additional microcracks can appear in the computational domain. Additionally, the size effect in this study is inherent in the definition of the energy release rate.

To suppress the size effect, one can keep the size of the VE fixed while increasing the number of grains which leads to a decrease in grain size. It is ensured that \(l^{\textrm{micro}}_{\textrm{c}}\) fulfills the separation of scales also for smaller grains. The evolution of the effective critical energy release rate over the number of grains for a fixed size of the VE is shown in Fig. 12. Now, the trend of the effective critical energy release rate shows a possible convergence with respect to the number of grains in the VE (variation of the mean value of 5%).

[36] gave a physical explanation of their size effect with a dimensional analysis of the dissipated energy in a zone of localized damage. However, it has to be clarified if the size effect in the present study is also physically reasonable. We conclude that the observed size effect is not physically reasonable as an increasing number of grains in the VE as well as an increasing grain size, which both increase the necessary dimension of the component, would lead to an increased fracture toughness. Hence, the effective critical energy release rate \(G^{\textrm{micro}}_{\textrm{c}}\) can only serve as a qualitative measure as it depends on the length scale \(l_{\textrm{VE}}\) that results from finding a compromise between a macrocrack being sharp enough relative to the component dimension (maximum of \(l_{\textrm{VE}}\)) and the volume element being representative (minimum of \(l_{\textrm{VE}}\)).

Fig. 11
figure 11

Evolution of effective values of critical strain energy density and critical energy release rate over an increasing number of grains inside the VE for a fixed grain size leading to an increasing VE size (linear surface energy density). The error bars represent the standard deviation normalized to the mean value for five different artificial microstructures

Full size image
Fig. 12
figure 12

Evolution of effective values of critical strain energy density and critical energy release rate over an increasing number of grains inside the VE for a fixed VE size leading to a decreasing grain size (linear surface energy density)

Full size image

4.3 Procedure for calibration and validation

Based on the studies in the previous sections regarding \(l^{\textrm{micro}}_{\textrm{c}}\) and the requirements for a valid RVE, the following procedure for calibration and validation of the phase field-based damage criterion is derived:

  1. 1.

    Find an upper limit for \(l^{\textrm{micro}}_{\textrm{c}} /l_{\textrm{heterogeneity}}\) for which the condition of the separation of scales between a heterogeneity and a microcrack is satisfied.

  2. 2.

    Choose a sufficient amount of heterogeneities, here the number of grains \(n_{\textrm{grains}}\), inside of the VE for it to be representative of the microstructure of interest. Together with the grain size \(d_{\textrm{grain}}\) this gives the size of the RVE which is approximately two times the macroscopic dimension parameter \(l^{\textrm{macro}}_{\textrm{c}} \approx \frac{1}{2} n_{\textrm{grains}} \, d_{\textrm{grain}}\).

  3. 3.

    Check if the crack on the macroscale is sharp enough. This serves as an upper limit for \(l^{\textrm{macro}}_{\textrm{c}}\) and so for \(g^{\textrm{macro}}_{\textrm{c}}\). If this value is too large, further decrease the number of grains if possible. If the lower limit in the grain number for the VE to be representative is already reached, the proposed method is not successful and a different method like, e.g., the embedded cell approach [22] has to be employed instead.

  4. 4.

    Choose \(W^{\textrm{micro}}_{\textrm{c}}\) so that the calculated fracture strength \(\sigma ^{\textrm{macro}}_{\textrm{max}}\) matches the one obtained from a uni-axial tensile test. This can be done directly for the linear formulation of surface energy density (13) by calculating the maximum of the strain energy density in the RVE when the volume-averaged stress reaches the tensile strength of the material. For the quadratic formulation of surface energy density (12), one needs to conduct phase field simulations of the evolution of microdamage iteratively while adjusting the critical local energy density \(W^{\textrm{micro}}_{\textrm{c}}\) until the volume-averaged stress at the Considère point matches the tensile strength.

  5. 5.

    Calculate the local value of the critical energy release rate on the macroscale \(g^{\textrm{macro}}_{\textrm{c}} = 2W^{\textrm{macro}}_{\textrm{c}}l^{\textrm{macro}}_{\textrm{c}}\) and compare it to the effective critical energy release rate \(G^{\textrm{micro}}_{\textrm{c}}\) calculated from the growth of microcracks in the RVE for plausibility (29).

  6. 6.

    Compare the calculated values of the effective critical energy release rate \(G^{\textrm{micro}}_{\textrm{c}}\) to experimental values (e.g., \(G^{\textrm{macro}}_{\textrm{c}} = \frac{K^2_{\textrm{Ic}}}{E}\)) for qualitative validation.

The calibrated damage parameters for Ni\(_{\textrm{3}}\)Si as a typical nickel silicide are given in table 2. The grain size is fixed to 30\(\upmu \)m in the further course of this study, and every simulation is scaled to a reference RVE with 15 grains per edge and \(d_{\textrm{grain}}/l^{\textrm{micro}}_{\textrm{c}} = 17\) to isolate the size effect in \(G^{\textrm{micro}}_{\textrm{c}}\). In the linear formulation of surface energy density (13), the critical energy density \(W_{\textrm{c}}\) is a constant threshold value for damage initiation. In the quadratic formulation of surface energy density (12), the resistance for damage is increasing, starting from an initial value of zero. This leads to much more dissipation of energy during the damage process and therefore the corresponding energy values \(W^{\textrm{micro}}_{\textrm{c}}\), \(G^{\textrm{micro}}_{\textrm{c}}\) and \(g^{\textrm{micro}}_{\textrm{c}}\) are significantly higher in the case of a quadratic surface energy density compared to a linear surface energy density. According to the results of [23] the effective critical energy release rate \(G^{\textrm{macro}}_{\textrm{c}}\) and the local value \(g^{\textrm{macro}}_{\textrm{c}}\) are similar for a sharp crack on the macroscale, so that one can assume \(G^{\textrm{macro}}_{\textrm{c}} \approx g^{\textrm{macro}}_{\textrm{c}}\) for a qualitative model validation. The effective critical energy release rate on the macroscale can be approximated based on the Young’s modulus E and the fracture toughness \(K_{\textrm{Ic}}\) for the plane stress case and mode I crack opening as \(G^{\textrm{macro}}_{\textrm{c}} = \frac{K^2_{\textrm{Ic}}}{E}\). Comparing the macroscopic and effective critical energy release rate (\(g^{\textrm{macro}}_{\textrm{c}}\) and \(G^{\textrm{micro}}_{\textrm{c}}\)), the standard formulation predicts values closer to the experiment from the literature compared to the modified linear formulation. Here it should be noted that one could technically still further increase the predicted values for \(G^{\textrm{micro}}_{\textrm{c}}\) and \(g^{\textrm{macro}}_{\textrm{c}}\) by increasing the size of the RVE and thereby \(l^{\textrm{macro}}_{\textrm{c}}\). However, the value of \(l^{\textrm{macro}}_{\textrm{c}}\) is already at the upper limit for a clear separation of scales when employing standard specimens of fracture mechanics (e.g., a Chevron-notched beam as in [6]).

Table 2 Calibrated damage parameters for the nickel silicide Ni\(_{\textrm{3}}\)Si calculated with standard (quadratic) and modified (linear) surface energy density formulation
Full size table

5 Damage in dual-phase brittle–ductile microstructures

The presence of a second phase with ductile behavior introduces a second source of heterogeneity in addition to the mismatch of crystallographic orientation of the individual grains. Therefore, the influence of two key parameters in a dual-phase microstructure will be discussed in the following sections. As outlined in Sect. 2, damage is restricted to the brittle phase. This is implemented by setting the value of the local critical strain energy density on the microscale \(W^{\textrm{micro}}_{\textrm{c}}\) artificially high in the ductile phase.

5.1 Influence of phase contrast on microdamage behavior

The first microstructural parameter of interest is the mechanical contrast between the brittle and the ductile phase. In this work, the phase contrast is defined as the ratio of the critical strain energy density in the brittle phase and the initial yield limit in the ductile phase. The dual-phase microstructure of interest is the composition of a typical brittle nickel silicide and the ductile nickel-based superalloy Haynes 214. For the study of a varying phase contrast, the volume fractions of the brittle and the ductile phase are set equal. Suitable damage parameters for the brittle nickel silicide are calibrated according to Sect. 4.3 using the quadratic surface energy density formulation based on values for fracture toughness and tensile strength taken from [5, 6, 38], and the crystal elastic–plastic material parameters for Haynes 214 are taken from [7]. For this configuration, the phase contrast is moderate. This means that microcracking in the brittle phase happens at very small values of plastic deformation in the ductile phase. The corresponding microcrack pattern is characterized by a dominant single crack as shown on the left in Fig. 13. This large single crack leads to a softening and therefore unstable response of the aggregate. For elevated temperatures, the phase contrast would increase significantly as the yield limit of the ductile phase would be strongly reduced [39], while the mechanical behavior of the temperature-resistant brittle phase would only be mildly affected. Here, an increase of the phase contrast by a factor of ten is chosen, which represents the extreme case of the temperature being close to the melting point of the ductile phase. In this case, the amount of plastic deformation in the ductile phase increases. This leads to a different microcrack pattern with multiple cracks as can be seen on the right side of Fig. 13. Apparently, the higher contrast in the stress field between the phases leads to a stronger tendency toward localization of damage in the brittle phase. As a consequence, many potential sites of crack initiation are formed.

Fig. 13
figure 13

Top: microcrack pattern for moderate (left) and large (right) phase contrast at a macroscopically critical state of deformation, bottom: first principle stress \(\sigma _{\textrm{I}}\) [GPa] for moderate (left) and large (right) phase contrast at a macroscopically critical state of deformation (quadratic surface energy density)

Full size image

5.2 Role of the volume fraction of the ductile phase

The second microstructural parameter of interest is the volume fraction of the ductile phase \(P_{\textrm{ductile}}\). The volume fraction of the ductile phase is incrementally increased from 0 \(\%\) (single brittle phase) to 25\(\%\), 50\(\%\) and 75\(\%\). Figure 14 shows the corresponding microcrack patterns. For volume fractions of the ductile phase of \(\le \)50\(\%\), one observes a single crack that leads to failure of the whole aggregate. If the volume fraction is further increased, the characteristics of the microcrack pattern change from a single crack to several cracks. Obviously, increasing the volume fraction of the ductile phase has the same impact as increasing the mechanical contrast between the brittle and the ductile phases. The reason for this tendency is most likely the higher stresses in the brittle phase caused by the larger amount of plastic deformation in the ductile phase and the associated reduced load-carrying capability of the ductile phase.

Fig. 14
figure 14

Microcrack pattern for a varying volume fraction of the ductile phase at a macroscopically critical state of deformation (quadratic surface energy density)

Full size image

5.3 Limits of model validity

Certain microstructural configurations lead to a serrated volume-averaged stress–strain curve of the dual-phase aggregate which is depicted in Fig. 15. For the quadratic formulation of the surface energy density, the stress shows a step-wise descent in the softening regime. For the linear formulation, re-hardening is predicted after partial softening. This unexpected behavior can be observed for large fractions of the ductile phase (see bottom right of Fig. 14) as well as for a large phase contrast (see right side of Fig. 13). In these cases, the evaluation of effective energy quantities at the Considère point is not unique anymore and therefore a limit of the approach is reached. A potential way to reduce the partial abrupt softening and thereby the serrated flow would be to further increase the number of heterogeneities in the VE. This would decrease the averaged free length that a microcrack can grow without encountering an obstacle, in the case at hand the ductile phase, relative to the VE edge length. Another way to reduce the serrated flow could be a full 3D resolution of the microstructure, which would provide additional obstacles for a microcrack in the third dimension. Despite these limitations given by the available computational resources, the proposed damage model allows to analyze a wide range of microstructures without the need of any a priori information about locations and pathways of microcracks.

Fig. 15
figure 15

Serrated volume-averaged stress–strain curves in case of a large phase contrast for a quadratic (left) and a linear (right) formulation of the surface energy density

Full size image

6 Conclusion and outlook

A phase field-based criterion for damage in heterogeneous microstructures as found in brazed nickel-based alloys is presented. The sources of heterogeneity considered are the crystallographic mismatch between individual grains and the mechanical contrast between a brittle and a ductile phase. Uni-axial tensile tests on a virtual polycrystalline microstructure have shown that the microscopic local critical strain energy density is better suited as the model input than the microscopic local critical energy release rate due to its lower sensitivity toward microstructural and numerical resolutions. Furthermore, the effective critical strain energy density on the macroscale is independent of the absolute size of the microstructural volume element and is therefore well suited for predicting macroscopic damage of a material with a heterogeneous microstructure. The effective critical energy release rate on the macroscale can only serve for qualitative validation or parameter studies due to an artificial size effect originating from the length scale parameter needed in the phase field approach. Regarding the formulation of the regularized crack surface the quadratic surface density functional provides good accordance with experimental values for the fracture toughness, but an increased effort for the calibration is required. The linear surface density functional produces sharper microcracks but shows less accordance with experimental values for the fracture toughness and is mathematically not consistent. The presented microstructure-based damage model approaches computational limits for the case of a large phase contrast or a large volume fraction of the ductile phase. Nevertheless, this modeling approach gives valuable insights in the strong influence of microstructural heterogeneity on the damage behavior of quasi-brittle materials.

Further investigations could focus on the influence of different loading conditions like compression and temperature or time-dependent material behavior. Such loading conditions occur in sealing systems of turbomachinery which is an important application of brazed nickel-based superalloys.