1 Introduction

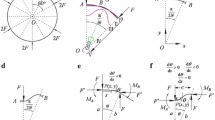
Spira mirabilis, i.e., the marvelous spiral, as the mathematician Jakob Bernoulli named the logarithmic spiral, is a motif somewhat recurring in nature. Many examples of structures organized with this shape can be found indeed. For instance, structures approximately similar to the logarithmic spiral might be recognized in some shells of many mollusks. It is no coincidence that in some topological optimizations, an arrangement of the material following these curves is obtained, as shown by some results obtained after the frequently cited work of the mechanical engineer Anthony G. M. Mitchell [1]. These last results can be used as the starting point for designing a net of curved fibers. The mechanics of elastic networks made of fibers is a challenging and fruitful topic since the pioneering works of Tchebychev on nets composed of inextensible fibers [2]. Systems constituted by an orthogonal network of fibers lying on a plane that can deform, while remaining embedded onto a surface could be conceived for many engineering applications as well as regarded as the reinforcement in a composite material. Especially nowadays, having at our disposal 3D printing technology [3,4,5,6,7,8,9,10,11], it is possible to build curved fiber networks optimized for many demanding tasks. In this paper, stepping in Mitchell’s footprints, we analyze a network of fibers arranged following logarithmic spirals (see [1] and later on [12]). The key idea for Mitchell is to find optimal “frame structures” to attain as much as possible the limit of the material economy under considered applied actions. This result can be accomplished, for small deformations, if the lengths in all the bars of the frame increase by equal fractions but not less than the fractional change of length of any element of the space occupied by the frame. In this context, Mitchell’s frames are truss systems of bars where they are arranged in orthogonal systems of curves both before and after the deformation. Among the solutions proposed by Mitchell is the case of a perpendicular network of curves made of logarithmic spirals (see Fig.1).

Fig. 1
figure 1

Michell’s cantilever truss

Full size image

An efficient way to model this kind of network systems consists in employing equivalent continuum elastic models based on strain-gradient [13,14,15,16,17,18,19,20], micro-morphic [21,22,23,24,25,26], or micro-polar [27,28,29,30,31,32] theories. In this paper, we adopt a second-gradient model that is able to describe the storage of elastic energy of a continuous distribution of fibers with several mechanisms of deformations. Specifically, we consider (1) the elongations of fibers, (2) a macroscopic shear deformation related to a change in the angle between the fibers connected to each other, (3) their curvature related to a deformation in the tangent plane to the net as well as for the out-of-plane bending and, finally, (4) the twisting of the fibers. Herein, we aim to characterize this kind of 2D material from a mechanical point of view. The cantilever truss proposed by Mitchell can be generalized by conceiving a polar symmetric prototype to fit a broader range of applications. With this intent, we consider an annular plate made with this arrangement of fibers and investigate its mechanical responses using numerically executed tests.

2 The model

2.1 Second-gradient sheet made by a fiber net

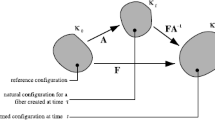
In this section, a bidimensional and second-gradient continuum model, embedded in the 3D space, for a net of curved fibers lying on a plane is described. First, the general framework is recalled. Then, it is specialized for a net made of orthogonal fibers disposed along logarithmic spirals [33,34,35,36,37,38]. This model is based on the following assumptions: (i) The homogenized surface is made of an infinite distribution of two families of fibers; (ii) for every fiber, the shear deformation is negligible; therefore, all the fiber cross-sections remain orthogonal to the tangent vector to the middle line of the fiber in the current configuration; (iii) the intersection points between the two families of the fibers constituting the network share the same position in any configuration, namely no relative motions are allowed at these points; (iv) the only degree of freedom permitted at these intersection points is a relative rotation of the fiber cross sections with respect to the orthogonal vector to the current tangent plane generated as the span of the two tangent vectors at the middle lines of the two fiber families. The considered elastic surface, \({\mathcal {S}}\), is represented by means of the positions in the current configuration, \({\varvec{x}}=(x_{1}, x_{2}, x_3) \in \mathbb {R}^{3}\), of the material points defining the reference configuration, \({\varvec{X}}=(X_{1}, X_{2}) \in \Omega \subset \mathbb {R}^{2}\).

The map \(\varvec{\chi }\) that links the reference configuration \({\varvec{X}}\) and the current one \({\varvec{x}}\), through the displacement vector of components \(u_{i}\), is:

$$\begin{aligned} {\varvec{x}}=\varvec{\chi }({\varvec{X}})=X_{\alpha }{\textbf{e}}_{\alpha }+u_{i}({\varvec{X}})\,{\textbf{e}}_{i} \end{aligned}$$
(1)

in which Greek indexes range from 1 to 2, while Latin ones from 1 to 3. Einstein’s convention is adopted for both of them, and the unit vectors \(\{{\textbf{e}}_{i}\}\) define the basis used to describe the surface \({\mathcal {S}}\). The central lines of the fibers are described by a parametric representation in the framework of a Lagrangian description using the two ‘material’ abscissae \(S_\beta \) \((\beta =1,2)\) in the reference configuration as \({\varvec{X}}={\varvec{X}}(S_\beta )\). In the case in which \(S_\beta \) characterizes a unit-speed parametrization, the tangent vectors to the fibers in the reference configuration are of norm one and can be expressed as

$$\begin{aligned} {\varvec{D}}_\beta ({\varvec{X}})=\frac{\textrm{d} X_{\alpha }}{\textrm{d} S_\beta }{\textbf{e}}_{\alpha } \end{aligned}$$
(2)

The tangent vectors in the current configuration are instead given by

$$\begin{aligned} \lambda _\beta ({\varvec{X}})\,{\varvec{d}}_\beta ({\varvec{X}})=\frac{\textrm{d} \varvec{\chi }}{\textrm{d} S_\beta }({\varvec{X}}) = {\varvec{F}}({\varvec{X}}) \,{\varvec{D}}_\beta ({\varvec{X}}) \end{aligned}$$
(3)

where \(\lambda _\beta = \Vert {\varvec{F}}\,{\varvec{D}}_\beta \Vert \), \({\varvec{F}}=\nabla \!_{_{{\varvec{X}}}}\varvec{\chi }\), that is the deformation gradient tensor, which is represented by a \(3\times 2\) matrix, and \({\varvec{d}}_\beta \) are the unit fiber tangent vectors in the current configuration. The unit vector orthogonal to the surface \({\mathcal {S}}\) is

$$\begin{aligned} {\varvec{n}}({\varvec{X}})=\frac{{\varvec{d}}_1\times {\varvec{d}}_2}{\left\| {\varvec{d}}_1\times {\varvec{d}}_2 \right\| } \end{aligned}$$
(4)

which can be simplified as

$$\begin{aligned} {\varvec{n}}({\varvec{X}})=\frac{\varepsilon _{ijk}\,F_{j2}\,F_{k1}\,{\textbf{e}}_i}{\left\| \varepsilon _{ijk}\,F_{j2}\,F_{k1}\,{\textbf{e}}_i\right\| } \end{aligned}$$
(5)

when the fibers in the reference configuration are orthogonal (\({\varvec{D}}_1 \cdot {\varvec{D}}_2 =0\)); \(\varepsilon _{ijk}\) stands for the Levi-Civita symbol.

In the framework of Kirchhoff’s model of rods [39,40,41,42,43], the cross-section orientation of fibers can be described by a rotation tensor as follows:

$$\begin{aligned} {\varvec{R}}_\beta : \{{\textbf{e}}_i\}\mapsto \{{\varvec{d}}_{\beta },\ {\varvec{n}} \times {\varvec{d}}_{\beta },\ {\varvec{n}}\} \end{aligned}$$
(6)

and, consequently, the curvature tensor can be given by

$$\begin{aligned} {\varvec{W}}_\beta = {\varvec{R}}_\beta ^\top \, \frac{\textrm{d} {\varvec{R}}_\beta }{\textrm{d} S_\beta } \end{aligned}$$
(7)

which is a skew-symmetric tensor whose significant components are the twisting, the out-of-plane curvature, and the geodesic one, namely

$$\begin{aligned} \kappa _{T\beta }= \left( {\varvec{n}}\times {\varvec{d}}_\beta \right) \cdot \frac{\textrm{d} {\varvec{n}}}{\textrm{d} S_\beta }, \quad \kappa _{n\beta }= {\varvec{n}} \cdot \frac{\textrm{d} {\varvec{d}}_\beta }{\textrm{d} S_\beta }, \quad \kappa _{g\beta }= - \left( {\varvec{n}}\times {\varvec{d}}_\beta \right) \cdot \frac{\textrm{d} {\varvec{d}}_\beta }{\textrm{d} S_\beta } , \end{aligned}$$
(8)

respectively. The differentiation with respect to the curvilinear abscissa \(S_\beta \) gives

$$\begin{aligned} \frac{\textrm{d} {\varvec{d}}_\beta }{\textrm{d} S_\beta } = \frac{1}{\lambda _\beta }\left[ \nabla \!_{_{{\varvec{X}}}}{\varvec{F}} \vert {\varvec{D}}_\beta \otimes {\varvec{D}}_\beta + {\varvec{F}}\!\left( \nabla \!_{_{{\varvec{X}}}}{\varvec{D}}_\beta \, {\varvec{D}}_\beta \right) \right] - \frac{\textrm{d} \lambda _\beta }{\textrm{d} S_\beta }\frac{{\varvec{d}}_\beta }{\lambda _\beta } \end{aligned}$$
(9)

where the above-mentioned expressions are evaluated by

$$\begin{aligned} \begin{aligned} (\nabla \!_{_{{\varvec{X}}}}{\varvec{F}} \vert {\varvec{D}}_\beta \otimes {\varvec{D}}_\beta )_i&= \frac{\partial F_{i\alpha }}{\partial X_\eta }({\varvec{D}}_\beta )_\eta ({\varvec{D}}_\beta )_{\alpha } \\ (\nabla \!_{_{{\varvec{X}}}}{\varvec{D}}_\beta \, {\varvec{D}}_\beta )_\alpha&= \frac{\textrm{d}^2 X_{\alpha }}{\textrm{d} {S_\beta }^2}. \end{aligned} \end{aligned}$$

The derivative of \({\varvec{n}}\) with respect to \(S_\beta \) can be performed from Eq. (4). The measures of deformation used to describe the behavior of the elastic surface \({\mathcal {S}}\) incorporating the effects due to the fibers are therefore:

  1. 1.

    The fiber stretching

    $$\begin{aligned} \varepsilon _\beta =\lambda _\beta -1 \end{aligned}$$
    (10)
  2. 2.

    The shear distortion angle

    $$\begin{aligned} \gamma =\textrm{asin} \left( {\varvec{d}}_1 \cdot {\varvec{d}}_2\right) \end{aligned}$$
    (11)
  3. 3.

    The curvature change

    $$\begin{aligned} \Delta \kappa _{T\beta }=\kappa _{T\beta } -\kappa _{T\beta }^0, \quad \Delta \kappa _{n\beta }=\kappa _{n\beta } -\kappa _{n\beta }^0, \quad \Delta \kappa _{g\beta }=\kappa _{g\beta } -\kappa _{g\beta }^0 \end{aligned}$$
    (12)

    where the superscript ‘0’ refers to the reference configuration.

In the case of a planar surface in the reference configuration, \(\kappa _{T\beta }^0=0\) and \(\kappa _{n\beta }^0=0\), the geodesic curvature can be evaluated as follows:

$$\begin{aligned} \kappa _{g\beta }^0= - \left( {\textbf{e}}_{3}\times {\varvec{D}}_\beta \right) \cdot \frac{\textrm{d} {\varvec{D}}_\beta }{\textrm{d} S_\beta } \end{aligned}$$
(13)

The elastic energy of the considered surface is assumed to be

$$\begin{aligned} 2 U\left[ \varvec{\chi }(\cdot )\right] =&\int _{\Omega } \sum _{\beta =1}^2 K_{e\beta } \left( \lambda _\beta -1\right) ^2 \,\textrm{d}\Omega + \int _{\Omega } K_{s} \gamma ^2 \,\textrm{d}\Omega \nonumber \\&+ \int _{\Omega } \sum _{\beta =1}^2 K_{g\beta } (\kappa _{g\beta } -\kappa _{g\beta }^0)^2 \,\textrm{d}\Omega + \int _{\Omega } \sum _{\beta =1}^2 K_{n\beta } (\kappa _{n\beta })^2 \,\textrm{d}\Omega \nonumber \\&+ \int _{\Omega } \sum _{\beta =1}^2 K_{T\beta } (\kappa _{T\beta })^2 \,\textrm{d}\Omega \end{aligned}$$
(14)

where \(K_{e\beta }\), \(K_{s}\), \(K_{g\beta }\), \(K_{n\beta }\), and \(K_{T\beta }\) are the significative stiffnesses for the two families of fibers, namely related to stretching, shearing, geodesic and normal bending, and twisting, respectively.

Fig. 2
figure 2

A possible prototype that could be made with 3D printing: a top view; b perspective view

Full size image

2.2 Logarithm spiral lattices

A net of orthogonal fibers disposed along logarithmic spirals is now considered and analyzed numerically with the aim of illustrating its mechanical responses in view of potential applications. The fibers are connected to each other through cylindrical pivots [44,45,46] that behave as deformable hinges to provide a relative motion between the fibers. This type of connection is able to provide a sufficiently yielding link that can satisfy the hypothesis iv stated in Sect. 2. A prototype that fits this description is shown in Fig. 2. Nowadays, since the enormous progress made by 3D printing technology, it is increasingly easy to conceive and produce complex substructures that can provide significant resistance with a limited amount of material. The system under study falls in that line of research.

In what follows, a representative sample is considered. It is made of fibers with a rectangular cross section of size \(b\times h\), namely the base \(b=1.6\) mm and the height \(h=1\) mm. They are connected through cylindrical pivots having radius \(r_p=0.45\) mm and height \(h_p=1\) mm. In the examined case, the middle lines of the fibers are represented by the two families of curves

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{1} = R_0\, e^{(\varphi +\psi )}\cos (\varphi -\psi )\\ X_{2} = R_0\, e^{(\varphi +\psi )}\sin (\varphi -\psi ) \end{array}\right. } \end{aligned}$$
(15)

obtained by varying the parameters \(\varphi \) and \(\psi \).Footnote 1 The constant \(R_0\) is the radius of the inner circle and is assumed to be 50 mm. The outer radius delimiting the annular plate is \(R_e = 260\) mm.

The stiffnesses characterizing the strain-gradient plate are computed with the expressions:

$$\begin{aligned} K_{e}= & {} \eta _e \frac{\text {Y A}}{p}, \quad K_s = \eta _s \frac{\text {G J}_p}{h_p\, p^2}, \quad K_{T} = \eta _T \frac{\text {G J}_t}{p}, \nonumber \\ K_{g}= & {} \eta _g \frac{\text {Y J}_{fg}}{p}, \quad K_{n} = \eta _n \frac{\text {Y J}_{fn}}{p} \end{aligned}$$
(17)

where \(\eta _i\) are corrective coefficients and, moreover, A is the area of the fibers cross section, \( J_t=0.196\, h^3\,b\), \(J_{fn}=h^3\,b/12, and J_{fg}=b^3\,h/12\) are the torsional, the normal bending, and the in-plane bending second moment of area of the fiber cross sections, respectively; in addition, \(J_p = \pi \, r_p^4/2\) is the torsional second moment of area of the cylindrical pivot. Here, the two families of fibers are perfectly equal; therefore, it is not necessary to distingue the stiffnesses belonging to different families. The variable p represents the pitch between two adjacent fibers. In particular, the pitch is determined by employing the three-dimensional sample shown in Fig. 2. This procedure has shown a linear dependence on the radial distance from the center of the annular plate that can be expressed with the relationship:

$$\begin{aligned} p = m \sqrt{2\,\left( {X_1}^2+{X_2}^2\right) } + q \end{aligned}$$
(18)

where \(q=-4 \times 10^{-2}\) mm and \(m=0.1085\).

The corrective coefficients \(\eta _i\) have been estimated by a micro-macro-identification as the one proposed in [47, 48]. The obtained values are listed in Table 1. In this procedure, the material considered for the 3D model is homogeneous and isotropic and, thus, characterized by Young’s modulus \(Y=1600\) MPa and Poisson’s ratio \(\nu =0.4\).

Table 1 Tuned coefficients \(\eta \)
Full size table

Moreover, the unit tangent vectors to the logarithmic spiral fibers are found to be

$$\begin{aligned} {\varvec{D}}_{1} \equiv \left( \frac{\left( X_1-X_2\right) }{\sqrt{2\,\left( {X_1}^2+{X_2}^2\right) }} , \frac{\left( X_1+X_2\right) }{\sqrt{2\,\left( {X_1}^2+{X_2}^2\right) }},0\right) , \quad {\varvec{D}}_{2} = {\varvec{D}}_{1}\times {\textbf{e}}_3 \end{aligned}$$
(19)

and their derivatives with respect to \(S_\beta \) are given by

$$\begin{aligned} \frac{\textrm{d} {\varvec{D}}_1}{\textrm{d} S_1}\equiv & {} \left( \frac{-\left( X_1+X_2\right) }{2\,\left( {X_1}^2+{X_2}^2\right) }, \frac{\left( X_1-X_2\right) }{2\,\left( {X_1}^2+{X_2}^2\right) } ,0\right) , \nonumber \\ \frac{\textrm{d} {\varvec{D}}_2}{\textrm{d} S_2}\equiv & {} \left( \frac{-\left( X_1-X_2\right) }{2\,\left( {X_1}^2+{X_2}^2\right) }, \frac{-\left( X_1+X_2\right) }{2\,\left( {X_1}^2+{X_2}^2\right) } ,0\right) ; \end{aligned}$$
(20)

consequently, the curvatures in the reference configuration become

$$\begin{aligned} \kappa _{g1}^0 = \kappa _{g2}^0 = -\frac{1}{\sqrt{2\,\left( {X_1}^2+{X_2}^2\right) }} \end{aligned}$$
(21)
Fig. 3
figure 3

Schematic representation of the performed tests: a circumferential shear test; b radial shear test; c hole expansion test d pull-off test; e angular misalignment test

Full size image

3 Numerical simulations and discussion

This section is devoted to numerically investigating the mechanical behavior of a 2D material made of an orthogonal net of curved fibers arranged following equiangular logarithmic spirals. To this end, several significative tests are performed on an annular plate showing the nonlinear responses when large displacements are applied to the boundaries. The employed model, sketched in the previous section, is programmed into a finite element software, namely COMSOL Multiphysics, directly through its weak formulation deduced from the elastic energy (14). For technical details related to the implementation, the reader can refer to the works [36, 49, 50], while for possible improvements, see [51,52,53,54].

Specifically, tests that are conceived to illustrate the peculiar responses of the considered bidimensional elastic material are (see Fig. 3):

  1. 1.

    Circumferential shear test;

  2. 2.

    Radial shear test;

  3. 3.

    Hole expansion test;

  4. 4.

    Pull-off test;

  5. 5.

    Angular misalignment test.

Only kinematic essential boundary conditions have been implemented in all the performed tests because of their simplicity. Since the model employed is a second-gradient one, proper boundary conditions involve assigning the displacement and its gradient.

Fig. 4
figure 4

Circumferential shear test: a Reference configuration; b Current configuration at the maximum angle attained of 23 degrees. Black solid lines represent material lines following some paths of logarithmic spirals. The same material point is highlighted in red in the two configurations for better understanding of the setup

Full size image

In the first simulation, a circumferential shear test is carried out. Here, we fix the inner circle and rotate the outer one at an increasing angle. The simulation is stopped at the angle of 23 degrees because, after this threshold, an out-of-plane buckling occurs. Regarding the boundary condition related to the displacement gradient, the in-plane normal derivative of the out-of-plane displacement component is set to zero to describe a clamping condition. In detail,

$$\begin{aligned} \nabla \!_{_{{\varvec{X}}}}u_3 \cdot \varvec{\nu } =0 \end{aligned}$$
(22)

where \(\varvec{\nu }\) is planar unit normal to the boundaries.

Figure 4 shows the annular plate prior the deformation and the equilibrium shape for the maximum angle imposed, namely 23 degrees. To facilitate the characterization of the deformed configuration, we put a red spot fixed on the plate. In Figs. 5, 6, and 7, the significant measures of deformation are displayed. In this case, one family of fibers is stretched, and the other is compressed, especially in the central zone close to the inner circle; the shear distortion angle is almost negligible; the change of geodesic curvature localizes near the boundary circles as it could be expected.

Fig. 5
figure 5

Circumferential shear test: elongation a \(\varepsilon _1\); b \(\varepsilon _2\)

Full size image
Fig. 6
figure 6

Circumferential shear test: shear distortion angle \(\gamma \)

Full size image
Fig. 7
figure 7

Circumferential shear test: geodesic curvature change a \(\Delta \kappa _{g1}\); b \(\Delta \kappa _{g2}\)

Full size image

Figure 8 exhibits the characteristic diagram of the reaction torque versus the applied angle to the outer circle. In the examined range, the behavior is predominantly linear. This plot has been evaluated using Castigliano’s theorem by numerically differentiating the elastic energy with respect to the imposed angle.

Fig. 8
figure 8

Circumferential shear test: torque vs angle

Full size image

In the second test, we clamp the outer circle and rigidly translate the inner one radially, keeping the condition (22) also for this boundary. The outcome of this radial shear test is shown in Fig. 9, where the current equilibrium shape is reported alongside the inner circle with a solid black line in the reference position for a displacement of \(0.386 R_0\).

Fig. 9
figure 9

Radial shear test: Current configuration after a radial displacement of \(0.386 R_0\)

Full size image
Fig. 10
figure 10

Radial shear test: elongation a \(\varepsilon _1\); b \(\varepsilon _2\)

Full size image
Fig. 11
figure 11

Radial shear test: shear distortion angle \(\gamma \)

Full size image
Fig. 12
figure 12

Radial shear test: geodesic curvature change a \(\Delta \kappa _{g1}\); b \(\Delta \kappa _{g2}\)

Full size image

The deformation measures related to this test are plotted in Figs. 10, 11, and 12. Here, both families of fibers are subject simultaneously to stretch and compression, having a mirror symmetry pattern. The shear distortion angle is more significant than in the previous case reaching the value of about 10 degrees. The change of geodesic curvature is also localized nearby the boundaries but with a more complex distribution.

Fig. 13
figure 13

Radial shear test: radial force vs imposed displacement

Full size image

Figure 13 depicts the force versus displacement plot that characterizes this radial shear test. Notwithstanding the relatively large enforced displacement, the whole behavior of the annular plate is still linear.

In this case, if a small amount of pressure normal to the plane of the annular plate is applied, a buckled shape occurs after a critical value of the radial displacement (\(R_0/5\)), as shown in Fig. 14a. The pattern of this shape is characterized by a prominent bulge in the compressed zone, while the left region affected by overall stretching presents several wrinkling. To confirm this complex shape, a numerical simulation has been performed with a more detailed and time-consuming 3D finite element model using the Saint Venant–Kirchhoff constitutive behavior for hyperelastic materials in nonlinear regime with an accurate description of the geometry of the fibers. Figure 14b reproduces the plot of the buckled shape with the 3D model. Comparing the results obtained by the two formulations, namely the 2D and 3D ones, shows a good agreement between the models corroborating the validity of the simplified bidimensional second-gradient plate theory adopted.

Fig. 14
figure 14

Buckling occurring during the radial shear test: a 2D model; b 3D model

Full size image

In the third case, we analyze a hole expansion test, where the inner circle is radially and isotropically expanded, holding the clamp condition of Eq. (22) on both boundaries (see, Fig. 15, for the current configuration at maximum imposed displacement).

Fig. 15
figure 15

Hole expansion test: current configuration for the maximal radial displacement of \(0.44\, R_0\)

Full size image

The significant measures of deformation for this case are plotted in Figs. 16 and 17. Due to the symmetry of the applied displacement, the deformation is also symmetric. Therefore, the elongations, which are negative, of the two fiber families are the same, as well as the change in the geodesic curvature. Let us remark that the compression is almost linearly distributed over the entire annular plate having the maximum located in the correspondence of the outer circle. Only a very narrow boundary layer of stretched fiber is localized on the inner circle. On the contrary, the distribution of the shear distortion angle tends to localize around the inner ring and becomes flat, approaching the outer boundary. As regards the change in the geodesic curvature, the most prominent deformation is localized near the inner circle and is zero almost everywhere except the boundaries.

Fig. 16
figure 16

Hole expansion test: a elongation \(\varepsilon _{\beta }\); b shear distortion angle \(\gamma \)

Full size image
Fig. 17
figure 17

Hole expansion test: geodesic curvature change \(\Delta \kappa _{g\beta }\)

Full size image

Figure 18 displays the inner radial pressure versus the radial applied displacement. In this case, an appreciable nonlinear behavior is present.

Fig. 18
figure 18

Hole expansion test: inner radial pressure vs displacement

Full size image

Subsequently, a pull-off test is performed on the annular plate. The outer circle is fixed, while the inner circle is rigidly translated in the out-of-plane direction until a displacement of \(2 R_0\) is reached. As the two boundary circles always remain parallel during the test starting from the reference configuration, the clamp conditions are once again given by Eq. (22). Figure 19 shows the current configuration for the maximum displacement.

Fig. 19
figure 19

Pull-off test: Current configuration for an out-of-plane displacement of the inner ring equal to \(2 R_0\)

Full size image
Fig. 20
figure 20

Pull-off test: a elongation \(\varepsilon _{\beta }\); b shear distortion angle \(\gamma \)

Full size image

In this new case, the set of deformation measures is richer than in the previous instances since the out-of-plane curvature and the torsion of fibers become different from zero. Figures 20, 21, and 22 illustrate all of them. The elongations, which are positive for all the fibers, have a linear distribution depending on the radius with the maximum value at the outer circle as shown in Fig. 20a. The shear distortion angle is also almost linear in the body of the annular plate with the maximum value near the inner circle but with more evident deviations close to the boundaries. The shear distortion angle also has almost a linear distribution in the body of the annular plate; on the contrary, the maximum value is near the inner circle, and more evident deviations can be noticed close to the boundaries (see Fig. 20b).

Fig. 21
figure 21

Pull-off test: curvature change a geodesic \(\Delta \kappa _{g\beta }\); b out-of-plane \(\kappa _{n\beta }\)

Full size image
Fig. 22
figure 22

Pull-off test: twisting change a \(\kappa _{T1}\); b \(\kappa _{T2}\)

Full size image

All the deformation measures related to the second-gradient contribution, namely the curvatures and the torsions, are almost negligible in the body of the annular plate but become significant in boundary layers nearby the two circles that define the considered elastic surface as apparent from Figs. 21 and 22.

Fig. 23
figure 23

Pull-off test: out-of-plane force vs imposed displacement

Full size image

Figure 23 shows the resultant out-of-plane component of the reaction force versus the applied displacement in the same direction. In this case, the nonlinear behavior is predominant, entailing a feeble resistance for small displacements that quickly grows as the displacement increases.

Finally, an angular misalignment test is performed on the annular plate imposing a relative rotation until \(\pi /2\) of the two out-of-plane normal axes of the boundary circles. Specifically, the outer ring is fixed, while the inner one is rotated at an increasing angle with respect to a radial axis lying on the plane of the plate. The clamp condition is the same Eq. (22) for the outer circle. The inner ring has been subject to a different treatment instead. Since the condition ensuring the clamp is much more complicated from a mathematical point of view due to the large rotation of the ring, the same condition has been obtained equivalently, as explained in the following. A narrow annular ring is added in correspondence with the hole, and the desired rigid rotation is imposed to this additional part (see Fig. 24). This simple trick clearly sets an equivalent differential condition for the clamp inside the annular plate forcing the tangent plane to the surface to be parallel to the plane of the inner circle.

Fig. 24
figure 24

Angular misalignment test: current configuration for a rotation of the inner ring of angle of \(\pi /2\)

Full size image
Fig. 25
figure 25

Angular misalignment test: elongation a \(\varepsilon _{1}\); b \(\varepsilon _{2}\)

Full size image
Fig. 26
figure 26

Angular misalignment test: shear distortion angle \(\gamma \)

Full size image
Fig. 27
figure 27

Angular misalignment test: geodesic curvature change a \(\Delta \kappa _{g1}\); b \(\Delta \kappa _{g2}\)

Full size image

Figures 25, 26, and 27 display the deformation measures characteristic of the tangent behavior to the elastic surface, namely the fiber elongations, the shear distortion angle, and the geodesic curvature changes of the fibers. In this case, these deformation measures have small amplitudes and hence are less significant, especially for what concerns the shear distortion angle and the geodesic curvature change because of the smaller values of the related stiffnesses.

Fig. 28
figure 28

Angular misalignment test: out-of-plane curvature change a \(\kappa _{n1}\); b \(\kappa _{n2}\)

Full size image
Fig. 29
figure 29

Angular misalignment test: twisting change a \(\kappa _{T1}\); b \(\kappa _{T2}\)

Full size image

Figures 28 and 29 exhibit the deformation measures related to the out-of-plane behavior, i.e., the out-of-plane curvature change and the twisting change of the fibers. The out-of-plane measures of deformations, as expected, have more pronounced amplitudes in this case representing an essential part of the overall deformation.

Fig. 30
figure 30

Angular misalignment test: reaction torque vs imposed angle

Full size image

Figure 30 reports the resultant reaction torque versus the applied angle. Analogously to the previous case, the nonlinear behavior is significant, showing a very weak resistance for small angles that quickly raises as the angle increases.

4 Conclusions

In this paper, we have numerically studied the behaviors of an archetypal prototype, namely an annular plate with fibers arranged according to logarithmic spirals following the framework proposed by David J. Steigmann [33, 55, 56] for describing a system made by an orthogonal net of fibers. The model falls in the category of continuum elastic surfaces of higher-order gradients [57,58,59]. This formulation is reasonably comprehensive since it is able to treat several mechanisms of deformations, including the bending and twisting of the fibers. Moreover, it has been proven in many experimental tests that the model is actually accurate and predictive [60,61,62,63,64].

The numerical tests show the nonlinear character of the system as well as its strength within the elastic regime, making it suitable for many technical applications such as separating septum with some shield capabilities, reinforcement for membranes in a valve, and flexible joints.

A final word for the future directions of this research is noteworthy. In this paper, we have only analyzed the elastic behavior in a static regime, although nonlinear. For a complete assessment of the full potential of the system under study, a thorough examination related to its dynamic properties [65,66,67,68,69,70,71,72,73] and inelastic behavior, i.e., in case of plasticity and damage [46, 74,75,76,77,78,79,80,81,82], is also compelling.