1 Introduction

Peridynamics (PD), introduced by Silling [1], is a nonlocal continuum theory and thus an alternative formulation for continuum mechanics. According to dell’Isola et al. [2], the concept of nonlocal continuum mechanics was already conceived by Gabrio Piola. In contrast to classical continuum mechanics (CCM) and similar to the fundamental idea of molecular dynamics, a continuum point in PD is in interaction with continuum points in its finite-sized neighbourhood. However, in contrast to molecular dynamics, PD also satisfies the underlying concept of continuum mechanics. Due to the nonlocal characteristics of PD, the divergence terms, present in CCM, are replaced by integro-differential terms, which is why PD is appropriate to use for problems including discontinuities. PD was initially introduced to overcome the limitation of modelling material damage and is thus widely used in fracture mechanics and related fields, e.g. [3,4,5,6,7,8]. The peridynamics review of Javili et al. [9] shows that the application of PD has extended significantly in recent years, even in fields unrelated to fracture mechanics, e.g. [10,11,12,13].

The original PD framework of Silling [1], called bond-based PD, accounts for pairwise interactions and shows to not reflect the Poisson effect correctly. To overcome the limitation of a fixed Poisson ratio of 1/3 in two-dimensional and 1/4 in three-dimensional problems [14], Silling extended the original PD theory to (ordinary and non-ordinary) state-based PD [15]. Alternatively, Javili et al. [9] recently introduced continuum-kinematics-inspired peridynamics (CPD), where the interactions that govern the nonlocal material behaviour are referred to as one-, two- and three-neighbour interactions dependent on the contributing number of neighbours. Since the interactions in CPD are governed by the change of pair-length, triplet-area and tetrad-volume, the CPD framework represents a kinematically exact formulation. Since one-neighbour interactions are equivalent to bond-based interactions, the Poisson effect is captured by considering two- and three-neighbour interactions [16].

Although the range of applications for PD has grown tremendously in recent years, the number of theoretical contributions is rather limited. To name a few, besides the already mentioned theoretical contributions of Silling et. al [1, 15] and Javili et al. [9], additional theoretical contributions involve the one of Silling and Lehoucq [17], where the first and second law of thermodynamics are exploited based on peridynamic quantities. Ostoja-Starzewski et al. [18] discuss the restrictions imposed by the second law of thermodynamics in bond-based and state-based PD. Further theoretical contributions, e.g. the ones of Kilic et al. [19], Bobaru and Duangpanya [20] and Oterkus et al. [21], address thermomechanical problems. Additionally, Javili et al. extended recently the CPD formulation to account for thermomechanical coupling [22] and elasto-plastic material behaviour [23].

However, to the author’s knowledge, only formulations for closed system peridynamics have been introduced in recent years. Therefore, the aim of this contribution is to propose a formulation for open system (continuum-kinematics-inspired) peridynamics for the first time. In contrast to closed systems, where the system can exchange energy in terms of heat and work with its surrounding, open systems can additionally exchange matter with its surrounding and generate mass locally. Thus, closed systems represent special cases of an open system, where the conservation of mass has to be satisfied. In the literature, mainly closed systems are considered in continuum mechanics, although it is a simplification for most mechanical problems. Particularly for chemomechanical and biomechanical processes, the concept of open systems holds. Since additional mass sources influence not only the balance of mass, but also the balances of momentum, energy and entropy, all balance equations have to be reconsidered. Thus, in terms of open system mechanics it is appropriate to start with the balance of mass and continue with the balances of momentum, energy and entropy. For open system CCM, Kuhl and Steinmann [24] showed that with the help of the balance of mass all other balance equations can be reformulated to reduced balance equations, which are comparable to the ones valid in closed system CCM.

To propose a formulation for open system (continuum-kinematics-inspired) peridynamics, the paper is structured as follows. In Sect. 2, we revisit the kinematic description relevant for PD and state general forms for the global, point-wise and neighbour-wise balance equations. In Sect. 3, the governing equations valid for open system peridynamics are stated. First, the balance of mass is introduced. Subsequently, the balance of linear and angular momentum are discussed, where the balance of mass is incorporated to obtain a reduced form for both balance equations. Following this, the kinetic energy theorem is examined to identify the external and internal power that are helpful to establish the balance of internal energy. Lastly, the balance of entropy is stated that is required to obtain the dissipation inequality, discussed in Sect. 4. In Sect. 5, we obtain the structure and constraints of the constitutive expressions by applying the Coleman–Noll procedure. For the sake of demonstration, we present in Sect. 6 an example for a nonlocal mass source and constitutive expressions for modelling the process of bone remodelling in a peridynamic sense. Section 7 concludes the main findings of the paper and provides further outlook.

2 Kinematics in peridynamics

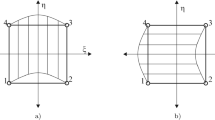
As illustrated in Fig. 1, we consider a continuum body in its material configuration \({\mathcal {B}}_0 \subset {\mathbb {R}}^3 \) at time \( t_0 \subset {\mathbb {R}}_+ \) with its boundary \(\partial {\mathcal {B}}_0\). The material coordinates \({\varvec{X}}\) that identify points of \({\mathcal {B}}_0\) are mapped via the nonlinear deformation map \({\varvec{y}}\) to their spatial coordinates as \( {\varvec{x}} = {\varvec{y}}({\varvec{X}},t):~{\mathcal {B}}_0 \times {\mathbb {R}}_+ \rightarrow {\mathcal {B}}_t \), where \({\mathcal {B}}_t \subset {\mathbb {R}}^3\) at \(t > t_0 \subset {\mathbb {R}}_+ \) denotes the continuum body in its spatial configuration.

Fig. 1
figure 1

A continuum point \({\varvec{X}}\) of the continuum body in its material configuration \({\mathcal {B}}_0 \subset {\mathbb {R}}^3 \) interacts with continuum points in its finite-sized neighbourhood, the horizon \({\mathcal {H}}_0\). \({\mathcal {B}}_0\) is mapped to its spatial configuration \({\mathcal {B}}_t \) via the deformation map \({\varvec{y}}\)

Full size image

In contrast to local continuum mechanics, the peridynamic theory is based on the fundamental idea that every continuum point is in interaction with continuum points in its finite neighbourhood, the so-called horizon \({\mathcal {H}}_0 \subset {\mathcal {B}}_0\). The interaction region is typically a spherical neighbourhood measured via its radius \(\delta \) in the material configuration. The horizon \({\mathcal {H}}_t\) in the spatial configuration is obtained via the deformation map by \({\mathcal {H}}_t = {\varvec{y}}({\mathcal {H}}_0)\). The horizon size \(\delta \) is considered a material parameter of PD as it influences the degree of nonlocality at \({\varvec{X}}\). Note that the local continuum theory can be recovered in the limit of \(\delta \rightarrow 0\). The vector between a continuum point \({\varvec{X}}\) and any of its neighbours \({\varvec{X}}^{{{\,\mathrm{ {}^{\vert } }\,}}} \in {\mathcal {H}}_0\) is expressed via the line vector \(\varvec{\Xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} := {\varvec{X}}^{{{\,\mathrm{ {}^{\vert } }\,}}} - {\varvec{X}}\) in the material configuration and \(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} := {\varvec{x}}^{{{\,\mathrm{ {}^{\vert } }\,}}} - {\varvec{x}}\) in the spatial configuration with \({\varvec{x}}^{{{\,\mathrm{ {}^{\vert } }\,}}} = {\varvec{y}}({\varvec{X}}^{{{\,\mathrm{ {}^{\vert } }\,}}},t)\). Note that we mark quantities of neighbours with a superscript line \( \{\bullet \}^{{{\,\mathrm{ {}^{\vert } }\,}}}\) to distinguish quantities of the continuum point and its neighbours within \({\mathcal {H}}_0\).

In the following, we state the governing equations in the material configuration, where the material time derivative of a quantity \(\{ \bullet \}\) at fixed material placement \({\varvec{X}}\) is denoted by \(\text {D}_t \{ \bullet \}\). We distinguish between densities per unit volume \(\{\bullet \}_0\) and per unit mass \(\{ \bullet \}\). In PD, the conversion of both densities is dependent on the nature of the quantity. For local quantities the conversion \(\{\bullet \}_0 = \rho _0 \{\bullet \}\) holds in the material configuration, where \(\rho _0\) is the material density of the continuum point. In contrast, the conversion

$$\begin{aligned} \{\bullet \}_0 = \displaystyle \int _{{\mathcal {H}}_0} \{\bullet \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \qquad \text {with} \qquad \{\bullet \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \{\bullet \}^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$

applies for nonlocal quantities, where \(\rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) is the material density of the respective neighbour. Both material densities, \(\rho _0\) and \(\rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}\), are local continuum quantities and considered homogenised versions of the underlying heterogeneous material. Note that \(\{ \bullet \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) is a neighbour-wise quantity per volume squared and \(\{ \bullet \}^{{{\,\mathrm{ {}^{\vert } }\,}}}\) consequently per volume and per mass.

Next, we establish general forms for balance equations in our peridynamic formulation and compare them to their counterparts in local classical continuum theory. To proceed, we first address the difference between the PD and CCM theory in terms of flux or flux-like quantities. Therefore, we consider a continuum body \({\mathcal {B}}_0 := {\mathcal {B}}_1 \cup {\mathcal {B}}_2\) exposed to external loads on its boundary \(\partial {\mathcal {B}}_0\). To analyse the current state of a continuum point \({\varvec{X}}\), we fictitiously divide the body \({\mathcal {B}}_0\) into two sub-domains, \({\mathcal {B}}_1\) and \({\mathcal {B}}_2\), schematically illustrated in Fig. 2. The resultant force measures acting on the continuum point \({\varvec{X}}_{\alpha }\) in CPD theory that result only from one-neighbour interactions (left) are compared to the resultant force measures acting on \({\varvec{X}}\) in CCM theory (right). In CCM, the resultant force is measured via the Cauchy theorem by the traction vector \({\varvec{t}} = {\varvec{P}} \cdot {\varvec{N}}\), as depicted in Fig. 2 (right). Therein, \( {\varvec{P}}\) denotes the Piola stress and \({\varvec{N}}\) the outward-pointing unit normal vector on the area element \(\text {d}A\). In PD, however, we cannot apply the Cauchy theorem due to the nonlocal characteristic of PD. As depicted in Fig. 2 (left), the force densities \({\varvec{p}}_{i\alpha }^{{{\,\mathrm{ {}^{\vert } }\,}}}\) with \(i = \{\beta , \gamma \} \) originate from interactions of the continuum point \({\varvec{X}}_{\alpha }\) with the continuum points \({\varvec{X}}_{\beta }^{{{\,\mathrm{ {}^{\vert } }\,}}}\) and \({\varvec{X}}_{\gamma }^{{{\,\mathrm{ {}^{\vert } }\,}}}\), which exemplarily represent the neighbourhood of \({\varvec{X}}_{\alpha }\) in the sub-domain \({\mathcal {B}}_2\). The resultant force is consequently computed by an integral of the force density per volume squared over the entire horizon \({\mathcal {H}}_0\). Note that Fig. 2 corresponds only to one-neighbour interactions in CPD or bond-based PD, wherein the interactions are pairwise by nature, unlike two- and three-neighbour interactions in CPD [9].

Fig. 2
figure 2

Resultant force measures acting on the continuum point \({\varvec{X}}_\alpha \) of the subdomain \({\mathcal {B}}_1\) in CPD (left) considering only one-neighbour interactions and on the continuum point \({\varvec{X}}\) in CCM (right) due to a fictitious division of the continuum body \({\mathcal {B}}_0 := {\mathcal {B}}_1 \cup {\mathcal {B}}_2\) into two subdomains, \({\mathcal {B}}_1\) and \({\mathcal {B}}_2\). The greek subindices distinguish the continuum point \({\varvec{X}}_\alpha \) from its neighbours \({\varvec{X}}_\beta ^{{{\,\mathrm{ {}^{\vert } }\,}}}\) and \({\varvec{X}}_\gamma ^{{{\,\mathrm{ {}^{\vert } }\,}}}\) (left), which exemplarily represent the neighbourhood of \({\varvec{X}}_\alpha \) in the subdomain \({\mathcal {B}}_2\)

Full size image

In continuum mechanics, the rate of a balanced quantity of a continuum body \({\mathcal {B}}_0\) is in general equal to the sum of source terms and flux or flux-like terms [24]. Generalising the above example to “flux” densities \(\{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) as nonlocal quantities, assuming sufficient smoothness regarding the balanced quantity \(\{ * \}_0\), the “flux” density \(\{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) and the source quantity \(\{ \circ \}_0\) and integrating over the continuum body \({\mathcal {B}}_0\), the general global balance equation in PD is given by

$$\begin{aligned} \text {D}_t \int _{{\mathcal {B}}_0} \{ * \}_0 \, \text {d}V = \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} \{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V + \int _{{\mathcal {B}}_0} \{ \circ \}_0 \, \text {d}V \, , \end{aligned}$$
(1)

where \(\{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) is in particular a “flux” density per volume squared that additionally needs to be integrated over the horizon \({\mathcal {H}}_0\).

Remark 1

In PD, the term flux has to be used very carefully, since a flux quantity is a local quantity that defines the flux through a surface. Due to the nonlocal characteristic of the PD theory the term flux density is not the physically correct description for the neighbour-wise density \(\{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\). However, we maintain the term flux and put it in quotation marks to highlight that \(\{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) is the nonlocal counterpart to the flux quantity \(\{ \square \}\) per area in CCM. Consequently, we rather speak of a “flux” or flux-like quantity in PD.

After localisation, the point-wise and yet nonlocal balance equation in PD reads

$$\begin{aligned} \text {D}_t \{ * \}_0 = \int _{{\mathcal {H}}_0} \{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + \{ \circ \}_0 \, . \end{aligned}$$
(2)

Note that the balanced and source quantity themselves can be local or nonlocal quantities. In case of the latter, we define these quantities also in integral form over the horizon \({\mathcal {H}}_0\) as

$$\begin{aligned} \{ * \}_0 = \int _{{\mathcal {H}}_0} \{ * \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \qquad \text {and} \qquad \{ \circ \}_0 = \int _{{\mathcal {H}}_0} \{ \circ \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(3)

respectively. For balance equations with only nonlocal quantities the point-wise form reads

$$\begin{aligned} \text {D}_t \int _{{\mathcal {H}}_0} \{ * \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = \int _{{\mathcal {H}}_0} \{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + \int _{{\mathcal {H}}_0} \{ \circ \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(4)

that can be further localised to a neighbour-wise and also local form

$$\begin{aligned} \text {D}_t \{ * \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \{ \diamond \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} + \{ \circ \}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(5)

This consequently provides a more restrictive balance equation than the point-wise form (4).

In contrast to Eq. (1), the general balance equation in global form in CCM is stated by integrating a flux term \(\{ \square \} \cdot {\varvec{N}}\) over the boundary \(\partial {\mathcal {B}}_0\) of the continuum body and is given by

$$\begin{aligned} \text {D}_t \int _{{\mathcal {B}}_0} \{ * \}_0 \, \text {d}V = \int _{\partial {\mathcal {B}}_0} \{ \square \} \cdot {\varvec{N}} \, \text {d}A + \int _{{\mathcal {B}}_0} \{ \circ \}_0 \, \text {d}V \, , \end{aligned}$$
(6)

where \({\varvec{N}}\) is the outward-pointing unit normal vector to \(\partial {\mathcal {B}}_0\) and \(\{ \square \}\) is the flux quantity per area [24]. After localisation and via the Gauss theorem, the point-wise balance equation in CCM reads

$$\begin{aligned} \text {D}_t \{ * \}_0 = \text {Div}\{ \square \} + \{ \circ \}_0 \, . \end{aligned}$$
(7)

Remark 2

Balance equations can also be formulated in the spatial configuration. The conversion of the material and spatial configuration can be accomplished in CCM via the deformation gradient \( {\varvec{F}}:=\text {Grad}{\varvec{y}}\), its Cofactor \( {\varvec{K}}:=\text {Cof}{\varvec{F}}\) and its determinant \( J :=\text {Det}{\varvec{F}} \). Similar holds for CPD [9] as it provides a geometrically exact framework.

3 Governing equations

Based on the general forms of the balance equation, we will elaborate in the following the mechanical and thermodynamic governing equations that are valid for open system peridynamics. The respective governing equations for closed systems can be found in [9, 22] and are recovered in the present formulation by setting the temporal rate of mass to zero. Table 1 provides a comparison of the governing equations in the peridynamic and classic continuum formulation.

Table 1 Comparison of governing equations in the peridynamic and classic continuum formulation
Full size table

3.1 Balance of mass

In the case of open system mechanics, the mass contained in \({\mathcal {B}}_0\) can no longer be considered a conservative property, since in- or out-“flux” of mass or creation of mass influence the temporal rate of mass. In this contribution, we only consider a mass source \({\mathcal {R}}_0\) for the sake of simplicity. The balance of mass in its global form is consequently given by

$$\begin{aligned} \int _{{\mathcal {B}}_0} \text {D}_t \rho _0 \, \text {d}V = \int _{{\mathcal {B}}_0} {\mathcal {R}}_0 \, \text {d}V \, , \end{aligned}$$
(8)

for the PD and CCM formulation, where the material density \(\rho _0\) at the continuum point is the balanced quantity. For both formulations, the point-wise form of Eq. (8) reads

$$\begin{aligned} \text {D}_t \rho _0 = {\mathcal {R}}_0 \, . \end{aligned}$$
(9)

Although the balance of mass (9) is a point-wise balance equation without any nonlocal contribution due to the omitted “flux” term, the mass source \({\mathcal {R}}_0\) of our peridynamic formulation can be a nonlocal quantity by its constitutive expression, providing the balance of mass with a nonlocal characteristic.

Remark 3

In case of an in- or out-“flux” of mass, the balance of mass (9) needs to be enhanced by an additional “flux” term. In PD, we would introduce a mass term \(\int _{{\mathcal {H}}_0} r_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}}\) with the mass “flux” density \(r_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) per volume squared that governs the mass “flux” in a peridynamic sense. The balance of mass is established following the general point-wise form (2) with \(\rho _0\) being the balanced quantity and \({\mathcal {R}}_0\) being the source quantity. In CCM, on the other hand, we would introduce a mass flux \({\varvec{R}}\) per area as flux quantity resulting in the mass flux term \(\text {Div} {\varvec{R}}\).

3.2 Balance of linear and angular momentum

We begin with the balance of linear and angular momentum in their global form. For both balance equations the momentum density \(\varvec{\pi }_0 = \rho _0 {\varvec{v}}\), defined as the velocity \({\varvec{v}}\) of the continuum point \({\varvec{X}}\) weighted with the continuum point density \(\rho _0\), is or contributes to the balanced quantity.

The balance of linear momentum embodies Newton’s second law and states that the temporal rate in \(\varvec{\pi }_0\) integrated over the body \({\mathcal {B}}_0\) is in equilibrium with the internal body force density \({\varvec{b}}_0^\text {int}\) and the external body force density \({\varvec{b}}_0^\text {ext}\) integrated over \({\mathcal {B}}_0\) as

$$\begin{aligned} \int _{{\mathcal {B}}_0} \text {D}_t \varvec{\pi }_0 \, \text {d}V = \int _{{\mathcal {B}}_0} {\varvec{b}}_0^\text {int} \, \text {d}V + \int _{{\mathcal {B}}_0} {\varvec{b}}_0^\text {ext} \, \text {d}V \, . \end{aligned}$$
(10)

Therein, the internal body force density \({\varvec{b}}_0^\text {int}\) of a continuum point in PD is an integral over the horizon \({\mathcal {H}}_0\) of the neighbour-wise force density \({\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) between the continuum point \({\varvec{X}}\) and its neighbours \({\varvec{X}}^{{{\,\mathrm{ {}^{\vert } }\,}}}\) as

$$\begin{aligned} {\varvec{b}}_0^\text {int} = \int _{{\mathcal {H}}_0} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(11)

see [9]. In CPD, the neighbour-wise force density \( {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) can be further subdivided into

$$\begin{aligned} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = {{\varvec{p}}_0}_1^{{{\,\mathrm{ {}^{\vert } }\,}}} + {{\varvec{p}}_0}_2^{{{\,\mathrm{ {}^{\vert } }\,}}} + {{\varvec{p}}_0}_3^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(12)

where \({{\varvec{p}}_0}_1^{{{\,\mathrm{ {}^{\vert } }\,}}}\), \({{\varvec{p}}_0}_2^{{{\,\mathrm{ {}^{\vert } }\,}}}\) and \({{\varvec{p}}_0}_3^{{{\,\mathrm{ {}^{\vert } }\,}}}\) denote the neighbour-wise force densities according to one-, two- and three-neighbour interactions [9], respectively. The amount of force density invoked by the mass source \({\mathcal {R}}_0\) is included in the external body force density by \({\varvec{b}}_0^\text {ext} := \bar{{\varvec{b}}}_0^\text {ext} + {\varvec{v}} {\mathcal {R}}_0\), whereby \(\bar{{\varvec{b}}}_0^\text {ext}\) is accordingly called the reduced external body force density.

Localising Eq. (10) and incorporating the expressions for the internal and external body force densities result in the point-wise balance of linear momentum

$$\begin{aligned} \text {D}_t \varvec{\pi }_0 = \int _{{\mathcal {H}}_0} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + {\varvec{\bar{b}}}_0^\text {ext} + {\varvec{v}} {\mathcal {R}}_0 \, . \end{aligned}$$
(13)

In comparison, the balance of linear momentum in CCM reads

$$\begin{aligned} \text {D}_t \varvec{\pi }_0 = \text {Div} {\varvec{P}} + {{\varvec{\bar{b}}}_0^\text {ext} + {\varvec{v}} {\mathcal {R}}_0} \, . \end{aligned}$$
(14)

Incorporating the balance of mass (9) into Eqs. (13) and (14), results in the reduced balance of linear momentum

$$\begin{aligned} \rho _0 \text {D}_t {\varvec{v}} = \int _{{\mathcal {H}}_0} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + \bar{{\varvec{b}}}_0^\text {ext} \, , \end{aligned}$$
(15)

in PD and

$$\begin{aligned} \rho _0 \text {D}_t {\varvec{v}} = \text {Div} {\varvec{P}} + {{\varvec{\bar{b}}}_0^\text {ext}} \, , \end{aligned}$$
(16)

in CCM, respectively.

The balance of angular momentum in PD is derived by starting with the global form of the momentum balance

$$\begin{aligned} \int _{{\mathcal {B}}_0} \text {D}_t \left[ {\varvec{y}} \times \varvec{\pi }_0 \right] \, \text {d} V = \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} {\varvec{y}}^{{{\,\mathrm{ {}^{\vert } }\,}}} \times {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d} V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V + \int _{{\mathcal {B}}_0} {\varvec{y}} \times {\varvec{b}}_0^\text {ext} \, \text {d} V \, . \end{aligned}$$
(17)

With \(\text {D}_t {\varvec{y}} \times \varvec{\pi }_0 = {\varvec{0}}\), \({\varvec{y}}^{{{\,\mathrm{ {}^{\vert } }\,}}} = \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} + {\varvec{y}} \) and the internal body force density (11) at hand, the global balance of angular momentum can be rewritten to

$$\begin{aligned} \int _{{\mathcal {B}}_0} {\varvec{y}} \times \left[ \text {D}_t \varvec{\pi }_0 \right] \text {d} V = \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \times {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d} V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V + \int _{{\mathcal {B}}_0} {\varvec{y}} \times \left[ {\varvec{b}}_0^\text {int} + {\varvec{b}}_0^\text {ext} \right] \text {d} V \, . \end{aligned}$$
(18)

The point-wise balance of angular momentum is obtained via localisation and reads

$$\begin{aligned} {\varvec{y}} \times \left[ \text {D}_t \varvec{\pi }_0 \right]&= \int _{{\mathcal {H}}_0} \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \times {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d} V^{{{\,\mathrm{ {}^{\vert } }\,}}} + {\varvec{y}} \times \left[ {\varvec{b}}_0^\text {int} + {\varvec{b}}_0^\text {ext} \right] \, . \end{aligned}$$
(19)

Incorporating the balance of mass (9) into Eq. (19) yields the reduced point-wise balance of angular momentum

$$\begin{aligned} {\varvec{y}} \times \left[ \rho _0 \text {D}_t {\varvec{v}} \right]&= \int _{{\mathcal {H}}_0} \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \times {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d} V^{{{\,\mathrm{ {}^{\vert } }\,}}} + {\varvec{y}} \times \left[ {\varvec{b}}_0^\text {int} + \bar{{\varvec{b}}}_0^\text {ext} \right] \, . \end{aligned}$$
(20)

Given the balance of linear momentum (15), the point-wise balance of angular momentum (20) can be further reduced to

$$\begin{aligned} \int _{{\mathcal {H}}_0} \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \times {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d} V^{{{\,\mathrm{ {}^{\vert } }\,}}} = {\varvec{0}} \, . \end{aligned}$$
(21)

Javili et al. [9] discuss the required conditions for the interaction potentials of one-, two- and three-neighbour interactions such that the balance of angular momentum is satisfied a priori. With the balance of linear momentum (16) in CCM, the balance of angular momentum results in the following statement

$$\begin{aligned} \varvec{\varepsilon } : \left[ {\varvec{F}} \cdot {\varvec{P}}^\text {t} \right] = {\varvec{0}} \qquad \Rightarrow \qquad {\varvec{F}} \cdot {\varvec{P}}^\text {t} = {\varvec{P}} \cdot {\varvec{F}}^\text {t} \, , \end{aligned}$$
(22)

with the third-order permutation tensor \(\varvec{\varepsilon }\).

3.3 Kinetic energy theorem

Next, we consider the balance equations for internal energy and entropy and establish the dissipation inequality. First, however, we examine the kinetic energy in order to identify the external and internal mechanical power. Therefore, we introduce the global kinetic energy K in the material configuration as

$$\begin{aligned} K := \displaystyle \int _{{\mathcal {B}}_0} k_0 \, \text {d}V \qquad \text {with} \qquad k_0 = \frac{1}{2} \rho _0 {\varvec{v}} \cdot {\varvec{v}} \, , \end{aligned}$$
(23)

being the kinetic energy density per volume. The mass-specific counterpart of the global kinetic energy reads

$$\begin{aligned} K := \displaystyle \int _{{\mathcal {B}}} k \, \text {d}M \qquad \text {with} \qquad k = \frac{1}{2} {\varvec{v}} \cdot {\varvec{v}} \, , \end{aligned}$$
(24)

where k is the kinetic energy density per mass. The temporal rate of the volume-specific kinetic energy is consequently given by

$$\begin{aligned} {\mathcal {K}} := \text {D}_t K = \displaystyle \int _{{\mathcal {B}}_0} \text {D}_t k_0 \, \text {d}V \end{aligned}$$
(25)

with the identity

$$\begin{aligned} \text {D}_t k_0 = k \text {D}_t \rho _0 + \rho _0 \text {D}_t k = {\varvec{v}} \cdot \text {D}_t \varvec{\pi }_0 - k \text {D}_t \rho _0 \, . \end{aligned}$$
(26)

Given the balance of linear momentum (10) and balance of mass (8), we obtain the kinetic energy theorem

$$\begin{aligned} {\mathcal {K}} = \displaystyle \int _{{\mathcal {B}}_0} {\varvec{v}} \cdot {\varvec{b}}^\text {int}_0 \, \text {d}V + \displaystyle \int _{{\mathcal {B}}_0} {\varvec{v}} \cdot {\varvec{b}}^\text {ext}_0 \, \text {d}V - \displaystyle \int _{{\mathcal {B}}_0} k {\mathcal {R}}_0 \, \text {d}V \, . \end{aligned}$$
(27)

The definition of the internal body force density (11), the external body force density \({\varvec{b}}^\text {ext}_0:=\bar{{\varvec{b}}}^\text {ext}_0 + {\varvec{v}} {\mathcal {R}}_0\) and the relations \({\varvec{v}} \cdot {\varvec{v}} = 2k\) and \({\varvec{v}} = {\varvec{v}}^{{{\,\mathrm{ {}^{\vert } }\,}}} - \text {D}_t\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}\) yield the more detailed form of the kinetic energy theorem

$$\begin{aligned} {\mathcal {K}} =&\displaystyle \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} {\varvec{v}}^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V + \displaystyle \int _{{\mathcal {B}}_0} {\varvec{v}} \cdot \bar{{\varvec{b}}}^\text {ext}_0 \, \text {d}V + \displaystyle \int _{{\mathcal {B}}_0} k {\mathcal {R}}_0 \, \text {d}V \nonumber \\&- \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V \, . \end{aligned}$$
(28)

Incorporating the virtual power equivalence

$$\begin{aligned} \displaystyle \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} \delta {\varvec{y}}^{{{\,\mathrm{ {}^{\vert } }\,}}}\cdot {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V = \int _{\partial {\mathcal {B}}_0} \delta {\varvec{y}} \cdot {\varvec{t}}_0^\text {ext} \, \text {d}A \qquad \forall \delta {\varvec{y}} \, , \end{aligned}$$
(29)

proposed in [9], with particularising \(\delta {\varvec{y}} = {\varvec{v}}\) results in

$$\begin{aligned} {\mathcal {K}} =&\displaystyle \int _{\partial {\mathcal {B}}_0} {\varvec{v}} \cdot {\varvec{t}}_0^\text {ext} \, \text {d}A + \displaystyle \int _{{\mathcal {B}}_0} {\varvec{v}} \cdot \bar{{\varvec{b}}}^\text {ext}_0 \, \text {d}V + \displaystyle \int _{{\mathcal {B}}_0} k {\mathcal {R}}_0 \, \text {d}V \nonumber \\&- \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V \, , \end{aligned}$$
(30)

where we can identify the external mechanical power

$$\begin{aligned} {\mathcal {P}}^\text {ext} = \displaystyle \int _{\partial {\mathcal {B}}_0} {\varvec{v}} \cdot {\varvec{t}}_0^\text {ext} \, \text {d}A + \displaystyle \int _{{\mathcal {B}}_0} {\varvec{v}} \cdot \bar{{\varvec{b}}}^\text {ext}_0 \, \text {d}V + \displaystyle \int _{{\mathcal {B}}_0} k {\mathcal {R}}_0 \, \text {d}V \, , \end{aligned}$$
(31)

due to the mass source and externally prescribed body forces and tractions. In addition, we identify the internal mechanical power due to interaction forces as

$$\begin{aligned} {\mathcal {P}}^\text {int} = \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V \, . \end{aligned}$$
(32)

The kinetic energy theorem can eventually be summarised in terms of the externally and internally generated mechanical power as

$$\begin{aligned} {\mathcal {K}} = {\mathcal {P}}^\text {ext} - {\mathcal {P}}^\text {int} \, . \end{aligned}$$
(33)

3.4 Balance of internal energy

Let U denote the global internal energy that is obtained by the integral of the internal energy density \(u_0\) over \({\mathcal {B}}_0\) as

$$\begin{aligned} U := \displaystyle \int _{{\mathcal {B}}_0} u_0 \, \text {d}V \, , \end{aligned}$$
(34)

and its temporal rate

$$\begin{aligned} {\mathcal {U}} := \text {D}_t U \qquad \Rightarrow \qquad {\mathcal {U}} = \displaystyle \int _{{\mathcal {B}}_0} \text {D}_t u_0 \, \text {d}V \, . \end{aligned}$$
(35)

We consider that the internal energy density \(u_0\) per volume of a continuum point is a nonlocal quantity, which is why it is given by an integral over \({\mathcal {H}}_0\) of the internal energy density \(u_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) per volume squared as

$$\begin{aligned} u_0 = \displaystyle \int _{{\mathcal {H}}_0} u_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \qquad \text {with} \qquad u_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} u^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(36)

To proceed, we briefly address the balance of total energy \(E = K + U\). In closed and open systems the temporal rate of the total energy \({\mathcal {E}} = {\mathcal {K}} + {\mathcal {U}}\) is equal to the external power of the system that is composed of a mechanical and non-mechanical contribution. Denoting the external thermal power as \({\mathcal {Q}}^\text {ext}\) yields the balance of total energy

$$\begin{aligned} {\mathcal {E}} = {\mathcal {P}}^\text {ext} + {\mathcal {Q}}^\text {ext} \, . \end{aligned}$$
(37)

Note that in contrast to closed systems, we have additional external power contributions in \({\mathcal {P}}^\text {ext}\) and \({\mathcal {Q}}^\text {ext}\) due to the mass source \({\mathcal {R}}_0\).

With the balance of kinetic energy (33) and the balance of total energy (37) at hand, it follows that the temporal rate of internal energy is equal to the sum of the internal mechanical power \({\mathcal {P}}^\text {int}\) and the external thermal power \({\mathcal {Q}}^\text {ext}\), that is

$$\begin{aligned} {\mathcal {U}} = {\mathcal {P}}^\text {int} + {\mathcal {Q}}^\text {ext} \, . \end{aligned}$$
(38)

The external thermal power \({\mathcal {Q}}^\text {ext}\) summarises the thermal power induced by externally prescribed heat within the body \({\mathcal {B}}_0\) and heat “flux” on the boundary \(\partial {\mathcal {B}}_0\) as

$$\begin{aligned} {\mathcal {Q}}^\text {ext} = {\mathcal {Q}}_{\mathcal {B}}^\text {ext} + {\mathcal {Q}}_{\partial {\mathcal {B}}}^\text {ext} \, , \end{aligned}$$
(39)

with

$$\begin{aligned} {\mathcal {Q}}_{\mathcal {B}}^\text {ext} := \displaystyle \int _{{\mathcal {B}}_0} {\mathscr {R}}_0^\text {ext} \, \text {d}V \qquad \text {and} \qquad {\mathcal {Q}}_{\partial {\mathcal {B}}}^\text {ext} := - \displaystyle \int _{\partial {\mathcal {B}}_0} {\mathscr {Q}}_0^\text {ext} \, \text {d}A \, . \end{aligned}$$
(40)

Therein, \({\mathscr {R}}_0^\text {ext}\) is the external heat source that is composed of the reduced external heat source \(\bar{{\mathscr {R}}}^{ext}_0\) and a nonlocal source term caused by the mass source \({\mathcal {R}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) and the internal energy density \(u^{{{\,\mathrm{ {}^{\vert } }\,}}}\) of the neighbour as

$$\begin{aligned} {\mathscr {R}}_0^\text {ext} = \bar{{\mathscr {R}}}^{ext}_0 + \displaystyle \int _{{\mathcal {H}}_0} u^{{{\,\mathrm{ {}^{\vert } }\,}}} {\mathcal {R}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(41)

The external heat “flux” density \({\mathscr {Q}}_0^\text {ext}\) per area is equivalently expressed in the peridynamic formulation as a nonlocal quantity by

$$\begin{aligned} \displaystyle \int _{\partial {\mathcal {B}}_0} {\mathscr {Q}}_0^\text {ext} \, \text {d}A = \displaystyle \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} q_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V \end{aligned}$$
(42)

with the heat “flux” density \(q_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) per volume squared.

In CCM, the external heat source \({\mathscr {R}}_0^\text {ext} := \bar{{\mathscr {R}}}^{ext}_0 + u {\mathcal {R}}_0\) of Eq. (40) is a local quantity, dependent on the internal energy u and mass source \({\mathcal {R}}_0\) of a continuum point [24]. Furthermore, the external heat flux density \({\mathscr {Q}}_0^\text {ext}\) is expressed by the heat flux vector \({\varvec{Q}}\) per area as \({\mathscr {Q}}_0^\text {ext} = {\varvec{Q}} \cdot {\varvec{N}}\) that is comparable to \({\varvec{t}}_0^\text {ext} = {\varvec{P}} \cdot {\varvec{N}}\) for the mechanical problem and yields the counterpart to Eq. (42)

$$\begin{aligned} \displaystyle \int _{\partial {\mathcal {B}}_0} {\mathscr {Q}}_0^\text {ext} \, \text {d}A = \displaystyle \int _{{\mathcal {B}}_0} \text {Div}{\varvec{Q}} \, \text {d}V \, . \end{aligned}$$
(43)

Equipped with the detailed expressions of the external thermal power, we obtain via localisation the point-wise form in PD

$$\begin{aligned} \displaystyle \int _{{\mathcal {H}}_0} \text {D}_t u_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} =&- \displaystyle \int _{{\mathcal {H}}_0} q_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}}+ \bar{{\mathscr {R}}}^{ext}_0 + \displaystyle \int _{{\mathcal {H}}_0} u^{{{\,\mathrm{ {}^{\vert } }\,}}} {\mathcal {R}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \nonumber \\&+ \int _{{\mathcal {H}}_0} \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(44)

and its counterpart in CCM

$$\begin{aligned} \text {D}_t u_0 = - \text {Div} {\varvec{Q}} + \bar{{\mathscr {R}}}^{ext}_0 + u {\mathcal {R}}_0 + {\varvec{P}} : \text {D}_t {\varvec{F}} \, . \end{aligned}$$
(45)

Next, we incorporate the balance of mass into both balance equations, (44) and (45). However, for the peridynamic balance equation (44) we use the balance of mass of the neighbours instead of the continuum point as the internal energy \(u_0\) is considered a nonlocal quantity. Consequently, we obtain the reduced balance of internal energy

$$\begin{aligned} \displaystyle \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \text {D}_t u^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = - \displaystyle \int _{{\mathcal {H}}_0} q_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + \bar{{\mathscr {R}}}^{ext}_0 + \int _{{\mathcal {H}}_0} \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(46)

in PD and its local counterpart in CCM

$$\begin{aligned} \rho _0 \text {D}_t u = - \text {Div} {\varvec{Q}} + \bar{{\mathscr {R}}}^{ext}_0 + {\varvec{P}} : \text {D}_t {\varvec{F}} \, . \end{aligned}$$
(47)

3.5 Balance of entropy

Based on the second law of thermodynamics, we introduce a new extensive quantity, the entropy of the system, which dictates the direction of a thermodynamical process. For this purpose, let S denote the global entropy that is obtained by the integral of the entropy density \(s_0\) per volume over \({\mathcal {B}}_0\) as

$$\begin{aligned} S := \displaystyle \int _{{\mathcal {B}}_0} s_0 \, \text {d}V \, , \end{aligned}$$
(48)

and its temporal rate

$$\begin{aligned} {\mathcal {S}} := \text {D}_t S \qquad \Rightarrow \qquad {\mathcal {S}} = \displaystyle \int _{{\mathcal {B}}_0} \text {D}_t s_0 \, \text {d}V \, . \end{aligned}$$
(49)

We consider that the entropy density \(s_0\) of a continuum point is a nonlocal quantity, which is obtained by an integral over \({\mathcal {H}}_0\) of the entropy density \(s_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) per volume squared, that is

$$\begin{aligned} s_0 = \displaystyle \int _{{\mathcal {H}}_0} s_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \qquad \text {with} \qquad s_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} s^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(50)

The entropy of an open system is balanced by the input of entropy as

$$\begin{aligned} {\mathcal {S}} = {\mathcal {H}}^\text {ext} + {\mathcal {H}}^\text {prd} \, , \end{aligned}$$
(51)

where \({\mathcal {H}}^\text {ext}\) is the external entropy contribution and \({\mathcal {H}}^\text {prd} \ge 0\) is the positive entropy production. Similar to the external heat source \({\mathcal {Q}}^\text {ext}\), the external entropy input \({\mathcal {H}}^\text {ext}\) is composed of a source term \({\mathcal {H}}_{{\mathcal {B}}}^\text {ext}\) within the body \({\mathcal {B}}_0\) and a flux term \({\mathcal {H}}_{\partial {\mathcal {B}}}^\text {ext}\) on the boundary \(\partial {\mathcal {B}}_0\) as

$$\begin{aligned} {\mathcal {H}}^\text {ext} = {\mathcal {H}}_{{\mathcal {B}}}^\text {ext} + {\mathcal {H}}_{\partial {\mathcal {B}}}^\text {ext} \, . \end{aligned}$$
(52)

Next, we establish a relation between the external entropy source on the boundary \({\mathcal {H}}_{\partial {\mathcal {B}}}^\text {ext}\) and the external heat “flux” density \(q_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) in dependency on the absolute neighbour-wise temperature \(T^{{{\,\mathrm{ {}^{\vert } }\,}}} > 0\), that reads

$$\begin{aligned} {\mathcal {H}}_{\partial {\mathcal {B}}}^\text {ext} = - \displaystyle \int _{{\mathcal {B}}_0} \int _{{\mathcal {H}}_0} \dfrac{q_0^{{{\,\mathrm{ {}^{\vert } }\,}}} }{T^{{{\,\mathrm{ {}^{\vert } }\,}}} } \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V \, . \end{aligned}$$
(53)

The external entropy source within the body \({\mathcal {H}}_{{\mathcal {B}}}^\text {ext}\) is expressed in terms of an external entropy density \({\mathfrak {H}}_0^\text {ext}\) as

$$\begin{aligned} {\mathcal {H}}_{{\mathcal {B}}}^\text {ext} = \displaystyle \int _{{\mathcal {B}}_0} {\mathfrak {H}}_0^\text {ext} \, \text {d}V \qquad \text {with} \qquad {\mathfrak {H}}_0^\text {ext} = \dfrac{\bar{{\mathscr {R}}}^{ext}_0}{T} + \displaystyle \int _{{\mathcal {H}}_0} s^{{{\,\mathrm{ {}^{\vert } }\,}}} {\mathcal {R}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} +{\mathscr {S}}_0 \, . \end{aligned}$$
(54)

Therein, the external entropy density \({\mathfrak {H}}_0^\text {ext}\) is composed of the reduced external heat source \(\bar{{\mathscr {R}}}^{ext}_0\) divided by the absolute temperature T, a nonlocal source term resulting from the mass source \({\mathcal {R}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) and the entropy density \(s^{{{\,\mathrm{ {}^{\vert } }\,}}}\) and an extra entropy source \({\mathscr {S}}_0\) as a characteristic of open systems.

Introducing the dissipation density \({\mathscr {D}}_0 \ge 0\) of a continuum point, we can express the positive entropy production as

$$\begin{aligned} {\mathcal {H}}^\text {prd} = \displaystyle \int _{{\mathcal {B}}_0} \frac{{\mathscr {D}}_0}{T} \, \text {d}V \ge 0 \, . \end{aligned}$$
(55)

Thus, we obtain the point-wise balance of entropy

$$\begin{aligned} \displaystyle \int _{{\mathcal {H}}_0} \text {D}_t s_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = - \displaystyle \int _{{\mathcal {H}}_0} \dfrac{q_0^{{{\,\mathrm{ {}^{\vert } }\,}}}}{T^{{{\,\mathrm{ {}^{\vert } }\,}}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + \dfrac{\bar{{\mathscr {R}}}^{ext}_0}{T} + \displaystyle \int _{{\mathcal {H}}_0} s^{{{\,\mathrm{ {}^{\vert } }\,}}} {\mathcal {R}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} +{\mathscr {S}}_0 + \dfrac{{\mathscr {D}}_0}{T} \, . \end{aligned}$$
(56)

Since the entropy density \(s_0\) is a nonlocal quantity, we further reduce the balance of entropy with the help of the balance of mass of the neighbours, resulting in

$$\begin{aligned} \displaystyle \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \text {D}_t s^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = - \displaystyle \int _{{\mathcal {H}}_0} \dfrac{q_0^{{{\,\mathrm{ {}^{\vert } }\,}}}}{T^{{{\,\mathrm{ {}^{\vert } }\,}}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + \dfrac{\bar{{\mathscr {R}}}^{ext}_0}{T} +{\mathscr {S}}_0 + \dfrac{{\mathscr {D}}_0}{T} \, . \end{aligned}$$
(57)

Under isothermal conditions with \(T = T^{{{\,\mathrm{ {}^{\vert } }\,}}}\), we eventually obtain

$$\begin{aligned} T \displaystyle \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \text {D}_t s^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = - \displaystyle \int _{{\mathcal {H}}_0} q_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} + \bar{{\mathscr {R}}}^{ext}_0 +T{\mathscr {S}}_0 + {\mathscr {D}}_0, \end{aligned}$$
(58)

that should be compared to its local counterpart in CCM

$$\begin{aligned} T \rho _0 \text {D}_t s = - \text {Div}{\varvec{Q}} + \bar{{\mathscr {R}}}^{ext}_0 +T{\mathscr {S}}_0 + {\mathscr {D}}_0 \, . \end{aligned}$$
(59)

4 Dissipation inequality

We first introduce the Helmholtz energy density in the material configuration that can be expressed by the internal energy \(u_0\) and the entropy \(s_0\) multiplied with the absolute temperature T, i.e. via a Legendre transformation as

$$\begin{aligned} \Psi _0 := u_0 - T s_0 \end{aligned}$$
(60)

with its time derivative

$$\begin{aligned} \text {D}_t \Psi _0 = \text {D}_t u_0 - \text {D}_t T s_0 - T \text {D}_t s_0 \, . \end{aligned}$$
(61)

Under isothermal conditions Eq. (61) reduces to

$$\begin{aligned} \text {D}_t \Psi _0 = \text {D}_t u_0 - T \text {D}_t s_0 \, , \end{aligned}$$
(62)

since \(\text {D}_t T = 0\). Note that we only state the quantities per unit volume for the sake of brevity.

To continue, we first need to express nonlocal quantities in integral form. In PD, we consider the Helmholtz energy density \(\Psi _0\) per volume as a nonlocal quantity that is given by

$$\begin{aligned} \Psi _0 = \int _{{\mathcal {H}}_0} \psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \qquad \text {with} \qquad \psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}} = {{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}\psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(63)

where \(\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) denotes the Helmholtz energy density per volume squared and \(\psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}\) the Helmholtz energy density per mass and per volume.

Since \(\Psi _0\), \(u_0\) and \(s_0\) are considered nonlocal quantities, Eq. (60) of our peridynamic formulation can accordingly be rewritten in integral form

$$\begin{aligned} \int _{{\mathcal {H}}_0} \psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} := \int _{{\mathcal {H}}_0} u_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T \int _{{\mathcal {H}}_0} s_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(64)

for isothermal conditions with \(T = T^{{{\,\mathrm{ {}^{\vert } }\,}}}\). The respective time derivative reads

$$\begin{aligned} \int _{{\mathcal {H}}_0} \text {D}_t \psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = \int _{{\mathcal {H}}_0} \text {D}_t u_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T \int _{{\mathcal {H}}_0} \ \text {D}_t s_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(65)

Expressing Eq. (65) in terms of the density \({{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}\) of the neighbour and the quantities per unit mass and volume yields

$$\begin{aligned} \int _{{\mathcal {H}}_0} \text {D}_t ({{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}\psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} ) \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = \int _{{\mathcal {H}}_0} \text {D}_t ({{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}u^{{{\,\mathrm{ {}^{\vert } }\,}}} ) \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T \int _{{\mathcal {H}}_0} \ \text {D}_t ({{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}s^{{{\,\mathrm{ {}^{\vert } }\,}}}) \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(66)

Next, incorporating the neighbour-wise counterpart per volume and per mass of Eq. (64), that is

$$\begin{aligned} \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} := u^{{{\,\mathrm{ {}^{\vert } }\,}}} - T s^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(67)

multiplied with the temporal rate of the density \({{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}\) of the neighbour into Eq. (66) results in

$$\begin{aligned} \int _{{\mathcal {H}}_0} {{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}\text {D}_t \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = \int _{{\mathcal {H}}_0} {{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}\text {D}_t u^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T \int _{{\mathcal {H}}_0} \ {{\,\mathrm{ \rho _0^{{}^{\vert }} }\,}}\text {D}_t s^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(68)

In a last step, inserting the balances of internal energy (46) and entropy (58) in Eq. (68), yields the dissipation inequality in PD

$$\begin{aligned} {\mathscr {D}}_0 = \int _{{\mathcal {H}}_0} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \text {D}_t \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T{\mathscr {S}}_0 \ge 0 \, . \end{aligned}$$
(69)

Under the same conditions, the counterpart in CCM reads

$$\begin{aligned} {\mathscr {D}}_0 = {{\varvec{P}}} : \text {D}_t {{\varvec{F}}} - \mathrm {\rho _0 \text {D}_t \Psi - T{\mathscr {S}}_0 \ge 0} \, . \end{aligned}$$
(70)

Additionally to the point-wise dissipation inequality, we can formulate a neighbour-wise form for our peridynamic formulation. Therefore, we introduce the extra entropy source \({\mathscr {S}}_0\) and the dissipation \({\mathscr {D}}_0\) in integral form as

$$\begin{aligned} {\mathscr {S}}_0 = \displaystyle \int _{{\mathcal {H}}_0} {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \qquad \text {and} \qquad {\mathscr {D}}_0 = \displaystyle \int _{{\mathcal {H}}_0} d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, , \end{aligned}$$
(71)

respectively. Therein, \({\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \) denotes the extra entropy source density per volume squared and \(d_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) the dissipation density per volume squared. The resulting point-wise dissipation inequality reads

$$\begin{aligned} \displaystyle \int _{{\mathcal {H}}_0} d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = \int _{{\mathcal {H}}_0} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \text {D}_t \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T \int _{{\mathcal {H}}_0} {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \ge 0 \, . \end{aligned}$$
(72)

Via localisation we obtain the more restrictive neighbour-wise dissipation inequality

$$\begin{aligned} d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} - \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \text {D}_t \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} - T {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \ge 0 \, . \end{aligned}$$
(73)

The condition \(d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \ge 0\) for all neighbours yields \({\mathscr {D}}_0 \ge 0\), but conversely \({\mathscr {D}}_0 \ge 0\) does not imply the condition \(d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \ge 0\).

5 Coleman–Noll procedure

Based on the Coleman–Noll procedure, we gain the structure and constraints of the constitutive equations that define the material behaviour. Recall the neighbour-wise energy density per mass and per volume

$$\begin{aligned} \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} = \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}(\rho _0, \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}, \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}, {\varvec{a}}^{{{\,\mathrm{ {}^{\vert , \vert \vert } }\,}}}, v^{{{\,\mathrm{ {}^{\vert , \vert \vert , \vert \vert \vert } }\,}}}) \, , \end{aligned}$$
(74)

that is dependent on the material densities, \(\rho _0\) and \(\rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}\), and the line vector \(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}\), the vectorial area element \({\varvec{a}}^{{{\,\mathrm{ {}^{\vert , \vert \vert } }\,}}}\) and the finite volume element \(v^{{{\,\mathrm{ {}^{\vert , \vert \vert , \vert \vert \vert } }\,}}}\) in the spatial configuration. The vectorial area element and the finite volume element are defined in terms of the line elements \(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}\), \(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert \vert } }\,}}}\) and \(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert \vert \vert } }\,}}}\), respectively, as

$$\begin{aligned} {\varvec{a}}^{{{\,\mathrm{ {}^{\vert , \vert \vert } }\,}}} := \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \times \varvec{\xi }^{{{\,\mathrm{ {}^{\vert \vert } }\,}}} \qquad \text {and} \qquad v^{{{\,\mathrm{ {}^{\vert , \vert \vert , \vert \vert \vert } }\,}}} := \left[ \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \times \varvec{\xi }^{{{\,\mathrm{ {}^{\vert \vert } }\,}}} \right] \cdot \varvec{\xi }^{{{\,\mathrm{ {}^{\vert \vert \vert } }\,}}} \, , \end{aligned}$$

see [9]. The temporal rate of the neighbour-wise energy density consequently reads

$$\begin{aligned} \text {D}_t \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}(\rho _0, \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}, \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}, {\varvec{a}}^{{{\,\mathrm{ {}^{\vert , \vert \vert } }\,}}}, v^{{{\,\mathrm{ {}^{\vert , \vert \vert , \vert \vert \vert } }\,}}}) = \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0} \text {D}_t \rho _0 + \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} + \frac{\delta \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\delta \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}} \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(75)

Therein, \(\delta \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} / \delta \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \) denotes the variational derivative due to one-, two- and three-neighbour interactions that is defined in [9].

Given the detailed form of \(\text {D}_t \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}(\rho _0, \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}, \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}, {\varvec{a}}^{{{\,\mathrm{ {}^{\vert , \vert \vert } }\,}}}, v^{{{\,\mathrm{ {}^{\vert , \vert \vert , \vert \vert \vert } }\,}}})\) and Eq. (72), we obtain the extensive point-wise dissipation inequality

$$\begin{aligned} {\mathscr {D}}_0 =&\displaystyle \int _{{\mathcal {H}}_0} d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = \int _{{\mathcal {H}}_0} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \nonumber \\&- \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \left[ \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0} \text {D}_t \rho _0 + \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} + \frac{\delta \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\delta \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}} \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \right] \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \nonumber \\&- T\int _{{\mathcal {H}}_0} {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \ge 0 \end{aligned}$$
(76)

that can be rewritten as

$$\begin{aligned} {\mathscr {D}}_0 =&\displaystyle \int _{{\mathcal {H}}_0} d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} = \int _{{\mathcal {H}}_0} \left[ {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} - \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \frac{\delta \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\delta \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}} \right] \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}}\nonumber \\&- \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \left[ \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0} \text {D}_t \rho _0 + \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \right] \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T \int _{{\mathcal {H}}_0} {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \ge 0 \, . \end{aligned}$$
(77)

In case of an isothermal elastic problem, solely contributions from the open system cause energy dissipation. Thus, the mechanical contribution of Eq. (77) should vanish, yielding the constitutive expression for the pairwise force density

$$\begin{aligned} {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \frac{\delta \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\delta \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}} \, . \end{aligned}$$
(78)

The more restrictive neighbour-wise dissipation inequality

$$\begin{aligned} d_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \left[ {\varvec{p}}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} - \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \frac{\delta \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\delta \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}} \right] \cdot \text {D}_t \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} - \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \left[ \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0} \text {D}_t \rho _0 + \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \right] - T {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \ge 0 \, , \end{aligned}$$
(79)

is obtained by further localising the point-wise dissipation inequality (77).

In a last step, we can formulate a reduced point-wise dissipation inequality

$$\begin{aligned} {{\mathscr {D}}_0}_\text {\tiny red} = - \int _{{\mathcal {H}}_0} \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \left[ \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0} \text {D}_t \rho _0 + \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \right] \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - T \int _{{\mathcal {H}}_0} {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \ge 0 \, , \end{aligned}$$
(80)

and further reduced neighbour-wise dissipation inequality

$$\begin{aligned} {d_0^{{{\,\mathrm{ {}^{\vert } }\,}}}}_\text {\tiny red} = - \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \left[ \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0} \text {D}_t \rho _0 + \frac{\partial \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\partial \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \right] - T {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \ge 0 \, , \end{aligned}$$
(81)

in addition to the constitutive expression (78). Note that the extra entropy source is here needed to assure positive dissipation.

6 Example for the nonlocal mass source

As an example for a nonlocal mass source, we present in the following constitutive expressions to model the complex process of bone remodelling in a peridynamic way. Therefore, we maintain the mass source function

$$\begin{aligned} {\mathcal {R}}_0 = c \left[ \left[ \dfrac{\rho _0}{\rho _0^*}\right] ^{-m} \Psi _0 - \Psi _0^* \right] \, , \end{aligned}$$
(82)

that is commonly used in local continuum models [25,26,27,28,29] to govern the temporal change in bone density. In Eq. (82), the energy density \(\Psi _0\) is weighted with a power of the nominal relative density of the material density \(\rho _0\) at the continuum point with respect to the initial material density \(\rho _0^*\) homogenised at the macroscale. The attractor stimulus \(\Psi _0^* \) indicates the energy state to reach homeostasis. The parameter c is introduced in Eq. (82) to govern the velocity of the bone remodelling process. The stability of the mass source function is determined by the dimensionless exponent m.

Up to this point, the balance of mass (9) and the expression of the mass source (82) is equivalent in the PD and CCM formulation. However, in our peridynamic formulation the nonlocal energy density \(\Psi _0\), given in Eq. (63), imparts the mass source \({\mathcal {R}}_0\) its nonlocal characteristic.

As we only consider one-neighbour interactions for the sake of demonstration, the Helmholtz energy density per volume squared is specified by

$$\begin{aligned} \psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}(\rho _0, \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}, \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}) = \dfrac{1}{2} {\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}_1(\rho _0, \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}, \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}) \, , \end{aligned}$$
(83)

where the subindex 1 indicates the one-neighbour interaction property. Considering the global form of the balance equations and only one-neighbour interactions, we are visiting every continuum point twice, which is why we introduced the factor one half in Eq. (83) to avoid double counting of energy [9].

Since bone tissue is classified as open-pored hard tissue, the energy density in local models is typically weighted with the nth-power of the nominal relative density, see [25, 30]. Extending this approach to the peridynamic case, the pairwise energy density per volume squared is weighted by the nth-power of the (nonlocal) nominal relative density as

$$\begin{aligned} {\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}_1(\rho _0, \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}, \varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}) = \left[ \dfrac{{\widehat{\rho }}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\rho _0^*} \right] ^n {\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}^{\text {\tiny {PD}}}_1(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}) \qquad \text {with} \qquad {\widehat{\rho }}_0^{{{\,\mathrm{ {}^{\vert } }\,}}} = \tfrac{1}{2} [ \rho _0 + \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} ] \, , \end{aligned}$$
(84)

where the superscript PD is introduced to distinguish between the density-dependent pairwise energy density \({\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}_1\) and the density-independent pairwise energy density \({\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}^{\text {\tiny {PD}}}_1\) that determines the purely mechanical material behaviour. With Eqs. (63)\(_2\), (83) and (84)\(_1\) at hand, the neighbour-wise energy density per mass and per volume reads

$$\begin{aligned} \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} = \dfrac{1}{2} \dfrac{1}{\rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \left[ \dfrac{{\widehat{\rho }}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\rho _0^*} \right] ^n {\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}^{\text {\tiny {PD}}}_1(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}) \, . \end{aligned}$$
(85)

In contrast to Eq. (82), the nominal relative density in Eq. (84) and (85), respectively, is nonlocal as it is determined by the arithmetic mean density \({\widehat{\rho }}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}\) that can be interpreted as a pairwise density. With this approach, we model a material behaviour, wherein two continuum points exert forces with same magnitude on each other, which corresponds to the fundamental idea of bond-based PD [15]. The dimensionless exponent n in Eq. (84) that governs the porosity of bone tissue is determined empirically in CMM [31] and varies between \(1 \le n \le 3.5\). In CCM, numerical stability and uniqueness of solutions is ensured for \(n<m\), see [25] and [32], respectively.

Accordingly, the Helmholtz energy density per volume that enters the mass source function \({\mathcal {R}}_0\) reads

$$\begin{aligned} \Psi _0 = \dfrac{1}{2} \int _{{\mathcal {H}}_0} \left[ \dfrac{{\widehat{\rho }}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\rho _0^*} \right] ^n {\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}^{\text {\tiny {PD}}}_1(\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}}) \, \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} \, . \end{aligned}$$
(86)

For the underlying purely mechanical material behaviour, we utilise the harmonic pairwise energy density function

$$\begin{aligned} {\psi _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}^{\text {\tiny {PD}}}_1 = \dfrac{1}{2} C L \left[ \dfrac{l}{L} - 1\right] ^2 \, , \end{aligned}$$
(87)

that is typically used in PD literature [9, 15], since an elastic energy density is typically employed to model open-pored hard tissue [33]. In Eq. (87), \(L = |\varvec{\Xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} |\) and \(l = |\varvec{\xi }^{{{\,\mathrm{ {}^{\vert } }\,}}} |\) are the bond lengths in the material and spatial configuration, respectively. The peridynamic material parameter C indicates the resistance against the change of bond length.

The more detailed expression of the mass source function in our peridynamic model for bone remodelling,

$$\begin{aligned} {\mathcal {R}}_0 = c \left[ \left[ \dfrac{\rho _0}{\rho _0^*}\right] ^{-m} \dfrac{1}{2} \int _{{\mathcal {H}}_0} \left[ \dfrac{{\widehat{\rho }}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}}{\rho _0^*} \right] ^n \dfrac{1}{2} C L \left[ \dfrac{l}{L} - 1\right] ^2 \text {d}V^{{{\,\mathrm{ {}^{\vert } }\,}}} - \Psi _0^* \right] \, , \end{aligned}$$
(88)

clearly emphasises the nonlocal characteristic of the mass source \({\mathcal {R}}_0\). From the neighbour-wise dissipation inequality (81) the entropy source \({\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0\) follows as

$$\begin{aligned} {\mathfrak {s}}^{{{\,\mathrm{ {}^{\vert } }\,}}}_0 \le - \dfrac{1}{T} \psi ^{{{\,\mathrm{ {}^{\vert } }\,}}} \left[ \dfrac{1}{2} n \dfrac{\rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}}}{{\widehat{\rho }}_0^{{{\,\mathrm{ {}^{\vert } }\,}}}} \left[ \text {D}_t \rho _0 + \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \right] - \text {D}_t \rho _0^{{{\,\mathrm{ {}^{\vert } }\,}}} \right] \, . \end{aligned}$$
(89)

7 Conclusion

This contribution proposes a framework for the thermodynamics of open system (continuum-kinematics-inspired) peridynamics. We introduced the balance of mass as a local balance equation that allows the system to gain or lose mass dependent on the (nonlocal) mass source. Equivalent to classical continuum open system mechanics, we assume that the change in mass affects the balances of linear momentum, internal energy and entropy. For the peridynamic formulation we distinguish between local and nonlocal balance equations. By incorporating the balance of mass into the volume-specific balance equations, we obtained the corresponding reduced balance equations, whose structures are comparable to the ones valid in closed system peridynamics.

We have presented an example for a nonlocal mass source, where we exploit the constitutive equations of bone remodelling processes. In order to demonstrate the influence of nonlocality on the governing equations, a numerical example of a biaxial deformation test is shown in Fig. 3. The relative density evolution for different horizon sizes \(\delta \) that results from a stepwise applied deformation function highlights the influence of nonlocality on the temporal change in relative density. Further numerical examples and information on the computational implementation can be found in [12].

Fig. 3
figure 3

In peridynamics, a continuum body \({\mathcal {B}}_0\) (top left) is discretised into a finite number of collocation points \({\mathcal {P}}^a\) (top right). The relative density evolution (bottom) for different horizon sizes \(\delta \), resulting from a stepwise biaxial deformation \({\varvec{u}} = \bar{{\varvec{u}}}\) with a stepwise incremental strain of \(\Delta \varepsilon \ = 0.015\) in horizontal and vertical direction applied on a unit square, shows the influence of nonlocality. For all simulations, we uniformly set \(\delta /\Delta = 3.01\), \(\rho _0^* = 1.0\), \(c = 1000\), \(m = 3\), \(n = 2\), \(\Psi _0^* = 0.001\) and \(E = 1.0\). The peridynamic parameter C in Eq. (87) for one-neighbour interactions is computed by the relation \(C = 9E/\delta ^3 \pi \) with the Young’s modulus E [34]

Full size image

In summary, this contribution proposes a thermodynamically consistent framework for open system (continuum-kinematics-inspired) peridynamics for the first time. We believe that this framework can be used to study and better understand nonlocal material behaviour in biomechanical and chemomechanical processes where the material density changes in time due to a (nonlocal) mass source.

In future research, our open system (continuum-kinematics-inspired) peridynamic framework will be exploited to model and study nonlocal material behaviour occurring in implant-bone-interfaces between non-living and living material. Furthermore, we will use this framework to account for material density changes during bone healing processes, revisiting the initial scope of PD in fracture mechanics. Regarding the example of a nonlocal mass source, this contribution has focused, for the sake of demonstration, on one-neighbour interactions of the CPD framework of Javili et al. [9]. In future, we will also study the influence of two- and three-neighbour interactions on the density evolution. In a next step, the balance of mass can be enhanced by a mass “flux” density, allowing in- or out-“flux” of mass.