1 Introduction

The continuum-mechanics-based theory of elasticity, see, e.g., Timoshenko and Goodier [28], serves as benchmark for the assessment of the accuracy of various structural mechanics beam theories of increasing complexity. The latter beam theories intend to approximate multi-dimensional elasticity solutions by one-dimensional solutions, stemming from the fundamental formulations of continuum mechanics, see Altenbach and Öchsner [5], by one-dimensional solutions, see, e.g., Krommer and Vetyukov [21]. Particularly, the plane stress formulation of two-dimensional linear elasticity ever since has been used for a comparison in case of plane bending and stretching of beams with rectangular cross sections. This strategy dates back to von Karman [16] and Seewald [26], who, using integral transform techniques, studied an isotropic homogeneous rectangular strip in plane stress according to the elasticity theory and compared their results to the classical Bernoulli–Euler (BE) theory of beams. Von Karman [16] eventually showed that the curvature of the axis of an infinitely extended strip can be expressed as an infinite series in the bending moment and its spatial derivatives. The second (non-vanishing) term in the curvature series, containing the second derivative of the bending moment, was explicitly communicated in [16]. Von Karman’s work [16] was accompanied by a study of Seewald [26], who gave a corresponding series representation for the stresses across the strip. The first terms in the series representations of [16, 26] for the curvature, the axial stress and the shear stress turned out to be equal to the formulations provided by the classical BE theory of beams. For smoothly varying external loadings and for slender beams, this explained the success of the BE theory in a relatively wide range of practical applications. The next terms in [16, 26] represent corrections of the classical beam theory that are of an increasingly minor refinement, if the loadings, and thus the bending moments, are smooth enough. The work of von Karman [16] and Seewald [26] suggested developing step-by-step procedures for deriving these correction terms for various load cases. A review on such successive approximation techniques was provided by Ghugal and Shimpi [12]. A first step-by-step procedure for stresses was introduced in a brief note by Donnell [8], who studied transverse loadings that are continuously distributed at both the upper and the lower edges of rectangular beams. The corresponding computation of the beam displacements was also sketched in [8]. Independently, Boley and Tolins [7] used a convenient iterative procedure in order to derive, from the continuum mechanics-based two-dimensional elasticity theory, the stresses and deflections due to transverse and shear loadings that vary smoothly along the outer edges of rectangular beams. The iterative procedure used in [7] was derived previously for thermally loaded rectangular beams by Boley [6]. For an introduction into the iterative computation of stresses in rectangular beams, we refer to the book of Altenbach and Naumenko [4] where some instructive applications to cantilever beams are to be found also. In Boley’s step-by-step technique, use is made of the properties of the Airy stress function, where the traction (stress) boundary conditions at the upper and lower faces of the beam are exactly satisfied. In [7], results for the first three steps were presented in the form of tables, the highly informative form of which represent a strong motivation for the present work. The tables given by Boley and Tolins [7] demonstrate how displacements and stresses within the rectangular beam do depend on bending moment and axial force, i.e., on integrals or derivatives of the latter, where a single order only appears in each of the steps of the successive computation of the stresses. From the latter, displacements are derived by integration the elastic constitutive relations. Again, only one order of derivative is kept in the columns of the tables presented in [7]. This means that, for the displacements, some results from one respective step of successive approximation were shifted tacitly to the next column in [7]. Since derivatives of bending moment and axial force are related to the known loading of the beam by ordinary differential equations via equilibrium considerations, the higher-order correction terms in the columns of the tables of [7] are known. For an application of Boley’s method to the problem of piezoelectric rectangular beams, see Krommer and Irschik [20]. Duva and Simmonds [9] modified the expressions in the step-by-step expansions in [7, 8] to account for orthotropic beams weak in shear and gave an explicit presentation of computable error estimates. The step-by-step formulations in [7, 8, 16, 26] refer to beams that are infinitely extended in axial direction. They satisfy exactly the stress boundary conditions at the upper and lower edges of the rectangular beam, as well as the equilibrium relations within the beam, while constitutive relations are generally satisfied only approximately. For polynomial loadings of a finite order, only a limited number of terms in the step-by-step procedures is necessary to satisfy constitutive relations exactly. For beams of finite length, three boundary conditions can be assigned at each of the lateral ends in a more or less straightforward manner, e.g., normal force, shear force and bending moment at a free end or bending moment and two displacements of the axis point at a simply supported end. The resulting solutions do coincide with some analytic results for plane stress problems presented in Timoshenko and Goodier [28]. It was shown by Irschik [15] that the corresponding two-dimensional elasticity results for beams of finite length can be obtained conveniently from enhanced BE beam problems by analogy, since BE problems are also assigned with three boundary conditions at a lateral end. Enhancement suggested in [15] concerns fictitious, but known additional eigenstrain loadings, the latter corresponding to the correction terms in the above step-by-step solutions in [7, 8]. However, the solutions with only three boundary conditions at each of the lateral beam ends generally cannot satisfy the boundary conditions that must be required to hold at each of the cross-sectional points on a lateral end, in order to obtain a completely exact two-dimensional elasticity solution. Solutions for beams of a finite length with only three selected boundary conditions at each lateral end therefore often are denoted as interior solutions. The difference between an interior solution and the completely exact two-dimensional elasticity solution should vanish away from the lateral ends according to St. Venant’s principle, which, however, must be considered with certain care, see, e.g., Karp and Durban [17] and the literature cited there. For elastic interior solutions for orthotropic beams, see Tullini and Savoia [29], who provided a successive approximation technique involving Fredholm equations of the second kind and stated a sufficient condition for the convergence of their series expansion. An exact interior solution for a beam with span-wise constant transverse loading was presented by Karttunen and von Hertzen [18], see [19] for the anisotropic case. In extension on studies on homogeneous beams, an extensive literature has been published on problems of the deformation of functionally graded and layered or laminated beams. For reviews, see Irschik [14], and Altenbach [3], Ghugal and Shimpi [12], as well as Sayyad and Ghugal [23]. For advanced topics in laminated beams concern, e.g., deformable interfaces, see Schulze [25], Weps [30], Adam and Heuer [2], or for spatially varying interfaces see Li and Liu [22]. Concerning Boley’s successive method, an anisotropic beam theory has been given recently by Gahleitner and Schöftner [11], and an application to bimorph piezoelectric beams of finite length composed of two layers with equal material parameters was recently presented by Schöftner and Benjeddou [24]. Nir Enuma [10] presented an extension of the works of von Karman [16], Seewald [26], Donnell [8] and Boley and Tolins [7] by developing a successive procedure for functionally graded orthotropic rectangular beams with transverse loading over the upper surface. A strategy for extending Boley’s method to laminated rectangular beams was also sketched in [10], but no explicit analytic formulas were presented.

Although the more recent literature refers to advanced topics in composite beams, such as mentioned above, there is a lack of systematic extensions of Boley’s successive method to layered rectangular beams. Successive methods would allow to obtain analytic solutions of increasing accuracy for the sake of comparison. It is the scope of the present contribution to extend the successive presentation given in Boley and Tolins [7] to the case of a composite rectangular beam of constant total height, made of two isotropic homogeneous layers with different material parameters and heights, the two layers being connected rigidly by a common straight interface. This problem has the advantage of including the original single-layer problem treated in [7, 8, 16, 28] as a special case. As simple as the problem may appear, the analytic results for the two-layer beam turn out to be quite complex. Therefore, from space limitations, we subsequently restrict to the corresponding extension of Case I of [7], where results for a single-layer beam under transverse loading applied at the upper edge of the beam were considered. Our intent is to enable formulations for the two-layer beam in a compact manner, in the form of tables, analogous to the ones given in [7]. The method presented below, however, can be easily applied to the other two load cases treated in [7] by analogy. Our subsequent methodology is different from the one in [10], since we satisfy the stress continuity conditions at the interface between the two layers from the onset. We also take the opportunity of clarifying some mathematical aspects of the Boley method of successive approximation, which were not explicitly addressed in the above cited literature. Particularly, we explain the consequences of the above-mentioned shifting process of bringing the results into a form, in which only one order of derivative appears in a single step, i.e., in each of the columns of the tables in [7]. Moreover, as a main result, we present formal mathematical expressions, which allow to compute the results for any number of considered successive steps, enabling to obtain complete analytic results for any order of polynomial loading. This is not directly possible from the results presented originally, e.g., in Boley and Tolins [7], where results for the first three steps were presented, which, however, do not allow extensions by complete induction.

Our paper is organized as follows: Notations and basic relations of our problem are stated in Sect. 2. Boley’s successive approximation technique is shortly discussed in Sect. 3. Extended Boley-type tables for the single layer of the composite two-layer beam, which are needed subsequently, are provided in Sect. 4. A strategy for extending Boley’s method to two-layer beams is given in Sect. 5. Displacement and stress continuity conditions at the interface are treated, eventually leading to a form that is indeed in complete analogy to the results for a single-layer beam treated in Table I of Boley and Tolins [7], namely in dependence from the bending moment and from the axial force, as well as from their respective integrals and derivatives. A Boley-type table representation for considering three successive steps is presented for the two-layer beam, as well as more general formulas allowing the consideration of any number of steps, see Table 1 and Eqs. (60)–(62) for the Airy stress functions. In Sect. 6, emphasis is given to the computation of displacement fields and the necessary shifting process for obtaining the desired successive form, see Table 1 for three successive steps, and the more general representation in Eqs. (74) and (75) for formal displacement representations that are applicable to any number of steps. Completeness of the successive representation for a given polynomial order of the applied loading is discussed. Also, for the sake of comparison with numerical computations, specific entries to Table 1 are presented for some special ratios between the elastic parameters, as well as between the thicknesses of the layers. In Sect. 7, using these specific entries, comparisons to numerical computations are presented, where a comparatively thick clamped–clamped beam of finite length with a linearly varying applied loading is used. For this case, the three steps considered in Table 1 give a complete analytic set of solutions for the infinitely extended beam. For the beam of finite length, analytic results are obtained by imposing additionally three advantageous boundary conditions for a clamped end that were suggested by Szabo [27]. Since these three boundary conditions are approximate, displacement distributions are obtained at the beam ends, which do not vanish completely there, although they satisfy Szabo’s three boundary conditions. Numerical comparison is performed utilizing the computer-code ABAQUS [1], on the basis of a sufficiently fine net of 1000 Elements. A first set of comparisons is obtained by prescribing the non-vanishing end displacements of the analytic solution to the finite element model at the beam ends. In this case, the exterior solution should vanish, and the analytic solution should completely coincide with the numerical solution. It is found that this is indeed the case, for both stresses and displacements. A second comparison is performed by prescribing vanishing displacements at the beam ends to the ABAQUS model. Then, an exterior solution should represent the differences between the ABAQUS solution and the analytic solution, the latter one representing the interior solution. These differences can be expected to fade away from the beam ends, due to the principle of St. Venant, see, e.g., [17] and Ziegler [31]. This also is nicely reflected by the presented results. These successful comparisons give strong evidence for the appropriateness of our Boley-type analytic solutions for the two-layer composite beam.

2 Problem statement

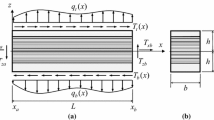
Consider an initially straight rectangular beam under the action of a distributed transverse loading that is applied at the upper edge of the beam. The beam is composed of two rectangular, homogeneous, isotropic and linear elastic layers, which are firmly bondedFootnote 1 together at their common interface, see Fig. 1.

Fig. 1
figure 1

Composite beam made of two layers under transverse loading q(x)

Full size image

Young’s modulus, Poisson’s ratio and thickness of a layer are denoted by \(E,\nu \) and c, respectively. These entities are assumed to be different in the two layers. Index l refers to the lower layer, while index u corresponds to the upper one. Numbers \(\alpha ,\,\beta ,\,\gamma \) are introduced in order to denote the ratios between the values of \(E,\,\nu \) and c in the two layers:

$$\begin{aligned} \alpha = \frac{E_l}{E_u} =\frac{E_l}{E} \quad \beta = \frac{c_l}{c_u}= \frac{c_l}{c} \quad \gamma = \frac{\nu _l}{\nu _u}= \frac{\nu _l}{\nu } \end{aligned}$$
(1)

In the following, the thickness of the upper layer is abbreviated with \(c_u = c\), and we write shortly \(E_u =E, \nu _u = \nu \). The two layers have an equal width b, see Fig. 1, which is used as unit reference length, \(b = 1\) in the following. It is more over assumed that the thickness of each layer is sufficiently larger than b, i.e., that the rectangular cross section is sufficiently narrow, such that a state of plane stress can be taken into account. A global Cartesian (x, y)-coordinate system is attached to the interface of the layers, where the axial coordinate is denoted by x, and y is the transverse coordinate. The transverse loading is denoted as q(x); it is applied at \(y = c\), see Fig. 1, and it is assumed to be sufficiently smooth. Suppressing the index that indicates a specific layer, the plane stress field equations in each of the layers read, see, e.g., Timoshenko and Goodier [28]:

$$\begin{aligned}&\frac{\partial {\sigma _x}}{\partial x}+\frac{\partial {\tau _{xy}}}{\partial y}= 0 \quad \frac{\partial {\tau _{xy}}}{\partial x} +\frac{\partial {\sigma _y}}{\partial y} = 0 \end{aligned}$$
(2)
$$\begin{aligned}&E \frac{\partial {u}}{\partial x} = \sigma _x - \nu \sigma _y \quad E \frac{\partial {v}}{\partial y} = \sigma _y - \nu \sigma _x\quad E\left( \frac{\partial {u}}{\partial y} + \frac{\partial {v}}{\partial x}\right) = 2 ( 1 + \nu ) \tau _{xy} \end{aligned}$$
(3)

Normal stresses are denoted as \(\sigma _x\) and \(\sigma _y\), and \(\tau _{xy}\) stands for the shear stress; axial and transverse displacements are denoted by u and v, respectively. The stress boundary conditions at the upper and lower edges of the beam are, see Fig. 1:

$$\begin{aligned}&\sigma _y(x,c)= q(x) \quad \tau _{xy}(x,c) =0 \end{aligned}$$
(4)
$$\begin{aligned}&\sigma _y(x, -\beta c) = 0 \quad \tau _{xy}(x,-\beta c) = 0 \end{aligned}$$
(5)

3 Boley’s successive approximation technique

Our strategy for solving the above stated problem is to apply and to extend a methodology originally developed by Bruno A. Boley for single-layer rectangular beams, Boley and Tolins [7], see Boley [6] also. Boley’s methodology consists in expanding Airy’s stress function \(\varphi \) in the form of a step-by-step series solution:

$$\begin{aligned} \varphi = \varphi _1 + \varphi _2 +\varphi _3 +\cdots \end{aligned}$$
(6)

with

$$\begin{aligned} \frac{\partial ^4 \varphi _{i}}{\partial y^4} = - 2 \frac{\partial ^4 \varphi _{(i-1)}}{\partial x^2\partial y^2} - \frac{\partial ^4 \varphi _{(i-2)}}{\partial x^4} \quad \varphi _i = 0 \;\;\;\;\;\; \text {for}\; i < 1 \end{aligned}$$
(7)

This formulation ensures that \(\varphi \) satisfies the bi-harmonic differential equation, as this should be, see Timoshenko and Goodier [28]. Note that Eq. (7) are to be understood as ordinary differential equations in the coordinate y. The nonzero stress boundary conditions at the upper and lower edges of the single layer are satisfied by means of the first term, \(\varphi _1\). The stress boundary conditions for \(\varphi _i\), \( i>1\), thus become trivial at the upper and lower edges, which means that there is

$$\begin{aligned} \varphi _i = \frac{\partial \varphi _i}{\partial y} = 0 \quad \text { for }i > 1 \end{aligned}$$
(8)

Having solved these one-dimensional boundary value problems step by step, the stresses follow as, see [28]:

$$\begin{aligned} \sigma _x = \frac{\partial ^2 \varphi }{\partial y^2} \quad \sigma _y = \frac{\partial ^2 \varphi }{\partial x^2} \quad \tau _{xy} = -\frac{\partial ^2 \varphi }{\partial x\partial y} \end{aligned}$$
(9)

Airy stress functions subsequently will be shortly denoted as potential functions or potentials. From the stresses, displacements are eventually computed by integrating the constitutive relations, Eq. (3), and by adjusting the arbitrary functions which arise so as to satisfy the third of Eq. (3). In [7], stresses and displacements were computed step-wise for three loading cases, and the results were presented in the form of three tables, each showing the respective results of the first three steps of the procedure. The loading cases considered in [7] were a transverse loading at the upper edge of the single-layer beam (Table I of [7]), and a symmetric as well as an anti-metric shear loading applied at the upper and lower edges (Tables II and III of [7]). Some short explanations seem to be in order. The tables presented in [7] are formulated in terms of bending moments and normal forces and their integrals and derivatives. As already mentioned, for the displacements a single order of derivative only was used also in each of the columns of the tables in [7], the rest of the results of the respective steps being shifted tacitly to the next columns. The first columns in the tables by Boley and Tolins [7] correspond to \(\varphi _1\) in Eq. (7) and coincide with the results of the elementary Bernoulli–Euler beam theory, see, e.g., Ziegler [31] for the latter theory. The second column, corresponding to \(\varphi _2\) in Eq. (7), dates back to fundamental contributions by Karman [16] and Seewald [26], who obtained their results via an integral transform technique. The third columns in the tables of [7], corresponding to the third step in Eq. (7), were presented for the first time in [7]. Nowadays, results of a higher-order multi-step procedure can be easily obtained by means of symbolic computation. It is the scope of our present paper to extend the Boley-type integrate technique to two-layer beams.

4 Extended Boley-type tables for the single layer of the composite two-layer beam

In a first step, the composite beam presented in Fig. 1 is cut along the common interface of the two layers into two single-layer beams, in \(y=0\). The resulting free-body diagrams are shown in Figs. 2 and 3, which result in five loading cases, three for the upper layer and two for the lower one.

Fig. 2
figure 2

Free-body diagrams of the two layers of the composite beam

Full size image
Fig. 3
figure 3

Stress resultants in the two layers of a differential beam element

Full size image

In Fig. 2, the interfacial stresses are denoted by \(\sigma = \sigma _y(x,0)\) and \(\tau = \tau _{xy}(x,0)\), respectively. Note that the interfacial stress continuity conditions at \(y=0\) are satisfied automatically by this convention. Results for the Airy stress functions and the displacements for the five loading cases are gathered in abbreviated Boley-type tables, which are given in “Appendix A.” Captions for these tables are denoted as follows: Table 2 belongs to Fig. 2a, and Table 3 is due to the loading case in Fig. 2b. Two Tables, 4 and 5, are needed for the shear loading case in Fig. 2c. These follow by representing the \(\tau \)-loading case as the sum of a symmetric and an antimetric loading, likewise to Case II and Case III in [7]. Correspondingly, the lower layer, see Fig. 2d, e, is represented in Tables 6, 7 and 8, respectively. The potentials and displacements presented in the tables of “Appendix A” are to be understood for the single layer of the composite beam, see Fig. 3 for positive directions of bending moments M, shear forces Q and normal forces P. Note that bending moments in “Appendix A” are to be understood with reference to the respective axis of the layer.

Bending moments, shear and axial forces are assigned with additional indices in order to distinguish between the load cases indicated in Fig. 2; e.g., \(M_{\tau u}\) and \(P_{\tau u}\) denote bending moments and normal forces due to the loading case \(\tau \) in the upper layer, see Fig. 2c and Tables 4 and 5, respectively. The tables of “Appendix A” have been independently derived using the step-wise original method of Boley and Tolins [7], but they are formulated already in the global interfacial coordinate system shown in Fig. 1, using the coordinate y introduced there. The following convention for abbreviating x-derivatives is used:

$$\begin{aligned} ()'= \frac{\hbox {d}()}{\mathrm{{d}}x}, \quad ()^{(n)}=\frac{\hbox {d}^n()}{\mathrm{{d}}x^n} \end{aligned}$$
(10)

Particularly, we have for the upper layer

$$\begin{aligned} M_{u}&= \int _{-c/2}^{c/2} \sigma _x y_u \mathrm{{d}}y_u \quad P_u= \int _{- c/2}^{c/2} \sigma _x\mathrm{{d}}y_u \end{aligned}$$
(11)
$$\begin{aligned} M_u&= M_{ qu} + M _{\sigma u} + M_{\tau u} \quad P_u = P_{\tau u} \end{aligned}$$
(12)

Analogously, there is for the lower layer

$$\begin{aligned} M_{l}&= \int _{-\beta c/2}^{\beta c/2} \sigma _x y_l \mathrm{{d}}y_l \quad P_l= \int _{-\beta c/2}^{\beta c/2} \sigma _x\mathrm{{d}}y_l \end{aligned}$$
(13)
$$\begin{aligned} M_l&= M _{\sigma l} + M_{\tau l} \quad P_l = P_{\tau l} \end{aligned}$$
(14)

The following layer-wise differential equilibrium relations do hold, see Fig. 3

$$\begin{aligned} P_{u}' - \tau&= 0 \quad Q_u' + q - \sigma = 0 \quad M_{u}^{(2)} + q -\sigma + \frac{c}{2} \tau ' =0 \end{aligned}$$
(15)
$$\begin{aligned} P_{l}' + \tau&= 0 \quad Q_l' +\sigma = 0 \quad M_{l}^{(2)} +\sigma + \beta \frac{c}{2}\tau ' =0 \end{aligned}$$
(16)

The tables of “Appendix A” can be used for single-layer homogeneous beams, in addition to the ones that were presented before by Boley and Tolins [7]. As in the latter reference, displacements in these tables are to be understood modulo rigid-body displacements.

5 A strategy for extending Boley’s method to two-layer beams

In the Boley-type tables of “Appendix A,” the expressions for potential functions and displacements in the two layers are expressed as functions of the respective internal forces and moments and their axial integrals and derivatives. Continuity of the interfacial stress components \(\sigma \) and \(\tau \), see Fig. 2, is automatically taken into account. What remains is to assure continuity of the displacements of the two layers at the common interface at \(y=0\),

$$\begin{aligned} \Delta u_0 = u_{0u} - u_{0l} = 0 \quad \Delta v_0 = v_{0u} - v_{0l} = 0 \end{aligned}$$
(17)

The index 0 refers to the interface of the two firmly bonded layers.

In order to reduce the unknowns in the tables of “Appendix A,” namely \(M_{qu}\), \(M_{\sigma u}\), \(M_{\tau u}\), \(P_{\tau u}\) and their counterparts in the lower layer, \(M_{\sigma l}, \,M_{\tau l}, \,P_{\tau l}\), it turns out that it is sufficient to study the difference at \(y=0\) of the first derivatives of the axial displacements, \(\Delta u'_0\), and of the second derivatives of the transverse displacements, \(\Delta v^{(2)}_0\), which also must vanish:

$$\begin{aligned} \Delta u_0' = \sum _{ i = 1}^n \left( u_{0ui}' - u_{0li}' \right) = 0 \quad \Delta v_0^{(2)} = \sum _{ i = 1}^n \left( v_{0ui}^{(2)} - v_{0li}^{(2)}\right) = 0 \end{aligned}$$
(18)

For instance, \(u_{0u1}'\) follows as the sum of the first derivatives of the axial displacements in the first columns of Tables 2, 3, 4 and 5 . This also holds for the next columns in the latter tables.

In a first step, we replace the unknowns \(M_{qu},\,M_{\sigma u},\,M_{\tau u},\,M_{\sigma l},\,M_{\tau l}\) and \(P_{\tau l}\), by four quantities, which we choose as \(M,\,M_{u0},\,P\) and \(P_{\tau u}\). This can be performed by using the following relations of static equivalence:

$$\begin{aligned} M_{u0} = M_{ qu} + M _{\sigma u} + M_{\tau u} + \frac{c}{2}P_{\tau u} \quad M_{l0}= M_{\sigma l} + M_{\tau l} - \frac{\beta c}{2} P_{\tau l} \end{aligned}$$
(19)

The bending moment \(M_{u0}\) denotes the moment of the axial stress \(\sigma _x\) in the upper layer with respect to the interface \(y=0\). \(M_{l0}\) is defined analogously. The total bending moment with respect to \(y=0\), and the resulting normal force P becomes:

$$\begin{aligned} M_0=M_{u0} + M_{l0} = M \quad P = P_{\tau u} +P_{\tau l} \end{aligned}$$
(20)

Note that we suppress the subscript 0 for M in the following. The subsequent differential relations are also needed:

$$\begin{aligned} M^{(2)}&= - q\quad P' = 0 \end{aligned}$$
(21)
$$\begin{aligned} M_{qu}^{(2)}&= M^{(2)} \quad P_{\tau u}' +P_{\tau l}' = 0 \end{aligned}$$
(22)
$$\begin{aligned} M_{\tau u}'&= -\frac{c}{2}P_{\tau u}', \quad M_{\tau l}' = \beta \frac{ c}{2}P_{\tau l}' \end{aligned}$$
(23)

Equation (21) represent equilibrium relations for the composite two-layer beam, with no external loadings at the lower edge, at \(y = -\beta c\), and no shear force loadings at the upper and lower edge. Equation (22) are immediate consequences of Eq. (21). The two relations in Eq. (23) follow from the vanishing of shear stresses at the upper edge, in \(y=c\), superposing Tables 4 and 5. Analogously, at the lower edge, at \(y=- \beta c\), we use Tables 7 and 8, respectively. Differentiating Eq. (19) twice, substituting the derivative of Eqs. (23), (22) and the second derivative of Eq. (20) as well yields:

$$\begin{aligned} M_{\sigma u}^{(2)} = M_{u0} ^{(2)} - M^{(2)} \quad M_{\sigma l}^{(2)} = M ^{(2)} - M_{u0}^{(2)} \end{aligned}$$
(24)

We eventually obtain the following expressions:

$$\begin{aligned} E \Delta u_1'&= -\frac{6 }{\alpha \beta ^2}\frac{M}{c^2}+\frac{6 \left( 1 - \alpha \beta ^2\right) }{\alpha \beta ^2}\frac{M_{u0}}{c^2}+ \frac{4 ( 1 +\alpha \beta )}{\alpha \beta }\frac{P_{\tau u}}{c} -\frac{4 }{\alpha \beta }\frac{P}{c} \end{aligned}$$
(25)
$$\begin{aligned} E \Delta u_2'&=\frac{1+ 5 \nu ( \alpha - \gamma )}{5 \alpha } M^{(2)} -\frac{1 -\alpha + 5 \nu (\alpha - \gamma )}{5 \alpha }M_{u0}^{(2)} -\frac{4 (\alpha +\beta )}{15 \alpha }cP_{\tau u}^{(2)} \end{aligned}$$
(26)
$$\begin{aligned} E \Delta u_3'&=\frac{ \left( 175 \alpha -104 \beta ^2\right) }{2100 \alpha }c^2M^{(4)}-\frac{26 \left( \alpha -\beta ^2\right) }{525 \alpha } c^2 M_{u0}^{(4)} +\frac{4 \left( \alpha +\beta ^3\right) }{1575 \alpha }c^3P_{\tau u}^{(4)} \end{aligned}$$
(27)
$$\begin{aligned} E \Delta v_1^{(2)}&=\frac{12}{\alpha \beta ^3 }\frac{M}{c^3}-\frac{12 \left( 1+\alpha \beta ^3\right) }{\alpha \beta ^3}\frac{M_{u0}}{c^3} - \frac{6 \left( 1-\alpha \beta ^2\right) }{\alpha \beta ^2}\frac{P_{\tau u} }{c^2} + \frac{6}{\alpha \beta ^2}\frac{P}{c^2} \end{aligned}$$
(28)
$$\begin{aligned} E \Delta v_2^{(2)}&= -\frac{12}{5 \alpha \beta } \frac{M^{(2)}}{c} + \frac{12 (1+\alpha \beta )}{5 \alpha \beta }\frac{M_{u0}^{(2)}}{c}+\frac{1 -\alpha +5\nu (\alpha -\gamma ) }{5 \alpha }P_{\tau u}^{(2)} \end{aligned}$$
(29)
$$\begin{aligned} E \Delta v_3^{(2)}&= \frac{ (175 \alpha +128 \beta )}{350 \alpha }cM^{(4)}-\frac{64 (\alpha +\beta )}{175 \alpha } cM_{u0}^{(4)} + \frac{26 \left( \alpha -\beta ^2\right) }{525 \alpha }c^2P_{\tau u}^{(4)} \end{aligned}$$
(30)

Recall that in the original tables of Boley and Tolins [7], all entities were expressed by the bending moment M and the normal force P of the single-layer beam, as well as by their integrals and differentials. In order to approach Boley-type tables for the two-layer composite beam, it is straightforward to further express \(M_{u0}\) and \(P _{\tau u}\) by a series in the bending moment M, its even-order derivatives and the normal force P. Hence, we write

$$\begin{aligned} M_{u0}&=a_0 M + a_1c P + a_2 c^2 M^{(2)}+ a_4 c^4 M^{(4)} +\cdots \end{aligned}$$
(31)
$$\begin{aligned} P_{\tau u}&=\frac{b_0}{c} M + b_1 P + b_2 c M^{(2)}+ b_4 c^3 M^{(4)} +\cdots \end{aligned}$$
(32)

Recall that P is taken as constant, see Eq. (21), since no distributed external axial loading is present for the case at hand. The shear stress at both sides of the interface of the two layers cancels out, and a constant total axial force P, if any, remains. Substituting Eqs. (31) and (32) into Eqs. (25)–(30) yields

$$\begin{aligned} \begin{aligned} E \Delta u_1'&= -\frac{6}{\alpha \beta ^2 c^2}M -\frac{4 }{\alpha \beta c}P +\frac{6 \left( 1 - \alpha \beta ^2\right) }{\alpha \beta ^2 c^2}\left( a_0 M + a_1 c P + a_2 c^2 M^{(2)} + a_4c^4 M^{(4)} \right) \\&\quad + \frac{4 ( 1 +\alpha \beta )}{\alpha \beta c}\left( \frac{b_0}{c} M + b_1 P + b_2 c M^{(2)}+ b_4 c^3 M^{(4)} \right) \end{aligned} \end{aligned}$$
(33)
$$\begin{aligned} \begin{aligned} E \Delta u_2'&= \frac{1+ 5 \nu ( \alpha - \gamma )}{5 \alpha } M^{(2)} -\frac{1 -\alpha + 5 \nu (\alpha - \gamma )}{5 \alpha }\left( a_0 M^{(2)} + a_2c^2 M^{(4)}+ a_4c^4 M^{(6)}\right) \\&\quad -\frac{4 c (\alpha +\beta )}{15 \alpha }\left( \frac{b_0}{c} M^{(2)} + b_2 c M^{(4)}+ b_4 c^3M^{(6)}\right) \end{aligned} \end{aligned}$$
(34)
$$\begin{aligned} \begin{aligned} E \Delta u_3'&= \frac{c^2 \left( 175 \alpha -104 \beta ^2\right) }{2100 \alpha }M^{(4)} -\frac{26 c^2 \left( \alpha -\beta ^2\right) }{525 \alpha } \left( a_0 M^{(4)} + a_2c^2 M^{(6)}+ a_4c^4 M^{(8)} \right) \\&\quad +\dfrac{4 c^3 \left( \alpha +\beta ^3\right) }{1575 \alpha }\left( \dfrac{b_0}{c} M^{(4)} + b_2 c M^{(6)}+ b_4 c^3M^{(8)} \right) \end{aligned} \end{aligned}$$
(35)
$$\begin{aligned} \begin{aligned} E \Delta v_1^{(2)}&= \frac{12}{\alpha \beta ^3 c^3}M+ \frac{6}{\alpha \beta ^2 c^2}P-\frac{12 \left( 1+\alpha \beta ^3\right) }{\alpha \beta ^3 c^3}\left( a_0 M + a_1 c P + a_2c^2 M^{(2)}+ a_4 c^4M^{(4)} \right) \\&\quad - \frac{6 \left( 1-\alpha \beta ^2\right) }{\alpha \beta ^2 c^2}\left( \frac{b_0}{c} M + b_1 P + b_2 c M^{(2)}+ b_4c^3 M^{(4)} \right) \end{aligned} \end{aligned}$$
(36)
$$\begin{aligned} \begin{aligned} E \Delta v_2^{(2)}&= -\frac{12}{5 \alpha \beta c} M^{(2)} + \frac{12 (1+\alpha \beta )}{5 \alpha \beta c}\left( a_0 M^{(2)} + a_2c^2 M^{(4)}+ a_4 c^4M^{(6)}\right) \\&\quad + \frac{5\nu (\alpha -\gamma ) +1 -\alpha }{5 \alpha }\left( \frac{b_0}{c} M^{(2)} + b_2 c M^{(4)}+ b_4 c^3 M^{(6)}\right) \end{aligned} \end{aligned}$$
(37)
$$\begin{aligned} \begin{aligned} E \Delta v_3^{(2)}&= \frac{c (175 \alpha +128 \beta )}{350 \alpha }M^{(4)}-\frac{64 c (\alpha +\beta )}{175 \alpha } \left( a_0 M^{(4)} + a_2 c^2 M^{(6)}+ a_4 c^4 M^{(8)} \right) \\&\quad + \frac{26 c^2 \left( \alpha -\beta ^2\right) }{525 \alpha }\left( \frac{b_0}{c} M^{(4)} + b_2 c M^{(6)}+ b_4 c ^3M^{(8)} \right) \end{aligned} \end{aligned}$$
(38)

In order to find expressions for the unknown coefficients a and b in Eqs. (33)–(38), we re-substitute Eqs. (33)–(38) into Eq. (18). Since the solution must hold for arbitrary functions M, we require that Eq. (18) must be satisfied for P and for each order of derivative of M separately. This yields the following set of equations gathered in Eqs. (39)–(46), which allows to compute the coefficients a and b in a step-by-step manner:

$$\begin{aligned}&1 - a_0 \left( 1 -\alpha \beta ^2\right) -b_0\frac{2\beta }{3}(1 + \alpha \beta ) = 0 \end{aligned}$$
(39)
$$\begin{aligned}&1 - a_0 \left( 1 + \alpha \beta ^3\right) - b_0\frac{\beta }{2} \left( 1 - \alpha \beta ^2\right) = 0 \end{aligned}$$
(40)
$$\begin{aligned}&1 - b_1 (1 +\alpha \beta )-a_1 \frac{3}{{2 \beta }}\left( 1 - \alpha \beta ^2\right) = 0 \end{aligned}$$
(41)
$$\begin{aligned}&1 -b_1 \left( 1 - \alpha \beta ^2\right) -a_1\frac{2}{\beta }\left( 1 +\alpha \beta ^3\right) =0 \end{aligned}$$
(42)
$$\begin{aligned}&1 + 5 \nu (\alpha - \gamma ) -\left[ 5 \nu ( \alpha - \gamma ) -\alpha +1\right] a_0- \dfrac{4}{3} (\alpha +\beta )b_0 \nonumber \\&\quad + \frac{30 \left( 1 - \alpha \beta ^2\right) }{\beta ^2}a_2 + \frac{20 (1 + \alpha \beta )}{\beta }b_2 =0 \end{aligned}$$
(43)
$$\begin{aligned}&1 - (1 +\alpha \beta ) a_0 - \frac{\beta }{12}\left[ 1 - \alpha + 5 \nu ( \alpha -\gamma ) \right] b_0\nonumber \\&\quad + \dfrac{5}{\beta ^2 } (1 + \alpha \beta ^3)a_2 + \frac{5}{2 \beta }( 1 - \alpha \beta ^2) b_2=0 \end{aligned}$$
(44)
$$\begin{aligned}&1-\frac{104 \beta ^2}{175 \alpha } - \frac{104(\alpha - \beta ^2)}{175\alpha }a_0 +\frac{16 (\alpha + \beta ^3)}{525\alpha }b_0 - \frac{12 \left[ 1- \alpha + 5 \nu (\alpha - \gamma )\right] }{5 \alpha }a_2\nonumber \\&\quad -\frac{16( \alpha + \beta ) }{5\alpha }b_2 -\frac{72 \left( \alpha \beta ^2-1\right) }{\alpha \beta ^2}a_4 + \frac{48 (\alpha \beta +1)}{\alpha \beta }b_4 =0 \end{aligned}$$
(45)
$$\begin{aligned}&1+ \frac{128 \beta }{175 \alpha } -\frac{128(\alpha +\beta )}{175 \alpha }a_0 +\frac{52\left( \alpha -\beta ^2\right) }{525 \alpha } b_0 + \frac{24(\alpha \beta +1)}{5 \alpha \beta }a_2 \nonumber \\&\quad + \frac{2\left[ 5\nu (\alpha -\gamma ) -\alpha +1\right] }{5 \alpha }b_2 -\frac{24\left( \alpha \beta ^3+1\right) }{\alpha \beta ^3}a_4 + \frac{12 \left( \alpha \beta ^2-1\right) }{\alpha \beta ^2}b_4 =0 \end{aligned}$$
(46)

One obtains from the first four relations, see Eqs. (39)–(42):

$$\begin{aligned} a_0&=\frac{\alpha \beta (3 \beta +4)+1}{\alpha ^2 \beta ^4+2 \alpha \left( 2 \beta ^2+3 \beta +2\right) \beta +1} \end{aligned}$$
(47)
$$\begin{aligned} b_0&=\frac{6 \alpha \beta (\beta +1)}{\alpha ^2 \beta ^4+2 \alpha \left( 2 \beta ^2+3 \beta +2\right) \beta +1} \end{aligned}$$
(48)
$$\begin{aligned} a_1&=\frac{2 \alpha \beta ^2 (\beta +1)}{\alpha ^2 \beta ^4+2 \alpha \left( 2 \beta ^2+3 \beta +2\right) \beta +1} \end{aligned}$$
(49)
$$\begin{aligned} b_1&=\frac{\alpha (4 \beta +3) \beta ^2+1}{\alpha ^2 \beta ^4+2 \alpha \left( 2 \beta ^2+3 \beta +2\right) \beta +1} \end{aligned}$$
(50)

This results for \(a_0\) and \(b_0\) can be substituted into the next two relations, Eqs. (43) and (44), in order to compute \(a_2\) and \(b_2\), etc. The expressions for \(a_2\), \(b_2\), \(a_4\) and \(b_4\) are already lengthy, but can be easily obtained via symbolic computation.

Now that \(M_{u0}\) and \(P_{\tau u}\) have been obtained according to Eqs. (31) and (32), the potentials in the upper and lower layers of the composite beam can be computed. We exemplary show this for the first part \(\varphi _{u1}\) of the upper layer’s potential. The corresponding transversal stress \(\sigma _{yu1}\) is computed from the potentials of the first columns of Tables 2, 3, 4 and 5 by using Eq. (9):

$$\begin{aligned} \begin{aligned} \sigma _{yu1} = \left( \frac{2 y^3}{c^3}-\frac{3 y^2}{c^2}\right) \left( M_{qu}^{(2)}+M_{\sigma u}^{(2)}+M_{\tau u}^{(2)}\right) +\frac{y}{c}M_{\tau u}^{(2)}+M_{\sigma u}^{(2)}+\left( \frac{y^2}{2 c}-\frac{y}{2}\right) P_{\tau u}^{(2)}\end{aligned} \end{aligned}$$
(51)

Substituting derivatives of Eqs. (19), (22), (23) and (24) into Eq. (51), \(\sigma _{yu1}\) is expressed via \(M^{(2)}\), \(M_{u0}^{(2)}\) and \(P_{\tau u}^{(2)}\) only:

$$\begin{aligned} \begin{aligned} \sigma _{yu1} =- M^{(2)} + \left( 1 +\frac{2 y^3}{c^3}-\frac{3 y^2}{c^2}\right) M_{u0}^{(2)} - \left( \frac{y^3}{c^2}-\frac{2 y^2}{c}+y\right) P_{\tau u}^{(2)}\end{aligned} \end{aligned}$$
(52)

Following an argument by Seewald [26], the functional dependency on the y-coordinate in the potentials and in \(\sigma _y\), which is the second axial derivative of the former, see Eq. (9), can be taken as equal. Hence, we find:

$$\begin{aligned} \begin{aligned} \varphi _{u1} =- M + \left( 1 +\frac{2 y^3}{c^3}-\frac{3 y^2}{c^2}\right) M_{u0} - \left( \frac{y^3}{c^2}-\frac{2 y^2}{c}+y\right) P_{\tau u} \end{aligned} \end{aligned}$$
(53)

Analogously, in order to compute \(\varphi _{u2}\) and \(\varphi _{u3}\), the relations in Eqs. (19)–(24) as well as their derivatives with respect to x are substituted into the potentials of the second and third column of Tables 2, 3, 4 and 5 . The same procedure has to be applied to the lower layer to get \(\varphi _l\). Substituting \(M_{u0}\) and \(P_{\tau u}\) from Eqs. (31) and (32) and resorting with respect to M, P, \(M^{(2)}\) and \(M^{(4)}\), we get the counterparts for the two-layer beam of Case I of the original single-layer table in Boley and Tolins [7]. In order to demonstrate the procedure, we note the result for the first term \(\varphi _{u1}\) and \(\varphi _{l1}\) in more detail:

$$\begin{aligned} \varphi _ {u1}&=M\bigg [a_0 -1 - b_0 \dfrac{y }{c}+(2 b_0-3 a_0)\dfrac{y^2}{c^2} + (2 a_0 - b_0) \dfrac{y^3}{c^3}\bigg ]\nonumber \\&\quad +cP \bigg [ (-3a_1+2 b_1) \dfrac{y^2}{c^2} + (2 a_1 - b_1) \dfrac{y^3}{c^3}\bigg ] \end{aligned}$$
(54)
$$\begin{aligned} \varphi _ {l1}&=M\bigg [a_0 -1 - b_0 \dfrac{y }{c}+(3- 3a_0-2 b_0) \bigg (\dfrac{y}{\beta c}\bigg )^2+ (2- 2a_0 - b_0) \bigg (\dfrac{y}{\beta c}\bigg )^3\bigg ] \nonumber \\&\quad -cP \bigg [ (3a_1+ 2 b_1) \dfrac{y^2}{(\beta c)^2} + (2 a_1 + b_1) \dfrac{y^3}{(\beta c)^3}\bigg ] \end{aligned}$$
(55)

For a compact notation, a dimensionless parameter \(\lambda \) has been introduced:

$$\begin{aligned} \lambda&= \frac{\alpha ^2 \beta ^4+4 \alpha \beta ^3+6 \alpha \beta ^2+4 \alpha \beta +1}{12 (\alpha \beta +1)} \end{aligned}$$
(56)

It is noted that \(E\lambda c^3\) can be interpreted as an effective flexural rigidity, reducing to \(E2c^3/3\) for the homogeneous beam of thickness 2c. Equations (54) and (55) now transform to:

$$\begin{aligned} \begin{aligned} \varphi _ {u1}&=\dfrac{M}{\lambda }\bigg [ k_{10} + k_{11} \dfrac{y}{c} + k_{12} \left( \dfrac{y}{c}\right) ^2 + k_{13} \left( \dfrac{y}{c}\right) ^3\bigg ] +\dfrac{cP}{\lambda } \bigg [ \bar{k}_{12}\left( \dfrac{y}{c}\right) ^2 +\bar{k}_{13}\left( \dfrac{y}{c}\right) ^3 \bigg ] \end{aligned} \end{aligned}$$
(57)
$$\begin{aligned} \begin{aligned} \varphi _ {l1}&=\dfrac{M}{\lambda }\bigg [ g_{10} + g_{11} \dfrac{y}{c} + g_{12} \left( \dfrac{y}{c}\right) ^2 + g_{13} \left( \dfrac{y}{c}\right) ^3\bigg ] +\dfrac{cP}{\lambda } \bigg [ \bar{g}_{12}\left( \dfrac{y}{c}\right) ^2 +\bar{g}_{13}\left( \dfrac{y}{c}\right) ^3 \bigg ] \end{aligned} \end{aligned}$$
(58)

For instance, the following abbreviations have been introduced in Eq. (57):

$$\begin{aligned} k_{10}&= -\frac{\alpha \beta ^2 \left( \alpha \beta ^2+4 \beta +3\right) }{12 (\alpha \beta +1)}&k_{11}&= -\frac{\alpha \beta (\beta +1)}{2 (\alpha \beta +1)}&k_{12}&=\frac{\alpha \beta ^2-1}{4 (\alpha \beta +1)}&k_{13}&= \frac{1}{6} \end{aligned}$$
(59)

Repeating the procedure for the next successive steps and applying the method of complete induction, the potentials \(\varphi _{u}\) and \(\varphi _{l}\) can be represented in the following compact series form, which allows to consider any number n of steps in the successive procedure:

$$\begin{aligned} \varphi _{u} = \frac{1}{\lambda }\left[ \sum _{ i = 1}^n c^{2(i-1)} M^{(2(i-1))} f_i + c P\, f_p\right] \end{aligned}$$
(60)
$$\begin{aligned} \varphi _{l} = \frac{1}{\lambda }\left[ \sum _{ i = 1}^n c^{2(i-1)} M^{(2(i-1))} g_i + c P\, g_p\right] \end{aligned}$$
(61)

with i as the number of iterations and f, g as polynomials in y:

$$\begin{aligned} f_i&= \sum _{j =0}^{2i+1} k_{ij}\left( \frac{y}{c}\right) ^j&f_p&= \sum _{j =2}^{3} {\bar{k}}_{1j}\left( \frac{y}{c}\right) ^j&g_i&= \sum _{j =0}^{2i+1} g_{ij}\left( \frac{y}{c}\right) ^j&g_p&= \sum _{j =2}^{3} {\bar{g}}_{1j}\left( \frac{y}{c}\right) ^j \end{aligned}$$
(62)

The coefficients for f and g can be taken from Tables 9 and 10 in “Appendix B,” where \(k_{ij}\), \({\bar{k}}_{1j}\) correspond to the upper layer and \(g_{ij}\), \({\bar{g}}_{1j}\) to the lower layer. Now, using Eqs. (60) and (61) and restricting to the first three steps lead to a Boley-type table for the two-layer composite beam, see Table 1. Together with the formal series representation in Eqs. (60) and (61), Table 1 represents the main results of our paper. Table 1 extends Case I in the table of Boley and Tolins [7] also with respect to a non-vanishing constant axial force P: For the homogenous beam, \(\alpha =\beta =\gamma =1\), Table 1 reduces to the Case I in the table of Boley and Tolins [7], if we set P equal zero in Eq. (20). For the sake of comparison to numerical computations, coefficients corresponding to a two-layer composite beam with \(\alpha =4,\,\beta =1,\,\gamma =3\) are presented in Tables 11 and 12 in “Appendix C.”

We now add a brief note on criteria to truncate the number of iterations. For polynomial loadings of order \(n \ge 0\), the number of iterations

$$\begin{aligned} i(n) = {\left\{ \begin{array}{ll} 2+ n/2 &{} \text {if }n\text { is even} \\ (3+n)/2&{} \text {if }n\text { is odd} \end{array}\right. } \end{aligned}$$
(63)

is necessary for an exact solution which follows from Table 1. Furthermore, the magnitude of the correction terms for \(i>1\) depends on the thickness-to-length ratio (aspect ratio) \(\mu \). This is exemplarily shown subsequently for the non-dimensional potential for a homogeneous beam (Case I of [7]) with reference bending moment M, non-dimensional transverse coordinate \(\eta = y/c\), aspect ratio \(\mu = 2 c \beta /L <1\), beam length L and parameter \(\beta \) of Eq. (1).

$$\begin{aligned} {\bar{\varphi }} = \frac{M(x)}{M}\left[ \frac{(\eta -2) (\eta +1)^2}{4}\mu ^0 -\frac{\eta \left( \eta ^2-1\right) ^2}{160} \mu ^2 +\left( \dots \right) \mu ^{2(i-1)}+ \cdots \right] \end{aligned}$$
(64)

Since the methodology is comparatively fast converging, a three-step procedure often is accurate enough, dependent on the aspect ratio, which is exemplarily shown for the upper fiber normal stress \(\sigma _x(x,c)\) of a homogeneous beam in Fig. 4. The results are normalized to the elementary (first iteration) normal stress. The exact solution is a polynomial of 11th order which approximates a sine half-wave and leads to \(i=7\) necessary iterations, see Eq. (63).

Fig. 4
figure 4

Dependency of the upper fiber normal stress \(\sigma _x(x,c)\) on the iterations i and aspect ratio \(\mu \)

Full size image

For non-polynomial loads, such as sine and cosine, the half-wave number must be taken into account in order to achieve convergence of the iteratively obtained results. Exemplarily, this is shown for a simply supported, homogeneous beam loaded by a distributed load \(q(x) = q_0 \sin (m \pi x/L)\) with the integer odd half-wave number \(m \ge 1\), see Fig. 5. For this special case of loading and supporting conditions, a closed-form solution can be determined with the Ansatz \(\phi (x,y) = M(x)f(y)\) where the bending moment is computed from \(M^{(2)}=- q(x)\) satisfying boundary conditions at the lateral ends. Substituting the Ansatz into the bi-potential equation leads to an ordinary differential equation of fourth order for f(y). Four constants of f(y) are to be adjusted so that the stress boundary conditions at the horizontal surfaces are satisfied, see Fig. 5. To demonstrate the convergence behavior of the introduced iterative procedure, the iteratively determined entities are compared to those obtained from the closed-form solution. Exemplarily, this is shown for the upper fiber normal stress \(\sigma _x(c,L/2)\) evaluated at \(x = L/2\) where the closed-form solution reads

Fig. 5
figure 5

Simply supported beam loaded by a sinusoidal load exemplarily with half-wave numbers \(m=1\), \(m=5\)

Full size image
$$\begin{aligned} \sigma _x(c,L/2)=\sigma _x^* = q_0\sin \left( \frac{\pi m}{2}\right) \frac{ 2 \pi ^2 \mu ^2 m^2+\cosh (2 \pi \mu m)-1}{-2 \pi ^2 \mu ^2 m^2+\cosh (2 \pi \mu m)-1} \end{aligned}$$
(65)

including the parameters \(\mu \) and m. Convergence studies are presented for two half-wave numbers (\(m=1\), \(m=5\)) and for two aspect ratios (\(\mu =1/5\), \(\mu =1/4\)), see Fig. 6. In Fig. 6a, the iterative and closed-form results agree already at the third and fourth iteration i for a sine half-wave with \(m=1\). For a half-wave number \(m=5\), the iteratively obtained results agree for \(i=7\) and \(i=8\), see Fig. 6b. This gives evidence for the statement by Boley and Tolins in their Paper [7] concerning the limited usage of the method for non-smoothly varying forces.

Fig. 6
figure 6

Convergence behavior of the upper fiber normal stress dependent on the aspect ratio \(\mu \), the half-wave number m and the number of iterations i

Full size image

6 Computation of the displacement fields

We demonstrate the displacement–computation procedure for the upper layer in more detail, since it performs analogously for the lower layer. The displacements are computed according to Eq. (3), where the normal stresses \(\sigma _x \) and \(\sigma _y\) from Table 1 are substituted. By integration, one finds for the axial displacement:

$$\begin{aligned} \begin{aligned} u&= \frac{1}{\lambda E} \bigg [f_1^{(II)}\!\int M \,\hbox {d}x + f_p^{(II)} cPx + c^2f_2^{(II)} M' +c^4f_3^{(II)}M^{(3)} \\&\quad - \nu \left( f_1M' + c^2f_2 M^{(3)}+c^4f_3 M^{(5)}\right) \bigg ] + G(y) \end{aligned} \end{aligned}$$
(66)

and for the transversal displacement:

$$\begin{aligned} \begin{aligned} v&= \frac{1}{\lambda E} \bigg [M^{(2)}\int f_1 \hbox {d}y + c^2M^{(4)}\int f_2 \hbox {d}y +c^4M^{(6)} \int f_3\hbox {d}y\\&\quad -\nu \left( f_1^{(I)}M + f_p^{(I)} cP + c^2f_2^{(I)} M^{(2)}+c^4f_3^{(I)}M^{(4)}\right) \bigg ] + F(x) \end{aligned} \end{aligned}$$
(67)

where roman superscripts denote derivatives with respect to y. In the course of the integration procedure, two unknown functions, G(y) and F(x), are to be introduced. The latter functions have to be determined so that the third of Eq. (3) is satisfied. Derivatives of Eq. (66) with respect to y, and of Eq. (67) with respect to x, as well as the shear stress \(\tau _{xy}\) from Table 1 are substituted into the third of Eq. (3). This gives

$$\begin{aligned} \begin{aligned}&f_1^{(III)}\int M \hbox {d}x + f_p^{(III)} cPx + M' \underbrace{\left( c^2f_2^{(III)}+ 2f_1^{(I)}\right) }_{2 ( k_{11} + 3 k_{23})/c} +M^{(3)}\underbrace{\left( c^4f_3^{(III)} + 2c^2 f_2^{(I)} +\int f_1 \hbox {d}y \right) }_{2 ( k_{21} + 3 k_{33}) c} \\&\quad + M^{(5)}\left( c^2 \int f_2 \hbox {d}y +2 c^4f_3^{(I)}\right) +M^{(7)} c^4\int f_3\hbox {d}y + \lambda EF'+ \lambda E G^{(I)} =0 \end{aligned} \end{aligned}$$
(68)

Substituting the coefficients according to “Appendix B” shows that the terms containing \(\int M {\hbox {d}}x,\; cPx,\;M'\) and \(M^{(3)}\) are functions of x only. However, the terms containing \(M^{(5)}\) and \(M^{(7)}\) are y dependent also. To satisfy the requirement that Eq. (68) must contain functions of x and y only, but no mixed terms, we assume that \(M^{(5)}=\text {const}\) for the time being. One then finds the following ordinary differential equation to compute G(y):

$$\begin{aligned} \begin{aligned} M^{(5)}\left( c^2 \int f_2 \hbox {d}y +2c^4f_3^{(I)}\right) + \lambda E G^I =0 \end{aligned} \end{aligned}$$
(69)

In the framework of this reasoning, we obtain for F(x):

$$\begin{aligned} \begin{aligned} f_1^{(III)}\int M {\hbox {d}}x + f_p^{(III)} cPx + M' \left( c^2f_2^{(III)}+ 2f_1^{(I)}\right) \\ +M^{(3)}\left( c^4f_3^{(III)} + 2c^2 f_2^{(I)} +\int f_1 \hbox {d}y \right) + \lambda EF'=0 \end{aligned} \end{aligned}$$
(70)

The displacements are determined by integration of Eqs. (69) and (70) and re-substituting the results into Eqs. (66) and (67). Modulo rigid-body displacements, this leads to

$$\begin{aligned} u(x,y)= & {} \frac{1}{\lambda E} \bigg [f_1^{(II)}\int M {\hbox {d}}x + f_p^{(II)} cPx +M'\left( c^2f_2^{(II)} - \nu f_1\right) \nonumber \\&\quad +M^{(3)}\left( c^4f_3^{(II)}-\nu c^2 f_2 \right) - M^{(5)}\left( c^2 \iint f_2 \hbox {d}y^2 + c^4 (2 + \nu )f_3\right) \bigg ] \end{aligned}$$
(71)
$$\begin{aligned} v(x,y)= & {} \frac{1}{\lambda E} \bigg [- f_1^{(III)}\iint M {\hbox {d}}x^2 - f_p^{(III)} cP\frac{x^2}{2} -\nu f_p^{(I)} cP - M \left( c^2f_2^{(III)}+ (2 +\nu ) f_1^{(I)}\right) \nonumber \\&\quad - M^{(2)}\left( c^4f_3^{(III)} + c^2(2+\nu ) f_2^{(I)} \right) + M^{(4)}\left( c^2 \int f_2 \hbox {d}y -\nu c^4f_3^{(I)}\right) \bigg ] \end{aligned}$$
(72)

The so-determined displacements do satisfy the constitutive relations in Eq. (3). With respect to the displacement continuity conditions, see Eq. (17), we find from the coefficients of Tables 9 and 10 in “Appendix B” that

$$\begin{aligned} \Delta u_0 =\frac{c^4 k_{30}(\gamma -\alpha ) (2+\nu ) }{\alpha E \lambda }M^{(5)} \quad \Delta v_0 =\frac{c^3 k_{31}(\gamma -\alpha )}{\alpha E \lambda } M^{(4)} \end{aligned}$$
(73)

Thus, Eq. (17) are satisfied with \(M^{(4)}= -q^{(2)} = 0\), or for the homogeneous case with \(\alpha =\beta =\gamma = 1\). First, some short remarks concerning the homogeneous case seem to be instructive. In order that the interface displacement continuity conditions are satisfied, \(M^{(4)}\) and \(M^{(5)}\) need not to vanish here. In order to include corresponding non-vanishing terms into a Boley-type table, an additional column \(n=4\) must be opened, to which the terms containing \(M^{(4)}\) and \(M^{(5)}\) have to be shifted. But additional terms containing \(M^{(4)}\) and \(M^{(5)}\), as well as derivatives of M of higher order, come into the play from integrating the stress contributions in the newly opened columns, and these terms must be included in the table also. So, it is to be noted that the displacement terms in the ith column of a Boley-type table, say, do not only stem from the stresses in this ith column, but also include contributions from column \(i-1\). We have designed our present notation by introducing functions \(f_i\) in order to make this fact more visible and tractable than this is possible from the original tables in Boley and Tolins [7]. The above remarks on the shifting procedure of course apply to the composite two-layer beam also, c.f. the columns in our Table 1. However, for this case of an inhomogeneous beam, the situation is complicated in so far, as it has turned out above to be necessary to assume that \(M^{(4)}= -q^{(2)} = 0\), in order that the displacement continuity conditions at the interface \(y=0\) are satisfied in the course of a three-step procedure, \(n=3\), see Eq. (73). Now, in order that complete solutions can be obtained for polynomial loadings q of a higher order than one, the situation again turns out to be resolvable by opening additional columns and repeating the above procedure. Analogous to our above discussion for \(n=3\), the vanishing of derivatives of the loading of a properly increased order has to be required, in order to satisfy the respective extended forms of Eq. (73). Following the above reasoning, the displacements presented in Table 1 have been eventually obtained, restricting to the first three columns, \(n = 3\); likewise this was done in Boley and Tolins [7]. Note that our Table 1 reduces to Case I of [7] for the homogeneous case, \(\alpha =\beta =\gamma = 1\). However, as already shortly noted above, our present notation allows to formulate the displacements of the composite beam in the following series form, without restricting the number n of columns, with \(n > 1\). By complete induction, the results in Table 1 for the displacements can thus be written as:

$$\begin{aligned}&u(x,y) = \frac{1}{\lambda E} \bigg [f_1^{(II)}\int M {\hbox {d}}x + f_p^{(II)} cPx +\sum _{i=2}^n M^{(2i-3)} c^{2(i-2)}\left( c^2 f_i^{(II)} - \nu f_{i-1}\right) \bigg ] \end{aligned}$$
(74)
$$\begin{aligned} v(x,y)= & {} - \frac{1}{\lambda E} \bigg [f_1^{(III)}\iint M {\hbox {d}}x^2 + cP\left( f_p^{(III)}\frac{x^2}{2} + \nu f_p^{(I)}\right) \nonumber \\&\quad + \sum _{i=2}^n M^{(2(i-2))} c^{2(i-2)}\left( c^2 f_i^{(III)}+ (2 +\nu ) f_{i-1}^{(I)}\right) \bigg ] \end{aligned}$$
(75)

Note that such an inductive reasoning is not directly possible when starting the original forms presented in [7]. Recall that, for displacements in the lower layer, \(f_i\) and \(f_p\) have to be replaced by \(g_i\) and \(g_p\) in Eqs. (74) and (75).

Table 1 Boley-type table for a two-layer beam
Full size table

7 Numerical example

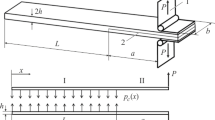
For the sake of comparison to numerical computations, the previously determined results are applied to a clamped–clamped two-layer beam, see Fig. 7, with length L, thickness 2c, a stiffer lower layer with \(E_l = 4E\), \(\nu _l = 3 \nu \) and a thickness-to-length ratio \(\mu = 2c/L = 1/4\).

Fig. 7
figure 7

Redundant two-layer beam subjected to a linear distributed loading, acting on the upper surface at \(y=c\)

Full size image

Stresses and displacements are computed and compared to a two-dimensional (2D) finite element analysis (FEA), using the commercial software ABAQUS [1]. The example beam with \(L=50\,\mathrm {mm}\), \(2c =12.5 \; \mathrm {mm}\), \(\nu =0.1\), \(E =10^4 \; \mathrm {N/mm^2}\) and \(q_0 =12 \; \mathrm {N/mm}\) is meshed with elements of the type CPS8, an 8-node bi-quadratic plane stress quadrilateral element. A comparatively high number of 200 elements in axial direction and 50 elements in transverse direction, respectively, are used in order to obtain sufficiently converged solutions.

The boundary conditions that are applied at the clamped ends read

$$\begin{aligned} u(-L/2,0)&= 0 \quad v(-L/2,0) = 0\quad \phi (-L/2) = 0\nonumber \\ u(L/2,0)&= 0 \quad v(L/2,0) = 0\quad \phi (L/2) = 0 \end{aligned}$$
(76)

The following convenient definition for a generalized cross-sectional rotation, suggested by Szabo [27], is used as trivial boundary condition in order to obtain the analytic solutions according to the above formulations:

$$\begin{aligned} \phi (x)&=\frac{u(x,c) - u(x,-c)}{2c} \end{aligned}$$
(77)

The FEA is performed by setting up two different types of boundary conditions, which are denoted as “elastic” and “rigid” in the following, and are abbreviated by the superscripts “E” and “R,” respectively. For the elastic case “E,” the set of boundary conditions reads at \(x=\pm L/2\):

$$\begin{aligned} u^{\text {E}}(\pm L/2,y) = u(\pm L/2,y)\quad v^{\text {E}}(\pm L/2,y) = v(\pm L/2,y) \end{aligned}$$
(78)

where u and v mean the analytic solutions derived by our above theory. Hence, since in our case of a linearly distributed loading, see Fig. 7, the three-step formulation in Table 1 gives a complete solution, the FEA for case “E” should coincide with our analytic solution.

For the rigid case “R,” the following trivial constraints are prescribed at \(x=\pm L/2\) for the FEA:

$$\begin{aligned} u^{\text {R}}(\pm L/2,y) = 0 \quad v^{\text {R}}(\pm L/2,y) = 0 \end{aligned}$$
(79)

This corresponds to the model of a completely undeformable clamped end.

In order to obtain the analytic solution according to Table 1, taking into account the reduced clamping boundary conditions in Eq. (76), the corresponding bending moment M and normal force P are needed. They are obtained by integration of the beam equilibrium relations, Eq. (21), with the three redundant static integration constants. We now take into account the displacements in Table 1 and substitute the coefficients of Tables 11 and 12, which refer to our present example with \(\alpha = 4,\beta = 1,\gamma =3\). Adding rigid-body displacement fields with three further kinematic unknown constants, satisfaction of the six boundary conditions in Eq. (76) leads to a set of six linear relations for the three static redundant constants and the three kinematic constants. Bending moment and normal force eventually follow in analytic form to:

$$\begin{aligned} M(x)= & {} q_0L^2 \bigg [ \frac{x^3}{12 L^3}-\frac{3 x^2}{8 L^2}-\frac{x}{80 L}+\frac{1}{32} \nonumber \\&\quad + \nu \mu ^2 \frac{25 \left( 1459 \mu ^2+328\right) L-2 \left( 3755 \mu ^2+13156\right) x}{11680 \left( \mu ^2 (73 \nu +40)+20\right) L} \nonumber \\&\quad +\mu ^2\frac{1100 \left( 2 \mu ^2+1\right) L-3 \left( 1529 \mu ^2+144\right) x}{46720 \left( 2 \mu ^2 +1\right) L}\bigg ] \nonumber \\ P(x)= & {} c q_0\frac{3 (229 \nu -90)}{584} \end{aligned}$$
(80)

Note that our analytic formulation indeed reflects the presence of a normal force, the sign of which is governed by the value of Poisson’s ratio \(\nu \). Such a result cannot be obtained in the framework of the kinematic Bernoulli–Euler assumptions.

7.1 Stress field

For determining the analytic stress solutions, we substitute bending moment M and normal force P into Table 1 by using the coefficients of Tables 11 and 12 in “Appendix C.” Corresponding non-dimensionalized stress distributions are shown in Fig. 8 where the stresses \(\sigma _x\), \(\sigma _y\) and \(\tau _{xy}\) are evaluated at three axial coordinates:

(a):

in the vicinity of a clamped end, at \(x =- 49 L/100\)

(b):

in the mid of the left field, at \(x =- L/4\)

(c):

in the middle of the span, at \(x =0\)

The stresses are normalized by introducing the non-dimensional transverse coordinate \(\eta = y/c\) in the following form:

$$\begin{aligned} \sigma _x = \frac{\sigma _x(x,\eta )}{|\sigma _{x}^*|} \quad \sigma _y = \frac{\sigma _y(x,\eta )}{|\sigma _{y}^*|} \quad \tau _{xy} = \frac{\tau _{xy}(x,\eta )}{|\tau _{xy}^*|} \end{aligned}$$
(81)

where the terms in the denominators of Eq. (81) denote the results from our theory evaluated at the respective x-coordinate, where \(\sigma _{x}^*\) is evaluated at the lower fiber, at \(\eta = -1\), \(\sigma _{y}^*\) is evaluated at the upper fiber, at \(\eta = 1\), and \(\tau _{xy}^*\) is taken at the common interface, in \(\eta =0\), respectively.

It turns out that the stress distributions derived from our theory are in full agreement with the FEA results for case “E,” as this should be, since in this case the exterior solution does vanish, because boundary conditions do coincide, see Eq. (76). For rigid constraints, case “R,” the FEA solution deviates from our analytical solution, since boundary conditions are different, see Eq. (79), and case “R” thus takes into account end effects, which are not covered in this work. It is seen from Fig. 8, however, that, in accordance with Saint-Venant’s principle, the non-vanishing exterior solution, which represents the difference with respect to our analytic solution, decays nicely here within a short distance away from the clamped ends, also in the present case of a comparatively thick composite beam. At the clamped ends, the exterior solution obviously shows stress concentrations and a jump-type behavior, which cannot be well reflected by the FEA. That is why we have performed our comparison for a cross section in the vicinity of the clamped end only, at \(x = -49L/100\), see Fig. 8a.

Fig. 8
figure 8

Stress distributions in non-dimensional form, see Eq. (81). The analytic results are represented by the continuous lines, FEA results corresponding to the markers. The superscript “E” denotes elastic and “R” rigid supporting constraints for the FEA model, see Eqs. (76) and (78) for the elastic case and Eq. (79) for the rigid case, respectively

Full size image

7.2 Displacements

Cross-sectional deformations in axial and transverse direction are presented in Fig. 9. The deformations u and v are normalized to

$$\begin{aligned} u = \frac{u(x,\eta )}{|u^*|} \quad v = \frac{v(x,\eta )}{|v^*|} \end{aligned}$$
(82)

where \(u^*\) and \(v^*\) denote the displacements, derived from our theory evaluated at the upper fiber at \(\eta = 1\) and at the respective x-coordinates. Analogous to the stress fields presented in Fig. 8, the analytical results are in excellent agreement to the FEA results for case “E,” i.e., when elastic constraints are prescribed on the FEA model. Near the clamped end, the analytical solution and the FEA-rigid solution “R” again deviate from the analytic solution due to end effects. Away from the clamped end, see Fig. 9b, c, the transverse displacements do coincide, and the shape of the axial displacements is similar to the FEA-rigid result “R,” but shifts are to be observed.

Fig. 9
figure 9

Cross-sectional displacements in axial and transverse direction in non-dimensional form, see Eq. (82). The analytic results are represented by the continuous lines, FEA results corresponding to the markers. The superscript “E” denotes elastic and “R” rigid supporting constraints for the FEA model, see Eqs. (76) and (78) for the elastic case and Eq. (79) for the rigid case, respectively

Full size image
Fig. 10
figure 10

Transverse and axial displacements of the beam axis, at \(\eta =0\), by introducing the non-dimensional axial coordinate \(\xi =x/L\). The analytic results are represented by the continuous lines, FEA results corresponding to the markers. The superscript “E” denotes elastic and “R” rigid supporting constraints for the FEA model, see Eqs. (76) and (78) for the elastic case and Eq. (79) for the rigid case, respectively. Results following from considering the first column in Table 1 only are shown as red lines

Full size image

The deflection cure \(v(\xi ,0)\) of the axis and the axial cross-sectional mid-span displacement \(u(\xi ,0)\) are presented in Fig. 10 by introducing the non-dimensional axial coordinate \(\xi =x/L\). The entities are normalized to

$$\begin{aligned} u = \frac{u(x,0)}{|u^{**}|} \quad v = \frac{v(x,0)}{|v^{**}|} \end{aligned}$$
(83)

with \(u^{**}=u(1/4,0)=0.00086\;\mathrm {mm}\) and \(v^{**}=v(0,0)=0.033\;\mathrm {mm}\) as the analytical results for the displacements at \(\xi = 0\) and \(\eta = 0\) exemplarily. Likewise to the latter results, the FEA results for case “E” are in agreement with the analytic solution. This also holds for the deflection curve of the “R” solution. Additionally, the results obtained from the first column in Table 1 are shown in Fig. 10. A deviation to our analytic solution of \(37\%\) can be observed for the deflection at the mid-span \(\xi =0\).

8 Conclusion

In the present contribution, analytic plane stress linear elasticity results for two-layer composite rectangular beams of infinite axial extension have been obtained, in extension and in analogy to Boley’s successive approximation procedure, see Boley and Tolins [7] for the single-layer case. To the best knowledge of the present authors, our results for the two-layer beam have not been published elsewhere in the open literature so far. Although results have turned out to be quite complex, a compact notation has allowed us presenting them in a form analogous to the one stated by Boley and Tolins [7] for the single-layer beam, see Table 1, which contains Case I of [7] as a special case. Our two-layer formulation automatically satisfies the stress continuity conditions at the interface of the two layers. In order to enable this, we above have started from successive approximation results for appropriate load cases that are applied to the single layer separately and that are put together properly. Eventually enforcing displacement continuity at the interface between the two layers, we have succeeded to derive results for the composite beam that exactly do satisfy the equilibrium field equations, the stress continuity conditions at the interface and the stress boundary conditions at the upper and lower edges of the beam. Moreover, our compact notation allows considering more than the three successive steps that were considered in [7], see Eqs. (60)–(62) and Eqs. (74) and (75) for stress functions and displacements, respectively. In extension of previous successive approximation formulations from the literature, it is thus possible to obtain complete solutions for beams for imposed loadings of an arbitrary polynomial order, meaning that the solutions do satisfy exactly the stress boundary conditions at the upper and lower edges of the composite beam, the stress transition conditions at the interface of the two layers, as well as the equilibrium relations within the layers. When the number of steps needed for the respective polynomial order of the imposed load is taken into account, the displacement continuity relations at the interface as well as the linear constitutive relations within the two layers are also satisfied exactly by our results. However, Boley’s successive approximation procedure is known to converge rather fast. Boley and Tolins [7] restricted their presentation on single-layer beams to three steps. We have presented corresponding three-step results for the two-layer beam in more detail in the Boley-type Table 1. Entries for specific ratios between the elastic parameters and between the thicknesses of the layers have also been given, for the sake of subsequent comparison to finite element computations. Interior solutions for beams of finite length have been derived in a straightforward manner. Particularly, we have presented corresponding analytic results for a comparatively thick clamped–clamped beam under the action of a linearly varying applied load, for which Table 1 is sufficient. As can be seen from Figs. 8, 9 and 10, the results of our proposed method agree well with the results of the finite element solutions. As far as the present authors can see, there are nevertheless two main advantages of the proposed analytical formulation: First, from a theory point of view, the method allows a comparison of the present semi-exact results for displacements and stresses with the assumptions of numerous refined beam theories that have been developed in literature, the basic Bernoulli–Euler theory being contained directly in the first column of Table 1, as mentioned above. For analogies between the Bernoulli–Euler theory and some refined beam theories, see, e.g., Irschik [13]. Table 1 allows to relate the appropriateness of assumptions of refined theories to the polynomial order of the loading. Moreover, from the point of engineering practice, formulations of the present type allow to perform parametric symbolic computations in the design process of composite beams. It is hoped that our results will serve as further benchmark solutions for performing comparisons to higher-order theories for composite rectangular beams, and that our above discussion on some mathematical aspects of Boley’s successive approximation procedure, such as on the shifting process, will stimulate extensions of this method to more advanced topics, such as non-isotropic and non-homogeneous layers, or non-rigid interfaces.