Refined zigzag theory for homogeneous, laminated composite, and sandwich beams derived from Reissner’s mixed variational principle

Abstract

A highly accurate and computationally attractive shear-deformation theory for homogeneous, laminated composite, and sandwich laminates is developed for the linearly elastic analysis of planar beams. The theory is derived using the kinematic assumptions of Refined Zigzag Theory (RZT) and a two-step procedure that implements Reissner’s Mixed Variational Theorem (RMVT). The basic expression for the transverse-shear stress that satisfies a priori the equlibrium conditions along the layer interfaces is obtained from Cauchy’s equilibrium equations. The resulting transverse-shear stress consists of second-order derivatives of the two rotation variables of the theory, which subsequently are restated as the unknown stress functions. As the first step in fulfilling RMVT, the Lagrange-multiplier functional is minimized with respect to the unknown stress functions, resulting in the stress functions consisting of first-order derivatives of the kinematic variables. Subsequently, the second term of RMVT is minimized, producing four beam equilibrium equations and consistent boundary conditions. For any number of material layers the new theory maintains only four kinematic variables. The theory is labeled RZT^(m), where the superscript (m) stands for mixed formulation. The RZT^(m) can accurately model the axial stretch, bending, and transverse-shear deformations, without shear-correction factors. Analytic solutions are derived for simply supported beams subjected to transverse-normal and transverse-shear tractions on the top and bottom surfaces. It is demonstrated that RZT^(m) has a wide range of applicability which includes sandwich construction and the laminates with embedded thin compliant layers that can potentially model progression of delaminations. The main advantage of RZT^(m) over RZT is in the superior predictions of transverse-shear stresses that are obtained directly from the low-order transverse-shear strain measures of the theory without resorting to a post-processing integration procedure. Importantly, the methodology can be readily extended to plate theory, and it can be applied effectively for developing simple and efficient C⁰-continuous finite elements.

Appendices

Appendix 1: Constitutive relations

The stress–strain relations for a two-dimensional (2-D) stress state corresponding to the x–z plane can be readily developed for plane strain and plane stress. Both constitutive relations are derived from the 3-D state of stress and strain for an orthotropic material layer in the material reference frame. The orthotropic layers of a composite laminate may have arbitrary orientation in the x–y plane of the beam. Employing the appropriate tensor transformations for stresses and strains, and the assumptions for plane strain (ɛ ^(k) _y  = γ ^(k) _yz  = γ ^(k) _xy  = 0) or plane stress (σ ^(k) _y  = τ ^(k) _yz  = τ ^(k) _xy  = 0), the 2-D strain–stress equations relating the infinitesimal strains to the Cauchy stresses in the x–z beam reference frame may be expressed as

$$ \left\{{\begin{array}{*{20}c} {\varepsilon_{x}^{(k)}} \\ {\varepsilon_{z}^{(k)}} \\ {\gamma_{xz}^{(k)}} \\ \end{array}} \right\} = \left[{\begin{array}{*{20}c} {S_{11}^{(k)}} & {S_{13}^{(k)}} & 0 \\ {S_{13}^{(k)}} & {S_{33}^{(k)}} & 0 \\ 0 & 0 & {S_{55}^{(k)}} \\ \end{array}} \right]\left\{{\begin{array}{*{20}c} {\sigma_{x}^{(k)}} \\ {\sigma_{z}^{(k)}} \\ {\tau_{xz}^{(k)}} \\ \end{array}} \right\} $$

(50)

where the S ^(k) _ij ’s denote the transformed compliance coefficients; they are given by different expressions depending on whether or not there is the plane stress or plane strain condition.

Since $\sigma_{z}^{(k)}$, transverse-normal stress, is commonly much smaller than $\sigma_{x}^{(k)}$, axial stress, then by setting $\sigma_{z}^{(k)} = 0$, the reduced constitutive relations are obtained

$$ \left\{{\begin{array}{*{20}c} {\varepsilon_{x}^{(k)}} \\ {\gamma_{xz}^{(k)}} \\ \end{array}} \right\} = \left[{\begin{array}{*{20}c} {S_{11}^{(k)}} & 0 \\ 0 & {S_{55}^{(k)}} \\ \end{array}} \right]\left\{{\begin{array}{*{20}c} {\sigma_{x}^{(k)}} \\ {\tau_{xz}^{(k)}} \\ \end{array}} \right\} $$

(51)

Alternatively, Eq. (51) can be inverted to yield the stress–strain relations

$$ \left\{{\begin{array}{*{20}c} {\sigma_{x}^{(k)}} \\ {\tau_{xz}^{(k)}} \\ \end{array}} \right\} = \left[{\begin{array}{*{20}c} {C_{11}^{(k)}} & 0 \\ 0 & {C_{55}^{(k)}} \\ \end{array}} \right]\left\{{\begin{array}{*{20}c} {\varepsilon_{x}^{(k)}} \\ {\gamma_{xz}^{(k)}} \\ \end{array}} \right\} $$

(52)

where [C ^(k)₁₁ , C ^(k)₅₅ ] ≡ [1/S ^(k)₁₁ , 1/S ^(k)₅₅ ] are the corresponding stiffness coefficients.

Appendix 2: RZT equilibrium equations derived from Cauchy equilibrium equations

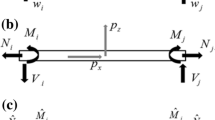
Consider a straight planar beam of rectangular cross-section having the length L, height 2h, and width b. The beam is composed of N orthotropic material layers that are perfectly bonded to each other (Fig. 1), where each layer is denoted by the superscript (k). The beam is referred to the Cartesian coordinate system (x, y, z), where x ∊ [x _a , x _b ] denotes the beam longitudinal axis, and z ∊ [−h, h] the thickness coordinate.

The 2-D Cauchy equilibrium equations of elasticity theory may be expressed as

$$ \sigma_{x, x}^{(k)} (x, z) + \tau_{xz, z}^{(k)} (x, z) = 0 $$

(53)

$$ \tau_{xz, x}^{(k)} (x, z) + \sigma_{z, z}^{(k)} (x, z) = 0 $$

(54)

Integrating Eq. (53) over the cross-sectional area yields

$$ N_{x, x} (x) + b\left[{T_{t} (x) - T_{b} (x)} \right] = 0 $$

(55)

where the axial force is given by

$$ N_{x} (x) \equiv \int\nolimits_{A} {\sigma_{x}^{(k)} (x, z)dA} $$

(56)

In addition, the following equilibrium conditions are fulfilled

$$ \tau_{xz}^{\left(N \right)} \left({x, h} \right) \equiv T_{t} \left(x \right), \quad \tau_{xz}^{(1)} \left({x, - h} \right) \equiv T_{b} \left(x \right) $$

(57)

These relations state that the shear tractions T _t (x) and T _b (x) that are prescribed on the top (z = h) and bottom (z = −h) surfaces, respectively, are in equilibrium with the transverse-shear stresses on the corresponding surfaces.

Next, multiplying Eq. (53) by the z coordinate, and integrating over the cross-sectional area gives

$$ \int\nolimits_{A} {z\left[{\sigma_{x, x}^{(k)} (x, z) + \tau_{xz, z}^{(k)} (x, z)} \right]dA = 0} $$

(58)

Defining the total bending moment M _x (x) and the total shear force V _x (x) in the usual manner as

$$ \left[{\begin{array}{*{20}c} {M_{x} (x),} & {V_{x} (x)} \\ \end{array}} \right] \equiv \int_{A} {\left[{z\sigma_{x}^{(k)} (x, z),\tau_{xz}^{(k)} (x, z)} \right]dA} $$

(59)

and integrating the second term in Eq. (58) by parts, results in

$$ \begin{aligned} \int\nolimits_{A} {z\tau_{xz, z}^{(k)} (x, z)dA} & = - \int\nolimits_{A} {\tau_{xz}^{(k)} (x, z)dA} + hb\left[{\tau_{xz}^{(N)} (x, h) +\, \tau_{xz}^{(1)} (x, - h)} \right] \\ & = - V_{x} (x) + hb\left[{T_{t} (x) + T_{b} (x)} \right] \\ \end{aligned} $$

(60)

This gives rise to the second equilibrium equation for the beam

$$ M_{x, x} (x) - V_{x} (x) + hb\left[{T_{t} (x) + T_{b} (x)} \right] = 0 $$

(61)

Integrating Eq. (54) over the cross section yields the third equilibrium equation of the beam

$$ \begin{aligned} \int\nolimits_{A} {\left[{\tau_{xz, x}^{(k)} (x, z) + \sigma_{z, z}^{(k)} (x, z)} \right]dA} & = V_{x, x} (x) + b\left[{\sigma_{z}^{(N)} (x, h) - \sigma_{z}^{(1)} (x, - h)} \right] \\ & = V_{x, x} (x) + b\left[{q_{t} (x) - q_{b} (x)} \right] = 0 \\ \end{aligned} $$

(62)

where σ ^(N) _z (x, h) ≡ q _t (x) and σ ⁽¹⁾ _z (x, −h) ≡ q _b (x). Equation (62) can now be written in the familiar form as

$$ V_{x, x} (x) + q(x) = 0 $$

(63)

where the transverse-normal traction, q(x), is defined as

$$ q(x) \equiv b\left[{q_{t} (x) - q_{b} (x)} \right] $$

(64)

Finally, the fourth RZT equilibrium equation is obtained by multiplying Eq. (53) by the zigzag function ϕ ^(k)(z), and then integrating over the cross section

$$ \begin{aligned} & \int\nolimits_{A} {\phi^{(k)} (z)\left[{\sigma_{x, x}^{(k)} (x, z) + \tau_{xz, z}^{(k)} (x, z)} \right]dA} \hfill \\ & = \int\nolimits_{A} {\left[{\phi^{(k)} (z)\sigma_{x}^{(k)} (x, z)} \right]_{,x} dA - \int\nolimits_{A} {\phi_{,z}^{(k)} (z)\tau_{xz}^{(k)} (x, z)dA}} \hfill \\ & \quad + b\left[{\phi^{(N)} (h)\tau_{xz}^{(N)} (x, h) - \phi^{(1)} (- h)\tau_{xz}^{(1)} (x, - h)} \right] = 0 \hfill \\ \end{aligned} $$

(65)

Now defining the bending moment M _ϕ (x) and shear force V _ϕ (x) related to the zigzag distortion, as in the original RZT formulation [36], as

$$ \left[{\begin{array}{*{20}c} {M_{\phi} (x),} &; {V_{\phi} (x)} \\ \end{array}} \right] \equiv \int_{A} {\left[{\phi^{(k)} (z)\sigma_{x}^{(k)} (x, z),{\phi^{(k)}_{,z}} {(z)}\tau_{xz}^{(k)} (x, z)} \right]dA} $$

(66)

and recognizing that the last two terms in Eq. (65) vanish identically due to the vanishing property of the zigzag function ϕ ^(N)(h) = ϕ ⁽¹⁾(−h) = 0, gives rise to the fourth and final equilibrium equation for this beam theory, i.e.,

$$ M_{\phi, x} (x) - V_{\phi} (x) = 0 $$

(67)

Finally, the four equilibrium equations are summarized as

$$ N_{x, x} (x) + T_{d} (x) = 0 $$

(68a)

$$ M_{x, x} (x) - V_{x} (x) + hT_{s} (x) = 0 $$

(68b)

$$ V_{x, x} (x) + q(x) = 0 $$

(68c)

$$ M_{\phi, x} (x) - V_{\phi} (x) = 0 $$

(68d)

where

$$ T_{d} \left(x \right) \equiv b\left[{T_{t} \left(x \right) - T_{b} \left(x \right)} \right], \quad T_{s} \left(x \right) \equiv b\left[{T_{t} \left(x \right) + T_{b} \left(x \right)} \right] $$

(68e)

It is remarked herein that the same equilibrium equations, Eq. (68a–68d), have been obtained using the virtual work principle in Ref. [36]. In addition, the variational approach gives rise to a set of variationally consistent boundary conditions at the two ends x = (x _a , x _b ) of the beam, where the edge tractions (T_xa, T_xb) and (T_za, T_zb), are prescribed. The applied loads acting along the bounding surfaces z = (−h, h), namely, q _b (x), q _t (x), T _b (x), and T _t (x), enter into the equilibrium equations, Eq. (68a–68d), meaning that all of the stresses on z = (−h, h) are fully equilibrated with the applied tractions on these surfaces. Finally, the homogeneous conditions of the zigzag functions, ϕ ^(N)(h) = ϕ ⁽¹⁾(−h) = 0, have been used in the derivation of the fourth equilibrium equation, Eq. (68d). Because of these homogeneous conditions, the transverse-shear tractions, T _b (x) and T _t (x), do not contribute to the relationship between the zigzag-related bending moment M _ϕ (x) and the shear force V _ϕ (x). This is in contrast to Eq. (68b), where the moment-shear force equilibrium involves the prescribed shear tractions. For the special case of zero shear tractions, T _b (x) = T _t (x) = 0, Eq. (68b) and (68d) have an analogous form.

The constitutive equations relating the stress resultants, N _x (x), M _x (x), and M _ϕ (x), to the strain measures u _,x (x), θ _,x (x), and ψ _,x (x) are obtained by substituting Eqs. (4) and (5) into Eq. (52) and then integrating Eqs. (56), (59) and (66) over the cross section, resulting in

$$ \left\{{\begin{array}{*{20}c} {N_{x}} \\ {M_{x}} \\ {M_{\phi}} \\ \end{array}} \right\} = \left[{\begin{array}{*{20}c} {A_{11}} & {B_{12}} & {B_{13}} \\ {B_{12}} & {D_{11}} & {D_{12}} \\ {B_{13}} & {D_{12}} & {D_{22}} \\ \end{array}} \right]\left\{{\begin{array}{*{20}c} {u_{,x}} \\ {\theta_{,x}} \\ {\psi_{,x}} \\ \end{array}} \right\} $$

(69)

where the stiffness coefficients are given by

$$ \left[{A_{11}, B_{12}, D_{11}} \right] \equiv \int_{A} C_{11}^{(k)} \left[{1, z, z^{2}} \right]dA, \quad \left[{B_{13}, D_{12}, D_{22}} \right] \equiv \int_{A} C_{11}^{(k)} \phi^{(k)} \left[{1, z, \phi^{(k)}} \right]dA $$

(70)

The constitutive equations for the transverse-shear forces, defined by Eqs. (59) and (66), depend on the definitions for τ ^(k) _xz ; for RZT^(m), they are given by Eqs. (42) and (43a–43c).