Abstract
This work describes an approach for strain determination at the “in-plane” torsional test using digital image correlation (DIC) without brushing a statistical pattern on the specimen. It is well known that the in-plane torsion test represents a appropriate test method for material characterization of sheet metal in terms of yielding and kinematic hardening (Wagner et al. in Application of the in-plane torsion test in an industrial environment—recent advances and remaining challenges. In: Conference Paper of the 12th Forming Technology Forum, Herrsching, Germany, 2019). However, the gained measurement data do not allow the exact reading of material models for direct use in numerical analysis. The determination of shear values represents thereby the main challenge. Besides well-established methods for stress–strain analysis mentioned in this contribution, the applicability of DIC methods for the direct reading of distortion on the specimen has been investigated. Therefore, a torsion test rig has been developed and torsion tests using specimen out of mild- and high-strength steel have been conducted. The in-plane situation allows the distortion tracking of single points on the specimen by using a 2D image correlation software. The needed pictures were taken by using a common digital lens reflex camera. It has been shown that the resolution of the inherent specimen pattern is sufficient for the use of common 2D image correlation software. Torsional test results in the form of computed yield curves of mild- and advanced high-strength steels are aimed to be presented in this contribution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Calibration and identification of parameter of material models for forming and crash simulation have become a major issue in the material development. To get comprehensive simulation results, knowledge of the material behavior in the form of material models is required. Different kinds of material tests are available for calibration of material models. However, the in-plane torsion test gives therefore the advantage of gaining test data far beyond uniform elongation as seen in the uniaxial tensile test [1, 2]. This available amount of data from the in-plane torsional test lifts the prediction quality of calibrated flow curves to a more precise level. Additionally, the in-plane torsional test provides the possibility of load reversal, without the usage of any stabilizing devices as usually needed at common tensile–compression tests [3], and enables furthermore the determination of shear fracture strains for calibration of damage models [4]. In order to perform in-plane torsional tests, a test rig has been designed at the Institute of Structural Lightweight Design, JKU Linz, in cooperation with the voestalpine Stahl GmbH, and successfully tested in terms of flow curve determination as well as for calibrating of kinematic hardening models [5, 6]. However, the gained measurement data in the form of measured torque T and the twist angle \(\alpha \) do not allow the direct reading of material models. For this reason, the extraction of the stress and strain values represents a very important issue and requires an closer examination. Approximation of the calculated stress–strain curves assuming a defined material model according to Bauer and Pöhlandt, [7] and the manual measurement of the shear angle on deformed scribed lines [6] represent established methods for computation of strain values. However, several issues render this methods in terms of accuracy and practicability, including reading errors or assumptions of material models. Thus, the application of digital image correlation in terms of strain determination has been initiated. Recent advances of the use of digital image correlation for strain determination are aimed for being presented herein.
2 Experimental setup
2.1 Current test setup
In order to perform torsional tests at sheet metals, a test rig was developed and designed. The load transmission is here done by friction to avoid influence on fracture load due to micro-cracks or stress concentration caused by mechanical applied pattern or bores [8]. Figure 1 shows the functional principle together with the general dimensions of the specimen where D describes the overall diameter, \(r_i\) and \(r_a\) are the respective groove radii, s is the sheet thickness, and \(s_\mathrm{g}\) is the groove thickness listed in Table 1. The target values to be measured are the resulting torque T and the overall twist angle \(\alpha \).
In Fig. 2, finally the torsion test rig, built up at the Institute of Structural Lightweight Design of the Johannes Kepler University Linz, is pointed out. The rig is driven by a servo-hydraulic test cylinder.
This cylinder is pulling the lever arm with distance of 500 mm to the center of the specimen in an adjustable speed range of 0.004–500 mm/s with a maximum force of 25 kN (see Fig. 2). As already mentioned, the load transmission takes place by friction; therefore, the specimen is clamped at its inner and outer diameter, where the inner diameter of the specimen is free of rotation. The clamping device is designed in a way to provide a steady contact force distribution in order to avoid bending of the specimen. For optical observation of the deformation, a common digital single lens reflex (DSLR) camera, equipped with an self-made micro-optic lens system, is taking pictures during the test. The camera is applied at the test rig supported by an integrated LED lightning system. The specimen will be twisted until fracture occurs. During the test, the cylinder force and the displacement of the hydraulic drive cylinder are recorded. The twist angel \(\alpha \) is calculated from the recorded cylinder displacement values, and the torque T is calculated from the recorded force values and the lever arm length. For the presented results in this contribution, specimen out of mild- and high-strength steels has been subjected to be tested at quasi-static strain rate conditions. Strain rate dependency is not taken into account in this contribution.
2.2 Test sample
Figure 3 shows the current specimen geometry used at the “in-plane” torsion test procedure described in this contribution. The specimen is manufactured out of sheet metal and contains a linear groove with constant groove thickness. This groove represents an overload breaking part, where the groove thickness is kept in a defined range to realize the torque transmission by static friction without sliding. A torque transmission by static friction offers the advantage of using simple clamping devices without any form of fit equipment like diamond pattern or locking pins. These devices are usually affecting the measurement results due to pre-deformation of the specimen [8]. The groove is actually manufactured by fine turning. This kind of manufacturing causes slight notches which are taking influence on the gain-able strain and stress values and have to be considered therefore. According to the literature, manufacturing of the groove by milling leads to the lowest variance of the extractable material strength values [9]. To use the entire clamping force of the test rig in order to transmit the torque to specimen characterized by high strength, the used sheet metals have to be free of any coatings. Additionally, a lasered scribed line is applied on the specimen for visualizing the deformation.
3 Determination of material strength values under pure shear by back-calculation methods
In the following different established approaches for calculation of material strength, values based on a back-calculation methods and post-measurement methods are described and shortly summarized.
3.1 Shear strength determination by analytical back-calculation from shaft rotation
This analysis process is based on Bauer and Pöhlandt [7]. The values for shear stress can be calculated easily according to Eq. (1), where T represents the measured torque, r the radial distance to the specimen center, t the time and \(s_\mathrm{g}\) the fillet thickness at the groove of the specimen.
The nonlinear relation between shear angel \(\gamma \) and the twist angle \(\alpha \) is expressed in Eq. 2.
where the shear strain \(\gamma \) can be derived by series expansion. Therefore, a material model has to be assumed for approximation of the computed yield curve to the real yield curve. The first approximation for the shear strain \(\gamma _0\) is derived by assuming the material model according to Ludwik with \(\sigma _f=C\varphi ^n\). In the literature, the first approximation is also called the zero approximation [5] and is described in Eq. (3)
where \(\beta =2\) in terms of equivalent stress formulation according to Tresca, and \(\beta =\sqrt{3}\) in case of using the equivalent stress formulation according to von Mises. The variables A and C are fit parameters to be determined. After comparison of the computed results based on the assumed constitutive law with the measurement result, the zero approximation can be replaced by a second-order approximation described in [5].
3.2 Shear strength determination by manual measuring of a deformed scribed line
This method is based on the manual measurement of a deformed scribed line (see Fig. 4) and is enabled due to the circumstance that every instant of time during plastic deformation and stress and strain gradient is existing [6]. The shear stress distribution \(\tau (r,t)\) can be calculated according to Eq. (1). Manual measuring of the shear deformation \(\gamma (r,t)\) described in Eq. (4) at an defined state of deformation, together with the corresponding torque, allows to extract a full yield curve based on at least one state of the deformed scribed line.
The error proneness due to reading errors during the manual measurement of the scribed line can be named as main handicap of this strength analysis procedure [8]. Due to the fact that high deformation gradients are concentrated in small areas of observation, a slight reading error causes a strong deviation in the final results for material strength values.
4 Determination of material strength values under pure shear using digital image correlation methods
A further powerful method for strain evaluation is digital image correlation (DIC), which has been successfully applied to the current “in-plane” torsion test. The “in-plane” situation of the test provides the possibility to utilize 2D DIC, using a single camera observing a defined area of the test sample. For this, a common single lens reflex camera (DSLR camera, see Fig. 2) has been used for taking images of the region of interest (ROI). To be able to use the commercially available reflex camera and to capture suitable pictures from the ROI, a special achromatic camera lens was built, where the macro-focus is set on the specimen surface to be observed. Figure 5 shows the mounting situation of the DSLR camera equipped with an applied special lens system on the test rig, and Fig. 6 shows the achromatic lens system. A fixed mounted LED light ring ensures the appropriate illumination of the sample section to be observed, and furthermore, that there is—without applied load—no distortion of the gray pattern due to moving of the lighting.
Figure 7 shows the image size calibration based on the sensor size and focal distance. Due to the small image section (ROI) in the center of the taken pictures required for evaluation, a constant pixel pitch was assumed and a distortion due to curvature in particular was not considered.
The images were taken at defined time steps during the twisting and assigned to the corresponding torque values. The observation of a small area of interest together with a camera lens built on special purpose enables the utilization of the inherent material texture of the uncoated sheet metal surface. Instead of applying an additional brushed speckle pattern, the distortion of the natural gray pattern is tracked using DIC methods. This approach in the specimen preparation gives the advantage of cost and time savings. Furthermore, it is ensured that the deformation is observed directly on the specimen instead on a brushed coating. For investigations on deformation observation using DIC, the software VIC-2D (Correlated Solution Inc., USA) has been applied. Therefore, two different methods in image correlation have been investigated using images of mild steel specimen characterized by a well-developed kinematic hardening behavior. Figure 8 shows the initial image together with the marked ROI including a size-defined subset mesh and reference points. Based on this image, the following correlation methods have been analyzed in terms of statistical correlation error \(\sigma \) and distortion observation:
-
Absolute correlation: Distortion is referenced to the first (origin) taken picture
-
Incremental correlation: Distortion is referenced to the picture previously taken.
The main source of error in 2D DIC is thereby the image correlation error \(\sigma \), which means the error in the pattern matching process between different image frames. It is a function of the camera noise, image distortion, illumination conditions, speckle pattern, how parallel the camera sensor and specimen are and matching process (subset size, shape function, sub-pixel interpolation scheme, correlation criterion) and means the average confidence margin for the data set where lower numbers indicate a better quality match [10, 11].
Figure 9 shows a comparison of the results of this two image correlation methods based on a mild steel specimen.
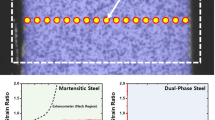
The use of the absolute image correlation method causes a loss of traceable points during the correlation, while the incremental correlation procedure provides distortion images without loss of traceable points or fragmentation. Therefore, the statistical correlation error is decreasing compared to the absolute correlation method. Strain determination at high-strength steels, where the low developed kinematic hardening rate leads to a shear deformation concentrated in a small shear band, can be performed by—in principle—tracing at least one single point throughout the test. Tracing of several (available) subsets within the observed area enables a accurate determination of the yield curve based on the computed strain. Figure 10 shows the different shear band characteristic of mild- and high-strength steels. At the mild steel samples, the shear band is distributed throughout the observed area, while at the high-strength steel specimen, a small concentrated shear band is observable. Particularly at this kind of steels, the application of DIC methods is advantageous, due to the fact that strain determination by manual measuring of the scribed line in a small shear band is inevitably inaccurate [6]. Furthermore, the computation of the stress–strain curves by back-calculation requires an substantiated assumption of the material model for high-strength steels with low kinematic hardening. Figure 11 shows the computed stress–strain curve of a high-strength steel using three selected subsets at different radial distances to be traced for strain determination within a small observed ROI compared to the stress values gained by the common tension test. Due to the “in-plane” situation, it is assumed that there is no out-of-plane movement. The shear stress values \(\tau (r)\) are calculated according to Eq. (5)
and the equivalent stress \(\sigma _{\mathrm {eq.}}(r)\) under assumption of the von Mises flow rule according to Eq. (7) with
The values for equivalent strain \(\varphi _{\mathrm{eq.}}(r)\) are computed based on the calculation by the software VIC-2D for the shear angel \(\gamma \) according to
The “in-plane” torsion test was therefore performed at quasi-static deformation speed. Every marker at the shown stress–strain curve represents a digital image. The material strength determination based on at least three observed points in the concentrated shear area showed good results in terms of deviation. The stress deviation between the maximum and the minimum stress values computed by data at the selected points \({P_0}\), \({P_1}\) and \({P_2}\) is \(<2.2\%\)
5 Conclusion and remaining remarks
A developed torsion test rig, driven by a common hydraulic cylinder using a lever arm, has been described. Besides well-established back-calculation methods for computation of materials strength values out of the “in-plane” torsion test, an approach for yield curve determination by DIC has been described in this contribution. It could be shown that the usage of 2D DIC by utilizing the inherent surface texture provides a appropriate method for strain measurement, i.e., no additional brushed speckle pattern is needed for reliable strain determination. Therefore, two different correlation methods were investigated in terms of correlation error at mild steel specimen characterized by a high kinematic hardening rate and a well-developed shear band. It turns out that an incremental correlation procedure, where the distortion of the subsets is referenced to the picture previously taken, represents a more accurate method in terms of statistical correlation error compared to the absolute correlation procedure. Furthermore, DIC supported strain measurements at high-strength steels were performed in order to approve the usability of DIC methods for determining strength values of materials characterized by a low kinematic hardening rate and a small shear band. It could be shown that by using the inherent surface pattern, at least a sufficient number of traceable subsets can be observed for computing reliable yield curves of high-strength steels. Next to the main idea of using DIC for computing material strength values based on “in-plane” torsional test values described herein, several issues still remain to be mentioned, for instance, the diversity of sheet metals to be tested in terms of coatings and inherent material texture as well as the comparison of the determined material strength values to well-established test methods. Gaining knowledge of the error evolvement of this method is a topic of further investigations.
References
Tekkaya, A., Pöhlandt, K., Lange, K.: Determining stress–strain curves of sheet metal in the plane torsion test. CIRP Annu. Manuf. Technol. 31, 171–174 (1982)
Marciniak, Z.: Influence of the sign change of the load in the strain hardening curve of the copper test subject to torsion. Archiwum mechanici Stosowanej 13, 743–751 (1961)
Röhrig, C., Scheffer, T., Diebels, S.: Mechanical characterization of a short fiber-reinforced polymer at room temperature: experimental setups evaluated by an optical measurement system. Contin. Mech. Thermodyn. 5, 1093–1111 (2017)
Yin, Q., Tekkaya, A., Traphöner, H.: Influence of the sign change of the load in the strain hardening curve of the copper test subject to torsion. CIRP Ann.Manuf. Technol. 64, 261–264 (2015)
Schagerl, M., Grillenberger, M.: On the back calculation of material strength values from strength test resutls. Proc. Appl. Math. Mech. 18, e201800342 (2018)
Till, E., Hackl, B., Walch, C.: Enhanced characterization of pure shear deformation and failure behaviour of AHSS sheets using plane torsion tests. In: Proceedings of the 34th International Deep Drawing Research Group Conference, pp. 868–878 (2015)
Bauer, M., Pöhlandt, K.: Fundamentals of the plane torsion test for determining flow curve of thin sheet. Matrialprüfung 28(3), 220–225 (1986)
Yin, Q.: Verfestigungs-und Schädigungsverhalten von Blechwerkstoffen im ebenen Torsionsversuch. Dissertation, 211 Seiten, Fakultät für Maschinenbau der Technischen Universität Dortmund (2014)
Traphöner, H., Heibel, S., Clausmayer, T., Tekkaya, A.: Infuence of manufacturing processes on material characterization with the grooved in-plane torsion test. Int. J.Mech.Sci. 146, 544–555 (2018)
Siebert, T.: Error estimations in digital image correlation technique. Appl. Mech. Mater. 7–8, 265–270 (2007)
Wang, Z., Li, H., Tong, J., Ruan, J.: Statistical analysis of the effect of intensity pattern noise on the displacement measurement precision of digital image correlation using self-correlated images. Exp. Mech. 47(5), 701–707 (2007)
Wagner, L., Gross, T., Gruger, P., Grillenberger, M., Schagerl, M.: Application of the in-plane torsion test in an industrial environment—recent advances and remaining challenges. In: Conference Paper of the 12th Forming Technology Forum, Herrsching, Germany (2019)
Acknowledgements
This work has been supported by the COMET-K2 Center of the Linz Center of Mechatronics (LCM) and funded by the Austrian federal government and the federal state of Upper Austria.
Funding
Open access funding provided by Johannes Kepler University Linz.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andreas Öchsner.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grillenberger, M., Schagerl, M. Enhanced characterization of the yield behavior of sheet metal at torsional load using digital image correlation methods. Continuum Mech. Thermodyn. 33, 475–483 (2021). https://doi.org/10.1007/s00161-020-00920-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00161-020-00920-1