Distributed design optimization of multi-component systems using meta models and topology optimization

Abstract

Distributed optimization architectures decompose large monolithic optimization problems into sets of smaller and more manageable optimization subproblems. To ensure consistency and convergence towards a global optimum, however, cumbersome coordination is necessary and often not sufficient. A distributed optimization architecture was previously proposed that does not require coordination. This so-called Informed Decomposition is based on two types of optimization problems: (1) one for system optimization to produce stiffness requirements on components using pre-trained meta models and (2) one for the optimization of components with two interfaces to produce detailed geometries that satisfy the stiffness requirements. Each component optimization problem can be carried out independently and in parallel. This paper extends the approach to three-dimensional structures consisting of components with six degrees of freedom per interface, thus significantly increasing the applicability to practical problems. For this, an 8-dimensional representation of the general 12 x 12 interface stiffness matrix for components is derived. Meta models for mass estimation and physical feasibility of stiffness targets are trained using an active-learning strategy. A simple two-component structure and a large robot structure consisting of four components subject to constraints for 100 different loading scenarios are optimized. The example results are at most 12.9% heavier than those of a monolithic optimization.

1 Introduction

The holistic or monolithic design of systems involving multiple components can be a difficult task. Firstly, from a product development perspective, the development process itself requires decomposition (Sobieszczanski-Sobieski and Haftka 1997). Therefore, in classical top-down development processes, requirements are first formulated at the system level and then broken down, and passed on to lower levels and finally to the respective departments (Forsberg and Mooz 1991; Ulrich and Eppinger 2003). The hierarchical process offers advantages, allowing designers to focus on parts rather than the entire system (Eckert and Clarkson 2005). Secondly, from a computational perspective, the sheer size of the system can make monolithic design prohibitively expensive, requiring decomposition to reduce the size of the problem and the computational time (Martins and Lambe 2013). For both views, therefore, decomposition is often preferred over a monolithic design approach.

Consequently, in the context of design optimization, distributed design optimization architectures were developed. These architectures break down a given monolithic optimization problem into smaller optimization subproblems, enabling individual design by separate groups (Martins and Ning 2022). Over recent years, numerous distributed architectures have emerged and successfully applied across different use cases. Many of these architectures build upon classical approaches such as Collaborative Optimization (Braun 1996), Analytical Target Cascading (Kim et al. 2003), BLISS-2000 (Sobieszczanski-Sobieski et al. 2000, 2003), or Quasiseparable Decomposition (Haftka and Watson 2005).

However, despite their potential benefits, distributed optimization architectures have not seen widespread adoption in industry. This is often due to their increased computational time requirements or their inability to accurately mirror real-world distributed product development processes (Martins and Ning 2022). One key challenge is that the optimization problems decomposed by most distributed architectures are not entirely separable and necessitate a coordination strategy to ensure consistency. Achieving such coordination within an industrial setting requires an optimization architecture that connects all involved departments, a task that is challenging to implement. Moreover, employing such a coordination strategy carries the risk of incurring coordination overhead, where the cost of coordination surpasses that of the original optimization problem (Alexandrov and Hussaini 1997; Tosserams et al. 2009).

Therefore, a decomposition scheme without any need for coordination is advantageous. In the context of distributed optimization architectures, we define the term decoupling as a horizontal decomposition between system and component level and vertical decomposition between different components without the need for coordination after the decomposition. This type of decomposition was, e.g., introduced by Zimmermann and von Hoessle (2013) and embedded in a design procedure in Zimmermann et al. (2017). The procedure differs from classical design optimization methods that it is not based on point solutions, but so-called solution spaces, which represent sets of good designs, i.e., designs that satisfy all requirements. In general, decoupled architectures run into the risk of

• 1. accidentally ruling out the optimal but initially unknown solutions on the system level and

• 2. committing to a physically infeasible design, i.e., a design that cannot be realized on a detail level afterwards.

One way to address these problems is to provide a priori information from the component level to the system level using meta models that are trained before performing a decoupling (Hou and Jiao 2020). Meta models have a long history in systems design because they can reduce the high computational cost of large-size computer models (Viana et al. 2014).

Papadrakakis et al. (1998) were one of the first authors that successfully applied meta models into a structural optimization problem, yet for size and shape optimization only. In the field of topology optimization, the combination of high-fidelity solutions of finite element models together with a large number of design variables lead to high computational cost for the design optimization process (Bendsøe and Sigmund 2004). Hence, meta models have recently been used to speed up the optimization process of these large-scale optimization problems, see, for example, the reviews of Mukherjee et al. (2021), Ramu et al. (2022) or Woldseth et al. (2022). Here, the deformation energy, referred to as compliance in the context of topology optimization, is often utilized as a performance measure. Since the compliance is a load-dependent quantity, corresponding mechanical detailed designs are only valid for the respective load case. By using a sufficiently broad dataset that spans variations in loads, boundary conditions, material models, objective function, and design domains, one can train a regressor for a general mapping.

Inherent component characteristics, which are independent of changing boundary conditions, can be used to reduce the amount of needed training data. For linear analyses, a stiffness matrix incorporates all information about the geometrical and physical constitution of mechanical components and is therefore load-independent. Hence, stiffness modeling plays an important role, e.g., in the design of robots, where multiple poses and loads are often considered. For example, Wang et al. (2019) performed a stiffness matrix optimization of a serial robot based on a parameterization of a topology, using linear regression. Similarly, Wang et al. (2022) topology optimized a parallel robot using a stiffness matrix-mass meta model. In multi-scale optimization, expensive macro- and microscale connections can be replaced by meta models to reduce computational costs. For example, Wu et al. (2019) utilized substructuring for hierarchical lattice structures to estimate microstructure mass and stiffness matrix. Additionally, White et al. (2019) proposed a neural network to map parameterized microstructures to their elastic material properties. Moreover, Wang et al. (2021) optimized various parameterized microstructures using meta models for material properties such as stiffness matrix or thermal conductivity. In Xia and Breitkopf (2015), topology optimization without parameterization predicted the effective strain energy density and constitutive tensor of microstructures. Furthermore, Kollmann et al. (2020) determined the stiffness matrix of topology-optimized microstructures using equivalent load cases, training a regression model for multi-scale optimization, however, not directly with a stiffness matrix as an input. In summary, most meta model approaches in literature either utilize parametrized topologies, limiting lightweight potential, or do not directly incorporate a stiffness matrix as an input for the meta models.

Besides the risk of excluding optimal designs, ensuring physical feasibility is also a relevant and difficult challenge for decoupled optimization architectures. Theoretically, all positive (semi-)definite stiffness matrices can be realized by a mechanical design. Milton and Cherkaev (1995) demonstrated that any positive definite elasticity tensor meeting necessary symmetry conditions can be achieved with a two-phase composite. Moreover, Huang and Schimmels (1998) and Huang and Schimmels (2000) established that arbitrary spatial stiffness matrices can be realized using screw springs. Consequently, designs not meeting positive definiteness criteria could be discarded to ensure physical feasibility, as exemplified by Wang et al. (2020), who explicitly included positive definiteness as an inequality constraint in multi-scale optimization. However, in continuous structural component design, factors like limited geometric design domain, available materials, and minimum member size further constrain the feasible design space of positive definite stiffness matrices (Milton et al. 2017; Wu et al. 2021). To prevent committing to infeasible designs, more stringent feasibility constraints are necessary, with design space limits not yet explicitly defined. Utilizing existing data, machine learning classifiers can approximate the physically feasible region. Classifiers are frequently employed in top-down design to ensure feasibility across various domains, such as analog circuit design (Ding and Vemur 2005; Boolchandani et al. 2011), air conditioners (Jeong et al. 2012), or the physically feasible workspace of robots (Kulick et al. 2013). In mechanical material design, Jung et al. (2019) used support vector machines to model feasibility constraints for optimization. Similarly, Qiu et al. (2021) developed a deep learning-based strategy for efficiently selecting fiber materials and stacking orientations of composites, estimating physical feasibility with a classifier based on a given database. Regenwetter and Ahmed (2022) introduced a metric considering physical feasibility, expressed as geometrical compatibility, for inverse design tasks like bicycle frames. However, no prior work has been identified for the direct and explicit classification of stiffness matrices.

Krischer and Zimmermann (2021) and Krischer et al. (2022) introduced meta models that take target stiffness matrices as input. They are part of a novel hierarchical and decoupled distributed optimization architecture. This approach separates monolithic optimization problems by employing stiffness matrix-based meta models to estimate both physical feasibility and optimality. However, the method has been restricted to planar mechanical design problems involving components with two interfaces, each possessing one vertical translational degree of freedom and one rotational degree of freedom (Krischer and Zimmermann 2021; Krischer et al. 2022).

The goal of this paper is now to extend the existing approach to three-dimensional linear mechanical design problems with components that possess two interfaces with three translational and three rotational degrees of freedom. Note that the results presented in this article are based on the findings of the PhD thesis by Krischer (2023).

The paper is organized as follows: in the subsequent chapter, the design problem concerned with the lightweight design of serial mechanical multi-component systems is introduced. Afterwards, the general framework of the decoupled optimization architecture Informed Decomposition based on Krischer and Zimmermann (2021) and Krischer et al. (2022) is presented in Sect. 3. Next, Sect. 4 provides the three-dimensional problem extension to components with two interfaces and six degrees of freedom. In Sect. 5, the validity of the approach is demonstrated by investigating a two-component system and comparing the results to a monolithic optimization. Sect. 6 outlines a practical implementation of this approach in analyzing the positioning accuracy of industrial robots, detailing the design of a four-component, low-cost lightweight robot. Finally, the results are discussed in Sect. 7 and concluded in the last Sect. 8.

2 Design problem

A mechanical multi-component system is defined as a collection of mechanical components that interact with each other. According to this definition, a large number of industrial products can be considered as mechanical multi-component systems. For research purposes, the following investigations are restricted to serial systems, yet an extension to parallel systems is straight-forward without any changes of the proposed approach.

Fig. 1

A generic serial mechanical multi-component system clamped on the left side of the first component and subject to a load ${\varvec{f}}$ on the right end of the system resulting in a translational end effector displacement ${\varvec{u}}_{\text {ee}}$

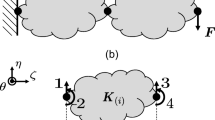
A generic serial mechanical multi-component system, Fig. 1, has $n_{\text {c}}$ components that can be oriented with respect to each other by prescribed rotations $\varvec{\theta }_{(i)} = [\alpha , \beta , \gamma ]^\text {T}$ at the joint positions ${\varvec{p}}_{(i)}$, where the set of rotations defines a specific system pose. Each component i consists of deformable parts and two rigid connectors on both sides. The deformable parts of length $l_{(i)}$ are modeled as linear elastic and have two mechanical interfaces ${\varvec{a}}_{(i)}$ and ${\varvec{b}}_{(i)}$. The first component is clamped on the left side ${\varvec{p}}_{(0)}$ and a static payload ${\varvec{f}}$ is applied on the right side of the last component of the system ${\varvec{p}}_{(n_{\text {c}})}$. The combination of pose $\varvec{\theta }_{(i)}$ and total system load ${\varvec{f}}_{\text {s}}$ is called load case. There are $n_{\text {p}}$ different load cases. The requirement on the system stiffness is for all load cases

$$\begin{aligned} u \le { } u_{\text {ub}}, \end{aligned}$$

(1)

with $u_{\text {ub}}$ being the upper bound for u.

Fig. 2

Dependencies between all relevant quantities on the system level (I), component performance level (II), and component detail level (III) in a monolithic optimization and the proposed approach consisting of b system and c component optimization

Figure 2a illustrates the dependencies between all relevant quantities that are needed to solve the given design problem. The detailed design variables ${\varvec{x}}_{(i)}$ include all design details for component i. For a given material, ${\varvec{x}}_{(i)}$ determines the detailed stiffness matrix ${\varvec{K}}_{\text {d},(i)}$, including all degrees of freedom of each structural element, and subsequently the interface stiffness matrix ${\varvec{K}}_{(i)}$ that defines the component’s elastic behavior with respect to the two interfaces ${\varvec{a}}_{(i)}$ and ${\varvec{b}}_{(i)}$. The components are then assembled to the system stiffness matrix ${\varvec{K}}_{s}={\text A}_{i=1}^{n_{c}} \varvec{K}_{(i)}$. Under a given system load vector ${\varvec{f}}_{\text {s}}$, the system deforms, resulting in the general system displacements ${\varvec{q}}_{\text {s}}$. Since the requirement is only on the translational part of the deformation ${\varvec{q}}_{\text {s}}$, the system stiffness is measured as the inverse of

$$\begin{aligned} u = || {\varvec{u}}_{\text {ee}} ||_{2}, \end{aligned}$$

(2)

where ${\varvec{u}}_{\text {ee}}$ contains the translational displacements at the end effector of the system. Similarly, the detailed design variables ${\varvec{x}}_{(i)}$ also define the mass ${m_{(i)}}$ of each component and consequently the system mass

$$\begin{aligned} m = m_{\text {s}} =\sum _{i=1}^{n_{\text {c}}} m_{(i)}. \end{aligned}$$

(3)

The quantities of the design problem can be hierarchically organized on three levels:

• (I) system level: ${\varvec{z}} = [m,u]$,

• (II) component performance level: ${\varvec{y}}_{(i)} = [m_{(i)},{\varvec{K}}_{(i)}]$,

• (III) component detail level: ${\varvec{x}}_{(i)}$.

The design problem can be solved using monolithic optimization which will be referred to as approach (A). It can be formally expressed as

$$\begin{aligned} {}&\quad \min \limits _{{\varvec{x}}_{(i)}}\sum _{i=1}^{n_{\text {c}}} m_{(i)} \left( {\varvec{x}}_{(i)}\right) , \nonumber \\ \text {s. t.:}&\quad u_{c} \left( {\varvec{x}}_{(i)}\right) - u_{\text {ub}} { }\le { } 0,&\text {for}\; c=1,\ldots ,n_{\text {p}},\nonumber \\ {}&{\varvec{x}}_{\text {lb}} { }\le { } {\varvec{x}}_{(i)} { }\le { } {\varvec{x}}_{\text {ub}},&\text {for}\; i=1,\ldots ,n_{\text {c}}. \end{aligned}$$

(4)

The objective function $m= \sum _{i=1}^{n_{\text {c}}} m_{(i)}$ is separable, i.e., it can be expressed as a sum of functions, each of which depend only on the corresponding local design variables ${\varvec{x}}_{(i)}$. On the other hand, the constraint function $g({\varvec{x}}) = u_{c} ({\varvec{x}}) - u_{\text {ub}}$ depends on all design variables ${\varvec{x}} = [{\varvec{x}}_{(1)},\ldots ,{\varvec{x}}_{(n_{\text {c}})}]$. If the constraints ${\varvec{g}}({\varvec{x}}) {\le } 0$ did not exist, this optimization problem could be simply decomposed into $n_{\text {c}}$ independent optimization subproblems. In literature, this kind of monolithic design optimization problem is called complicating constraints problem (Conejo et al. 2002).

3 Informed Decomposition

The monolithic optimization problem (4) of Sect. 2 is then decomposed, see Fig. 2b and c, using the Informed Decomposition approach (Krischer and Zimmermann 2021; Krischer et al. 2022). It is divided into a decoupled optimization architecture consisting of a surrogate-based system optimization that decouples the problem and subsequent $n_{\text {c}}$ independent and parallel component optimizations, Fig. 3a, and an offline database consisting of physical feasibility estimators $\hat{p}(\varvec{\kappa })$ and mass estimators $\hat{m}(\varvec{\kappa })$, Fig. 3b. Note, that established meta models $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$ can be reused for different design problems.

$\varvec{\kappa }$ is a lower-dimensional representation of the interface stiffness matrix $\varvec{\varPhi }(\varvec{\kappa }) = {\varvec{K}}$. So far this approach has only been applied to problems with $n_{\text {dof}}=2$ degrees of freedom (one rotational and one translational) per interface Krischer and Zimmermann (2021). For this setup and a given geometrical design domain $\varOmega$, ${\varvec{K}}$ can be represented by three independent values $\varvec{\kappa } \in {\mathbb {R}}^{1 \times 3}$. The extension to interfaces with $n_{\text {dof}}=6$ degrees of freedom follows in the subsequent Sect. 4.

Fig. 3

Overview over the proposed approach consisting of: a system optimization and decoupled component optimizations and b establishing feasibility estimators $\hat{p}(\varvec{\kappa })$ and mass estimator $\hat{m}(\varvec{\kappa })$

3.1 System optimization

The system optimization problem is a variation of the monolithic optimization (A) of (4). However, the system optimization uses $\varvec{\kappa }$ (II) instead of ${\varvec{x}}$ (III) as design variables, see Fig. 2a and b. This means, that the system optimization is carried out without knowing the component details. To ensure feasibility and optimality, a surrogated-based system optimization using the meta models $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$ is adopted

$$\begin{aligned} {}&\quad \min \limits _{\varvec{\kappa }_{(i)}} \sum _{i=1}^{n_{\text {c}}} \hat{m}(\varvec{\kappa }_{(i)}),&\nonumber \\ \text {s. t.:}&\quad -\hat{p}\left( \varvec{\kappa }_{(i)}\right) + 1 { }={ } 0,&\nonumber \\ {}&\quad u_{c} \left( \varvec{\kappa }_{(i)}\right) - u_{\text {ub}} { }\le { } 0,&\text {for}\; c=1,\ldots ,n_{\text {p}}, \nonumber \\ {}&\qquad \varvec{\kappa }_{\text {lb}} { }\le { } \varvec{\kappa }_{(i)} { }\le { } \varvec{\kappa }_{\text {ub}},&\text {for} \, i=1,\ldots ,n_{\text {c}}. \end{aligned}$$

(5)

The mass estimator $\hat{m}(\varvec{\kappa }_{(i)})$ enables mass estimates with respect to $\varvec{\kappa }_{(i)}$. The feasibility estimator $\hat{p}(\varvec{\kappa }_{(i)})$ indicates whether the component’s stiffness ${\varvec{K}}=\varvec{\varPhi }(\varvec{\kappa })$ corresponds to an actual physical design ${\varvec{x}}_{(i)}$, hence $\hat{p}(\varvec{\kappa }_{(i)})=1$. In comparison with the monolithic optimization, the system optimization problem is extended with constraints on the physical feasibility estimator $\hat{p}(\varvec{\kappa })$ for each component i.

The formulation with respect to $\varvec{\kappa }$ has two advantages: First, the system optimization does not need to compute the high-dimensional detailed stiffness matrices ${\varvec{K}}_{d,(i)}$, but only the low-dimensional interface stiffness matrices ${\varvec{K}}_{(i)}=\varvec{\varPhi }(\varvec{\kappa }_{(i)})$. This reduces the computational cost of solving the bottom-up mapping for computing the displacements ${\varvec{q}}_{s}$ on the system level needed for the requirement on the translational displacements $u = || {\varvec{u}}_{\text {ee}} ||_{2}$. Second, the optimization has usually fewer design variables. When using, e.g., topology optimization, the number of design variables equals the number of elements in the design domain, whereas for the system optimization only the reduced stiffness vectors $\varvec{\kappa }_{(i)}$ needs to be optimized.

Due to the binary classification characteristic of $\hat{p}(\varvec{\kappa })$ and the possibly non-convex design domain spanned by $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$, a gradient-free and global-search algorithm, namely a particle swarm optimization (PSO) is utilized (Kennedy and Eberhart 1995).

In order to establish the bottom-up mapping for the system optimization, a given multi-component system is assembled, see also Fig. 4. Therefore, each interface stiffness matrix ${\varvec{K}}_{(i)}$ related to ${\varvec{a}}_{(i)}$ and ${\varvec{b}}_{(i)}$ is first rigidly connected to the joint positions ${\varvec{p}}_{(i-1)}$ and ${\varvec{p}}_{(i)}$, i.e.,

$$\begin{aligned} {\varvec{K}}_{\text {p},(i)} = {\varvec{T}}_{\text {p},(i-1,i)}^\text {T} {\varvec{K}}_{(i)} {\varvec{T}}_{\text {p},(i-1,i)}, \end{aligned}$$

(6)

utilizing a RBE2 formulation via the condensation matrix ${\varvec{T}}_{\text {p},(i-1,i)}$. Then, ${\varvec{K}}_{\text {p},(i)}$ is transformed into the global coordinate system $^{(0)} {\varvec{K}}_{\text {p},(i)} = {\varvec{R}}_{(0)}^\text {T}... {\varvec{R}}_{(i-1)}^\text {T} {\varvec{K}}_{\text {p},(i)} {\varvec{R}}_{(i-1)}... {\varvec{R}}_{(0)},$ applying the rotation matrices ${\varvec{R}}_{(j)}$ with the respective rotations $\varvec{\theta }_{(j)}$ at the joint positions ${\varvec{p}}_{(j)}$ for $j=0,\ldots ,i{-}1$. Finally, the global multi-component system stiffness matrix can be assembled

$${\varvec{K}}_{s}=\mathop{\text A}\limits_{i=1}^{n_{c}} (0)\varvec{K}_{\text p, (i)},$$

(7)

and the system displacement is computed as

$$\begin{aligned} {\varvec{q}}_{\text {s}} = {\varvec{K}}_{\text {s}}^{-1} {\varvec{f}}_{\text {s}}, \end{aligned}$$

(8)

with ${\varvec{u}}_{\text {ee}} \in {\varvec{q}}_{\text {s}}$ as the translational displacements of the end effector. The design variables for the system optimization of a $n_{\text {c}}$-component system are

$$\begin{aligned} \varvec{\kappa } = [\varvec{\kappa }_{(1)},\ldots ,\varvec{\kappa }_{(n_{\text {c}})}]. \end{aligned}$$

(9)

Fig. 4

Assembly consisting of (1) the condensation matrix ${\varvec{T}}_{\text {p},(i-1,i)}$ that connects ${\varvec{a}}_{(i)}$ and ${\varvec{b}}_{(i)}$ via rigid body elements to ${\varvec{p}}_{(i-1)}$ and ${\varvec{p}}_{(i)}$, and (2) the rotation matrix ${\varvec{R}}_{(i)}$

After the system optimization, each optimized $\varvec{\kappa }_{(i)}^*$ can be now taken as a target stiffness for the subsequent $n_{\text {c}}$ decoupled component optimization problems, i.e.,

$$\begin{aligned} \varvec{\kappa }^t_{(i)} = \varvec{\kappa }_{(i)}^*. \end{aligned}$$

(10)

3.2 Component optimization

The component optimization seeks the optimal design variables ${\varvec{x}}_{(i)}$ (III) in the geometrical design domain $\varOmega _{(i)}$ with minimum mass $m_{(i)}$ for a given target interface stiffness $\varvec{\kappa }^t_{(i)}$ (II), see Fig 2 (c). The component optimization problem statement reads

$$\begin{aligned} {}&\quad \min \limits _{{\varvec{x}}_{(i)}} m_{(i)}({\varvec{x}}_{(i)} ),&\nonumber \\ \text {s. t.:}&\quad \Vert \varvec{\kappa }_{(i)}({\varvec{x}}_{(i)}) - \varvec{\kappa }^t_{(i)}\Vert&{ }\le { } \epsilon , \nonumber \\ {}&{\varvec{x}}_{\text {lb}} { }\le { } {\varvec{x}}_{(i)} { }\le { } {\varvec{x}}_{\text {ub}},&\end{aligned}$$

(11)

where ${\varvec{x}}_{\text {lb}}$ and ${\varvec{x}}_{\text {ub}}$ are the lower and upper bounds on the design variables ${\varvec{x}}_{(i)}$, $\varvec{\kappa }_{(i)}$ is the low-dimensional representation of the interface stiffness matrix $\varvec{\varPhi }(\varvec{\kappa }_{(i)}) = {\varvec{K}}_{(i)}$ associated with ${\varvec{x}}_{(i)}$ and $\epsilon$ is a small positive value.

The optimization problems (11) can be solved in parallel and independently of each other due to the decoupling of the system optimization (5).

The modeling process to connect the detailed design variables ${\varvec{x}}$ of level (III) to the level (II) interface stiffness matrix ${\varvec{K}}$ with respect to ${\varvec{a}}$ and ${\varvec{b}}$, see also Fig. 5, consists of three steps:

• (1) Discretization of the design domain $\varOmega$ of the mechanical body with three-dimensional brick elements ${\varvec{K}}_{e}$,

• (2) Static condensation of the design domain with respect to the left $({\varvec{A}})$ and right side $({\varvec{B}})$ of the domain using Guyan reduction,

• (3) Kinematic condensation with respect to the $n_{\text {dof}}=6$-dimensional interfaces at ${\varvec{a}}$ and ${\varvec{b}}$ using a RBE2 formulation.

Fig. 5

Modeling process of the interface stiffness matrix ${\varvec{K}}$ consisting of (1) discretization, (2) static condensation, and (3) kinematic condensation

First (1), the geometrical design domain $\varOmega$ of each mechanical body is discretized with $n_{\text {ele}}$ three-dimensional brick elements ${\varvec{K}}_{e}$. Within this work, the design domain $\varOmega$ is realized with a box of height h, width w, and length l. The elastic behavior of the entire mechanical body is described by the global stiffness matrix ${\varvec{K}}_{\text {d}}$

(12)

while $\rho _e$ are the detailed design variables of the design domain $\varOmega$ and $p=3$ is a penalty factor utilized in SIMP-based topology optimization methods (Bendsøe and Sigmund 2004). The sensitivity filter radius is set to $r=\sqrt{2}$.

Then (2), a static condensation is performed with respect to the master degrees of freedom located on the left ${\varvec{A}} \cup {\varvec{a}}$ and right side ${\varvec{B}} \cup {\varvec{b}}$ of the design domain, Fig. 5 (2),

$$\begin{aligned} {\varvec{K}}_{\text {g}} = {\varvec{T}}^{\text {T}}_{\text {g}} {\varvec{K}}_{\text {d}} {\varvec{T}}_{\text {g}}, \end{aligned}$$

(13)

where ${\varvec{T}}_{\text {g}}$ is the Guyan condensation matrix (Guyan 1965).

Finally (3), the remaining degrees of freedom on ${\varvec{A}}$ and ${\varvec{B}}$ are rigidly connected to the interfaces ${\varvec{a}}$ and ${\varvec{b}}$ using a RBE2 formulation of a rigid body element (Heirman and Desmet 2010; Liu and Quek 2013). The interface stiffness matrix ${\varvec{K}}$ can be computed as

$$\begin{aligned} {\varvec{K}} = {\varvec{K}}_{\text {rg}} = {\varvec{T}}^{\text {T}}_{\text {r}} {\varvec{K}}_{\text {g}}{\varvec{T}}_{\text {r}} = {\varvec{T}}^{\text {T}}_{\text {r}} {\varvec{T}}^{\text {T}}_{\text {g}} {\varvec{K}}_{\text {d}} {\varvec{T}}_{\text {g}} {\varvec{T}}_{\text {r}}, \end{aligned}$$

(14)

with ${\varvec{T}}_{\text {r}}$ being the second condensation matrix related to the rigid body elements on both sides. $\varvec{\kappa }$ can then be computed using the linear mapping $\varvec{\varPhi }(\varvec{\kappa }) = {\varvec{K}}$.

The so-called Method of Moving Asymptotes (MMA), developed by Svanberg (1987), can be utilized to compute the solution of each component optimization problem. Note, that the masses $m_{(i)}$ are processed as volume fractions $v_{(i)}$. Since the MMA is a gradient-based optimization algorithm, it needs the derivatives of the interface stiffness matrix ${\varvec{K}}={\varvec{K}}_{\text {rg}}$,

$$\begin{aligned} \frac{\partial \varvec{K_{\text {rg}}}}{\partial \rho _{e}} =&{\varvec{T}}_{\text {r}}^{\text {T}} \left( {\varvec{T}}_{\text {g}}^{\text {T}} \frac{\partial {\varvec{K}}_{\text {d}}}{\partial \rho _{e}} {\varvec{T}}_{\text {g}}\right) {\varvec{T}}_{\text {r}}, \end{aligned}$$

(15)

with

$$\begin{aligned} \frac{\partial {\varvec{K}}_{\text {d}}}{\partial \rho _{e}} =&p \rho _{e}^{p-1} {\varvec{K}}_{e}, \qquad \end{aligned}$$

(16)

as well as the volume fraction gradients

$$\begin{aligned} v =&\frac{1}{n_{\text {ele}}}\, \sum _{e=1}^{n_{\text {ele}}} \rho _{e}, \end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial v}{\partial \rho _{e}} =&\frac{1}{n_{\text {ele}}}, \qquad \qquad \end{aligned}$$

(18)

where the element volume $V_{e}$ is the same for all elements and the gradients are constant and relate to a $100\%$ filled reference unit volume.

The stiffness constraint $g({\varvec{x}}_{(i)}) \le 0$ of (11) is reformulated for numerical processing as

$$\begin{aligned} - \epsilon \le \left[ \frac{\kappa _{j} - \kappa _{j}^t}{\kappa _{\text {ub},j} - \kappa _{\text {lb},j}} \right] \le \epsilon ,&\;\;\;&\text {for} \, j=1,\ldots ,n_{\text {k}}, \end{aligned}$$

(19)

where $\kappa _{\text {ub}}$ and $\kappa _{\text {lb}}$ are the upper and lower bounds on the stiffness entries, respectively.

3.3 Establishing feasibility and mass estimator

If no appropriate physical feasibility estimator $\hat{p}$ and mass estimator $\hat{m}$ can be found in the offline database, new meta models need to be established, see Fig. 3b. To provide the necessary training data ${\varvec{y}}_{A}$, for $A=1,\ldots ,N$, first the input space needs to be sampled

$$\begin{aligned} {\varvec{y}}_{A}= [\varvec{\kappa }_{A}]&\in {\mathbb {R}}^{ n_{\text {y}}}, \end{aligned}$$

(20)

within the bounds $[{\varvec{y}}_{\text {lb}},{\varvec{y}}_{\text {ub}}]$. The sample output vector contains information about physical feasibility p and the mass m

$$\begin{aligned} {\varvec{z}}_{A} = [p_{A},m_{A}]&\in {\mathbb {R}}^{n_{z}}, \end{aligned}$$

(21)

while $m_{A}$ is again processed as $v_{A}$. In order to compute the sample output data ${\varvec{z}}_{A}$, the component optimization of (11) is utilized. It determines whether a corresponding detailed design ${\varvec{x}}$ exists for the given $\varvec{\kappa }$. If the component optimization converges, the feasibility flag is set to $p_{A}=1$, otherwise $p_{A}=\text {-}1$. The sample data consist then of the input and output data

$$\begin{aligned}{}[{\varvec{Y}},{\varvec{Z}}]&\in {\mathbb {R}}^{N \times (n_{y} + n_{z})}. \end{aligned}$$

(22)

The sample data can then be used to train a new physical feasibility estimator $\hat{p}$ and a mass estimator $\hat{m}$ for the offline database. The physical feasibility estimator $\hat{p}$ is evaluated by the false positive rate, FPR, true positive rate, TPR, and the accuracy, ACC, while the mass estimator $\hat{m}$ is evaluated by the mean squared error, MSE, and the $R^2$-value.

Most combinations of stiffness entries cannot be realized leading to imbalanced datasets. Therefore, an active-learning undersampling strategy was developed to produce a well-balanced dataset and enabling an efficient sampling procedure. For more information, see Krischer et al. (2022).

The resulting sample data are used to train the meta models $\hat{p}$ and $\hat{m}$, which can then be utilized for the system optimization of (5).

4 Extension to six degrees of freedom interfaces

4.1 Kernel of interface stiffness matrix K

In the following, the extensions to $n_{\text {dof}}=6$ degrees of freedom interfaces is presented based on Krischer (2023). For an arbitrary three-dimensional mechanical body with $n_{\text {int}}=2$ interfaces and $n_{\text {dof}}=6$ degrees of freedom per interface, see Fig. 6, the interface stiffness matrix ${\varvec{K}} \in {\mathbb {R}}^{12 \times 12}$ determines the elastic behavior of the component with respect to the interfaces ${\varvec{a}}$ and ${\varvec{b}}$

Fig. 6

A three-dimensional mechanical body with $n_{\text {int}}=2$ interfaces and $n_{\text {dof}}=6$ degrees of freedom per interface

Each interface possesses $n_{\text {dof}}=6$ degrees of freedom, three translational and three rotational, with the corresponding displacements, ${\varvec{u}}$ and $\varvec{\varphi }$, respectively,

$$\begin{aligned} {\varvec{q}}^{a} =\, [{\varvec{u}},\varvec{\varphi }]^{a\text {T}} =&[q_{1},q_{2},\ldots ,q_{6}]^\text {T}&\in {\mathbb {R}}^{6}, \end{aligned}$$

(23)

and

$$\varvec{q}^{b} = [\varvec{u},\varvec{\varphi}] ^{{b{\text{T}}}} = [q_{7} ,q_{8} , \ldots ,q_{{12}} ]^{{\text{T}}} \in \mathbb{R}^{6} .$$

(24)

Moreover, for the following investigations, the two mechanical interfaces ${\varvec{a}}$ and ${\varvec{b}}$ are fixed on the local x-axis with same orientation. Also, we define

$$\begin{aligned} {\varvec{b}} - {\varvec{a}} = [l,0,0]^\text {T}. \end{aligned}$$

(25)

Feasible interface stiffness matrices ${\varvec{K}} \in {\mathbb {R}}^{12 \times 12}$ must satisfy the following four requirements:

• (R1) ${\varvec{K}}$ must be symmetric, i.e.,  ${\varvec{K}}={\varvec{K}}^\text {T}$,

• (R2) rigid body modes $\varvec{\phi }_{r}$ result in zero forces, i.e.,

  ${\varvec{K}} \varvec{\phi }_{r} = {\varvec{0}}$,

• (R3) ${\varvec{K}}$ must be positive semi-definite, i.e.,

   ${\varvec{q}}^\text {T} {\varvec{K}} {\varvec{q}} \ge 0$, and

• (R4) there exists a detailed design ${\varvec{x}}$ corresponding to ${\varvec{K}}$.

Thus, not all interface stiffness matrices ${\varvec{K}}$ can be realized. If the requirements (R1)-(R4) are all satisfied, ${\varvec{K}}$ is said to be physically feasible.

Due to the symmetry requirement (R1), ${\varvec{K}}$ has at most $n_k=78$ independent entries. Moreover, the mechanical body possesses $n_{\phi }=6$ rigid body modes $\varvec{\phi }_{r}$, see Fig. 7, corresponding to three translational and three rotational ones. Based on the requirement (R2) the rigid body modes $\varvec{\phi }_{r}$ can be used to remove dependent stiffness entries by solving the following equation

$$\begin{aligned} {\varvec{K}} \varvec{\phi }_{r} = {\varvec{0}}&\;\;\;&\text {for}\; r=1,\ldots ,6. \end{aligned}$$

(26)

Fig. 7

$n_{\phi }=6$ rigid body modes of a mechanical body with $n_{int}=2$ interfaces and $n_{\text {dof}}=6$ degrees of freedom. (1–3) show the translational rigid body modes, while (4–6) show the rotational rigid body modes

These six rigid body modes $\varvec{\phi }_{r}$ correspond to six eigenvectors with eigenvalues of zero $\lambda _{r}=0$. Equation (26) comprises the six-dimensional null space or also called kernel of the interface stiffness matrix ${\varvec{K}}$. In order to assess the number of independent entries of ${\varvec{K}}$, the rank-nullity theorem can be used (Meyer 2008). Here, the rank of ${\varvec{K}}$ can be calculated as the difference between the dimension of the vector space of $\text {dim}({\varvec{K}})=12$ and the dimension of the null space, also called the $\text {nullity}({\varvec{K}})=n_{\phi }=6$,

$$\begin{aligned} \text {rank}({\varvec{K}}) + \text {nullity}({\varvec{K}}) = \text {dim}({\varvec{K}}). \end{aligned}$$

(27)

It follows that $\text {rank}({\varvec{K}})=6$ and thus the dimension of the non-degenerated vector space, i.e., the vector space where the linear dependencies are removed, is also ${\mathbb {R}}^{6}$. This can be illustrated with a small example, see Fig. 8.

Fig. 8

A three-dimensional mechanical body a without support, represented by ${\varvec{K}} \in {\mathbb {R}}^{12 \times 12}$, and b clamped on the right interface ${\varvec{b}}$, represented by ${\varvec{K}} \in {\mathbb {R}}^{6 \times 6}$

If a mechanical body is without any support, Fig. 8a, ${\varvec{K}} \in {\mathbb {R}}^{12 \times 12}$ has the earlier mentioned $n_{\phi }=6$ rigid body modes $\varvec{\phi }_{r}$ and can freely move in space without any force ${\varvec{f}}={\varvec{0}}$. Only by adding boundary conditions as, e.g., a displacement boundary condition, this system can be solved by removing those rigid body modes. If the mechanical body is, for instance, clamped on one side, Fig. 8b, then the interface stiffness matrix is ${\varvec{K}} \in {\mathbb {R}}^{6 \times 6}$, while still possessing all information of the mechanical body. Thus, requirement (R2) combined with the symmetry requirement (R1) lead to $n_{\text {k}}=21$ independent stiffness entries $k_{i,j}$ of ${\varvec{K}} \in {\mathbb {R}}^{6 \times 6}$. Since ${\varvec{K}} \in {\mathbb {R}}^{12 \times 12}$ can be recomputed from ${\varvec{K}} \in {\mathbb {R}}^{6 \times 6}$ by just taking the geometrical information of the rigid body modes $\varvec{\phi }_{r}$ into account, also ${\varvec{K}} \in {\mathbb {R}}^{12 \times 12}$ possesses $n_{\text {k}}=21$ independent stiffness entries $k_{i,j}$.

A linear map $\varvec{\varPhi }$ can be set up by solving (26) for specific ${\varvec{K}}=(k_{i,j})$. Since (26) is an underdetermined system of equations, different parametrizations of the linear map with 21 input values $k_{i,j}$ exist. One representation is

$$\begin{aligned} \varvec{\varPhi }(\varvec{\kappa }) = {\varvec{K}},\; &\varvec{\varPhi }: {\mathbb {R}}^{21} \rightarrow {\mathbb {R}}^{12 \times 12}, \end{aligned}$$

(28)

with

$$\begin{aligned} \varvec{\kappa } =&[k_{1,1},k_{2,1},k_{3,1},k_{4,1},k_{5,1},k_{6,1},k_{2,2}, \nonumber \\&k_{2,3},k_{2,4},k_{2,5},k_{3,3},k_{3,4},k_{3,6}, k_{4,4}, \nonumber \\&k_{4,5},k_{4,6},k_{5,5},k_{5,6},k_{6,6},k_{11,11},k_{12,12}], \end{aligned}$$

(29)

where $\varvec{\kappa } \in {\mathbb {R}}^{21}$. Thus $n_{\text {k}}=21$ stiffness entries determine the total deformation of the mechanical body with $n_{\text {int}}=2$ and $n_{\text {dof}}=6$.

Note that unlike ${\varvec{K}} \in {\mathbb {R}}^{6 \times 6}$ of the clamped body in Fig. 8b, the diagonal entries $k_{11,11}$ and $k_{12,12}$ of interface ${\varvec{b}}$ are taken instead of the non-diagonal entries $k_{2,6}$ and $k_{3,5}$ of ${\varvec{a}}$. This is done because the diagonal entries of the positive semi-definite stiffness matrix ${\varvec{K}}$ are strictly positive. Therefore, the lower bound on the diagonal entries is always known a priori, which facilitates subsequent design optimization for the stiffness entries.

4.2 Symmetry conditions

To further reduce the dimensions of $\varvec{\kappa } \in {\mathbb {R}}^{21}$, additional restrictions are imposed on the physically feasible detailed designs ${\varvec{x}}$. First, it is assumed that the geometrical shape of the design domain $\varOmega$ is invariant with respect to the x-axis, i.e., the dimension of the outer hull of the design domain $\varOmega$ remains constant along the x-axis, as is the case, for example, for the rectangular design domain used, see Fig. 9. Thus, for topology optimization, only the design variables within the design domain can be changed. Second, a planar symmetry condition for the mechanical body is enforced with respect to the

• (S1) $x{-}y$ plane and

• (S2) $x{-}z$ plane.

Fig. 9

Exemplary box-shaped design domain with enforced plane symmetry on the x-y and x-z plane

The invariant design domain together with the symmetry conditions (S1) and (S2) lead to a beam-like deformation behavior of the mechanical component with respect to the interfaces ${\varvec{a}}$ and ${\varvec{b}}$. Following the idea of three-dimensional elastic beam theory, see, e.g., Andersen and Nielsen (2008), the interfaces now lie on the bending center of the mechanical body, meaning normal forces $f_{1}$ or $f_{7}$ only induce axial displacements with respect to $d_{1}$ and $d_{7}$. Thus,

$$\begin{aligned} k_{i,j} = 0&\quad \text {for} \; i=1,7 \;\text {and} \; \; j \ne 1,7. \end{aligned}$$

(30)

Also, the interfaces ${\varvec{a}}$ and ${\varvec{b}}$ coincide with the principal axis of the bending moments $f_{5}$, $f_{11}$ and $f_{6}$, $f_{12}$ causing that only their associated shear loads $f_{3}$, $f_{9}$ and $f_{2}$, $f_{8}$, respectively, are coupled to these bending degrees of freedom. Hence, also all other stiffness entries $k_{i,j}$ are zero,

$$\begin{aligned} k_{i,j} = 0&\quad \text{for} \; i=2,6,8,12 \;\text {and} \; j \ne 2,6,8,12, \end{aligned}$$

(31)

and

$$\begin{aligned} k_{i,j} = 0&\quad \text{for} \; i=3,5,9,11\; \text {and} \; j \ne 3,5,9,11. \end{aligned}$$

(32)

Finally, for double symmetric cross sections, as it holds for (S1) and (S2), also the bending center coincides with the shear center, meaning that torsional displacements $d_{4}$ and $d_{10}$ are only caused by the torsional loads $f_{4}$ or $f_{10}$. Therefore,

$$\begin{aligned} k_{i,j} = 0& \quad \text {for} \; i=4,10 \; \text {and} \; j \ne 4,10. \end{aligned}$$

(33)

With these assumptions, the interface stiffness matrix can represented as

$$\begin{aligned} {\varvec{K}}= \left[ \begin{array}{cccccccccccc} k_{1,1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} k_{1,7} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} k_{2,2} &{} 0 &{} 0 &{} 0 &{} k_{2,6} &{} 0 &{} k_{2,8} &{} 0 &{} 0 &{} 0 &{} k_{2,12} \\ &{} &{} k_{3,3} &{} 0 &{} k_{3,5} &{} 0 &{} 0 &{} 0 &{} k_{3,9} &{} 0 &{} k_{3,11} &{} 0 \\ &{} &{} &{} k_{4,4} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} k_{4,10} &{} 0 &{} 0 \\ &{} &{} &{} &{} k_{5,5} &{} 0 &{} 0 &{} 0 &{} k_{5,9} &{} 0 &{} k_{5,11} &{} 0 \\ &{} &{} &{} &{} &{} k_{6,6} &{} 0 &{} k_{6,8} &{} 0 &{} 0 &{} 0 &{} k_{6,12} \\ &{} &{} &{} &{} &{} &{} k_{7,7} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} {\text {sym}} &{} &{} &{} &{} k_{8,8} &{} 0 &{} 0 &{} 0 &{} k_{8,12} \\ &{} &{} &{} &{} &{} &{} &{} &{} k_{9,9} &{} 0 &{} k_{9,11} &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} k_{10,10} &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} k_{11,11} &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} k_{12,12} \\ \end{array}\right] {.} \end{aligned}$$

(34)

Incorporating (34) into (28) and (29) leads to a further reduced stiffness description

$$\begin{aligned} \varvec{\varPhi }_{\text {sym}}(\varvec{\kappa }_{sym}) = {\varvec{K}}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$

(35)

with

$$\begin{aligned} \varvec{\kappa }_{\text {sym}} = [ k_{1,1},k_{2,2},k_{3,3}, k_{4,4}, k_{5,5},k_{6,6},k_{11,11},k_{12,12}]. \end{aligned}$$

(36)

where $\varvec{\kappa }_{\text {sym}} \in {\mathbb {R}}^{8}$. In conclusion, $n_{\text {k}}=8$ diagonal stiffness entries are necessary to fully describe the deformation behavior ${\varvec{K}} \in {\mathbb {R}}^{12 \times 12}$ of a mechanical component with respect to ${\varvec{a}}$ and ${\varvec{b}}$ for an invariant design domain $\varOmega$ and enforced symmetry planes $x{-}y$ and $x{-}z$.

5 Physical feasibility and optimality

5.1 Setup

First, a simple two-component system, with a rectangular design domain $\varOmega$ of width and height $w_{(i)}=h_{(i)}=30$ mm, and length $l_{(i)}=100$ mm for both components, is investigated for a required system displacement of up to $u_{\text {ub}}=1$ mm. The box-shaped design domain $\varOmega$ is discretized with $n_{\text {ele}} = [20,8,8]^\text {T}$ elements in x-, y-, and z-direction for each component i. The material used is a synthetic resin for additive manufacturing, see Table 1. The given design problem (P1) is solved for $n_{\text {p}} =6$ load cases, see Fig. 10. Each load case represents a main load in one coordinate direction.

Table 1 Material data of a synthetic resin for the components i of both design problems

Fig. 10

Design problem (P1) with a a simple two-component system and b the $n_{\text {p}}=6$ respective load cases that are investigated

As introduced in Sect. 4, symmetry conditions are enforced leading to the reduced $\kappa$-representation (36) with eight entries $\varvec{\kappa }_{\text {sym}} \in {\mathbb {R}}^{8}$.

5.2 Offline database

First, two new meta models $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$ for the offline database of the Informed Decomposition (B) have to be established. The sample data $[{\varvec{Y}},{\varvec{Z}}]$ computed by the active-learning strategy are shown in Fig. 11. Since only diagonal values are utilized for the $\kappa$-representation, a completely filled design domain $\varOmega$ represents the maximum value, while the minimum value is obtained for a void design domain $\varOmega$. The projections of the scatter plots show that the sampling strategy was not capable of completely sampling the physically feasible design space, failing to cover the void and filled reference design domains $\varOmega$. Especially the upper limit is clearly not included in the sample data.

Fig. 11

Predictions by (i) physical feasibility and (ii) mass estimators after training using active learning for (P1)

The active-learning strategy suffers from the curse of dimensionality, which despite of the higher number of sample points $N_{\text {C}}$ prevents the sampling strategy from covering the whole design space. The sample data are then used to train the final meta models $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$. The performance measures for both estimators are listed in Table 2.

Table 2 Performance measures of $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$ for (P1)

5.3 System optimization

The $\kappa$-representations of level (II) for the given design problem (P1) of the monolithic approach (A) and the system optimization (5) of (B) in Table 3. Both (A) and (B) produce results with similar $\varvec{\kappa }_{(i)}$, yet deviations can be observed. In particular, the system optimization of (B) is not able to realize stiffness values close to the lower bound, e.g., the $k_{2,2}$ and $k_{3,3}$ values for the second component of load case (LC6). Meta models do not have sufficient sample data in this region, hence labeling it as falsely infeasible.

5.4 Component optimization

Next, the optimized $\varvec{\kappa }_{(i)}$ of level (II) are utilized for the component optimization of (B) to derive the final topologies ${\varvec{x}}_{(i)}$ of level (III). The system optimization and the component optimization operate on volume fractions $v_{(i)}$ and $\varvec{\kappa }_{(i)}$, i.e., ${\varvec{y}}_{(i)}=[v_{(i)},\varvec{\kappa }_{(i)}]$, see Table 3. The resulting topologies are shown in Fig. 12.

For load case (LC1) in straight pose for both components, the first component experiences a mixed load, a z-bending moment and a y-shear load. Therefore, on the one hand, the material is distributed farthest from the axis, while on the other hand, a slightly tapered tip in the beginning with reinforcements in the center for the occurring shear loads can be observed. By contrast, the second component shows a classical cantilever beam topology with a more pronounced tip, where the y-shear load is applied, and reinforcements in the center between the upper and lower side of the component. The difference between component 1 and 2 is only the ratio between shear load and bending moment. The proposed approach (B) produces a slightly lighter first component compared to the reference design obtained by monolithic optimization,i.e., approach (A), while the second component is heavier. Overall, the total mass of the Informed Decomposition is $3.87\%$ heavier than the reference design. Both satisfy the requirement $u {\le } u_{\text {ub}}$ for system stiffness, see Table 3.

The z-bending load in load case (LC2) yields a topology for (A), with material only at the boundary of the design domain $\varOmega$ to compensate for the bending normal stresses. It resembles a classical i-beam without web. For the second component of (LC2), a mixture of shear and bending loads is applied, resulting in a similar topology to (LC1). The first component of approach (B) differs significantly from the one of approach (A) and does not show a clear pure bending characteristic with also a slightly higher volume fraction. The second component of approach (B) is even bulkier than the counterpart of (A), resulting in a total system mass deviation of $8.06\%$.

In (LC3) pure normal load is applied to the vertical second component, resulting in a bar-shaped topology in approach (A), while the first component experiences both shear and normal loads. While component one is similar in both approaches, component two is different. Approach (A) forms the familiar rod-like structure, while approach (B) develops a tube-like design. For the pure normal load case, this is generally not a problem, since the cross-sectional area provided by each slice of the topology is relevant. However, the second component is also considerably heavier and results in the highest deviation of all load cases at $8.18\%$, which is also in contrast to the previous section’s more accurate solution of $1.87\%$.

Load case (LC4) is similar to (LC1), however, rotated about the x-axis by $90^\circ$. It is utilized to evaluate approach (B) for the same load case but for different stiffness inputs. Since the active-learning strategy automatically samples the design space, small differences are expected. While the topologies for approach (A) are the same as for (LC1), only $90^{\circ }$ rotated, approach (B) deviates slightly from (LC1), resulting in a slightly higher component mass for the first component and a slightly lower component mass for the second component. The mass deviation compared to (A) is $5.83\%$, which is worse than the $3.87\%$ of (LC1).

Table 3 Component performance (II), ${\varvec{y}}_{(i)}=[v_{(i)},\varvec{\kappa }_{(i)}]$, and the quantities on the system level (I), ${\varvec{z}}=[m,u]$, of design problem (P1) for monolithic optimization (A) and the proposed Informed Decomposition (B)

Fig. 12

Optimized component designs ${\varvec{x}}_{(i)}$ for (P1) of the A monolithic optimization and B Informed Decomposition

The next load case (LC5) is also a rotated variant of (LC2), resulting in a bending moment about the y-axis instead of the z-axis. In comparison with (LC2), approach (B) yields better results for the z-bending load case, resulting in a system mass deviation of $6.90\%$ compared to $8.06\%$ of (LC2).

In (LC6), the first component is mainly under the influence of torsion while the second component experiences shear forces, also in the z-direction as in (LC4). Approach (A) therefore forms a closed tubular topology for the first component, while the second component has the classical cantilever beam shape. Approach (B) reproduces the topology for the first component quite accurately, but the second component is bulkier, with a total mass deviation of $7.20 \%$.

In summary, the Informed Decomposition (B) was able to produce physically feasible designs for all load cases (LC1–6) while satisfying the system stiffness requirement $u {\le } u_{\text {ub}}$. The mass deviation of the proposed approach (B) assumes a minimum at $3.87\%$ for the y-shear load case (LC1) and a maximum at $8.18\%$ for the x-normal load case (LC3). It should be noted that for the investigated load cases, always the second component with the lower volume fraction shows higher deviations. This could hint at a degradation of the performance of meta models for stiffnesses with low (extreme) volume fractions.

6 Towards practical application

6.1 Setup

A four-component system, with a box-shaped design domain $\varOmega$ of width and height $w_{(i)}=h_{(i)}=30$ mm, and respective lengths ${\varvec{l}}= [150,100,50,50]^\text {T}$ mm, is investigated in the design problem (P2), see Fig. 13. It presents a three-dimensional robot architecture with $n_{\text {dof}}=6$ degrees of freedom per interface. The deformable parts of the components i are connected with joints by so-called connectors that are modeled as rigid. The robot is designed for a given specific trajectory $\varvec{\theta }_{(i)}(t) = [\alpha , 0, 0 ]^\text {T}$ of a pick-and-place task and a payload of $m=1$ kg is applied to the end effector. From the given trajectory $\varvec{\theta }_{(i)}(t)$, $n_{\text {p}}=100$ static load cases are derived for each of which the system stiffness requirement is $u{\le }1$ mm.

Fig. 13

Design problem (P2) with a a three-dimensional four-component system, i.e., a low-cost lightweight robot and b the pick-and-place trajectory $\varvec{\theta }_{(i)}(t)$

The respective monolithic optimization problem (A) of (4) is decoupled utilizing the Informed Decomposition approach (B). Like in the previous chapter, the reduced $\varvec{\kappa }$-representation (36) with eight entries $\varvec{\kappa }=\varvec{\kappa }_{\text {sym}} \in {\mathbb {R}}^{8}$ is adopted.

Note that unlike in the earlier investigated design problem, gravity forces ${\varvec{f}}_\text {cog}$are also considered. The respective gravity forces at the center of gravity can be recalculated with respect to the interface positions $p_{(i)}$, adding an offset moment for the lever arm distance between the joint position ${\varvec{p}}$ and the center of gravity ${\varvec{x}}_\text {cog}$, see Fig. 14.

Fig. 14

a Actual gravity loads ${\varvec{f}}_{\text {cog}}$ of the rigid connectors and b substitute loads acting on the join positions ${\varvec{p}}_{(i)}$

6.2 Offline database

The Informed Decomposition approach (B) can take advantage of the offline database since meta models for $l=100$ mm already exist. Therefore, component $i=2$ can reuse the meta models of Sect. 5. For the other three components, two new meta models with input $\varvec{\kappa } \in {\mathbb {R}}^{8}$ are needed for physical feasibility estimate, $\hat{p}_{l=50}(\varvec{\kappa }), \hat{p}_{l=150}(\varvec{\kappa }),$ and mass estimator $\hat{m}_{l=50}(\varvec{\kappa }), \hat{m}_{l=150}(\varvec{\kappa }).$

The sample data $[{\varvec{Y}},{\varvec{Z}}]$ for $l=50$ mm and $l=150$ mm computed by the active-learning strategy are shown in Fig. 15a and b, respectively. Similar to Sect. 5, the active-learning strategy is not capable of sampling the upper bound of the design space for both lengths corresponding to filled design domains $\varOmega$.

Fig. 15

Predictions by (i) physical feasibility and (ii) mass estimators after training using active learning for (P2) for a $l=50$ mm and b $l=150$ mm

It is also noticeable that during the classification phase (i) for $l=150$ mm, see Fig. 15b, one of the temporary classifiers failed, resulting in several infeasible sample data points at the upper boundary of the design space. The sample data are used to train the final meta models $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$. The performance measures for both estimators are listed in Table 4. Even though one of the temporary classifiers failed during classification phase (i), the performance measures of the meta models, for $l=150$ mm, are still acceptable.

Table 4 Performance measures of $\hat{p}(\varvec{\kappa })$ and $\hat{m}(\varvec{\kappa })$ for (P2)

6.3 System optimization

Approach (A) and (B) are applied to the design problem (P2) with $n_{\text {p}}=100$ static load cases. First, the level (II) $\kappa$-representations are computed, see Table 5.

Table 5 Component performance (II), ${\varvec{y}}_{(i)}=[v_{(i)},\varvec{\kappa }_{(i)}]$, and the quantities on the system level (I), ${\varvec{z}}=[m,u]$, of design problem (P2) for monolithic optimization (A) and the proposed Informed Decomposition (B)

The Informed Decomposition approach yields results for $\varvec{\kappa }_{(i)}$ that differ significantly from the monolithic optimization results, for components $i=1, 3$ and 4, while the results for the second component $i=2$ are very similar. Like in Sect. 5, the system optimization seems to have problems in realizing small stiffness values, e.g., $k_{2,2}$ for $\varvec{\kappa }_{(1)}$, and $k_{2,2}$ and $k_{3,3}$ for $\varvec{\kappa }_{(4)}$. It is possible that the meta models do not have sample data in this region, which prevents the system optimization from computing those values. In summary, the experienced outliers indicate a non-optimal decoupling of the multi-component system by the system optimization of (B).

6.4 Component optimization

Next, the optimized $\varvec{\kappa }_{(i)}$ values of level (II) are utilized to derive the final topologies ${\varvec{x}}_{(i)}$ of level (III) using the decoupled component optimizations (11) of (B). The resulting volume fractions $v_{(i)}$ and the quantities ${\varvec{z}}=[m,u]$ on the system level (I) are listed in Table 5. The maximum displacement observed in one of the load cases is denoted as max($u_{c}$).

Note that the last pose of the given trajectory turned is the dominant load case. Therefore, the plausibility is best established by analyzing this load case (LC100), see also Fig. 16, and comparing it with the resulting topologies for approach (A) and (B) in Fig. 17.

Fig. 16

Dominant load case (LC100)

Approach (A), for $n_{\text {p}}=100$ load cases, shows some specific properties for each component i of the multi-component system. The last component $i=4$ on which the pay load ${\varvec{f}}$ acts, has a topology that evolved mainly to provide stiffness to resist a z-shear load suggesting that it is not only optimal for the last load case (LC100), but is the dominant load case over the entire discretized trajectory $\varvec{\theta }_{(i)}(t)$. The third component $i=3$ has a closed profile, with more material accumulating on the outer edges of the y-axis than on the z-axis. This is again consistent with the orientation of component $i=3$ for the last pose, associated with bending about the z-axis, requiring more material at the y-axis boundaries. Component $i=2$ is a closed tubular profile experiencing the highest torsional load of all components, which can also be concluded from the system pose for load case (LC100). Moreover, it exhibits high stiffness against shear and bending loads. Finally, the first component $i=1$ has a topology that mainly supports bending about the z-axis and normal loads in the local x-axis. The open profile lacks stiffness against any torsional load or shear forces.

Fig. 17

Optimized component designs ${\varvec{x}}_{(i)}$ for (P2) of the monolithic optimization (A) and Informed Decomposition (B)

For a static analysis, all topologies are plausible with respect to the last load case (LC100) and hence also support the hypothesis of one dominant load case. However, these results also show a clear drawback of the chosen approach. The static poses of the original dynamic trajectory do not consider dynamic loads. Therefore, especially the first component $i=1$ shows significant weaknesses in practical applications. The low-cost lightweight robot architecture derived for the given trajectory rotates around the local x-axis of the first component to perform its task. In a dynamic load case, this leads to torsional loads on the first component, for which it provides little stiffness due to its non-closed structure. Nevertheless, for a static consideration, these poses are optimal. This is consistent with the idea of a pure top-down design process, where only the explicit requirements for the system are met and not formally stated requirements may be violated.

For the detailed design of approach (B), the components $i=1$, $i=3$ and $i=4$ of the multi-component system significantly deviate from both, the component volume fractions $v_{(i)}$ and their respective topologies ${\varvec{x}}_{(i)}$ compared to (A). However, the components $i=1$ and $i=3$ exhibit the same main characteristics for the experienced loads of the investigated load cases. In contrast, the high deviation of $\varvec{\kappa }_{(4)}$ of component $i=4$ of the system optimization, also leads to a topology that does not show the expected features against a dominating z-shear load. Additionally, the component mass produced by (B) deviates by $70.7\%$ from (A). In contrast, component $i=2$ not only agrees for the $\varvec{\kappa }_{(2)}$-values, but also with respect to the topology and the component mass, which turns out to be even identical.

In summary, the total mass deviation is $12.9\%$, while both approaches (A) and (B) produce feasible designs with respect to the system displacement requirement $u {\le } u_{\text {ub}}$. Once again, approach (B) had most problems for the component with the lowest volume fraction $v_{(4)}$.

The resulting topologies of Fig. 17 produced by the proposed Informed Decomposition (B) were subsequently post-processed, additively manufactured and assembled into a robot arm demonstrator, see Fig. 18.

Fig. 18

Resulting low-cost lightweight robot with topology-optimized and post-processed components for $n_{\text {p}}=100$ load cases

7 Discussion

Physical feasibility and optimality. The validity of the approach was assessed by analyzing the results for physical feasibility and mass optimality, comparing them to a classical monolithic optimization problem. While all outcomes met the system stiffness requirements, deviations were observed, particularly for the second design problem (P2). The quality of results depends on the meta models, which distribute stiffness properties to components for physical feasibility and mass optimality. Sampling may not cover the entire design space, leading to lower quality predictions for stiffness regions with low and high volume fractions, and incomplete capture of design domain bounds. Improved sample data can enhance meta model generalization and result quality.

Offline database. Generating sample data for the offline database is computationally expensive. In optimization architectures, some approaches integrate this expensive sampling and training process into the optimization itself. Informed Decomposition generates an offline database, employing pre-trained meta models for various design problems. Similitude theory enables the reuse of meta models for similar designs across different geometric domains (Coutinho et al. 2016; Casaburo et al. 2019). However, for arbitrary changes, meta models need retraining with explicit geometric parameters, as was shown in Krischer et al. (2022). The generalization of the meta models represents a pivotal stage in the development of an offline database that can be applied to a range of mechanical design problems. This eliminates the necessity for costly new training processes to be undertaken for each new design problem at hand.

Product development processes. One of the primary motivations for implementing distributed optimization architectures is to mimic the structure of classic product development processes, where different departments can design their subsystems independently (Martins and Ning 2022). Decoupling, as implemented in the proposed Informed Decomposition approach, facilitates application in industry by eliminating the need for coordination between different subsystems and hierarchy levels. As demonstrated in both design problems (P1) and (P2), all problems can be solved independently at the component level after the system optimization has been completed.

Computational time. The second motivation for distributed architectures is to reduce computational time by decomposing large-size monolithic optimization problems. Although this study did not explicitly investigate time, decoupling the costly component optimization offers significant potential for time reduction. The independence of the number of components and load cases, due to system-level decoupling, particularly benefits the optimization of the second design problem (P2) with a high number of load cases. Moreover, since no overarching coordination scheme is required, coordination overhead is eliminated, further supporting a reduction in computational time. However, this does not take training of meta models into account.

Applicability. So far, only serial mechanical multi-component systems with two system quantities, i.e., system mass and displacement, within linear statics were investigated. The authors believe that there is no fundamental restriction that prevents the application to parallel structures. An extension to dynamics is also considered feasible, e.g., by training meta models estimating the mass, physical feasibility, center of mass and inertia of a structure.

Mesh resolution. The finite element models utilized in this study employ coarse meshes, ensuring a minimum member size in resulting structures. However, in SIMP-based topology optimizations, mesh dependency is inevitable, typically addressed using filters (Sigmund and Petersson 1998; Bendsøe and Sigmund 2004). Finer meshes may yield different structures. Despite this, the computational time advantage of a decoupled optimization architecture persists, even with finer meshes, albeit at potentially higher sampling costs. Furthermore, decoupled component optimizations, can employ finer meshes than those used for the training of the meta models. The system optimization using these meta models would then decouple the system in a non-optimal yet potentially sufficient manner. The finer meshes of the decoupled component optimizations may lead to equivalent or superior designs compared to the reference design obtained with coarse meshes.

8 Conclusion

Informed Decomposition introduced by Krischer and Zimmermann (2021) is a decoupled optimization architecture consisting of system optimization and independent component optimization. The system optimization incorporates pre-trained meta models that provide estimates of component mass and physical feasibility for target stiffness matrices. Stiffness targets produced by the system optimization are then used for the optimization of all components. While previous work had already demonstrated the viability of this approach, this paper extended it to be applicable to real-world three-dimensional structures with six degrees of freedom per interface. For this, an 8-dimensional stiffness matrix representation was developed to replace the high-dimensional 12x12 interface stiffness matrices. Active learning was adopted to efficiently train meta models in the 8-dimensional space of stiffness matrices. The proposed approach was applied to a simple two-component system and a 4-component robot structure subject to a large number of stiffness requirements. The results were physically feasible and at most $12.9 \%$ heavier than the results obtained by monolithic optimization.

The results demonstrate the practical applicability to real-world three-dimensional structures consisting of two-interface components. Informed Decomposition produces results that are worse than those obtained by monolithic optimization. However, each optimization problem is significantly smaller and computation time may be significantly reduced. Unlike in other distributed architectures, no coordination is required.

In future, the active-learning undersampling strategy could be modified to improve the quality of point selection and thus the estimations of the meta models. An extension to parallel mechanical multi-component systems should be possible without changing the method. Also, components with a higher number of interfaces could be modeled with a new $\kappa$-representation. The same holds for including dynamic system behavior into the component optimizations. This is particularly useful for the presented use case of a robotic arm. Finally, an investigation of classical multidisciplinary design optimization problems involving different disciplines would be interesting. A comparison between the established distributed architectures and the proposed Informed Decomposition for specific benchmark problems would further validate the approach.