1 Introduction

The design of systems with a large number of interacting components can be a difficult task. Two different views are particularly relevant for this paper. First, from a computational performance point of view, the size of the system can make an overall optimization prohibitively expensive demanding a decomposition to reduce the size of the problem (ElMaraghy et al. 2012). Second, from a designer’s perspective, it is often beneficial to think about the entire system without its details. In top-down development processes, requirements are formulated on the system level and then broken down into requirements on components. The components are then typically designed by separate engineering groups (Martins and Lambe 2013; Zimmermann et al. 2017). A decomposition is therefore often preferred over a monolithic optimization utilizing complete system analyses.

In a distributed optimization, the given problem is decomposed into smaller subproblems containing subsets of the objectives, design variables and constraints. However, common approaches as analytical target cascading (Kim et al. 2003), multidisciplinary design optimization of independent subspaces (Shin and Park 2005), or collaborative optimization (Braun et al. 1996) are not fully separable architectures and need a coordination strategy to maintain consistency between shared quantities of components and/or the system.

Complete decoupling, i.e., horizontal decomposition between system and component level and vertical decomposition between different components, can avoid further coordination between the components after the decomposition. This kind of quantitative top-down design was introduced by Zimmermann and von Hoessle (2013) and embedded into a design procedure in Zimmermann et al. (2017). Based on system targets, so-called solution spaces are computed representing sets of good, i.e. feasible, designs. The edges of box-shaped solution spaces are permissible intervals for component properties and can be used to formulate completely decoupled component requirements.

Unfortunately, for complete decoupling there is a risk of excluding the optimal, but so far unknown solution beforehand. In Zimmermann and von Hoessle (2013) this is referred to as loss of solution space. One possible way of solving this so-far unsolved problem is to incorporate a-priori information from the component level with the help of meta models into the decoupling procedure.

Meta models have a long history in systems design as they can reduce the high computational cost of large size computer models (Viana et al. 2014). For example, deformation energy, referred to as compliance in the context of structural optimization, is often utilized as a performance measure. Since compliance is a load dependent quantity, corresponding mechanical detailed designs are only valid for the respective load case. Kim et al. (2016) carried out a dynamic system optimization with a decomposition of the structure based on a regression model that maps mass on compliance for equivalent static loads of different time steps. Oh et al. (2019) utilized deep learning techniques for estimating topologies with respect to minimal compliance for given normal and shear load cases of a car-wheel. A further generalization to estimate detailed designs with respect to arbitrary load cases is presented in Ulu et al. (2015), Lei et al. (2019), and Yu et al. (2019), where the regression models were trained for multiple load cases. In conclusion, meta models based on compliance need extensive sampling procedures with varying load case conditions to allow for general applicability. Also, compliance does often not accurately represent stiffness related requirements of components as, e.g., maximum displacement. Using compliance here would impose an unnecessary strict constraint to a problem.

Yet, also the displacement of a structure is load dependent. Therefore, quantities are needed that represent inherent component characteristics that are independent of changing boundary conditions as constraints or forces. For linear static analyses, a stiffness matrix incorporates all information about the geometrical and physical constitution of mechanical components and is therefore load-independent. Moreover, it can be directly related to a displacement requirement for a given load case and contains all relevant information regarding the deformation behavior. In Wang et al. (2019), a stiffness matrix–based optimization of a serial robot based on a parametrization of a topology was conducted utilizing a linear regression for the stiffness estimate of the components with respect to mass. In the context of multi-scale optimization, the connection of the macro and micro scale of the structure is sometimes replaced by meta models to reduce the computational cost. In Wu et al. (2019) and Wu et al. (2020) a substructuring technique for hierarchical lattice structures was used to estimate the mass and the stiffness matrix of microstructures. For this purpose, a regression model based on a reduced basis description was established, where the microstructure properties are determined by samples of parametrized unit cells. Furthermore, Wang et al. (2021) carried out a multi-scale topology optimization where meta models of different parameterized microstructures were considered with respect to material properties as stiffness matrix or thermal conductivity. However, due to prescribed parametrization of the geometry, the design freedom in the presented approaches is limited and hence one does not exploit the full lightweight potential. Kollmann et al. (2020) utilized topology optimization to estimate microstructure designs. In order to determine the stiffness matrix, substitute load cases were set up, which were used to optimize different topologies with respect to mass. Utilizing those topologies, a regression model was trained to predict optimal microstructures. However, those meta models do not work directly with a stiffness matrix as an input, but with volume fraction, filter radius, and either maximum bulk modulus, shear modulus, or minimum poison ratio as input variables.

Besides the risk of excluding optimal designs, also ensuring feasibility is a relevant and difficult challenge. In theory, all positive semi-definite stiffness matrices can be realized by a mechanical design. Huang and Schimmels (1998) and Huang and Schimmels (2000) showed that arbitrary spatial stiffness matrices can be realized with a set of so-called screw springs. In practice however, limitations like available geometrical space or the material choice do restrict the feasible design space of stiffness matrices. To avoid requirements on component stiffness that cannot be satisfied, feasibility classification is adopted. In Ding and Vemur (2005), an active learning strategy for feasibility classification of analog circuits was implemented. Jeong et al. (2012) used a support vector machine classifier for mathematical test problems and air-conditioner pipe design. In the context of material design, Jung et al. (2019) modeled feasibility constraints to carry out a material optimization for inverse crystallographic texture problems. For the classification of stiffness matrices, no previous work could be identified.

This paper presents an approach to decouple system and component optimization of mechanical systems. For this purpose, two sequential optimization steps are proposed. First, a system optimization, where requirements on the elastic behavior of the components, in particular their stiffness matrices, are defined, and the mass and feasibility are estimated by meta models. Thus, the loss of solution space will be reduced. The resulting stiffness matrix requirements are then propagated down to the components. Second, independent component optimization problems are solved. The components are designed via structural optimization techniques, without any coordination with the system level or each other.

The paper is organized as follows: In Section 2, the demonstrator problem setup is explained. The proposed approach is introduced in Section 3. For comparison, in Section 4, two alternative design approaches are shortly described. In Section 5, results for three different component models are presented. The results are discussed in Section 6 and the conclusions presented in Section 7.

2 Demonstrator problem

The overall development goal is to design a lightweight mechanical system, consisting of two components, see Fig. 1a, e.g., representing a two-component robot arm. The mechanical structure is clamped on the left side and consists of two components each with length l(i)= 300 mm. The requirement on the system stiffness is:

The system must sustain a vertical load of F= 50 N with a maximum tip displacement of d0= 1 mm.

Fig. 1
figure 1

A simple mechanical two-component system (a), and the respective degrees of freedom, length l(i) and stiffness matrix K(i) for each component i (b)

Full size image

The payload is applied on the right end of the structure. Each component is modeled as linear elastic and has two mechanical interface points. Each interface possesses two degrees of freedom: one translational and one rotational, see Fig. 1b. The design variable vector x(i) includes all design details for component i on the component-detail level. In the following, three exemplary component models will be considered:

  1. (M1)

    a beam with constant cross-section,

  2. (M2)

    a beam with varying cross-sections,

  3. (M3)

    an arbitrary body represented by a 2-dimensional topology.

For a given material (see Table 1), detailed design variables x(i) determine the component stiffness matrices \(\boldsymbol {K}_{(i)} \in \mathbb {R}^{4 \times 4}\) for both components i on the component-performance level. Under a given load F, the structure deforms resulting in a system displacement d. Similarly, the detailed description x(i) also defines the mass m(i) of each component and consequently the system mass is m = m(1) + m(2). Figure 2a illustrates the dependencies between all relevant quantities that are needed to solve the given demonstrator problem.

Table 1 Material data
Full size table
Fig. 2
figure 2

Dependency graph of all relevant quantities on the system level (I), component-performance level (II), and component-detail level (III) in a monolithic (a) and the proposed approach (b)

Full size image

3 Informed decomposition

3.1 κ-representation of the component stiffness matrix K

Not all component stiffness matrices can be realized. Feasible component stiffness matrices \(\boldsymbol {K} \in \mathbb {R}^{4 \times 4}\) must satisfy the following requirements:

  1. (R1)

    K must be symmetric

  2. (R2)

    rigid body deformations should result in zero forces,

  3. (R3)

    K must be positive semi-definite, for stability,

  4. (R4)

    there exists a detail design x corresponding to K, that satisfies the problem-specific restriction, e.g., related to geometry.

Requirements (R1)–(R3) shall be satisfied by an appropriate representation of component stiffness matrices K using eigenvectors φ of the generalized eigenvalue problem

$$ \boldsymbol{K} \boldsymbol{\varphi} = \lambda \boldsymbol{B} \boldsymbol{\varphi}, $$
(1)

where \(\boldsymbol {B} \in \mathbb {R}^{4 \times 4}\) is chosen to adjust the physical units using a reference displacement dr, i.e.,

$$ \boldsymbol{B} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & {d_{r}^{2}} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & {d_{r}^{2}} \end{bmatrix}. $$
(2)

Then, (1) can be rewritten with respect to Φ = [φ1,...,φ4] as KΦ = BΦΛ, and K can be expressed as

$$ \boldsymbol{K} = \boldsymbol{B} \boldsymbol{{{\varPhi}}} \boldsymbol{{{\varLambda}}} \boldsymbol{{{\varPhi}}}^{-1}, $$
(3)

where \( \boldsymbol {{{\varLambda }}} = diag\left (\lambda _{1}, ..., \lambda _{4} \right )\). This satisfies (R1). Choosing eigenvectors as rigid body deformations with zero-valued eigenvalues

$$ \boldsymbol{\varphi}_{1} = \begin{bmatrix} d_{r} \\ 0 \\ d_{r} \\ 0 \end{bmatrix}, \quad \lambda_{1} = 0 $$
(4)

and

$$ \boldsymbol{\varphi}_{2} = \begin{bmatrix} {- d_{r}} \\ \phantom{-} \frac{2 d_{r}}{l} \\ \phantom{-} d_{r} \\ \phantom{-} \frac{2 d_{r}}{l} \end{bmatrix}, \quad \lambda_{2} = 0, $$
(5)

will ensure (R2). (R3) will be satisfied by choosing only eigenvalues equal or greater than zero,

$$ \lambda_{3} \ge 0, \quad \lambda_{4} \ge 0. $$
(6)

The remaining eigenvectors φ3 and φ4 need to be orthogonal to the already defined φ1 and φ2, representing rigid body modes, and each other. The length of the vectors is normalized for uniqueness, i.e.

$$ \boldsymbol{\varphi}_{m}^{T} \boldsymbol{B} \boldsymbol{\varphi}_{j} = \begin{cases} 0 & \text{for } m \neq {j}\\ {d_{r}^{2}} & \text{for } m = {j}\\ \end{cases} $$
(7)

These equations can be solved to express φ3 and φ4 for any given reference displacement dr and component length l in terms of one remaining degree of freedom γ, denoted as the eigenvector orientation (see Appendix A.1). For \(l^{2} \gg {d_{r}^{2}}\), the expressions can be simplified to

$$ \boldsymbol{\varphi}_{3} = \begin{bmatrix} \frac{{d_{r}^{2}}}{l} \left( \gamma - (1- \gamma^{2})^{\frac{1}{2}}\right) \\ \gamma \\ -\frac{{d_{r}^{2}}}{l} \left( \gamma - (1- \gamma^{2})^{\frac{1}{2}}\right) \\ \frac{-2 \gamma {d_{r}^{2}}}{l^{2}} - (1 - \gamma^{2})^{\frac{1}{2}} \end{bmatrix}, $$
(8)
$$ \boldsymbol{\varphi}_{4} = \begin{bmatrix} -\frac{{d_{r}^{2}}}{l} \left( \gamma + (1- \gamma^{2})^{\frac{1}{2}} \right) \\ - \left( 1 - \gamma^{2}\right)^{\frac{1}{2}}\\ \frac{{d_{r}^{2}}}{l} \left( \gamma + (1- \gamma^{2})^{\frac{1}{2}} \right) \\ \frac{2 {d_{r}^{2}}}{l^{2}} (1 - \gamma^{2})^{\frac{1}{2}} - \gamma \end{bmatrix}, $$
(9)

with 0 ≤ γ < 1. In the following l= 300 mm and dr= 1 mm is set. All component stiffness matrices K satisfying (R1)-(R3) are therefore determined by

$$ \boldsymbol{\kappa} = [\gamma,\lambda_{3},\lambda_{4}]^{T}. $$
(10)

Satisfying (R4) is less straightforward. Whether or not a component stiffness matrix can be realized will depend on the provided design space and the utilized material. A vector of feasibility estimators \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa }){=}\boldsymbol {f}\) will be established to express feasibility fj= 1 or any infeasibility fj= − 1 of a given component stiffness matrix with respect to (R4).

In contrast to the classical problem setup in Fig. 2a, the masses for the κ-representation of K are not computed by the detailed design variable vector x, but with a mass estimator \(\hat {m}(\boldsymbol {\kappa })\) for κ. Thus, a mass estimate is available without knowing the detailed design, see Fig. 2b.

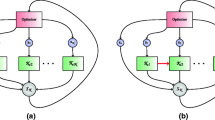
Based on the κ-representation of K, the new top-down approach is proposed (see Fig. 3). It is divided into (a) a pure design procedure based on a horizontal and vertical decomposition of a system, enabling a completely independent component design and (b) establishing feasibility estimators \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and mass estimator \(\hat {m}(\boldsymbol {\kappa })\), if appropriate models are not available. Note that established meta models can be reused for different design tasks.

Fig. 3
figure 3

Overview over the proposed approach consisting of (a) system optimization and decoupled component optimizations and (b) establishing feasibility estimators \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and mass estimator \(\hat {m}(\boldsymbol {\kappa })\)

Full size image

3.2 System optimization

For available \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\), the system optimization decomposes the problem horizontally and vertically into two completely independent component optimizations. The system optimization problem reads:

$$ \begin{array}{@{}rcl@{}} & \quad \min\limits_{\scriptsize \boldsymbol{\kappa}_{(1)},\boldsymbol{\kappa}_{(2)}} \hat{m}_{(1)}\left( \boldsymbol{\kappa}_{(1)}\right) & + \hat{m}_{(2)}\left( \boldsymbol{\kappa}_{(2)}\right) \\ \text{s. t.:} & \quad d\left( \boldsymbol{\kappa}_{(1)}, \boldsymbol{\kappa}_{(2)}\right) - d_{0} &{ }\le{ } 0 \\ & \quad -\hat{\boldsymbol{f}}\left( \boldsymbol{\kappa}_{(1)}\right) & { }\le{ } 0 \\ & \quad -\hat{\boldsymbol{f}}\left( \boldsymbol{\kappa}_{(2)}\right) & { }\le{ } 0 \\ & \qquad \boldsymbol{\kappa}_{lb} { }\le{ } \boldsymbol{\kappa}_{(1)} { }\le{ } \boldsymbol{\kappa}_{ub} & \\ & \qquad \boldsymbol{\kappa}_{lb} { }\le{ } \boldsymbol{\kappa}_{(2)} { }\le{ } \boldsymbol{\kappa}_{ub}. & \end{array} $$
(11)

The system optimization produces a mass-optimal stiffness κ(i) for each component with the help of \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\), while not knowing the detailed designs. Note that the system optimization problem between level (I) and (II), see Fig. 2, is significantly less expensive than a monolithic optimization all the way down to level (III) including the detailed design variable vector x(i) for both components. The first requires solving for all component interface displacements, say \(\boldsymbol {d}_{s} \in \mathbb {R}^{6}\). This is accomplished by inverting the linear equation system Ksds = Fs, with \(\boldsymbol {K}_{s}\left (\boldsymbol {\kappa }_{(1)}, \boldsymbol {\kappa }_{(2)}\right ) \in \mathbb {R}^{6 \times 6}\) being a system stiffness matrix assembled with the two component stiffness matrices K(1) and K(2) represented by κ(1) and κ(2), respectively, and Fs being a vector of loads on component interfaces. By contrast, the second, i.e., monolithic optimization, requires solving for all nodal displacement of a detailed Finite Element mesh by inverting the linear equation system Ksddsd = Fsd, with \(\boldsymbol {K}_{sd} \in \mathbb {R}^{n_{sd} \times n_{sd}}\) being the detailed system stiffness matrix with nsd degrees of freedom, dsd being the nodal displacement vector, and Fsd, being the vector of external nodal forces.

A particle swarm algorithm is utilized to solve the given system optimization problem. Note that the algorithm suffers from stochastic perturbations, therefore in the following, N= 10 optimizations are carried out and the best result is taken.

The resulting κ(i) is used to formulate component stiffness target values K0(i) for the two components

$$ \boldsymbol{K}_{0(i)} = \boldsymbol{B}\boldsymbol{{{\varPhi}}}_{(i)}(\boldsymbol{\kappa}_{(i)})\boldsymbol{{{\varLambda}}}_{(i)}(\boldsymbol{\kappa}_{(i)}) \boldsymbol{{{\varPhi}}}_{(i)}^{-1}(\boldsymbol{\kappa}_{(i)}). $$
(12)

3.3 Component optimization

The component optimization between level (II) and (III), see Fig. 2, identifies the optimal detailed design x(i) for each component with minimum mass for a given reference component stiffness matrix K0(i). The associated problem statement reads

$$ \begin{array}{@{}rcl@{}} & \quad \min\limits_{\boldsymbol{x}_{(i)} } m(\boldsymbol{x}_{(i)} ) & \\ \text{s. t.:} & \quad \lVert \boldsymbol{K}(\boldsymbol{x}_{(i)}) - \boldsymbol{K}_{0(i)}\lVert &{ }\le{ } \epsilon \\ & \quad g(\boldsymbol{x}_{(i)} ) & { }\le{ } 0 \\ & \boldsymbol{x}_{lb} { }\le{ } \boldsymbol{x}_{(i)} { }\le{ } \boldsymbol{x}_{ub}, & \end{array} $$
(13)

where xlb and xub are the lower and upper bounds on the detailed design variables x(i), K(x(i)) is the candidate component stiffness matrix associated with x(i). g(x(i)) is an inequality constraint function including additional restrictions for the respective component models.

The optimization problem is solved utilizing the method of moving asymptotes (MMA) by Svanberg (1987). Since the problem was completely decoupled, the system stiffness measured by the total displacement d is assumed to satisfy the requirement d ≤ d0 as long as the component optimizations are feasible.

3.4 Establishing feasibility and mass estimator

When the feasibility estimators \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and the mass estimator \(\hat {m}(\boldsymbol {\kappa })\) are not available in closed form solution, meta models are established by first sampling the input space of κ satisfying (R1)-(R3), and, second, numerical optimization to assess whether (R4) is satisfied. To create the input samples, first κA is generated within the bounds [κlb,κub]. The sample vector of the inputs reads

$$ \boldsymbol{X}_{A}=[\boldsymbol{\kappa}_{A}]. $$
(14)

For each κA, a reference component stiffness matrix K0A is computed using (3). The corresponding detailed design x with minimal mass m is sought using the component optimization of (13). If the component optimization converges, the feasibility flag will be set to fA= 1 otherwise fA= − 1. The sample output vector containing the feasibility flag and the realized mass for feasible designs reads

$$ \boldsymbol{Y}_{A} = [ f_{A},m_{A}]^{T}. $$
(15)

The resulting sample data [XA,YA] is used to train the meta models \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\), which can then be utilized for the system optimization of the design procedure of Section 3.2. In Section 5, \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\) are derived for each given component model.

4 Alternative design approaches for comparison

The informed decomposition in Section 3 will be referred to as approach (A) and will be compared to a complete monolithic optimization, which is assumed to be the benchmark result, and an uninformed decomposition, where both components are assigned a certain stiffness budget α.

Monolithic optimization, approach (B). This is the standard approach to structural optimization where the mass and the system displacement are directly computed from the detailed design variables x of each component, see Fig. 2a. The associated monolithic optimization problem for approach (B) reads

$$ \begin{array}{@{}rcl@{}} & \quad \min\limits_{\boldsymbol{x}_{(1)},\boldsymbol{x}_{(2)} } m \left( \boldsymbol{x}_{(1)}\right) {+} &m \left( \boldsymbol{x}_{(2)}\right) \\ \text{s. t.:} & \quad d\left( \boldsymbol{x}_{(1)},\boldsymbol{x}_{(2)}\right) - d_{0} &{ }\le{ } 0 \\ & \quad \boldsymbol{g}\left( \boldsymbol{x}_{(1)},\boldsymbol{x}_{(2)}\right) & { }\le{ } 0 \\ & \boldsymbol{x}_{lb} { }\le{ } \boldsymbol{x}_{(1)} { }\le{ } \boldsymbol{x}_{ub} & \\ & \boldsymbol{x}_{lb} { }\le{ } \boldsymbol{x}_{(2)} { }\le{ } \boldsymbol{x}_{ub}. & \end{array} $$
(16)

Uninformed decomposition, approach (C). This type of vertical decomposition was previously introduced in Krischer et al. (2020) for a similar two-component structure. As an important difference to the proposed approach (A), no mass estimation is used to balance the requirement on the stiffness matrices of each component. Instead, a stiffness distribution is motivated by a reference structure that is not necessarily optimal. Also, no feasibility estimate is taken into account. The total deformation

$$ d = d_{(1)} + \theta_{(1)} l_{(2)} + d_{(2)} $$
(17)

can be additively decomposed into the translational displacement d(1) and the rotational displacement 𝜃(1) of the first component and translational displacement d(2) of the second component (see Fig. 4). The system requirement d ≤ d0 will be satisfied, whenever the following component requirements are satisfied,

$$ \begin{array}{@{}rcl@{}} b_{(1)}(\boldsymbol{x}) & = & \left( d_{(1)} + \theta_{(1)} l_{(2)} \right) - \alpha d_{0} \le 0, \end{array} $$
(18)
$$ \begin{array}{@{}rcl@{}} b_{(2)}(\boldsymbol{x}) & = &d_{(2)} - \left( 1-\alpha \right) d_{0} \le 0, \end{array} $$
(19)

where α can assume any value between 0 and 1. α controls how much stiffness will be contributed by each component in order to meet the system stiffness requirement. The component optimization of each component reads

$$ \begin{array}{@{}rcl@{}} & \quad \min\limits_{\boldsymbol{x}_{(i)}} m(\boldsymbol{x}_{(i)}) & \\ \text{s. t.:} & \quad b(\boldsymbol{x}_{(i)}) &{ }\le{ } 0 \\ & \quad g(\boldsymbol{x}_{(i)}) & { }\le{ } 0 \\ & \boldsymbol{x}_{lb} { }\le{ } \boldsymbol{x}_{(i)} { }\le{ } \boldsymbol{x}_{ub}. & \end{array} $$
(20)
Fig. 4
figure 4

Additive decomposition of the system displacement d into the respective component displacements d(1), 𝜃(1) and d(2)

Full size image

Two stiffness distributions are chosen for comparison in the following chapters: α = 0.5 (C.1) and α = 0.6 (C.2).

5 Results for three component models

5.1 Beam with constant cross-section

To point out the main features of the proposed approach (A), the simplest component model (M1) containing all necessary ingredients is considered first. For this component model, the feasibility and mass estimators, \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\), are established. To validate the proposed approach, they are derived in a closed form. A simple mechanical representation with an i-beam and constant cross-sections (see Fig. 5 (M1), for W(ζ) = const.) is utilized.

Fig. 5
figure 5

Design variables of the component models for a beam with constant cross-section (M1), a beam with varying cross-sections (M2), and an arbitrary body represented by a 2-dimensional topology (M3)

Full size image

The detailed design variables for both components are

$$ \boldsymbol{x} = \left[\begin{array}{c} w \\ W \end{array}\right] \qquad 0 < w \le W \le 40 \text{ mm} , $$
(21)

where w = h and W = H are prescribed.

The component stiffness matrix K and the mass m for a constant cross-section Euler-Bernoulli beam are according to Bathe (2006)

$$ \begin{array}{@{}rcl@{}} & \boldsymbol{K} &= EI \boldsymbol{k}(l), \end{array} $$
(22)
$$ \begin{array}{@{}rcl@{}} & m & = \rho l \left( W H - wh \right), \end{array} $$
(23)

with the moment of inertia \(I = 1/12 \left (W H^{3} - w h^{3} \right )\). For physical feasibility, the outer flange width W must be greater than w, i.e.,

$$ g (\boldsymbol{x}) = w - W \le 0. $$
(24)

The component stiffness matrix K for a given length l and a given material depends solely on the moment of inertia I, see (22). Therefore, the stiffness matrix constraint can be simplified to

$$ \lVert \boldsymbol{K}(\boldsymbol{x}) - \boldsymbol{K}_{0}\lVert = I - I_{0} = 0. $$
(25)

Utilizing these simplifications, the solution of the component optimization (13) is

$$ \begin{array}{@{}rcl@{}} w & =& \left( W^{4} - 12 I\right)^{\frac{1}{4}}, \end{array} $$
(26)
$$ \begin{array}{@{}rcl@{}} W & =& 40 \text{ mm}, \end{array} $$
(27)
$$ \begin{array}{@{}rcl@{}} m & =& \rho l \left( W^{2} - (W^{4} - 12 I)^{\frac{1}{2}} \right), \end{array} $$
(28)

and the sample data can be created as

$$ \begin{array}{@{}rcl@{}} X_{A} & = &[\lambda_{3 A},\lambda_{4 A},\gamma_{A}], \end{array} $$
(29)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{Y}_{A} & = & \left[ g_{A},m_{A},I_{A} \right]^{T}, \end{array} $$
(30)

where the mass sample data is enriched by the inertia information IA to derive the mass estimator with respect to κ. Since the stiffness only depends on one structural quantity I, also the κ-representation of K can be reduced to one entry. In κ, the eigenvalues λ3 and λ4 represent the stiffness of the beam, which therefore must possess a constant ratio to each other. Consequently, the orientation vector γ must be constant. Finally, the upper stiffness bound is needed, which corresponds to a completely filled cross-section. To incorporate all the needed information, only one sample point N= 1 with the maximum stiffness property is needed. The feasibility estimators \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) can then be derived as

$$ \begin{array}{@{}rcl@{}} && \hat{f}_{1}(\boldsymbol{\kappa}) = \frac{\lambda_{4 A}}{\lambda_{3 A}} \lambda_{3} - \lambda_{4} = c_{1} \lambda_{3} - \lambda_{4} = 0, \end{array} $$
(31)
$$ \begin{array}{@{}rcl@{}} && \hat{f}_{2}(\boldsymbol{\kappa}) = \gamma - \gamma_{A} = \gamma - c_{2} = 0, \end{array} $$
(32)
$$ \begin{array}{@{}rcl@{}} && \hat{f}_{3}(\boldsymbol{\kappa}) = \lambda_{3} - \lambda_{3 A} = \lambda_{3} - c_{3} \le 0. \end{array} $$
(33)

The constant ratio is considered in (31). The constant orientation vector γ in (32). The upper bound of the first eigenvalue is captured by (33).

For setting up the mass estimator \(\hat {m}(\boldsymbol {\kappa })\) with respect to λ3, the relation between the moment of inertia I and the third eigenvalue is needed λ3

$$ I = \frac{\lambda_{3 A}}{I_{A}} \lambda_{3} = c_{4} \lambda_{3}, $$
(34)

which can be inserted into equation (28)

$$ \hat{m}(\boldsymbol{\kappa}) = \rho l \left( W^{2} - (W^{4} - 12 c_{4} \lambda_{3})^{\frac{1}{2}} \right). $$
(35)

The established feasibility and mass estimators, \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\) are shown in Table 2. In Fig. 6, the first row shows the stiffness design space with the accessible space as a one-dimensional line of designs with constant ratio λ3 and λ4 and constant eigenvector orientation γ. Additionally, samples of infeasible designs are shown. Note that most of the design space is infeasible.

Table 2 Explicit formulation of \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \( \hat {m}(\boldsymbol {\kappa }) \) for the component model (M1)
Full size table
Fig. 6
figure 6

Sampled stiffness design spaces for the component models (M1)–(M3)

Full size image

Having set up \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\), the system optimization (11) can be solved. The results of the system optimization can be seen in the first row of Fig. 7 and in Table 5. The monolithic optimization of approach (B) and the proposed systems design approach (A) have coinciding designs, due to the explicit description of the feasibility and mass estimator. Due to a non-optimal stiffness distribution α, the eigenvalues λ3 and λ4 of approach (C.1) and (C.2) deviate from the known optimal design, where the eigenvalues of the first component are larger and of the second component lower than in approach (B).

Fig. 7
figure 7

Feasible and optimized stiffness κ for the component models (M1)–(M3)

Full size image

Due to the explicit formulations of \(\hat {\boldsymbol {f}}(\boldsymbol {\kappa })\) and \(\hat {m}(\boldsymbol {\kappa })\) and (26), (27) and (34), the component-detail design x can be derived directly from the system optimization results κ. The results of all approaches are shown in Table 6 and Fig. 8. All approaches use the full width W and height H, as calculated analytically before. Approaches (A) and (B) show the same cross-sectional description. Consistent with the higher eigenvalues, approach (C) assigns more stiffness to the first component and less to the second component, resulting in a heavier overall structure. In conclusion, all approaches satisfy the given system requirement.

Fig. 8
figure 8

Optimized component designs x of the component models (M1)–(M3)

Full size image

5.2 Beam with varying cross-sections

To increase complexity, varying cross-section widths W(ζ) are utilized for the second component model (M2). Each structural component is discretized with ne= 10 cross-sections, see Fig. 5 (M2). The detailed design variables for both components are the flange widths We, i.e.,

$$ \begin{array}{@{}rcl@{}} && \boldsymbol{x} = [W_{e}] \qquad t_{w} \le W_{e} \le 40 \text{ mm}, \\ && \text{for } e=1,...,10, \end{array} $$
(36)

where H= 40 mm, h = H − 2th, with th= 3 mm, and tw= 1 mm are fixed for both components. The width w is calculated as w = W − tw. In order to determine the behavior of the components with respect to the defined two interface degrees of freedom, the static Guyan condensation technique is applied to the structure

(Guyan 1965), with the element stiffness matrix Ke formulated for the element length \(l_{e} = \frac {l}{n_{e}}\)

$$ \begin{array}{@{}rcl@{}} && \boldsymbol{K}_{d} = \sum\limits_{e=1}^{n_{e}} \boldsymbol{K}_{e}, \end{array} $$
(37)
$$ \begin{array}{@{}rcl@{}} && \boldsymbol{K}_{d} \boldsymbol{d}_{d} = \boldsymbol{F}_{d}, \end{array} $$
(38)
$$ \begin{array}{@{}rcl@{}} && \left[\begin{array}{c c} \boldsymbol{K}_{mm} & \boldsymbol{K}_{ms} \\\boldsymbol{K}_{sm} &\boldsymbol{K}_{ss} \end{array}\right] \left[\begin{array}{c} \boldsymbol{d}_{m} \\ \boldsymbol{d}_{s} \end{array}\right] = \left[\begin{array}{c} \boldsymbol{F}_{m} \\ \boldsymbol{0} \end{array}\right], \end{array} $$
(39)

where the suffix m is used for the master-degrees of freedom related to the two interfaces, and the suffix s is used for the condensated interior degrees of freedom of the detailed component stiffness matrix Kd. The equation is solved for the master degrees of freedom and can be represented by

$$ \begin{array}{@{}rcl@{}} & &\boldsymbol{K}_{g} \boldsymbol{d}_{m} = \boldsymbol{F}_{m}, \end{array} $$
(40)
$$ \begin{array}{@{}rcl@{}} && \boldsymbol{K}_{g} = \boldsymbol{T}_{g}^{T} \boldsymbol{K}_{d} \boldsymbol{T}_{g}, \end{array} $$
(41)
$$ \begin{array}{@{}rcl@{}} && \boldsymbol{T}_{g} = \left[\begin{array}{c} \boldsymbol{1} \\ -\boldsymbol{K}^{-1}_{ss}\boldsymbol{K}_{sm} \end{array}\right], \end{array} $$
(42)

where \(\boldsymbol {K}_{g} \in \mathbb {R}^{4x4}\) is the condensed interface component stiffness matrix.

The sensitivities of the reduced component stiffness matrix are derived in O’Connell et al. (1976) as

$$ \frac{\partial \boldsymbol{K}_{g}}{\partial W_{e}} = \boldsymbol{T}_{g}^{T} \frac{\partial \boldsymbol{K}_{d}}{\partial W_{e}} \boldsymbol{T}_{g}, $$
(43)

where the derivative of the detailed component stiffness matrix Kd for We is

$$ \frac{\partial \boldsymbol{K}_{d}}{\partial W_{e}} = \frac{H^{3} -h^{3}}{12} E \boldsymbol{k}_{e}(l_{e}). $$
(44)

The mass sensitivities read

$$ \frac{\partial m}{\partial W_{e}} = \rho l_{e} \left( H-h\right). $$
(45)

For K=Kg, the stiffness matrix requirement of the component optimization problem (13) can be reformulated to ensure that requirements (R1)–(R3) are satisfied as (see Appendix A.2)

$$ -\epsilon \le \left[\begin{array}{c} \frac{K_{11} - K_{11,0}}{K_{11,0}} \\ \frac{K_{22} - K_{22,0}}{K_{22,0}} \\ \frac{K_{44} - K_{44,0}}{K_{44,0}} \end{array} \right] \le \epsilon. $$
(46)

Note that no constraint function g(x) is necessary.

To establish the meta models, N= 1800 sample points were generated utilizing a Latin hypercube sampling procedure (McKay et al. 1979), see Fig. 6, where Nf= 416 samples were feasible. In contrast to component model (M1), a volume of feasible designs can be observed in the stiffness design space. Due to the lower bound We≥tw, the feasible stiffness design space has also lower bounds greater than zero κ>0. The sample data is used to train a scalar-valued feasibility estimator \(\hat {f}(\boldsymbol {\kappa })\) and mass estimator \(\hat {m}(\boldsymbol {\kappa })\). Therefore, machine learning methods are applied.

For estimating the feasibility f, support vector machines (SVM) are chosen, due to their simplicity combined with convexity also for non-linear classification problems (Cortes and Vapnik 1995). Thus, the binary SVM classifier from MATLAB is utilized and denoted in the following with \(\hat {f}_{SVM}(\boldsymbol {\kappa })\). As a kernel function, radial basis functions are used. The data is split into 80% training and 20% test samples. The hyperparameters are determined using a Bayesian optimization with a five-fold cross-validation on the training data. To assess the performance of the classifier, the false positive rate (FP), the true positive rate (TP) and the accuracy (acc) were analyzed, see Table 3. Since a decision for an infeasible design on the system level, makes the whole design approach invalid, the most important quantity is a low FP. Secondly, the mass estimator has to be established using a regression analysis. Feedforward artificial neural networks (ANN), with their capacity of approximating any function with any desired accuracy for a suitable parameter choice, have been frequently applied to a wide variety of regression problems (Hornik et al. 1989; Bishop 2009). Hence, the mass estimator is realized with an ANN \(\hat {m}_{ANN}(\boldsymbol {\kappa })\) trained with the Levenberg-Marquardt algorithm in MATLAB. The sample data is split into 80% training, 10% validation and 10% test samples. For choosing the best configuration of hidden layers and respective neurons, a grid search was carried out for nhl= 1,...,5 hidden layers and nn= 1,...,10 neurons. The configuration with the lowest R2-value was chosen. The final ANN possesses nhl= 2 hidden layers and nn= 7 neurons. Additionally, the mean squared error (mse) of the mass was taken as a second performance measure, see Table 3. Note that the meta models are valid for both components.

Table 3 Performance measures of \(\hat {f}_{SVM}(\boldsymbol {\kappa })\) and \( \hat {m}_{ANN}(\boldsymbol {\kappa }) \) for the component model (M2)
Full size table

Having established the meta models, the system optimization (11) is carried out. The results of the system optimization can be seen in in Fig. 7 and in Table 5. Approaches (A) and (B) again produce similar system designs for both components. In contrast, the uninformed approaches (C.1) and (C.2) show higher and lower eigenvalues for the first and second component, respectively. However, now not only the eigenvalues λ3 and λ4, but also the eigenvector orientation γ differs.

The results of the subsequent component optimization and the corresponding alternative approaches are shown in Fig. 8 and in Table 6. The width W decreases along the ζ-axis of both components, as it would be expected. The lightest designs are achieved by approaches (A) and (B), which slightly differ in the weight of the components and the overall mass. Both approaches (A) and (B) satisfy the system requirement. Note that approach (C.1) is not capable of fulfilling the component requirement of the first component and hence also the system requirement is violated resulting in a constant full width We of component one. In contrast, approach (C.2) satisfies the system requirement, however resulting in a higher total weight compared to (A) and (B).

5.3 2-dimensional topology

Finally, arbitrary 2-dimensional bodies are designed utilizing topology optimization (M3). Both sides of each body are connected rigidly to interface points. The height is set to H= 98 mm and the thickness to W= 1 mm for both components, see Fig. 5 (M3).

The body is discretized with uniform 2d-plane stress elements with stiffness matrices Ke (Bathe 2006) and nζ= 48 elements in the ζ- and nη= 16 elements in the η-direction. The total number of elements is ne= 768 and the respective element lengths are \(l_{e}{=}\frac {0.98 l}{n_{e\zeta }}\), leaving 1% of the length for the connection between the body and the interface points on both sides, \(H_{e}{=}\frac {H}{n_{e\eta }}\), and We=W. For the component optimization, the classical SIMP approach (Bendsøe and Sigmund 2004) is used with the element densities ρe as the detailed design variables, a penalty factor of p = 3 and a sensitivity filter radius of r = 1.2:

$$ \begin{array}{@{}rcl@{}} && \boldsymbol{K}_{d} = \sum\limits_{e=1}^{n_{e}} {\rho^{p}_{e}} \boldsymbol{K}_{e}, \end{array} $$
(47)
$$ \begin{array}{@{}rcl@{}} && \boldsymbol{x} = [\rho_{e}], \qquad \qquad 0 < \rho_{e} \le 1. \end{array} $$
(48)

The optimization code is based on Sigmund (2001). First, the known static condensation technique (Guyan 1965) is applied, with respect to the boundary degrees of freedom of both, the left and the right side of the plate, as the master nodes

$$ \boldsymbol{K}_{g} = \boldsymbol{T}^{T}_{g} \boldsymbol{K}_{d} \boldsymbol{T}_{g}. $$
(49)

In order to connect both sides of the body to the interface points, master-slave elimination via a multi-freedom constraint is applied, see Liu and Quek (2013). The slave nodes of both sides are eliminated enforcing a geometrical constraint with respect to the master interface nodes yielding

$$ \boldsymbol{K}_{rg} = \boldsymbol{T}^{T}_{r} \boldsymbol{K}_{g}\boldsymbol{T}_{r}. $$
(50)

The derivatives of the component stiffness matrix \(\boldsymbol {K}_{rg} \in \mathbb {R}^{4x4}\) are

$$ \begin{array}{@{}rcl@{}} && \frac{\partial \boldsymbol{K}_{rg}}{\partial \rho_{e}} = \boldsymbol{T}_{r}^{T} \left( \boldsymbol{T}_{g}^{T} \frac{\partial \boldsymbol{K}_{d}}{\partial \rho_{e}} \boldsymbol{T}_{g}\right) \boldsymbol{T}_{r}, \end{array} $$
(51)
$$ \begin{array}{@{}rcl@{}} & & \frac{\partial \boldsymbol{K}_{d}}{\partial \rho_{e}} = p \rho_{e}^{p-1} \boldsymbol{K}_{e}, \end{array} $$
(52)

and the mass gradients are constant

$$ \frac{\partial m}{\partial \rho_{e}} = \rho l_{e} H_{e} W_{e}, $$
(53)

with ρ as the density of aluminum.

Having computed the derivatives, the component optimization problem (13) can be set up utilizing the reduced stiffness constraint of Section 5.2. Again, no extra constraint g(x) is required.

The component optimization problem is then used to establish the meta models. While sampling, it could be observed that for low-valued eigenvalues λ3 and λ4 the designs tend to be infeasible. Also, the component mass m exhibited a more nonlinear behavior for both eigenvalues in the low-value region. Therefore, the basic sample data Xlhs ∈ [0,1] created by Latin hypercube sampling is mapped onto a cubic space \(\boldsymbol {X}_{lhs} \rightarrow \boldsymbol {X}_{lhs}^{3}\) for both eigenvalues λ3 and λ4 and is then applied to the stiffness design space κ ∈ [κlb,κub] allowing for more sample data in the crucial low-value region, see Fig. 6. The increased design freedom of the topology optimization provides a broad feasible design space with Nf = 1026 feasible sample points.

The created sample data is used to train the meta models \(\hat {f}_{SVM}(\boldsymbol {\kappa })\) and \(\hat {m}_{ANN}(\boldsymbol {\kappa })\) similar to Section 5.2. The ANN has nhl = 3 hidden layers and nn = 9 neurons. The training results are shown in Table 4.

Table 4 Performance measures of \(\hat {f}_{SVM}(\boldsymbol {\kappa })\) and \( \hat {m}_{ANN}(\boldsymbol {\kappa }) \) for the component model (M3)
Full size table

Next, the system optimization is carried out. The results are shown in Fig. 7 and Table 5. The designs of the first component of approaches (A) and (B) differ slightly with respect to both eigenvalues λ3, λ4 and the eigenvector orientation γ. The approaches (C.1) and (C.2) assign again more stiffness, i.e. larger eigenvalues, to the first component than to the second one. It is also noticeable that the second component of approach (C.1) produces an eigenvector orientation γ close to the upper bound with a larger third eigenvalue λ3 and a smaller fourth eigenvalue λ4, in contrast to the other approaches with an eigenvector orientation close to the lower bound and a higher λ4 eigenvalue compared to λ3.

Table 5 Optimized stiffness κ for the component models (M1)-(M3)
Full size table

The final topologies of the component optimization are shown in Fig. 8. For all design models, the second components converge to the known cantilever beam design for classical bending load cases. The proposed approach (A) exhibits a more tapered right end compared to (B), whereas (C.1) and (C.2) only differ in the assigned densities of the existing beam-like structure resulting in lower component masses (see Table 6). Even though the results of the system optimization of component one are different for (C.1) compared to (A), (B), and (C.2), the results of the component topology optimization in Fig. 8 show only slight differences. The first component of approaches (A) and (B) show thick beam-like structures at the outer regions of the design domain, with crossbars for transferring the shear loads. Yet, the position for these differs in both approaches. Approach (C.2) produces a similar topology, with a slightly higher material fraction in component one. In contrast, the domain of approach (C.1) is completely filled with material, stemming from a component requirement that is too challenging. The required system displacement for approach (C.1) is therefore violated, while approaches (A), (B) and (C.2) are all feasible.

Table 6 Optimized component designs x of the component models (M1)–(M3)
Full size table

6 Discussion

Validity

The proposed approach (A) was capable of successfully solving the given demonstrator problem for three different component models (M1)–(M3) (see Fig. 9). For the component model (M1), the exact expression for the feasibility and the mass estimator led to the same component-detail designs as for the monolithic system optimization of approach (B). For the component models (M2) and (M3), approach (A) utilized machine learning–based meta models. Here, the system mass m only slightly differed with a deviation below 1%.

Fig. 9
figure 9

Post-processing results of the optimized component designs of the component models (M1)–(M3) for approach (A)

Full size image

Informed vs. uninformed decomposition

The key ingredients, the feasibility and the mass estimators, proofed to be crucial within the scope of completely decoupled optimization schemes. The uninformed approach (C) turned out to be both, at risk of proposing infeasible designs (C.1) and producing no mass-optimal solutions (C.2). For more complex design tasks with multiple load cases, the intuition for reasonable component requirements will eventually fail. Therefore, the proposed approach presents a promising way of decomposing multi-component systems in a feasible and mass-optimal way.

Computational cost

One motivation of decomposing multi-component systems is the high computational cost. For the given problem, the computational cost of a monolithic system optimization is still small compared to the sampling process, where each sample point needs to be generated by carrying out a single component optimization. However, adding complexity to the problem by, e.g., a higher number of components, multiple load cases with different boundary conditions or a selection of available materials, can greatly increase the cost of a monolithic system optimization. In such a scenario, complete decoupling with separate component optimizations could be less expensive (Krischer et al. 2020). Moreover, the training process must not be carried out for every single system optimization. Meta models with a validity over a range of geometrical quantities such as length, width, and height would enhance the applicability to more complex and therefore more expensive problems with a need for higher training cost only once.

Establishing meta models

The generation of sample data for the training process of the meta models is a critical step. Besides the great computational cost, the infeasible regions for highly detailed description of components are often located in small areas that need to be captured within the procedure. While training, even if captured, they might be not considered by the feasibility estimator due to unbalanced training data. Therefore, a sufficiently balanced training data set needs to be ensured.

κ-representation of K

The unique representation of component stiffness matrices via an eigenvalue decomposition helps to enable an efficient sample data generation (see Section 3.1). However, a drawback of the approach is that for eigenvector orientations γ close to the lower or upper bound, the respective eigenvectors of the opposite bound resemble each other. Hence, the results of the system optimization in terms of κ can sometimes differ significantly in γ for similar detailed design vectors x (see Section 5.3). Also, since the sample data is not directly derived with respect to κ, but in terms of the entries of the component stiffness matrix K, see (13), the accuracy of the component optimization can only indirectly be ensured by setting a low threshold 𝜖. Especially during the sampling procedure, a compromise between a high accuracy and the computational effort must be made.

Post-processing

Finally, structural optimization results often need a post-processing step. In Fig. 9, a manual post-processing was carried out. However, small changes might cause a invalid component behavior violating system requirements. Hence, a requirement-based post-processing is necessary to transfer the results into a feasible component.

7 Conclusion and future work

The proposed approach in this paper has two main ingredients: (a) a top-down design procedure and (b) establishing meta models for feasibility and mass estimation. The top-down design procedure is based on two subsequent optimization problems. First, a system optimization is carried out, that decomposes the problem horizontally and vertically into completely independent component optimization problems. The elastic properties of the mechanical components are hereby defined by component stiffness matrices, which are parametrized by eigenvalues and eigenvectors, enabling better access to the space of stiffness matrices. To assess feasibility and mass of the given component stiffness matrices, meta models are utilized. Feasibility is taken into account by considering geometrical restrictions and material properties. In order to distribute the requirements in a mass-optimal way, a mass estimator is established that provides the lowest possible mass for a given stiffness. As a result of the system optimization, required stiffness properties for both components are assigned, while not knowing their detailed descriptions. In a second step, a subsequent component optimization is using the stiffness properties as constraints. The component optimizations can be carried out completely independently of each other, making any coordination between the components or the system level unnecessary.

For a linear mechanical two-component system, the proposed approach (A) was compared to two alternative design approaches. The approach (B) is a monolithic system optimization, for designing an entire system at once. The uninformed approach (C) distributes a predefined stiffness budget to the components without knowing the effect on mass and feasibility on the component-detail level. Afterwards, two independent component optimization problems are solved with respect to the assigned stiffness budgets. Three different component models were tested: (M1) a i-beam with constant cross-section, (M2) a i-beam with varying flange width, and (M3) an arbitrary body represented by a 2-dimensional topology. It could be shown that the proposed approach (A) is capable of assigning component requirements in a feasible and mass-optimal manner, resulting in designs that only slightly differ from the results of the monolithic optimization of approach (B). The uninformed approaches (C) exhibited problems, in either producing non-feasible requirements (C.1) and/or requirements that lead to suboptimal designs (C.2).

In the future, the approach will be enhanced to problems with (a) multiple interfaces and (b) more degrees of freedom per interface. In order to widen the applicability of meta models, varying geometrical boundary conditions will be considered during the training phase. To reduce the computational effort of the training phase, active-learning sample procedures are to be investigated.