Abstract
In this work, an algorithm for topology optimization of incompressible structures is proposed, in both small and finite strain assumptions and in which the loads come from the interaction with a surrounding fluid. The algorithm considers a classical block-iterative scheme, in which the solid and the fluid mechanics problems are solved sequentially to simulate the interaction between them. Several stabilized mixed finite element formulations based on the Variational Multi-Scale approach are considered to be capable of tackling the incompressible limit for the numerical approximation of the solid. The fluid is considered as an incompressible Newtonian fluid flow which is combined with an Arbitrary-Lagrangian Eulerian formulation to account for the moving part of the domain. Several numerical examples are presented and discussed to assess the robustness of the proposed algorithm and its applicability to the topology optimization of incompressible elastic solids subjected to Newtonian incompressible fluid loads.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fluid–Structure Interaction (FSI) problems involve the interaction between a fluid and a deformable solid structure. These problems arise in various engineering and scientific applications, including aerospace (Kamakoti and Shyy 2004), civil engineering (Rhyzhakov and Oñate 2017), biomechanics (Bodnár et al. 2014; Rhyzhakov et al. 2019), and offshore structures (Yan et al. 2016). Numerical methods play a significant role in solving FSI problems by providing efficient and accurate solutions. These methods combine fluid dynamics and structural mechanics algorithms to simulate the coupled behavior of fluids and structures. The interaction between the fluid and the structure is typically modeled by exchanging information at the fluid–structure interface (Richter and Wick 2010). Understanding and accurately simulating FSI phenomena is crucial for designing and optimizing systems where fluid and structure interact (Rhyzhakov et al. 2010; Richter 2017).
One common approach for simulating FSI problems is the partitioned approach, where separate solvers are used for the fluid and structural domains. In this approach, the fluid solver calculates the fluid flow field while treating the structure as a rigid body or prescribing its motion based on the interaction forces. The structural solver computes the deformation and stress response of the solid structure based on the fluid-induced loads. The coupling between the two solvers is achieved by iteratively exchanging information at the fluid–structure interface until convergence is reached (Küttler and Wall 2008; Moreno et al. 2023).
FSI problems involving incompressible structures are a subset of FSI phenomena where the solid component undergoes negligible volume changes when subjected to external forces or deformations. In such problems, the fluid interacts with a solid object that remains essentially incompressible, maintaining its volume throughout the interaction (Treloar 1975). The study of FSI involving incompressible solids is crucial in numerous fields, including biomechanics, bioengineering, soft robotics, and material science (Comellas et al. 2016; Martínez-Frutos et al. 2021). Examples of incompressible structures include soft tissues, elastomers, gels, and certain biological materials (Wex et al. 2015; Comellas et al. 2016, 2020). Understanding the complex interactions between the fluid and the incompressible solid is essential for designing and optimizing systems in these domains.
Mixed formulations are commonly used in the context of incompressible structures to handle the incompressibility constraint. These formulations introduce additional unknowns, such as the pressure field, to enforce volume conservation. The most widely used mixed formulations are the displacement-pressure mixed formulations (Baiges and Codina 2017; Castañar et al. 2020) or the three-field formulations which add some extra unknowns to increase its accuracy (Chiumenti et al. 2015, 2021; Castañar et al. 2023). These formulations provide stable and accurate solutions for incompressible problems by coupling the displacement and pressure fields; in this work, they are employed to model FSI simulations involving incompressible structures.
Topology Optimization (TO) is a powerful computational design approach that aims to optimize the material distribution within a given design domain to achieve desired performance objectives. The goal is to find the optimal arrangement or layout of material that meets specified criteria while considering design constraints (Bendsøe and Sigmund 2013). The primary objective of TO of incompressible structures is to improve structural stiffness while ensuring volume conservation. In these problems, the incompressibility constraint needs to be satisfied throughout the optimization process, meaning that the total volume or the fraction of occupied material within the design domain remains constant (Novotny and Sokolowski 2013; Novotny et al. 2019).
TO is an efficient method to improve mechanical systems design in engineering. In the last decades, several methods have been developed to find optimal structures inside predefined design domains by minimizing objective functions and constraints (Bendsøe and Sigmund 2013; Bendsøe and Kikuchi 1988; Huang and Xie 2010; van Dijk et al. 2013; Deaton and Grandhi 2014). In Castañar et al. (2022) the TO of incompressible structures is studied by considering stabilized mixed formulations and using the topological derivative (TD) concept. It is observed that the optimal topology for structural elements in the incompressible limit can significantly differ from that of compressible or slightly compressible ones. The TO of hyperelastic materials is also studied in Ortigosa et al. (2019, 2020) with the combination of a level-set method and the well-known SIMP approach.
Although the field of structural optimization has become mature, many applications, such as aeronautics or biomechanics, require multiphysics design (Deng et al. 2013; Shu et al. 2014; Sigmund and Clausen 2007; Wang et al. 2016; Andreasen and Sigmund 2013). As a consequence, methodologies for structural TO in FSI problems have become popular as they provide a framework to include FSI models in the TO design procedure.
These methodologies are classified in Jenkins and Maute (2015) according to the treatment applied on the interface between the fluid flow and the structure. Therefore, those cases in which only the internal part of the structure is optimized are named “dry” or design-independent optimization, whereas the “wet” or design-dependent optimization are those cases in which the geometry of the FSI boundary can be changed during the TO process.
Regarding the latter, several methodologies have been proposed during the last years. In Yoon (2010) the idea of using a monolithic approach to interpolate both structural and fluid equations based on the density method was proposed for steady-state FSI problems. These ideas were lately extended to stress-based TO (Yoon 2014). Another option was proposed in Jenkins and Maute (2016) to extend the XFEM-Level-set method reported in Jenkins and Maute (2015) to “wet” optimization. The bi-directional evolutionary structural optimization is also applied in Picelli et al. (2017) to disjoint the problem into two subdomains and be able to tackle them in a separate way. A body-fitted mesh evolution technique integrated into a level-set method can be found in Feppon et al. (2020). Finally, reaction-diffusion equation-based level-set methods are applied to solve the FSI optimization problem presented in Li et al. (2022). All these works concern the interaction between a linear elastic compressible structure and viscous fluid flows governed by the incompressible Navier–Stokes equations. In Silva et al. (2022) the TO of structures subject to stationary FSI is adressed.
In this work, we are interested in “dry” TO for FSI problems which may involve incompressible structures. In particular, FSI problems which are two-way coupled. The flow depends on the structural displacements and the structural behavior depends upon the fluid forces. As the FSI boundary remains constant over the TO procedure, we can use a staggered approach to solve individually the fluid and the structure sub-problems and satisfy the interface conditions in a strongly coupled manner (Küttler and Wall 2008).
In this study, we propose a new “dry” TO framework for strongly coupled FSI systems with incompressible structures. To the best of our knowledge, this is the first attempt to use TD-based TO of incompressible structures in FSI problems. Furthermore, the structural model can be either linear elastic or hyperelastic, allowing for finite strain deformations. In addition, the study of transient FSI problems is also performed.
This work is organized as follows. In Sect. 2 some preliminaries are introduced. Next, in Sect. 3 we present several stabilized mixed formulations which are able to tackle the incompressible limit to model solid dynamics in both linear elasticity and finite strain hyperelasticity. Section 4 provides the governing equations to deal with incompressible fluid flows with moving domains. Afterward, Sect. 5 outlines the setting of the whole TO problem of incompressible structures subjected to FSI loads. Several numerical examples are shown in Sect. 6 to assess and validate the proposed methodology. The work is closed with some conclusions in Sect. 7.
2 Preliminaries
This section provides a foundational introduction to the key concepts, theories, methodologies and background knowledge necessary for understanding the main content for all sub-problems presented in this work.
Let us introduce some notation for deriving the weak formulation of the problems we need to develop. As usual, the space of square integrable functions in a domain \(\omega\) is denoted by \(L^2\left( \omega \right)\), whereas the space of functions whose first derivative is square integrable is denoted by \(H^1\left( \omega \right)\). The space \(H^1_0\left( \omega \right)\) consists of functions in \(H^1\left( \omega \right)\) vanishing on boundaries. We shall use the symbol \(\left( \cdot , \cdot \right) _\omega\) to refer to the \(L^2(\omega )\) inner product and \(\left\langle \cdot , \cdot \right\rangle _\omega\) to refer to the integral of the product of two functions in a domain \(\omega\), not necessarily in \(L^2(\omega )\). The subscript is omitted when \(\omega = \Omega\), being \(\Omega\) the domain of study for each sub-problem.
For the sake of conciseness, in this work only the implicit second order backward differences scheme (BDF2) is considered. Let us now consider a partition of the time interval [0, T] into N time steps of size \(\delta t\), assumed to be constant. Given a generic time dependent function at a time step \(t^{n+1} = t^n + \delta t\), for \(n=0,1,2,\dots\), the approximation of both the first and the second time derivatives of second order are written using information from already computed time instants and \(f^{n+1}\) which is being computed at this time step according to the following approximation:
Appropriate initializations are required for \(n=1,2\).
For all formulations, the standard Galerkin approximation is considered as follows. Let \(\mathcal {P}_h\) denote a finite element (FE) partition of the domain of study \(\Omega\). The diameter of an element domain \(K \in \mathcal {P}_h\) is denoted by \(h_K\) and the diameter on the FE partition by \(h=\text { max} \lbrace h_K | K \in \mathcal {P}_h \rbrace\). We can now construct conforming FE spaces \(\mathbb {X}_h \subset \mathbb {X}\) being \(\mathbb {X}\) any proper functional space where an unknown solution is well-defined, as well as the corresponding subspace \(\mathbb {X}_{h,0} \subset \mathbb {X}_0\), \(\mathbb {X}_{0}\) being made with functions that vanish on the Dirichlet boundary.
Furthermore, all the formulations used in this work must be stabilized so as to avoid satisfying inf-sup conditions among the unknowns of the problem and to tackle the incompressible limit (see, e.g., Boffi et al. (2013)). The stabilized FE method we propose to use in the following is based on the Variational Multi-Scale (VMS) concept (Hughes et al. 1998; Codina et al. 2017). Let \(\mathbb {X}= \mathbb {X}_h \oplus \tilde{\mathbb {X}}\), where \(\tilde{\mathbb {X}}\) is any space to complete \(\mathbb {X}_h\) in \(\mathbb {X}\). The elements of this space are denoted by \(\tilde{{\textbf {X}}}\) and they are called subgrid scales (SGSs). Likewise, let \(\mathbb {X}_0 = \mathbb {X}_{h,0} \oplus \tilde{\mathbb {X}}_0\). In this work, we consider Orthogonal SubGrid Scales (OSGS), where the SGS space is considered to be orthogonal to the FE space, as it is argued in Codina (2000). Furthermore, a key property of the OSGS stabilization is that, thanks to the projection onto the FE space, we keep the consistency of the formulation in a weak sense in spite of including just the minimum number of terms to stabilize the solution (Moreno et al. 2019, 2020), allowing us to define a term-by-term stabilization technique called Split OSGS (S-OSGS), which is the one we consider in this work.
3 Solid dynamics problem
This section focuses on the analysis and behavior of solid structures that can reach the incompressible limit under dynamic loading conditions. It explores the response of materials and structures. Let us start by summarizing the conservation equations for both linear elasticity and finite strain hyperelasticity in solid dynamics.
3.1 Mixed formulations in linear elasticity
3.1.1 The continuum problem
In this section, the equations of motion of an elastic body under the linear theory of elasticity are considered. Let the solid domain \(\Omega _{\text {s}}(t)\) be an open, bounded and polyhedral domain of \(\mathbb {R}^d\), where d is the number of space dimensions. Any point of the body is labeled with the vector \({\textbf {x}}\). The boundary of the domain is denoted as \(\Gamma _{\text {s}}(t) :=\partial \Omega _{\text {s}}(t)\). We denote as \(\left]0,T\right[\) the time interval of analysis for all problems to be considered. Let \(\mathfrak {D}_{\text {s}}=\left\{ ({\textbf {x}},t) |~{\textbf {x}}\in \Omega _{\text {s}}(t), 0<t<T \right\}\) be the space-time domain where the solid problem is defined.
The continuum problem for solid dynamics, suitable for reaching the incompressible limit, is defined by the following system of equations:
where \({\textbf {u}}_{\text {s}}\) is the displacement field, \({\textbf {s}}_{\text {s}}\) the deviatoric stress field, \(p_{\text {s}}\) the pressure field and \({\textbf {e}}_{\text {s}}\) the deviatoric strain field. Equation (1) is the balance of momentum equation, where \(\rho _{\text {s}}\) is the density field and \(\rho _{\text {s}}{\textbf {b}}\) represents the external load per unit of volume. Here, \(\nabla \cdot (\cdot )\) is the divergence operator and \(\nabla (\cdot )\) is the gradient operator. Equation (2) is the deviatoric constitutive equation, where \(\mathbb {C}^{\text {dev}}\) is the 4th-order deviatoric constitutive tensor, which for isotropic materials is defined as
Here, \(\mathbb {I}\) and \({\textbf {I}}\) are the 4th and 2nd-rank identity tensors, respectively, \(\mathbb {D}\) the 4th-order deviatoric operator and \(\mu _{\text {s}}=\frac{E_{\text {s}}}{2(1+\nu _{\text {s}})}\) the shear modulus, being \(E_{\text {s}}\) the Young modulus and \(\nu _{\text {s}}\) the Poisson ratio. Equation (3) is the volumetric constitutive equation which imposes the incompressibility constraint, where \(\kappa _{\text {s}}=\frac{E_{\text {s}}}{3(1-2\nu _{\text {s}})}\) is the bulk modulus. Finally, Eq. (4) is the deviatoric kinematic equation which relates the deviatoric strain field with the displacement field, where \(\nabla ^{\text {s}}(\cdot )\) denotes the symmetric gradient operator.
A set of boundary conditions is considered which can be split into Dirichlet boundary conditions (5), where prescribed displacements \({\textbf {u}}_{\text {s},D}\) are specified, Neumann boundary conditions (6) where a prescribed value for the tractions \({\textbf {t}}_{\text {s},N}\) are applied, and the transmission conditions on the interface boundary (7), where \({\textbf {t}}_{\text {f}}\) are the tractions coming from the surrounding fluid (the continuity of velocities will be assigned as transmission condition to the flow problem). Vector \({\textbf {n}}_{\text {s}}\) is the geometric unit outward normal vector on the boundary \(\Gamma _{\text {s}}(t)\) and \({\textbf {n}}_{\text {i}}\) the unit normal pointing from the fluid side to the solid one on the interface boundary. The governing equations must be supplied with initial conditions for displacements (8) and velocities (9) in \(\Omega _{\text {s}}(0)\), with \({\textbf {u}}_{\text {s}}^0\) and \({\textbf {v}}_{\text {s}}^0\) given.
Two different mixed formulations are considered in this subsection. On the one hand, the well-known \({\textbf {u}}\text {-}p\) formulation, which is introduced in order to deal with nearly and fully incompressible scenarios (Baiges and Codina 2017). On the other hand, the \({\textbf {u}}\text {-}p\text {-}{\textbf {e}}\) formulation, which includes the \({\textbf {u}}\text {-}p\) formulation to tackle the incompressible limit and introduces deviatoric strains to obtain a higher accuracy in the computation of both stresses and strains (Codina 2009; Chiumenti et al. 2015, 2021). Both formulations are explained in detail in Castañar et al. (2022).
3.1.2 The \({\textbf {u}}\text {-}p\) formulation
The first formulation we consider is the well-known mixed \({\textbf {u}}\text {-}p\) formulation, which is introduced to deal with nearly and fully incompressible materials. The problem consists of finding both a displacement \({\textbf {u}}_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}^d\) and a pressure \(p_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}\) such that
The problem must be supplied with the already-defined boundary and initial conditions.
Let \(\mathbb {U} = \left[ H^1(\Omega _{\text {s}}) \right] ^d\) and \(\mathbb {P} =L^2(\Omega _{\text {s}})\) be, respectively, the proper functional spaces where displacement and pressure solutions are well-defined. We denote by \(\mathbb {U}_0\) functions in \(\mathbb {U}\) which vanish on the Dirichlet boundary \(\Gamma _{\text {s},D}\). We shall be interested also in the spaces \(\mathbb {W} :=\mathbb {U} \times \mathbb {P}\) and \(\mathbb {W}_0 :=\mathbb {U}_0 \times \mathbb {P}\). The variational statement of the problem is derived by testing the system presented in Eqs. (10–11) against arbitrary test functions \(\breve{{\textbf {U}}}_{\text {s}}:=[\breve{{\textbf {u}}}_{\text {s}},\breve{p}_{\text {s}}]^T\), \(\breve{{\textbf {u}}}_{\text {s}}\in \mathbb {U}_0\) and \(\breve{p}_{\text {s}}\in \mathbb {P}\). The weak form of the problem reads: find \({\textbf {U}}_{\text {s}}:=\left[ {\textbf {u}}_{\text {s}}, p_{\text {s}}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}\) such that initial and Dirichlet boundary conditions are satisfied and
where \(\mathcal {A} \left( {\textbf {U}}_{\text {s}}, \breve{{\textbf {U}}}_{\text {s}}\right)\) is a bilinear form defined on \(\mathbb {W} \times \mathbb {W}_0\) as
and \(\mathcal {F} \left( \breve{{\textbf {U}}}_{\text {s}}\right)\) is a linear form defined on \(\mathbb {W}_0\) as
The VMS stabilized \({\textbf {u}}\text {-}p\) formulation of the problem for a discrete Galerkin approximation and with a BDF2 time discretization reads: find \({\textbf {U}}_{\text {s},h}:=\left[ {\textbf {u}}_{\text {s},h}, p_{{\text {s}},h}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}_{h}\) such that initial and Dirichlet boundary conditions are satisfied and
where \(\Pi ^{\bot }_h\) is the \(L^2(\Omega _{\text {s}})\) projection onto the orthogonal FE space and \(\tau _{{\textbf {u}}}\) and \(\tau _p\) are coefficients coming from a Fourier analysis of the problem for the SGSs. In this work, we use the stabilization parameters proposed in Codina (2009) for linear elastic cases
where \(c_1 = 4\) and \(c_2 = 2\) are the algorithmic parameters used in the numerical examples (using linear elements). Note that it is possible to write the formulation in a symmetric form by applying \(\Pi ^{\bot }_h\) also to the operators acting on the test functions.
3.1.3 The \({\textbf {u}}\text {-}p\text {-}{\textbf {e}}\) formulation
In this subsection we present the mixed three-field formulation used to deal with the solid dynamics problem. We introduce the mixed \({\textbf {u}}\text {-}p\text {-}{\textbf {e}}\) problem, which consists of finding a displacement field \({\textbf {u}}_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}^d\), a pressure \(p_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}\) and a deviatoric strain field \({\textbf {e}}_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}^d \otimes \mathbb {R}^d\) such that
The governing equations must be supplied with the already-defined boundary and initial conditions.
Let us consider the same spaces and test functions we have defined previously for the mixed \({\textbf {u}}\text {-}p\) formulation. Let also \(\mathbb {E} = \left[ L^2(\Omega _{\text {s}}) \right] ^{d\times d}\) be the proper functional space where deviatoric strain components are well-defined. We shall be interested also in the spaces \(\mathbb {W} :=\mathbb {U} \times \mathbb {P} \times \mathbb {E}\) and \(\mathbb {W}_0 :=\mathbb {U}_0 \times \mathbb {P} \times \mathbb {E}\). The variational statement of the problem is derived by testing system (12–14) against arbitrary test functions \(\breve{{\textbf {U}}}_{\text {s}}:=\left[ \breve{{\textbf {u}}}_{\text {s}}, \breve{p}_{\text {s}}, \breve{{\textbf {e}}}_{\text {s}}\right] ^T\), \(\breve{{\textbf {e}}}_{\text {s}}\in \mathbb {E}\). The weak form of the problem reads: find \(\normalsize {\textbf {U}}_{\text {s}}:=\left[ {\textbf {u}}_{\text {s}}, p_{\text {s}}, {\textbf {e}}_{\text {s}}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}\) such that initial and Dirichlet boundary conditions are satisfied and
where \(\mathcal {A} \left( {\textbf {U}}_{\text {s}}, \breve{{\textbf {U}}}_{\text {s}}\right)\) is a bilinear form defined on \(\mathbb {W} \times \mathbb {W}_0\) as
and \(\mathcal {F} \left( \breve{{\textbf {U}}}_{\text {s}}\right)\) is the same linear form as the one defined for the \({\textbf {u}}\text {-}p\) formulation. To avoid overloading the notation, we shall always use \(\mathcal {A}\) to denote the form that defines the problem, regardless of the formulation employed.
The VMS stabilized \({\textbf {u}}\text {-}p\text {-}{\textbf {e}}\) formulation of the problem for a discrete Galerkin approximation and with a BDF2 time discretization reads: find \({\textbf {U}}_{\text {s},h}:=\left[ {\textbf {u}}_{\text {s},h}, p_{{\text {s}},h}, {\textbf {e}}_{\text {s},h}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}_{h}\) such that initial and Dirichlet boundary conditions are satisfied and
where \(\tau _{{\textbf {e}}} = c_3\), being \(c_3=0.1\) the algorithmic parameter used in the numerical examples.
3.2 Mixed formulations in finite strain hyperelasticity
In this subsection the equations of motion of an elastic body under the finite strain theory of hyperelasticity are presented in a total Lagrangian formulation framework. We employ the super index zero for quantities acting at the reference configuration. Let \(\Omega _{\text {s}}^0:=\Omega _{\text {s}}\left( 0 \right)\) be the reference configuration of the solid body, whereas the current configuration of the body at time t is denoted by \(\Omega _{\text {s}}\left( t \right)\). The motion is described by a function \(\pmb {\psi }\) which links a material particle \({\textbf {X}}\in \Omega _{\text {s}}^0\) to the spatial configuration \({\textbf {x}}\in \Omega _{\text {s}}\left( t \right)\) according to
The boundary of the reference configuration is denoted as \(\Gamma _{\text {s}}^0:=\partial \Omega _{\text {s}}^0\). The interface boundary with the fluid at the reference configuration is \(\Gamma _{\text {i}}^0:=\Gamma _{\text {i}}(0)\). Let now \(\mathfrak {D}_{\text {s}}=\left\{ ({\textbf {X}},t) |~{\textbf {X}}\in \Omega _{\text {s}}^0, 0<t<T \right\}\) be the space-time domain where the solid problem is defined. All the spatial derivatives are understood to be taken with respect to the material coordinates \({\textbf {X}}\).
We want to deal with compressible materials that can reach the incompressible limit. The governing equations in finite strain hyperelasticity are:
where \({\textbf {S}}^\prime _{\text {s}}\) is the deviatoric second Piola Kirchhoff (PK2) stress tensor and \(p_{\text {s}}\) the pressure field. Equation (15) is the balance of momentum equation, where \({\textbf {F}}_{\text {s}}= \frac{\partial {\textbf {x}}}{\partial {\textbf {X}}}\) is the deformation gradient and \(J_{\text {s}}= \hbox {det}~{\textbf {F}}_{\text {s}}>0\) is the Jacobian of the deformation. Equation (16) is the volumetric constitutive equation, which imposes the incompressibility constraint when \(\kappa _{\text {s}}\rightarrow \infty\), and where \(G_{\text {s}}\) is a function which depends on the volumetric part of the strain energy model. In this work, we select the Simo-Taylor law (Simo et al. 1985), which is defined as
Finally, Eq. (17) is the deviatoric constitutive equation, which allows us to relate the displacement field with the deviatoric PK2 stress tensor through the deviatoric part of the strain energy function \(W_{\text {s}}\). In this work, we restrict ourselves to a neo-Hookean material model (Scovazzi et al. 2016), which is defined as
where \({\textbf {C}}_{\text {s}}={\textbf {F}}^T_{\text {s}}{\textbf {F}}_{\text {s}}\) is the right Cauchy–Green tensor and \(\hbox {tr }{\textbf {C}}_{\text {s}}={\textbf {C}}_{\text {s}}:{\textbf {I}}\) is the trace of \({\textbf {C}}_{\text {s}}\).
With regards to the boundary conditions (18–20), \({\textbf {u}}_{\text {s},D}\) is a prescribed value for the displacements on the Dirichlet boundary, \({\textbf {T}}_{\text {s},N}\) a prescribed value for the tractions on the Neumann boundary and \({\textbf {t}}_{\text {f}}\) are the tractions coming from the fluid on the interface boundary. Note that a pull-back transformation must be applied to fluid tractions \({\textbf {t}}_{\text {f}}\) to apply them on the boundaries at the reference configuration. Vector \({\textbf {N}}_{\text {s}}\) is the geometric unit outward normal vector on the boundary \(\Gamma _{\text {s}}^0\) and \({\textbf {N}}_{\text {i}}\) the unit normal pointing from the fluid side to the solid one on the interface boundary at the reference configuration. The governing equations must be supplied with initial conditions for displacements (21) and velocities (22) in \(\Omega _{\text {s}}^0\), with \({\textbf {u}}_{\text {s}}^0\) and \({\textbf {v}}_{\text {s}}^0\) given.
As for the linear case, two different mixed formulations are considered to manage this problem. On the one hand, the mixed two-field \({\textbf {u}}\text {-}p\) formulation presented in Castañar et al. (2020), in which the addition of the pressure field as an extra primary variable with respect to the classical displacement-based formulation is considered to be able to enforce the incompressibility constraint. On the other hand, a novel mixed three-field \({\textbf {u}}\text {-}p\text {-}{\textbf {S}}^\prime\) formulation which is presented in Castañar et al. (2023), in which the deviatoric PK2 stress tensor is added as unknown of the problem. The final goal is to design a FE technology able to tackle simultaneously problems which may involve incompressible behavior together with a high degree of accuracy of the stress field.
3.2.1 The \({\textbf {u}}\text {-}p\) formulation
The first formulation we consider is the mixed two-field \({\textbf {u}}\text {-}p\) formulation, which is introduced to deal with nearly and fully incompressible materials. The problem consists of finding both a displacement \({\textbf {u}}_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}^d\) and a pressure \(p_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}\) such that
where \({\textbf {S}}^\prime _{\text {s}}\), \({\textbf {F}}_{\text {s}}\), \(J_{\text {s}}\) and \(\frac{dG_{\text {s}}}{dJ_{\text {s}}}\) are functions of the displacement field. The problem must be supplied with the already-defined boundary and initial conditions.
Let \(\mathbb {U}\) and \(\mathbb {P}\) be, respectively, the proper functional spaces where displacement and pressure solutions are well-defined. We denote by \(\mathbb {U}_0\) functions in \(\mathbb {U}\) which vanish on the Dirichlet boundary \(\Gamma _{\text {s},D}^0\). We shall be interested also in the spaces \(\mathbb {W} :=\mathbb {U} \times \mathbb {P}\) and \(\mathbb {W}_0 :=\mathbb {U}_0 \times \mathbb {P}\). The variational statement of the problem is derived by testing the system presented in Eqs. (23–24) against arbitrary test functions \(\breve{{\textbf {U}}}_{\text {s}}:=[\breve{{\textbf {u}}}_{\text {s}},\breve{p}_{\text {s}}]^T\), \(\breve{{\textbf {u}}}_{\text {s}}\in \mathbb {U}_0\) and \(\breve{p}_{\text {s}}\in \mathbb {P}\). The weak form of the problem reads: find \({\textbf {U}}_{\text {s}}:=\left[ {\textbf {u}}_{\text {s}}, p_{\text {s}}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}\) such that initial and Dirichlet boundary conditions are satisfied and
where \(\mathcal {A} \left( {\textbf {U}}_{\text {s}}, \breve{{\textbf {U}}}_{\text {s}}\right)\) is a semi-linear form defined on \(\mathbb {W} \times \mathbb {W}_0\) as
and \(\mathcal {F} \left( \breve{{\textbf {U}}}_{\text {s}}\right)\) is a linear form defined on \(\mathbb {W}_0\) as
In order to solve the problem, the system needs to be linearized, so that a bilinear operator which allows to compute a correction \(\delta {\textbf {U}}_{\text {s}}\) of a given guess for the solution at time \(t^{n+1}\) is obtained, that we denote by \({\textbf {U}}_{\text {s}}\). Iteration counters will be omitted to simplify the notation. After using a Newton-Raphson scheme, we obtain the following linearized form of the problem. Given \({\textbf {U}}_{\text {s}}\) as the solution at time \(t^{n+1}\) and the previous iteration, find a correction \(\delta {\textbf {U}}_{\text {s}}:=\left[ \delta {\textbf {u}}_{\text {s}}, \delta p_{\text {s}}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}_0\) such that
where \(\mathcal {B} \left( \delta {\textbf {U}}_{\text {s}}, \breve{{\textbf {U}}}_{\text {s}}\right)\) is the bilinear form obtained through a Newton–Raphson linearization and it is defined on \(\mathbb {W}_0 \times \mathbb {W}_0\) as
where \(f_{\text {s}}(J_{\text {s}})\) is a function coming from the linearization of \(\frac{dG_{\text {s}}}{dJ_{\text {s}}}\) and \(\mathbb {C}^\prime\) is the deviatoric constitutive tangent matrix; these terms are:
The VMS stabilized \({\textbf {u}}\text {-}p\) formulation of the linearized problem for a discrete Galerkin approximation and with a BDF2 time discretization is given by
where
\(\Pi ^{\bot }_h\) is the \(L^2(\Omega _{\text {s}}^0)\) projection onto the orthogonal FE space and \(\tau _{{\textbf {u}}}\) is defined in Castañar et al. (2020) as
where \(c_1 = 1.0\) is the algorithmic parameter applied in the numerical examples (using linear elements).
3.2.2 The \({\textbf {u}}\text {-}p\text {-}{\textbf {S}}^\prime\) formulation
In this subsection we present the mixed three-field formulation used to deal with the solid dynamics problem. It consists of finding a displacement field \({\textbf {u}}_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}^d\), a pressure \(p_{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}\) and a deviatoric PK2 stress field \({\textbf {S}}^\prime _{\text {s}}:\mathfrak {D}_{\text {s}} \rightarrow \mathbb {R}^d \otimes \mathbb {R}^d\) such that
where \({\textbf {F}}_{\text {s}}\), \(J_{\text {s}}\), \(\frac{dG_{\text {s}}}{dJ_{\text {s}}}\) and \(\frac{\partial W_{\text {s}}}{\partial {\textbf {C}}_{\text {s}}}\) are functions of the displacement field. The problem must be supplied with the already-defined boundary and initial conditions. Note that tensor \({\textbf {S}}^\prime _{\text {s}}\) is in fact not deviatoric, but it comes from the volumetric-deviatoric splitting of the Cauchy stress tensor.
Let us consider the same spaces and test functions we have defined previously for the mixed \({\textbf {u}}\text {-}p\) formulation. Let \(\mathbb {S}\) be the proper functional space where the deviatoric PK2 stress components are well-defined. We shall be interested also in the spaces \(\mathbb {W} :=\mathbb {U} \times \mathbb {P} \times \mathbb {S}\) and \(\mathbb {W}_0 :=\mathbb {U}_0 \times \mathbb {P} \times \mathbb {S}\). The variational statement of the problem is derived by testing system (25–27) against arbitrary test functions \(\breve{{\textbf {U}}}_{\text {s}}:=\left[ \breve{{\textbf {u}}}_{\text {s}}, \breve{p}_{\text {s}}, \breve{{\textbf {{S}}}}^{\prime }\right] ^T\), \(\breve{{\textbf {{S}}}}^{\prime }\in \mathbb {S}\). The weak form of the problem reads: find \({\textbf {U}}_{\text {s}}:=\left[ {\textbf {u}}_{\text {s}}, p_{\text {s}}, {\textbf {S}}^\prime _{\text {s}}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}\) such that initial and Dirichlet boundary conditions are satisfied and
where \(\mathcal {A} \left( {\textbf {U}}_{\text {s}}, \breve{{\textbf {U}}}_{\text {s}}\right)\) is a semi-linear form defined on \(\mathbb {W} \times \mathbb {W}_0\) as
and \(\mathcal {F} \left( \breve{{\textbf {U}}}_{\text {s}}\right)\) is the same linear form as the one defined for the \({\textbf {u}}\text {-}p\) formulation.
After using a Newton–Raphson scheme, we obtain the following linearized form of the problem. Given \({\textbf {U}}_{\text {s}}\) as the solution at time \(t^{n+1}\) and the previous iteration, find a correction \(\delta {\textbf {U}}_{\text {s}}:=\left[ \delta {\textbf {u}}_{\text {s}}, \delta p_{\text {s}}, \delta {\textbf {S}}^\prime _{\text {s}}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}_0\) such that
where \(\mathcal {B} \left( \delta {\textbf {U}}_{\text {s}}, \breve{{\textbf {U}}}_{\text {s}}\right)\) is a bilinear form defined on \(\mathbb {W}_0 \times \mathbb {W}_0\) as
The VMS stabilized \({\textbf {u}}\text {-}p\text {-}{\textbf {S}}^\prime\) formulation of the linearized problem for a discrete Galerkin approximation and with a BDF2 time discretization is given by:
\(\forall\, \breve{{\textbf {U}}}_{\text {s},h}\in \mathbb {W}_{h,0}\), where
and \(\tau _{{\textbf {S}}^\prime } = c_3\) is defined as in Castañar et al. (2023), being \(c_3 = 0.5\) the algorithmic parameter applied in the numerical examples.
4 Fluid flow problem
The next step is to define the governing equations that model the flow problem for an incompressible Newtonian fluid, which is modeled with the well-known Navier–Stokes equations. The approach followed can be understood as the traditional one, where the fluid problem is solved by means of an ALE formulation to cope with the time dependency of the fluid domain.
4.1 ALE formulation of the fluid flow equations
Let \(\Omega _{\text {f}}(t)\) be the domain where the fluid flows, with boundary \(\Gamma _{\text {f}}(t) :=\partial \Omega _{\text {f}}(t)\), where Dirichlet boundary conditions are prescribed on \(\Gamma _{\text {f},D}(t)\) and Neumann conditions on \(\Gamma _{\text {f},N}(t)\). These boundaries may be moving.
Let \({\pmb \chi }_t\) be a family of invertible mappings, which for all \(t\in [0,T]\) map a point \({\textbf {X}}\in \Omega _{\text {f}}(0)\) to a point \({\textbf {x}}= {\pmb \chi }_t({\textbf {X}})\in \Omega _{\text {f}}(t)\), with \({\pmb \chi }_0 = {{\textbf {I}}}\), the identity. If \({\pmb \chi }_t\) is given by the motion of the particles, the resulting formulation would be Lagrangian, whereas if \({\pmb \chi }_t= {{\textbf {I}}}\) for all t, \(\Omega _{\text {f}}(t) = \Omega _{\text {f}}(0)\) and the formulation would be Eulerian. Let now \(t'\in [0,T]\), with \(t'\le t\), and consider the mapping
Let \(\mathfrak {D}_{\text {f}} =\{({\textbf {x}},t)\vert {\textbf {x}}\in \Omega _{\text {f}}(t),~0<t<T\}\) be the space-time domain where the fluid problem is defined. Given a function \(f: \mathfrak {D}_{\text {f}} \longrightarrow {\mathbb R}\) we define
In particular, the domain velocity taking as a reference the coordinates of \(\Omega _{\text {f}}(t')\) is given by
When the flow equations are approximated using the FE method, \({\textbf {v}}_{\text {dom}}\) needs to be computed. It is assumed to be given on the boundary \(\Gamma _{\text {f}}(t)\). To compute the values for the interior of the domain, a mesh equation must be solved. The mesh equation we use is proposed in Chiandussi et al. (1999). The method considers the mesh as a fictitious linear elastic body subjected to prescribed displacements at the selected moving boundaries. The mechanical properties of each mesh element are appropriately selected in order to minimize the deformation and the distortion of the mesh elements. Let us directly show here the system of equations that is solved for a given velocity field in the interface boundary with the solid domain \({\textbf {v}}_{\Gamma _{\text {i}}}\) at time \(t^n\):
where \(\mathbb {C}\left( E_{\text {dom}}\left( {\textbf {x}}\right) ,\nu _{\text {dom}} \right)\) is the constitutive 4th order tensor in linear elasticity, \(E_{\text {dom}}\left( {\textbf {x}}\right)\) is the Young modulus of the mesh and \(\nu _{\text {dom}}\) is the Poisson coefficient of the mesh.
Using the ALE reference, the only modification with respect to the purely Eulerian formulation is to replace the transport velocity \({\textbf {v}}_{\text {f}}\) of the advective term by \({\textbf {v}}_{\text {c}}:={\textbf {v}}_{\text {f}}- {\textbf {v}}_{\text {dom}}\). If \({\textbf {v}}_{\text {dom}}= {{\textbf {0}}}\) we would recover a purely Eulerian formulation for the fluid.
4.2 The continuum problem statement
The equations of the Newtonian incompressible fluid flow assumption are now presented. The continuum Navier–Stokes problem for incompressible Newtonian fluid flows is defined by the following system of equations:
where Eq. (28) is the balance of linear momentum and Eq. (29) the incompressibility constraint. In these equations, \({\textbf {v}}_{\text {f}}\) is the velocity field, \(p_{\text {f}}\) the pressure, \({\textbf {f}}\) the vector of body forces, \(\rho _{\text {f}}\) the density of the fluid and \(\mu _{\text {f}}\) its dynamic viscosity.
With regards to the boundary conditions (30–32), \({\textbf {v}}_{{\text {f}},D}\) is a prescribed value for the velocities on the Dirichlet boundary, \({\textbf {t}}_{\text {f},N}\) the prescribed value for the tractions on the Neumann boundary and \({\textbf {v}}_{\Gamma _{\text {i}}}\) is the velocity field coming from the solid on the interface boundary. The governing equations must be supplied with an initial condition for the velocity field (33) in \(\Omega _{\text {f}}(0)\), with \({\textbf {v}}_{\text {f}}^0\) given.
In this work, the stabilized two-field \({\textbf {v}}\text {-}p\) formulation proposed in Codina (2001) is considered. Details can be found in Codina et al. (2018). Here we just write the resulting numerical formulation.
4.3 The \({\textbf {v}}\text {-}p\) formulation
In this subsection, the well-known mixed \({\textbf {v}}\text {-}p\) formulation is introduced in order to deal with incompressible Newtonian fluid flows. In the presented formulation the velocity field \({\textbf {v}}_{\text {f}}:\mathfrak {D}_{\text {f}} \rightarrow \mathbb {R}^d\) and the pressure field \(p_{\text {f}}:\mathfrak {D}_{\text {f}} \rightarrow \mathbb {R}\) are used as independent variables.
Let \(\mathbb {V} = \left[ H^1(\Omega _{\text {f}}) \right] ^d\) and \(\mathbb {P} =L^2(\Omega _{\text {f}})\) be, respectively, the proper functional spaces where velocity and pressure solutions are well-defined. We denote by \(\mathbb {V}_0\) functions in \(\mathbb {V}\) which vanish on the Dirichlet boundary \(\Gamma _{\text {f},D}\). We shall be interested also in the spaces \(\mathbb {W} :=\mathbb {V} \times \mathbb {P}\) and \(\mathbb {W}_0 :=\mathbb {V}_0 \times \mathbb {P}\). The variational statement of the problem is derived by testing the system presented in Eqs. (28–29) against arbitrary test functions \(\breve{{\textbf {V}}}_{\text {f}}:=[\breve{{\textbf {v}}}_{\text {f}},\breve{p}_{\text {f}}]^T\), \(\breve{{\textbf {v}}}_{\text {f}}\in \mathbb {V}_0\) and \(\breve{p}_{\text {f}}\in \mathbb {P}\). The weak form of the problem reads: find \({\textbf {V}}_{\text {f}}:=\left[ {\textbf {v}}_{\text {f}}, p_{\text {f}}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}\) such that initial and Dirichlet boundary conditions are satisfied and
where, for a fixed \(\hat{{\textbf {v}}}\), \(\mathcal {A} \left( \hat{{\textbf {v}}}; {\textbf {V}}_{\text {f}}, \breve{{\textbf {V}}}_{\text {f}}\right)\) is a bilinear form defined on \(\mathbb {W} \times \mathbb {W}_0\) as
\(\mathcal {F} \left( \breve{{\textbf {V}}}_{\text {f}}\right)\) is a linear form defined on \(\mathbb {W}_0\) as
Note that the Navier–Stokes problem to be solved has one source of nonlinearity, namely, the convective term. For the sake of conciseness, we will consider only a fixed-point iterative scheme. In particular, \(\hat{{\textbf {v}}}\) will be taken as the velocity computed in a previous iteration of a fixed-point scheme.
In this case, we consider the SGSs to be time-dependent; these are solutions of:
where \(\tau _{{\textbf {v}}}\) and \(\tau _p\) are coefficients coming from a Fourier analysis of the problem for the SGSs. In this work, we use the stabilization parameters proposed in Codina et al. (2018) as
where \(\left|{\hat{{\textbf {v}}}_h}\right|\) is the Euclidean norm of the velocity guess and \(c_1=4.0\) and \(c_2=2.0\) are the algorithmic parameters used in the numerical examples using linear elements.
The VMS stabilized \({\textbf {v}}\text {-}p\) formulation of the problem for a discrete Galerkin approximation and with a BDF2 time discretization reads: find \({\textbf {V}}_{\text {f},h}:=\left[ {\textbf {v}}_{{\text {f}},h}, p_{{\text {f}},h}\right] ^T: \left]0,T\right[\rightarrow \mathbb {W}_{h}\) such that initial and Dirichlet boundary conditions are satisfied and
This stabilized ALE formulation for the linear convection-diffusion equation using also BDF2 as time integrator is analyzed in Badia and Codina (2006). Let us also remark that if discontinuous pressure interpolations are used (which is not our case), terms involving SGSs on the element boundaries need to be introduced (Codina et al. 2009).
5 Topology optimization of incompressible structures subject to FSI
5.1 Fluid–structure interaction
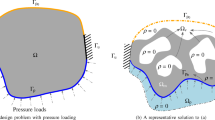
Let \(\Omega (t)\) be the whole domain of the problem, formed by a fluid sub-domain \(\Omega _{\text {f}}(t)\) and a solid one \(\Omega _{\text {s}}(t)\), which will be optimized during the process. These two sub-domains do not overlap, so that \(\bar{\Omega }(t) = \overline{\Omega _{\text {f}}(t) \cup \Omega _{\text {s}}(t)}\) and \(\mathring{\Omega _{\text {f}}}(t) \cap \mathring{\Omega _{\text {s}}}(t)= \emptyset\). Recall that the sub-domains have their own boundaries \(\Gamma _{\text {f}}(t)\) and \(\Gamma _{\text {s}}(t)\), and the interface between them is \(\Gamma _{\text {i}}(t)\). Its unit normal with respect to the spatial configuration is denoted as \({\textbf {n}}_{\text{ i }}\), pointing from the fluid side to the solid one. We also define \(\Gamma _{\text {s}}^0\) as the solid boundary in the reference configuration and its unit normal with respect to the material configuration is denoted by \({\textbf {N}}_{\text {i}}\).
In this work, a classical block-iterative coupling is considered, in which the solid and the fluid problems are solved sequentially with a strong coupling. A Dirichlet-Neumann coupling is considered: the solid is solved with the loads computed from the fluid in a given iteration and then the fluid is computed with the velocities on the interface obtained from the solid. To enhance the convergence rate of the coupled solvers, an Aitken relaxation scheme is implemented. By accelerating the convergence, it reduces the number of iterations required to reach a desired level of accuracy, thereby reducing computational time and resources. This is particularly beneficial for complex FSI problems that involve large-scale simulations or real-time applications (Küttler and Wall 2008; Codina et al. 2023). Obviously, other iteration-by-subdomain schemes could be used, as those proposed in Codina and Baiges (2011) emanating from the concept of boundary SGSs.
5.2 Topology optimization of incompressible structures
In the following, the TO problem is summarized under the assumption of both linear elastic and finite strain hyperelastic isotropic materials. As we are considering a total Lagrangian formulation framework when dealing with finite strain theory, let us use the material coordinates \({\textbf {X}}\) and work in the reference configuration for the solid. Obviously, in the linear elastic case we can consider both configurations due to the fact that they are supposed to be very close to each other.
One common objective in TO is minimizing the total potential energy of a structure. The total potential energy is a measure of the internal energy stored within the solid, which is directly related to its stiffness and deformation behavior. By minimizing the potential energy, engineers can design structures that are lightweight yet strong, leading to improved performance and efficiency. In addition to minimizing the potential energy, TO often incorporates volume constraints. These constraints ensure that the resulting optimized design does not exceed a certain volume or mass limit, which is often dictated by practical considerations, such as manufacturing capabilities or weight restrictions. By imposing volume constraints, engineers can ensure that the optimized design remains feasible and practical for real-world applications.
The description of the topology is determined by a characteristic function defined as
where the solid domain at the reference configuration \(\Omega _{\text {s}}^0\) is split into two parts. The sub-domains \(\Omega _{\text {str}}\) and \(\Omega _{\text {wea}}\) are made of different materials. The characteristic function is in charge of determining in the whole domain \(\Omega _{\text {s}}^0\) what part corresponds to either material. Such kind of problems are typically termed bi-material TO problems. The material corresponding to the domain \(\Omega _{\text {wea}}\) exhibits a very small stiffness, approximating the absence of material. The material parameters of the strong domain \(\Omega _{\text {str}}\) are denoted by \(\rho _{\text {str}}\), \(E_{\text {str}}\) and \(\nu _{\text {str}}\), and the parameters of the weak domain \(\Omega _{\text {wea}}\) are taken as \(\rho _{\text {wea}}=\gamma \rho _{\text {str}}\), \(E_{\text {wea}} = \gamma E_{\text {str}}\), and thus \(\gamma\) stands for the jump of density and stiffness. Note that \(\gamma > 0\) is a parameter, small enough to model void regions and large enough to entail invertibility properties to the stiffness matrix. To simplify the problem in the void region, we take the fictitious material there as compressible, i.e., \(\nu _{\text {wea}} < 0.5\). This is especially important if the optimization process leads to confined regions of fictitious material, if the material was incompressible there, significant loading could occur in the fictitious region, which would lead to incorrect results (see Castañar et al. (2022)).
The TO problem is then formulated as the minimization of the total potential energy functional subjected to the material allowed, which is written as follows
where \(\Psi _{\text {s}}= W_{\text {s}}+ \kappa _{\text {s}}G_{\text {s}}\) is the strain energy function and \(\mathbb {X}_L\) is the feasible domain restricted to a volume constraint denoted as a fraction \(0<L<1\) of the domain \(\Omega _{\text {s}}^0\).
Several approaches exist to solve the TO problem (34) for elastic materials. In this work we apply the Topological Derivative (TD) concept (Novotny et al. 2019) together with a level-set approach in order to advance to the optimal topology. The TD is a measurement of the sensitivity of a given functional with respect to the apparition of an infinitesimal inclusion in a given point of the domain of interest.
In the linear elastic case, the TD of this functional at a point \({\textbf {X}}\) suitable to reach the incompressible limit can be formally computed according to Castañar et al. (2022) as
where \(\mathbb {P}^{\text {dev}}\) and \(\text {P}^{\text {vol}}\) are the deviatoric polarization tensor and the volumetric polarization coefficient, which are defined in Castañar et al. (2022).
Unfortunately, there is no way to obtain an analytical expression for the TD for finite strain hyperelastic materials. However, an approximation can be found in Pereira and Bittencourt (2008, 2010). In this set of works, the topological sensitivity analysis is applied to finite strain deformation based on the total Lagrangian formulation framework. The numerical study of the asymptotic behavior of the function \(\mathcal {D}_T\mathcal {J} \left( \chi , {\textbf {X}} \right)\) with relation to the radius of the hole is developed. It is concluded that the TD of this functional at a point \({\textbf {X}}\) can be approximated by
which is nevertheless expected to be a minimization direction.
Remark 5.1
Let us discuss some important aspects about the TD approximation we are using when the infinitesimal strain assumption is considered. In such case, the TD approximation is written as
where \(\pmb {\varepsilon }_{\text {s}}\) is the infinitesimal strain tensor and \(\pmb {\sigma }_{\text {s}}\) the Cauchy stress tensor. By comparing this approximation with the analytical TD obtained for linear elastic materials given in Lopes et al. (2015) it is seen that these two equations match, if and only if, the polarization tensor \(\mathbb {P}\) reduces to the 4th-order identity tensor \(\mathbb {I}\) (up to constant values, which do not affect the direction of the TD). This only happens when \(\nu _{\text {s}}=0.25\). Therefore, the TD approximation only matches the exact one when \(\nu _{\text {s}}=0.25\), being just an approximation otherwise. Also in the context of linear elasticity, this approximate TD is justified in Oliver et al. (2019) using the concept of relaxed TD. A comparison of this and other approaches can be found in Yago et al. (2022).
We can now define a signed TD such that
Let us now introduce the signed TD interpretation. For a given topology, computing the TD allows one to know, for each given material point, how the cost functional would change if the material switches. Once the optimal value for the characteristic function \(\chi \left( {\textbf {X}}\right)\) is reached, the following condition holds
Note that at the interface \(\overline{\Omega _{\text {str}}}\cap \overline{\Omega _{\text {wea}}}\), the TD presents a jump, but the signed TD is continuous. Equation (37) allows one to construct a level set function, which will implicitly characterize \(\Omega _{\text {str}}\) and \(\Omega _{\text {wea}}\). This level set function is defined as
where \(\lambda \in \mathbb {R}\) is a scalar, responsible for ensuring that the volume restriction in Eq. (34) is fulfilled. The level-set function also allows us to characterize the description of the topology:
Furthermore, the level-set function allows us to keep a sharp interface between materials when \(\psi \left( \chi , {\textbf {X}}\right) = 0\). The scalar \(\lambda\) can be computed by enforcing
where H is the Heaviside step function. From Eq. (38), it can be observed that for the solution of Eq. (34) there holds
We can perform the TO procedure according to the flowchart in Fig 1 (see Baiges et al. (2019) and Castañar et al. (2022)) to see further details on the TO procedure). Let us comment some details about this flowchart.
Topology optimization algorithm flowchart
Initially, the level set function \(\psi\) is defined with unit initial value, which means that we consider the structure to be composed of strong material everywhere. Obviously, this first approach does not fulfill the volume constraint. We thus take
Let \(\psi ^{i-1}\) be a known level set, where the superscript indicates the TO iteration counter. From this level set value, a characteristic function can be built
which allows one to solve the solid dynamics problem and compute the signed TD. This is independent from the use of any formulation. For convergence aspects, the algorithm also requires an intermediate function \(\phi ^i \left( \chi ^i, {\textbf {X}}\right)\). This function is initially defined as the projection onto the FE space of the normalized TD in order to bound the level-set function with a relaxation scheme introduced as the iterative process advances, i.e.,
The relaxation parameter \(\kappa ^i\) is computed according to Baiges et al. (2019), and \(\Pi _h\) indicates a projection onto the FE space. In the numerical examples, \(\Pi _h\) is computed by using a lumped mass matrix approach for computational efficiency. This approach plays the role of standard filtering in TO. Finally, the level set function at the current iteration is defined as
where \(\lambda ^i\) is computed by using the secant method to solve the volume constraint equation at iteration i:
As a stopping criterion we consider the evolution of the objective functional. The algorithm concludes if the functional has not decreased more than a given minimum during a maximum number of iterations. Also, a maximum number of total iterations to be performed is set.
To determine \(\kappa ^i\), a spatial oscillation indicator is computed:
Note that \(\xi ^i \left( \chi ^i, {\textbf {X}}\right) = 1\) if the iterative algorithm for computing the TD is advancing monotonically in the preceding iterations and \(\xi ^i \left( \chi ^i, {\textbf {X}}\right) = -1\) otherwise. This indicator allows one to detect if there are oscillations in the iterative process. If there are oscillations, the value for \(\kappa ^i\) needs to be decreased, otherwise it can be increased up to a maximum of 1. An intermediate function \(\mu ^i \left( \chi ^i, {\textbf {X}}\right)\) is introduced as
Since \(\xi ^i \left( \chi ^i, {\textbf {X}}\right)\) is a spatial function, the information on the oscillations needs to be averaged, so that a scalar value for \(\kappa ^i\) can be obtained; this is done as follows:
where \(k_1 \ge 1\), \(k_2 \le 1\) and \(k_3 \le 1\) are algorithmic parameters. In the numerical examples to be presented, \(k_1 = 1.1\), \(k_2 = 0.5\) and \(k_3 = 0.1\) are used.
5.3 Algorithm for the topology optimization of incompressible structures subject to FSI
The sequence of the individual steps is shown in Algorithm 1. Let us explain in detail the proposed strategy.
The main goal of the proposed methodology is to obtain optimized incompressible structures which are subjected to FSI loads. In this sense, we need to specify both a delay for the TO to start, \(n_{\text {del}}\), and a time window \(N_\text {w}\), which will take into account the number of steps to do a TO iteration. Obviously, the selection of this time window is not simple, and it depends upon the FSI problem. For real transient FSI problems, the problem is supposed to be statistically stationary, i.e., some statistics such as the mean or the standard deviation, remain constant (Hughes et al. 2001; Codina et al. 2010; Colomes et al. 2015). In this work, as a first approximation, a fixed value for the time window is imposed during the whole procedure.
The following ingredient is to compute an additive TD for all the steps along the time window. In each time step, we iterate until convergence of the block-iterative FSI method. Once a converged solution is obtained, we can compute the TD associated with the solid converged state according to Eq. (35) for linear elastic materials or to Eq. (36) for hyperelastic ones. The idea is to sum the contributions for all the time steps inside the time window. To do so, a simple additive function is defined as
where \(n_\text {w}\) is the time window counter. Once the time window is achieved, \(n_\text {w}=N_\text {w}\), a single TO step is performed for the solid domain with the additive TD according with the flowchart presented in Fig. 1. The counter of steps and the additive TD are reset to zero.
An important aspect to mention is that “dry” TO is performed. This means that only the interior of the structure is optimized, whereas the interface boundary remains constant along the problem. To do so, we split the solid domain \(\Omega _{\text {s}}^0\) into two sub-domains, \(\Omega _{\text {var}}\) and \(\Omega _{\text {fix}}\). The former contains the interior of the structure and it is allowed to be optimized during the TO procedure, the latter contains the external layer of the structure in contact with the fluid and is fixed as strong material during the whole TO procedure.
TO of incompressible structures subject to FSI
6 Numerical examples
In this section, three numerical examples are presented to assess the performance of the proposed methodology to perform TO of incompressible structures subject to FSI. All numerical examples have been implemented in our in-house code FEMUSS, a multiphysics platform implemented in object oriented Fortran 2008. In the first one, a flow through a channel with a flexible wall is considered to study a stationary solution. The main idea is to analyze the differences between mixed formulations when considering either linear elastic structures or hyperelastic ones. Next, so as to examine the effect of transient FSI solutions, the well-known Turek’s test FSI2 is presented. In this case, the behavior of a laminar channel flow around an elastic object is studied when several volume fractions are considered for the optimized structure. To end up, a three-dimensional case with an incompressible flexible plate in a channel flow is considered.
On the one hand, for the fluid sub-problem we select the S-OSGS method with time-dependent SGSs. A maximum of 10 iterations is set, and the numerical tolerance in the \(L^2 \left( \Omega _{\text {f}}\right)\) norm is \(10^{-5}\). On the other hand, for the solid sub-problem the stabilization technique is also selected to be the S-OSGS method. A maximum of 10 iterations is set, and the numerical tolerance in the \(L^2 \left( \Omega _{\text {s}}^0\right)\) norm is \(10^{-5}\).
In order to solve the monolithic system of linear equations for each sub-problem, we use the Biconjugate Gradients solver, BiCGstab (Van der Vorst 1992), which is already implemented in the PETSc parallel solver library (Balay et al. 2015).
Concerning the iterative scheme, a strong-coupling staggered approach is considered, as previously mentioned. For the transmission conditions on the interface boundary \(\Gamma _{\text {i}}\), the relative tolerance is set to \(10^{-3}\). For the mapping between domains, the aforementioned ALE formulation is applied in the fluid domain, together with the Total Lagrangian approach for the solid mechanics problem
With regards to the TO parameters, the weak material is considered to be compressible, with \(\nu _{\text {wea}}=0.4\). The mixed formulation for the solid is used in this region even if it is not strictly required to avoid switching formulations and changing the number of total unknowns during the simulation. The jump of stiffness \(\gamma\) is fixed to \(10^{-2}\). As a stopping criterion for the TO algorithm, we impose a relative tolerance for the objective functional \(\text {tol} = 10^{-3}\), unless otherwise specified. The volume fraction is reduced at once except where otherwise stated. In all presented figures, only the positive part of the level set is plotted, therefore only the strong material part is shown. The rest is filled of weak material elements, and thus interpreted as the void region.
6.1 Beam in a channel flow
In this first problem, we seek to determine the optimal topology of a structure immersed in a channel flow. This example is very similar to the one presented in Jenkins and Maute (2015) and Li et al. (2022). The problem presented here has a fixed interface boundary between the fluid flow and the structure. Therefore, we optimize the interior of the solid. The geometry of the problem is shown in Fig. 2
Beam in a channel flow. Geometry
Regarding the channel measures, the rigid channel has height \(H=1\ \text {m}\). The flexible wall is located at 2H from the channel entrance. The length of the whole channel is \(L=5\ \text {m}\). The structure bar has length \(l = 0.1\) m and height \(h = 0.5\) m. The solid domain \(\Omega _{\text {s}}^0\) is divided into two subdomains \(\Omega _{\text {var}}\) and \(\Omega _{\text {fix}}\). The former contains the interior of the structure and it is allowed to be optimized during the TO procedure, the latter contains the external layer of the structure of width \(r = 0.01\) m which is in contact with the fluid and is fixed as strong material during the whole TO procedure.
Regarding the properties of the fluid, the density is \(\rho_{\text{f}}=1\) \({\text {kg}}/\text {m}^3\) and the dynamic viscosity is \(\mu _{\text {f}}=1\ {\text {Pa}}\, \text {s}\). For the elastic plate the properties are as follows: an initial density \(\rho _{\text {s}}^0=1\ {\text {kg}}/\text {m}^3\), a Young’s modulus \(E_{\text {s}}=40\ \text {kPa}\) and a Poisson’s ratio \(\nu _{\text {s}}=0.5\). A plane strain assumption is considered. A final volume of 50% of the initial one is stated as a volume restriction for \(\Omega _{\text {var}}\).
Concerning the boundary conditions, in the inlet boundary of the fluid domain \(\Gamma _{\text {in}}\), a steady Poiseuille flow with average velocity \(\bar{v}_{\text {in}}\) is assumed, given by
On the walls \(\Gamma _{\text {wall}}\), no-slip boundary conditions are imposed, and in the outlet \(\Gamma _{\text {out}}\), the pressure is set to \(p_{\text {out}}=0\) Pa. A rectangular plate is considered as the solid domain, and it is clamped at the bottom side.
The domains are discretized using \(P_1\) (linear) elements for both fluid and solid domains. Regarding the distribution of the elements, both meshes are unstructured. In total, the fluid mesh is formed by 12,446 elements, and the solid mesh by 12,720 elements as it is shown in Fig 3.
Beam in a channel flow. Mesh domains
Beam in a channel flow. Distribution of the velocity field (top) and pressure (bottom) in the fluid domain with average velocity \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\). Velocities are plotted using their Euclidean norm
To start the problem, a smooth increase of the velocity profile in time is prescribed, given by
We select the time step \(\delta t=0.005\) s. During the first 2.5 s, we let the FSI problem run without performing any TO iteration. To do so, we impose a delay in the TO procedure of \(n_{\text {del}}=500\). At this moment, the problem has already converged to a stationary solution. From this point on, we select a time window of \(N_\text {w}=50\), so that \(N_\text {w}{\delta t}= 0.25\) s, to store the additive TD and perform a TO iteration. We continue the same procedure until a converged optimized solution is obtained for the structure.
First of all, let us consider the case \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\), which results in a fluid flow with Reynolds number \({\text {Re}}=1\). For this case, the final stationary FSI solution is supposed to produce very small strains in the structure, which can be approximated with the infinitesimal strain theory. Let us start by showing the final stationary solution for the fluid domain once the optimized structure has been obtained for a linear elastic material. Both velocity and pressure fields in the channel are depicted in Fig. 4.
Beam in a channel flow. Distribution of the displacement field (left), pressure (middle), and deviatoric strain field (right) in the linear elastic incompressible beam with \({\textbf {u}}\text {-}p\) formulation and with average velocity \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\). Displacements and deviatoric strains are plotted using their Euclidean norm
Beam in a channel flow. Distribution of the displacement field (left), pressure (middle), and deviatoric strain field (right) in the linear elastic incompressible beam with \({\textbf {u}}\text {-}p\text {-}{\textbf {e}}\) formulation and with average velocity \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\). Displacements and deviatoric strains are plotted using their Euclidean norm
We consider the two different formulations presented in Sect. 3.1 for the structure. In Fig. 5 the final optimized solution with the \({\textbf {u}}\text {-}p\) formulation is shown, whereas in Fig. 6 the one obtained for the three-field \({\textbf {u}}\text {-}p\text {-}{\textbf {e}}\) formulation is presented. Both solutions display different features, although they are supposed to converge to the same one with finer meshes. We refer the readers to Castañar et al. (2023) for an in-depth comparison of the accuracy and performance of both formulations.
Let us consider now a hyperelastic material. The solution of the channel flow is very similar as the one obtained for the linear elastic case. Again, the two different formulations presented in Sect. 3.2 are applied. Figure 7 presents the final solution obtained with the two-field \({\textbf {u}}\text {-}p\) formulation and Fig. 8 displays the solution for the \({\textbf {u}}\text {-}p\text {-}{\textbf {S}}^\prime\) formulation. Again quite different solutions are obtained due to the nonlinearities of the problem, the iterative TO algorithm and the coarse mesh of the solid domain that we are considering.
Beam in a channel flow. Distribution of the displacement field (left), pressure (middle), and deviatoric PK2 stress field (right) in the hyperelastic incompressible beam with \({\textbf {u}}\text {-}p\) formulation and with average velocity \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\). Displacements and deviatoric stresses are plotted using their Euclidean norm
Beam in a channel flow. Distribution of the displacement field (left), pressure (middle), and deviatoric PK2 stress field (right) in the hyperelastic incompressible beam with \({\textbf {u}}\text {-}p\text {-}{\textbf {S}}^\prime\) formulation and with average velocity \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\). Displacements and deviatoric stresses are plotted using their Euclidean norm
For the sake of completeness, Table 1 shows the forces exerted by the fluid flow on the whole submerged beam structure and the displacement at point A for the different cases we have studied. As it was expected, all cases display the same final properties due to the fact that infinitesimal strain theory can be considered.
Finally, in Fig. 9 the total potential energy is plotted against the TO iterations during the whole procedure for all the formulations considered. As expected, all formulations are decreasing the objective functional during the TO iterations until a minimum is achieved. Due to the high accuracy of strains and stresses that are obtained using the three-field formulations, we can see different values for the total potential energy. Obviously, this difference is expected to be reduced while refining the solid mesh.
Beam in a channel flow. Convergence diagrams for all formulations with average velocity \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\). LE states for a linear elastic material and HE for a hyperelastic one
Beam in a channel flow. Distribution of the velocity field (top) and pressure (bottom) in the fluid domain with average velocity \(\bar{v}_{\text {in}}=10\ \text {m}/\text {s}\). Velocities are plotted using their Euclidean norm
Let us now consider a case which involves finite strains. To do so, we increment the average velocity to \(\bar{v}_{\text {in}}=10\ \text {m}/\text {s}\), which results in a fluid flow with Reynolds number \({\text {Re}}=10\). To perform this study we employ only the \({\textbf {u}}\text {-}p\) formulation for both linear elastic and hyperelastic materials. Figure 10 shows the solution for the fluid domain which is quite similar in both cases. Figures 11 and 12 show the final optimized structure for a linear elastic material and for a hyperelastic one, respectively. In this case, we can observe that strains are not infinitesimal anymore.
Beam in a channel flow. Distribution of the displacement field (left), pressure (middle), and infinitesimal strain tensor field (right) in the linear elastic incompressible beam with \({\textbf {u}}\text {-}p\) formulation and with average velocity \(\bar{v}_{\text {in}}=10\ \text {m}/\text {s}\). Displacements and strains are plotted using their Euclidean norm
Beam in a channel flow. Distribution of the displacement field (left), pressure (middle), and Green Lagrange strain tensor field (right) in the hyperelastic incompressible beam with \({\textbf {u}}\text {-}p\) formulation and with average velocity \(\bar{v}_{\text {in}}=10\ \text {m}/\text {s}\). Displacements and strains are plotted using their Euclidean norm
To show that the linear elastic theory hypothesis is not suitable in this case, Table 2 shows the fluid forces on the beam interface and the displacement at point A. As it can be clearly seen, quite different solutions are obtained between the linear elastic model and the finite strain hyperelastic one. This example clearly shows that even in stationary FSI problems, the linear theory of elasticity must be considered only when very small strains (smaller than \(10^{-3}\), typically) are produced in the structure. From the conceptual point of view, in this case there is no physical interaction, as the solid configuration does not change and thus the solid does not affect the fluid dynamics.
6.2 Turek’s test
In this second case, we study the TO of an incompressible hyperelastic structure subject to FSI with a laminar flow. This case derives from the well-known benchmark in FSI used by many authors (Turek and Hron 2007). The configuration consists of a laminar channel flow around an elastic object which results in self-induced oscillations of the structure.
The geometry of the problem is displayed in Fig. 13. The rigid channel has height \(H = 0.41\) m and length \(L=2.5\) m. The circle center is positioned at point \(C = (0.2,0.2)\) m (measured from the left bottom corner of the channel) and its radius is \(r = 0.05\) m. The solid bar has a length \(l = 0.35\) m and a height \(h = 0.02\) m. The right bottom corner is positioned at (0.6, 0.19) m, and the left end is fully attached to the fixed cylinder. The solid domain \(\Omega _{\text {s}}^0\) is divided into two subdomains \(\Omega _{\text {var}}\) and \(\Omega _{\text {fix}}\). The former contains the interior of the structure and it is allowed to be optimized during the TO procedure, the latter contains the external layer of the structure of width \(d = 0.001\) m, which is in contact with the fluid and is fixed as strong material during the whole TO procedure.
Turek’s test. Geometry
With regards to boundary conditions, a parabolic profile is prescribed at the left channel inflow, given by
such that the mean inflow velocity is \(\bar{v}_{\text {in}}\) and the maximum of the inflow velocity profile is \(1.5 \bar{v}_{\text {in}}\). A smooth increase of the velocity profile in time is prescribed, given by
The outflow condition is considered stress free. Finally, a no-slip condition is prescribed for the fluid on the other boundary parts. Concerning the boundary conditions of the structure, fixed null displacement is considered at the left edge.
The main goal of this example is to perform a TO procedure of a transient FSI solution. Therefore, the FSI2 parameter settings are taken from the benchmark. The mean flow velocity is fixed to \(\bar{v}_{\text {in}}=1\ \text {m}/\text {s}\). Regarding the properties of the fluid, the density is \(\rho_{\text{f}}=1000\) \({\text {kg}}/\text {m}^3\) and the dynamic viscosity is \(\mu _{\text {f}}=1\ {\text {Pa}}\, \text {s}\). This results in a flow with Reynolds number \({\text {Re}}=100\). For the incompressible elastic plate the properties are as follows: an initial density \(\rho _{\text {s}}^0=10{,}000 \ {\text {kg}}/\text {m}^3\), a Young’s modulus \(E_{\text {s}}=14\ \text {kPa}\) and a Poisson’s ratio \(\nu _{\text {s}}=0.5\). The plane strain assumption is considered.
The domains are discretized using \(P_1\) (linear) elements for both sub-domains. Regarding the distribution of the elements in the fluid domain, the mesh is finer around the cylinder and the bar, while downstream the mesh is coarser. In total, the fluid mesh is formed by 13,537 unstructured elements, and the solid mesh by 15,608 unstructured elements equally distributed over the bar as it can be observed in Fig. 14
Turek’s test. Mesh domains
We select the time step \(\delta t=0.005\) s. During the first 12 s, we let the FSI problem run without performing any TO iteration. This is the time needed to arrive to a periodic solution. To do so, we impose a delay in the TO procedure of \(n_{\text {del}}=2400\). From this point on, we select a time window of \(N_\text {w}=50\), so that \(N_\text {w}{\delta t}= 0.25\) s, to store the additive TD and perform a TO iteration. This time is very close to the period in the case without TO. We continue the same procedure until a converged optimized solution is obtained for the structure. For this example, only the \({\textbf {u}}\text {-}p\) formulation is considered.
To show the effect of the TO procedure in a transient FSI problem, we select several volume fractions, ranging from 90 to 70%. Let us first impose a final volume of 90% of the initial one. Figure 15 shows both the velocity and the pressure fields at different times of the final transient solution. The final optimized structure is depicted in Fig. 16. As expected, all the extracted material is taken from the right edge of the beam. Next, we select a final volume of 80% of the initial one. Figures 17 and 18 display both the final solutions for the fluid domain and the optimized solid structure at different times, respectively. In this case, oscillations decrease compared to the ones presented in the first case. This reduction is clearly explained due to the loss of mass in the structure. Finally, we impose a final volume of 70% of the initial one. In this case, an almost stationary solution is achieved as it can be seen in Figs. 19 and 20. From this study, we can draw the conclusion that TO optimization cannot only be used for reducing material volumes while minimizing an objective function, but to modify transient solutions in time by changing oscillations in some coupled problems.
Turek’s test. Distribution of the velocity field (left) and pressure (right) in the fluid domain with 90% of final volume at several times. Velocities are plotted using their Euclidean norm
Turek’s test. Distribution of the displacement field (left) and pressure (right) in the solid domain with 90% of final volume at several times. Displacements are plotted using their Euclidean norm
Turek’s test. Distribution of the velocity field (left) and pressure (right) in the fluid domain with 80% of final volume at several times. Velocities are plotted using their Euclidean norm
Turek’s test. Distribution of the displacement field (left) and pressure (right) in the solid domain with 80% of final volume at several times. Displacements are plotted using their Euclidean norm
Turek’s test. Distribution of the velocity field (top) and pressure (bottom) in the fluid domain with 70% of final volume. Velocities are plotted using their Euclidean norm
Turek’s test. Distribution of the displacement field (top) and pressure (bottom) in the solid domain with 70% of final volume. Displacements are plotted using their Euclidean norm
To show clearly the effects that are exposed in the previous paragraph, both forces exerted by the fluid in the whole submerged body (cylinder plus beam) and displacement at point A are plotted in Fig. 21 for all volume fractions considered. All volume fractions arrive with the same oscillations at time \(t=12\) s. At this point each one decreases to the final volume fraction required. As it can be seen, drag and lift are decreasing while decreasing the final volume fraction and therefore, the displacement at point A is also decreasing. For the case of 70% of the final volume, we can see that all figures end with a stationary solution.
Turek’s test. Displacement at point A and forces exerted by the fluid on the whole submerged body
To end this example, in Fig. 22 the evolution of the total potential energy for the three cases along TO iterations is shown. As it is expected, the functional decreases for the three cases until a point in which we consider that a minimum is achieved. It is worth to mention that in the 70% case, the stationary solution means that almost no forces are done by the fluid flow to the solid, and this is the reason why the energy is almost 0. Let us also point out that some oscillations appear in the 90% case due to the fact that the compliance in this case depends also upon time. If we want to remove this effect, a higher time window for the TO iterations should be considered.
Turek’s test. Convergence diagram for all the volume fractions studied
6.3 Flexible plate in a channel flow
As a final example we study the optimization of the internal structural layout of a three-dimensional test case which exhibits high nonlinearities and a final stationary FSI solution. The problem geometry is depicted in Fig. 23. A plate of length \(l=0.07\) m, width \(w=0.6\) m and height \(h=0.35\) m is mounted at the bottom of a channel. The plate is located at \(L_1=0.49\) m from the channel entrance. The channel is a cuboid-shaped domain of length \(L=1.5\) m, width \(W=1.2\) m and height \(H=0.6\) m. The solid domain \(\Omega _{\text {s}}^0\) is divided into two subdomains \(\Omega _{\text {var}}\) and \(\Omega _{\text {fix}}\). The former contains the interior of the structure and it is allowed to be optimized during the TO procedure, the latter contains the external layer of the structure of width \(r = 0.007\) m which is in contact with the fluid and is fixed as strong material the whole TO procedure.
Flexible plate in a channel flow. Geometry
A parabolic profile for the velocity at the channel inlet face is prescribed, given by
where the maximum velocity is \(\bar{v}_{\text {max}}=1\ \text {m}/\text {s}\) and it is varied by a temporal factor
The time \(t= 0.1\) s denotes the final time of the excitation phase. Therefore, the flow entering the domain excites the structural flap to initially bend and deform. No-slip wall boundary conditions at the four sides perpendicular to the inlet prevent the flow to escape. A stress-free condition is applied on the outlet boundary. The bottom face of the flexible plate is considered clamped.
The material properties are chosen as follows: the flow is assumed incompressible with dynamic viscosity \(\mu _{\text {f}}=0.01 \ {\text {Pa}}\, \text {s}\) and a density \(\rho _{\text {f}}=1\) \({\text {kg}}/\text {m}^3\). Based on the maximum inflow velocity and the width of the flap, the Reynolds number \({\text {Re}}\) ranges from 0 to 60. The structure is assigned a Young’s modulus \(E_{\text {s}}= 3000\) Pa, a Poisson’s ratio \(\nu _{\text {s}}=0.5\) and an initial density \(\rho _{\text {s}}^0=250 \, {\text {kg}}/\text {m}^3\), for which finite and dynamic deformations are expected. A final volume of 60% of the initial one is fixed as a volume restriction for \(\Omega _{\text {var}}\).
The domains are discretized using tetrahedral elements for both fluid and solid domains. Regarding the distribution of the elements, both meshes are unstructured and with smaller elements concentrated on the interface boundary. In total, the fluid mesh is formed by 140, 600 elements, and the solid mesh by 660, 000 elements.
We select the time step \(\delta t=0.001\) s. During the first 0.6 s, we let the FSI problem run without performing any TO iteration. To do so, we impose a delay in the TO procedure of \(n_{\text {del}}=600\). At this moment, the problem converges to a stationary solution. From this point on, we select a time window of \(N_\text {w}=50\), so that \(N_\text {w}{\delta t}= 0.05\) s, to store the additive TD and perform a TO iteration. We continue the same procedure until a converged optimized solution is obtained for the structure. For this example, only the \({\textbf {u}}\text {-}p\) formulation is considered.
Flexible plate in a channel flow. Final stationary solution
First of all, let us show the final stationary FSI solution in Fig. 24. As explained before, “dry” TO is performed and therefore the boundary of the solid which is in contact with the fluid flow remains constant. It is important to mention that strains of the order of \(10^{-1}\) are obtained, which means that the infinitesimal strain theory is not suitable in this case and finite strain theory fits better with the kind of problem that we are modeling. Both velocity and pressure fields in the channel flow from different points of view are depicted in Fig. 25.
Flexible plate in a channel flow. Distribution of the velocity field (left) and pressure (right) in the fluid domain. Velocities are plotted using their Euclidean norm
Flexible plate in a channel flow. Distribution of the displacement field (top) and pressure (bottom) in the final optimized structures. Displacements are plotted using their Euclidean norm
Let us move now to the solid domain. Figure 26 displays the final optimized incompressible structure once a stationary solution is achieved and the objective function is not decreasing anymore (according to the tolerance). To show the interior of the solid, which is the one which is optimized, a cut of the middle of the structure is depicted from different viewpoints and the fixed part and the empty region are shown in gray. For the sake of completeness, in Fig. 27 the evolution of both the total potential energy and the volume fraction during the TO iterations is shown. As expected, the objective function increases while we start decreasing the volume fraction progressively, just to avoid numerical problems due to the highly nonlinear behavior of the whole problem. Once the volume fraction of 60% is fixed, the objective function starts decreasing until a minimum is obtained and, therefore, the problem is ended.
Flexible plate in a channel flow. Convergence curves
7 Conclusions
In this work, a TO algorithm has been presented to deal with incompressible structures subjected to FSI loads. The main goal of this work was to combine an additive TD with a level set method to optimize the internal structural layout of FSI problems. The structural response is modeled assuming either infinitesimal strains or finite ones. The fluid model is studied with the incompressible Navier–Stokes model and the coupling problem is treated in a staggered way with strong-coupling between sub-problems.
The key to solving problems involving incompressible structures was the introduction of the mixed stabilized FE formulations presented in Sect. 3.1 for linear elastic materials and in Sect. 3.2 for hyperelastic ones. On the one hand, the well-known \({\textbf {u}}\text {-}p\) formulation, in which the pressure is added as an unknown—the fundamental one, when dealing with incompressible materials. On the other hand, three-field formulations which also add stresses as unknowns of the problem to increase their accuracy.
Thanks to the TD formulae that are presented in Castañar et al. (2022), the TO algorithm of incompressible structures is possible for linear elastic materials by means of the topological derivative concept. Furthermore, the approximation applied to the TD in the finite strain cases, replacing it by the minimization direction given in Eq. (36), shows good performance in the numerical examples presented in this work, in the sense that the objective functional certainly decreases along the TO steps.
In Sect. 6 several numerical examples have been shown to assess the performance of the new TO algorithm for incompressible structures subjected to FSI loads. First of all, a flow through a channel with a flexible wall is considered. This case is supposed to converge to a stationary solution. Several cases have been performed, showing different optimized structures depending upon the kind of solid that is considered and the employed stabilized mixed formulation. The evolution of the total potential energy is also shown to decrease along the TO steps. Next, the well-known Turek’s FSI2 test, adapted to the present setting, is performed. The main idea of this problem is to show how the TO algorithm works in transient FSI problems. To do so, several volume fractions for the final structure are considered. Two final transient solutions are obtained for 90% and 80% of the final volume, but a stationary one is achieved when considering a 70% of material. Fluid forces and solid displacements are shown to see the effect of reducing the mass in the beam and how this can modify the physics of the FSI problem. To end up, a 3D case is performed to show the good performance of the methodology in three-dimensional cases.
References
Andreasen CS, Sigmund O (2013) Topology optimization of fluid-structure-interaction problems in poroelasticity. Comput Methods Appl Mech Eng 258:55–62
Badia S, Codina R (2006) Analysis of a stabilized finite element approximation of the transient convection-diffusion equation using an ALE framework. SIAM J Numer Anal 44:2159–2197
Baiges J, Codina R (2017) Variational Multiscale error estimators for solid mechanics adaptive simulations: an Orthogonal Subgrid Scale approach. Comput Methods Appl Mech Eng 325:37–55
Baiges J, Martínez-Frutos J, Herrero-Pérez D, Otero F, Ferrer A (2019) Large-scale stochastic topology optimization using adaptive mesh refinement and coarsening through a two-level parallelization scheme. Comput Methods Appl Mech Eng 343:186–206
Balay S, Abhyankar S, Adams MF, Brown J, Brune P, Buschelman K, Dalcin L, Eijkhout V, Gropp WD, Kaushik D, Knepley MG, May DA, Curfman McInnes L, Mills RT, Munson T, Rupp K, Sanan P, Smith BF, Zampini S, Zhang H, Zhang H (2015) PETSc Web page. http://www.mcs.anl.gov/petsc
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224
Bendsøe MP, Sigmund O (2013) Topological optimization: theory. Springer, Berlin
Bodnár T, Galdi GP, Nečasová S (2014) Fluid-structure interactions and biomedical applications. Springer, Berlin
Boffi D, Brezzi F, Fortin M (2013) Mixed finite element methods and applications. Springer, Berlin
Castañar I, Baiges J, Codina R (2020) A stabilized mixed finite element approximation for incompressible finite strain solid dynamics using a total Lagrangian formulation. Comput Methods Appl Mech Eng 368:113164
Castañar I, Baiges J, Codina R, Venghauss H (2022) Topological derivative-based topology optimization of incompressible structures using mixed formulations. Comput Methods Appl Mech Eng 390:114438
Castañar I, Codina R, Baiges J (2023) A stabilized mixed three-field formulation for stress accurate analysis including the incompressible limit in finite strain solid dynamics. Int J Numer Methods Eng 124(10):2341–2366
Chiandussi G, Bugeda G, Oñate E (1999) A simple method for automatic update of finite element meshes. Commun Numer Methods Eng 16:1–19
Chiumenti M, Cervera M, Codina R (2015) A mixed three-field FE formulation for stress accurate analysis including the incompressible limit. Comput Methods Appl Mech Eng 283:1095–1116
Chiumenti M, Cervera M, Moreira CA, Barbat GB (2021) Stress, strain and dissipation accurate 3-field formulation for inelastic isochoric deformation. Finite Elem Anal Des 192:103534
Codina R (2000) Stabilization of incompressibility and convection through orthogonal sub-scales in finite element methods. Comput Methods Appl Mech Eng 190:1579–1599
Codina R (2001) A stabilized finite element method for generalized stationary incompressible flows. Comput Methods Appl Mech Eng 190:2681–2706
Codina R (2009) Finite element approximation of the three field formulation of the Stokes problem using arbitrary interpolations. SIAM J Numer Anal 47:699–718
Codina R, Baiges J (2011) Finite element approximation of transmission conditions in fluids and solids introducing boundary subgrid scales. Int J Numer Methods Eng 87:386–411
Codina R, Principe J, Baiges J (2009) Subscales on the element boundaries in the variational two-scale finite element method. Comput Methods Appl Mech Eng 198:838–852
Codina R, Principe J, Avila M (2010) Finite element approximation of turbulent thermally coupled incompressible flows with numerical sub-grid scale modelling. Int J Numer Methods Heat Fluid Flow 20:492–516
Codina R, Badia S, Baiges J, Principe J (2017) Variational multiscale methods in computational fluid dynamics. Wiley, Hoboken
Codina R, Badia S, Baiges J, Principe J (2018) Variational multiscale methods in computational fluid dynamics. In: Encyclopedia of computational mechanics, 2nd ed, pp 1–28,
Codina R, Baiges J, Castañar I, Martínez-Suárez I, Moreno L, Parada S (2023) An embedded strategy for large scale incompressible flow simulations in moving domains. J Comput Phys 488:112181
Colomes O, Badia S, Codina R, Principe J (2015) Assessment of variational multiscale models for the large eddy simulation of turbulent incompressible flows. Comput Methods Appl Mech Eng 285:32–63
Comellas E, Bellomo FJ, Oller S (2016) A generalized finite-strain damage model for quasi-incompressible hyperelasticity using hybrid formulation. Int J Numer Methods Eng 105:781–800
Comellas E, Gasser T, Bellomo FJ, Oller S (2016) A homeostatic-driven turnover remodelling constitutive model for healing in soft tissues. J R Soc Interface 13:20151081
Comellas E, Budday S, Pelteret JP, Holzapfel GA, Steinmann P (2020) Modeling the porous and viscous responses of human brain tissue behavior. Comput Methods Appl Mech Eng 369:113128
Deaton JD, Grandhi RV (2014) A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct Multidisc Optim 49:1–38
Deng Y, Liu Z, Wu Y (2013) Topology optimization of steady and unsteady incompressible Navier-Stokes flows driven by body forces. Struct Multidisc Optim 47(4):555–570
Feppon F, Allaire G, Dapogny C, Jolivet P (2020) Topology optimization of thermal fluid-structure systems using body-fitted meshes and parallel computing. J Comput Phys 417:109574
Huang X, Xie Y (2010) A further review of ESO type methods for topology optimization. Struct Multidisc Optim 41:671–683
Hughes TJR, Feijóo GR, Mazzei L, Quincy J (1998) The variational multiscale method–a paradigm for computational mechanics. Comput Methods Appl Mech Eng 166:3–24
Hughes TJR, Oberai AA, Mazzei L (2001) Large eddy simulation of turbulent channel flows by the variational multiscale method. Phys Fluids 13:1784–1799
Jenkins N, Maute K (2015) Level set topology optimization of stationary fluid-structure interaction problems. Struct Multidisc Optim 52:179–195
Jenkins N, Maute K (2016) An immersed boundary approach for shape and topology optimization of stationary fluid-structure interaction problems. Struct Multidisc Optim 54:1191–1208
Kamakoti R, Shyy W (2004) Fluid-structure interaction for aeroelastic applications. Prog Aerosp Sci 40:535–558
Küttler U, Wall WA (2008) Fixed-point fluid-structure interaction solvers with dynamic relaxation. Comput Mech 43(1):61–72
Li H, Kondoh T, Jolivet P, Furuta K, Yamada T, Zhu B, Izui K, Nishiwaki S (2022) Three-dimensional topology optimization of a fluid-structure system using body-fitted mesh adaption based on the level-set method. Appl Math Model 101:276–308
Lopes CG, Batista dos Santos R, Novotny AA (2015) Topological derivative-based topology optimization of structures subject to multiple load-cases. Latin Am J Solids Struct 12:834–860
Martínez-Frutos J, Ortigosa R, Gil AJ (2021) In-silico design of electrode meso-architecture for shape morphing dielectric elastomers. J Mech Phys Solids 157:104594
Moreno L, Codina R, Baiges J, Castillo E (2019) Logarithmic conformation reformulation in viscoelastic flow problems approximated by a VMS-type stabilized finite element formulation. Comput Methods Appl Mech Eng 354:706–731
Moreno L, Codina R, Baiges J (2020) Solution of transient viscoelastic flow problems approximated by a term-by-term VMS stabilized finite element formulation using time-dependent subgrid-scales. Comput Methods Appl Mech Eng 367:113074
Moreno L, Castañar I, Codina R, Baiges J, Cattoni D (2023) Numerical simulation of Fluid-Structure Interaction problems with viscoelastic fluids using a log-conformation reformulation. Comput Methods Appl Mech Eng 410:115986
Novotny AA, Sokolowski J (2013) Topological derivatives in shape optimization. Springer, Berlin
Novotny AA, Sokolowski J, Zochowski A (2019) Topological derivatives of shape functionals. Part I. Theory in singularly perturbed geometrical domains. J Optim Theory Appl 180:341–373
Oliver J, Yago D, Cante J, Lloberas-Valls O (2019) Variational approach to relaxed topological optimization: closed form solutions for structural problems in a sequential pseudo-time framework. Comput Methods Appl Mech Eng 355:779–819
Ortigosa R, Martínez-Frutos J, Gil AJ, Herrero-Pérez D (2019) A new stabilisation approach for level-set based topology optimisation of hyperelastic materials. Struct Multidisc Optim 60:2343–2371
Ortigosa R, Ruíz D, Gil AJ, Donoso A, Bellido JC (2020) A stabilisation approach for topology optimisation of hyperelastic structures with the SIMP method. Comput Methods Appl Mech Eng 364:112924
Pereira CEL, Bittencourt ML (2008) Topological sensitivity analysis in large deformation problems. Struct Multidisc Optim 37:149–163
Pereira CEL, Bittencourt ML (2010) Topological sensitivity analysis for a two-parameter Mooney-Rivlin hyperelastic constitutive model. Latin Am J Solids Struct 7:391–411
Picelli R, Vicente WM, Pavanello R (2017) Evolutionary topology optimization for structural compliance minimization considering design-dependent FSI loads. Finite Elem Anal Des 135:44–55
Rhyzhakov PB, Oñate E (2017) A finite element model for fluid-structure interaction problems involving closed membranes, internal and external fluids. Comput Methods Appl Mech Eng 326:422–445
Rhyzhakov PB, Rossi R, Idelsohn SR, Oñate E (2010) A monolithic Lagrangian approach for fluid-structure interaction problems. Comput Mech 46:883–899
Rhyzhakov P, Soudah E, Dialami N (2019) Computational modeling of the fluid flow and the flexible intimal flap in type B aortic dissection via a monolithic arbitrary Lagrangian/Eulerian fluid-structure interaction model. Int J Numer Methods Biomed Eng 35:e3239
Richter T (2017) Fluid-structure interactions. Springer, Berlin
Richter T, Wick T (2010) Finite elements for fluid-structure interaction in ALE and fully Eulerian coordinates. Comput Methods Appl Mech Eng 199:2633–2642
Silva KE, Sivapuram R, Ranjbarzadeh S, Gioria RD, Silva EC, Picelli R (2022) Topology optimization of stationary fluid-structure interaction problems including large displacements via the TOBS-GT method. Struct Multidisc Optim 65(11):337
Scovazzi G, Carnes B, Zeng X, Rossi S (2016) A simple, stable, and accurate linear tetrahedral finite element for transient, nearly, and fully incompressible solid dynamics: a dynamic variational multiscale approach. Int J Numer Methods Eng 106:799–839
Shu L, Wang MY, Ma Z (2014) Level set based topology optimization of vibrating structures for coupled acoustic-structural dynamics. Comput Struct 132:34–42
Sigmund O, Clausen PM (2007) Topology optimization using a mixed formulation: an alternative way to solve pressure load problems. Comput Methods Appl Mech Eng 196:1874–1889
Simo JC, Taylor RL, Pister KS (1985) Variational and projection methods for the volume constraint in finite deformation elasto-plasticity. Comput Methods Appl Mech Eng 51(1–3):177–208
Treloar LRG (1975) The physics of rubber elasticity. Oxford University Press, Oxford
Turek S, Hron J (2007) Proposal for numerical benchmarking of fluid-structure interaction between an elastic object and laminar incompressible flow. In: Fluid-structure interaction. Lecture notes on computational science and engineering, pp 371–385
Van der Vorst HA (1992) Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM 13(2):631–644
van Dijk NP, Maute K, Langelaar M, van Keulen F (2013) Level-set methods for structural topology optimization: a review. Struct Multidisc Optim 48:437–472
Wang X, Xu S, Zhou S, Xu W, Leary M, Choong P, Qian M, Brandt M, Xie YM (2016) Topological design and additive manufacturing of porous metals for bone scaffols and orthopaedic implants: a review. Biomaterials 83:127–141
Wex C, Arndt S, Stoll A, Bruns C, Kupriyanova Y (2015) Isotropic incompressible hyperelastic models for modelling the mechanical behaviour of biological tissues: a review. Biomed Eng 60:577–592
Yago D, Cante JC, Lloberas-Valls O, Oliver J (2022) Topology optimization methods for 3d structural problems: a comparative study. Arch Comput Methods Eng 29:1525–1567
Yan J, Korobenko A, Deng X, Bazilevs Y (2016) Computational free-surface fluid-structure interaction with application to floating offshore wind turbines. Comput Fluids 141:155–174
Yoon GH (2010) Topology optimization for stationary fluid-structure interaction problems using a new monolithic formulation. Int J Numer Methods Eng 82:591–616
Yoon GH (2014) Stress-based topology optimization method for steady-state fluid-structure interaction problems. Comput Methods Appl Mech Eng 278:499–523
Acknowledgements
Inocencio Castañar gratefully acknowledges the support received from the Agència de Gestió d’Ajut i de Recerca through the predoctoral FI grant 2019-FI-B-00649. R. Codina gratefully acknowledges the support received through the ICREA Acadèmia Research Program of the Catalan Government. This work was partially funded through the TOP-FSI: RTI2018-098276-B-I00 project of the Spanish Government. CIMNE is a recipient of a “Severo Ochoa Programme for Centers of Excellence in R &D” grant (CEX2018-000797-S) by the Spanish Ministry of Economy and Competitiveness.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Replication of results
All the information required for replicating the paper results was duly presented. Data files for the results are available upon request from the authors.
Additional information
Responsible Editor: Emilio Silva
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Castañar, I., Baiges, J. & Codina, R. Topology optimization of incompressible structures subject to fluid–structure interaction. Struct Multidisc Optim 67, 90 (2024). https://doi.org/10.1007/s00158-024-03770-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-024-03770-6