Topography optimisation using a reduced-dimensional model for convective heat transfer between plates with varying channel height and constant temperature

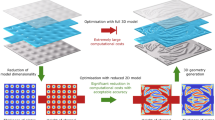
Abstract

This paper proposes a reduced-dimensional model for the structural optimisation of conjugate heat transfer between parallel plates with constant temperature and a fluid channel of varying height. The model considers heat conduction and convection through a planar reduced-dimensional version of the convection-diffusion equation. To significantly reduce the computational time for the optimisation process, assumptions on the through-thickness velocity and temperature fields are made, allowing to transform a three-dimensional problem to a two-dimensional one. The accuracy and limitations of the model are investigated through an in-depth parametric analysis and are seen to be acceptable in the context of optimisation when considering the reduced computational cost. To allow for the optimisation of varying topology and topography, the local channel height is linearly interpolated based on the design field. The height parametrisation combined with the reduced-dimensional model provides physical meaning to intermediate design variables and removes the traditional requirement of 0–1 discrete solutions for topology optimisation. This allows the free switch between topology and topography optimisation, but it is illustrated through various examples that only topography changes are relevant for the treated problems. Two optimisation examples, a square heat exchanger and a manifold heat exchanger, demonstrate that the reduced-dimensional model is sufficiently accurate to be applied to structural optimisation. In comparison with shape optimisation using a full three-dimensional model, it is demonstrated that topography optimisation using the reduced-dimensional model can achieve equivalent optimised designs at a significantly lower computational cost.

Graphical abstract

1 Introduction

1.1 Motivation

Fig. 1

Graphical overview of the proposed methodology and the difference between topography and topology designs

Thermal management is critical for both large industrial equipment and micro electronic devices, and as the performance and integration of the equipment improve, increasing requirements are imposed on the performance of heat exchangers. Plate heat exchangers are widely used due to their high heat transfer coefficient and compact structure (Elmaaty et al. 2017). Plate heat exchangers consist of a group of thin plates with undulating surfaces stacked in parallel, and the topography of the plates significantly affects the performance of the system (Tsai et al. 2009; Subramaniam et al. 2019). Therefore, more and more attention is being paid to the structural optimisation of plate heat exchangers (Dbouk 2017; Alexandersen and Andreasen 2020; Fawaz et al. 2022).

The particular system that inspired this work is a thermal energy storage (TES) system based on stacks of compact storage module plates filled with phase change material (PCM) (Hassan et al. 2023; Dallaire et al. 2022) to be integrated into building ventilation systems (Veje et al. 2019). To simplify the model for initial developments and demonstrations of the power of reduced-dimensional models, the plate temperatures are assumed to be predefined and constant. This could be seen as a special case during the phase transition of the PCM from solid to fluid, or vice versa, where the temperature is approximately constant.

The TES system, as well as many common plate heat exchangers, have a large span in scale between the length and thickness of the plates. To accurately capture the variations in surface topography during the optimisation process, it is necessary to ensure that there are enough elements in the thickness direction. This results in extremely fine meshes for the entire model, which introduces significant computational costs. Moreover, structural optimisation usually requires hundreds of analyses, making it highly challenging and costly to perform topology optimisation with a full three-dimensional model (Alexandersen and Andreasen 2020). Therefore, it is necessary to propose a simplified heat transfer model that can accurately calculate the performance of varying heat transfer plates during optimisation at a low computational cost.

Figure 1 shows a graphical overview of the design methodology proposed herein with a reduced-dimensional model for the flow and heat transfer between plates of varying topography. The concept of topography optimisation for fluid flow in channels of varying height was introduced by Alexandersen (2022). Figure 1 illustrates the difference between topology (adding holes) and topography (changing thickness). As will be demonstrated in this paper, topographical designs are preferable due to their increased heat transfer surface area, in contrast to topological changes.

1.2 Literature

Many investigations have been performed to find better structural forms using parametric optimisation, size optimisation and shape optimisation methods to improve the flow and heat transfer performance of the structure. Zhai et al. (2021) investigated the effect of the geometry of a plate heat exchanger on the performance of the absorption refrigeration cycle using parametric optimisation; Garcia et al. (2022) applied genetic algorithms to optimise the geometric parameters of the flat-tubed microchannel heat exchanger for a smaller volume and fan power for a given capacity; Liu et al. (2017) performed shape optimisation of the plate fins of the heat exchanger based on CFD simulations to enhance heat transfer and reduce flow resistance. All of the above studies improve the performance, but they all rely on the initial design and their final structural form is restricted. Hoon Lee et al. (2017) performed a parametric optimisation of the contact surface topography for full-film lubrication problems and demonstrated that the optimisation of arbitrary shapes gives a better design than the parametric optimisation dependent on the initial design. However, the number of design variables in their work is still small, which may limit the complexity of the optimised design. While topology optimisation has a larger design space than the above methods and enables one to obtain a non-intuitive structure independent of the initial design (Bendsøe and Sigmund 2004).

Topology optimisation was initially applied in the field of solid mechanics (Bendsøe and Kikuchi 1988; Bendsøe and Sigmund 2004), and then it was gradually extended to acoustic, thermal, and electromagnetic fields (Deaton and Grandhi 2013). Building on the extension of topology optimisation to the fields of fluid flow (Borrvall and Petersson 2003; Evgrafov 2005; Gersborg-Hansen et al. 2005; Alexandersen and Andreasen 2020) and solid heat transfer (Li et al. 1999; Bendsøe and Sigmund 2004; Gersborg-Hansen et al. 2006), applying topology optimisation to the design of conjugate heat transfer systems such as heat exchangers has become an active area of research (Alexandersen and Andreasen 2020; Fawaz et al. 2022). For thermal fluid problems, there is an enormous computational cost for fine three-dimensional models, and topology optimisation will multiply the computational cost by hundreds of times due to its serial nature. Therefore, it has become a research direction to reduce the computational cost of the topology optimisation of thermal fluids (Haertel et al. 2018; Zeng et al. 2018).

Researchers have made numerous attempts to reduce the computational cost of topology optimisation for thermal fluids. An early approach was to approximately model convection on a fluid-solid surface using Newton’s law of cooling, with the fluid-solid surface determined in different ways (Zhou et al. 2016; Coffin and Maute 2015). Instead of modelling and calculating the fluid, this approach uses the convection coefficient to calculate the heat flux transferred by the fluid, saving considerable computational costs. However, it is challenging to determine a convective coefficient that provides accurate results, especially for topology optimisation. In addition to the above approach, the multi-layer model approach has been proposed to reduce the computational cost of topology optimisation for thermal fluids. The multi-layer model approach is to simplify the three-dimensional parallel plate model into a two-dimensional multi-layer model consisting of a heated substrate or top plate with a fluid-solid mixed layer. Zeng et al. (2018) used a two-layer model for the topology optimisation design of air-cooled heat sinks and liquid-cooled microfluidic heat sinks (Zeng and Lee 2019) and verified the performance through manufacture and experiments. Yan et al. (2019) proposed a new two-layer model based on the assumption of planar flow, assuming that the temperature profile of the thermal fluid layer is a fourth-order polynomial and that the temperature of the substrate is linearly distributed. Zhao et al. (2021) proposed a three-layer model that takes into account the heat transfer of the upper cover of the two-layer model, with a varying temperature profile function. All of the above research can yield simulation results with acceptable accuracy and significantly reduce the computational cost. Although the multi-layer model approach can solve other thermal fluid problems well, it still has some problems when applied to a plate heat exchanger. First, the current multi-layer model only considers the case where a single layer contains a heat source, whereas a plate heat exchanger usually contains heat sources on all surfaces. Although the three-layer model considers heat transfer with the upper cover, it increases computational cost compared to the two-layer model (Zhao et al. 2021). Second, and more importantly, the structure obtained using the multi-layer model approach has no variation in height out of the plane, and this extruded structure from the plane cannot be used to design plate heat exchangers with varying surface heights.

The above reduced-dimensional models are similar to homogenisation-based models, where a local microstructure is introduced and the effective material parameters, such as permeability and thermal conductivity, are found based on homogenisation. Examples include poroelasticity (Andreasen and Sigmund 2011) and conjugate heat transfer (Takezawa et al. 2019; Geng et al. 2022).

1.3 Contributions

This paper proposes a reduced-dimensional model for forced convection heat transfer between a fluid channel and parallel plates with constant temperature. The model can provide fluid velocity and temperature distributions with acceptable accuracy at a low-dimensional computational cost. The reduced-dimensional model accounts for the heat conduction in all directions and convection in-plane, providing accurate energy and temperature gradients.

This paper takes the height of the channel as the design variable and applies a linear interpolation to the structural optimisation of forced convection, which gives physical meaning to the intermediate design variables and makes it possible to achieve a free switch between topology and topography optimisation. This makes it similar to the variable thickness sheet problem of structural mechanics (Rossow and Taylor 1973). This interpolation combines the reduced-dimensional model with structural optimisation, enabling free structure optimisation while significantly reducing computational costs.

1.4 Paper layout

The rest of the paper is organised as follows: Sect. 2 presents the governing equations and the reduced-dimensional model for the heat transfer problem. Section 3 validates the reduced model using the full 3D model and investigates the effect of different parameters on accuracy through parametric analysis. Section 4 presents the implementation of combining the reduced-dimensional model with the optimisation and the formulation of two optimisation problems. Sect. 5 shows the optimisation results and discussion. Finally, Sect. 6 presents conclusions and future work.

2 Governing equations and reduced-dimensional models

This section presents the governing equations for convective heat transfer and proposes a reduced-dimensional model for heat transfer between the fluid channel and the parallel plates of constant temperature.

Fig. 2

Schematic diagram of the reduced-dimensional model, which uses velocity and temperature in the mid-plane to represent velocity and temperature in three dimensions

2.1 Governing equations

For heat transfer between fluid channels and constant temperature parallel plates, as shown in Fig. 2, convection and conduction are the mechanisms of heat transfer. Temperature and fluid velocity are weakly coupled, i.e. velocity is independent of temperature, while temperature is influenced by velocity due to convection effects. The Navier–Stokes equations and heat transfer equations governing fluid flow and heat transfer are as follows:

$$\begin{aligned} \rho u_{j}\frac{\partial u_{i}}{\partial x_{j}} - \mu \frac{\partial }{\partial x_{j}}\left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} \right) + \frac{\partial p}{\partial x_{i}}&= 0 \end{aligned}$$

(1a)

$$\begin{aligned} \rho \frac{\partial u_{i}}{\partial x_{i}}&= 0 \end{aligned}$$

(1b)

$$\begin{aligned} \rho c_\text {p} u_{i}\frac{\partial T}{\partial x_{i}} - \frac{\partial }{\partial x_{i}} \left( k \frac{\partial T}{\partial x_{i}} \right)&= 0 \end{aligned}$$

(1c)

where $\rho$ is the density of the fluid, $u_{i}$ is the i-th component of the velocity vector. $\mu$ is the dynamic viscosity of the fluid, p is the pressure field, $x_{i}$ denotes the spatial coordinate, T is the temperature field, $c_\text {p}$ is the heat capacity of the fluid, and k is the thermal conductivity of fluid.

2.2 Reduced-dimensional model

In the proposed reduced-dimensional model, it is assumed that the fluid flow is an incompressible, fully developed laminar flow. With the assumption, the distributions of the velocity and temperature along the height direction are assumed to be parabolic and fourth-order polynomials, respectively. Therefore, the spatial distributions of velocity and temperature can be represented by the velocity and temperature in the mid-plane, as shown in Fig. 2. This makes it possible to obtain the spatial distribution of velocity and temperature at low-dimensional computational cost.

2.2.1 Fluid flow model

The concept of simplification of fluid flows is based on approximating velocity profiles and reducing the dimensions of the problem through transformation. To the knowledge of the authors, Borrvall and Petersson (2003) first proposed the model for fluid topology optimisation. Recently, Alexandersen (2022) modified the proposed model by Borrvall and Petersson (2003) and Gersborg-Hansen et al. (2005) to simulate fluid flow between parallel plates with varying heights. This work uses the model proposed by Alexandersen (2022) for fluid flow, which is as follows:

$$\begin{aligned} \bar{\rho } \bar{u}_{j} \frac{\partial \bar{u}_{i}}{\partial x_{j}} - \mu \frac{\partial }{\partial x_{j}}\left( \frac{\partial \bar{u}_{i}}{\partial x_{j}} + \frac{\partial \bar{u}_{j}}{\partial x_{i}} \right) - \alpha \bar{u}_{i} + \frac{\partial \bar{p}}{\partial x_{i}}&= 0 \end{aligned}$$

(2a)

$$\begin{aligned} h \frac{\partial \bar{u}_{i}}{\partial x_{i}} + \bar{u}_{i}\frac{\partial h}{\partial x_{i}}&= 0 \end{aligned}$$

(2b)

where $i, j = 1, 2$, $\bar{u}$ is the velocity at the mid-plane ($x_{3} = 0$), h is the spacing height between the two plates, $\bar{\rho }=\frac{6}{7}\rho$ is the effective density, $\bar{p}=\frac{5}{4}p$ is the in-plane scaled pressure field, and $\alpha = \frac{10\mu }{h^2}$ is the through-height/out-of-plane viscous resistance factor. $-\alpha \bar{u}_{i}$ is the resistance term, which represents the local resistance of the fluid and is positively related to the local height. The detailed derivations of the coefficients are given in (Borrvall and Petersson 2003; Gersborg-Hansen et al. 2005; Alexandersen 2022).

2.2.2 Heat transfer model

For the heat transfer problem shown in Fig. 2, the temperature profile in the height direction is assumed to be fourth-order polynomial. The spatial temperature can be expressed using the temperature in the mid-plane, which is expressed as follows:

$$\begin{aligned} T \left( x_{1},x_{2},x_{3} \right)&= \bar{T}\left( x_{1},x_{2} \right) \nonumber \\&\quad + \theta \left( \bar{T}\left( x_{1},x_{2} \right) - \bar{T}_\text {s}\left( x_{1},x_{2} \right) \right) \end{aligned}$$

(3)

with:

$$\begin{aligned} \theta = \frac{1}{5} \left( \frac{2 x_{3}}{h \left( x_{1},x_{2} \right) } \right) ^2 \left( \left( \frac{2 x_{3}}{h \left( x_{1},x_{2} \right) } \right) ^2 -6 \right) \end{aligned}$$

(4)

where $\bar{T}$ is the temperature field in the mid-plane and $\bar{T}_\text {s}$ is the temperature field of the plates, where the temperature is assumed to be constant and predefined - this is an approximation of the phase transition of a PCM, as mentioned in the introduction. $\theta$ is the temperature profile function of the fluid channel, which is obtained from several simulations and accurately fits the practical temperature profile at different Peclét numbers. The effect of the height variation is also considered in the heat transfer, the reduced-dimensional model for heat transfer is obtained by substituting the profile functions of velocity and temperature into the modified energy conservation equation and simplifying it. To make the article concise and readable, the detailed derivation can be found in the Appendix A. The final equation for heat transfer is as follows:

$$\begin{aligned}&\rho c_\text {p} \frac{\partial }{\partial x_{i}} \left( \bar{u}_{i} h \left( {\scriptstyle \frac{17}{21}} \bar{T} + {\scriptstyle \frac{13}{56}} \bar{T}_\text {s}\right) \right) - k\frac{\partial }{\partial x_{i}} \left( \frac{\partial h}{\partial x_{i}}\left( \bar{T} - \bar{T}_\text {s} \right) \right. \nonumber \\&\quad + \left. h \frac{\partial }{\partial x_{i}} \left( \bar{T} + {\scriptstyle \frac{9}{16}} \bar{T}_\text {s} \right) \right) + \frac{10k}{h} \left( \bar{T} - \bar{T}_\text {s} \right) = 0 \end{aligned}$$

(5)

3 Model verification

This section investigates the heat transfer between the fluid channel and parallel plates with varying heights and displays the results obtained using the full three-dimensional model and the reduced-dimensional model. Errors in temperature and temperature gradients between the different models are calculated to validate the reduced-dimensional models. A parametric analysis of the Peclét number, channel height, and other parameters is also carried out to investigate the effect of different parameters on the accuracy of the reduced-dimensional model.

Fig. 3

Three-dimensional fluid channel geometries for different parameters

3.1 Simulation details

All simulations for this work are completed on COMSOL Multiphysics Version 6.0 (COMSOL 2022). The “Laminar Flow” interface and the “Heat Transfer in Fluids” interface are used for the full model, while the “Weak Form Boundary PDE” interface is used for the simplified model, which defines the mid-plane surface of the full model geometry as the boundary and solves the modified governing equations. Second-order shape functions are used for velocity fields, and first-order shape functions are used for pressure and temperature fields. The geometry of the reduced-dimensional model and the full 3D is discretised using quadrilateral elements and tetrahedral elements, respectively. The meshes used in this section and the verification of the independence of the meshes are shown in Appendix B.

For the solver setting, a separate solver is used for the full three-dimensional model and the reduced two-dimensional model. Since the fluid properties are independent of the temperature in this work, it saves more time to use the separate solver to solve the flow field first and then the temperature field.

3.2 Verification example

In this section, the heat transfer between the fluid channel and the parallel plates with temperature is analysed using the full three-dimensional model and the reduced-dimensional model, respectively, and the results are compared to verify the effectiveness of the reduced-dimensional model. The boundary conditions are shown in Fig. 3: the temperature of the parallel plate $T_s$ is kept constant, the fluid with temperature $T_\text {in}$ flows from the inlet at a velocity of $U_\text {in}$, and the pressure at the outlet is $P_\text {out}$. Figure 3 depicts the geometry of the fluid channel between the parallel plates, obtained by rotating the following profile around the $x_3$ axis:

$$\begin{aligned} h\left( x \right) =\,&h_\text {mid} + \left( h_\text {in}-h_\text {mid} \right) \nonumber \\&\quad \frac{ \tanh \left( \frac{\beta }{2} \right) + \tanh \left( \frac{\beta }{2} \cos \left( 2\pi \frac{x_1}{L} \right) \right) }{ 2\tanh \left( \frac{\beta }{2} \right) } \end{aligned}$$

(6)

where $h\left( x \right)$ represents the height between the parallel plates, $h_\text {in}$ and $h_\text {mid}$ represent the heights at the inlet and at the middle, respectively, L is the length of the plates, and $\beta$ controls the sharpness of the height transition; the larger the $\beta$ value, the steeper the height transition. The effect of $\beta$ and $h_\text {mid}$ on the geometric profile of the fluid channel is shown in Fig. 3.

3.3 Results of parametric analysis

This section defines the investigated problem using dimensionless quantities to generally discuss the effect of some heat transfer parameters on the validity of the reduced-dimensional model; the specific parameters are given in Table 1.

Table 1 Parameters for dimensionless analysis of comparisons between reduced and full models. The units of the parameters are in the International System of Units

3.3.1 Different Peclét numbers, middle heights, transition sharpness

A parametric analysis of the fluid temperature and the temperature gradient with respect to the various Peclét numbers, middle height, and transition sharpness is performed. The Peclét number describes the proportional relationship between the two heat transfer effects, advection and conduction, in the heat exchange process ${Pe} = \frac{L u \rho c_\text {p}}{k}$. In this example, the range of Peclét number is defined as ${Pe} \in [10^{-1},10^4]$. When ${Pe} = 10^{-1}$, conduction is the dominant heat transfer mechanism and when ${Pe} = 10^{4}$, advection is the dominant heat transfer mechanism. Next comes the middle height $h_{mid}$ and the transition sharpness $\beta$, the range of values of which is defined as:

$$\begin{aligned} h_\text {mid} \in [0.6,1.4] \qquad \beta \in [1,32] \end{aligned}$$

(7)

where when $h_\text {mid}>1$ means that the plate is protruding in the middle, and when $h_\text {mid}<1$ means that the plate is dimpled in the middle. When $\beta =1$ the height varies very smoothly, and when $\beta =64$, the height varies close to a step change.

The temperature distribution at the mid-plane and the temperature gradient distribution along the wall obtained for the two models with different parameters are shown in Appendix C. The results clearly demonstrate that for the considered range of parameters, the reduced-dimensional model can obtain very similar temperature distributions and temperature gradient distributions to those of the full three-dimensional model. Further, to quantify the effect of different parameters on the accuracy of the reduced-dimensional model, the average relative error of the temperature at the mid-plane and the average relative error of the temperature gradient along the wall with different parameters are calculated in this section. The average relative error of the temperature at the mid-plane is defined as follows:

$$\begin{aligned} \epsilon _\text {T} = \frac{1}{| \omega _\text {m} |} \int _{\omega _\text {m}} \frac{|\bar{T}_\text {3D}-\bar{T}_\text {2D}|}{\bar{T}_\text {3D}-T_\text {ref}} \ dS \end{aligned}$$

(8)

where $\omega _\text {m}$ is the mid-plane of the three-dimensional model. The average relative error for the temperature gradient along the wall is defined as follows:

$$\begin{aligned} \epsilon _\text {Tg} = \frac{1}{| \omega _\text {s} |} \int _{\omega _\text {s}} \frac{|\nabla \bar{T}_\text {3D}-\nabla \bar{T}_\text {2D}|}{\max (\nabla \bar{T}_\text {3D},10^{-3})} \ dS \end{aligned}$$

(9)

where $\omega _\text {s}$ is the upper surface of the three-dimensional model and $\nabla \bar{T}$ is the vertical sum of all directions of the temperature gradient.

Fig. 4

Average relative error of temperature between the reduced and the full models. Same colour indicate the same $\beta$, the same line type indicate the same $h_\text {mid}$

Figure 4 shows the error of temperature between the reduced model and the full model with different parameters. It is clear that the Peclét number has a significant effect on the temperature error, the temperature error increases as the Peclét number increases. This is because when the Peclét number is small, the convection effect is weak, the temperature difference between the fluid and the channel is small, and the overall temperature is high. Therefore, the error is small. When the Peclét number increases, the convective effect increases, the temperature difference between the fluid and the channel increases, and the overall temperature is lower; therefore, the temperature error is large. It should be noted that when ${Pe}>1000$, convection becomes the dominant heat transfer mechanism and the temperature distribution in the channels remains almost constant. Therefore, the larger Peclét number is not studied here and the use of the reduced-dimensional model should be reconsidered if the practical application has ${Pe}>1000$. When ${Pe}<1000$, the error is less than 5%, so the model can be considered to have good accuracy within a reasonable range of Peclét numbers, especially given the significant reduction in computational cost shown later. Furthermore, for the same Peclét number, the temperature error varies within less than 1% for different transition sharpnesses or different intermediate heights, indicating that the global temperature error is weakly dependent on the transition sharpness and middle height; only the Peclét number determines the temperature error. The reason for this is that although excessive transition sharpness and height variations affect the temperature to some extent, the effect on the temperature is localised, so that the global temperature distribution has good accuracy.

Fig. 5

Average relative error of gradient of temperature between the reduced and full model. Same colour indicate the same $h_\text {mid}$, same line type indicate the same $\beta$

Figure 5 shows the error of the temperature gradients along the wall between the reduced model and the full model with different parameters. It can be seen that the error of the temperature gradient is affected by both the height transition sharpness and the middle height, i.e. the temperature gradient is sensitive to the height variation. When the difference between the middle height and the surrounding height is large, the gradient error increases significantly with the increase of the height transition sharpness. When the height transition sharpness is large, a large height change produces a larger gradient error, whereas when the height transition sharpness is small, the errors from even large height variations are small and remain within acceptable ranges. The above errors arise because the assumed temperature profile function is in error with the actual temperature profile when there is a dramatic variation in height. As can be seen from the temperature gradient distributions in Appendix C, only the temperature gradients at locations with large height variations differ significantly, the temperature gradients at the other locations match very well.

3.3.2 Further decreasing heights

For optimisation problems, very small minimum channel height is often taken as the optimisation lower limit and there will be many areas of very small height in the optimised design. Therefore, the influence of the very small minimum height on the accuracy of the reduced-dimensional model is investigated in this part to evaluate the feasibility of using the reduced-dimensional models for optimisation.

A parametric analysis is performed on middle heights in the range $h_\text {mid}\in [0.01, 0.3]$. When $h_\text {mid} = 0.01$, the fluid flow is blocked and no heat exchanges between the fluid and the plate at this point, which can be considered as a topological change of the channel. Figure 6 shows the variation of the temperature error with the middle height. As in previous sections, the error in temperature is still dependent on the Peclét number; the larger the Peclet, the larger the error in temperature. However, unlike the previous sections, the temperature error increases slightly with the decrease of the middle height when $\beta = 8$, i.e. when the height transition is sharp. When $\beta = 1$, the temperature error is not sensitive to the variation in the middle height. The above shows that dramatic height variations can have a certain effect on the accuracy of the temperature but remain within acceptable ranges and that errors from height variations can be greatly eliminated by limiting the height transition sharpness.

Fig. 6

Average relative error of temperature between the reduced and full model at different very small middle heights

Figure 7 shows the errors in the temperature gradient for different parameters. The error in the temperature gradient is still influenced by both the height transition sharpness and the middle height. As the middle height decreases, the effect of the height transition sharpness becomes more significant. When $h_\text {mid} = 0.01$, the temperature gradient error can become very large from 30 to 45%. However, when using a small height transition sharpness, the error in the temperature gradient is significantly reduced.

From the above analysis, it can be concluded that the reduced-dimensional model has good first-order accuracy. Even when the height varies dramatically, the error of the reduced-dimensional model remains within an acceptable range. The second-order accuracy of the reduced-dimensional model is very sensitive to height variations, and when the difference between the middle position and the surrounding height is large, a small transition sharpness is required to keep the accuracy acceptable. In the optimisation, PDE filter is used to ensure that height variations are smooth, the implementation and impact of which will be described subsequently.

Fig. 7

Average relative error of the gradients of temperature between the reduced and full models at different very small middle heights

4 Optimisation formulation

This section presents a linear interpolation scheme that combines the proposed reduced-dimensional model with the density-based method and implementation details for the topography and topology optimisation of the fluid channels. In this section, two heat exchanger optimisation examples are also presented, and the optimisation problem formulations for each are given.

4.1 Design parameterisation

The local height of the channel between the parallel plates is coupled to a design variable field $\gamma \in [0,1]$, and the height of the channel is defined as:

$$\begin{aligned} h\left( x_1,x_2 \right) = h_\text {min} + \left( h_\text {max}-h_\text {min} \right) \gamma \left( x_1,x_2 \right) \end{aligned}$$

(10)

where $h_\text {min}$ is the minimum height, $h_\text {max}$ is the maximum height. The intermediate design variable corresponds to the intermediate channel height, which gives it physical meaning and breaks the restriction of the design variable of the traditional density-based method to a binary value of 0–1. Design variables are defined at the nodes of the elements and interpolated within the elements using a linear shape function. Similarly, the optimised height field is interpolated within the elements using a linear shape function and the 3D geometry surface can be generated directly from the nodal heights via the parametric surface function in the geometry interface of COMSOL. A Helmholtz-type PDE filter (Lazarov and Sigmund 2010) is employed to avoid potential numerical problems during the optimisation process and to limit channel height variations to avoid inaccurate representation of the reduced model caused by drastic variations. The filter radii $R_\text {min}$ is determined by the following equation:

$$\begin{aligned} R_\text {min} = \max \left( \frac{h_\text {max}-h_\text {min}}{\nabla h_\text {max}},2.4 h_\text {elem} \right) \end{aligned}$$

(11)

where $\nabla h_\text {max}$ is the predefined maximum gradient of height variation and $h_\text {elem}$ is the size of the element. The height gradient constraint is introduced by the requirement of model accuracy, by sacrificing some optimisation space to achieve an acceptable accuracy.

4.2 Implementation details

All optimisation work in this section are carried out completely within COMSOL Multiphysics Version 6.0 (COMSOL 2022). The “Weak Form PDE” interface is used to implement the proposed reduced model and to simulate fluid flow and heat transfer. The “Coefficient Form PDE” interface is used to implement the PDE filter. The “Optimisation module” is used to define the design variable field and the objectives and constraints of the optimisation problem. It is worth noting that the entire derivation and calculation of the sensitivity is done within COMSOL, and the adjoint sensitivity for the optimisation problem is calculated using the built-in algebraic differentiation method. The GCMMA method is also implemented in COMSOL to solve optimisation problems. The parameter settings for GCMMA will be given in the specific optimisation problem.

4.3 Square heat exchanger

4.3.1 Geometry and boundaries

Fig. 8

Problem setup for the square heat exchanger optimisation problem. Parameters are given in Table 2

Figure 8 shows the setup for the square heat exchanger optimisation problem. The square heat exchanger consists of a large square heat transfer area and two small square inlet and outlet areas. The height range of the fluid channels is $[h_\text {min}, h_\text {max}]$, the height of the boundary $\Gamma _\text {min}$ is $h_\text {min}$ and the height of the inlet $\Gamma _\text {in}$ and the outlet $\Gamma _\text {out}$ is $h_\text {max}$. The temperature of the upper and lower surfaces of the channel is $T_\text {s}$. The fluid inflow velocity is parabolic with a maximum velocity of $U_\text {in}$ and the temperature is polynomial with a minimum temperature of $T_\text {in}$. The fluid flows out of the outlet and the pressure is 0 Pa. The heat transfer fluid is a concentration of 50% of ethylene glycol, a commonly used cooling agent in engineering, with a density of $\rho$ and a viscosity of $\mu$. The parameters of the dimensional and physical properties of the problem are shown in Table 2.

Table 2 Parameters for the square heat exchanger

4.3.2 Problem formulation

The aim of this example is to maximise the heat transfer performance of the square heat exchanger, while constraining the pressure drop of the flow to ensure a fluent internal flow. Heat transfer performance can be represented as the heat flux difference between the inlet and outlet, since a fixed velocity and temperature boundary is employed at the inlet, this objective can be simplified to maximise the heat flux at the outlet. The pressure at the outlet is set to 0 Pa, so the pressure drop of the flow channel is equal to the inlet pressure. This optimisation problem is established as follows:

$$\begin{aligned} \underset{\gamma }{\text {Maximise: }}&\phi _\text {out} \nonumber \\ \text {Subject to: }&\Delta P < P^* \end{aligned}$$

(12)

with

$$\begin{aligned} \phi _\text {out}= & {} \frac{1}{|\Gamma _\text {out}|} \int _{\Gamma _\text {out}} \rho c_\text {p}Tu \ dL \end{aligned}$$

(13)

$$\begin{aligned} \Delta P= & {} \frac{1}{|\Gamma _\text {in}|} \int _{\Gamma _\text {in}} P \ dL \end{aligned}$$

(14)

where $\Gamma _\text {out}$ is the boundary of the outlet, $\Gamma _\text {in}$ is the boundary of the inlet, $P^*$ denotes the upper limit of pressure drop, which is typically determined by scaling the pressure drop of initial or reference design. It is important to stress that the pressure drop constraint is essential in this optimisation problem. Without the pressure drop constraint, the channel height would be minimised driven by the objective to maximise the outlet temperature, but this is not practically efficient. The pressure drop constraint ensures that the flow channel is continuous, making the optimised design practically effective.

4.4 Manifold heat exchanger

4.4.1 Geometry and boundaries

Fig. 9

Problem setup for the manifold heat exchanger. Parameters are given in Table 3

Figure 9 shows the setup for the manifold heat exchanger optimisation problem. The manifold heat exchanger consists of a narrow inlet, a rectangular region where heat exchange takes place, and three narrow outlets. The difference from the square heat exchanger is that the manifold heat exchanger has multiple outlets and is asymmetrically distributed, making the heat flux uniform across the different outlets is the main challenge of this optimisation problem. The boundary conditions and the properties of the heat transfer fluid are consistent with previous examples and the parameters are shown in the Table 3.

Table 3 Parameters for the manifold heat exchanger example

4.4.2 Problem formulation

The aim of this example is to improve the total heat transfer performance while keeping the heat flux of three outlets consistent. The objective is still to maximise the outlet heat flux. The heat exchanger has three outlets, so the objective is to optimise the average heat flux across the three outlets. This example aims to achieve equal heat energy delivered by each outlet. Therefore, in addition to the pressure drop constraint, the heat flux at each outlet needs to be constrained to be within a given range of the average outlet heat flux. The optimisation problem is established as follows:

$$\begin{aligned} \underset{\gamma }{\text {Maximise: }}&\phi _\text {out} \nonumber \\ \text {Subject to: }&\Delta P < P^* \nonumber \\&\phi _\text {out}^{i} \le \phi _\text {out} + \varepsilon \quad \text {for} \quad i=1,2,3\nonumber \\&\phi _\text {out}^{i} \ge \phi _\text {out} - \varepsilon \quad \text {for} \quad i=1,2,3 \end{aligned}$$

(15)

with

$$\begin{aligned} \phi _\text {out}= & {} \frac{1}{|\Gamma _\text {out}|} \int _{\Gamma _\text {out}} \rho c_\text {p}Tu \ dL \end{aligned}$$

(16)

$$\begin{aligned} \phi _\text {out}^{i}= & {} \frac{1}{|\Gamma _\text {out}^{i}|} \int _{\Gamma _\text {out}^{i}} \rho c_\text {p}Tu \ dL \end{aligned}$$

(17)

where $\Gamma _\text {out}=\Gamma _\text {out}^{1} \cup \Gamma _\text {out}^{2} \cup \Gamma _\text {out}^{3}$ is the boundary of three outlets, $\Gamma _\text {out}^{i}$ is the boundary of the i-th outlet, $\varepsilon$ is a small value that constrains the heat flux at each outlet to a range of $[\phi _\text {out}-\varepsilon$, $\phi _\text {out}+\varepsilon ]$, herein set to $\varepsilon = 0.025\phi _\text {out}$.

5 Optimisation results

5.1 Square heat exchanger

The setup for the square heat exchanger optimisation example is shown in Fig. 8. It is discretised using quadrilateral elements with lengths of 0.25 mm and mesh refinement for the inlet and outlet areas. A total of around 64,000 elements and 40,000 design variables are generated. The maximum height gradient $\nabla h_\text {max}=2$ and the filter radii $R_\text {min}=0.9$ mm calculated by Eq. 11. The maximum number of outer iterations is 300, the number of inner iterations of the GCMMA solver is 3, and the convergence criterion is $10^{-4}$.

5.1.1 Different pressure drop constraints

This subsection shows the optimisation results for different pressure drop constraints. The minimum height of the channel is kept constant and set to 0.2 mm. Taking the pressure drop of the initial design with $\gamma =1$ as the reference pressure drop $P_\text {0}$, the pressure drop constraint can be expressed as $P^* = f_\text {p} P_\text {0}$. where $f_\text {p} \in \{1, 1.1, 1.2, 1.3, 1.4, 1.5\}$.

Fig. 10

Height distribution for optimised designs with different pressure drop constraints $\Delta P < f_\text {p} P_0$

Figure 10 shows the optimised designs for different pressure drops. The optimised height distribution can be considered as consisting of two parts: the part near the inlet, shaped like an unfolded leaf, which increases the contact area with the incoming fluid; and the part near the outlet, which exchanges heat with the fluid bypassing the inlet part and helps the fluid to converge at the outlet, allowing a sufficient heat exchange between the fluid and the channel. Furthermore, the height distribution is strongly dependent on the pressure drop constraint, the minimum height area increases as the pressure drop increases. This is because the small height area has a larger contact area with the fluid, which enhances heat transfer, and the optimisation algorithm is driven by the objective to produce the minimum height area. However, this area also provides high resistance, generating a large pressure drop and is therefore strictly limited by the pressure drop constraint.

Fig. 11

Temperature, velocity, pressure distribution for optimised designs with different pressure drop constraints: a is the initial design; b–e are optimised designs with constraint $\Delta P < f_\text {p} P_0$

Figure 11 shows the temperature, velocity, and pressure distributions of optimised designs with different pressure drops. As can be seen from the figure, the overall temperature of the fluid increases as the pressure drop constraint is relaxed, i.e. the heat transfer efficiency is improved and all the optimised designs are significantly improved compared to the initial design. For the pressure distribution, it can be seen that the pressure drop between the inlet and outlet also increases, but always satisfies the pressure constraint.

Fig. 12

Height distribution of the optimised design obtained with different lower height limits $h_\text {min} = f_\text {h} h_\text {max}$. The colour scale of the height distribution is the same for all subfigures

5.1.2 Different minimum height limits

This subsection investigates the effect of different minimum height limits on the optimised design and its performance. The pressure drop constraint is set to $P^*=1.1P_0$ and the minimum height $h_\text {min} = f_\text {h} h_\text {max}$, where $f_\text {h} \in \{0.001, 0.01, 0.1, 0.2, 0.3, 0.4\}$.

Figure 12 shows the optimised height distribution at different minimum height limits. It can be seen that the basic layout of the height distribution is not affected by the minimum height variation, which affects only local details. As the minimum height limits increase, the minimum height area gradually increases and merges into a continuous area. The reason for this is that as the minimum height increases, the minimum area has less resistance to flow and produces a lower pressure drop. With a constant pressure drop constraint, larger minimum height areas can be generated. Furthermore, when $f_\text {h}$ is equal to 0.001 and 0.01, there is no minimum height area in the optimised height layout. This is because the intermediate heights can provide better heat transfer performance, and therefore the optimised design prefers to generate intermediate heights rather than minimum heights.

Fig. 13

The outlet heat flux and the minimum height in the optimised design obtained for different lower height limits. The initial design has an inlet heat flux of $5.315\times 10^7$ W/m$^2$ and an outlet heat flux of $5.698\times 10^7$ W/m$^2$

To show the effect of minimum height limits on the optimisation results, Fig. 13 shows the outlet heat flux, minimum height and minimum design variables for optimised designs with different limits. The graph shows that the outlet heat flux increases as the minimum height limit decreases: when the minimum height limit is greater than 0.4 mm, the outlet heat flux increases more rapidly; when the limit reaches 0.2 mm, the heat flux gradually converges. When the height limit is greater than 0.4 mm, the minimum design variable is almost 0, and the minimum height almost coincides with the height limit, which means that the design variable is limited during the optimisation process. This results in a lower heat flux. When the limit decreases, the optimisation design space expands and the objective improves, which explains the significant increase in heat flux in this interval. When the height limit is less than 0.2 mm, it can be found that the minimum height gradually converges and the corresponding heat flux changes slowly. At this stage, the minimum height in the design is higher than the limit, and the corresponding design variables are greater than 0. This indicates that when the design variables are not restricted during the optimisation process, the design with the intermediate design variable has a greater outlet heat flux than the design with a minimum design variable of 0, i.e. the topography design has better heat transfer performance than the topology design. This conclusion is validated by the verification example in Appendix D.

Fig. 14

Comparison of velocity, temperature and pressure obtained using the full three-dimensional model and the reduced-dimensional model

Fig. 15

Comparison of temperature profiles in the height direction between the reduced-dimensional model and the full three-dimensional model at selected positions. The figure on the left shows the selected position on the plane $x_1 = l_\text {des}/2$

Table 4 Comparison of calculation results between the reduced-dimensional model and the full three-dimensional model

5.1.3 Verification with three-dimensional model

In order to verify the optimisation results using the reduced-dimensional model, this subsection will take the previous optimised design with the pressure drop constraint $f_\text {p} = 1.3$ as an example, generate a 3D geometry based on its optimised height distribution, and analyse it using the reduced-dimensional model and the full 3D model, respectively. Where the reduced-dimensional model is defined on the mid-plane of the 3D model, the same mesh is used for the computation to allow for a fair comparison. Figure 14 shows the 3D geometry and the comparison of temperature, velocity, and pressure between the two models. The figure shows that the distributions of temperature, velocity, and pressure for the 3D model are all consistent with those obtained from the reduced-dimensional model.

The above comparison shows the temperature in the mid-plane. To demonstrate that the reduced-dimensional model is still accurate in the height direction, this subsection compares the temperature distribution in the height direction for the three-dimensional model with the reduced-dimensional model at three representative positions. The selected positions are shown in Fig. 15. Position 1 has the maximum channel height, where the fluid is fully exchanged and the temperature difference in the height direction is small; Position 2 has a slightly lower channel height than the maximum height, where the fluid is not fully exchanged and the temperature difference in the height direction is large; Position 3 has a very small channel height and the fluid temperature is low. The comparison of the temperatures at the three positions is shown in Fig. 15. For different heights and different temperature differences, the temperature profiles in the height direction of the two models are in good agreement, which fully demonstrates the accuracy of the reduced-dimensional model. In addition, the temperature profiles obtained from the 3D model are not smooth. This is because the mesh in the height direction is not fine enough. If finer meshes were used, the temperature error between the two models would probably be smaller, which demonstrates the requirement for finer meshes to use the 3D model and further demonstrates the high computational cost required for the 3D model.

To quantify the error between the two models, Table 4 shows a comparison of the temperature and pressure drop and the calculation time between the two models. Where the errors in both temperature and pressure drop between the two models are kept at acceptable levels. It is notable that the computation times between the two models show a significant difference. With the same mesh, the computation time for the reduced-dimensional model is only 1.2% of that for the three-dimensional model, which allows the optimisation design problem of 3D conjugate heat transfer problems to be performed at an extremely low computational cost.

5.2 Manifold heat exchanger

The setup for the manifold heat exchanger optimisation problem is shown in Fig. 9. Quadrilateral elements with side lengths of 0.25 mm are used for discretization. A total of around 48,000 elements and 32,000 design variables are obtained by mesh refinement of the inlet and outlet areas. The maximum height gradient $\nabla h_\text {max}=2$ and the filter radii $R_\text {min}=0.9$ mm. The maximum number of outer iterations is 300, the number of inner iterations of the GCMMA solver is 3, and the convergence criterion of the optimisation objective is $10^{-4}$.

5.2.1 Different pressure drop constraints

As demonstrated in the previous examples, the pressure drop constraint has a significant effect on the optimisation results, so in this section different pressure drop constraints are used for optimisation and analyses and compares the different designs. The minimum height of the channel $h_\text {min} = 0.2$ mm and the maximum pressure drop $P^* = f_\text {p} P_0$, where $P_0$ is the reference pressure drop at the maximum height $h_\text {max}$ and $f_\text {p} \in \{1.00, 1.05, 1.10, 1.15, 1.20\}$.

Fig. 16

Height distribution, temperature, velocity, pressure distribution for optimal designs with different pressure drop constraints $\Delta P < f_\text {p} P_\text {0}$

Table 5 Heat flux at the outlets of optimised design with different pressure drop constraints

Table 5 shows the total corrected heat flux, the average heat flux, and the standard deviation of the heat fluxes for the optimised design obtained with different pressure drop constraints. To emphasises the increased heat flux of the system, the corrected total heat flux was calculated with the following equation:

$$\begin{aligned} \phi _\text {corrected} = \frac{1}{|\Gamma _\text {out}|} \int _{\Gamma _\text {out}} \rho c_\text {p}\left( T-T_\text {ref} \right) u \ dL \end{aligned}$$

(18)

Compared to the initial design, the corrected heat flux of the optimised design significantly increased. As $f_p$ increases, the heat exchange performance improves. Furthermore, it can be observed that the standard deviation of the heat flux at the outlets is significantly reduced compared to the initial design, which means that the energy output from each outlet tends to be equal.

Figure 16 shows the optimised channel height distribution, as well as the temperature, velocity, and pressure distributions for different pressure drop constraints. The minimum height area increases as the pressure drop constraint is relaxed, which is consistent with the previous conclusion. The optimised height distribution can be divided into three sections according to the outlet, each of which increases the contact surface area with the incoming flow through a curved structure to enhance heat transfer. As shown in Table 5, the initial design has the largest average heat flux at outlet $\Gamma ^1_\text {out}$ and the smallest heat flux at outlet $\Gamma ^3_\text {out}$. Driven by the objective of maximising the outlet heat flux and the constraint on the heat flux, the algorithm will improve the heat flux at the outlet $\Gamma ^3_\text {out}$ and slightly reduce the heat flux at the outlet $\Gamma ^1_\text {out}$ to the average value. From the point of view of structural variation, the algorithm focusses on optimising the structure near the outlet $\Gamma ^1_\text {out}$ and the outlet $\Gamma ^2_\text {out}$ when the pressure drop constraint is strict. On the one hand, the contact area between the two outlets and the incoming flow is increased to enhance heat transfer; on the other hand, the flow at the two outlets is restricted so that the outlet $\Gamma ^3_\text {out}$ can receive sufficient flow to improve the heat flux at the outlet $\Gamma ^3_\text {out}$. When the pressure drop constraint is relaxed, the algorithm increases the details of the structure while maintaining the main layout of the structure, allowing for a larger heat exchange area and, therefore, the overall heat transfer performance is improved.

Fig. 17

Three-dimensional geometry of the initial design and the optimised design obtained with different filter radii

Fig. 18

Temperature distributions in the full three-dimensional model and the reduced-dimensional model for the initial design, the optimised design with $\nabla h_\text {max}=1$, the optimised design with $\nabla h_\text {max}=2$, and the optimised design with $\nabla h_\text {max}=3$

5.2.2 Different filter radii and Verification using 3D model

As shown in previous sections, drastic height variations can introduce additional model errors and this paper limits the height variation gradient by changing the radii of the PDE filter. This subsection investigates the effect of different filter radii on the 3D optimised design and verifies the reliability of the 3D optimised design obtained from the reduced-dimensional model by comparing the results with those of the full three-dimensional model. In this subsection, the minimum height $h_\text {min} = 0.1 h_\text {max}$ and the maximum pressure $P^* = 1.05P_0$. The filter radii are determined by Eq. 11, where $\nabla h_\text {max}$ is taken as $\{$1, 2, 3$\}$.

Figure 17 shows the 3D geometry of the optimised designs with different filter radii. The topography of the channel changes significantly after optimisation. The main layout of the channel heights is essentially the same for the different designs, but the design with a large $\nabla h_\text {max}$, i.e. a smaller filter radii, has more details and the height of the channel varies more dramatically, whereas the design with a small $\nabla h_\text {max}$, i.e. a larger filter radii, has a gentler variation in height. The 3D geometry is discretised and analysed using fine meshes. The mesh used for validation is given in Appendix B.

Table 6 Error between reduced-dimensional model and full three-dimensional model for optimised designs with different filter radii

Fig. 19

Temperature gradient distributions in the full three-dimensional model and the reduced-dimensional model for the initial design, the optimised design with $\nabla h_\text {max}=1$, the optimised design with $\nabla h_\text {max}=2$, and the optimised design with $\nabla h_\text {max}=3$

Figure 18 compares the temperature distributions for different designs between using the reduced-dimensional model and the three-dimensional model. The temperature distribution obtained using the reduced-dimensional model matches the results of the three-dimensional model very well. In addition, compared to the initial design, both optimised designs increase the temperature at the outlet and improve the uniformity of the temperature at the outlet. To more intuitively compare the performance of the different optimised designs and the error between the reduced-dimensional model and the three-dimensional model, Table 6 shows the total power of heat exchange, the outlet heat flux and its standard deviation, and the overall temperature error obtained using the different models.

Table 6 shows that the optimised design significantly improves the heat transfer performance and the uniformity of the heat flux at the outlet compared to the initial design. There is little difference in performance between the optimised designs for different filter radii, and the performance of the optimised designs increases as the filter radii decreases. The optimised design performs best when the filter radii are the smallest, i.e. $\nabla h_\text {max}=3$: the average heat flux at the outlet is highest, the total power of heat exchange is highest, and the uniformity of the heat flux at the outlet is best. This makes sense, as a smaller filter radii means less restriction on the optimisation, and therefore the optimised design has better performance. However, as the filter radii become smaller, the errors in the total heat exchange power increase. This could be attributable to: 1. As the filter radii decreases, the height variation in the optimised design becomes steeper, which leads to increased errors in the reduced-dimensional model. 2. The geometric features of the model are lost when generating the three-dimensional geometry, and the detailed variation is not fully represented in the full three-dimensional model, which leads to an increase in error between the three-dimensional model and reduced model. However, the error in total heat exchange power is kept within 5%, the error in overall temperature is kept within 3%, and the error in average outlet heat flux is kept within 3%. These errors are all within acceptable ranges, which demonstrates that the reduced-dimensional model has sufficient accuracy for optimisation.

The above results show the overall error in the optimised design for the reduced-dimensional model. To further investigate the local errors, Fig. 19 shows the temperature gradient distributions along the surface for the optimised designs with different filter radii for both the reduced-dimensional model and the full model. For comparison purposes, all gradient distributions are plotted on the same scale. Firstly, the full model has a larger temperature gradient at the inlet, which explains why the temperature at the inlet of the full model rises faster than that of the reduced-dimensional model. In addition, as $\nabla h_\text {max}$ increases, the full model exhibits a higher temperature gradient at the height variations close to the inlet. However, the above errors are only observed at the tip of the height variation, and the overall temperature gradient distribution still fits very well. The above temperature gradient distribution demonstrates that all the optimised designs with filter radii considered in this paper satisfy the height variation requirements of the reduced-dimensional model.

6 Concluding remarks

This paper extends the reduced-dimensional model proposed by Alexandersen (2022) for fluid optimisation to the optimisation of conjugate heat transfer between parallel plates with constant temperature and a fluid channel with varying height. The plates are assumed to be of a predefined and constant temperature as an initial approximation and can be seen as a special case of the phase transition of a PCM inside the plates. The proposed model includes conduction and convection in the fluid based on a generalised convection-diffusion equation arising from the assumptions of the out-of-plane profiles. In addition, the present work applies the reduced-dimensional model to the free topology and topography optimisation of the structure using a linear interpolation of the height with respect to the design variable. This ensures full physical interpretation of all design variables, including intermediate values.

The reduced-dimensional model demonstrates its reasonable accuracy and limitations through in-depth parametric analysis. Reduced-dimensional models can obtain accurate temperature distributions even with dramatic height variations. However, for temperature gradients normal to the surface, the reduced-dimensional model needs to impose certain limits on the gradient of height variation to obtain accurate temperature gradients when the height difference is large. When applying the reduced-dimensional model to optimisation, this work achieves the restriction of the height gradient during optimisation by limiting the filter radius, the effectiveness of which is also demonstrated in the verification example of the optimised design. During the optimisation process, it is found that with the use of linear height interpolation, the optimisation algorithm avoids generating very small heights, i.e. topological variations, and prefers to generate intermediate heights, i.e. topographical variations. It is verified by the three-dimensional physical model that the topography design has better heat transfer performance than the topology design and that topography optimisation can result in a better design than traditional optimisation. Furthermore, in comparison with traditional optimisation using the full three-dimensional model, it is demonstrated that optimisation using the reduced-dimensional model can achieve an equivalent optimised design at a lower computational cost.

Regarding future work, the model is being further extended to consider temperature variations in solid plates and more complex boundary conditions. It is also planned to extend the model to transient heat transfer problems, as well as plates filled with phase change materials. In addition, to solve practical engineering problems, the strength and manufacturability of the structure will be further considered in the future.

Appendices

Appendix A: Derivation of the reduced-dimensional model for heat transfer

Fig. 20

Schematic diagram of the height-varying control volume used to calculate the energy conservation equation

$$\begin{aligned}&\iint _{-\frac{h\left( x_2 \right) }{2}}^{\frac{h\left( x_2 \right) }{2}} \rho c_{p} u_{2} T - k\frac{\partial T}{\partial x_2} \,dx_{3}\,dx_{1} \nonumber \\&\quad - \iint _{-\frac{h\left( x_2+\Delta x_2 \right) }{2}}^{\frac{h\left( x_2+\Delta x_2 \right) }{2}} \rho c_{p} u_{2} T - k\frac{\partial T}{\partial x_2} \,dx_{3}\,dx_{1}\nonumber \\&\quad + \iint _{-\frac{h\left( x_1 \right) }{2}}^{\frac{h\left( x_1 \right) }{2}} \rho c_{p} u_{1} T - k \frac{\partial T}{\partial x_1} \,dx_{3}\,dx_{2}\nonumber \\&\quad - \iint _{-\frac{h\left( x_1+\Delta x_1 \right) }{2}}^{\frac{h\left( x_1+\Delta x_1 \right) }{2}} \rho c_{p} u_{1} T - k \frac{\partial T}{\partial x_1}\,dx_{3}\,dx_{2} \nonumber \\&\quad + \iint _{}^{} k\frac{\partial T}{\partial x_3}|_{x_3= \frac{h}{2}} - k\frac{\partial T}{\partial x_3}|_{x_3=-\frac{h}{2}} \,dx_{1}\,dx_{2} = 0 \end{aligned}$$

(A1)

$$\begin{aligned}&\left. \left( \frac{\rho c_\text {p}}{525} \left( \bar{u}_2 h \left( 272\bar{T} + 78\bar{T}_\text {s} \right) \right) \right. \right. \nonumber \\&\quad \left. \left. - \frac{16k}{25}\left( \frac{\partial h}{\partial x_2}\left( \bar{T} -\bar{T}_\text {s} \right) - h \frac{\partial }{\partial x_2} \left( \bar{T} + \frac{9}{16} \bar{T}_\text {s} \right) \right) \right) \right| _{x_2=x_2}\Delta x_1 \nonumber \\&\quad - \left. \left( \frac{\rho c_\text {p}}{525} \left( \bar{u}_2 h \left( 272\bar{T} + 78\bar{T}_\text {s} \right) \right) \right. \right. \nonumber \\&\quad \left. \left. - \frac{16k}{25}\left( \frac{\partial h}{\partial x_2}\left( \bar{T} -\bar{T}_\text {s} \right) - h \frac{\partial }{\partial x_2} \left( \bar{T} + \frac{9}{16} \bar{T}_\text {s} \right) \right) \right) \right| _{x_2=x_2+\Delta x_2}\Delta x_1 \nonumber \\&\quad + \left. \left( \frac{\rho c_\text {p}}{525} \left( \bar{u}_1 h \left( 272\bar{T} + 78\bar{T}_\text {s} \right) \right) \right. \right. \nonumber \\&\quad \left. \left. - \frac{16k}{25}\left( \frac{\partial h}{\partial x_1}\left( \bar{T} -\bar{T}_\text {s} \right) - h \frac{\partial }{\partial x_1} \left( \bar{T} + \frac{9}{16} \bar{T}_\text {s} \right) \right) \right) \right| _{x_1=x_1}\Delta x_2 \nonumber \\&\quad - \left. \left( \frac{\rho c_\text {p}}{525} \left( \bar{u}_1 h \left( 272\bar{T} + 78\bar{T}_\text {s} \right) \right) \right. \right. \nonumber \\&\quad \left. \left. - \frac{16k}{25}\left( \frac{\partial h}{\partial x_1}\left( \bar{T} -\bar{T}_\text {s} \right) - h \frac{\partial }{\partial x_1} \left( \bar{T} + \frac{9}{16} \bar{T}_\text {s} \right) \right) \right) \right| _{x_1=x_1+\Delta x_1}\Delta x_2 \nonumber \\&\quad - \left( \frac{16k}{5}\left( \frac{\bar{T}-\bar{T}_\text {s}}{h} \right) + \frac{16k}{5}\left( \frac{\bar{T}-\bar{T}_\text {s}}{h} \right) \right) \Delta x_1\Delta x_2 =0 \end{aligned}$$

(A2)

$$\begin{aligned}&-\frac{\rho c_\text {p}}{525}\frac{d}{dx_{2}}\left( \bar{u}_{2} h \left( 272\bar{T}+ 78\bar{T}_\text {s} \right) \right) \nonumber \\&\quad + \frac{16 k}{25} \frac{d}{dx_{2}} \left( \frac{\partial h}{\partial x_{2}}\left( \bar{T} - \bar{T}_\text {s} \right) + h \frac{\partial }{\partial x_{2}} \left( \bar{T} + \frac{9}{16} \bar{T}_\text {s} \right) \right) \nonumber \\&\quad - \frac{\rho c_\text {p}}{525}\frac{d}{dx_{1}}\left( \bar{u}_{1} h \left( 272\bar{T}+ 78\bar{T}_\text {s} \right) \right) \nonumber \\&\quad + \frac{16 k}{25} \frac{d}{dx_{1}} \left( \frac{\partial h}{\partial x_{1}}\left( \bar{T} - \bar{T}_\text {s} \right) + h \frac{\partial }{\partial x_{1}} \left( \bar{T} + \frac{9}{16} \bar{T}_\text {s} \right) \right) \nonumber \\&\quad - \frac{32k}{5} \left( \frac{\bar{T} - \bar{T}_\text {s}}{h} \right) = 0 \end{aligned}$$

(A3)

$$\begin{aligned}&\frac{\rho c_\text {p}}{525} \frac{\partial }{\partial x_{i}} \left( \bar{u}_{i} h \left( 272 \bar{T} + 78 \bar{T}_\text {s} \right) \right) \nonumber \\&\quad - \frac{16 k}{25}\frac{\partial }{\partial x_{i}} \left( \frac{\partial h}{\partial x_{i}}\left( \bar{T} - \bar{T}_\text {s} \right) + h \frac{\partial }{\partial x_{i}} \left( \bar{T} + \frac{9}{16} \bar{T}_\text {s} \right) \right) \nonumber \\&\quad + \frac{32k}{5} \left( \frac{\bar{T} - \bar{T}_\text {s}}{h} \right) = 0 \end{aligned}$$

(A4)

The control volume shown in Fig. 20 considers the variation in height. Based on the dimensions of the control volume and the heat exchange on the control volume surfaces shown in the figure, the heat conservation equation is given in Eq. A1.

The above equation assumes that the control volume is symmetric about the plane $x_3=0$. Substituting the velocity and temperature profile functions (Eq. 3) into Eq. A1 and solving the integration yields Eq. A2.

Rearranging the Eq. A2 and dividing by $\Delta x_{1}\Delta x_{2}$, since the size of the control volume $\Delta x_{1}\rightarrow 0$ and $\Delta x_{2}\rightarrow 0$, the differential Eq. A3 can be obtained according to the relationship between limits and derivatives.

Sorting Eq. A3 gives the final heat conservation equation as shown in Eq. A4.

Appendix B: Mesh validity study

1.1 B.1 Validation example

Section 3 validates the reduced-dimensional model using a three-dimensional model. In this subsection, the parameter group with $Pe = 500$, $h_\text {mid} = 0.6$, $\beta = 8$ is chosen as an example for the demonstration of mesh validity. The 3D mesh consists mainly of tetrahedral elements with a total number of 334,754. As this validation example investigates the temperature error in the mid-plane and the temperature gradient error along the surface, this section uses the average temperature in the mid-plane and the heat flux difference between the inlet and outlet as the measure of mesh validity, and the number of elements is expressed in terms of the DOFs solved instead, and the objective varies with DOFs as shown in Fig. 21. The blue line in the graph represents the average temperature of the mid-plane, and the yellow line shows the heat flux difference. Both the indices gradually decrease and converge as the number of DOFs increases. After considering both computational cost and accuracy, the validation example in Sect. 3 uses the mesh with DOFs = 1,825,249, which provides relatively accurate results.

The mesh for the reduced-dimensional model consists entirely of quadrilateral elements, with a total of 66,500 elements. Although the 2D mesh for the reduced-dimensional model has only 1/5 of the number of elements of the 3D mesh, it is finer than the 3D mesh in the mid-plane. Based on this framework, the independence of the mesh is investigated by changing the size of the elements. The average temperature and the heat flux difference are used as measures of the effectiveness of the mesh, and the measures varied with DOFs as shown in Fig. 22. The blue line in the graph represents the average temperature, and the yellow line shows the heat flux difference. The temperature converges quickly, and the heat flux difference converges gradually as the number of DOFs increases. Section 3 takes the mesh with DOFs = 668,100, which can achieve satisfactory precision for both the temperature and energy calculations.

Fig. 21

The average temperature and heat flux difference of the full three-dimensional channels in Sect. 3 varies with the number of DOFs

Fig. 22

The average temperature and heat flux difference of the channels using reduced-dimensional model in Sect. 3 varies with the number of DOFs

1.2 B.2 Square heat exchanger optimisation example

Section 5.1 shows the optimisation results for the square heat exchanger. The mesh used for the optimisation consists of quadrilateral elements. Since the design variables are defined at the nodes, the number of elements is related to the computational cost. In addition, the meshes at the inlet and outlet are refined to improve the accuracy of the results. Figure 23 shows the effect of the number of elements on the optimisation objective and optimisation time.

Fig. 23

The heat flux difference of the optimised design in Sect. 5.1 and the optimisation time varies with the number of design variables

The blue line in Fig. 23 shows the heat flux difference of the optimised design, and the yellow line shows the corresponding optimisation time consumed. Both the objective value and the optimisation time increase as the number of design variables increases, but the objective value increases more slowly while the optimisation time increases more rapidly. This is because when there are few design variables, the increase in design variables mostly changes the main part of the structure and substantially improves the optimisation objective, while when there are more design variables, the increase in design variables mainly changes the details of the structure and therefore improves the optimisation objective less. The graph shows that when the design variables are greater than 40,501, the objective is not greatly improved, but the optimisation time grows faster. Therefore, considering the optimisation objective and the computational cost, a mesh of 40,501 design variables is selected for optimisation.

1.3 B.3 manifold heat exchanger optimisation example

Section 5.2.2 produces 3D geometry based on optimised designs with different filter radii and uses the full 3D model to calculate the heat flux and other performance. As the optimised design with $\nabla h_\text {max}=3$ is more complex than the other designs, this section takes the optimised design with $\nabla h_\text {max}=3$ as an example to demonstrate the validity of the verification mesh. The verification mesh consists mainly of tetrahedral elements and the number of DOFs to be solved is 19,212,857. In this section, the total power of heat exchange is used as a measure of the effectiveness of the mesh, the number of DOFs to be solved for are used instead of the number of elements, and the heat flux difference varies with the number of DOFs as shown in Fig. 24.

Fig. 24

The heat flux difference of the 3D optimised design with $\nabla h_\text {max}=3$ using the verification mesh varies with the number of DOFs

As can be seen from the figure, when the mesh is coarse, the oscillation of the total power is larger; when the mesh is finer, the total power also oscillates with the number of DOFs to be solved, but the oscillation becomes significantly smaller. When the number of DOFs is 19,212,857, it can be assumed that the total power converges with this mesh. Therefore, the verification mesh used is sufficiently fine, and the obtained results are accurate and reliable.

Appendix C: Results of the parametric analysis

Fig. 25

Comparison of the mid-plane temperature distribution of the reduced model with the full model at different Peclét numbers. The middle height $h_\text {mid}=0.6$ and the transition sharpness $\beta =8$

Fig. 26

Comparison of the mid-plane temperature distribution of the reduced-dimensional model with the full model at different middle heights and transition sharpness when ${Pe}=100$

Fig. 27

Comparison of the surface temperature gradients of the reduced-dimensional model with the full model at different Peclét numbers. The middle height $h_\text {mid}=0.6$ and the transition sharpness $\beta =1$

Fig. 28

Comparison of the surface temperature gradients of the reduced-dimensional model with the full model at different middle heights and transition sharpness when ${Pe}=100$

Figure 25 shows the temperature distribution in the mid-plane for the reduced and full models for different Peclét numbers when $h_\text {mid} = 0.6$ and $\beta = 8$. The reduced model can obtain the same temperature distribution as the full three-dimensional model for different Peclét numbers, i.e. different effects of the heat transfer mechanism. Even for the temperature distribution at and around the depressions, the reduced model still gives satisfactory results.

Figure 26 shows the temperature distribution in the mid-plane for the reduced and full models for different $h_\text {mid}$ and $\beta$ when $Pe = 100$. For both cases of channel height protrusion or depression, the reduced model gives temperature distributions consistent with the full three-dimensional model. It is also observed that when the transition sharpness is large and the height of the channel varies considerably, the temperature of the reduced model varies more rapidly at the height transition than the full model. In contrast, when the height variation is small, the effect of an increasing transition sharpness on the temperature is small.

Figure 27 shows the temperature gradient distribution along the wall for different Peclét numbers when $h_\text {mid} = 0.6$ and $\beta = 1$. The reduced-dimensional model gives an accurate temperature gradient distribution, which suggests that the model can also accurately account for the energy exchange between the fluid and the solid. It can also be seen that when $P_e = 1000$, there is an oscillation in the temperature gradient at height variations. This is due to the increased convective effect and the large change in temperature gradient, which would be mitigated by using a finer mesh, whereas the planar mesh of the reduced-dimensional model is sufficiently fine to obtain a smooth temperature gradient distribution.

Figure 28 shows the distribution of temperature gradients along the wall for different $h_\text {mid}$ and $\beta$ when $Pe = 100$. It can be seen that when the beta increases, the error in the temperature gradient is mainly concentrated at the height variation, and the rest of the temperature gradient is very similar. In addition, $h_\text {mid}$ also has an effect on the temperature gradient; the smaller the height variation, the more accurate the distribution of the temperature gradient in the reduced model.

Appendix D: Verification of the topography design

Fig. 29

Average heat flux at the outlet of fluid channels at different middle heights and corresponding heat flux slices inside the channels

The Sect. 5.1.2 shows that although when the minimum height $h_\text {min} = 0.001 h_\text {max}$, no minimum height region is generated in the optimised design, and the optimised result remains a topography design rather than a topology design. To obtain a topology design, volume constraints, intermediate design variable constraints, and other methods have been introduced to force a discrete 0–1 design. However, all of them did not obtain a topology design. This again demonstrates that topography design possesses better performance than topology design, such that the optimisation algorithm refuses to generate a topology design. To verify this conclusion, this section uses the example of the parallel plate channel with varying middle heights in Sect. 3.2 to investigate the effect of topology variation and topography variation on the heat flux at the outlet. In this subsection, the Peclét number ${Pe}=500$ and the middle height $h_\text {mid}\in \{0.001, 0.1, 0.2, 0.3, 0.4, 0.6\}$ m.

Figure 29 shows the heat flux inside the channel at different middle heights. The solid blue line indicates the average heat flux at the outlet, which corresponds to the previous optimisation objective, and in addition, the heat flux slices inside the channel (the back half of the channel) at different heights are also shown in the figure. The trend of the average heat flux at the outlet shows that the channel has the maximum average outlet heat flux when $h_\text {mid} = 0.3$ m, which confirms that the topology design is not the optimal option and that the topography design can have better heat transfer performance. The heat flux slices in the channel explain the reason for this. When $h_\text {mid} = 0.001$ m, which corresponds to the topology variation, the fluid flows around the middle area, and the fluid does not exchange heat with the middle of the plate, only with the wall and the area on the sides. Although there is an increase in the heat flux locally in the areas on the sides due to the increased velocity, the heat flux in the middle of the outlet is extremely low, resulting in a low average outlet heat flux. Whereas when $h_\text {mid} = 0.6$ m, the fluid obtains good heat transfer in the middle region, but due to the small area of the wall due to the height variation, the heat flux on both sides is not high, and therefore the average heat flux at the outlet is also low. When $h_{mid} = 0.3$ m, which corresponds to the topography variation, the fluid exchanges heat both with the middle area and with the wall areas on the sides, and the maximum heat flux at the outlet is obtained in coordination between the two.

Appendix E: Shape optimisation

Fig. 30

Optimisation boundary conditions of the initial design for shape optimisation and the mesh used for the optimisation

Fig. 31

Comparison of shape-optimised design obtained with full three-dimensional model and topography-optimised design obtained with reduced two-dimensional model

Table 7 Comparison of the parameters of the shape-optimised design obtained with the full three-dimensional model and the topography-optimised design obtained with the reduced two-dimensional model

To verify the effectiveness of topology/topography optimisation using the reduced-dimensional model, this subsection compares the topography-optimised design obtained from the reduced-dimensional model with the shape-optimised design obtained from the full three-dimensional model. All the shape optimisation parameters were set to keep the same as for the optimisation using the reduced-dimensional model. The pressure constraint is $P=1.3P_0$. The mesh and boundary conditions used for the shape optimisation are shown in Fig. 30.

Fig. 31 shows the optimised designs obtained with the different models and their velocity and temperature distributions. The main structure of the shape-optimised design using the full three-dimensional model is the same as that of the topography-optimised design using the reduced-dimensional model, while the topography-optimised design has more detail and a larger heat transfer area between the fluid and the channels, the shape-optimised design has less detail and smoother structure variations. The main reasons for the above differences in the optimised designs are: 1. Due to the limitations of computational resources, the number of design variables for shape optimisation is less than for topography optimisation, resulting in the optimised structure being unable to produce more detail. 2. Due to the limitations of computational resources, the mesh used for the shape optimisation has difficulty representing the desired minimum height in the thickness direction, resulting in the shape optimised design being very similar to the limited design for $h_\text {min} = 0.3$ in the previous section.

Table 7 shows the optimisation performance in terms of heat flux difference, pressure drop, and calculation time for the two designs. Firstly, the topography-optimised design using the reduced-dimensional model has a larger heat flux difference than the shape-optimised design using the full three-dimensional model, which indicates that the topography-optimised design using the reduced-dimensional model has better heat transfer performance. It is also observed that the pressure drops in both designs slightly exceeds the pressure drop constraint, which is an acceptable error due to the re-modelling. In addition, the topography optimisation using the reduced-dimensional model consumes significantly less time than the shape optimisation using the full three-dimensional model. It should be noted that the full three-dimensional model uses only 1/4 of the geometry based on boundary symmetry but still consumes much longer computation time than the reduced-dimensional model, and the design variables for optimisation are also less than those for topography optimisation using the reduced-dimensional model.

This subsection therefore demonstrates that topology/topography optimisation using reduced-dimensional models can produce designs with the same or better performance while significantly reducing computational costs compared to traditional optimisation using full three-dimensional models. This enables the algorithm to optimise while considering more design variables with the same computational resources, resulting in surprisingly detail-rich designs.