Level set topology optimization of cooling and heating devices using a simplified convection model

Abstract

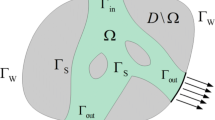
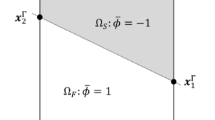
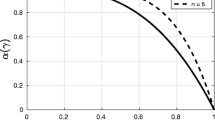
This paper studies topology optimization of convective heat transfer problems in two and three dimensions. The convective fluxes are approximated by Newton’s Law of Cooling (NLC). The geometry is described by a Level Set Method (LSM) and the temperature field is predicted by the eXtended Finite Element Method (XFEM). A constraint on the spatial gradient of the level set field is introduced to penalize small, sub-element-size geometric features. Numerical studies show that the LSM-XFEM provides improved accuracy over previously studied density methods and LSMs using Ersatz material models. It is shown that the NLC model with an iso-thermal fluid phase may over predict the convective heat flux and thus promote the formation of very thin fluid channels, depending on the Biot number characterizing the heat transfer problem. Approximating the temperature field in the fluid phase by a diffusive model mitigates this issue but an explicit feature size control is still necessary to prevent the formation of small solid members, in particular at low Biot numbers. The proposed constraint on the gradient of the level set field is shown to suppress sub-element-size features but necessitates a continuation strategy to prevent the optimization process from stagnating as geometric features merge.

Appendix : A: Parameterized petal geometry level set field

In the petal optimization study of Section 4.2 the level set field is constructed from an overlay of individual level set fields which define the semi-circular base and a sequence of petal shapes swept around the base. The design variables are: the relative petal width, $\tilde {w}$, the combined petal and base length, $\tilde {h}_{t}$, the radius of the circular base, $\tilde {h}_{b}$, and the amplitude of the sinusoidal shaped petal sides, $\tilde {a}$. A single petal and base are depicted in Fig. 10. The fields are combined as follows:

$$ \phi(\tilde{\mathbf{x}}) = min(\phi_{c}(\tilde{\mathbf{x}}), \phi_{p}(\tilde{\mathbf{x}})), $$

(31)

where $\phi _{c}(\tilde {\mathbf {x}})$ is the level set field of the circular base:

$$ \phi_{c}(\tilde{\mathbf{x}}) = \left | \tilde{\mathbf{x}} \right | - h_{b}. $$

(32)

The level set field for each petal is conveniently defined in a local coordinate system:

$$ \left[ \begin{array}{llll} \tilde{x}^{\prime} \\ \tilde{y}^{\prime} \end{array} \right] = \left[ \begin{array}{llll} cos\left( \theta \right) & -sin\left( \theta \right) \\ sin\left( \theta \right) & cos\left( \theta \right) \end{array} \right] \left[ \begin{array}{llll} \tilde{x} \\ \tilde{y} \end{array} \right], $$

(33)

where the angle of the j−t h petal is:

$$ \theta = -\frac{\pi}{2} + \frac{\pi}{n_{p} -1} j \ , $$

(34)

assuming j to be a zero based index. The level set field of each petal describes a cuboid:

$$ \phi_{p}(\tilde{\mathbf{x}}) = \left( \left[ \frac{2 \tilde{x}_{x} \tilde{h}_{b}}{\tilde{w}_{w}} \right]^{p} + \left[ \frac{\tilde{y}_{y} \tilde{h}_{b}}{\tilde{h}_{p}} \right]^{p} \right)^{\frac{1}{p}}, $$

(35)

where p is the sharpness of the cuboid shape and $\tilde {h}_{p}$ is the petal length:

$$ \tilde{h}_{p} = \tilde{h}_{t} - \tilde{h}_{b} \ . $$

(36)

The width, $\tilde {w}_{w}$, varies in radial direction, i.e. $\tilde {y}^{\prime }$, and is defined as:

$$ \tilde{w}_{w} = \frac{\pi}{n_{p} -1} \left( \tilde{h}_{b} \left( \tilde{w}-1\right) - \tilde{y}^{\prime} \right) . $$

(37)

Note the maximum width depends on the number of petals n _p . The axillary coordinates $\tilde {x}_{x}$ and $\tilde {y}_{y}$ are defined as functions of the local coordinates $\tilde {x}^{\prime }$ and $\tilde {y}^{\prime }$:

$$ \tilde{x}_{x} = \tilde{x}^{\prime} - sign\left( -\tilde{x}^{\prime} \right) \tilde{a} \tilde{w}_{w} sin\left( \frac{3}{2} \pi \frac{1}{\tilde{h}_{p}} \left( \tilde{y}^{\prime} - \tilde{h}_{b} \right) \right), $$

(38)

$$ \tilde{y}_{y} = \tilde{y}^{\prime} - \tilde{h}_{b} \ . $$

(39)