Stacking sequence optimisation of an aircraft wing skin

Abstract

This paper demonstrates a stacking sequence optimisation process of a composite aircraft wing skin. A two-stage approach is employed to satisfy all sizing requirements of this industrial sized, medium altitude, long endurance drone. In the first stage of the optimisation, generic stacks are used to describe the thickness and stiffness properties of the structure while considering both structural requirements and discrete guidelines such as blending. In the second stage of the optimisation, mathematical programming is used to solve a Mixed Integer Linear Programming formulation of the stacking sequence optimisation. The proposed approach is suitable for real-world thick structures comprised of multiple patches. Different thickness discretisation strategies are examined for the retrieval of the discrete stacking sequences, with each one having a different influence on the satisfaction of all structural constraints across the various sub-components of the wing. The weight penalty introduced between the continuous and final discrete design of the proposed approach is negligible.

1 Introduction

Fibre-reinforced composite materials have been increasingly used over the last decades due to the reduced weight and enhanced mechanical characteristics that they offer. In the aerospace industry, large composite parts are constructed by stacking multiple unidirectional, pre-impregnated plies of equal thickness but of different orientation on top of each other. By altering the number, stacking sequence and orientation of the plies, the properties of the laminated structure can be tailored to a significantly bigger extent compared to traditional metallic structures. However, this opportunity for increased tailoring simultaneously leads to a more challenging design task.

Various constraints must be considered during the optimisation process. On the one hand the structure must comply with multiple physical constraints such as stability, buckling and damage tolerance. Besides those, design rules (Irisarri et al. 2014; Fedon et al. 2021) enforcing restrictions on the stacking sequence design of individual patches must also be taken into account. Finally, the structure must also fulfil manufacturing rules which regulate the stacking sequence transitions between neighbouring patches. Amongst those, continuity or blending between patches is of significant importance. Even though composite design and manufacturing rules are not always applied to academic studies they are commonly applied in the industry to reduce the risks associated with the certification of an aircraft. Therefore, the challenges associated with the stacking sequence optimisation of large-scale composite parts are the combination of continuous and discrete characteristics of the optimisation, stemming from both composite design rules and structural constraints and the computational needs when performing this task for real-world structures.

Many different approaches have been proposed over the past years (Ghiasi et al. 2009, 2010) concerning stacking sequence optimisation. However, when it comes to dealing with the challenges mentioned above, two stage approaches have been established as the norm in both academia and the industry. The first stage involves a gradient-based optimiser being used to derive a continuous thickness and stiffness distribution across the structure, which also satisfies all the physical constraints linked with the responses of the Finite Element Model. The second stage of the optimisation aims to retrieve a discrete manufacturable stacking sequence, which fulfils composite guidelines, with blending between all neighbouring patches being the minimum requirement. The aim of the second stage optimisation is to perform a satisfactory stiffness match, so that physical constraints of the discretised design are not violated.

Lamination (IJsselmuiden 2011; Setoodeh et al. 2006; Liu et al. 2019; Ijsselmuiden et al. 2008; Irisarri et al. 2021) and polar (Montemurro et al. 2012b, 2018) parameters have been the two main alternative formulations used to describe the stiffness of each patch in the structure. Heuristic algorithms (Liu et al. 2010; IJsselmuiden et al. 2009; Bruyneel et al. 2014; Jing et al. 2015) are usually employed in the second stage of the process. A lot of emphasis has been placed on deriving the correct boundaries for the design space of lamination parameters and on the incorporation of blending constraints in the first stage of the optimisation, in both lamination (Diaconu et al. 2002; Macquart et al. 2016, 2018) and polar parameter (Panettieri et al. 2019) formulations. This is important as it increases the chances of deriving a discrete stacking sequence for which the stiffness is close to the continuous optimum value.

Such two-stage approaches have been applied multiple times to academic case studies (IJsselmuiden et al. 2009; Macquart et al. 2016; Picchi Scardaoni et al. 2020), however, there have only been few realistic applications to larger sized problems. Silva Caprio et al. (2018) applied aeroelastic tailoring to a regional jet following a two-stage process. Satisfaction of the physical constraints is achieved due to a surrogate model employed in the second stage of the optimisation. Bordogna et al. (2020) also performed aeroelastic tailoring on the wing of a regional wing using lamination parameters. Physical constraint violations are observed for the discretised design even when applying blending constraints in the first stage of the optimisation. Recently, Scardaoni et al. (2022) applied a two stage process using polar parameters to the sizing of a box-wing. Buckling constraint violations occurred in some of the sub-components studied.

The current study focuses on the application of a two-stage optimisation process to the detailed sizing of the wing skin of an aircraft. Within the first stage of the optimisation, generic stacks which have been previously introduced by the authors (Ntourmas et al. 2021a), are used to model the thickness and stiffness properties of the structure and a Mixed Integer Linear Programming (MILP) formulation of the problem (Ntourmas et al. 2021b) is solved in order to retrieve manufacturable stacking sequences. An improved decomposition of the original optimisation problem is presented for the second stage of the optimisation and it is shown that the process can efficiently handle industrial size problems. Emphasis is placed on the retrieval of manufacturable stacking sequences that fulfil all physical constraints. It is shown that, the influence on the physical constraint satisfaction differs depending on the composite design rules applied in the second stage of the optimisation and the thickness discretisation performed between the two stages. Overall, the weight penalty introduced between the continuous and finalised discrete design which satisfies all constraints is negligible.

The rest of this paper is structured as follows: In Sect. 2, the composite design and manufacturing rules commonly applied in the aerospace industry are summarised. The two stages of the optimisation process and an alternative thickness discretisation are briefly presented in Sect. 3. The aircraft model is described in Sect. 4 and results from the application of the optimisation process on the industrial example are demonstrated in Sect. 5. The findings of this work are summarised in Sect. 6.

2 Composite design guidelines

Composite design and manufacturing rules (Schwartz 1983) often serve as guidelines when designing laminated structures. These guidelines are utilised for manufacturing laminates which are less prone to high stress concentration and unwanted mechanical coupling effects or to avoid problems during manufacturing. Most of these rules have also been presented and used in previous works (Irisarri et al. 2014; Bermell-Garcia et al. 2012; Fedon et al. 2021). It is worth noting that while some of these design rules are omitted in some academic studies by using more sophisticated analyses (Vannucci and Verchery 2001; Montemurro 2015a, b) and manufacturing methods (Raju et al. 2012; Montemurro et al. 2012a; Montemurro and Catapano 2019), the industry is following most of these rules (Thompson and Blom-Schieber 2017). Using well known and understood principles ensures a robust process and thus mitigates the risks associated with the certification of the aircraft. Below, the composite rules applied in this work are summarised.

Composite rules consist of design and manufacturing rules. Design rules concern restrictions applied on the stacking sequence design of a single patch.

• 1. Symmetry. In order to avoid coupling between bending and extension symmetric laminates are usually preferred.

• 2. Balance. Balanced laminates can be used to remove coupling between shear and extension. Balanced laminates are formed by an equal number of layers with $+\theta$ and $-\theta$ orientations $(\theta \ne 0^{\circ},90^{\circ})$.

• 3. Damage tolerance. Plies placed on the external part of the laminate should not be in the direction of the principal load path. In most cases, a layer oriented at $45^{\circ}$ or $-45^{\circ}$ is placed on the outer part of the laminate.

• 4. Minimum percentage. In favour of minimising matrix degradation and encouraging a fibre-dominated failure mode, a minimum percentage of all fibre orientations might be desirable in a laminate. The minimum percentage rule makes sense for laminates which use the four standard fibre orientations $(0,90,45,-45)$. This design rule is commonly used in conjunction with a maximum allowed percentage.

• 5. Grouping. In order to decrease the coupling between bending and twist, $+\theta$ and $-\theta$ layers may be grouped together.

• 6. Contiguity. According to the contiguity design rule, the maximum number of consecutive layers placed in the same orientation is limited. This is done in order to minimise interlaminar stresses and encourage a more uniform stress distribution.

• 7. Disorientation. To minimise inter-laminar shear effects, the absolute difference between the fibre orientations of adjacent laminae might be limited to a maximum of $45^{\circ}$.

Even though both the effects of the grouping and disorientation design rules might be desirable during the design process, they cannot be enforced simultaneously as they are contradicting and would lead to an infeasible optimisation problem.

Manufacturing rules regulate the transitions of the stacking sequences between neighbouring patches.

• 1. Continuity/Blending. Blending, also referred to as continuity, guarantees the structural integrity of a composite structure. In this work, generalised blending which was introduced by Campen et al. (2008) is employed. The concept of generalised blending does not limit the position of the ply drops within the laminate as long as all plies belonging to the thinner patch continue across the neighbouring thicker laminates, as shown in Fig. 1.

• 2. Maximum dropping. Concerning transitions between neighbouring patches, the maximum number of ply drops might be restricted in order to achieve a homogeneous load distribution across the structure.

• 3. External covering ply. to achieve structural integrity, at least one of the plies placed in the external part of the laminate is not dropped.

• 4. Internal covering ply. In an attempt to avoid zones in which delamination might me initiated, the maximum number of plies which are allowed to be dropped simultaneously is capped to an upper limit. This means that the number of consecutive layers than are allowed to be dropped is restricted and once this limit is reached, at least one ply must be preserved before further plies can be dropped in the laminate.

Fig. 1

Generalised blending example between three patches

3 Optimisation process

A two-stage optimisation approach is employed to design manufacturable laminated composite structures. A brief overview of the process is presented before going into more details in the specifics of each step.

3.1 Overview of the process

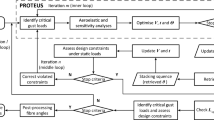
The first stage of the process is a gradient-based optimisation employing generic stacks (Ntourmas et al. 2021a) to model the thickness and stiffness of the structure. In this stage, all physical constraints of the problem are considered, while simultaneously, as many discrete design and manufacturing constraints must also be applied to minimise the disparity between the continuous and the discrete optimisation. In the most simple case, the total continuous thickness of each patch is rounded up to the nearest integer or the nearest even number of plies in the intermediate thickness discretisation task between the two optimisation stages. In this work, an alternative to this simple discretisation is also presented, to cope with the satisfaction of strength constraints after the discrete optimisation. More details on this will follow in Sect. 3.3. In the discrete optimisation, the thickness of the structure remains constant. Only design and manufacturing rules are taken into consideration while retrieving a discrete laminated structure. The objective function of the discrete optimisation is minimising the absolute difference between the stiffness characteristics of the continuous and discrete design, to avoid violation of the physical constraints of the discretised structure. Eventually, the discretised structure must be analysed using the Global Finite Element Model (GFEM) model of the gradient-based optimisation to check whether the physical constraints are still satisfied. In case they are not, the usually applied remedy is to increase the design factor and perform the entire two-stage process again.

Fig. 2

Flowchart of the two-stage stacking sequence optimisation process. The discrete stacking sequence graph has been created using the code developed in the work of Macquart (2016)

3.2 Continuous optimisation

The continuous optimisation is performed using LAGRANGE, (Schuhmacher et al. 2012) which is an in-house Multidisciplinary Design and Optimisation platform being developed at Airbus Defence and Space over the last four decades. The optimisation algorithm used in this work is NLPQLP Schittkowski (1986, 2011), a sequential quadratic programming algorithm which is one of the available algorithms in LAGRANGE. In the current study, a sizing optimisation is performed meaning that the geometry and configuration of the aircraft remain constant and only the thickness and stiffness of the wing structure of the aircraft are modified. The objective function of the gradient-based optimisation is the mass of the aircraft. The structural model and the optimisation problem are presented in more detail in Sect. 4. In the following subsections, emphasis is placed on how the fibre-reinforced composite skin of the aircraft wing, which is the focus of this study, is modelled in the first stage of the optimisation.

3.2.1 Generic stacks formulation

A generic stack is comprised of multiple generic layers. The exact orientation and stacking sequence of these plies remains fixed throughout the optimisation, whereas the individual thickness of each generic ply acts as a design variable able to take any real positive value. In a very simple case, a generic stack can be comprised of 8 generic plies as shown in Fig. 2. In reality, the number and stacking sequence of the generic stack must be chosen so that the resulting thickness and stiffness distribution does not depend on the modelling decisions applied. Knowing the thickness of each generic ply and the stacking sequence of the stack, the extensional stiffness matrix ${\varvec{A}}$, the coupling stiffness matrix ${\varvec{B}}$ and the bending stiffness matrix ${\varvec{D}}$ can be computed as:

$$\begin{aligned} A_{ij}= & {} \sum _{k=1}^{n} \left( {\bar{Q}}_{ij} \right) _k \left( z_k - z_{k-1}\right) \end{aligned}$$

(1)

$$\begin{aligned} B_{ij}= & {} \frac{1}{2} \sum _{k=1}^{n} \left( {\bar{Q}}_{ij} \right) _k \left( z_k^2 - z_{k-1}^2\right) \end{aligned}$$

(2)

$$\begin{aligned} D_{ij}= & {} \frac{1}{3} \sum _{k=1}^{n} \left( {\bar{Q}}_{ij} \right) _k \left( z_k^3 - z_{k-1}^3\right) . \end{aligned}$$

(3)

In Eqs. 1–3, $z_k$ is the distance between the midplane of the laminate and the side of the $k{\textrm{th}}$ layer which is further away from the midplane. The elements of the transformed reduced stiffness matrix ${\varvec{{\bar{Q}}}}$ are computed as:

$$\begin{aligned} \begin{aligned}&{\bar{Q}}_{11} = Q_{11} \cos ^4\theta + 2 \left( Q_{12} +2Q_{66} \right) \cos ^2\theta \sin ^2\theta + Q_{22} \sin ^4\theta \\&{\bar{Q}}_{12} = Q_{12} \left( \cos ^4\theta + \sin ^4\theta \right) +\left( Q_{11} +Q_{22} -4Q_{66} \right) \cos ^2\theta \sin ^2\theta \\&{\bar{Q}}_{16} = \left( Q_{11} -Q_{12} -2Q_{66} \right) \cos ^3\theta \sin \theta \\&\quad - \left( Q_{22} -Q_{12} -2Q_{66} \right) \cos \theta \sin ^3\theta \\&{\bar{Q}}_{22} = Q_{11} \sin ^4\theta + 2 \left( Q_{12} +2Q_{66} \right) \cos ^2\theta \sin ^2\theta + Q_{22} \cos ^4\theta \\&{\bar{Q}}_{26} = \left( Q_{11} -Q_{12} -2Q_{66} \right) \cos \theta \sin ^3\theta \\&\quad - \left( Q_{22} -Q_{12} -2Q_{66} \right) \cos ^3\theta \sin \theta \\&{\bar{Q}}_{66} = \left( Q_{11} +Q_{22} -2Q_{12} -2Q_{66} \right) \cos ^2\theta \sin ^2\theta \\&\quad +Q_{66}\left( \cos ^4\theta + \sin ^4\theta \right) .\\ \end{aligned} \end{aligned}$$

(4)

In Eq. 4, $\theta$ is the orientation at which the unidirectional lamina is laid and ${\varvec{Q}}$ is the reduced stiffness matrix:

$$\begin{aligned} {\varvec{Q}} = \begin{bmatrix} \frac{E_{11}^2}{E_{11}-\nu _{12}^2E_{22}} &{} \frac{\nu _{12}E_{11}E_{22}}{E_{11}-\nu _{12}^2E_{22}} &{} 0 \\ \frac{\nu _{12}E_{11}E_{22}}{E_{11}-\nu _{12}^2E_{22}} &{} \frac{E_{11}E_{22}}{E_{11}-\nu _{12}^2E_{22}} &{} 0\\ 0&{} 0 &{} G_{12}\\ \end{bmatrix} \end{aligned}$$

(5)

where $E_{11}$ is the modulus of elasticity across the fibre direction, $E_{22}$ the modulus of elasticity across the transverse direction, $G_{12}$ the shear modulus and $\nu _{12}$ the principal Poisson’s ratio for a specific material type.

The main benefit of modelling the structural properties using generic stacks is that design and manufacturing rules can be formulated easily and accurately in their design space, so that the gap between the continuous and the discrete optimisation stage is minimised. The formulation of the composite rules used in this study are summarised in the following paragraphs. The reader is addressed to previous work by the authors (Ntourmas et al. 2021a) for the formulation of more of these rules.

• 1. Symmetry. Symmetry can be achieved by linking the design variables on the two sides of the laminate formed by the midplane surface.

• 2. Balance. Similarly to symmetry, balance can be achieved by linking the design variables corresponding to the $\pm \theta$ oriented layers.

• 3. Damage tolerance. This design rule can be facilitated in the optimisation by choosing a generic stack with a $45^{\circ}$ or $-45^{\circ}$ generic layer on the outer part of the laminate, in combination with increasing the minimum gauge of the relevant design variable to the thickness of the tape to be used during manufacturing.

• 4. Minimum percentage. A minimum percentage (p) of any fibre orientation $\theta _c$ used in a laminate is formulated as:

  $$\begin{aligned} p \sum _{i=1}^{I} t_{ij} - \sum _{i'=1}^{I'} t_{i'j} \le 0 \quad \forall j, i' \in \{I \cap {\theta _{ij}=\theta _c} \} \end{aligned}$$

  (6)

  where $t_{ij}$ is thickness of the $i\text {th}$ layer in patch number j. The symbols I and $I'$ stand for the total number of layers and number of layers satisfying the condition $i' \in \{I \cap {\theta _{ij}=\theta _c} \}$ respectively.

Manufacturing rules affect the transitioning between laminates placed in neighbouring patches.

• 1. Blending. The mathematical formulation of blending for two neighbouring patches $j_1$ and $j_2$ is expressed as:

  $$\begin{aligned} \begin{aligned}&\text {if } \sum _{i=1}^{I}t_{ij_1} \le \sum _{i=1}^{I}t_{ij_2}\\&\text {then }t_{ij_1} \le t_{ij_2} \quad \forall i \in I \\&\text {else } \sum _{i=1}^{I}t_{ij_1}> \sum _{i=1}^{I}t_{ij_2} \\&\text {then }t_{ij_1} > t_{ij_2} \quad \forall i \in I. \end{aligned} \end{aligned}$$

  (7)

  Essentially, if the total thickness of patch $j_1$ is less or equal than the total thickness of patch $j_2$, then the thickness of each individual generic layer in patch $j_1$ must also be less or equal than the thickness of the equivalent generic layer in patch $j_2$.

• 2. Maximum dropping. The maximum number of plies dropped in transitions between neighbouring laminates $j_1$ and $j_2$ is limited, to assist smooth load distribution throughout the structure. On a lamina level this is formulated as:

  $$\begin{aligned} t_l - \left| t_{ij_1} - t_{ij_2} \right| \ge 0 \quad \forall i \in I \end{aligned}$$

  (8)

  and on a laminate level as

  $$\begin{aligned} t_s - \left| \sum _{i=1}^{I} t_{ij_1} - \sum _{i=1}^{I} t_{ij_2} \right| \ge 0. \end{aligned}$$

  (9)

  In Eqs. 8 and 9$t_l$ and $t_s$ are the absolute allowable differences in thickness for a ply and stack, respectively.

• 3. External covering ply. This manufacturing rule can be enforced by setting the minimum gauge of the corresponding design variable to the thickness of the pre-impregnated unidirectional tape and is automatically fulfilled when the damage tolerance guideline is also enforced.

3.3 Thickness discretisation under consideration of strength constraints

The optimal, continuous number of layers resulting from the first stage of the optimisation must be converted to a discrete number of layers which remains constant during the second optimisation stage. Since the nominal cured ply thickness of the pre-impregnated unidirectional tape that will be used during manufacturing is known, the total thickness of each patch can be rounded up to either the nearest integer number of layers or the nearest even number of layers.

During the examination of the large-scale demonstrator studied in this work, issues were observed with the satisfaction of strength constraints of the discretised design, especially when buckling and strength criteria simultaneously drove the design of a patch. One of the solutions to this problem is rounding-up all or some of the total individual fibre orientations e.g. $[0^{\circ},\,90^{\circ},\pm 45^{\circ}]$ in the structure. More specifically, if the total continuous number of individual fibre orientations is denoted by $\nu _{j\theta }$ and the total discrete number of plies per fibre orientation and patch in the structure is denoted by $n_{j\theta }$, where index $\theta \in \{1,2,...,\Theta \}$ denotes the different available fibre orientations and $j \in \{1,2,...,J\}$ the patches in the structure, then the individual thicknesses can be rounded up based on the following condition:

$$\begin{aligned} \begin{aligned}&\text {if } \nu _{j\theta } - \lfloor \nu _{j\theta } \rfloor \le l \text { then}\\&n_{j\theta } \ge \lfloor \nu _{j\theta } \rfloor \\&\text {else} \\&n_{j\theta } \ge \nu _{j\theta }. \\ \end{aligned} \end{aligned}$$

(10)

In Eq. 10, $l \in [0,1)$ is a value corresponding to the fractional part of $\nu _{j\theta }$ above which the individual number of layers for an orientation $n_{j\theta }$ are rounded up.

To maximise the benefits of this discretisation scheme , the discrete $n_{j\theta }$ values for the fibre orientations $\theta$ of interest must also be enforced as constraints in the upcoming discrete optimisation. However, if the number of layers for some fibre orientations is to remain fixed in the discrete optimisation, we must take special considerations to ensure that the number of layers used comply with the design and manufacturing rules which will be used afterwards. More specifically, if strictly balanced laminates are to be derived then:

$$\begin{aligned} n_{j{\theta _1}} = n_{j{\theta _2}} \quad \forall j, \theta _1=-\theta _2\ne \{0,90\}. \end{aligned}$$

(11)

If slight imbalances of $n_{imb}$ layers are allowed then:

$$\begin{aligned} \begin{aligned}&n_{j{\theta _2}} - n_{j{\theta _1}} \le 0 \\&n_{j{\theta _1}} - n_{j{\theta _2}} \le n_{imb} \quad \forall j, \theta _1=-\theta _2\ne \{0,90\}. \\ \end{aligned} \end{aligned}$$

(12)

The minimum $p_1$ and maximum percentage $p_2$ design rules are formulated as:

$$\begin{aligned} \begin{aligned}&n_{j\theta } \ge p_1 \sum _{\theta =1}^\Theta n_{j\theta } \quad \forall j, \theta \\&n_{j\theta } \le p_2 \sum _{\theta =1}^\Theta n_{j\theta } \quad \forall j, \theta . \end{aligned} \end{aligned}$$

(13)

Finally, blending between any two neighbouring patches $j_1$ and $j_2$ is expressed as:

$$\begin{aligned} \left( n_{j_1\theta _1} - n_{j_2\theta _1} \right) \left( n_{j_1\theta _2} - n_{j_2\theta _2} \right) \ge 0 \quad \forall j_1,j_2, \theta _1 \ne \theta _2. \end{aligned}$$

(14)

The constraints in Eqs. 10–14 are satisfied by multiple laminates. Therefore, the thickness discretisation task must be converted in an optimisation task of its own, albeit much simpler to solve than the continuous and discrete optimisation stages. Essentially, a third optimisation stage is added to the process. However, the optimisation process is still referred to as a two-stage process to avoid confusion in cases where the thickness discretisation task is simply performed by a rounding operation of the thickness of the laminate. The goal of this thickness discretisation optimisation is to retrieve a solution which satisfies the aforementioned requirements while adding the minimum number of extra plies, hence the objective function is formulated as:

$$\begin{aligned} \text {min} \sum _{j=1}^{J} \sum _{\theta =1}^{\Theta } n_{j\theta }. \end{aligned}$$

(15)

The optimisation described above is an integer quadratically constrained programming problem which is solved using the commercial mathematical programming tool Gurobi (Gurobi Optimization LLC 2022).

3.4 Discrete optimisation

The goal of the discrete optimisation is to retrieve a manufacturable stacking sequence across all patches which fulfils all of the imposed discrete composite guidelines. The total number of layers across the patches remains constant throughout the discrete optimisation. In the case that the modified thickness discretisation which considers strength requirements has been applied, then the number of plies per individual fibre orientation shall also be fixed for all or some of the fibre orientations. The objective for this optimisation problem is to minimise the absolute difference between the continuous stiffness at which the first stage of the optimisation converged $({\xi }{_{kj}^{A,B,D}})_{\text {optimal}}$ and the discrete stiffness characteristics of the retrieved discrete stack ${\xi }{_{kj}^{A,B,D}} \in [-1,1]$.

$$\begin{aligned} \text {min} \sum _{j=1}^{J} {w}{_{k}^{A,B,D}} |{\xi }{_{kj}^{A,B,D}} - ({\xi }{_{kj}^{A,B,D}})_{\text {optimal}} |\quad \forall k. \end{aligned}$$

(16)

When the first stage of the optimisation has converged, the continuous thicknesses of each generic stack are translated into lamination parameters. This is done to allow for a more compact representation of the stiffness attributes of each patch and also enable a straightforward comparison with similar approaches available in the literature. The weight coefficients ${w}{_{k}^{A,B,D}}$ in Eq. 16, may be used to prioritise the matching of specific stiffness components. In all numerical examples presented in this work, the value of the weight coefficients is set to ${w}{_{k}^{A,B,D}}=1$.

Two distinct Mixed Integer Linear Programming (MILP) formulations of the blended stacking sequence optimisation problem, namely explicit and implicit, have been developed by the authors in previous work (Ntourmas et al. 2021b). The major difference between the two formulations is the way blending is modelled, even though both formulations provide the same stacking sequence for a given optimisation problem using the same design rules. For the case study presented in this work, the implicit formulation has been employed. A combination of discrete an continuous design variables are used in order to model the optimisation problem. The objective function and constraints of the optimisation must both be expressed as linear functions with respect to the design variables. The commercial mathematical programming tool Gurobi (Gurobi Optimization LLC 2022) is used to solve this second stage optimisation problem. A wide range of design and manufacturing rules can be activated depending on the requirements of the design.

3.4.1 Decomposition

The implicit MILP formulation of the stacking sequence optimisation problem considers all design variables and constraints simultaneously for the entire arrangement of patches in the structure. However, this complete optimisation problem can become too computationally expensive for industrial scale structures consisting of hundreds of layers. What is more, Gurobi and similar software based on branch and bound algorithms can significantly benefit from good initial feasible solutions by reducing the size of the search tree. Therefore, a technique for decomposing the stacking sequence optimisation problem has been developed, to speed up the overall convergence of the optimisation and to retrieve acceptable solutions in a fraction of the original computational time.

The flowchart of the decomposition strategy is presented in Fig. 3. A decomposition of the problem requires the definition of at least one path traversing all patches in the structure. A path is essentially an ordered set containing all patches in the structure. The connectivity between the patches can be presented using an undirected graph where vertices represent patches and edges indicate the shared boundaries between neighbouring patches. All patches belonging to the same structural component are connected with at least one other patch. As for the paths to be examined during the decomposition of the problem, these can either be manually defined by the user or automatically generated using one of the algorithms shown in the “Define paths” module of Fig. 3. The MAX and MIN algorithm generates a path by starting from the thickest or thinnest patch in the structure, respectively, and sequentially adding the next thickest or thinnest patch which shares an edge with one of the patches already existing in the path. BFS stands for a Breadth First Search algorithm during which, starting from any chosen root patch, all neighbouring patches are added to the path until all patches have been included. On the other hand, DFS is the Depth First Search algorithm which explores all patches in a branch before expanding to other branches.

Fig. 3

Flowchart of the optimisation using decomposition developed for the implicit formulation

Once a path or set of paths have been defined, each of them is solved using the decomposed approach. Initially, only the first patch in the path is optimised individually, without any blending requirements with neighbouring patches. Afterwards, depending on the order of the patches in the path, one patch is added at a time to the optimisation sub-problem until all patches in the path have been added. Each time a new patch is added to the sub-problem, the stacking sequence of the patch or the patches optimised in the previous sub-problem is fixed. Therefore, the purpose of each sub-problem after the first one is to find the optimum solution that satisfies all requirements and blends with all the established neighbouring stacking sequences. However, in many cases, these optimisation sub-problems might be infeasible given the fixed stacking sequence of the neighbouring patches. In such cases, constraints restricting the stacking sequence of these neighbouring patches must be lifted to allow for more design freedom. This is performed using one of the methods shown in the “Remove fixation constraints” module of Fig. 3 which are also visually demonstrated in Fig. 4. The sub-problem can be altered by backtracking to the previously added patch in the path and removing the fixation constraints for it. This is repeated until a feasible solution can be obtained as shown in Fig. 4a. In the specific example of Fig. 4a, where only 3 neighbouring patches exist, the rightmost one being the one added last to the sub-problem, the first step of the fixation constraint removal process would be to remove the constraints for the second patch. If the optimisation problem is still infeasible, then a second step can be performed to remove the stacking sequence fixation constraints applied to the first patch. These potential fixation constraint removal steps are illustrated by the usage of different colour schemes in Fig. 4. Alternatively, instead of removing the fixation constraints for an entire patch, the constraints can be relaxed for all patches and for a certain number of layers around the midplane of the laminate as demonstrated in Fig. 4b. This number of layers increases until eventually a feasible solution is obtained. Finally, a combination of the two previously mentioned techniques depicted in Fig. 4c can be applied. More specifically, an increasing number of layers are removed for the patch added last in the path. In case the sub-problem remains infeasible, the process of removing an increasing number of layers around the midplane is repeated after backtracking to the previously added patch in the path. The goal of all of these techniques for removing the fixation constraints is to keep the size of the decomposition small and not turn the decomposed problem into one which is of a similar complexity as the original complete optimisation problem. Once all the paths have been explored, the solution with the best objective function can be used as an initial solution for the complete optimisation.

Fig. 4

Visual representation of the fixation constraints removal strategies during the decomposition of the second stage of the optimisation for an example of 3 neighbouring patches. In all examples the rightmost patch is the one added last to the sub-problem. The different colour schemes of each step indicate the layers for which the stacking sequence fixation constraints would be removed. The number of steps required depends on whether the optimisation problem still remains infeasible or not after fixation constraints have been removed from the optimisation

4 Model description

The two-stage optimisation process has been applied to the wing covers of a modified OptiMALE model (Elssel et al. 2018), an industrial-scale demonstrator shown in Fig. 5. More specifically, OptiMALE is a Medium Altitude Long Endurance (MALE) aircraft which operates as an unmanned aerial vehicle. The wing span and length of the aircraft are approximately 30 and 15 m respectively. In this study the focus is placed on the detailed design of the fibre-reinforced composite skins around the wing box of the aircraft. These wing skins are split up into 4 different sub-components, 2 for the lower and upper side of the wing and 2 for the inner and outer parts of the wing, with the latter designed to be detachable for storage and transportation purposes.

Fig. 5

Structural model of the Medium Altitude Long Endurance OptiMALE aircraft. The red line indicates the boundary between the inner and outer sub-components of the wing

4.1 Elements and materials

The aircraft is modelled using a coarse GFEM model consisting of 1D and 2D structural elements. The skins of the wing are modelled using isoparametric membrane bending triangular and quadrilateral 2D plate elements. More specifically, the elements used are LAGRANGE native elements CQUAD4 and CTRIA3, with mathematical formulation similar to that of the homonymous Nastran MSC elements. A composite material is assigned to these skin regions of the wing box. The spar webs and ribs of the wing are also modelled using the same plate elements, however, the spar webs are modelled with a composite material while the ribs are metallic.

The remaining components in the wing box assembly are modelled using 1D elements. Particularly, rib caps and spar caps are modelled with CROD tension-compression elements and stringers are modelled using CBAR Timoshenko Beam elements of a “T” cross section. The difference in modelling stems from the fact that stringers must also be able to bear out-of-plane loading, which, in the case of spar and rib caps, is transmitted to and carried by the spar and rib webs accordingly. To that extent, the modelling of the reinforcements around a cutout area, which is designated for the main landing gear of the aircraft as shown in Fig. 6, is altered. More specifically, the reinforcements along the wingspan of the lower side of the wing are modelled using a CBAR “T” cross section element and the reinforcements along the chord of the upper side of the wing are modelled with CBAR “I” cross section elements. All the aforementioned 1D elements use an isotropic material which represents the elastic module of a composite material.

Fig. 6

Modelling of the spar and rib caps around the main landing gear cutout area of OptiMALE. CROD and CBAR elements are depicted with a red and green colour, respectively

4.2 Load cases

The model is subjected to 19 static load cases summarised in Table 1. These load cases cover critical cases of maximum and minimum vertical load factors originating from pull-up and push-over manoeuvres, respectively, as well as maximum roll accelerations and gust cases at the given mass configurations. Additionally cruise load cases are considered at different envelope points. More specifically, $n_z$ denotes the vertical load factor exerted on the aircraft and ${\dot{p}}$ the roll acceleration. The mass configurations considered are Maximum Take Off Weight (MTOW), Maximum Landing Weight (MLW) and Maximum Zero Wing Fuel Weight (MZWFW).

The aforementioned load cases were generated through an aeroelastic analysis of the flight states using a Doublet Lattice Method (DLM) coupled to the structural GFEM model. For this, the aerodynamic loads coming from the DLM model where combined with the inertia loads originating from accelerations on the structural FEM model. The resulting elastic deformations of the aircraft which alter the aerodynamic boundary conditions were then used to iteratively update the aerodynamic loads in DLM until convergence was reached. Each load case was trimmed to reach load equilibrium in the flight degrees of freedom using angles of attack and control surface deflections. The resulting loads on the model were frozen and applied as static loads during the first stage of the optimisation shown in this study.

Table 1 Flight load cases considered for the detailed sizing optimisation of OptiMALE

4.3 Patch definition and design variables

Design variables need to be assigned to all structural components which are being sized. In practise, the level of detail during the design process of an aircraft increases as the project matures. In this study a sensible, adequately detailed discretisation of the design space has been chosen for all components being sized based on experience gained from past projects. The minimum size of any structural element is of course limited by the coarseness of the GFEM model. In practise, multiple elements are grouped together during the definition of the design variables. To maintain consistency and to simplify the setup of the optimisation problem, the boundaries of the design variables for each component are defined using the components adjacent to it.

More specifically, for the skins of the aircraft, which are the focus of the study, the patches that eventually define the zones according to which the variable stiffness laminates will be formed, are defined using the ribs, spars and stringers of the wing of the aircraft. The patch layouts for the 4 skin components of the wing are shown in Fig. 7. A smaller patch size has been chosen for the area near the wing root of the inner upper and lower wing skins as steeper thickness gradients are usually expected in these areas.

The thickness and stiffness properties of each patch are modelled using a generic stack. The number of generic layers used must be adequate for the expected thickness of the laminate. As a general rule of thumb, the stiffness properties of a laminate with N number of plies can be properly modelled using a generic stack with at least N/4 generic plies. In this example, the maximum expected thickness for laminates towards the root of the wing is equal to approximately 120 layers and therefore 32 generic layers have been used. The generic stack used is $[(45,-45,90,0)_4]_s$. This generic stack is applied to all thicker regions of the skins of the wing which are known due to previously performed preliminary optimisations. More specifically, it is used for patches 1 through 52 and 1 through 20 in sub-components I and III respectively. All other patches across each sub-component are modelled using a generic stack with 8 plies $[45,-45,90,0]_s$. The reason for this choice, is that if the number of generic plies used is significantly bigger than the actual physical plies corresponding to the thickness of a laminate, then the permitted design freedom is greater than what can be achieved during the discrete optimisation. This leads to unattainable stiffness distributions which in turn result to significant physical constraint violations of the discrete design.

Fig. 7

Patch arrangement for all the skins of OptiMALE’s wing

Besides the aforementioned skins of the wing, all other structural components of the wing box are also sized during the optimisation. This includes the spar caps, stringers, rib webs, rib caps and the connecting structural elements between the detachable inner and outer part of the wing. These wing components are also discretised into design variables using their interfaces with neighbouring structural components. The exact definition of those design variables is not presented, since the focus of the study is on the design of the skin components of the wing. Due to local effects, the sizing of the spar webs and ribs has been performed outside of LAGRANGE and was kept constant during the optimization.

4.4 Constraints

In this subsection, the formulations of the physical constraints applied to the first stage of the optimisation are presented. Additionally, the details concerning the application of the composite design guidelines in the continuous optimisation are summarised. The information concerning the application of the composite design guidelines in the second stage of the optimisation is presented on a case-to-case basis in Sect. 5.

4.4.1 Physical

Buckling and strength constraints are applied to the model. Concerning the stability constraints on the skins of the wing, each buckling field is assumed to be simply supported, subjected to in-plane loads and specially orthotropic. The mathematical formulation of these constraints in the optimisation problem is:

$$\begin{aligned} \frac{1}{2}\left( \frac{N_{x}}{N_{x,cr}} + \sqrt{\left( \frac{N_{x}}{N_{x,cr}}\right) ^2+ 4\left( \frac{N_{xy}}{N_{xy,cr}}\right) ^2}\right) \le 1. \end{aligned}$$

(17)

The left hand-side in Eq. 17 indicates the combined Reverse Reserve Factor (RRF) of a buckling field for a combination of the critical normal loads and shear loads. In Eqs. 17 and 18, $N_{x}$ indicates the load applied on the longitudinal direction, $N_{xy}$ the shear load applied on the plate, $N_{x,cr}$ and $N_{xy,cr}$ the critical normal and shear buckling loads, respectively, and $N_{y}$ denotes the load applied on the transverse direction. The critical buckling load $N_{x,cr}$ across the longitudinal direction can be computed as:

$$\begin{aligned} N_{x,cr} = \frac{\pi ^2\left( D_{11} \left( \frac{m}{a}\right) ^4 +2 \left( D_{12}+2D_{66} \right) \left( \frac{mn}{ab} \right) ^2 + 2D_{22} \left( \frac{n}{b} \right) ^4 \right) }{\left( \frac{m}{a}\right) ^2+\frac{N_y}{N_x} \left( \frac{n}{b}\right) ^2}. \end{aligned}$$

(18)

In the equation above, a and b are the lengths of the plate in the longitudinal and transverse direction, respectively. The minimum load computed for a set of half wavelengths m and n across the length and width of the plate is the critical buckling load. Because the above equation is based on Classical Lamination Theory, the critical normal buckling load is less accurate for moderately thick and thick laminates. The critical shear load can be computed under the assumption of a long plate and is expressed as:

$$\begin{aligned} N_{xy,cr} = \left\{ \begin{array}{ll} \frac{4}{b^2} \root 4 \of {D_{11}{D_{22}}^3} \left( 8.12+\frac{5.05}{\delta }\right) &{} \text {for } \quad \delta \ge 1 \\ \frac{4}{b^2} \sqrt{D_{22}\left( D_{12}+2D_{66}\right) } \left( 11.7+0.532\delta + 0.938\delta ^2 \right) &{} \text {for } \quad \delta < 1 \end{array} \right. \end{aligned}$$

(19)

where

$$\begin{aligned} \delta = \frac{\sqrt{D_{11}D_{22}}}{D_{12}+2D_{66}}. \end{aligned}$$

(20)

Alternatively, Finite Element buckling can also be applied to thicker laminates. In this study, the analytical buckling formulation is chosen to maintain simplicity.

To ensure that the stringer provides enough stability to the skin, a column buckling constraint is used. The well-established Johnson-Euler column buckling method is applied to an assembly of the stringer and its adjacent skins (Shigley 1972). Local skin buckling under compression is taken into account by using the effective skin width via the Von-Kármán method (Von Kármán 1932). The critical buckling load of this assembly is computed in an iterative manner until convergence of the effective skin width is reached.

The maximum strain criterion is used in this study concerning strength constraints and more specifically fibre failure. Strength constraints are expressed as:

$$\begin{aligned} \left|\frac{\varepsilon _{1T}^u}{\varepsilon _1} \right|-1 \ge 0 \qquad \text{or} \qquad \left|\frac{\varepsilon _{1C}^u}{\varepsilon _1}\right|-1 \ge 0. \end{aligned}$$

(21)

The equations above, apply to extensional and compressive loads respectively, across the direction of the fibre. Moreover, $\varepsilon _{1T}^u$ denotes the ultimate strain of the composite material for tension, $\varepsilon _{1C}^u$ stands for the ultimate strain of the material for compression and $\varepsilon _1$ is the strain along the fibre direction for a single layer. The strains ${\varvec{\varepsilon }}$ and curvatures ${\varvec{\kappa }}$ can be computed since the stiffness of the laminate and therefore the force and moment resultants are known.

$$\begin{aligned} \begin{Bmatrix} {\varvec{N}}\\ {\varvec{M}}\\ \end{Bmatrix} = \begin{bmatrix} {\varvec{A}} &{} {\varvec{B}}\\ {\varvec{B}} &{} {\varvec{D}} \end{bmatrix} \begin{Bmatrix} {\varvec{\varepsilon }}\\ {\varvec{\kappa }}\\ \end{Bmatrix} \end{aligned}$$

(22)

In the equation above, ${\varvec{N}}$ and ${\varvec{M}}$ are the resultant forces and moments exerted on the laminate. The strain in each individual ply $\varepsilon _1$ can also be calculated when the global strain distribution is computed. This is possible because the local material directions are available due to the usage of generic stacks.

4.4.2 Manufacturing

Manufacturing constraints are applied to both the continuous and discrete stage of the optimisation. In the first stage of the optimisation, symmetry and balance are enforced by linking the appropriate design variables in each patch. The stacking sequence of the generic stacks used in combination with gauges applied to the outermost generic plies, also facilitates the enforcement of the damage tolerance and external covering ply composite rules. A minimum of 10% and maximum of 60% is also applied to all laminates of the wing skin. Finally, between all neighbouring laminates, a maximum dropping of 30 plies is applied and continuity constraints are enforced. The blending constraints of Eq. 7 can only be applied between laminates that share the same generic stack. As mentioned in Sect. 4.3, two different generic stacks are applied for sub-components I and III to appropriately model the stiffness of thinner and thicker patches. The blending constraints between neighbouring patches modelled with a different generic stack are applied to the sum of each fibre orientation instead of each generic ply. More specifically, the formulation of these constraints is:

$$\begin{aligned} \begin{aligned}&\text {if } \sum _{i=1}^{I}t_{ij_1} \le \sum _{i=1}^{I}t_{ij_2}\\&\text {then } \sum _{i'=1}^{I} t_{i'j_1} \le \sum _{i'=1}^{I} t_{i'j_2} \quad \forall i',\theta _c \in \{I \cap {\theta _{ij}=\theta _c} \} \\&\text {else } \sum _{i=1}^{I}t_{ij_1}> \sum _{i=1}^{I}t_{ij_2} \\&\text {then } \sum _{i'=1}^{I} t_{i'j_1} > \sum _{i'=1}^{I} t_{ij_2} \quad \forall i',\theta _c \in \{I \cap {\theta _{ij}=\theta _c} \} \end{aligned} \end{aligned}$$

(23)

where $\theta _c$ are the fibre orientations used in the generic stack.

The contiguity constraint which limits the maximum number of equally oriented plies stacked consecutively is not applied in this work, although it has been formulated in the framework of the generic stacks (Ntourmas et al. 2021a). The reason for this decision is that to provide meaningful results, it requires a laminate expected to be N layers thick, to be modelled with approximately 3N/4 generic layers. When compared to the N/4 generic layers guideline mentioned in Sect. 4.3, which is adequate to model the stiffness of the laminates, the application of the contiguity constraint would increase the number of design variables in the optimisation problem. However, most importantly, it would also lead to more neighbouring patches with a different number of generic plies, which would require the application of the blending constraints in the form of 23. This formulation of blending is less accurate than that of 7, since all plies of a specific orientation in a laminate are aggregated. Blending constraints have a greater influence on the stiffness output of the laminates than the contiguity constraint and therefore their exact application for as many neighbouring laminates as possible was preferred.

As for the composite rules applied to the discrete problem, these will be explained in more detail in the following section on a case-to-case basis.

5 Results

In this section, results of the two-stage methodology applied to OptiMALE are presented. Initially, the continuous thickness and stiffness distribution of the wing skins are presented as well as the convergence of the two stages of the optimisation. The emphasis is then placed on the retrieval of discrete stacking sequences and on how the intermediate thickness discretisation stage and the choice of composite rules influences the satisfaction of the physical constraints.

5.1 Size and convergence

In total, the first stage of the optimisation problem is comprised of approximately 600,000 constraints and 3000 design variables. LAGRANGE employs an active set strategy to filter out inactive constraints during each optimisation iteration. The continuous optimisation converges after 142 iterations with a Karush–Kuhn–Tucker condition of $10^{-5}$. The total computational time is approximately 40 h on a typical workstation employing 8 threads.

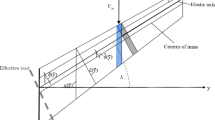
The continuous thickness and flexural stiffness distribution resulting from the first stage of the optimisation are shown in Fig. 8 for the four wing skin sub-components. As expected, the thickness of the wing decreases towards the tip. The flexural stiffness for each one of the patches is plotted in polar coordinates with a white colour. In these polar plots, the distance from the pole indicates the normalised modulus of elasticity, and the azimuth denotes the angle of rotation with respect to the reference axis of each laminate. More details on the visualisation of the membrane stiffness can be found in the work of Bordogna et al. (2020). It can be seen that thin areas such as the outer parts of the upper and lower side of the wing which are predominantly sized by buckling have a higher flexural stiffness across the 45° axis. On the contrary, thicker areas towards the wing root have increased flexural stiffness across the 0° axis since strength constraints are also sizing these patches as will be discussed in the following sections.

The structural mass of the aircraft, following the continuous optimisation, is 11,789 Kg.

Fig. 8

Thickness and flexural stiffness distribution across the wing skins of OptiMALE

Figure 9 illustrates the progress plot for the objective value of sub-component III, using the implicit MILP formulation and the process shown in Fig. 3 to retrieve a good feasible solution. Normally, one or two different path strategies are used to retrieve an initial discrete stacking sequence. In this case, 6 different paths are defined to demonstrate the impact of the chosen path to the objective function. The number indicated for the DFS and BFS strategies in Fig. 9 signifies the root patch used to initiate the path build. The average run-time of each individual run for the different paths is less than 5 min on a typical workstation employing 8 threads, including the overhead of setting up each of the many sub-problems for every path. One first observation is that paths generated using a thinner patch as the root i.e. MIN, BFS-11 and DFS-11 lead to a smaller objective function and therefore better stiffness match across all patches collectively. This can be attributed to the fact that in thinner patches, the placement of a layer influences the stiffness more compared to a thicker panel. Therefore, allowing the thinner patches to be optimised first can in many cases prevent the decomposition from getting stuck at a local minimum favouring some of the thickest patches. Secondly, the DFS strategy appears to also lead to a smaller objective function when compared to the BFS one. The reason behind this is that during the former, stiffness requirements of patches further across the structure are taken into consideration earlier on the decomposition, when there is still adequate design freedom to accommodate them.

Fig. 9

Comparison of different path generation strategies and convergence of the discrete stacking sequence optimisation problem for sub-component #3. The number indicated for the DFS and BFS strategies signifies the root patch used to initiate the path build

The solution used to initialise the complete optimisation problem is the one with the lowest objective function out of the solutions retrieved by the different explored paths. In Fig. 9 “best known objective” indicates the lowest value of the objective function for a solution which satisfies all constraints in the complete optimisation problem. The “objective lower bound” visualised with a dashed line, concerns the minimum bound of the objective function that has been discovered during the optimisation. This minimum bound is known because of the branch and bound algorithm on which the solver is based.When the value of the best possible objective is equal to that of the best known objective, then optimality has been proven. In this specific example, the runtime allotted to the optimisation of the complete MILP formulation is 2000 s. In the first half of it, a heuristic algorithm available in Gurobi Optimization LLC (2022) is employed to improve the best solution further, without solving the continuous relaxation of the MILP problem. In the latter half of the optimisation, the branch and bound algorithm of the commercial solver is used to prove optimality. The best possible bound for the objective is substantially increased throughout this process, due to the continuous relaxation of the MILP problem being solved. Actually proving optimality for large-scale problems becomes time consuming, and therefore, the optimisation is stopped earlier. The quality of the solutions obtained through the decomposition and subsequent complete optimisation process are satisfactory, as shown by the results in the following section.

5.2 Retrieval of discrete stacking sequences

Before performing the second stage of the optimisation to retrieve discrete stacking sequences for all sub-components of the wing skin, the total continuous thickness of each patch is rounded up to the nearest even number of discrete plies assuming a tape thickness of 0.125 mm. Initially, the design and manufacturing rules applied are the strict rules commonly employed in the industry, which have also been used in the first stage of the optimisation. More specifically, all composite design and manufacturing guidelines of Sect. 2 are applied, with the exception of the disorientation guideline which is not used because it contradicts the requirements of the grouping guideline which is used instead. The minimum and maximum percentages of layers allowed for each orientation in every patch are $10\%$ and $60\%$ respectively. No more than 4 plies of the same orientation are allowed to be grouped together and the number of consecutive plies that may be dropped simultaneously is capped to 4. The standard fibre orientations $[0,90,45,-45]$ commonly used in the industry are applied during the stacking sequence retrieval.

After obtaining the discrete stacking sequences satisfying these design guidelines, the continuous laminates of the wing skins are replaced by the discrete ones and an analysis of the model is performed. The minimum reserve factors and the number of fields in which violations appear for the buckling and strength constraints of the wing skins and the stringers are shown in Table 3. In the case of buckling constraints, each patch is usually comprised of 1-3 buckling fields depending on its size, while for strength constraints each element in the GFEM acts as a separate constraint field. The number of fields to which buckling and strength constraints are applied for the wings and stringers is shown in Table 2. The actual number of constraints in the optimisation and therefore the analysis model, is the number of fields to which constraints are applied multiplied with 19, the number of load cases applied to the model. Therefore, the actual constraint violations may be greater than the number of fields violated, shown in Table 3, if the constraint applied to one field is violated for multiple load cases.

Table 2 Number of fields to which strength and buckling constraints are applied, across the skins and stringers of the four sub-components of the wing of OptiMALE

Table 3 Minimum Reserve Factor and number of constraint violations for strength and buckling constraints across the skins and stringers of the four sub-components of the wing of OptiMALE. Strict design rules are used for the retrieval of discrete stacking sequences

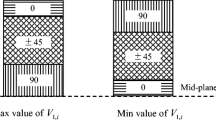
As can be seen in Table 3, significant violations appear for the majority of the wing skin sub-components in both buckling and strength. The minimum Reserve Factor (RF) equal to 0.586 appears on patch number 5 of the lower, outer part of the wing skin. As mentioned in Sect. 4.3 sub-component IV is modelled using the following generic stack $[45,-45,90,0]_s$. The continuous number of layers for this generic stack and for patch number 5 is $[2.790,2.790,0.698,0.699]_s$. The resulting discrete stack is $[45,-45,45,-45,0,90,90]_s$. First of all, the fact that the continuous thickness is 13.95 layers, which is rounded up to 14 layers for the stack retrieval, does not leave a generous safety margin for the inevitable stiffness change which occurs between the two stages. Most importantly, since symmetry, balance and minimum percentage are being strictly enforced, the stiffness match is sacrificed. The equivalent generic stack with a discrete thickness distribution of the discrete stack for patch 5 is $[2,2,2,1]_s$. Sacrificing the number of 45 and -45 layers, which had it not happened would probably lead to a smaller constraint violation, is necessary in order to satisfy the minimum percentage guideline for 0 and 90°. The adverse effects of the strict design rules on the stiffness matching between continuous and discrete are more evident in thinner patches.

Buckling constraint violations also occur for the stringers in all of these sub-components, even though the stringer design has not been discretised but rather remains fixed to the optimal solution found in the first, continuous stage of the optimisation. The reason behind the violations in the stringers is mainly internal load redistribution across the structure due to the discretisation of the wing skins. Essentially, some areas in the wing attract more load due to the increase in thickness or change in stiffness, which also leads to higher loads for the stringers which have not been sized for such loads.

5.3 Considerations for buckling and strength constraints

As seen previously, the strict design rules lead to a sparsely populated design space which makes stiffness matching difficult. The strong influence of the design rules can be seen if the strict design rules applied in the previous section are relaxed. In particular, asymmetries are allowed up to 3 plies away from the midplane of each patch. Additionally, grouping of 45 and − 45 layers is no longer strictly enforced and imbalances of up to one layer are permitted. Besides the relaxation of the design rules, the intermediate thickness discretisation step between the two stages of the optimisation is also modified, to allow rounding up the total patch thickness to the nearest integer number of plies, instead of rounding up to the nearest even number of plies. The analysis results for the new discrete stacking sequences are shown in Table 4, under the column named “2-Relaxed”. An average improvement of 6% is observed for the minimum values of the RFs and the number of constraint fields violated are reduced by 24%. The improvements are noticed for both buckling and strength constraints across the skins and stringers of the wing.

The remaining buckling violations on the wing skin mainly exist because of patches for which the difference between the total discrete and continuous thickness is very small. This difference is the thickness introduced during the intermediate rounding up step and acts as a safety net for the stiffness mismatches which inevitably occur whenever transitioning from a continuous to a discrete design. In order to highlight this effect, a Safety Factor (SF) is introduced during the thickness discretisation stage. Basically, the total continuous thickness of each patch is rounded up to the nearest integer number of plies for all patches, except the ones where this thickness difference is less than 0.2 layers. In those patches, the discrete thickness is further increased by an extra layer. The analysis results of this third alternative thickness discretisation, with the design rules remaining relaxed, are demonstrated in the column named “3-Relaxed with SF” of Table 4. The buckling RFs and the number of constraint violations are further improved in this case, since the discrete stiffness is increased for a sub-set of the patches. A negative side effect of the SF application in the thickness discretisations is that a lower minimum RF is observed for the stringers in sub-component one even though the number of fields in which the buckling constraints are violated is reduced. The introduction of this lower RF can be attributed to load redistribution in the structure, since the marginally thicker patches attract more load compared to what the stringers were designed for during the continuous optimisation.

Table 4 Minimum Reserve Factor and number of constraint violations for strength and buckling constraints across the skins and stringers of the four sub-components of the wing of OptiMALE. The discrete stacking sequences have been derived using relaxed design riles, relaxed design rules in combination with a thickness safety factor and the thickness discretisation considering strength constraints presented in Sect. 3.3

Finally, in order to improve the strength constraint violations on the wing skins, the intermediate thickness discretisation method presented in Sect. 3.3 is applied. The value of parameter l in Eq. 10 is set to 0. After the integer quadratically constrained programming problem is solved, the number of layers for each individual fibre orientation are derived and are then enforced by equality constraints in the second stage of the optimisation. However, for thicker patches, these equality constraints can lead to infeasible optimisation problems due to the simultaneous application of the contiguity constraint. This constraint, unlike blending, balance, and minimum percentage constraints, cannot be considered in the alternative thickness discretisation stage due to lack of detailed stacking sequence information. To overcome the obstacle of infeasible designs, the constraints enforcing the number of layers are only strictly applied to 0° fibers and are allowed to be violated for ±45 and 90 orientations. The constraint violations for the stacks derived using this method are shown in the column named “4-Strength” of Table 4. Although the minimum RF for the strength constraints on the wing skin is slightly increased and the number of fields violated is reduced, the number of buckling fields violated for the skins and stringers is increased. This is once again due to load redistribution being amplified by the introduction of thicker patches, which can be observed by the increase in structural weight which is the biggest across all derived discrete stacks.

5.4 Feasible design

As seen in Tables 3 and 4, none of the four derived discrete stacks fulfils all physical constraints. In order to achieve a discrete manufacturable design which fulfils all physical constraints, the first stage of the optimisation must be performed again using a design factor. Unfortunately, a design factor leads to an unnecessary overdimensioning of the structure. In the case of OptiMALE, the discrete stacks #2–4 derived by employing different thickness discretisation and design rule variations, all lead to smaller violations of the physical constraints when compared to the first discrete stack. All things considered, the best discrete stack is the second one using the relaxed design rules. The fact that it is the lighter solution out of all other candidates also leads to the best stiffness match and therefore to the least impact of load redistribution, as seen by the buckling constraint violations on the stringers.

To avoid introducing the design factor and because the constraint violations for the second discrete stack are rather insignificant, the following alternative procedure is followed. The continuous optimisation is performed again, only this time, the design variables corresponding to the skins of the wing are removed and the design is fixed to the derived discrete stacks. All physical constraints applied to the skins, as well as all other design variables and their respective constraints, remain intact. This modified optimisation converges in very few iterations to a design that satisfies all physical constraints in which the skin is discretised. Moreover, the structural weight of this final design is 11,791 Kg which is lighter than that of the starting point of this optimisation at 11,796 Kg. This means that the optimisation not only drives the design to a state at which no constraints are violated, but also manages to reduce the weight of other structural components because the discretised, thicker skins now attract part of the load previously carried by others. Compared to the initial 11,789 Kg weight of the continuous structure, only 2 Kg of mass were added for a design in which the wing skins have been discretised, while also satisfying all physical and composite constraints across the structure. This is virtually no change in structural weight considering the weight prediction precision of such a coarse GFEM structural model and in relation to the overall structural weight of the OptiMALE aircraft.

This study only examined the discretisation of the skins of the wing and no other composite parts of the structure. While it is true that discretising other components, such as the stringers, might once again lead to load redistribution and hence, constraint violations, the aforementioned strategy to fulfil all physical constraints can be realistically applied even in these cases. The reason for this is that other sub-components exist, whose stiffness is not only a function of the discrete stacking sequence but is also influenced by continuous design variables. For example, in the case of a stringer with a “T” cross section, the stiffness also depends on the lengths of the flange and the web which can vary in the continuous domain.

6 Conclusion

This paper demonstrates the detailed sizing of a composite aircraft wing skin using a two-stage optimisation approach. In the first gradient-based optimisation stage, the properties of the structure are modelled using generic stacks which allow for the exact formulation of laminate blending, among others. The second stage of the optimisation involves mathematical programming that solves a Mixed Integer Linear Programming formulation of the stacking sequence optimisation, which is subject to composite design rules aiming to accurately match the continuous optimisation stiffness characteristics. The improved decomposition strategies presented in this paper further assist in the retrieval of good quality solutions in the second stage of the optimisation.

Both stages of the presented approach can efficiently handle industrial-size optimisation problems. Concerning the capability of the methodology to retrieve manufacturable stacking sequences which fulfil all physical constraints, it is shown that the enforcement of strict design rules lead to large physical constraint violations especially for thin laminates. These violations are significantly reduced when the design rules imposed to the second stage of the optimisation are slightly relaxed.

Different thickness discretisation strategies are applied between the continuous and discrete optimisation stages, in an attempt to eliminate all physical constraint violations across all sub-components of the wing. As expected, a thickness safety factor introduced for patches in which the continuous thickness is marginally different than that of the discrete, reduces the number of buckling field violations in the wing skin. Alternatively, a newly developed thickness discretisation considering strength constraint requirements slightly improves the satisfaction of strength constraints. However, both of these thickness discretisations lead to a higher structural mass, which also sets the ground for a worse stiffness match during the stacking sequence retrieval, leading to a load redistribution and constraint violations across other sub-components. In general, discretising the total thickness of each patch up to the nearest integer number of plies and applying slightly relaxed design rules, such as allowing asymmetries close to the midplane, provides the overall best results.

The minor constraint violations can be easily handled by a repetition of the continuous optimisation, using the discretised stacking sequences. The optimiser can easily satisfy all remaining violations by a slight modification of the stiffness properties of other sub-components, whose stiffness characteristics can be easily manipulated in the continuous domain. Overall, the weight penalty introduced between the continuous and discrete result which satisfies all constraints is approximately 2 Kg.