An aeroelastic optimisation framework for manufacturable variable stiffness composite wings including critical gust loads

Abstract

This work presents a new aeroelastic optimisation framework for the preliminary design of variable stiffness composite wing structures. The framework is constructed by sequentially and iteratively solving two sub-problems: aeroelastic tailoring and lay-up retrieval, using gradient-based algorithms with full-analytical sensitivities provided. During aeroelastic tailoring, the wing mass is minimised by optimising the lamination parameters and thickness of wing laminates together with wing jig twist distribution. The load cases cover not only static loads, but also the critical gust loads that are identified across the entire flight envelop at every iteration of optimisation. Further, a cruise shape constraint is included in addition to other aerostructural constraints, so that the optimal aircraft performance can be ensured. During lay-up retrieval, the manufacturable stacking sequence is retrieved according to the optimal lamination parameters with the consideration of minimal steering radius constraint. Moreover, to fix the possible constraint violations caused by lay-up retrieval, a correction strategy is incorporated to tighten the violated constraints for repeating aeroelastic tailoring. Finally, several case studies on the design of NASA common research model wing are carried out and investigated. The results indicate that the critical gust loads and cruise shape constraint have a large influence on the design of tow-steered composite wing structures, which therefore demonstrate the usefulness and benefits of the proposed optimisation framework.

1 Introduction

In the structural design of aircraft wings, aeroelastic tailoring usually is used to introduce the beneficial coupling effects, e.g., wash-out twist, to passively alleviate the aerodynamic loads and thereby lead to the reduction of wing weight (Jutte and Stanford 2014). For composite aircraft wings, one way of aeroelastic tailoring is to elaborately design the stacking sequence of laminates, so that the wing stiffness can be tailored in desirable directions (Gasbarri et al. 2009; Bach et al. 2017; Bordogna et al. 2020).

Currently, the most common type of composites are stacked with $0/\pm 45/90^{\circ}$ angle unidirectional plies, because the knowledge and experience about these laminates was accumulated over years and, thus, they are often referred to as conventional laminates. However, the prescribed fibre angles of conventional laminates pose a limit on the design space. This issue, intuitively, can be tackled by making use of straight-fibre with arbitrary angles or even the curved-fibre. Accordingly, the so-called tow-steered or variable stiffness laminates (VSL) have drawn attention in the design of composite structures, thanks to the advent of automated fiber placement (AFP) machines (Marsh 2011; Brooks and Martins 2018). In contrast to the conventional laminates, the fibre trajectories of VSL are not necessary to be straight. As a result, tow-steering, i.e., allowing fibre angles to continuously vary within each ply of laminates, has the potential to further expand the benefits of aeroelastic tailoring, e.g., increasing the flutter speed (Stanford et al. 2014; Stodieck et al. 2013).

In order to take full advantage of aeroelastic tailoring and tow-steering for wing structure design, they have been incorporated into multidisciplinary design optimisation (MDO) frameworks. To date, the existing researches mainly focus on developing optimisation methodologies and quantifying the benefits of aeroelastic tailoring using VSL, and most of them are limited to the investigation of simple composite structures, such as flat plates and simplified aircraft wings (Stanford et al. 2014; Stodieck et al. 2013; Fazilati and Khalafi 2019; Akhavan and Ribeiro 2019; Guimarães et al. 2019; Akhavan and Ribeiro 2018; Haddadpour and Zamani 2012; Zhang et al. 2020).

Conversely, only very limited work has been done on the study of full-scale wing structures. The work done by Brooks et al. (2019) focuses on developing a high-fidelity aeroelastic optimisation approach, where the aerodynamics is modelled using the computational fluid dynamics (CFD) method. Applying this approach for wing-box design results in improvements of up to 2.4% in fuel burn and 24% in wing weight. In their follow-up study, the proposed method also has been employed to explore the tradeoff between fuel burn and wing weight (Brooks et al. 2020).

In another study, Stanford and Jutte (2017) compared the benefits of aeroelastic tailoring by minimising wing mass with the use of curvilinear stiffeners and VSL. They found both methods can reduce the wing mass compared to their non-curvilinear structural counterparts, but some degree of diminishing returns are observed when both methods are used simultaneously.

Moreover, Wang et al. (2021) took advantage of continuous tow shearing (CTS) manufacturing method for aeroelastic optimisation of a wing-box, such that the typical process-induced defects (i.e., gaps or overlaps) of VSL can be eliminated. However, CTS changes the thickness of wing laminates as the fibres are packed together for shearing.

For the aforementioned studies on aeroelastic optimisation of variable stiffness composite wings, several more research gaps and challenges may be identified to the best of the authors’ knowledge. Firstly, the fibre angle distribution obtained from the existing work usually are limited to the prescribed reference fibre paths (Wang et al. 2021) or patterns (Brooks et al. 2019), which overshadows the benefits of tow-steering due to the reduction of design space. Secondly, gust loads might be critical when the wing becomes more flexible as the result of aeroelastic tailoring, but the existing work has hardly included gust loads in optimisation. Additionally, it is important to maintain the cruise wing shape to ensure the optimal aircraft performance at cruise flight condition, which, however, has not been considered in the aforementioned studies.

To address these identified challenges, this work extends TU Delft aeroelastic tailoring framework PROTEUS (Werter and De Breuker 2016) by introducing a lay-up retrieval step, so that the extended framework can be applied for the conceptual design of variable stiffness composite wings. The aim of lay-up retrieval is to obtain fibre angle distribution based on the optimal distribution of lamination parameters given by PROTEUS, subject to manufacturability constraints (Peeters et al. 2015b). This is realised without any a priori definitions on fibre paths, therefore, the fibre angle distribution provided by the presented framework is not limited to any prescribed reference.

In terms of the consideration of gust loads, although it has been studied in the work of Stodieck et al. (2017), only three flight points are used to analyse gust loads and they are fixed throughout the optimisation process. Correspondingly, there is no guarantee that the applied gust loads are critical to wing sizing, because the critical gust loads might change with the updating of the wing design. This drawback is overcome in the proposed optimisation framework, whereby the critical gust loads are identified across the entire flight envelope at every iteration of optimisation using an efficient gust selection procedure developed by Rajpal et al. (2019a).

Further, Stodieck et al. (2017) considers a cruise shape constraint for wing sizing, so that the optimal aircraft performance at cruise flight condition can be ensured. This functionality has been also included in the proposed optimisation framework. For satisfying the cruise shape constraint, the jig (unloaded) shape of the wing is parameterised and considered as design variable in optimisation (Sodja et al. 2021), which is a more robust approach compared to the inverse method used in the work of Stodieck et al. (2017) for wing jig shape calculation.

Particularly, to account for the performance loss during lay-up retrieval, a strategy is proposed for tightening the violated constraints and correcting wing jig twist distribution after lay-up retrieval in the framework. As a result, the final manufacturable design provided by the proposed method always satisfies all design constraints. Additionally, in the proposed framework, all design variables are updated efficiently by making use of gradient-based optimisation algorithms with full-analytical gradients provided.

In summary, this paper continues the study on aeroelastic tailoring of aircraft wings with VSL. The presented optimisation framework is capable to address some challenges identified in the previous studies, which justifies the novelty and usefulness of the current work. The paper is organised as follows. Section 2 formulates the aeroelastic optimisation problem and proposes a solution framework. In Sect. 3, the correction strategies proposed for tightening the violated constraints and fixing the jig shape after lay-up retrieval are described. To demonstrate the features and benefits of the presented framework, some numerical examples are carried out in Sect. 4. Finally, Sect. 5 draws the main conclusions of the current study.

2 Optimisation problem and solution

In this work, composite wing structures are partitioned into a number of design sections with an independent stacking sequence assigned to each section. Further, the cruise and jig shape of the wing is described using corresponding distribution of twist angles along the wing span, and the out-of-plane deflection and dihedral of the wing are neglected because their influence on wing loads and drag is relatively small (Sodja et al. 2021). Accordingly, the aeroelastic optimisation problem defined for variable stiffness composite wings can be mathematically formulated in a general form as

$$\begin{aligned} \begin{aligned} \min \limits _{{\varvec{\theta }},{\varvec{N}},{\varvec{\varTheta }}}\qquad \,&M({\varvec{\theta }},{\varvec{N}},{\varvec{\varTheta }}) , \\ \text {subject to} \qquad&f_{i}^{j} ({\varvec{\theta }},{\varvec{N}},{\varvec{\varTheta }}) \le C_{i}^{0} , \\ \qquad&i =1,\ldots,I , \quad j =1,\ldots,J , \\ \text {with} \qquad&L_{k} \le x_{k} \le U_{k} , \\ \qquad&x_{k} \in \{\theta _{k}, N_{k}, \varTheta _{k} \} , \quad k =1,\ldots,K \\ \end{aligned} \end{aligned}$$

(1)

where M is the wing mass, ${\varvec{\theta }}$ and ${\varvec{N}}$ are the fibre angles and the number of layers in each wing section (laminate), and ${\varvec{\varTheta }}$ represents the jig twist distribution of the wing. For every design variable $x_{k}$, it is restricted by the predefined lower bound $L_{k}$ and upper bound $U_{k}$, and note that $L_{k}$, $U_{k}$ and K can take different values in corresponding to different types of design variables, i.e., fibre angle $\theta _{k}$, the number of layers $N_{k}$ and jig twist angle $\varTheta _{k}$. Further, $f_{i}^{j}$ refers to the ith design constraint under the jth load case, and $C_{i}^{0}$ is the prescribed limit value for constraint $f_{i}$ under all load cases. Additionally, I indicates the total number of constraints per load case and J is the total number of load cases.

In order to obtain a feasible and flightworthy wing design, the design constraints considered in problem (1) include aeroelastic stability, local angle of attack (AoA), buckling load, material strength, lamination feasibility and laminate manufacturability. On the other hand, the constraints on cruise shape and aileron effectiveness are also taken into account for ensuring the performance of the aircraft. Further, the load cases cover not only static loads in correspondence to cruise and manoeuvre flight conditions, but also dynamic loads induced by gust. The design constraints and load cases will be further discussed in Sects. 2.1, 2.2 and 4.2.

For efficiently solving the optimisation problem (1) using gradient-based algorithms, a solution framework, depicted in Fig. 1, is proposed. In the framework, optimisation problem (1) is resolved into two sub-problems: Aeroelastic tailoring and lay-up retrieval. In the sub-problem of aeroelastic tailoring, the stiffness properties of the laminates are parameterised by lamination parameters ${\varvec{V}}$ and laminate thicknesses ${\varvec{t}}$, which provides a continuous design space that enables the use of gradient-based optimisation methods. Accordingly, the problem of aeroelastic tailoring can be formulated as

$$\begin{aligned} \begin{aligned} \min \limits _{{\varvec{V}},\overline{{\varvec{t}}},\overline{{\varvec{\varTheta }}}} \qquad \,&\frac{M({\varvec{V}},\overline{{\varvec{t}}},\overline{{\varvec{\varTheta }}})}{M_0} , \\ \text {subject to} \qquad&\frac{f_{i}^{j} ({\varvec{V}},\overline{{\varvec{t}}},\overline{{\varvec{\varTheta }}})}{C_{i}^0} \le 1 , \\ \qquad&i =1,\ldots,I-I_{0} , \quad j =1,\ldots,J , \\ \text {with} \qquad&-1 \le \overline{x}_{k} \le 1 , \\ \qquad&\overline{x}_{k} \in \{V_{k}, \overline{t}_{k}, \overline{\varTheta }_{k} \} , \quad k =1,\ldots,K , \\ \end{aligned} \end{aligned}$$

(2)

where the vectors $\overline{{\varvec{t}}}$ and $\overline{{\varvec{\varTheta }}}$ with their elements $\overline{t}_{k}$ and $\overline{\varTheta }_{k}$ represent the normalised laminate thicknesses and jig twist distribution, respectively. Here the normalisation is necessary due to the scale difference of different types of design variables, and the normalised design variable $\overline{x}_{k}$ can be obtained by

$$\overline{x}_{k} = \frac{2}{U_{k}-L_{k}} \left( x_{k} - \frac{U_{k}+L_{k}}{2} \right) ,$$

(3)

with the original design variable $x_{k} \in \{ t_{k}, \varTheta _{k} \}$ and its lower bound $L_{k}$ and upper bound $U_{k}$.

Fig. 1

Flowchart of the aeroelastic optimisation framework for the design of tow-steered composite wings, with iterations l, m and n referring to different optimisation loops

Moreover, all design constraints of problem (1) are considered in sub-problem (2) excluding the manufacturability constraints. This is because the constraints on steering need to be imposed on the distribution of fibre angles ${\varvec{\theta }}$. Accordingly, constraint index i in sub-problem (2) ranges between one and $I-I_{0}$, where $I_{0}$ is the total number of manufacturability constraints. In the framework depicted in Fig. 1, the solution procedure of sub-problem (2) is illustrated by the inner loop (with iteration index m), in which the critical gust loads are identified at every iteration during optimisation. The aeroelastic tailoring is carried out using PROTEUS, which will be introduced in the following Sect. 2.1.

After solving sub-problem (2), on the one hand, the wing jig twist distribution can be updated, as shown in Fig. 1. On the other hand, a lay-up retrieval is required to be carried out in order to obtain the manufacturable stacking sequence of wing laminates. To this end, first the optimal thicknesses ${\varvec{t}}_{\text {opt}}$ are rounded up to the nearest number of plies according to the given ply thickness, which determines the number of layers in each design section, i.e., design variables ${\varvec{N}}$ in (1). Subsequently, the fibre angles of wing laminates can be obtained by solving the sub-problem of lay-up retrieval that is expressed as

$$\begin{aligned} \text {retrieve} \,\, &{\varvec{\theta }} , \\ \text {to match} \,\, &{\varvec{V}}_{\text {opt}} , \\ \text {subject to} \,\, &f_{i} ({\varvec{\theta }}) \le \zeta _{\text {U}} , \quad i =I-I_ {0}+1,\ldots ,I , \\ \text {with} \quad&L_{k} \le \theta _{k} \le U_{k} , \quad k =1,\ldots ,K , \\ \end{aligned}$$

(4)

where $\zeta _{\text {U}}$ represents the upper bound of steering curvature, here $f_{i}$ is the function of the steering $\zeta$. Further details on the steering constraint and the solution of sub-problem (4) will be given in Sect. 2.2.

Since the optimal lamination parameters ${\varvec{V}}_{\text {opt}}$ cannot be completely matched by solving sub-problem (4), the optimised design may no longer satisfy all design constraints after retrieving the manufacturable stacking sequence. To address this issue, the performance loss during retrieval is taken into account by tightening the violated constraints and then repeating aeroelastic tailoring procedure shown as the inner loop in Fig. 1. This process is referred to as the middle loop (with iteration index n) illustrated in Fig. 1, and it will be terminated once all design constraints, excluding cruise shape constraints, are satisfied under static load cases.

The possible violations on cruise shape constraints will be addressed by correcting wing jig twist distribution ${\varvec{\varTheta }}$ and checking the cruise lift distribution ${\varvec{L}}_{1\text {g}}$, which will be further discussed in Sect. 3. After that, the constraint violations under both static loads and critical gust loads are checked. The entire optimisation process will terminate if all design constraints under all load cases are satisfied. Otherwise, aeroelastic tailoring and lay-up retrieval are required to be repeated using the optimised design as a new start point, which is illustrated as the outer loop (with iteration index l) in Fig. 1. Finally, the manufacturable fibre paths of wing structures are obtained by post-processing the retrieved distribution of fibre angles.

2.1 Aeroelastic tailoring

The aeroelastic tailoring problem (2) is solved using a tool, PROTEUS, developed at TU Delft. For structural analysis, PROTEUS models the 3D wing using a geometrically nonlinear beam finite element model (FEM), where the stiffness properties of beam cross-sections are determined by a cross-sectional modeller. Further details on beam model and cross-sectional modeller refer to the work of De Breuker et al. (2011), Ferede and Abdalla (2014) and references therein.

The aerodynamic analysis is carried out by vortex lattice method based on potential flow theory, and the wing is modelled using vortex ring elements on its camber surface under a thin wing assumption, one can refer to the work of Werter et al. (2018) for more details on aerodynamic model implemented in PROTEUS.

Regarding to aeroelastic analysis, PROTEUS is capable to approximate both static and dynamic aeroelastic responses. The static aeroelastic system closely couples the geometrically nonlinear beam model and a steady aerodynamic model, and it is solved using Newton–Raphson root finding method. On the basis of static aeroelastic analysis, a dynamic structural model is constructed by linearising the nonlinear stiffness matrix around the static equilibrium solution and combining with a linear mass matrix. Then this structural model is coupled to an unsteady aerodynamic model to obtain the dynamic aeroelastic model which allows for predicting the aeroelastic response under gust loads. The detailed description on PROTEUS refers to the work of Werter and De Breuker (2016).

For the implementation of dynamic gust loads in PROTEUS, a discrete 1-cosine gust given by EASA CS-25 regulations (EASA 2020) is considered, and the shape of the gust is formulated as

$$U = \frac{U_{\text {ds}}}{2} \left[ 1 - \text {cos} \left( \frac{\pi s}{H} \right) \right] ,$$

(5)

where U represents the gust velocity, s is the distance penetrated into the gust, H refers to half of the gust length, and $U_{\text {ds}}$ is the design gust velocity which is given by

$$U_{\text {ds}} = U_{\text {ref}} F_{\text {g}} \left( \frac{H}{107} \right) ,$$

(6)

where $U_{\text {ref}}$ is the reference gust velocity that decreases linearly from 17.07 m/s at sea level to 13.41 m/s at 4572 m and then to 6.36 m/s at 18,288 m, $F_{\text {g}}$ is the flight profile alleviation factor, which is determined according to the maximum take-off weight and maximum landing weight of aircraft.

In order to identify the critical gust loads at every iteration over the entire flight envelope, the dynamic aeroelastic analysis is required to be computationally efficient. To this end, Rajpal et al. (2019a) have developed a critical gust selection procedure within the framework of PROTEUS based on a reduced-order aeroelastic model that couples the structural model and a reduced-order aerodynamic model. In the reduced-order aerodynamic system, the original states of full-order model are projected onto a reduced basis, which leads to a significant reduction of system dimension. Further, the reduced basis can be found using balanced proper orthogonal decomposition method (Willcox and Peraire 2002) according to the investigation on four commonly used model order reduction methods. To further reduce the computational costs, the reduced-order aerodynamic system is reformulated to isolate the effect of the airspeed and Mach number on the dominant aerodynamic modes, which enables the use of a single reduced-order model for aeroelastic analysis at all flight points over the entire flight envelope. More details on critical gust load identification refer to the work of Rajpal et al. (2019a) and references therein.

In aeroelastic tailoring, the optimisation constraints listed in Table 1 have been implemented in PROTEUS. The lamination feasibility formulations proposed by Hammer et al. (1997), Raju et al. (2014), and Wu et al. (2015) are applied to ensure the lamination parameters ${\varvec{V}}$ represent a feasible laminate. The composite strength failure criteria is considered based on a failure-free envelope derived using Tsai–Wu failure criterion in terms of lamination parameters and principal strains (IJsselmuiden et al. 2008; Khani et al. 2011). Similarly, the inverse buckling factor, defined as the ratio between the applied load and the critical buckling load, is used to assess the stability constraint in buckling of each wing skin panel delimited by the ribs and stiffeners (Dillinger et al. 2013).

Table 1 Summary of the optimisation constraints implemented in PROTEUS

Numerically, the aeroelastic stability is governed by the eigenvalues of the state matrix in aeroelastic equilibrium equation. Therefore, the aeroelastic stability constraints are implemented by restricting the real part of the eigenvalues. Namely, flutter happens when the real part of one of the eigenvalues becomes positive. To ensure the performance of the aileron, aileron effectiveness $\eta$ defined as a negative ratio between the roll coefficient $C_{\text {L} \delta }$ induced by the aileron deflection $\delta$ and the roll coefficient due to roll damping $C_{\text {Lp}}$, is required to be no less than a predefined minimum $\eta _{\text {min}}$. Then the aileron effectiveness constraint can be formulated as

$$\eta = - \frac{C_{\text {L}} \delta }{C_{\text {Lp}}} = \frac{p_{\text {roll}} s}{\delta V_{\infty }} \ge \eta _{\text {min}} ,$$

(7)

where $p_{\text {roll}}$ is the steady roll rate obtained from the solution of a roll moment equilibrium, s and $V_{\infty }$ refer to the wing semispan and the flight velocity, respectively.

Moreover, the cruise shape constraint is implemented based on the cruise twist distribution ${\varvec{\varTheta }}_{1{\text {g}}}$ of the wing, and it can be formulated as

$$\mid {\varvec{\varTheta }}_{1{\text {g}}} - {\varvec{\varTheta }}_{\text {target}} \mid \le {\varvec{\varDelta }} ,$$

(8)

where ${\varvec{\varTheta }}_{\text {target}}$ is the desired target twist distribution at cruise flight condition, and ${\varvec{\varDelta }}$ is a vector with its elements that represent the predefined tolerance values. Note that the cruise twist distribution ${\varvec{\varTheta }}_{1{\text {g}}}$ is the sum of the jig twist distribution ${\varvec{\varTheta }}$ and the elastic twist deformation of wing induced by the applied external loads. Moreover, in accordance with beam FEM, all twist distributions are parameterised by the corresponding twist angle at each node.

In addition, to ensure attached aerodynamic flow, a local AoA constraint is imposed on each aerodynamic cross-section, which is expressed as

$$-\alpha ^{*} \le \alpha _{s} \le \alpha ^{*} , \quad s =1,\ldots ,S ,$$

(9)

where the local AoA $\alpha$ is defined by the aircraft AoA, wing jig twist angle and the twist angle induced by wing deformation, $\alpha ^{*}$ is the predefined bound for local AoA, S represents the total number of aerodynamic cross-section, and it depends on the number of spanwise aerodynamic panels used to discretise wing aerodynamic surface.

For the update of design variables during optimisation, a gradient-based optimiser, globally convergent method of moving asymptotes (GCMMA) developed by Svanberg (2002), is employed in PROTEUS, in order to efficiently solve the aeroelastic tailoring problem (2) with full-analytical sensitivities provided.

2.2 Lay-up retrieval

Based on the solution of the aeroelastic tailoring problem (2) provided by PROTEUS, the manufacturable stacking sequence of wing laminates can be obtained by solving lay-up retrieval problem (4). In this work, an optimisation method developed by Peeters et al. (2015b) is adopted to carry out lay-up retrieval, and this method is briefly reviewed in this section.

Figure 2 illustrates the solution procedure of problem (4), in which the fibre angles ${\varvec{\theta }}$ are defined at the element nodes of a shell FEM obtained by discretising the composite structure (not to be confused with the beam FEM introduced in Sect. 2.1 because the aeroelastic tailoring and lay-up retrieval are carried out using different tools). In order to reduce computational costs and derive analytical sensitivities for optimisation, a bi-level approach is used to successively approximate the exact structural responses of composites, e.g., structural compliance c. At the first level, the structural response is approximated as a function of the in-plane (membrane) and out-of-plane (bending) stiffness matrices ${\varvec{A}}$ and ${\varvec{D}}$ and their reciprocals:

$$\begin{aligned} c^{(1)} \approx \sum _{n} \left( \begin{aligned}&{\varvec{\phi }}_{{\text {m}}} : {\varvec{A}}^{-1} + {\varvec{\phi }}_{{\text {b}}} : {\varvec{D}}^{-1} \\&+ {\varvec{\psi }}_{{\text {m}}} : {\varvec{A}} + {\varvec{\psi }}_{{\text {b}}} : {\varvec{D}} + c \end{aligned} \right) , \end{aligned}$$

(10)

where n runs over all the nodes of shell FEM, ${\varvec{\phi }}$ and ${\varvec{\psi }}$ are the reciprocal and linear approximation terms, the subscripts ${\text {m}}$ and ${\text {b}}$ denote the membrane and bending, respectively. The free term c equals to zero for the responses that enjoy homogeneity properties. Accordingly, the first level approximation is independent of fibre angles ${\varvec{\theta }}$ and it can be parameterised by lamination parameters ${\varvec{V}}$ and laminate thicknesses ${\varvec{t}}$. Conversely, the second level approximation of structural response is a function of fibre angles ${\varvec{\theta }}$, which can be formulated as

$$c^{(2)} \approx c^{(1)} + {\varvec{g}} \cdot \varDelta {\varvec{\theta }} + \varDelta {\varvec{\theta }}^{\text {T}} \cdot {\varvec{H}} \cdot \varDelta {\varvec{\theta }} ,$$

(11)

where ${\varvec{g}}$ and ${\varvec{H}}$ are the gradient vector and Hessian matrix of the first level approximation with respect to fibre angles ${\varvec{\theta }}$ at the approximation point.

According to Fig. 2, the lay-up retrieval procedure starts with an initial guess of fiber angles for the initialisation of the stiffness matrices ${\varvec{A}}$ and ${\varvec{D}}$. To build the first level approximation, the terms ${\varvec{\phi }}$ and ${\varvec{\psi }}$ in (10), which are the optimal stiffness matrix ${\varvec{A}}_{\text {opt}}$ or ${\varvec{D}}_{\text {opt}}$ and the corresponding inverse, are determined based on the optimal lamination parameters ${\varvec{V}}_{\text {opt}}$ and laminate thicknesses ${\varvec{t}}_{\text {opt}}$ provided by PROTEUS. Subsequently, by optimising fibre angles ${\varvec{\theta }}$, the second level approximation is carried out iteratively until the first level approximation is converged, see inner loop indicated in Fig. 2. Here the convergence means that the first level approximations obtained using the updated fibre angles at two consecutive iterations differ within a predefined tolerance or the predefined maximum number of iterations is reached. After that, the structural response approximated at the first level is compared to the response target which is the first level approximation obtained directly using ${\varvec{V}}_{\text {opt}}$ and ${\varvec{t}}_{\text {opt}}$ given by PROTEUS. If the difference between the approximated response and the target satisfies the predefined tolerance, then the stacking sequence of wing laminates is found. Otherwise, the updated fibre angles are used to build new approximation at the first level, where the stiffness matrices (${\varvec{A}}$ and ${\varvec{D}}$) are updated with the reciprocal and linear approximation terms (${\varvec{\phi }}$ and ${\varvec{\psi }}$) in (10) are fixed. The aforementioned process is required to be repeated until reaching the convergence of the outer loop shown in Fig. 2.

Fig. 2

Solution procedure of the lay-up retrieval

In the optimisation of fibre angles, a steering constraint is taken into account to avoid too small steering radius as it is one of the reasons causing fibre wrinkling during AFP process. The steering $\zeta$ is defined as the rate of change in fibre angle between nodes, and the steering constraint can be expressed as

$$\zeta ^{2} = \nabla \theta \cdot \nabla \theta = \frac{2}{\varOmega } \cdot {\varvec{\theta }}^\text {T} \cdot \mathbf{L} _{e} \cdot {\varvec{\theta }} \le \zeta _{\text {U}}^{2} ,$$

(12)

where $\varOmega$ is the area of the element e, $\mathbf{L}$ is the standard FEM discretisation of the Laplacian. Consequently, the steering of each element at each layer is restricted by a given maximum steering value $\zeta _{\text {U}}$ to ensure the manufacturability. The value of $\zeta _{\text {U}}$ is the inverse of the minimum radius of curvature, for example, a maximum steering value of 2 ${\text {m}}^{-1}$ corresponds to a minimum radius of curvature of 500 mm. More details on the method of lay-up retrieval can be found in the work of Peeters et al. (2015a, b, 2018). Additionally, a postprocessing procedure presented in the paper of Blom et al. (2010) is used to obtain the final fibre paths on the basis of the retrieved distribution of fibre angles.

3 Constraint and jig twist correction

In the framework illustrated in Fig. 1, although lay-up retrieval provides a manufacturable design, it often causes performance loss as the optimal lamination parameters and thickness cannot be matched exactly during lay-up retrieval. As a consequence, the violation of some design constraints might take place after retrieving the manufacturable stacking sequence. In order to obtain a manufacturable design that satisfies all design constraints, a constraint correction strategy is proposed and implemented in the presented optimisation framework, so that the loss in performance during retrieval can be taken into account through repeating aeroelastic tailoring (PROTEUS).

The correction strategy separately addresses the constraint of cruise twist distribution and the others considered in optimisation problem (2). When the design constraints, excluding cruise twist constraints, are violated after lay-up retrieval, the correction strategy applied for violated constraints is to tighten the original limit value of constraint by the percentage linked to the constraint violation. Accordingly, the limit value of the constraint used in PROTEUS can be obtained by

$$C_{i}^{n} = \left\{ \begin{array}{ll} \lambda _{i}^{n-1} C_{i}^{0} &{} \text {if}\, \lambda _{i}^{n-1}> \varLambda _{i} , \\ \varLambda _{i} C_{i}^{0} &{} \text {otherwise} , \end{array}\right. \quad \text {with} \;\; n>1 ,$$

(13)

where n is the iteration number of running PROTEUS (as indicated in Fig. 1) and i is the index of the design constraint as defined in (2). Accordingly, $C_{i}^{n}$ represents the limit value of the ith constraint at the nth time of running PROTEUS, and $C_{i}^{0}$ is the prescribed original limit value of the ith constraint as defined in (1). Furthermore, $\lambda$ represents a violation factor defined as $\lambda _{i}^{n-1}=c_{i}^{n-1}/C_{i}^{0}$ with $n > 1$, in which c is the constraint value obtained from reassessing wing aerostructural performance after lay-up retrieval. To prevent the requirement of too many iterations of running PROTEUS to reach a feasible design, a threshold value $\varLambda$ is predefined for violation factor $\lambda$, and it is used to tighten the original constraint limit $C_{0}$ if the violation factor $\lambda$ is lower than the threshold value $\varLambda$.

According to the proposed strategy for constraint correction, the original constraint limit $C_{i}^{0}$ is used at the first time of running PROTEUS (i.e., $n = 1$). When the constraint violations happen after lay-up retrieval, the constraint value $C_{i}^{n}$ required for rerunning PROTEUS (i.e., $n > 1$) is obtained by scaling the original constraint limit $C_{i}^{0}$ using the violation factor $\lambda _{i}^{n-1}$ or the threshold value $\varLambda _{i}$. For example, the threshold value $\varLambda _{i}=1.05$ means the original constraint limit $C_{i}^{0}$ need to be tightened 5% for rerunning PROTEUS. Generally, the larger the predefined threshold value, the less repetitions of PROTEUS are required, but that may make the design overly conservative.

Theoretically, the strategy formulated as (13) should also be applicable for correcting the constraint violations of wing cruise twist distribution ${\varvec{\varTheta }}_{1{\text {g}}}$. However, the twist distribution of the deformed wing has a large dependency on wing jig twist distribution ${\varvec{\varTheta }}$, and the main objective of including cruise twist constraint is to maintain the desired lift distribution of wing. Therefore, in the present work, the constraint violations of wing cruise twist distribution are addressed by iteratively correcting wing jig twist distribution ${\varvec{\varTheta }}$, such that the difference in lift distributions obtained before and after retrieval can be restricted. Figure 3 illustrates the correction procedure, where, at each iteration p ($p \geqslant 1$), the difference between the resulting cruise twist distribution after retrieval ${\varvec{\varTheta }}_{1{\text {g}}}^{\text {after}}$ and the target cruise twist distribution ${\varvec{\varTheta }}_{\text {target}}$ is calculated and subtracted from the previous wing jig twist distribution ${\varvec{\varTheta }}_{p-1}$. This procedure will be repeated until the maximum difference between cruise lift distributions obtained before (${\varvec{L}}_{1{\text {g}}}^{\text {before}}$) and after (${\varvec{L}}_{1{\text {g}}}^{\text {after}}$) lay-up retrieval satisfies a predefined tolerance. In this paper, it is assumed to be acceptable when the cruise lift distribution calculated after retrieval changes no more than 1% in comparison to that obtained before lay-up retrieval.

Fig. 3

Flowchart of correcting the jig twist distribution of the wing

4 Numerical examples

In this section, the proposed optimisation framework is applied to design a reference composite wing, whereby the objective is to minimise the normalised wing mass, subject to different load cases and design constraints. Accordingly, by means of analysing and comparing the optimisation results obtained in different case studies, the features and benefits of the presented optimisation framework will be demonstrated. Although it is difficult to carry out a detailed comparison between the simulation results obtained in this work and literature due to different numerical setups, some similarities can be observed when comparing the current results to those found in literature.

4.1 Baseline wing model

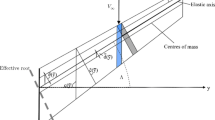
The NASA common research model (CRM) wing is selected as a baseline model for case studies, of which the design details refer to the work of Vassberg et al. (2008), Klimmek (2014), and Lacy and Sclafani (2016). The wing planform is depicted in Fig. 4, and the main parameters of wing planform are summarised in Table 2. Further, as illustrated in Fig. 4, ribs, engine, main landing gear, fuel, leading edge and trailing edge devices are modelled as lumped masses in accordance to the aeroelastic analysis framework of PROTEUS.

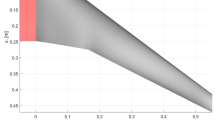
Figure 5 shows the wing geometry, where the wing-box is colored in red and it is divided into 20 segments along spanwise direction. For structural analysis, each segment is modelled using a beam element as mentioned in Sect. 2.1. Generally, to guarantee the accuracy of beam FEM, sufficient number of beam elements is required for modelling the wing structure. For computational efficiency, however, the number of design sections (i.e., wing laminates) defined along the wing spanwise direction is not necessary to be as many as that of beam elements. In the current work, the design sections are obtained by dividing the wing-box into 10 spanwise sections, of which each spanwise section of top and bottom skins consists of 2 chordwise sections and each spanwise section of spars has only 1 chordwise section. Further, since the middle spar has only 4 spanwise design sections, thus a total of 64 design sections ($10 \times 2 \times 2 = 40$ skin sections and $10 \times 2 + 4 = 24$ spar sections) are defined for wing optimisation. As mentioned in Sect. 2.1, the stiffness properties of beam elements depend on their corresponding cross-sections. Since the number of beam elements and design sections defined in this work are different (20 versus 10), so the properties of one design section may be assigned to multiple cross-sections according to the location of design sections and beam cross-sections.

Further, each section has independent design variables of lamination parameters and laminate thickness. Figure 6 gives an example of the wing laminates defined for wing top skin, where an auxiliary mesh is used to describe the connectivity of wing laminates. According to the method of lay-up retrieval introduced in Sect. 2.2, the fibre angles ${\varvec{\theta }}$ are defined at the nodes of the auxiliary mesh and the steering constraints are imposed on the elements of the auxiliary mesh. Note that the function of the auxiliary mesh is to describe the connectivity of wing laminates for lay-up retrieval, and it is not used to perform finite element analysis in the current work. In addition, the laminate adopted for wing optimisation is symmetric and its material properties are listed in Table 3.

Fig. 4

CRM wing planform with lumped mass distribution depicted

Table 2 Geometry parameters of CRM wing

Fig. 5

Virtualisation of the CRM wing geometry with the wing-box colored in red

Fig. 6

Illustration of the design sections (wing laminates) defined for wing top skin with their connectivity indicated using an auxiliary mesh (colored in red)

Table 3 Material properties of AS4/3501-6

The static load cases considered for the design of the CRM wing are listed in Table 4, and the load cases 1–3 represent cruise, 2.5 g symmetric pull up and $-1$ g symmetric push down flight conditions (points), respectively. Regarding to dynamic load cases induced by gust, 35 flight points that cover the entire flight envelope are selected for investigation. Figure 7 shows the flight envelope of the CRM aircraft and indicates the ID and location of the selected flight points. Note that, here, the ID number starts from 4 because the flight points 1–3 are in correspondence to static loads given in Table 4. Furthermore, the flight points 34–38 are determined based on the prescribed maximum operating altitude of the CRM aircraft. For each flight point, as described in EASA CS-25 regulations (EASA 2020), a sufficient number of gust lengths in the range 9 m to 107 m is required to be investigated to find the critical response. Accordingly, in this work, 22 gust lengths ranging from 9 to 107 m (11 positive lengths) and $-9$ m to $-107$ m (11 negative lengths) are considered for each flight point. Note that the magnitude of gust length is always positive, the positive and negative sign of gust length represent the upwash and downwash gust, respectively. Additionally, the fuel level is set to 0.8 for each gust length at each flight point. As a result, a total of 770 dynamic load cases are evaluated at every iteration of aeroelastic optimisation for identifying the critical gust loads.

Table 4 Static load cases defined for the aeroelastic optimisation of the CRM wing

Fig. 7

Flight points selected across the flight envelope of the CRM aircraft for the identification of the critical gust loads

4.2 Optimisation setup

The setup of design variables and constraints in optimisation is as follows:

• Since the wing-box is divided into 64 design sections and it is modelled using 20 beam elements, so there are $64 \times 8 = 512$ lamination parameters, 64 laminate thicknesses and 20 jig twist angles, which results in a total of 596 design variables.

• Similarly, as the lamination parameters of each laminate have to satisfy 6 feasibility formulations, so in total of $64 \times 6 = 384$ lamination parameter feasibility constraints are included.

• For aeroelastic stability constraint, only the 10 most critical eigenvalues for each load case are considered.

• The bound of local AoA $\alpha ^{*}$ in (9) is set to 12 deg and there are 34 local AoA constraints per load case due to 16 spanwise aerodynamic panels.

• The minimum aileron effectiveness $\eta _{\text {min}}$ in (7) is defined as 0.1, and only one constraint is imposed on aileron effectiveness for each load case.

• The failure constraint is implemented by restricting the strain responses of each beam element, which actually are composed of the strain distribution of two corresponding cross-sections (obtained using the cross-sectional modeller). Further, since only the 4 most critical Tsai–Wu strain factors are considered, so the total number of strain constraints per load case is formulated as $4 \times 2 \times (7 \times 8 + 6 \times 12) = 1024$, where the first 8 beam elements have 7 laminates (4 skin and 3 spar laminates) and the other 12 beam elements have 6 laminates because of 2 spars.

• For the buckling constraint, 8 most critical buckling panels are selected for each laminate and 8 bucking constraints are considered for each panel, which results in a total of $8 \times 8 \times 64 = 4096$ constraints per load case.

• According to (8), there are 42 constraints on cruise twist distribution in correspondence to 21 nodes of beam FEM. All values of the tolerance ${\varvec{\varDelta }}$ in (8) are set to 0.01 deg in order to better maintain the desired cruise shape of the wing.

• Regarding to steering curvature (radius), as mentioned in Sect. 2.2, one constraint is imposed on each element (of the auxiliary mesh shown in Fig. 6) at each layer to restrict the rate of change in fibre angle between element nodes. As a result, a total of $50 \times (18 \times 2 + 9 \times 2 + 3) = 2850$ constraints are included in lay-up retrieval, where 50 corresponds to the maximum number of layers (100) assumed for each symmetric laminate. Further, 18, 9 and 3 are the number of elements for skins, front and rear spars and the middle spar, respectively. Additionally, the value of the minimal steering radius is set to 0.5 m.

In the current work, three case studies are defined, see Table 5, and performed to investigate the effects of cruise shape constraints and critical gust loads on the design of wing structures.

• In Case 1, wing structures are sized under static loads (listed in Table 4) without the consideration of cruise (1 g) twist constraints and critical gust loads, which serves as a reference case.

• Case 2 considers both static loads and cruise twist constraints for wing sizing, thus it can be compared to Case 1 to show the effect of cruise shape constraints on wing design.

• On the basis of Case 2, Case 3 takes critical gust loads into consideration so that the influence of gust loads can be revealed by comparing Cases 2 and 3.

Note that the presented framework shown in Fig. 1 can be directly used for Case 3, but the module of identifying critical gust loads need to be removed from the framework in order to carry out Case 2. Moreover, the module that is to check ${\varvec{L}}_{1{\text {g}}}$ and correct ${\varvec{\varTheta }}$ is not necessary for Case 1 because there is no constraint on cruise twist distribution.

Table 5 Definition of case studies

4.3 Results and discussion

Figure 8 shows the convergence behaviour of the normalised wing mass and the number of violated constraints for Case 1. It can be seen that 10 constraints are violated after the first time of lay-up retrieval in Case 1, of which 9 constraints are related to strain factor and 1 constraint is on aileron control effectiveness. Due to the constraint violations, PROTEUS is repeated with stricter constraints and the original constraints are all satisfied after the second time of lay-up retrieval. Nevertheless, driving by the tighter constraints used in rerunning PROTEUS, the mass reduction gained from previous iteration ($n=1$) is decreased around 35%. Moreover, it can be observed that retrieving manufacturable lay-up slightly increases wing mass (around 3% at $n=1$) as a result of rounding up the optimal laminate thickness. A similar convergence behaviour is also observed in Case 2, as shown in Fig. 9, where 17 constraints are violated after the first time of lay-up retrieval, and the convergence is reached after the second time of retrieval (i.e., $n=2$).

Fig. 8

Convergence behaviour of the normalised mass and the number of violated constraints for Case 1

Fig. 9

Convergence behaviour of the normalised mass and the number of violated constraints for Case 2

According to the methodology described in Sect. 3, after reaching the convergence of the middle loop, the wing jig twist distribution will be corrected using the strategy depicted in Fig. 3, such that the wing lift distributions obtained before and after retrieval can be matched. The 1 g twist and lift distributions obtained after aeroelastic tailoring (PROTEUS), lay-up retrieval and jig twist correction in Case 2 are provided in Fig. 10. It shows that the 1 g twist distribution given by PROTEUS is very close to the desired target of 1 g twist distribution, which is because of the consideration of 1 g twist constraints in optimisation. However, due to the performance loss during retrieval, a clear difference can be found between the 1 g twist distribution obtained after lay-up retrieval and the target. Accordingly, the 1 g lift distribution obtained after lay-up retrieval differ somewhat (maximum 6%) from that provided by PROTEUS. After performing the correction of jig twist distribution, the difference between the final 1 g twist distribution and the target is reduced dramatically, and it is hard to be noticed. Further, the 1 g lift distribution obtained after jig twist correction maximally differs 0.4% compared to that given by PROTEUS, which is assumed to be an acceptable result as described in Sect. 3. This result indicates that it is necessary to separately address the constraint violations of 1 g twist and the others.

Fig. 10

Cruise twist and lift distribution obtained after aeroelastic tailoring (PROTEUS), lay-up retrieval and jig twist correction in Case 2

The convergence behaviour of Case 3 is similar to that of Case 2, and it terminates even without repeating the outer loop shown in Fig. 1. This means the wing optimised in the middle loop is safe under different gust loads represented in Fig. 7. One of the factors driven such convergence behaviour of Case 3 is the threshold value $\varLambda$ predefined for scaling constraint limit values, see (13). In the present work, $\varLambda =0.5$ is set for all three cases and it can observed that all cases require only two iterations within the middle loop to reach a converged solution. To investigate the effect of threshold value on final optimisation result, Case 3 is also carried out with the threshold value $\varLambda = 0.6$. As it can be expected, the wing mass increases with the increase of threshold value according to the optimisation results listed in Table 6. This is because the larger the threshold values the tighter constraints are used for repeating aeroelastic tailoring (PROTEUS), which leads to a larger reduction of the benefits gained from previous aeroelastic tailoring. Generally, larger threshold values require less iterations to converge as less gain is obtained in aeroelastic tailoring. Comparing the normalised wing masses (listed in Table 6) for Cases 1, 2 and Case 3 with threshold value $\varLambda = 0.5$, it shows that including cruise twist constraints and jig twist optimisation leads to a mass reduction of 10% (Case 2 versus Case 1), but the wing mass is increased around 5% when taking the dynamic gust loads into account for optimisation (Case 3 versus Case 2).

Table 6 Optimised wing mass in different case studies

To further explain the difference between the wing masses obtained in different case studies, the optimal thickness distribution of wing skins and spars for Cases 1, 2 and 3 is given in Fig. 11. It can be seen that all three cases have a similar trend in thickness distribution. Namely, the thickness increases from the wing root till the wing middle span and, in the inner half of the wing, the leading edge patches are thicker than those at the trailing edge. A thicker leading edge results in a forward shift of wing elastic axis, thus introducing wash-out (nose-down) twist upon wing bending to shift aerodynamic loads inboard and, consequently, leads to a reduction of wing mass due to lower wing root bending moment. Conversely, in the outer half of the wing, the thickness starts to decrease from the middle span up to the tip, and the trailing edge patches are thicker than those at the leading edge, which shifts the elastic axis aft to increase the aileron control effectiveness. The thickness distributions obtained in this work are similar to these given by Rajpal et al. (2019a, b).

Figure 12 shows the difference in thickness distribution of Cases 1, 2 and 3, where the thickness difference ranges from $-57$ to 25% except one region at which the laminate thickness increases 108% (Case 3 versus Case 2). It is clear that almost all laminates of wing skins in Case 3 are thicker than their counterparts in Case 2, showing that the gust loads are important to take into account because they are sizing the wing.

Comparing the thickness distribution in Cases 1 and 2, it indicates that the wing mass reduction (Case 2 versus Case 1) is mainly attributed to the thinner bottom skin and a large decrease of thickness at wing root regions. The reason of this difference is mainly because the wing jig twist distribution is allowed to change in Case 2 to satisfy the cruise twist constraint, but the jig twist in Case 1 is fixed. As a result of optimising wing jig twist distribution, the wing twist and lift distributions are adapted for gaining more wash-out effects, which leads to wing mass reduction in Case 2 although it includes additional constraints on cruise twist distribution compared to Case 1. The similar trend of thickness variation also can be observed when comparing the thickness distributions of Cases 1 and 3, but the thickness difference is smaller compared to that observed between Cases 1 and 2.

Fig. 11

Thickness distribution of the optimised wing components for Cases 1, 2 and 3

Fig. 12

Difference in thickness distribution of the optimised wing components for Cases 1, 2 and 3

The thickness distribution shown in Fig. 11 indicates that, as mentioned before, the wing tip region is mainly sized by aileron control effectiveness. To further validate this point, Case 1 is also carried out without the constraint of aileron control effectiveness. The optimal thickness distribution, shown in Fig. 13, shows that the leading patches generally are thicker than those at trailing edge throughout the wing span in order to gain more wash-out benefits. Further, no thickness increase close to the region of aileron can be observed.

According to the distribution of strain and buckling factor of the optimised wing shown in Fig. 14, it can be seen that the wing root region is sized by both strain and buckling, and the design of wing middle span is clearly strain driven. Note that Fig. 14 only plots the stain and buckling factor for Case 3 because all three cases have a similar distribution regarding to stain and buckling factor under static loads listed in Table 4.

Fig. 13

Thickness distribution of the optimised wing components for Case 1 without considering aileron effectiveness constraint

Fig. 14

Strain and buckling factor distribution of the optimised wing for Case 3

Figure 15 depicts the 1 g and jig twist distribution of the optimal wing in all three cases. This result is similar to the twist distributions obtained in the work of Kenway et al. (2014), Klimmek (2014), and Stodieck et al. (2017). It is clear that the 1 g twist distribution obtained in Case 1 is significantly different from these of Cases 2 and 3, because the 1 g twist constraint is not included in Case 1. Furthermore, as a result of satisfying the 1 g twist constraint, the jig twist distribution is changed in both Cases 2 and 3 in comparison to the initial jig twist distribution that is kept fixed in Case 1. Additionally, as mentioned before, the 1 g twist distribution in Case 2 shows further wash-out twists comparing to that in Case 1, which results in the reduction of wing mass. According to the difference observed between the cruise and jig twist distributions, the optimal wings obtained in all three cases seem to be stiff. This is attributed to the consideration of a relatively strict constraint on aileron effectiveness in the current work.

When the constraint of aileron effectiveness is removed from the optimisation of Case 1, the wing structure becomes more flexible and more wash-out twists can be observed as shown in Fig. 15. Additionally, it can be noticed that there is almost no difference between the jig twist distributions of Cases 2 and 3, which is because both 1 g twist distributions in Cases 2 and 3 have to match the desired target as the result of including 1 g twist constraint. For other two static load cases, the wing twist distributions obtained in Cases 2 and 3 are still similar because of the aileron effectiveness constraint. Conversely, the out-of-plane deflection of the wing is free as long as the strain and buckling constraints are satisfied. Consequently, the difference in wing thickness distribution of Cases 2 and 3 is reflected by the out-of-plane deflection (i.e., bending stiffness) of the wing as shown in Fig. 16.

Fig. 15

Cruise and jig twist distribution of the optimised wing for Cases 1, 2 and 3

Fig. 16

Out-of-plane deflection of the optimised wing for Cases 1, 2 and Case 3 under static loads listed in Table 4 (For clarity, the negative tip deflection is displayed for Load 3)

To better understand the importance and effect of dynamic gust loads on wing design, Fig. 17 shows the distribution of critical flight points and corresponding gust lengths of the wing in Case 3. For each wing laminate, all values of strain factor obtained at different static (listed in Table 4) and dynamic (see Fig. 7) loads are compared, and the critical flight point of the laminate is defined as the load case that results in the maximum strain factor. Accordingly, there is also a critical gust length if the critical flight point is corresponding to dynamic gust loads. Note that, in Fig. 17d–f, the wing laminate is colored as grey if the critical flight point ID of this laminate is 2 or 3 (i.e., static loads listed in Table 4). As shown in Fig. 17, the distribution of critical flight point is given at three different phase of optimisation process in Case 3, where the intermediate design is the wing obtained after the first time of lay-up retrieval.

The difference observed in these distributions of critical flight point confirms the finding given by Rajpal et al. (2019a): the critical gust loads can be different with the update of wing design during optimisation. Further, it can be seen that the critical gust length can also be different for the laminates with the same critical flight point. Looking at the distribution of the critical flight point of the final design, it is clear that a large part of the wing, especially wing tip region, is sized by dynamic gust loads. Therefore, it is of importance to be able to identify and include critical gust loads at every iteration of optimisation for wing sizing.

This point can be further demonstrated by applying the critical gust loads identified in Case 3 to the optimal wing structure provided by Case 2. Figure 18 gives the strain factor distribution obtained with static (flight point 2) and dynamic gust loads (flight points 8 and 28). It can be observed that the strain factor obtained under gust loads increases, even violates a bit (larger than 1), in contrast to that given by static load, which means the optimal wing sized with only static loads (Case 2) experiences failure under critical gust loads.

Fig. 17

Critical flight points and corresponding gust lengths for the wing in Case 3

Fig. 18

Strain factor obtained under static and critical gust loads for the wing provided by Case 2

As mentioned in Sect. 2, once the optimal distribution of fibre angles is determined by lay-up retrieval, the manufacturable fibre path can be obtained via a post-processing procedure based on the work of Blom et al. (2010). Further, as illustrated in Fig. 6, only one fibre angle per layer is defined for each laminate. To obtain more smooth fibre paths, the final distribution of fibre angles is enriched by interpolating more fibre angles according to the optimal fibre angles obtained in lay-up retrieval. This is performed only for the sake of the visualisation of fibre paths. Figure 19 shows the fibre paths of layers 1–4 of the optimised wing skins for Cases 1, 2 and 3. Note that the leading edge patch at wing tip of the top skin in Cases 3 is colored as black, because the layer 4 at this section is dropped. It can be seen that the retrieved fibre paths are diverse for different layers in different cases, and they are not restricted to any prescribed reference paths or patterns. This is one of the advantages of the proposed optimisation framework in comparison to the existing researches. Although the fibre paths indicate the stiffness directions of a single layer, they cannot be directly used to interpret the stiffness distribution of wing laminates. Therefore, in the current work, the laminate stiffness is represented by a polar plot of the membrane and bending thickness-normalised modulus of elasticity, $\hat{E}_{11}^{A} (\theta )$ and $\hat{E}_{11}^{D} (\theta )$, respectively. As introduced by Dillinger et al. (2013), the visualised laminate stiffness are obtained by

$$\hat{E}_{11}^{A} (\theta ) = \frac{1}{\hat{{\varvec{A}}}^{-1}_{11} (\theta )} , \quad \hat{E}_{11}^{D} (\theta ) = \frac{1}{\hat{{\varvec{D}}}^{-1}_{11} (\theta )} ,$$

(14)

where

$$\hat{{\varvec{A}}}^{-1} (\theta ) = {\varvec{T}}^{\text {T}} \hat{{\varvec{A}}}^{-1} {\varvec{T}} , \quad \hat{{\varvec{D}}}^{-1} (\theta ) = {\varvec{T}}^{\text {T}} \hat{{\varvec{D}}}^{-1} {\varvec{T}} ,$$

(15)

and

$${\varvec{T}}=\left[ \begin{array}{ccccc} \text {cos}^{2} (\theta ) &{} &{} \text {sin}^{2} (\theta ) &{} &{} 2 \text {cos} (\theta ) \text {sin} (\theta ) \\ \text {sin}^{2} (\theta ) &{} &{} \text {cos}^{2} (\theta ) &{} &{} -2 \text {cos} (\theta ) \text {sin} (\theta ) \\ -\text {cos} (\theta ) \text {sin} (\theta ) &{} &{} \text {cos} (\theta ) \text {sin} (\theta ) &{} &{} \text {cos}^{2} (\theta ) - \text {sin}^{2} (\theta ) \end{array} \right] ,$$

(16)

where $\hat{{\varvec{A}}}$ and $\hat{{\varvec{D}}}$ are the thickness-normalised laminate stiffness matrices, which are defined as $\hat{{\varvec{A}}}={\varvec{A}}/h$ and $\hat{{\varvec{D}}}=12 {\varvec{D}}/h^{3}$ with given laminate membrane stiffness matrix ${\varvec{A}}$, bending stiffness matrix ${\varvec{D}}$ and thickness h. ${\varvec{T}}$ refers to the axes transformation matrix with $\theta$ ranges from 0 to 360 deg. Accordingly, Fig. 20 shows the membrane and bending stiffness distribution of the wing laminates for Cases 1, 2 and 3, in which both the stiffness distributions obtained before and after the last time of lay-up retrieval are given. When looking at the membrane and bending stiffness distributions for all three cases, it can be seen that the bending stiffness properties are more pronounced at the wing root region compared to the rest of the wing, because the wing root is buckling critical as mentioned before. For the middle part of the wing, as it can be observed, the membrane stiffness is oriented along the wing axis to increase the load carrying capability of the wing. Comparing the stiffness distributions obtained before (colored blue) and after (colored red) retrieving the manufacturable stacking sequence, a good agreement can be observed when reaching a converged solution. This demonstrates the validity of the presented optimisation framework depicted in Fig. 1. Further, the difference observed in stiffness distributions indicates that the optimal lamination parameters cannot be completely matched. As a consequence, it will cause constraint violations (e.g., Fig. 8) when the difference in stiffness distributions becomes sufficient, which drives the rerunning of PROTEUS for aeroelastic tailoring.

Fig. 19

Fibre paths (layers 1–4) of the optimised wing skins for Cases 1, 2 and 3

Fig. 20

Membrane (in-plane) and bending (out-of-plane) stiffness distribution of the wing laminates obtained before and after the last time of retrieving the stacking sequence for Cases 1, 2 and 3

5 Conclusions

To enable the consideration of critical gust loads and cruise shape constraints for the preliminary design of manufacturable variable stiffness composite wings, a formulation of aeroelastic optimisation and its solution framework have been proposed. In this framework, the original optimisation problem is resolved into two sub-problems: aeroelastic tailoring and lay-up retrieval, so that it can be efficiently solved using gradient-based optimisers. Aeroelastic tailoring enables the minimising of wing mass through optimising the lamination parameters and thickness of wing laminates together with wing jig twist distribution, subject to a variety of design constraints and load cases. The load cases cover not only static loads but also dynamic gust loads. Further, the critical gust loads are identified across the entire flight envelop at every iteration of optimisation. The design constraints include aeroelastic stability, aileron effectiveness, local AoA, buckling load, material strength and lamination feasibility. Particularly, a desired prescribed cruise shape of the wing (i.e., cruise twist distribution) is maintained during optimisation to ensure the optimal aircraft performance. With the optimal lamination parameters, the manufacturable stacking sequence is retrieved in lay-up retrieval by including minimal steering radius constraint. Additionally, a strategy has been proposed for tightening the violated constraints and correcting wing jig twist distribution, so that the constraint violations caused by lay-up retrieval can be fixed.

To demonstrate the features and benefits of the proposed optimisation framework, several case studies on the design of the NASA CRM wing have been carried out. Accordingly, the effects of critical gust loads and cruise shape constraint on wing sizing have been investigated. The results show that including the cruise shape constraint together with jig twist optimisation can gain further reduction of wing mass, while the consideration of gust loads leads to the increase of wing mass, but is necessary since the the gust loads lead the statically optimised wing to fail. Further, it confirms that the critical gust loads might change with the update of wing design during optimisation. Therefore, it is of great importance to be able to identify critical gust loads at every iteration of optimisation and include cruise shape constraint for the design of wing structures. Moreover, the final distribution of fibre angles obtained in the current work are not restricted to any predefined reference paths or patterns, which also demonstrates the benefits of the presented optimisation framework for the design of variable stiffness composite wings.