Moving morphable curved components framework of topology optimization based on the concept of time series

Abstract

Topology optimization provides a powerful approach to structural design with its capability to find the optimal topology automatically. However, the optimal topologies achieved by the traditional density-based method are difficult to be manufactured. Recently, some explicit descriptions, like the Moving Morphable Components (MMC) approach, have been introduced to narrow the gap between design and manufacture. However, since only components with simple geometry are considered, it is still unsatisfactory regarding geometric arbitrariness in those studies. Here we demonstrate a new topology optimization approach originating from the MMC framework by replacing the straight components with the curved ones so as to enhance the geometric arbitrariness. The skeleton of the modified component is described by the non-uniform rational B-splines (NURBS) curve. The concept of time series is then proposed to directly generate the curved component from the 1D skeleton curve. It is shown that it’s much easier to achieve the variation of width by the new strategy when compared with other curve descriptions. Numerical examples demonstrate the effectiveness and robustness of the proposed approach based on the moving morphable curved components.

Appendix: Library of benchmark examples

To further show the good performance of the developed TSMMC, several representative examples are provided in this library.

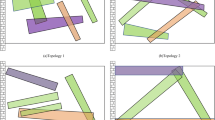
The Messerschmitt–Bölkow–Blohm (MBB) problem is illustrated in Fig. 

Fig. 13

The MBB problem (only a half beam is indicated here)

13. Because of the symmetry, the design domain is taken to be half of the beam. The vertical load is applied on the middle point of the top side with $F = 1$. The length and height of the design domain are taken to be 3 and 1 with a $120 \times 40$ FEM mesh. The upper bound of the available volume is set as $V_{bound} = 0.5$. The configuration is composed of 12 curved components, and 6 control points are assigned to draw each component. Figure 

Fig. 14

a Convergence history; b initial configuration; c final configuration of the MBB problem

14 shows the initial configuration, optimized configuration, and convergence history.

The second example is the bridge problem as shown in Fig. 

Fig. 15

The bridge problem

15. $150 \times 50$ FEM mesh is assigned to the $3 \times 1$ design domain and a $3 \times 0.1$ non-designable domain is set on the top. The load is uniformly distributed on the top surface with the total magnitude equal to 1. The upper bound of the available volume of this problem is taken as $V_{bound} = 0.3$. The numbers of components and control points are 8 and 6, respectively. The convergence history with its initial and final configurations of this bridge problem is illustrated in Fig. 

Fig. 16

a Convergence history; b initial configuration; c final configuration of bridge problem

16. Noted that some curved components are clearly seen in the optimized configuration which clarifies the need of using curved components in MMC.

The Michell truss problem for a single load with two supports (Fig. 

Fig. 17

The Michell truss problem for a single load with two supports

17) is considered here. The $2 \times 1$ rectangular design domain is meshed by $100 \times 50$ finite elements. A vertical load $F = 1$ is applied on the middle point of the bottom side. As in the previous case, the numbers of components and control points are 8 and 6, respectively. The volume constraint of this problem is set to be $V_{bound} = 0.4$. The convergence history with its initial and final configurations is shown in Fig. 

Fig. 18

a Convergence history; b initial configuration; c final configuration of Michell truss problem for a single load with two supports

18. The optimization converges very fast and the curved components are also seen in the optimized configuration. The jump is due to the fact that voids temporarily exist near the force-applied region. Actually, such a problem is also reported in the standard MMC-based framework (Zhu et al. 2018).

The Michell truss problem for a single load with a circular support (Fig. 

Fig. 19

The Michell truss problem for a single load with a circular support

19) is also considered here for demonstrating the advantages of TSMMC. The $3 \times 2$ rectangular design domain is meshed by $120 \times 80$ elements. A vertical load $F = 1$ is applied at the centre of the right boundary. The numbers of components and control points for each component are set as 2 and 6, respectively. The volume constraint of this case is $V_{bound} = 0.25$. The convergence history with its initial and final configurations is shown in Fig. 19. It converges fast. Curved components are seen in the optimized configuration which exactly implies the advantages of TSMMC.

Finally, we return to the short beam problem again. Given an initial configuration without symmetry, we examine whether the TSMMC can spontaneously generate a symmetric design. All parameters are set to be the same as before except for the initial configuration. The convergence history with its initial and final configurations is shown in Fig. 20. As observed from Fig. 21, the components can find their optimal shapes and positions even when an asymmetric initial configuration is adopted.

Fig. 20

a Convergence history; b initial configuration; c final configuration of Michell truss problem for a single load with a circular support

Fig. 21

a Convergence history; b initial configuration without symmetry; c final configuration of the short beam problem