Gradient-based optimisation of rectangular honeycomb core sandwich panels

Abstract

When subjected to bending loads, sandwich panels are highly efficient structural components with the potential to achieve substantial weight reduction. A successful design methodology for sandwich panels should aim at maximising this potential for weight reduction while considering the various possible failure mode in a simple yet accurate manner. This paper investigates the application of steel sandwich panels as two-way deck systems. Near-optimal designs for all-steel Rectangular Honeycomb Core Sandwich Panels (RHCSPs) under general out-of-plane loading are achieved using a gradient-based optimisation method. The method relies on continuously optimising the design limit state constraints while the response constraints are considered a priori in the analysis stage using simplified analytical assessment. Plate bending solutions and sandwich bending solutions are used as alternatives to estimate the internal stresses on each layer of the sandwich panel under out-of-plane loads, where comparisons are made between these two analysis methods in terms of computational efficiency and accuracy. The internal stresses are then used to formulate design limit state equations for each relevant failure mode, including material yielding, plate buckling and deformation control. The Method of Moving Asymptotes is used for the optimisation of RHCSPs, considering the limit states as the constraints of the optimisation problem and weight as the objective function to be minimised. The proposed methodology for simplified assessment is verified against detailed nonlinear finite element models for optimal design solutions. The implications of the results of the proposed optimisation strategy on the development of a systematic design methodology for RHCSPs are also highlighted, making specific reference to critical failure modes.

1 Introduction

Conventional steel deck systems, such as those used in offshore topsides and as shown in Fig. 1, consist of a steel plate spanning over a grid of primary and secondary beams, forming a grillage system. For applications where heavy equipment is installed, the provision of a dense grid of secondary beams underneath the equipment supports is required to ensure efficient load transfer, adequate capacity and sufficient stiffness of the deck plate locally. On the other hand, areas destined for light equipment and consumables are usually designed for uniform loads, leading to a uniform arrangement of the secondary structural components. Due to these design requirements, secondary deck beams are distributed throughout the deck in a nonuniform fashion, depending on the load magnitude and variability, predominantly dictated by the equipment arrangement over the deck. This convoluted beam distribution requires substantial welding activities to be performed on-site, steeply raising the construction costs associated with conventional deck systems. Additionally, conventional deck systems form an important contribution to the overall weight of industrial structures. Innovative solutions to substitute conventional configurations which are more beneficial in terms of weight, construction time, life span, safety, assembly process and overall cost are thus desirable.

Fig. 1

Plan view of primary and secondary steel layout of a conventional deck system

The popularity and effectiveness of sandwich components in weight-critical applications can be attributed to their attractive high specific strength and stiffness, resulting from their geometrical configuration. Formally, a sandwich panel can be defined as a composite structural component consisting of the following: (i) two thin and sufficiently stiff plates of dense material at the top and bottom of the panel, (ii) the core, which is an intermediate thick layer of a low density material between the plates, and (iii) a specific connection scheme between the plates and the core of the panel (Allen 1969).

The basic principle underlying the structural response of sandwich panels is analogous to that of an I-shape beam, extended in two planar dimensions. The relative strength and stiffness of I-sections can be attributed to the concentration of most of the material in the flanges, far from the bending neutral axis. In this manner, the component stiffness and capacity under flexural loading is significantly enhanced. The web provides the required shear resistance, maintaining a certain distance between the plates, while further providing stability to the flanges against buckling. Similarly, the behaviour of sandwich structures is defined by the sandwich effect: the top and bottom plates resist bending moments and the core resists transverse shear forces. These characteristics render sandwich components considerably more efficient in resisting flexural loading as compared to conventional solid components of equivalent weight (Zenkert 1995).

When considering their application as deck systems, the enhanced flexural behaviour of sandwich panels enables the design of larger spans, reducing the need for a dense grip of supporting secondary beams, as shown in Fig. 2a. This is further reduced by taking advantage of the two-way spanning action of sandwich panels. Beyond their inherent weight saving potential, sandwich panels demonstrate an impressive potential for achieving functional flexibility against the relocation of heavy equipment, due to the uniformity of the core geometry resulting in uniform local stiffness and strength characteristics throughout their planar domain.

Fig. 2

a Plan view of steel layout for an innovative sandwich panel deck system; b Rectangular Honeycomb Core Sandwich Panel

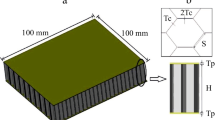
All-steel Rectangular Honeycomb Core Sandwich Panels (RHCSPs), as illustrated in Fig. 2b, are considered to be the topology of sandwich construction with the most potential to satisfy the deck system requirements of weight saving, adequate structural performance, and practical manufacturing and assembly processes. RHCSPs consist of an array of strips in the two planar dimensions, which intersect to form rectangular cells, capable of adapting to a wide range of spans with different aspect ratios as well as loading conditions. In this manner, an anisotropic response with pre-defined characteristics can be established, achieving the optimal performance in each bending direction. While previous work has focussed on one-way sandwich action, such as the I-core sandwich panel system (Kujala and Klanac 2005), this paper focuses on the optimisation of RHCSPs as two-way spanning sandwich systems.

There is a lack of clear and detailed guides for modelling the two-way behaviour of sandwich plates. Initial design guides for sandwich panels were specific for a given product, where the design was achieved through tables presenting the properties of a discrete set of sandwich panels (Hexcel Composites 2000). Additionally, analyses are based on one-way simply supported or cantilever beam theory. Even more recent guidelines use basic equations and tables for the design of sandwich panels (Lloyd's Register 2015).

The first specification for the structural application of steel sandwich panels was put forward by DNV—Det Norske Veritas (2012), particularly for applications to ship structures. For new sandwich constructions, DNV requires/recommends the following:

A steel sandwich panel subjected to local lateral pressure is to follow elastic design principles to avoid major plastic yielding of steel face plating and to limit too high shear stresses in the core.

In the absence of detailed FE analysis, which is normally preferred for complex cases with load and pressure variations over the sandwich plating and supporting structure, a simplified analytical assessment based on a simply supported plate model and uniform lateral pressure is acceptable.

A design methodology that follows both requirements/recommendations is deemed suitable for practical application since the trade-off between the efficiency of the design process and the accuracy of the final solution is seen as beneficial. In this regard, a suitable method of analysis based on analytical approaches could be considered since these can be easier and faster to apply than detailed numerical approaches. On the other hand, analytical approaches are valid only for idealised loading and support conditions (SAND.CORe Co-ordination Action 2006). Simplified FE models can overcome these restrictions, where common methods with improved efficiency rely on the employment of sandwich shell finite elements, using layerwise laminate theory (Carrera 1998), while still defining distinct material properties for the faceplates and the homogeneous core. An effective approach has previously been proposed by Liang and Izzuddin (2016) to perform linear and nonlinear analysis of sandwich structures using a 2D local shell system, where a co-rotational approach is employed to model geometric nonlinearity (Izzuddin 2007; Izzuddin and Liang 2016).

In contrast, for a sandwich panel with a discrete core, which can be highly orthotropic, a full discretisation in shell elements is recommended (SAND.CORe Co-ordination Action 2006). Orthotropic all-metal sandwich panels, such as the corrugated core (Chang et al. 2005; Ge et al. 2021) or the I-core (Yan and Jelovica 2021; Sun et al. 2015) sandwich panels, require a dense mesh of finite elements for both the plates and the core to capture several structural phenomena at sufficient levels of detail. The discretisation of the whole sandwich panel can, however, lead to significant computational demands, rendering these models unsuitable for practical application in design and optimisation. These benefits and drawbacks of detailed numerical models for RHCSPs have been previously investigated (Nordas et al. 2018), showing that the use of such high-fidelity models should be restricted to design scenarios of extreme significance where important local effects cannot be captured with simplified approaches.

As an alternative to classic iterative design methodologies, optimisation has become increasingly used for structural engineering problems which are relevant to industrial applications (Pedersen et al. 2015). For example, a weight optimisation tool, which can provide sufficiently accurate predictions at the early design phase is extremely valuable since it allows for the structure to be further optimised in the next executive phase (Cicconi et al. 2016). Optimisation problems for sandwich panels target a wide range of applications, materials and core topologies (Rathbun et al. 2005; Romanoff 2014; Lurie et al. 2017; Fang et al. 2017). The wide range that is covered in the research literature suggests that new problems require individual and innovative solution methods, as presented hereafter.

Initially, closed-form solutions established the fundamentals for minimum-weight structural optimisation of sandwich panels (Vinson 1999). However, complex engineering optimisation problems that require an increased number of variables and constraints do not typically have closed-form solutions. Accordingly, gradient-based algorithms have been developed to provide solutions for these problems, typically through using iterative methods based on the derivatives of the objective and constraints functions (Valdevit et al. 2004). An example of gradient-based optimisation of sandwich structures with varying core and face plate thickness was proposed by Löffelmann (2021), taking into consideration constraints on maximum stress, wrinkling, and crimping.

Other works take advantage of heuristic methods, such as Genetic Algorithms (GA), to perform the structural optimisation of sandwich panels, usually using nonlinear finite element analysis to assess the structural behaviour of each individual (Poirier et al. 2013). Alternatively, topology optimisation has also been used for the design of sandwich panels (Chu et al. 2019). These methodologies, although accurate, are less suitable for practical application due to the substantial computational time to create, run and post-process nonlinear FE models.

This paper proposes a practical optimisation methodology for the structural design of RHCSPs under combined out-of-plane uniformly distributed loads and patch loads, allowing their application as two-way spanning deck systems. Gradient-based optimisation algorithms are considered to be ideal for this problem due to a reduced number of variables and the continuity of the design limit state equations. To increase the applicability of the method, simplified numerical approaches, which are inherently less accurate but more computationally efficient, are preferred. Two distinct numerical modelling approaches are considered, based on analytical Reissner–Mindlin plate bending expressions and layered sandwich shell elements (Liang and Izzuddin 2016). These two methods are used to capture the stiffness characteristics of the panel and determine the internal force distribution within the domain of the panel. However, both these methods must be accompanied by local limit state checks to overcome their inability to capture some local failure modes. The efficiency of the method is based on solely optimising the design limit state constraints while the response constraints are considered during the analysis stage. The method, verified against numerical modelling, is shown to generate minimum-weight solutions in an efficient yet accurate manner, which is of particular importance in weight-sensitive applications including offshore structures.

2 Optimisation of RHCSPs

Besides the width $W$ and length $L$, RHCSPs are uniquely defined by seven geometric variables, as illustrated in Fig. 3: thicknesses of the top and bottom plates $t_{f,top}$ and $t_{f,bot}$, height $h$, core strip spacing in the $x$- and $y$-directions, $l_{x}$ and $l_{y}$ and web thickness in $x$ and $y$, $t_{w,x}$ and $t_{w,y}$.

Fig. 3

Geometric characteristics of RHCSPs

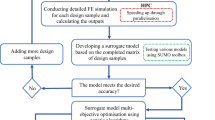
In this paper, two different methodologies for the design and optimisation of RHCSPs are proposed. The simplest one, envisioned for simply supported panels, uses Reissner–Mindlin (RM) plate theory to obtain the internal forces within the panel, followed by an optimisation of the geometric variables of RHCSPs according to its local failure criteria. This method does not require iterations because the internal bending moments and shear forces are independent of the candidate structural details, although this is only valid for isotropic or nearly isotropic sandwich panels under certain support conditions, specifically simply supported panels.

A more refined method of analysis uses a modelling approach based on layered sandwich shell elements (Izzuddin and Liang 2016) to re-assess a candidate optimal solution, update the internal forces, and optimise again for these new design internal forces. The initial candidate solution is obtained arbitrarily, and the procedure stops when weight convergence is achieved, based on a weight tolerance of 10^–2 kg/m². This iterative method can more realistically account for the influence of the core shear stiffness in the two directions, rendering it suitable to be applied to sandwich panels with general support boundary conditions.

Both approaches are schematically illustrated in Fig. 4.

Fig. 4

Schematic of the design and optimisation methods for RHCSPs

2.1 Methods of analysis

The development of a practical assessment and optimisation method for the design of RHCSP systems requires the evaluation of the accuracy and computational efficiency of several methods of analysis to obtain the internal forces in a sandwich panel, presented in Fig. 5. These methods include analytical expressions, plate FE elements, sandwich FE elements and detailed numerical models using full discretisation of the cover plates and the honeycomb core. As mentioned in the previous section, detailed high-fidelity models are not considered due to their substantial computational cost (Nordas et al. 2018).

Fig. 5

Internal forces on a sandwich plate element

Analytical expressions for plate bending are associated with a very limited field of application and have several assumptions embedded regarding the material response, the geometry and the range of loading and deformation. In fact, most of the analytical work can only be used for simply supported plates. Nonetheless, under these circumstances, plate bending theory, such as RM theory, is extremely useful for the initial design stages as it provides an accurate and efficient estimate of internal forces in the elastic range. These are valid for any given sandwich panel with thin faces and isotropic weak core (Zenkert 1995). This theory can be written in terms of partial deflections, which are the components of the total deflection due to bending $w_{b}$ and due to transverse shear $w_{s}$. The component of deformation due to shear is significant for sandwich panels due to the low shear stiffness of its core relatively to solid plates. Considering a simply supported sandwich panel, the partial deflections are obtained as follows (Zenkert 1995):

$$w_{b} \left( {x,y} \right) = \frac{1}{D}\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\frac{{p_{mn} }}{{\left[ {\left( {m\pi /L} \right)^{2} + \left( {n\pi /W} \right)^{2} } \right]^{2} }}} } \sin \frac{m\pi x}{L}\sin \frac{n\pi y}{W}$$

(1)

$$w_{s} \left( {x,y} \right) = \frac{1}{S}\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\frac{{p_{mn} }}{{\left( {m\pi /L} \right)^{2} + \left( {n\pi /W} \right)^{2} }}} } \sin \frac{m\pi x}{L}\sin \frac{n\pi y}{W}$$

(2)

where $D$ and $S$ represent, respectively, the bending and shear stiffness of the sandwich panel and $p_{mn}$ represents the Fourier coefficients associated with a given load. Under a uniformly distributed load, $p_{mn} = 16p_{0} /\pi^{2} mn$, where $p_{0}$ is the value of the UDL and $m$ and $n$ assume odd integer values.

This assumption is only exact for isotropic sandwich panels but still provides a good approximation of the internal force distribution for similar rigidities in the $x$- and $y$-direction, as demonstrated subsequently. Similar expressions are also available for simply supported plates under patch loads (Zenkert 1995). To consider general support boundary conditions or continuity between adjacent panels, resorting to FE models becomes necessary.

The sandwich element, as illustrated in Fig. 6, has been implemented in ADAPTIC (Izzuddin 1991), which is employed for all the numerical work in this paper. Sandwich FE models consist of layered shell elements with three layers, where the two plates and the core of the sandwich panels are embedded (Liang and Izzuddin 2016). When compared to RM plate models, sandwich elements offer a broad range of benefits, including practical application in design and a good balance between accuracy and computational demand. Since the intermediate layer is continuous in this modelling approach, the mechanical properties of the discrete core are equivalently obtained through a process of core homogenisation.

Fig. 6

Three-layered sandwich model and local coordinate system (Liang and Izzuddin 2016)

Sandwich element models can predict the stiffness characteristics of the panel, due to the intermediate layer having equivalent mechanical properties to the discrete core. Moreover, the planar stress distribution in the top and bottom plates can be captured with good accuracy and a nonprohibitive computational cost. The shear stiffness of the core S_x and $S_{y}$, can be determined by the conception of a transverse shear load acting only on the core in the $z$-direction. By applying Hooke’s law, the shear stiffness of the core is simply determined by:

$$\begin{array}{*{20}c} {S_{x} = G_{s} h\left( {\frac{{t_{w,x} }}{{l_{x} }}} \right)} \\ {S_{y} = G_{s} h\left( {\frac{{t_{w,y} }}{{l_{y} }}} \right)} \\ \end{array}$$

(3)

where $G_{s}$ represents the shear modulus of steel. On the other hand, the continuous nature of the intermediate core layer, as opposed to the actual discrete configuration, does not allow for some local failure modes to be accurately captured, such as intercellular plate buckling. Therefore, the sandwich element models provide a highly efficient approach of acceptable accuracy only in cases where the elastic response of the panel component or system is investigated. In fact, this is the main mode of application for assessment or design purposes, where the distribution of internal forces is required in the elastic range of response. However, this type of analysis must be accompanied by local limit state checks to overcome the inability to capture local failure modes.

2.2 Limit state criteria

A successful design methodology for sandwich panels requires the consideration of the various possible failure modes, where an accurate prediction of these modes is not only necessary, but it should also utilise a simple approach that is suitable for practical application. The aim is to enable designers to assess with confidence the critical failure mode under specific loading and support conditions, the magnitude of the corresponding load and, most importantly, the location of failure. With this information, the iterative optimisation process of a given design becomes simple and intuitive.

The limit states derived henceforth can be divided into three categories: material yielding, plate buckling and serviceability limit states. Material yielding is assumed to take place according to the von-Mises yield criterion, with a yield strength of the material $f_{y}$. Secondly, for plate buckling, the critical buckling load $N_{cr}$ and respective critical buckling stress $\sigma_{cr}$ are generally written as:

$$\sigma_{cr} = k\frac{{\pi^{2} E}}{{12(1 - \nu^{2} )}}\left( \frac{t}{b} \right)^{2} ;\quad \sigma_{cr} = \frac{{N_{cr} }}{t};\quad N_{cr} = k\frac{{\pi^{2} D_{plate} \left( t \right)}}{{b^{2} }}$$

(4)

where $E$ is the elastic Young’s modulus of the plate, $t$ is plate thickness, $\nu$ is Poisson’s ratio, $D_{plate} \left( t \right) = Et^{3} /12\left( {1 - \nu^{2} } \right)$ is the plate bending stiffness, $b$ is a dimension of the plate and $k$ is the buckling coefficient (Ventsel 2001). The definition of the buckling coefficient, hence the corresponding buckling load, depends on the aspect ratio of the plate, the stress state, and the support conditions, as elaborated in subsequent sections. Moreover, it should be noted that buckling limit states are constrained by the elastic buckling capacity of RHCSPs, as it is a common design philosophy in engineering codes.

The limit states considered for RHCSP and discussed hereafter are: face yielding, face intercellular buckling, core compressive yielding, core compressive buckling, core shear yielding, which includes punching shear, and core shear buckling. The only serviceability limit state considered in this paper is deflection control. Detailed FE analysis is used to guide the development and confirm the simplified analytical expressions for each limit state. The three buckling failure modes considered in this paper are illustrated in Fig. 7, referring to the face plate and the core strips shown in Fig. 3, which include the relevant geometric variables and the deformed shape consistent with simply supported conditions at the ends of the component plates.

Fig. 7

Buckling failure modes: a face intercellular buckling; b core shear buckling; c core compressive buckling

2.2.1 Face yielding

Consider a sandwich panel under general loading that leads to different bending moments in the principal directions, $M_{x}$ and $M_{y}$, as well as twisting moments $M_{xy}$, as shown in Fig. 5. According to the sandwich concept, the top and bottom plates will be under a general planar stress state. Plate yielding limit state will therefore be defined by the von-Mises yield criterion (Gozzi 2004) and the sandwich effect according to the following expression, derived per unit length:

$$\sigma_{d} = \sqrt {\left( {\frac{{M_{x} }}{{h \cdot t_{f} }}} \right)^{2} - \left( {\frac{{M_{x} }}{{h \cdot t_{f} }}} \right)\left( {\frac{{M_{y} }}{{h \cdot t_{f} }}} \right) + \left( {\frac{{M_{y} }}{{h \cdot t_{f} }}} \right)^{2} + 3\left( {\frac{{M_{xy} }}{{h \cdot t_{f} }}} \right)^{2} } \le f_{y}$$

(5)

where $t_{f}$ refers to the thickness of the face plate and $h$ refers to the height of the panel, as illustrated in Fig. 3. A single quantity, equivalent to a ‘von-Mises moment’ can be conveniently derived according to:

$$M_{vM} = \sqrt {M_{x}^{2} - M_{x} M_{y} + M_{y}^{2} + 3M_{xy}^{2} }$$

(6)

From the three maps of internal resulting moments, a ‘von-Mises moment’ map can, therefore, be obtained. This simplification helps to establish where yielding initiates in the panel according to the following:

$$M_{vM,\max } \le M_{rd} = h \cdot t_{f} \cdot f_{y}$$

(7)

2.2.2 Face intercellular buckling

Face intercellular buckling occurs when one of the face plates subject to a compressive stress state loses stability in between the supports provided by the core plates. The assessment of intercellular buckling under a general planar stress state can be achieved by considering a simply supported rectangular plate under biaxial planar stress, whose dimensions are the cell sizes of the core in the two directions, neglecting the effect of planar shear, as shown in Fig. 7a. Moreover, the biaxial stress resultants are defined by the bending moments of the panel divided by its height.

By introducing the cell sizes in the two directions into the exact solution for the stability equation applied to the buckling behaviour of rectangular simply supported plates under biaxial compressive stress, the bending moment resistance for intercellular buckling can be determined as:

$$M_{ed,x} \le M_{cr,x} = h \cdot t_{f} \cdot \frac{{\left[ {m^{2} \left( {l_{x} /l_{y} } \right)^{2} + n^{2} } \right]^{2} }}{{m^{2} \left( {l_{x} /l_{y} } \right)^{2} + \alpha n^{2} }}\frac{{\pi^{2} D_{plate} \left( {t_{f} } \right)}}{{l_{x}^{2} }}$$

(8)

where $\alpha = M_{ed,y} /M_{ed,x}$ defines the ratio between the bending moment resultants at a given point. It should be noted that the selection of the deformation mode, via parameters $m$ and $n$, is the one that leads to the smallest compressive load, referred to as the critical buckling load. For this, eight different constraints are added considering $m = 1,2,3,4$ for $n = 1$ and $n = 1,2,3,4$ for $m = 1$. These constraints lead to the exact buckling load for aspect ratios between the cell sizes of the core up to 4.0, since the incorrect choice of $m$ and $n$ would lead to higher capacity and therefore to nonactive constraints, i.e. constraints that do not influence the optimal solution.

The critical locations for design are considered to be where $M_{ed,x}$ is maximum, for both positive and negative values, with the corresponding $M_{ed,y}$, and where $M_{ed,y}$ is maximum, for both positive and negative values, with the corresponding $M_{ed,x}$. This approach is expected to provide conservative theoretical predictions and could accordingly be used to achieve safe designs.

2.2.3 Core shear yielding

According to the sandwich concept, the core is responsible for carrying shear forces and stabilising the face plates. Therefore, the core plates will be under a pure shear stress state which can cause yielding or buckling. The plastic shear resistance of a beam specimen of a RHCSP can be obtained similarly to an I-beam, by multiplying its shear area, which is the area of the web, by $f_{y} /\sqrt 3$. This accords with the von-Mises criterion, which leads to the following expressions for the orthogonal cores under a pure shear stress state in a RHCSP:

$$V_{ed,x} \le V_{rd,x} = h\left( {\frac{{t_{w,x} }}{{l_{x} }}} \right)\frac{{f_{y} }}{\sqrt 3 }$$

(9)

$$V_{ed,y} \le V_{rd,y} = h\left( {\frac{{t_{w,y} }}{{l_{y} }}} \right)\frac{{f_{y} }}{\sqrt 3 }$$

(10)

The verified analytical predictions for the shear yielding limit state specify that the resistance of the core in the two main directions is independent of each other. Therefore, the RHCSP is a versatile structural solution for rectangular sandwich panels, with two different orthogonal spans, with independent design checks for each direction, and the possibility of optimising the core in each direction, while taking advantage of the two-way flexural response.

2.2.4 Core shear buckling

Core shear buckling can be assessed by considering a simply supported rectangular plate under a pure shear stress state whose dimensions are the cell size of the core in the orthogonal direction and the height of the panel, as shown in Fig. 7b. This method neglects the combined effect of shear and compression, which could potentially be relevant in the vicinity of patch loads.

The general solution for the stability equation applied to the buckling behaviour of rectangular simply supported plates under pure shear stress $N_{xy}$ can be obtained. Under these conditions, by substituting the plate dimensions by the height and cell size in the orthogonal direction and considering $h \ge l$, the critical shear force resultant of a RHCSP in the two directions, as verified via detailed numerical analysis, can be determined as:

$$V_{ed,x} \le V_{cr,x} = \left( {\frac{h}{{l_{x} }}} \right) \cdot \left[ {5.35 + 4/\left( {h/l_{y} } \right)^{2} } \right] \cdot \frac{{\pi^{2} D_{plate} \left( {t_{w,x} } \right)}}{{l_{y}^{2} }}$$

(11)

$$V_{ed,y} \le V_{cr,y} = \left( {\frac{h}{{l_{y} }}} \right) \cdot \left[ {5.35 + 4/\left( {h/l_{x} } \right)^{2} } \right] \cdot \frac{{\pi^{2} D_{plate} \left( {t_{w,y} } \right)}}{{l_{x}^{2} }}$$

(12)

and for $h < l$:

$$V_{ed,x} \le V_{cr,x} = \left( {\frac{h}{{l_{x} }}} \right) \cdot \left[ {5.35 + 4/\left( {l_{y} /h} \right)^{2} } \right] \cdot \frac{{\pi^{2} D_{plate} \left( {t_{w,x} } \right)}}{{h^{2} }}$$

(13)

$$V_{ed,y} \le V_{cr,y} = \left( {\frac{h}{{l_{y} }}} \right) \cdot \left[ {5.35 + 4/\left( {l_{x} /h} \right)^{2} } \right] \cdot \frac{{\pi^{2} D_{plate} \left( {t_{w,y} } \right)}}{{h^{2} }}$$

(14)

These constraint functions, when applied simultaneously, do not result in the accurate shear buckling capacity, since the wrong geometrical assumptions generate active constraints. This inaccuracy can be easily resolved by writing the denominators as piecewise functions.

These verified design equations for the shear buckling capacity of the core indicate that the two main directions are no longer decoupled. As an example, decreasing the core spacing in the $y$-direction increases the resistance of the core against core shear buckling in $x$-direction.

2.2.5 Core compressive yielding

Under local concentrated loading, arising from the supports of heavy equipment, the core of the sandwich panel can fail through compressive yielding or compressive buckling. Compressive yielding is also governed by the von-Mises criterion applied for a uniaxial stress state. In this state, the ultimate capacity of a rectangular honeycomb core per unit area can be derived by the following expression:

$$C_{ed} \le C_{rd} = \left[ {\left( {\frac{{t_{w,x} }}{{l_{x} }}} \right) + \left( {\frac{{t_{w,y} }}{{l_{y} }}} \right)} \right]f_{y}$$

(15)

2.2.6 Core compressive buckling

The prediction of the elastic buckling of the core under compression can be achieved by considering a simply supported rectangular plate under a uniaxial compressive stress state. The dimensions of this unit-plate are the cell size of the core and the height of the panel, as shown in Fig. 7c. Taking into consideration rectangular cores, the buckling behaviour of a group of cells can be assessed by two different critical buckling loads arising from different orthogonal unit-plates. The elastic buckling capacity of the system is determined by the sum of the resistance of each unit-plate, leading to the following expression to assess the compressive buckling capacity of a rectangular core:

$$C_{ed} \le C_{cr} = \left( {\frac{{t_{w,x} }}{{l_{x} }}} \right)\left( {\frac{{m_{x} l_{y} }}{h} + \frac{h}{{m_{x} l_{y} }}} \right)^{2} \frac{{\pi^{2} D_{plate} \left( {t_{w,x} } \right)}}{{l_{y}^{2} t_{w,x} }} + \left( {\frac{{t_{w,y} }}{{l_{y} }}} \right)\left( {\frac{{m_{y} l_{x} }}{h} + \frac{h}{{m_{y} l_{x} }}} \right)^{2} \frac{{\pi^{2} D_{plate} \left( {t_{w,y} } \right)}}{{l_{x}^{2} t_{w,y} }}$$

(16)

where $m_{x}$ and $m_{y}$ are selected so that the critical buckling is minimised. The selection of the deformation mode, via parameters $m_{x}$ and $m_{y}$, is achieved via 25 different constraints considering the permutations of $m_{x} ,m_{y} = 1,2,3,4,5$. These constraints lead to the exact buckling load of welded cores in the practical range where the height of the optimal panel is less than five times the cell sizes in the two orthogonal directions.

Each component of (16) is valid only for elastic buckling. For elasto-plastic buckling, with material nonlinearity developing after buckling, the plate that buckles first could have lost a significant part of its resistance due to softening. Adding the two buckling loads provides an accurate estimation of the buckling capacity only if the buckling capacities of the two plates are similar. Nonetheless, the choice of using (16) as a design equation relies on three aspects: firstly, rectangular plates present a strong stable post-buckling response, characterised by a shift of the applied compressive stress from the centre of the plate towards its edges, reducing the bending moments in the centre of the buckled plate; secondly, compressive yielding is revealed to be the least critical limit state, decreasing the chances of compressive buckling to be shortly followed by material yielding; and thirdly, the difference between the buckling capacity of each set of plates is delimited by the set of design bounds for thicknesses and cell sizes.

2.2.7 Deflection control

Finally, a serviceability limit state regarding the deflection of the panel is considered as 1/360 of the smaller span of the sandwich panel. The maximum deflection $w_{b0}$ is obtained using considering a unit flexural stiffness $D$. The deflection constraint is then written as:

$$\frac{{w_{b0} }}{{D_{panel} }} \le \frac{{\min \left( {L,W} \right)}}{360}$$

(17)

Shear deformation can also be accounted in the constraint by considering a similar reference variable $w_{s0}$, corresponding to the maximum shear deflection, as shown in for $S = 1.0$. With $D_{panel} = E \cdot \left( {h^{2} t_{f,top} t_{f,bot} } \right)/\left( {t_{f,top} + t_{f,bot} } \right)$ and $S_{panel} = G \cdot h \cdot \min \left( {t_{w,x} /l_{x} ,\;\;t_{w,y} /l_{y} } \right)$, the updated deflection constraint is given by:

$$\frac{{w_{b0} }}{{E \cdot \frac{{h^{2} t_{f,top} t_{f,bot} }}{{t_{f,top} + t_{f,bot} }}}} + \frac{{w_{s0} }}{{G \cdot h \cdot \min \left( {\frac{{t_{w,x} }}{{l_{x} }},\frac{{t_{w,y} }}{{l_{y} }}} \right)}} \le \frac{{\min \left( {L,W} \right)}}{360}$$

(18)

In the case of orthotropic cores, two constraints are considered to prevent convergence issues arising from the $\min$ function in the denominator. Nonetheless, this approximation leads to conservative solutions since the shear deflection is calculated using the most flexible core in the two directions. In the case where the deflection is numerically obtained from the sandwich element models, as shown in Fig. 6, the flexural reference variable $w_{b0}$ is determined on a model with virtually large shear stiffness, while the shear reference variable $w_{s0}$ is estimated through the difference between the model with realistic shear stiffness and the model with large shear stiffness. This does not increase computational time since the two linear elastic models can be computed in parallel.

2.3 Gradient-based optimisation

It is recognised that the weight of an offshore facility significantly influences the cost, schedule, and complexity of offshore projects (Rui and Walker 2015), even though it is hard to quantify this influence (Kaiser et al. 2013). Moreover, fabrication costs for offshore topside structures are usually presented in cost per tonne, indicating the significance of weight on these costs. This is due to the cost per day of offshore transportation vessels being highly dependent on their weight capacity. Therefore, considering the application as deck systems for offshore topsides, minimising weight is seen as the main objective since it not only reduces material usage but significantly influences the cost of transportation and installation.

In this paper, the weight of the panels is the only parameter to be considered in the objective function $f_{0} \left( {\rm X} \right)$ for optimisation. The expression for the weight of the panel, expressed per unit area, is as follows:

$$f_{0} \left( {\rm X} \right) = {\text{Weight}} = \rho_{s} \left[ {t_{f,top} + t_{f,bot} + h\left( {\frac{{t_{w,x} }}{{l_{x} }} + \frac{{t_{w,y} }}{{l_{y} }}} \right)} \right]$$

(19)

This objective function as well as the constraint functions presented throughout Sect. 2.2 are continuous. Moreover, as shown in Fig. 3, this optimisation problem is defined solely by seven geometric variables, which renders gradient-based optimisation algorithms capable of efficiently solving this problem. A practical consideration in the context of gradient-based optimisation requires that the constraint functions be normalised to improve the performance of the method. Every structural constraint is then written in the following form:

$$f_{i} \left( {\rm X} \right) = \frac{C}{{g_{i} ({\text{X}})}} - 1.0 \le 0$$

(20)

where $C$ stands for a constant value combining all the constant inputs necessary to express a given limit state, and $g_{i} \left( {\rm X} \right)$ stands for a function that combines all the variables ${\rm X}$ of the optimisation problem in the same expression. Additionally, the value of 1.0 can be interpreted as the inverse of a target utilisation factor (or safety factor) for the considered limit state, as $C$ also refers to the design internal forces and $g_{i} \left( {\rm X} \right)$ to the respective resistance. This requires the internal forces to be independent of the variables, which is an assumption undertaken in this paper. This assumption is valid for simply supported sandwich panels of nearly isotropic cores. For general support boundary conditions, the refined methodology is needed to re-assess the internal forces at the end of each iteration, as illustrated in Fig. 4. Using different target utilisation factors for different limit states establishes a hierarchy of failure conditions, similar to the principles of capacity design presented in design codes for buildings under earthquake loading (British Standards Institution 2005). In this paper, the target utilisation factors are all set to 1.0.

Lower and upper design bounds (${\rm X}_{\min }$ and ${\rm X}_{\max }$) for the geometric variables that define a RHCSP are also established. A minimum value for the thickness of the plates of 3 mm is chosen due to fabrication limits. However, there is an interest in neglecting these design bounds initially, generalising the method to different applications. Consequently, the optimisation problem can be summarised as follows:

$$\begin{array}{*{20}l} {\min f_{0} ({\text{X}})\quad \quad \quad \quad} \\ {{\text{s.t.}}\,\left\{ {\begin{array}{*{20}l} {\frac{C}{{g_{i} ({\text{X}})}} - 1.0 \le 0} \\ {{\text{X}}_{\min } \le {\text{X}} \le {\text{X}}_{\max } } \\ \end{array} } \right.} \\ \end{array}$$

(21)

This work adopts the Method of Moving Asymptotes (MMA) (Svanberg 1987), which is a gradient-based numerical method to solve optimisation problems by creating, in each iteration, a subproblem where a function with the general shape of $y = 1/x$ approximates both the objective and the constraint functions in the vicinity of the current point. In short, the MMA algorithm replaces the objective and constraints functions with a set of convex functions that are equivalent in the vicinity of the current point and then solves the subproblem as a convex optimisation problem. These approximating functions are updated in each iteration, hence the name ‘moving asymptotes’. In detail, the approximation functions that constitute the subproblem are defined as:

$$\tilde{f}_{i}^{(k)} ({\text{X}}) = f_{i} \left( {{\rm X}^{(k)} } \right) + \sum\limits_{j = 1}^{n} {\left( {\frac{{p_{ij}^{(k)} }}{{u_{j}^{(k)} - {\text{X}}_{j} }} - \frac{{p_{ij}^{(k)} }}{{u_{j}^{(k)} - {\text{X}}_{j}^{(k)} }}} \right) + } \sum\limits_{j = 1}^{n} {\left( {\frac{{q_{ij}^{(k)} }}{{{\text{X}}_{j} - l_{j}^{(k)} }} - \frac{{q_{ij}^{(k)} }}{{{\text{X}}_{j}^{(k)} - l_{j}^{(k)} }}} \right)}$$

(22)

where the $i$-index refers to the objective and constraints functions, the $j$-index to the design bounds of each of the $n$ variables, $p_{ij}$ and $q_{ij}$ are scalar coefficients which guarantee the same local gradient in the current iterative step $k$, and $u_{j}$ and $l_{j}$ are the moving asymptotes. A representation of the approximation function $\tilde{f}({\text{X}})$ is illustrated in Fig. 8a, where the local gradient is negative $\left( {p_{ij} = 0} \right)$, while Fig. 8b illustrates the case where the local gradient is positive $\left( {q_{ij} = 0} \right)$.

Fig. 8

Approximation of functions by the MMA: a negative and b positive local gradient

2.3.1 Sensitivity analysis

The sensitivities of the objective function and the yielding, buckling and deformation constraints are obtained analytically and implemented in the algorithm. Since the geometric variables are treated as continuous, the objective and constraint functions presented throughout Sect. 2.2 are differentiable. The derivation of these sensitivities is presented in Appendix.

The objective and constraint functions that rule structural design optimisation problems, such as the one presented in this paper, are usually nonlinear and, most importantly, nonconvex. Therefore, gradient-based algorithms, such as MMA, may result in a local optimum instead of the global optimum. To confirm the suitability of the method, an exhaustive search was applied which consists of subdividing the parametric domain to obtain an estimate of the global minimum through brute force search. The solution found in the discrete space using this exhaustive search is similar to the one found in the continuous space using MMA. Moreover, the design space in the vicinity of the optimal solution was searched by permutating small increments of the geometric variables. This guarantees that the minimum solution that respects the constraints is found. Finally, since the initial candidate solution is obtained arbitrarily and multiple starts converged to the same solution, this strongly indicates the solutions provided in this paper are global optima.

For the problems described in this paper, MMA provided consistent global optimal solutions. It should be noted that some other gradient-based methods, such as the interior-point method (Maar and Schulz 2000) or sequential quadratic programming (Schittkowski et al. 1994), could have been used to solve this optimisation problem.

3 Verification against detailed numerical models

A simply supported rectangular sandwich panel with an area of 5.4 × 9.0 m² under a combination of distributed and patch loads is analysed and optimised. A schematic view of the example is presented in Fig. 9a, establishing the geometry of the problem and the loading conditions. The panel is subjected to a UDL of 20 kPa as well as four patch loads with varying dimensions and area loads. Design internal forces are obtained using RM plate bending theory with these being unaffected by the flexural and shear rigidities. An illustrative output of this method of analysis is presented in Fig. 9b depicting the top plate planar stress resultant in the $x$-direction in N/mm. On the other hand, Fig. 9c represents the same stress map as obtained from the sandwich FE model of the optimal solution. The numerical sandwich FE solution was obtained using 8640 elements corresponding to an element size of 75 mm while the RM plate bending theory was used to calculate the internal forces in 6000 points. The correspondence between the results from the RM analytical solution and the numerical sandwich FE solution is evident in this case.

Fig. 9

5.4 × 9.0 m² Model: a schematic view; b internal force maps using analytical RM model; c internal force maps using sandwich FE model

These two methods of analysis are used to obtain the following quantities relevant to the previously presented limit states: maximum equivalent von-Mises bending moment, $M_{vM,ed}$, for face yielding; maximum bending moment in $x$- and $y$-directions at critical locations, $M_{ed,x}$ and $M_{ed,y}$, for intercellular buckling; maximum shear forces in $x$- and $y$-directions, $V_{ed,x}$ and $V_{ed,y} ,$ for core shear yielding and buckling; maximum compressive stress, $C_{ed}$, for compressive yielding and buckling; the constants $w_{b0}$ and $w_{s0}$, for deformation control. The critical locations for intercellular buckling include the points with maximum bending moments in both $x$- and $y$-directions. These design internal forces are presented in Table 1, as obtained using the Reissner–Mindlin analytical expressions and as obtained using the sandwich FE model of the optimal panel. Some discrepancies can be observed mainly in the maximum shear forces in the vicinity of the patch loads, which can be associated with the different underlying assumptions of RM plate bending theory and sandwich FE modelling to analyse domains where shear is changing rapidly. Nonetheless, it can be ascertained from Fig. 9 and Table 1 that the analytical RM plate bending expressions can accurately estimate the distribution of internal forces in the domain of the panel, as compared to the numerical model based on sandwich FE elements, verifying that no iterations are required in this case.

Table 1 Design internal force resultants—5.4 × 9.0 m²

As previously mentioned, the target utilisation factors for all limit states are kept as 1.0, and the optimisation is performed without considering design bounds. Considering a yield strength $f_{y}$ of 235 MPa, the outcomes of the optimisation algorithm are the dimensions of the optimal panel, which are presented in Table 2, and the corresponding utilisation factors for the optimal panel are presented in Table 3. It can be observed that several limit states have a utilisation factor equal to 1.0, rendering them critical to the optimisation problem.

Table 2 Geometric variables of the optimal panel—5.4 × 9.0 m²

Table 3 Utilisation factors of the optimal panel—5.4 × 9.0 m²

The optimal panel, as obtained from the two different analysis methods, is approximately the same. To verify the optimisation sequence, a detailed nonlinear FE model, in which both the cover plates and core strips are modelled with nine-noded shell elements, is used to investigate the nonlinear structural behaviour of the optimal panel from the RM analytical solution. The panel geometry and the loading conditions are presented in Fig. 9a and Table 2. For the domain discretisation of RHCSPs, 9-noded quadrilateral (Izzuddin and Liang 2016, 2020) geometrically nonlinear co-rotational shell FEs have been employed. This high-fidelity numerical modelling strategy can capture various forms of local buckling and its progression over the panel domain, alongside the effects of material nonlinearity and sympathetic sinusoidal imperfections (Nordas et al. 2018).

A model of the optimal panel is depicted in Fig. 10a, which also shows the compressive stress maps in the $x$-direction, while Fig. 10b provides the predicted nonlinear response.

Fig. 10

Detailed model of the optimal panel: a Stress maps and failure b Nonlinear response

It can be seen from the core deformed shape in Fig. 10a that the critical failure mode is compressive buckling of the core plates below the 900 × 900 mm² patch loads, which occurs at a load factor LF = 0.95. The fact that this load factor is close to 1.0 indicates that the interaction between core compressive buckling and core shear buckling below the patch loads is not significant. The results from an identical model with linear elastic material are shown to identify material yielding, which occurs at LF = 1.02. At LF = 1.0, the maximum displacement is 13.62 mm, complying with the serviceability limit of 15.0 mm (i.e. 5400/360). As predicted by the optimisation sequence, structural instabilities should affect the nonlinear response of the panel at a load factor LF = 1.0, which is successfully observed in the detailed model. This fact serves as a verification tool for the proposed analysis methodology. In addition, the panel displays a hardening post-buckling response, which indicates that the proposed limit state criteria have the desirable characteristic of being marginally conservative.

4 Application examples

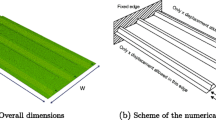
Benchmark results arising from the optimisation algorithm are provided and discussed in this section to assist in the development of practical rules and future design guidance. Firstly, it should be noted that both design methodologies presented in this paper provide the same solution for simply supported square panels under UDL. This is because plate models accurately estimate isotropic sandwich panels, which end up being optimal in these scenarios. It should also be noted the optimisation sequence based on the RM analytical solution is an order of magnitude faster than the algorithm based on sandwich FE elements since it does not require recalculation of design internal forces. More relevant conclusions arise from a 2 × 10 m² simply supported panel under a UDL of 0.2 MPa, as shown in Fig. 11a. Table 4 presents the design internal forces for the optimal panel.

Fig. 11

Schematic view of 2 × 10 m² panels: a simply supported under UDL; b simply supported under centred patch load; c three fixed edges and a free long edge under UDL

Table 4 Design internal force resultants—2 × 10 m², UDL, without design bounds

As expected, load transfer is achieved via the shorter span in the $x$-direction as indicated by the design bending moments in $x$- and $y$-directions in Table 4. The optimal panel is established for the unbounded problem, assuming a yield strength $f_{y}$ of 235 MPa, with the optimal geometric variables presented in Table 5, while Table 6 depicts the respective utilisation factors.

Table 5 Geometric variables of the optimal panel—2 × 10 m², UDL, without design bounds

Table 6 Utilisation factors of the optimal panel—2 × 10 m², UDL, without design bounds

The optimal panel has an approximately isotropic core ($S_{x} \approx S_{y}$). Even by artificially reducing $V_{y,ed}$ to a negligible number, the optimal panel is still interestingly nearly isotropic ($S_{x} \approx 1.3S_{y}$), with shear buckling in the two directions representing the critical limit states, as shown in Table 6. This nonintuitive result can be interpreted as follows: first of all, when the variables are kept unbounded, there are no lower bounds to the weight of the core and, therefore, the optimal panel is defined by a large height and a light core; secondly, the plates of the core, are extremely thin and prone to buckling; finally, the shear buckling limit state, as defined in (11) and (12), for $h \ge l$, denotes that the spacing of the strips in the orthogonal direction has a greater influence on the elastic buckling capacity, than the spacing of the strips in the direction of the shear forces; therefore, the optimal panel has thick plates with increased cell size in the direction of high shear force and thinner plates with reduced cell size in the direction of the lower shear force, leading to a panel which has similar core shear stiffness in both directions.

Now, to investigate the effect of introducing design bounds on the thicknesses of the plates, which are set as a minimum thickness of 3 mm due to fabrication limits, the optimal panel presented in Table 7 is obtained.

Table 7 Geometric variables of the optimal panel—2 × 10 m², UDL, with design bounds

In this case, the core of the optimal panel is orthotropic with $S_{x} = 2.15S_{y}$. This degree of orthotropy of the core might indicate that plate bending solutions do not provide an accurate distribution of internal forces in the panel. Nevertheless, it has been found that more accurate analysis using sandwich FE modelling does not significantly alter the weight of the optimal panel, indicating that the analytical RM approach, which runs around 10-times faster, can be still used to accurately estimate the optimal solution of simply supported rectangular panels with an orthotropic core and with large aspect ratio under UDL.

Another example considers the same 2 × 10 m² panel under a 2 MPa, 400 × 400 mm² centred patch load, as shown in Fig. 11b. Table 8 presents the geometric variables of the optimal panel.

Table 8 Geometric variables of the optimal panel—2 × 10 m², Patch load, with design bounds

In these two cases, using the iterative method achieves a lighter optimised panel, which is due to a reduction in the design shear forces. A final reference is considered for a 2 × 10 m² panel under a UDL of 0.2 MPa, but now with three fixed edges and a free long edge, as shown in Fig. 11.c. For general support boundary conditions, neither analytical nor numerical plate bending models can provide sufficiently accurate results since the internal force distribution is dependent on the ratio between flexural and shear stiffness of the plate. Hence, this method of analysis is not suitable to be used for optimisation of sandwich panels with general support boundary conditions. Table 9 presents the geometric variables of the optimal panel when excluding or considering design bounds for the thicknesses of the plates, obtained using the more general approach using sandwich FE model.

Table 9 Geometric variables of the optimal panel—2 × 10 m², three fixed edges—Sandwich FE model

In this last case, the shear forces at the corners of the free edge substantially influence the optimal panel. Since the panel is designed according to the maximum shear force, this fact leads to nearly isotropic core sandwich panels. A nonuniform core could be used in these cases, where core strips are used only near the supports and then interrupted towards the middle of the panel.

5 Conclusions

This paper proposes a methodology for structural design and optimisation of RHCSPs using a gradient-based optimisation approach, comprised of a method of analysis and the introduction of limit state equations based on pre-established failure modes, solved iteratively by the Method of Moving Asymptotes. This paper demonstrates that removing the response constraints from the optimisation sequence leads to an efficient yet accurate design method for simply supported panels.

The analysis of simply supported sandwich panels under combined out-of-plane UDL and patch loads can be based on the Reissner–Mindlin plate theory, which, when compared to sandwich FE models, allows for a relatively accurate optimisation sequence to run without recalculating the internal forces for every iterative step. When considering general support boundary conditions, the analytical RM approach is no longer suitable, and a more refined method of analysis, such as using sandwich FE models, is required to recalculate the internal force distribution at each iterative step.

Regardless of the method of analysis, the design methodology takes advantage of the sandwich concept, where it is assumed that top and bottom plates resist bending moments and the core resists the shear forces, to obtain the internal forces in each layer. The internal forces are used to generate the constraints of a structural optimisation problem to minimise weight. The constraints are based on the various limit states in the domain of the panel, including material yielding, plate buckling and deformation control. The optimal panel obtained from the proposed design methodology is verified against detailed numerical modelling.

The results considering different panel configurations demonstrate that the optimisation of the unbounded problem interestingly leads to nearly isotropic cores even for rectangular panels with a one-way load transferring mechanism, mainly due to core shear buckling being the critical limit state. By considering practical limits related to the manufacturing process, the cores of optimal rectangular panels become more orthotropic. Despite this, the analytical RM approach proved to provide sufficiently accurate results for simply supported panels at a substantially reduced computational cost, as it avoids a recalculation of the internal forces at each iterative step.

The proposed methodology enhances the prospects for the application of RHCSPs as two-way sandwich panel deck systems, a novel solution that is superior to the conventional one currently used in offshore structural engineering practice in terms of weight, construction time, life span, safety, assembly process and overall cost.

Appendices

Appendix

Analytical sensitivities

Analytical sensitivities of the objective function and the yielding, buckling and deformation constraints $f_{i} \left( {\rm X} \right)$ are presented hereafter, written in the following form:

$$\frac{{\partial f_{i} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial f_{i} }}{{\partial t_{f,top} }}}&{\frac{{\partial f_{i} }}{{\partial t_{f,bot} }}}&{\frac{{\partial f_{i} }}{\partial h}}&{\frac{{\partial f_{i} }}{{\partial t_{w,x} }}}&{\frac{{\partial f_{i} }}{{\partial l_{x} }}}&{\frac{{\partial f_{i} }}{{\partial t_{w,y} }}}&{\frac{{\partial f_{i} }}{{\partial l_{y} }}} \\ \end{array} } \right]^{T}$$

(23)

The objective function $f_{0} \left( {\rm X} \right)$, presented in (19), is differentiated as:

$$\frac{{\partial f_{0} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \rho_{s} \left[ {\begin{array}{*{20}c} 1&1&{\frac{{t_{w,x} }}{{l_{x} }} + \frac{{t_{w,y} }}{{l_{y} }}}&{\frac{h}{{l_{x} }}}&{ - h\frac{{t_{w,x} }}{{l_{x}^{2} }}}&{\frac{h}{{l_{y} }}}&{ - h\frac{{t_{w,y} }}{{l_{y}^{2} }}} \\ \end{array} } \right]^{T}$$

(24)

The sensitivities are obtained as follows for face yielding of the top plate:

$$\frac{{\partial f_{1} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{M_{vM,ed} }}{{f_{y} }}\left[ {\begin{array}{*{20}c} {\frac{ - 1}{{t_{f,top}^{2} h}}}\quad0\quad{\frac{ - 1}{{t_{f,top} h^{2} }}}\quad0\quad0\quad0\quad0 \\ \end{array} } \right]^{T}$$

(25)

face yielding of the bottom plate:

$$\frac{{\partial f_{2} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{M_{vM,ed} }}{{f_{y} }}\quad\left[ {\begin{array}{*{20}c} 0\quad{\frac{ - 1}{{t_{f,bot}^{2} h}}}&{\frac{ - 1}{{t_{f,bot} h^{2} }}}\quad0\quad0\quad0\quad0\\ \end{array} } \right]^{T}$$

(26)

core shear yielding in the $x$-direction:

$$\frac{{\partial f_{3} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{V_{ed,x} \sqrt 3 }}{{f_{y} }}\left[ {\begin{array}{*{20}c} 0\quad0&{\frac{{ - l_{x} }}{{h^{2} t_{w,x} }}}&{\frac{{ - l_{x} }}{{ht_{w,x}^{2} }}}&{\frac{1}{{ht_{w,x} }}}\quad0\quad0 \\ \end{array} } \right]^{T}$$

(27)

core shear yielding in the $y$-direction:

$$\frac{{\partial f_{4} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{V_{ed,y} \sqrt 3 }}{{f_{y} }}\quad\left[ {\begin{array}{*{20}c} 0\quad0&{\frac{{ - l_{y} }}{{h^{2} t_{w,y} }}}\quad0\quad0&{\frac{{ - l_{y} }}{{ht_{w,y}^{2} }}}&{\frac{1}{{ht_{w,y} }}} \\ \end{array} } \right]^{T}$$

(28)

and core compressive yielding:

$$\frac{{\partial f_{5} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{C_{ed} }}{{f_{y} \left( {\frac{{t_{w,x} }}{{l_{x} }} + \frac{{t_{w,y} }}{{l_{y} }}} \right)^{2} }}\quad\left[ {\begin{array}{*{20}c} 0\quad0\quad0\quad{\frac{ - 1}{{l_{x} }}}&{\frac{{t_{w,x} }}{{l_{x}^{2} }}}&{\frac{ - 1}{{l_{y} }}}&{\frac{{t_{w,y} }}{{l_{y}^{2} }}} \\ \end{array} } \right]^{T}$$

(29)

For buckling limit states, the derivatives require more terms. To simplify the notation, the following placeholders are defined first:

$$\begin{gathered} k_{mn} = m^{2} l_{x}^{2} + n^{2} l_{y}^{2} \hfill \\ k_{\alpha } = m^{2} l_{x}^{2} + \alpha n^{2} l_{y}^{2} \hfill \\ \end{gathered}$$

(30)

The sensitivities for face intercellular buckling applied to the top plate are then obtained as follows:

$$\frac{{\partial f_{6} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{M_{ed,x} 12\left( {1 - \nu^{2} } \right)l_{x}^{2} l_{y}^{2} }}{{E\pi^{2} k_{mn}^{2} }}\left[ {\begin{array}{*{20}c} {\frac{{ - 3k_{\alpha } }}{{t_{top}^{4} h}}} \\ 0 \\ {\frac{{ - k_{\alpha } }}{{t_{top}^{3} h^{2} }}} \\ 0 \\ {\frac{{k_{\alpha } }}{{t_{top}^{3} h}}\left( {\frac{{ - 4l_{x} m^{2} }}{{k_{mn} }} + \frac{2}{{l_{x} }}} \right) + \frac{{2l_{x} m^{2} }}{{t_{top}^{3} h}}} \\ 0 \\ {\frac{{k_{\alpha } }}{{t_{top}^{3} h}}\left( {\frac{{ - 4l_{y} n^{2} }}{{k_{mn} }} + \frac{2}{{l_{y} }}} \right) + \frac{{2l_{y} \alpha n^{2} }}{{t_{top}^{3} h}}} \\ \end{array} } \right]$$

(31)

Considering shear buckling in the $x$-direction and considering $h \ge l_{y}$, the following placeholder is first defined:

$$k_{s} = 5.35 + 4/\left( {h/l_{y} } \right)^{2}$$

(32)

where the sensitivities are expressed as:

$$\frac{{\partial f_{7} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{V_{ed,x} 12\left( {1 - \nu^{2} } \right)}}{{E\pi^{2} k_{s} t_{w,x}^{3} }}\left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{{ - l_{x} l_{y}^{2} }}{{h^{2} }} + \frac{{8l_{x} l_{y}^{4} }}{{h^{4} k_{s} }}} & {\frac{{ - 3l_{x} l_{y}^{2} }}{{ht_{w,x} }}} & {\frac{{l_{y}^{2} }}{h}} & 0 & {\frac{{ - 8l_{x} l_{y}^{3} }}{{h^{3} k_{s} }} + \frac{{2l_{x} l_{y} }}{h}} \\ \end{array} } \right]^{T}$$

(33)

On the other hand, for $h < l_{y}$, $k_{s}$ is given by:

$$k_{s} = 5.35 + 4/\left( {l_{y} /h} \right)^{2}$$

(34)

where the sensitivities are obtained as:

$$\frac{{\partial f_{8} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{V_{ed,x} 12\left( {1 - \nu^{2} } \right)}}{{E\pi^{2} k_{s} t_{w,x}^{3} }}\left[ {\begin{array}{*{20}c} 0 & 0 & {l_{x} + \frac{{ - 8h^{2} l_{x} }}{{k_{s} l_{y}^{2} }}} & {\frac{{ - 3hl_{x} }}{{t_{w,x} }}} & h & 0 & {\frac{{ - 8h^{3} l_{x} }}{{k_{s} l_{y}^{3} }}} \\ \end{array} } \right]^{T}$$

(35)

For shear buckling in the $y$-direction, and considering $h \ge l_{x}$, the following placeholder is first defined:

$$k_{s} = 5.35 + 4/\left( {h/l_{x} } \right)^{2}$$

(36)

where the sensitivities are obtained as:

$$\frac{{\partial f_{9} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{V_{ed,y} 12\left( {1 - \nu^{2} } \right)}}{{E\pi^{2} k_{s} t_{w,y}^{3} }}\left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{{ - l_{x}^{2} l_{y} }}{{h^{2} }} + \frac{{8l_{x}^{4} l_{y} }}{{h^{4} k_{s} }}} & 0 & {\frac{{ - 8l_{x}^{3} l_{y} }}{{h^{3} k_{s} }} + \frac{{2l_{x} l_{y} }}{h}} & {\frac{{ - 3l_{x}^{2} l_{y} }}{{ht_{w,y} }}} & {\frac{{l_{x}^{2} }}{h}} \\ \end{array} } \right]^{T}$$

(37)

On the other hand, for $h < l_{x}$, $k_{s}$ is defined as:

$$k_{s} = 5.35 + 4/\left( {l_{x} /h} \right)^{2}$$

(38)

and the sensitivities are expressed as:

$$\frac{{\partial f_{10} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{V_{ed,x} 12\left( {1 - \nu^{2} } \right)}}{{E\pi^{2} k_{s} t_{w,y}^{3} }}\left[ {\begin{array}{*{20}c} 0 & 0 & {l_{y} + \frac{{ - 8h^{2} l_{y} }}{{k_{s} l_{x}^{2} }}} & 0 & {\frac{{ - 8h^{3} l_{y} }}{{k_{s} l_{x}^{3} }}} & {\frac{{ - 3hl_{y} }}{{t_{w,y} }}} & h \\ \end{array} } \right]^{T}$$

(39)

To simplify the notation for compressive buckling, consider two placeholders:

$$\begin{gathered} k_{x} = \frac{{m_{x} l_{y} }}{h} + \frac{h}{{m_{x} l_{y} }} \hfill \\ k_{y} = \frac{{m_{y} l_{x} }}{h} + \frac{h}{{m_{y} l_{x} }} \hfill \\ \end{gathered}$$

(40)

The sensitivities can then be expressed as:

$$\frac{{\partial f_{11} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{C_{ed} 12\left( {1 - \nu^{2} } \right)}}{{E\pi^{2} }}\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{\frac{{2t_{w,x}^{3} }}{{l_{x} l_{y}^{2} }}k_{x} \left( {\frac{{m_{x} l_{y} }}{{h^{2} }} - \frac{1}{{m_{x} l_{y} }}} \right) + \frac{{2t_{w,y}^{3} }}{{l_{x}^{2} l_{y} }}k_{y} \left( {\frac{{m_{y} l_{x} }}{{h^{2} }} - \frac{1}{{m_{y} l_{x} }}} \right)}}{{\left( {\frac{{t_{w,x}^{3} }}{{l_{x} l_{y}^{2} }}k_{x}^{2} + \frac{{t_{w,y}^{3} }}{{l_{x}^{2} l_{y} }}k_{y}^{2} } \right)^{2} }}} \\ { - \frac{{3t_{w,x}^{2} }}{{l_{x} l_{y}^{2} }}\frac{{k_{x}^{2} }}{{\left( {\frac{{t_{w,x}^{3} }}{{l_{x} l_{y}^{2} }}k_{x}^{2} + \frac{{t_{w,y}^{3} }}{{l_{x}^{2} l_{y} }}k_{y}^{2} } \right)^{2} }}} \\ {\frac{{\frac{{t_{w,x}^{3} }}{{l_{x}^{2} l_{y}^{2} }}k_{x}^{2} - \frac{{2t_{w,y}^{3} }}{{l_{x}^{2} l_{y} }}k_{y} \left( {\frac{{m_{y} }}{h} - \frac{h}{{m_{y} l_{x}^{2} }}} \right) + \frac{{2t_{w,y}^{3} }}{{l_{x}^{3} l_{y} }}k_{y}^{2} }}{{\left( {\frac{{t_{w,x}^{3} }}{{l_{x} l_{y}^{2} }}k_{x}^{2} + \frac{{t_{w,y}^{3} }}{{l_{x}^{2} l_{y} }}k_{y}^{2} } \right)^{2} }}} \\ { - \frac{{3t_{w,y}^{2} }}{{l_{x}^{2} l_{y} }}\frac{{k_{y}^{2} }}{{\left( {\frac{{t_{w,x}^{3} }}{{l_{x} l_{y}^{2} }}k_{x}^{2} + \frac{{t_{w,y}^{3} }}{{l_{x}^{2} l_{y} }}k_{y}^{2} } \right)^{2} }}} \\ {\frac{{\frac{{t_{w,y}^{3} }}{{l_{x}^{2} l_{y}^{2} }}k_{y}^{2} - \frac{{2t_{w,x}^{3} }}{{l_{x} l_{y}^{2} }}k_{x} \left( {\frac{{m_{x} }}{h} - \frac{h}{{m_{x} l_{y}^{2} }}} \right) + \frac{{2t_{w,x}^{3} }}{{l_{x} l_{y}^{3} }}k_{x}^{2} }}{{\left( {\frac{{t_{w,x}^{3} }}{{l_{x} l_{y}^{2} }}k_{x}^{2} + \frac{{t_{w,y}^{3} }}{{l_{x}^{2} l_{y} }}k_{y}^{2} } \right)^{2} }}} \\ \end{array} } \right]$$

(41)

The sensitivities for the control of deflection considering $\frac{{t_{w,x} }}{{l_{x} }} < \frac{{t_{w,y} }}{{l_{y} }}$ are determined as:

$$\frac{{\partial f_{12} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{w_{b0} \left( {1 - \nu^{2} } \right)360}}{{E\min \left( {L,W} \right)}}\left[ {\begin{array}{*{20}c} {\frac{1}{{t_{f,top} t_{f,bot} h^{2} }} - \frac{{t_{f,top} + t_{f,bot} }}{{t_{f,top}^{2} t_{f,bot} h^{2} }}} \\ {\frac{1}{{t_{f,top} t_{f,bot} h^{2} }} - \frac{{t_{f,top} + t_{f,bot} }}{{t_{f,top} t_{f,bot}^{2} h^{2} }}} \\ { - 2\frac{{t_{f,top} + t_{f,bot} }}{{t_{f,top} t_{f,bot} h^{3} }}} \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] + \frac{{w_{s0} 360}}{{G\min \left( {L,W} \right)}}\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - \frac{{l_{x} }}{{t_{w,x} h^{2} }}} \\ { - \frac{{l_{x} }}{{t_{w,x}^{2} h}}} \\ {\frac{1}{{t_{w,x} h}}} \\ 0 \\ 0 \\ \end{array} } \right]$$

(42)

On the other hand, for $\frac{{t_{w,y} }}{{l_{y} }} < \frac{{t_{w,x} }}{{l_{x} }}$:

$$\frac{{\partial f_{13} \left( {\rm X} \right)}}{{\partial {\rm X}}} = \frac{{w_{b0} \left( {1 - \nu^{2} } \right)360}}{{E\min \left( {L,W} \right)}}\left[ {\begin{array}{*{20}c} {\frac{1}{{t_{f,top} t_{f,bot} h^{2} }} - \frac{{t_{f,top} + t_{f,bot} }}{{t_{f,top}^{2} t_{f,bot} h^{2} }}} \\ {\frac{1}{{t_{f,top} t_{f,bot} h^{2} }} - \frac{{t_{f,top} + t_{f,bot} }}{{t_{f,top} t_{f,bot}^{2} h^{2} }}} \\ { - 2\frac{{t_{f,top} + t_{f,bot} }}{{t_{f,top} t_{f,bot} h^{3} }}} \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] + \frac{{w_{s0} 360}}{{G\min \left( {L,W} \right)}}\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - \frac{{l_{y} }}{{t_{w,y} h^{2} }}} \\ 0 \\ 0 \\ { - \frac{{l_{y} }}{{t_{w,y}^{2} h}}} \\ {\frac{1}{{t_{w,y} h}}} \\ \end{array} } \right]$$

(43)