A data-driven Kriging model based on adversarial learning for reliability assessment

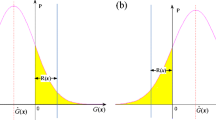
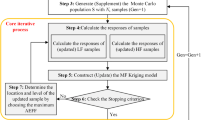
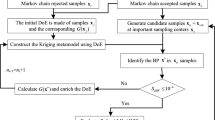
Abstract

The huge computational cost is a main barrier of structural reliability assessment for complex engineering. Surrogate models can release the CPU burden of reliability assessment, however, it is very challenging to guarantee the prediction accuracy of failure probability. In this study, we propose an Adversarial Learning-Based Kriging model (ALBK), where two models learn from and compete with each other to achieve an improved model accuracy. First, the initial models are established, and fitting accuracy is evaluated by each other with the proposed criterion. Then, the modeling parameters are optimized according to the evaluation results. The data-driven criteria and adversarial relationship promote the evolution of modeling parameters. Moreover, a triple-indicator method is provided to choose the final model and avoid oscillation. The ALBK adjusts modeling parameters with alternative evolution, while the predicted values are more accurate than those of Kriging. Finally, an adaptive ALBK method is provided with new samples added to improve the accuracy of reliability assessment. Through several numerical examples, it can be seen that the ALBK always provides the best results with the fewest assessment calls, and the robustness is also good.

Appendices

Appendix

Derivation of Kriging

The predicted function of Kriging can be written as

$$\hat{y}\left( x \right) = \mathop \sum \limits_{i = 1}^{n} \omega_{i} y_{i},$$

(27)

where $\omega_{i}$ denotes the weight coefficient of the ith response value. The regression function is defined as

$$Cov\left( {Z\left( {{\varvec{x}}^{i} } \right),Z\left( {{\varvec{x}}^{j} } \right)} \right) = \sigma^{2} R\left( {{\varvec{x}}^{i} ,{\varvec{x}}^{j} } \right),$$

(28)

where R is the kernel function of σ²and θ

$$R\left( {{\varvec{x}}^{i} ,{\varvec{x}}^{j} } \right){ = }\exp \left( { - \sum\limits_{k = 1}^{d} {\theta_{k} } \left( {x_{k}^{i} - x_{k}^{j} } \right)^{2} } \right),$$

(29)

where d is the number of dimensions, and $x_{k}^{i}$ is the kth dimension of ith point. The mean squared error (MSE) at x is

$$MSE\left( {\varvec{x}} \right) = {\varvec{E}}\left[ {\left( {\hat{y}\left( {\varvec{x}} \right) - y\left( {\varvec{x}} \right)} \right)^{2} } \right] = {\varvec{E}}\left[ {\left( {\mathop \sum \limits_{i = 1}^{n} \omega_{i} y_{i} } \right)^{2} } \right].$$

(30)

In order to satisfy the unbiasedness constraint, the mean of the estimated error must be zero as follows:

$$E\left[ {{\text{y}}\left( {\varvec{x}} \right)} \right] = E\left[ {\mathop \sum \limits_{i = 1}^{n} \omega_{i} y_{i} } \right].$$

(31)

So far, the weight coefficients can be calculated by solving the minimization problem about MSE(x) with the Lagrange multiplier approach. It can be found as follows:

$$\left\{ {\begin{array}{*{20}c} {\sum\nolimits_{{j = 1}}^{n} {\omega _{j} } Cov(Z\left( {x^{i} } \right),Z\left( {x^{j} )} \right){\mkern 1mu} \;\;,i = 1,2 \cdots ,n} \\ {\sum\nolimits_{{i = 0}}^{n} {\omega _{i} } = 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,i = 1,2 \cdots ,n} \\ \end{array} } \right.$$

(32)

And $\mu$ is the Lagrange multiplier. Then, according to Eqs. (28) and (32), the following function can be obtained:

$$\left\{ {\begin{array}{*{20}c} {\sum\nolimits_{{j = 1}}^{n} {\omega _{j} } R\left( {x^{i} ,x^{j} } \right) + \frac{\mu }{{2\sigma ^{2} }} = R\left( {x^{i} ,x} \right)\;\;\;,i = 1,2 \cdots ,n} \\ {\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,i = 1,2 \cdots ,n} \\ \end{array} } \right.$$

(33)

Also, Eq. (33) can be written as a matrix function as follows:

$$\left[ {\begin{array}{*{20}c} {\varvec{R}} & {\varvec{F}} \\ {{\varvec{F}}^{T} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{\lambda}} \\ {\tilde{\mu }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{r}}_{{\left( {\varvec{x}} \right)}} } \\ 1 \\ \end{array} } \right],$$

(34)

where

$$\begin{gathered} \tilde{\mu } = - \frac{\mu }{{2\sigma ^{2} }} = (F^{T} R^{{ - 1}} F)^{{ - 1}} (F^{T} R^{{ - 1}} r_{{(x)}} - 1) \hfill \\ F = [1,...,1,0,0,...,0]^{T} \in \Re ^{n} \hfill \\ \lambda = (\omega _{1} ,...,\omega _{n} )^{T} = R^{{ - 1}} (r_{{(x)}} - F\tilde{\mu }). \hfill \\ \end{gathered}$$

(35)

By solving Eq. (34), the prediction of unknown samples can be derived. As the samples have been adjusted to Eq. (27), the correlation matrix can be calculated easily. The correlation vector and the correlation matrix can be expressed as

$$r_{(x)} = [R(x,x^{1} ),R(x,x^{2} )...R(x,x^{n} )]^{T} \in \Re^{n}$$

(36)

$$R = \left[ {\begin{array}{*{20}c} {R(x^{1} ,x^{1} )} & {R(x^{1} ,x^{2} )} & \ldots & {R(x^{1} ,x^{n} )} \\ {R(x^{2} ,x^{1} )} & {R(x^{2} ,x^{2} )} & \ldots & {R(x^{2} ,x^{n} )} \\ \vdots & \vdots & \ddots & \vdots \\ {R(x^{n} ,x^{1} )} & {R(x^{n} ,x^{n} )} & \ldots & {R(x^{n} ,x^{n} )} \\ \end{array} } \right] \in \Re^{n \times n}.$$

(37)

The predicted MSE of $\hat{y}\left( x \right)$ is

$$s_{{\left( {\varvec{x}} \right)}}^{2} = \sigma^{2} (1 + ({\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}})^{ - 1} \left( {1 - {\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{r}}_{\left( x \right)} )^{2} - {\varvec{r}}_{\left( x \right)}^{T} {\varvec{R}}^{ - 1} {\varvec{r}}_{\left( x \right)} } \right).$$

(38)

As both $\hat{y}\left( x \right)$ and MSE are the functions of $\sigma^{2}$ and θ, θ can be calculated by the maximum likelihood estimation approach. Because Z(x) follows the normal distribution, $\hat{y}\left( x \right)$ follows the multidimensional normal distribution as

$$\begin{gathered} P\left( {Y\left( x \right)|\theta ,\sigma ^{2} ,\hat{y}\left( x \right)} \right) = L\left( {\theta ,\sigma ^{2} |\hat{y}\left( x \right) = Y\left( x \right)} \right) = \frac{1}{{(2\pi \sigma ^{2} )^{{\frac{n}{2}}} |R|^{{\frac{1}{2}}} }}{\text{exp}}\left[ { - \frac{{(Y - \beta F)^{T} R^{{ - 1}} \left( {Y - \beta F} \right)}}{{2\sigma ^{2} }}} \right] \hfill \\ {\text{Ln}}\left( {L\left( {\theta ,\sigma ^{2} ,\hat{y}\left( x \right)|Y\left( x \right)} \right)} \right) = - \frac{n}{2}\ln \left( {2\pi } \right) - \frac{n}{2}\ln \left( {\sigma ^{2} } \right) - \frac{1}{2}\ln \left| R \right| - \frac{{(Y - \beta F)^{T} R^{{ - 1}} \left( {Y - \beta F} \right)}}{{2\sigma ^{2} }}. \hfill \\ \end{gathered}$$

(39)

In order to obtain the maximum Ln(L), we can make the partial derivative about $\sigma^{2}$ of this function to be zero to obtain the maximum evaluation. Take the partial derivative with respect to $\sigma^{2}$ of this equation and set it as zero, $\sigma^{2}$ and ${\varvec{\beta}}$ can be obtained as

$$\begin{gathered} \sigma^{2} = \frac{1}{n}({\varvec{Y}} - \varvec{F}\beta )^{{\varvec{T}}} {\varvec{R}}^{ - 1} \left( {{\varvec{Y}} - \varvec{F}\beta } \right) \hfill \\ {\varvec{\beta}} = \left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}}} \right)^{ - 1} {\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{Y}} \hfill \\ \end{gathered}.$$

(40)

The following function called ‘concentrated log-likelihood’ can be obtained, with which θ is calculated as follows:

$$Find\;\theta \;\max \left[ { - \frac{n}{2}\ln \left( {\sigma ^{2} } \right) - \frac{1}{2}\ln \left| R \right|} \right] \to \min {\mkern 1mu} \sigma ^{2} \left| R \right|^{{\frac{1}{n}}} \;s.t.\;\theta > 0.$$

(41)