Robust multiscale optimization accounting for spatially-varying material uncertainties

Abstract

In this work we demonstrate a methodology for performing robust optimization using multivariable parameterized lattice microstructures. By introducing material uncertainties at the microscale, we are able to simulate the variations in geometry that occur during the manufacturing stage and design structures which are tolerant to variations in the microscale geometry. We impose both uniform and spatially-varying, non-uniform material uncertainties to generate structures which, in terms of standard deviation, are up to 77% more robust in the non-spatially uncertainty varying case, and 74% more robust in the spatially-varying case. We also explore the utility of imposing spatially-varying material uncertainties compared to using homogeneous, uniform material uncertainties, which are much less computationally expensive. It is found that when designs that have been optimized assuming uniform uncertainties are subject to spatially-varying uncertainties, their standard deviations of compliance are similar to designs optimized assuming spatially-varying uncertainties. However, their mean compliances are far higher in comparison to designs generated by assuming spatially-varying material uncertainties.

1 Introduction

Additive manufacturing (AM) has enabled the realization of geometries and designs which were previously impossible or highly impractical to achieve with traditional manufacturing processes. Ensuring that designs can be manufactured using subtractive manufacturing techniques leads to significant constraints on their geometric complexity. A good example of this is a cellular structure, whose global material properties is derived from the arrangement and configuration of (micro)structures on their finer scales. These structures, commonly found in wood, bones and coral, have been known for a long time to exhibit desirable properties, particularly useful for engineering design applications (Ashby 1983). However, due to the intricate geometries of the cellular structures existing across multiple scales, their fabrication was limited until the advent of reliable AM techniques.

Interest in cellular structures arises as a result of their highly adaptable material properties and potential for lightweight designs, which lend themselves towards high specific stiffness or strength (Sigmund et al. 2016; Xu et al. 2019), lightweighting (Lynch et al. 2018; Plocher and Panesar 2019), thermal (Sigmund and Torquato 1996) and energy absorption (Ashby 1983; Brennan-Craddock et al. 2012; Maskery et al. 2017) applications. Sigmund et al. (2016) show that closed thin-wall structures are able to attain stiffness values near the theoretical bound, as given by the Hashin–Shtrikman bounds. However, as the authors note, it may be impossible to manufacture these structures in reality, leading to the use of minimum length scale conditions or alternative, less optimal, microstructures. As their global properties are derived from the arrangement and configuration of the underlying (micro)structures, individual microstructures can be optimized to attain application specific material properties. This process, known as inverse homogenization (Sigmund 1994), involves generating microstructures with favourable material properties, such as maximum stiffness for compliance related applications, or enabling maximum, zero or negative thermal expansions (Sigmund and Torquato 1996) for thermal problems. Approaches for concurrently optimizing across two scales have also been proposed. Here, the optimization tailors the topology on the macroscale, as well as optimizing the configuration of the microstructures on the finer microscale. For example Liu et al. (2008) present a concurrent optimization methodology where microstructures are optimized on the microscale using a SIMP methodology, while the macrostructure material layout using the porous anisotropic material with penalization (PAMP) method at the same time to discourage intermediate densities. Methodologies for pre-defining or parameterizing unit cells using density or geometric design variables have also been presented in literature. As the unit cell designs are known prior to the optimization, one of the benefits of these methodologies is the ability to pre-compute the material properties of the microstructures. For example, Zhu et al. (2017) generated a database of multi-material microstructure prior to performing topology optimization (TO). To enable AM, the continuous optimized solution is then mapped to discrete microstructures. Imediegwu et al. (2019) presented a multiscale 3D optimization framework using a 7-design variable lattice parameterization. By creating a full factorial design of experiments (DOE), the authors assembled response surface models (RSMs) to generate continuous material models, which were used to perform gradient-based macroscale optimization. A variation of this framework, which concurrently couples the micro and macroscale models, significantly reduces the computational expense of optimisation, enabling a previously intractable number of design variables to be used in the parameterization of the microscale geometry (Murphy et al. 2021).

As with any manufacturing process, uncertainties arise during AM, particularly during the manufacturing of intricate cellular structures. These uncertainties, which typically lead to defects in the microscale geometry, ultimately cause the material properties of the additively manufactured parts to differ significantly from the material properties of the original intended design. For example, Boniotti et al. (2017) utilized 3D tomography to show that defects in a body-centred cubic (BCC) lattice structure, manufactured using selective laser melting (SLM), lead to local strain concentrations that may cause poorer strength or fatigue characteristics, evidence of which was later provided by Boniotti et al. (2019). Here, the authors found that strain concentrations, induced by local variations in the geometry, negatively impacted the fatigue strength of the lattice structures. Imperfections arising during the manufacturing process have been considered in topology optimization. Sigmund (2009) proposed a robust topology optimization formulation for a SIMP-based interpolation by simulating the erosion and dilation of the structure. More recently, Moussa et al. (2021) presented a methodology for considering material uncertainties within a multiscale optimization framework. In this work, the authors use the imperfect geometry of printed lattice structures to create a library of the typical non-uniform strut thicknesses and deviations of the truss centre lines found in the printed structures. Using the material properties of the imperfect microstructures, rather than the deterministic, ideal structures, the authors performed TO using a density variable to represent the underlying imperfect microstructure configurations.

In this work, we utilize the multiscale optimization framework presented by Imediegwu et al. (2019), which allows the optimizer to directly control the underlying lattice configurations, indirectly tailoring the distribution of stiffness tensors throughout the macroscale domain. To ensure that the performance of the design does not deteriorate as a result of the material uncertainties introduced during the AM process, we utilize the formulation presented by Thillaithevan et al. (2021a, b). This methodology introduces material uncertainties by directly perturbing the underlying lattice microstructure truss radii, simulating the variations in geometry that may arise during the AM process. By coupling this uncertainty model with a robust optimization formulation, it is possible to design structures which are more tolerant to variations in the microscale geometry.

To the authors’ best knowledge, this paper presents the first introduction of material uncertainties within multiscale optimization frameworks which are parameterized using multiple microstructure design variables. We extend the methodology proposed by Thillaithevan et al. (2021a, b), by utilizing a parameterized 7-design variable lattice microstructure and formulating spatially-varying material uncertainties within the robust optimization framework. We begin by introducing the standard deterministic optimization framework in Sect. 2. We then introduce the material uncertainty methodology in Sect. 3, including the consideration of uniform and spatially-varying uncertainties. Finally, in Sect. 4.2 we perform robust optimization using uniform and spatially-varying material uncertainties, tackling two classical geometries, a cantilever and bridge structure, to explore the efficacy of this material uncertainty formulation.

2 Deterministic formulation

2.1 Microscale modelling

The multiscale optimization framework consists of two scales: the microscale and the macroscale. The microscale is composed of periodic truss based lattice microstructures. In particular, the body-centred 7-truss unit cell design, as introduced by Imediegwu et al. (2019), is utilized. These lattice microstructures are parameterized by the 7-truss radii, each of which can be independently altered to give rise to a wide range of material properties during the optimization. This is somewhat similar to the free material optimization (FMO) (Zowe et al. 1997) approach, where the stiffness matrix at every cell in a discretized domain is optimized directly. In this case we are indirectly optimizing the stiffness matrices by varying the microstructure configuration in each cell. It should also be noted that although the final macroscale structures are composed of highly connected trusses, this work is not related to ground structure optimization schemes, where the layout of a set of highly connected discrete trusses is optimized. As shown in Fig. 1, the lattice is composed of three axis aligned trusses and four diagonal trusses, connecting each opposing vertex of the unit cell. The macroscale is constructed from a discretized 3D domain, where each cell is assigned the homogenized material properties of a chosen lattice configuration, as shown in Fig. 2. To avoid the need for expensive, fullscale finite element analysis (FEA) of macroscale structures consisting of several thousand lattices, the asymptotic homogenization method is employed (Bendsøe and Kikuchi 1988; Francu 1982; Hollister and Kikuchi 1992). Here is it assumed that the lattice microstructures can be represented as homogeneous solids on the macroscale, provided there is a sufficient scale of separation between the macro and microscales, as illustrated in Fig. 2. It should be noted that the micro and macroscale are agnostic to the actual length scales that are used, which means that the microscale unit cell size does not need to be below a certain predefined length for this assumption to hold. The important factor is the relative difference in the length scales. However, due to manufacturing constraints in practical applications, a minimum unit cell size is usually required. Typically, at least six layers of microstructures are required along each dimension (in 3D) to achieve sufficient scale separation for compression or tension dominated load cases (Thillaithevan et al. 2021a, b), with additional layers required for shear dominated cases.

Fig. 1

Lattice microstructure parameterization

Fig. 2

Illustration of multiscale modelling process

To obtain the homogenized material properties of the lattice microstructures, finite element analysis (FEA) using periodic boundary conditions (PBCs) is performed. From the FEA, the homogenized stiffness tensor, $\varvec{E}^H$ is obtained using

$$\begin{aligned} \varvec{E}^H = \frac{1}{\varOmega }\int _{\varOmega }\varvec{E}(\varepsilon ^0 - \varepsilon ^*)\text {d}\varOmega \end{aligned}$$

(1)

where $\varepsilon ^0$ represents the six unit macroscale strains applied, $\varepsilon ^*$ is the microscopic strain field resulting from the macroscopic strain field, $\varOmega$ is the domain volume and $\varvec{E}$ is the stiffness tensor of the bulk material. The full stiffness tensor is assembled by solving the finite element system six times, once for each independent unit macroscale strain applied. In this work, the bulk material is assumed to be a generic polymer with base stiffness E = 2 GPa and $\nu$ = 0.3. The finite element modelling is performed using a voxel-based method with a fixed hexahedral mesh to avoid remeshing each lattice microstructure, reducing the computational effort required for the homogenization process. Based on a mesh convergence study, the domain was discretized using 1 million linear hexahedral elements for the FEA. To improve the stability of the solver, a nodal averaging algorithm was employed, as outlined in Imediegwu et al. (2019). Here the perpendicular distance to the centre line of each truss from the vertices of every cell is used to determine the stiffness assigned to any given cell. By determining the number of vertices of a cell that lie ‘inside’ any of the lattice trusses, the stiffness assigned to the cell is calculated by linearly scaling between $E_{{{\text{void}}}}$ and E, where $E_{\text{void}}$ = 100 Pa. Any cells without vertices within the radius of the trusses are assigned a stiffness of $E_{\text{void}}$ to avoid numerical instabilities in the FEA. The FEA was performed using the open-source partial differential equation (PDE) solver FEniCS 2019.1.0 (Alnæs et al. 2015).

2.2 Response surface modelling

To efficiently link the micro and macroscales, RSMs are generated. The RSMs are used to quickly evaluate the homogenized material properties of any lattice microstructure in the macroscale domain during the optimization process and are also used to compute the gradients required for the gradient-based optimization algorithm used in this work. The data points used to generate the RSMs are obtained from a full factorial design of experiments (DOE). The lattice radii are independently perturbed in the range $0.08 \le r_i \le 0.38$, $i=\{1,..,7\}$, enabling fully dense cells, using 7 levels to generate a total of $7^7$ (823,543) lattice configurations within the DOE. However, as shown by Imediegwu et al. (2019), due to the symmetries present in the lattice parameterization, the number of unique lattice configurations that require simulation can be reduced to 40,817, significantly reducing the computational expense of constructing the DOE and by extension the RSMs. A non-zero lower bound, $r_{\text{min}} > 0$, is used as the number of cells required for convergence due to the increasingly thin trusses as $r \rightarrow 0$, becomes impractical for the construction of the DOE. To overcome the issue of non-zero radii during the optimization, we introduce a density parameter to simulate the effects of void cells during the optimization. Further details of this are outlined in Sect. 2.3.

To convert the discreet property space formed by the DOE, into continuous, differentiable RSMs, multivariate polynomials are used. To construct the polynomials a series of least squares problems are solved. The general form of the polynomials is given by

$$\begin{aligned} \begin{aligned} \hat{y} =&\beta _0 + \beta _1\big (\prod _{i=1}^k x_i^{n_i}\big ) + \dots + \beta _{j-1}\big (\prod _{i=1}^k x_i^{n_i}\big ) \\&\sum _{i=1}^k n_i \le m \end{aligned} \end{aligned}$$

(2)

where $k = 7$ is the number of independent variables, $\beta$ are the coefficients terms, $\hat{y}$ is the dependent variable, m denotes the maximum order of the polynomial, and j represents the number of coefficient terms in the polynomial. Here the independent variables are the 7-truss radii which can be altered to give rise to the desired material properties, in particular the homogenized stiffness and volume fraction, which are represented by the RSM approximations

$$\begin{aligned} \begin{aligned} \varvec{E}_{ij}^H&\approx \varvec{\tilde{E}}_{ij}^H(r_1,r_2,r_3,r_4,r_5,r_6,r_7)\\ v&\approx \tilde{v}(r_1,r_2,r_3,r_4,r_5,r_6,r_7) \end{aligned} \end{aligned}$$

(3)

where $\varvec{\tilde{E}}^H$ and $\tilde{v}$ are the approximations of the true functions $\varvec{{E}}^H$ and v. To assemble $\varvec{\tilde{E}}^H$, 21 RSMs are fitted, one for each unique term of the stiffness tensor, resulting in 22 RSMs in total, including the volume fraction model. Polynomials with a maximum order m = 7 were chosen heuristically, leading to an average ${R^2 = 0.99}$. Once the RSMs are constructed they can be used repeatedly in any subsequent optimization problems.

2.3 Macroscale optimization

The macroscale optimization is performed by varying the radii of each truss of each lattice in the macroscale domain. Here the optimizer is indirectly tailoring the local stiffness tensor in each cell to generate the ideal load path which minimizes or maximizes the given objective, which has similarities to the methodology used in free material optimization (Zowe et al. 1997). As mentioned earlier, to quickly evaluate the material properties of the lattices during the optimization, the RSMs shown in Eq. 3 are utilized. The radii used to evaluate the RSMs are constrained by a non-zero lower bound, as shown in the previous section. This limits the macroscale optimization to lattice-only designs, where lattices are present everywhere in the domain, without changes to the overall topology, albeit with local changes in truss radii. To enable binary, lattice/void designs, which allow for more efficient use of materials, an additional density parameter, $0 \le \rho \le 1$, is introduced into the multiscale lattice optimization framework. The density variable is used to penalize regions with low density lattices that offer little or no structural support by using

$$\begin{aligned} \begin{aligned} \varvec{\bar{{E}}} = \rho ^p\varvec{{E}}^H(r_1,r_2,r_3,r_4,r_5,r_6,r_7) \end{aligned} \end{aligned}$$

(4)

where $\varvec{{E}^H}$ is the RSM defined in Eq. 3 where the tilde and subscripts have been dropped for convenience, and $p = 3$ is the chosen penalty term. To accurately simulate void cells, the volume fraction model is also modified using

$$\begin{aligned} \begin{aligned} \bar{v} = \rho v(r_1,r_2,r_3,r_4,r_5,r_6,r_7) \end{aligned} \end{aligned}$$

(5)

where v is the RSM for the volume fraction as seen in Eq. 3.

Helmholtz filtering (Lazarov and Sigmund 2011) is applied to the design variables to avoid checkboarding (Díaz and Sigmund 1995), where low density and high density cells are found in an alternating pattern, and to generate mesh-independent designs. In this formulation, the filtered design variables are obtained from the solution of a Helmholtz type PDE

$$\begin{aligned} \tilde{\varvec{x}} = \varvec{x} + r_f^2\nabla ^2\tilde{\varvec{x}} \end{aligned}$$

(6)

where $\varvec{x}$ and $\tilde{\varvec{x}}$ are the unfiltered and filtered design variables. The filtering radius is defined by $r_f$, which can be considered as a 3D spherical region of influence where the filtering is performed. Choosing large values of $r_f$ leads to extreme filtering with very smooth variations in the design variables, limiting the scope of the optimization, and $r_f \rightarrow 0$ results in an unfiltered design with potentially checkerboarded layouts. In this work, $r_f$ is assigned a value of D, where D is the cell width used in the macroscale mesh. To overcome the artificial ‘sticking’ of material to the domain boundaries that occurs in standard Helmholtz filtering schemes, Robin boundary conditions are applied to any exterior surface which is unloaded and does not act as a support, as proposed by Wallin et al. (2020). Once the density variables and truss radii are filtered using the Helmholtz filter, a threshold filtering (Wang et al. 2011) scheme is applied to $\rho$, to ensure a ‘binary’ design containing only void and material (lattice) cells is achieved. The thresholded density variables, $\hat{\tilde{\rho }}$ are defined as

$$\begin{aligned} \begin{aligned} \hat{\tilde{\rho }} = \frac{\tanh {\big (\beta \eta \big )}+\tanh {\big (\beta ({\tilde{\rho }}-\eta )\big )}}{\tanh {\big (\beta \eta \big )}+\tanh {\big (\beta (1-\eta )\big )}} \end{aligned} \end{aligned}$$

(7)

where $\tilde{\rho }$ is the Helmholtz filtered density variable. The linearity of the thresholding is determined by $\beta$, where in the limit $\beta \rightarrow \infty$, the projection filter leads to a fully binary design. However, as large values of $\beta$ can lead to stability issues in the optimization, $\beta$ is updated adaptively throughout the optimization. In this work, $\beta$ is incremented by 0.5 every 30 iterations, from an initial value of 0.5 up to a maximum value of 3.5. These values were chosen heuristically to avoid stability issues. The thresholding level is determined by $\eta$, which is set to 0.5. Finally, the thresholded and filtered density variable are used in the scaling of the stiffness tensor and volume fraction, so the relationships shown in Eqs. 4 and 5, are updated to

$$\begin{aligned} \begin{aligned} \varvec{\hat{\tilde{{E}}}}&= \hat{\tilde{\rho }}^p\varvec{{E}}^H(r_1,r_2,r_3,r_4,r_5,r_6,r_7) \\ \hat{\tilde{v}}&= \hat{\tilde{\rho }} v(r_1,r_2,r_3,r_4,r_5,r_6,r_7) \end{aligned} \end{aligned}$$

(8)

The design variables used in the optimization, are defined through the design variable matrix, $\varvec{\chi }$, which is assembled from the truss radii and density variables

$$\begin{aligned} \varvec{\chi } = \begin{bmatrix} r_{1,1} &{} r_{2,1} &{} r_{3,1} &{} r_{4,1} &{} r_{5,1} &{} r_{6,1} &{} r_{7,1} &{} \rho _{1}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ r_{1,e} &{} r_{2,e} &{} r_{3,e} &{} r_{4,e} &{} r_{5,e} &{} r_{6,e} &{} r_{7,e} &{} \rho _{e} \end{bmatrix} \end{aligned}$$

(9)

where e is the number of cells or lattices in the macroscale domain, $r_{i,j}$ represents radii of the ith truss of the jth lattice and similarly, $\rho _j$ corresponds to the density variable attached to the jth lattice. For the optimization problems tackled in this work a compliance minimization formulation is adopted. This optimization problem can be defined as

(10)

where the maximum volume fraction and actual volume fractions are defined as $V_{\text{max}} =$ 0.3 and $V_f$ respectively. To compute $V_f$, the individual lattice volume fractions given by $v_j$ are summed. The global stiffness matrix, denoted by $\varvec{K}$, is a function of both the truss radii and the density parameter $\rho$, the force and displacement vectors are given by $\varvec{F}$ and $\varvec{U}$ respectively. To assemble $\varvec{K}$, the elemental stiffness matrices, $k_e$, are used, where

$$\begin{aligned} \varvec{k}_e = \int _{\varOmega _e} \varvec{B}^T{\varvec{\hat{\tilde{E}}}}\varvec{B} \partial \varOmega _e \end{aligned}$$

(11)

and ${\varvec{\hat{\tilde{E}}}}$ is the SIMP stiffness tensor shown in Eq. 8, $\varOmega _e$ is the volume of the cell and $\varvec{B}$ is the strain-displacement matrix. The gradients of the objective and constraints required for the optimization are obtained using the chain rule. The gradients relative to the truss radii are obtained using

$$\begin{aligned} \begin{aligned} \frac{\text{d} C}{\text{d} r_i}&= \frac{\text{d} C}{\text{d} \varvec{E}} \frac{\text{d} \varvec{E}}{\text{d} \tilde{r}_i} \frac{\text{d} \tilde{r}_i}{\text{d} r_i} \\ \frac{\text{d} V_f}{\text{d} r_i}&= \frac{\text{d} V_f}{\text{d} \tilde{r}_i} \frac{\text{d} \tilde{r}_i}{\text{d} r_i} \quad i \in \{1,\dots ,7\} \end{aligned} \end{aligned}$$

(12)

where $\frac{\text{d} C}{\text{d} \varvec{E}}$ is obtained using the algorithmic differentiation capabilities provided by the Python library dolphin-adjoint (Mitusch et al. 2019). The library is able to efficiently derive the adjoint and gradient of the FE model by manipulating the symbolic mathematical representation of the FE model implemented within the Python library FEniCS. The filtered radii gradients $\frac{\text{d} \varvec{E}}{\text{d} \tilde{r}_i}$ and $\frac{\text{d} V_f}{\text{d} \tilde{r}_i}$ are obtained by differentiating the polynomials used to construct the RSMs shown in the previous section. The filtering gradient, $\frac{\text{d} \tilde{r}_i}{\text{d} r_i}$, is computed by differentiating the Helmholtz PDE given in Eq. 6. The gradients of the density variable, $\rho$, are given by

$$\begin{aligned} \begin{aligned} \frac{\text{d} C}{\text{d} \rho }&= \frac{\text{d} C}{\text{d} \hat{\tilde{\rho }}} \frac{\text{d} \hat{\tilde{\rho }}}{\text{d}{\tilde{\rho }}} \frac{\text{d} \tilde{\rho }}{\text{d} \rho } \\ \frac{\text{d} C}{\text{d} \rho }&= \frac{\text{d} V_f}{\text{d} \hat{\tilde{\rho }}} \frac{\text{d} \hat{\tilde{\rho }}}{\text{d} \tilde{\rho }} \frac{\text{d} {\tilde{\rho }}}{\text{d} {\rho }} \end{aligned} \end{aligned}$$

(13)

where $\frac{\text{d} C}{\text{d} \hat{\tilde{\rho }}}$ is computed using algorithmic differentiation and $\frac{\text{d} V_f}{\text{d} \hat{\tilde{\rho }}}$ is derived by differentiating Eq. 8. Finally, the remaining gradients are computed using the differentials of the Helmholtz equation and the threshold projection.

3 Modelling manufacturing uncertainty

By definition, an efficient deterministic optimization algorithm should generate solutions which lie in local or (ideally) global minima. As a result, the objective or response of the optimal solution may be highly sensitive to changes in the design variables. This means that designs generated using deterministic optimization formulations can be particularly susceptible to uncertainties that arise in the real world. For example, components designed using a standard deterministic structural optimization formulation may perform worse than expected due to the uncertainties that occur during manufacturing or uncertainties in the loading conditions. In this paper we tackle the problem of material uncertainty that arises during the AM of optimized multiscale structures. As the solutions obtained by the deterministic optimization framework presented in Sect. 2.3 may contain highly tailored local material properties, the designs are likely to be highly sensitive to the variations in the geometry that can occur during the AM process. To counter this, it is important to consider the uncertainties that arise in the real world during the optimization stage to generate designs that are robust and behave as expected.

3.1 Non-spatially-varying uncertainties

To account for the material uncertainties that arise as a result of variations in the printed geometry, we utilize the methodology presented by Thillaithevan et al. (2021a, b). In this methodology, material uncertainties are introduced at the microscale by imposing uncertain perturbations to the lattice truss radii. The perturbation to each lattice is given by the relationship

$$\begin{aligned} \varvec{\check{r}}_i = \varvec{r}_i + \omega \quad i \in \{1, \dots , 7\} \end{aligned}$$

(14)

where $\omega$ is an uncertain perturbation and $\varvec{\check{r}}_i$ is the vector of perturbed truss radii for the ith truss. Here, $\omega$ represents the uncertainty in the additively manufactured geometry and gives rise to uncertain material properties. It should be noted that this formulation only considers the constant dilation and erosion of truss radii, rather than defects that may occur along the trusses themselves. As shown in Eq. 14, the uncertainties are assumed to be constant for all 7 trusses that make up each lattice cell within the optimization domain. In this section, the uncertainties are also assumed to be uniform and thus, non-spatially-varying. A methodology for introducing spatially-varying material uncertainty is presented in Sect. 3.2.

Although not tackled in this work, this methodology offers the potential to introduce truss dependent uncertainties or correlated truss uncertainties, where for example the uncertainty present in the horizontal trusses are assumed to be larger than those in the vertical trusses, to reflect the influence of the AM print direction on the uncertainties. This could easily be achieved by adding another dimension to the perturbation such that $\omega \rightarrow \omega _i$, albeit at increased computational cost. This methodology can also be applied to other parameterized unit cell designs, provided the microstructure geometry is explicitly defined. It should also be noted that the only source of uncertainty considered in this work is the manufacturing uncertainty. The underlying framework, including the FE modelling and RSM, is assumed to be deterministic.

To generate optimized designs which are resistant to variations in the printed geometry and the resulting uncertain material properties, we employ a robust optimization formulation. In this formulation, the optimizer is tasked with reducing both the mean compliance, as well as ensuring the deviation of the compliance remains low in the presence of material uncertainties. The robust formulation is defined as

(15)

where $\mathbb {E}[\cdot ]$ and $\sigma [\cdot ]$ denote the mean and standard deviation operators, respectively. The variable $\kappa$ is a scaling parameter used to vary the influence of the standard deviation within the optimization. In this work $\kappa = 3$ is chosen to favour robust designs. It should be noted that the choice of $\kappa$ is a trade-off between robustness (minimizing the standard deviation of compliance) and the mean performance (minimizing the mean compliance). Increasing the value of $\kappa$ is expected to lead to further reductions in the standard deviation at the cost of the mean performance, and reducing it is expected to lead to designs which on average, perform better, but may have larger variability in their performance. To ensure the RSMs defined in Sect. 2.2 remain valid once the perturbations are applied to the truss radii, the lower and upper bounds of radii are updated as $\check{r}_{\text{min}} = r_{\text{min}} + \omega _{\text{min}}$ and $\check{r}_{\text{max}} = r_{\text{max}} - \omega _{\text{max}}$ respectively. This reduction in the bounds is a drawback of the proposed methodology as it reduces the available design space. However, the reduction in design space is viewed as a trade-off between microstructure optimality and overall design robustness. As the radii are no longer deterministic, the stiffness matrix becomes an uncertain function and is assembled using the following equation

$$\begin{aligned} \hat{\varvec{k}}_e = \int _{\varOmega _e} \varvec{B}^T\check{{\varvec{E}}}\varvec{B} \partial \varOmega _e \end{aligned}$$

(16)

where $\check{{\varvec{E}}}$ is derived from the RSMs using the perturbed radii according to

$$\begin{aligned} \varvec{\check{{E}}} = \hat{\tilde{\rho }}^p{\varvec{{{E}}}}(\varvec{\check{r}}_1, \dots , \varvec{\check{r}}_7) \end{aligned}$$

(17)

where $\hat{\tilde{\rho }}$ is the Helmholtz and Heaviside projection filtered density variable and $\varvec{\check{r}}_i$ are the filtered uncertain truss radii. Using this formulation it is clear that using a range of uncertain perturbations, it is possible to derive a series of material properties which correspond to variations in the microscale truss radii which may arise during the manufacturing process.

One of the main difficulties of solving robust optimization problems is the increased computational burden that arises from calculating the statistical moments required for the objective function and constraints. In this work, the first two statistical moments, the mean and standard deviation, as shown in Eq. 15, are required to perform the optimization. While it is possible to easily implement Monte Carlo (MC) simulations to obtain the statistical moments, they are very inefficient; typically requiring hundreds of simulations to obtain converged results. Instead, in this work, non-intrusive polynomial chaos expansions (PCE) (Ghanem and Spanos 2003) are utilized to obtain the mean and standard deviation of compliance. As well as reducing the number of simulations required to obtain converged statistics, the non-intrusive PCE method requires no modifications to the underlying FE solver. For a discussion on intrusive and non-intrusive PCE methods, the reader referred to Keshavarzzadeh et al. (2016). In the PCE method a stochastic function, the objective in this case, is represented by a linear sum of deterministic coefficients, $c_i$ and orthogonal polynomials, $\psi _i$, expressed as

$$\begin{aligned} \begin{aligned} C(\omega ) = \sum _{i=0}^{\infty } c_i\psi _i(\omega ) \end{aligned} \end{aligned}$$

(18)

For practicality, the summation is truncated to $k = 3$ terms, which was chosen heuristically to ensure converged low-order statistics. The polynomials, $\psi _i$ are chosen to be orthogonal with respect to the probability density function of the underlying random variables, $\omega$, which in this case are chosen to be Legendre polynomials, since $\omega$ are drawn from a uniform distribution (Xiu and Karniadakis 2002). The polynomials are defined in such a way that $\psi _0 = 1$, and due to their orthogonality the relationship

$$\begin{aligned} \begin{aligned} \langle \psi _n, \psi _m \rangle = \delta _{mn} \end{aligned} \end{aligned}$$

(19)

is found, where $\delta$ is the Kronecker delta. Using this property, the mean can be derived as

$$\begin{aligned} \begin{aligned} \mathbb {E}[J]&= \mathbb {E}[\psi _0 C] \\&= \sum _{i=0}^{k}c_i \langle \psi _0, \psi _i \rangle \\&= c_0 \end{aligned} \end{aligned}$$

(20)

where we observe that the mean of the stochastic function can be determined simply from the first coefficient term, $c_0$. The variance (square of standard deviation) is computed using

$$\begin{aligned} \begin{aligned} \sigma [J]^2&= \mathbb {E}[C^2] - \mathbb {E}[C]^2 \\&= \sum _{i=0}^{k}c_i^2 \langle \psi _i^2 \rangle \\&= \sum _{i=0}^{k} c_i^2 \end{aligned} \end{aligned}$$

(21)

Lastly, the coefficients $c_i$ are obtained using a quadrature scheme

$$\begin{aligned} \begin{aligned} c_i&= \frac{\langle C\psi _i \rangle }{\langle \psi _i^2 \rangle } \\ \langle C\psi _i \rangle&= \sum _{j=1}^{n_q} C(\omega ^j)\psi _i(\omega ^j)w^j \end{aligned} \end{aligned}$$

(22)

where $n_q$ are the number of integration points, $\omega ^j$ are the integration points and $w^j$ are the weights corresponding to each integration point, which are generated using the Gauss--Legendre quadrature scheme, resulting in $n_q = 4$. Here $n_q$ represents the number of simulations of the compliance that are required. In comparison, for the problems tested in this work, the standard MC simulation approach required up to 1000 simulations to obtain converged statistics, representing a large saving in computational expense in terms of resources and time required to perform the optimization. As each $\omega ^j$ is independent, the simulations of $C(\omega ^j)$ ($j \in \{1,\dots ,n_q\}$) are performed in parallel to further reduce the computational effort. The sensitivities required for the gradient-based optimization algorithm are computed by extending the PCE method to the gradients defined in Eqs. 12 and 13, resulting in

$$\begin{aligned} \begin{aligned} \frac{\partial \mathbb {E}[C]}{\partial \varvec{\chi }}&= \mathbb {E}\Big [\frac{\partial C}{\partial {\varvec{\chi }}}\Big ] \\ \frac{\partial \sigma [C]}{\partial \varvec{\chi }}&= \frac{1}{(n_q-1)\sigma [C]}\Bigg ( \Big (\sum _{j=1}^{n_q} C(\omega ^j)\frac{\partial {C}}{\partial \varvec{\chi }} \Big ) - n_q\mathbb {E}[C]\frac{\partial \mathbb {E}[C]}{\partial \varvec{\chi }} \Bigg ) \end{aligned} \end{aligned}$$

(23)

where $\chi$ are the truss radii and density design variables shown in Eq. 9. It should be noted that the individual compliance derivatives, $\frac{\partial C}{\partial \chi }$, corresponding to each random field are computed using the same algorithmic differentiation approach employed in the deterministic framework, shown in Eqs. 12 and 13. These gradients are used to construct a PCE which provides the final gradients of the mean and standard deviation.

3.2 Spatially-varying uncertainties

The uncertainties which arise during the AM process are unlikely to be homogeneous or uniform, as assumed in the previous section. In reality, the perturbation or material uncertainty that occurs is likely to differ from one location to another during the AM process. To accurately represent the spatially-varying material uncertainties, the methodology shown in the previous section is modified by representing $\omega$ as a random field, $\varvec{\omega }(\varvec{\text {x}})$, where $\varvec{\text {x}}$ represents the spatial dimensions. The flowchart shown in Fig. 3 describes the updated methodology for including spatially-varying material uncertainties within the robust optimization framework.

The addition of the spatial dimensions to the perturbation requires careful treatment due to a phenomenon commonly referred to as the curse of dimensionality. As the number of stochastic dimensions are increased linearly, the number of simulations required to accurately represent the system increases exponentially. As we are now concerned with the spatial variation of material uncertainty, an infinite series of random variables would be required to capture the behaviour of the uncertain system. A widely used methodology for representing random fields using a finite number of random variables is the Karhunen–Loéve expansion (KLE) (Ghanem and Spanos 1991). Using a KLE a random field can be represented as

$$\begin{aligned} \begin{aligned} \varvec{\omega }(\varvec{\text {x}}) = \mu _{\varvec{\omega }}(\varvec{\text {x}}) + \sum _{m=1}^{\infty } \sqrt{\lambda _{m}}\phi _m(\varvec{\text {x}})\alpha _m \end{aligned} \end{aligned}$$

(24)

where $\lambda _{m}$ and $\phi _m$ are the ordered eigenvalue and eigenvector pair of the correlation matrix $\varvec{\text {C}}$, which is assumed to be of a squared exponential form

$$\begin{aligned} \begin{aligned} \varvec{\text {C}}[\varvec{\text {x}}_1, \varvec{\text {x}}_2] = \exp \Big (-\frac{|\varvec{\text {x}}_1 - \varvec{\text {x}}_2|^2}{2l^2}\Big ) \end{aligned} \end{aligned}$$

(25)

where l is the correlation length, which is assigned a value of 0.8L, where L is the length of the optimization domain. It should be noted that the choice of correlation length impacts the fineness of the random field shown in Eq. 24. Longer correlation lengths lead to fewer fine scale variations in the random field and shorter lengths create many more fine variations in the random field. As there is fast decay in the eigenmodes, meaning that higher modes provide increasingly smaller contributions to the random field, the series shown in Eq. 24 can be truncated to the first $n_{kl}$ modes. In this work the first $n_{kl} =3$ modes are used to compute the random field, the efficacy of which is further discussed in Sect. 4.1.

Fig. 3

Flowchart outlining the steps performed in the robust optimization using spatially-varying material uncertainty

In Eq. 24, $\alpha _m$ represents uncorrelated random variables with a mean of zero ($\mathbb {E}[\alpha _m]$ = 0). When employing KLE, for simplicity, the random field is typically modelled as a Gaussian random field by prescribing $\alpha$ as a Gaussian variable. However, the uncertainty model shown in Eq. 14 is not compatible with Gaussian distributions as they are unbounded and would therefore result in nonphysical radii values (due to overly large perturbations). To enable a more physical representation of the material uncertainties, the Gaussian random field is transformed into a random field bound by a uniform distribution as shown by Lazarov et al. (2012), ensuring that the resulting perturbed radii are physical and well defined by the RSMs. Using the Gaussian cumulative distribution function, $\Phi [\cdot ]$, the Gaussian random field is transformed according to

$$\begin{aligned} \begin{aligned} \varvec{\omega }_u(\varvec{\text {x}}) = \omega _{\text{min}} + (\omega _{\text{max}} - \omega _{\text{min}})\Phi [\varvec{\omega }(\varvec{\text {x}})] \end{aligned} \end{aligned}$$

(26)

where $\omega _{\text{min}}$ and $\omega _{\text{max}}$ are the lower and upper bounds of the uniform distribution.

The PCE method, as introduced in Sect. 3.1, is once again utilized to efficiently compute the low-order statistics required for the optimization. To reduce the number of integration points, the Leja nested quadrature scheme (Narayan and Jakeman 2014) is utilized. As this scheme is nested, the Smolyak sparse grid algorithm (Smolyak 1964) is used to further reduce the number of integration points. Traditionally, moving from univariate to multivariate quadratures requires full tensor grids, invoking the curse of dimensionality, where the number of integration points increases exponentially, i.e. $N^d$ where N is the number of points in the univariate case and d is the number of dimensions. Combined with the nested quadratures generated by the Leja scheme, the Smolyak algorithm reduces the number of integration points compared to a standard full tensor grid, which ultimately reduces the number of simulations required for each iteration of the optimization. Using $n_{kl} = 3$ eigenmodes in the generation of the random field and $k = 6$ PCE modes in the construction of the PCE, a total of $n_q = 84$ quadrature points are required to compute the low-order statistics. This leads to 84 random perturbation fields, $\varvec{\omega }^j_u(\varvec{\text {x)}}, j \in \{1,\dots ,n_q\}$, requiring 84 simulations of the compliance, $C^j(\hat{\tilde{\rho }}, \check{\varvec{r}}^j_1, \dots ,\check{\varvec{r}}^j_7)$, where $\hat{\tilde{\rho }}$ is the filtered and threshold projected density variables and $\check{\varvec{r}}^j_i$ are jth vector of perturbed truss radii, computed by perturbing the deterministic truss radii $\varvec{r}_i$

$$\begin{aligned} \begin{aligned} \check{\varvec{r}}^j_i = \varvec{r}_i + \varvec{\omega }^j_u(\varvec{\text {x)}} \quad j \in \{1,\dots ,n_q\} \end{aligned} \end{aligned}$$

(27)

To avoid stability issues during the optimization, the $n_q$ random fields are computed once at the beginning of each optimization and are reused in every iteration. Four examples of the random fields generated for the cantilever problem tackled in Sect. 4.2 is shown in Fig. 4. For further clarity, a flowchart of the entire robust optimization process using spatially-varying material uncertainty is shown in Fig. 3. To reduce the computational expense of the $n_q$ compliance simulations, 32 cores are utilized to perform some of the computations in parallel.

Fig. 4

Four examples of random fields, $\varvec{\omega }(\varvec{\text{x}})$, generated using KLE

Table 1 Energy captured using $n_{kl} = 3$ modes for each problem

4 Application to robust optimization

4.1 Optimization setup

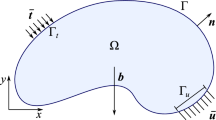
To demonstrate the efficacy of the uncertain perturbation method, we optimize two classical problems: a cantilever and a bridge problem, as shown in Fig. 5. For both problems the inclusion of uniform and spatially-varying material uncertainties is considered. The uncertain perturbation is heuristically chosen to be defined by a uniform distribution in the range $-0.05 \le \omega \le 0.05$, defined in terms of normalized radii units for both the uniform and spatially-varying cases. For a unit cell size of 10 mm, this uncertainty is equivalent to a tolerance of ±0.5 mm in the lattice truss radii. The two optimization problems were run for 300 iterations, with an adaptive $\beta$ value which is incremented by 0.5 every 30 iterations, up to $\beta _{\text{max}} = 3.5$. If the change in objective is less than 0.01% over three successive iterations, once $\beta _{\text{max}}$ is reached, the optimization is terminated. The compliance simulations required each iteration for the uniform ($n_q = 4$) and spatially-varying ($n_q = 84$) uncertainty cases were solved in parallel using the Multiprocessing library within Python. The Python library ChaosPy (Feinberg and Langtangen 2015) was used to implement the non-intrusive PCE method and to generate the Leja integration points. The gradients of the compliance $\frac{\text{d}\varvec{C}}{\text{d}\varvec{\hat{\tilde{{E}}}}}$ and $\frac{\text{d}\varvec{C}}{\text{d}\hat{\tilde{\rho }}}$ were obtained using algorithmic differentiation using the Python library dolfin-adjoint (Mitusch et al. 2019).

Prior to the tackling the optimization problems, we examine the effectiveness of the KLE construction, outlined in Sect. 3.2. Using the first 100 eigenmodes as a reference, we to quantify the percentage ‘energy’ captured when using $n_{kl} = 3$ modes in Table 1. From these results, we observe that over 95% of the ‘energy’ is captured by the first three modes for both problems, which is deemed sufficient for the present study.

Fig. 5

Optimization problem setups

4.2 Results

In this section we present two numerical examples of performing robust optimization using the lattice based multiscale framework considering material uncertainties on the microscale. In each example three material uncertainty cases are considered: deterministic (no material uncertainty), uniform uncertainty and spatially-varying material uncertainty. First, a detailed discussion of the cantilever case is provided, followed by a comparison to the bridge optimization case.

4.2.1 Cantilever

Non-spatially-varying uncertainty

This example examines the impact of considering material uncertainties on the design of a classical end-loaded cantilever, as shown in Fig. 5a. To examine the efficacy of the uncertainty model presented in this work, we first consider the uniform material uncertainty case. Compared to the standard deterministic design, the inclusion of uniform material uncertainties during the optimization process leads to a 21.8% reduction in the mean compliance and a 77.1% reduction in the standard deviation of compliance. These results indicate that the robust optimization model proposed in this work is able to generate designs which are more tolerant of uniform material uncertainties compared to the standard deterministic optimization framework.

Fig. 6

Lattice reconstruction of deterministic, uniform and spatially-varying uncertainty optimized cantilever designs (top row—iso view, bottom row—rear view)

To provide some context and examine the sensitivity of the original deterministic design we also computed the increase in compliance that would result from a fixed uniform perturbation of $\omega = -0.05$ (the most extreme perturbation allowed within this work) to the optimized truss radii. Compared to the deterministic compliance value (where $\omega = 0$), the compliance value increases by 62.9%, when the deterministically optimized design was exposed to a uniform perturbation of $\omega = -0.05$. While a uniform erosion of the truss radii everywhere in the structure during the AM process is unlikely, this result does highlight the sensitivity of the deterministic design. In contrast, exposing the robust design, obtained considering uniform uncertainties during the optimization, to the same perturbation results in a 17.0% increase in the compliance relative to the deterministic compliance value.

To visualize the impact of considering uniform uncertainties in the robust optimization, 3D reconstructions of the deterministic and uniform case designs are shown in Fig. 6a and b, respectively. Here, we observe significant differences in the topology between the two cases, with a hollow, shell structure generated in the deterministic case, whereas the uniform case leads to the formation of a I-beam type structure, as seen in Fig. 6b. The presence of a single central structure transferring the load from the loaded, free end to the fixed end of the cantilever, forms a single, more substantial load path. This leads to a structure which is more tolerant of variations in the lattice radii and contributes to the improved robustness, both in terms of the mean and the standard deviation of compliance, relative to the deterministic design. Based on optimized designs presented for similar setups in literature, we speculate that the shell like structure formed in the deterministic case may be due to a local minimum in the design space rather than the true global optimum solution for the deterministic case. For example, examples of designs similar to that observed in the uniform uncertainty case, shown in Fig. 6b, have been reported in deterministic optimizations (see for example Robbins et al. (2016)).

To further examine the mechanism by which the robust optimization model generates designs which are tolerant of the uniform material uncertainty, histograms showing the underlying material distribution for the design variables ($\rho$ and $r_i$) for both the deterministic and uniform material uncertainty cases are shown in Fig. 7. Focusing on the truss radii ($r_1, \dots , r_7$), shown in Fig. 7b–h, we note that there is a significantly larger number of trusses with radii in the upper bound ($0.29 \le r \le 0.33$) for the uniform uncertainty case in comparison to the standard deterministic result, for every one of the seven trusses. This makes sense as the gradient of the stiffness tensor ($\frac{\text{d}\varvec{E}}{\text{d}r_i}$) is much shallower for thicker lattice trusses, compared to thinner lattice trusses, indicating that denser lattices are more tolerant of variations in the truss radii. As a result, the optimizer pushes the lattice radii towards lattices with larger volume fractions (due to the increase in truss radii) in the optimization domain.

The symmetry present in the microstructure (both in the diagonal trusses and in the x and z axis aligned trusses), is also evident in the optimized designs. From the histograms, we observe that the distributions for the four diagonal trusses, $r_1$ to $r_4$ and the x and the z aligned trusses, $r_5$ and $r_7$, are identical due to the symmetries present on the macroscale. To ensure the volume fraction constraint is met, we observe an increase in the number of void cells, as indicated by the distribution of $\rho$, shown in Fig. 7a, which overall leads to fewer material regions. However, where lattices still exist, they have increased volume fractions, leading to increased robustness. It should also be noted that the effectiveness of the threshold filtering, as defined in Eq. 7, can be clearly observed from the binary distribution of the density variable in Fig. 7a, highlighting that the designs generated are composed of binary, material or void elements only.

Fig. 7

Material distribution histograms for the cantilever optimization problem

Spatially-varying uncertainty

In this section we examine the efficacy of the spatially-varying material uncertainty model proposed in Sect. 3.2, through the robust optimization of a cantilever design. Relative to the deterministic case, the design optimized considering spatially-varying material uncertainties is found to have a 16.2% reduction in the mean compliance and a 67.7% reduction in the standard deviation of compliance, giving confidence that the robust design is more tolerant of spatial variations in the microscale geometry that may occur during the manufacturing process.

Table 2 Comparison of the mean and standard deviation calculated using k = 6 and k = 14 PCE modes

To investigate the accuracy of the low-order statistics, computed using $k = 3$ PCE modes with $n_q = 84$ integration points, the ‘true’ mean and standard deviation of the final optimized designs are computed using $k = 14$ with $n_q = 680$ integration points, the results of which are shown in Table 2. Errors less than 0.1% for the mean and less than 10% for the standard deviation are observed, which is deemed sufficient for the present study. Improvements in the accuracy can be achieved by increasing the number of PCE modes, k, and or by utilizing Gaussian quadrature rules with a full tensor grid, which may perform better as they are less reliant on the smoothness of the stochastic space (Elesin et al. 2012). However, both of these modifications will result in a significant increase in the number of integration points, which can be highly impractical for optimization purposes.

The overall topology, shown in Fig. 6c, is very similar to the design seen in the uniform uncertainty case, shown in Fig. 6b, with an I-beam type structure carrying the load. As with the uniform case design, in the spatially-varying case larger lattice radii are utilized, compared to the deterministic case design, to improve the robustness, as shown in the histograms in Fig. 7b–h. To compensate for the resulting increase in volume, there is an increase in the number of void cells, which is highlighted in Fig. 7a by the increase in the number of cells with $\rho < 0.2$.

Spatially-varying uncertainty vs. uniform uncertainty

A natural question arises regarding the utility of imposing spatially-varying material uncertainties during the robust optimization. Relative to the uniform uncertainty case, there is more than a 20-fold increase in the number of simulations required each iteration (for the setup used in this work), alongside the added complexity of simulating random fields in the first place. In this section we investigate the benefit of considering spatially-varying material uncertainties during the robust optimization, compared to assuming uniform uncertainties. To do this, the low-order statistics of structures designed assuming uniform and spatially-varying material uncertainties were computed by imposing spatially-varying uncertainties on the optimized designs. To clarify, this study simulates the behaviour of structures optimized assuming uniform and spatially-varying material uncertainties in the presence of spatially-varying uncertainties. Therefore, this comparison helps to understand if there is any benefit in utilizing spatially-varying material uncertainties, which are much more computationally intensive, compared to the inclusion of uniform material uncertainties.

For the cantilever problem, based on the data presented in Fig. 8, the relative mean compliance values are − 21.7% and − 30.5% for the uniform and spatially-varying case designs respectively, when exposed to spatially-varying uncertainties, relative to the deterministic design. This result is somewhat expected and shows that the mean compliance is improved by considering spatially-varying uncertainties during the optimization process compared to considering uniform uncertainties. However, the relative standard deviation of compliance values are − 76.8% and − 74.1% for the uniform and spatially-varying case designs, respectively, when exposed to spatially-varying uncertainties, relative to the deterministic design. In the context of the standard deviations of compliance, for the cantilever problem, it appears that there is no real benefit in considering spatially-varying uncertainties during the optimization process. This may be due to the fact that the uniform uncertainty case imposes more extreme changes in material properties, since it always adds or removes material everywhere in the domain. On the other hand, in the spatially-varying case, material is added in some places and removed material in others, causing smaller variations in the compliance. This means that, designs which have been optimized using uniform material uncertainty are somewhat more tolerant to spatially-varying uncertainties, as the optimizer deals with more extreme scenarios in the uniform case.

Fig. 8

Comparison of the relative mean and standard deviation for the uniform and spatially-varying designs

Further evidence of this can also be found by comparing the underlying material distribution histograms, shown in Fig. 7. Here we note that the changes in material distribution relative to the deterministic case are much larger in the designs optimized using uniform uncertainty compared to those optimized using spatially-varying uncertainty. For example, there is a larger increase in the number of void cells meaning that there is a larger reduction in the number of cells containing lattices in the uniform uncertainty optimized designs compared to the spatially-varying uncertainty optimized designs. Similarly, the increase in number of thick truss radii are also much more significant in the uniform uncertainty optimized cases compared to those with non-uniform uncertainty.

Overall, when considering both the mean and standard deviation of compliance, there is a benefit to using spatially-varying uncertainties during the optimization process, despite the increased computational cost. Although, for the setup considered in this work, there is a slight increase in the standard deviation of compliance for the spatially-varying case design relative to the uniform case design, when exposed to spatially-varying material uncertainties, a significant reduction in the mean compliance is achieved. Further analysis is required to examine the impact of the standard deviation factor, $\kappa$, on these results, however this is outside the scope of the current work.

4.2.2 Bridge

Robust optimization was also used to tackle a bridge design problem, as shown in Fig. 5b, to further examine the efficacy of the proposed uncertainty model. As shown in the cantilever problem, the sensitivity of the deterministic and robust solutions for the bridge problem were examined by applying a fixed uniform perturbation to optimized designs. When a perturbation of $\omega = -0.05$ was applied to the deterministic bridge design, the compliance values increased by 63.1%, relative to the deterministic compliance (where $\omega = 0$). However, the increase in compliance was only 16.1% for the bridge design obtained by robust optimization considering uniform uncertainties, further highlighting the need for robust optimization techniques and the inherent sensitivity of deterministically optimized designs.

Similarly to the cantilever problem, the bridge design optimized considering uniform uncertainty was found to have a significantly lower standard deviation of compliance (− 72.9%), as seen in Table 3. This indicates that the robust optimized design has an increased tolerance of variations in the microscale geometry. However, the improvement in the mean compliance is considerably lower, almost negligible, in the bridge case with a reduction of 0.2% in the mean compliance relative to the deterministic design. Compared to the reduction of 21.8% for the mean compliance in the cantilever design, this result appears to be worse than expected, but it may be explained by two factors. Firstly, from the visualizations shown in Fig. 9, we note that the degree of change in topology is very small in comparison to the changes between the deterministic and uniform case designs for the cantilever problem shown in Fig. 6a and b. As there is a limited change in the topology, the improvement in mean compliance that is achieved by the optimized design is therefore also limited. Secondly, as noted in Sect. 3.1, the standard deviation weighting factor used in the objective function was $\kappa =3$, which forces the optimizer to prioritize the reduction of the standard deviation over reductions in the mean compliance, which may explain why, despite a significant reduction in the standard deviation of compliance, only a slight reduction in the mean compliance is observed in the bridge designs.

Table 3 Change in mean and standard deviation of compliance, for the robust optimized designs using uniform uncertainty compared to deterministic designs

Fig. 9

Lattice reconstruction of deterministic, uniform and spatially-varying uncertainty optimized bridge designs (top row—iso view, bottom row—side view)

Table 4 Relative mean and standard deviation of the robust optimized designs using spatially-varying uncertainty relative to the deterministic designs

As discussed in the cantilever problem in Sect. 4.2.1, when spatially-varying uncertainties are considered in the robust optimization the final designs are found to be more robust, due to reductions in the standard deviation of compliance, and more optimal, due to a reduction in the mean compliance, as summarized in Table 4. Once again the material distribution histograms for the bridge design, shown in Fig. 10, can be used to examine the underlying changes which lead to these improved statistics. From the histograms we note an increase in the number of dense lattices, which are less sensitive to variations in the truss radii. The symmetries noted in the cantilever problem are also observed in the bridge design histograms, with identical distribution for the diagonal trusses, as shown in Fig. 10b–e. Further evidence of this can be seen in the 3D reconstructions shown in Fig. 9. For example in the bottom row of Fig. 9a–c we can see that the trusses $r_1$ and $r_4$ are dominant on the left side of the arches and the trusses $r_2$ and $r_3$ are dominant on the right side of the arches to enable more efficient load paths from the loaded surface to the supports.

Fig. 10

Material distribution histograms for the bridge optimization problem

Finally, we can perform a comparison between the uniform and spatially-varying case designs, to examine any benefits of considering spatially-varying uncertainties. As previously discussed, this comparison is performed by imposing spatially-varying uncertainties on the final designs obtained by assuming uniform or spatially-varying material uncertainty during the optimization process. Similarly to the cantilever case, from the results displayed in Fig. 8, we find that considering uniform uncertainties during the optimization process leads to similar standard deviations of compliance in the presence of spatially-varying uncertainties, compared to designs obtained by assuming spatially-varying uncertainties during the optimization. As mentioned earlier, this is due to the fact that uniform uncertainties can be viewed as the extreme case of spatially-varying uncertainty, since material is always added or removed, leading to greater changes in the compliance. However, this leads to sub-optimal structures in terms of the mean compliance, when the uniform uncertainty case designs are exposed to spatially-varying uncertainties, as seen in Fig. 8a. For the bridge problem, the mean performance is almost identical to the deterministic solution (− 0.2%), when we only consider uniform uncertainty. However, in the spatially-varying uncertainty optimized designs, we find significant improvements in the mean compliance (− 16.2%). These results suggest that uniform uncertainty based robust optimized does provide some robustness (in terms of standard deviation), against spatially-varying uncertainties. However, these designs are sub-optimal in terms of the mean compliance and so spatially-varying uncertainty based robust optimization is beneficial when considering both the mean and standard deviation of compliance based on the setup used in this work and assuming that real-world uncertainties arising during the AM process are indeed spatially-varying.

5 Conclusions

Many efficient deterministic multiscale optimization frameworks exist. However, to ensure that designs generated by the optimization algorithms are viable in the real world, the impact of uncertainties must be considered within the optimization framework. In this work we have extended the flexible material uncertainty methodology proposed by Thillaithevan et al. (2021a, b) by performing robust optimization, utilizing a 7-truss lattice microstructure and by imposing spatially-varying material uncertainties. By directly perturbing the microstructure trusses, the uncertainty model simulates the linear erosion and dilation of the microstructures. While this does not capture local defects that may occur along individual trusses, it serves as a starting point for the inclusion of material uncertainty in multiscale optimization frameworks that utilize multiple variable parameterization, something that, to the authors’ best knowledge, has not yet been addressed in literature.

Two numerical examples were presented to highlight the efficacy of the proposed uncertainty model, considering both uniform and spatially-varying uncertainties. The main conclusions from these results are as follows:

• Deterministically optimized designs were shown to be highly sensitive to the type of manufacturing uncertainties that may occur in an AM process, highlighting the need for robust optimization.

• The proposed uniform and spatially-varying material uncertainty formulations generate structures which are significantly more robust in terms of the standard deviation of compliance. For both problems tackled in this work, reductions of $\sim$70% in the standard deviation of compliance were observed in the robust designs in comparison to the standard deterministic designs. These results give confidence that these robust optimized designs would be more tolerant to uncertainties arising during the AM process.

• Direct comparisons between the uniform and spatially-varying case designs indicate that, for the setup used in this work, the consideration of spatially-varying uncertainties during the optimization is beneficial. While the uniform case leads to similar standard deviations, the mean compliance is significantly worse than in the designs optimized using spatially-varying uncertainties.

As the characteristics of real-world defects are heavily influenced by the printer and print settings, in practical applications it will be necessary to tune the uncertain parameters presented in this work using experimental results. This will be the subject of future research.