Consistent boundary conditions for PDE filter regularization in topology optimization

Abstract

Design variables in density-based topology optimization are typically regularized using filtering techniques. In many cases, such as stress optimization, where details at the boundaries are crucially important, the filtering in the vicinity of the design domain boundary needs special attention. One well-known technique, often referred to as “padding,” is to extend the design domain with extra layers of elements to mitigate artificial boundary effects. We discuss an alternative to the padding procedure in the context of PDE filtering. To motivate this augmented PDE filter, we make use of the potential form of the PDE filter which allows us to add penalty terms with a clear physical interpretation. The major advantages of the proposed augmentation compared with the conventional padding is the simplicity of the implementation and the possibility to tune the boundary properties using a scalar parameter. Analytical results in 1D and numerical results in 2D and 3D confirm the suitability of this approach for large-scale topology optimization.

1 Introduction

Topology optimization is a computational design methodology that is widely used in industry, in particular for aerospace and automotive applications. Common structural objectives are to find optimal trade-offs between weight, stiffness, strength, and natural frequency. One of the leading approaches to topology optimization, which is also the one followed in this article, is the density-based approach where the topology is described by a density, i.e. volume fraction of solid isotropic material variable at each discretization point in the design domain (Bendsøe 1989; Bendsøe and Sigmund 2003). As the underlying density variables are continuous between zero and one, penalizing intermediate density values using certain material interpolation schemes is necessary to obtain crisp 0/1 layouts. The most popular material interpolation functions are the SIMP (Solid Isotropic Material with Penalization, cf. Bendsøe (1989), Zhou and Rozvany (1991), and Mlejnek (1992)) and the RAMP stiffness interpolation (Rational Approximation of Material Properties, cf. Stolpe and Svanberg (2001).)

A well-known issue associated with penalization of diffuse designs is that the penalized formulation is lacking an intrinsic length scale which causes numerous problems (Diaz and Sigmund 1995). A remedy to these problems uses a filter-based regularization, similar to those used in image processing, to introduce a length scale. One such early filter is the sensitivity filter (Sigmund 1994; Sigmund and Maute 2012) that essentially averages the design sensitivities over a neighborhood of each design point. This idea was later applied directly to the density variables, leading to the widely used density filter (Bruns and Tortorelli 2001; Bourdin 2001; Bruns and Tortorelli 2003). Filtering in topology optimization has evolved into a research topic as the filtering operation has tremendous impact on the geometry of the resulting design. Among many extensions and variations, one can find smooth Heaviside projections (Guest et al. 2004); morphological filters (Sigmund 2007); manufacturing-tolerant formulations (Sigmund 2009; Wang et al. 2011); density filters based on geomteric, harmonic and quasi-arithmetic means (Svanberg and Svärd 2013; Wadbro and Hägg 2015); and recently also spatial variation of the length scale (Amir and Lazarov 2018; Schmidt et al. 2019). Several alternatives to the filtering do exist, e.g., the perimeter control method (Haber et al. 1996), the gradient control scheme (Peterson and Sigmund 1998; Borrvall and Petersson 2001), and the MOLE method (Poulsen 2003); see also the surveys (Sigmund and Peterson 1998; Borrvall 2001). Furthermore, other, non density-based, topology optimization approaches use alternate means for controlling the length scale, for example phase-field methods (Wallin and Ristinmaa 2013, 2015) and level-set methods (Allaire et al. 2016; Wang et al. 2016). However, the density-based approach with a density filter remains the most widely used method, both in research and in practice. Hence, the current contribution focuses solely on issues arising with this method, specifically with boundary effects.

Recently, issues regarding the consistent treatment of filtering along the boundaries of the design domain have arose. Indeed, upon observing the many topology optimization results in the literature, it can clearly be seen that filtering causes an artificial “attraction” of the design towards the boundaries. This anomaly is a result of the nonuniformity of the filtering operation in the boundary regions. This matter is of particular importance for stress-constrained topology optimization since the maximum stress likely occurs at the design domain boundary.

The need for consistent treatment of length scale control at the boundaries was discussed by several authors, cf. Poulsen (2003) and Lazarov et al. (2016). A recent article demonstrates the artifacts clearly and resolves the issue by extending the design domain for the purpose of consistent filtering (Clausen and Andreassen 2017). Two techniques have been discussed in the literature: we will refer to both as “padding.” In the first padding method, the filter operation is performed on an extended design domain so that the boundary and interior regions of the original design domain (being solid or void) are filtered in a consistent manner (Zhou et al. 2014; Lazarov et al. 2016). In the second padding method, both the filter operation and the finite element analysis are performed on the extended design domain (Clausen and Andreassen 2017). The latter method has resolved stress concentrations at re-entrant corners in stress-based topology optimization (Amir and Lazarov 2018; de Troya and Tortorelli 2018).

Due to the maturity of 2D topology optimization, as well as the industrial need for 3D design, research focus is currently being shifted from 2D applications to 3D topology optimization. This trend puts new emphasis on efficient computational methods such as parallel computing, cf. e.g. Aage et al. (2015, 2017). Notably density filters which are costly to use in parallel algorithms are supplanted by the PDE filter introduced in Kawamoto et al. (2011) and Lazarov and Sigmund (2011). This requires the solution of an elliptic PDE, whose discretized form is solved using conventional finite elements and parallel algorithms. In most topology optimization procedures, the additional computational cost for solving the PDE filter equations is small compared to solving the state equations. Unfortunately, the anomalies in the boundary regions still arise. But fortunately, they are mitigated by using padding. In this paper, we discuss an alternative to padding whereby we augment the potential functional whose minimization generates the PDE filter. This augmentation results in a Robin boundary condition that eliminates the need for padding while preserving the effect of padding. As such, the proposed scheme will not resolve issues that are associated with padding (Clausen and Andreassen 2017). That said, the computational cost for the proposed scheme is slightly less than that of the padding procedure, but the implementation complexity is significantly reduced.

The remainder of the paper is organized as follows: Basic preliminary concepts are reviewed in Section 2, including a review of the standard density and PDE filters. The main contribution of the article is presented in Section 3 where we discuss the augmented PDE filter and shed light on the additional length scale parameter that controls the boundary condition of the filter. Several numerical examples of minimum compliance optimization in 2D and 3D are presented in Section 4. Finally, conclusions are drawn in Section 5.

2 Preliminaries

In this section, we first review several basic features of the topology optimization formulation considered throughout the article. Then, we provide background on density filtering, in its standard form and in the PDE-based approach.

2.1 Problem formulation

For simplicity, we consider the problem of minimum compliance topology optimization subject to a constraint on the total volume fraction, i.e.,

$$ \begin{array}{@{}rcl@{}} \underset{\boldsymbol{\rho}}{\text{minimize :}} && \textsf{\textbf{F}}^{T} \textsf{\textbf{a}} \\ \text{subject to :} && \frac{{\sum}_{e=1}^{N_{\text{elm}}} {\rho}_{e} V_{e}}{{\sum}_{e=1}^{N_{\text{elm}}} V_{e}} - V_{f} \leq 0 \\ : && 0 \leq \rho_{e} \leq 1,\quad e=1, \ldots,N_{\text{elm}} \\ \text{with :} && \textsf{\textbf{K}}_{s}(\boldsymbol{\rho}) \textsf{\textbf{a}} = \textsf{\textbf{F}} \end{array} $$

(1)

where K_s(ρ)a = F is the discretized equilibrium equations for a linear elastic body occupying the design domain volume V under the assumption of quasi-static conditions; is the structural stiffness matrix with the assembly operator denoted . The nodal displacement vector is a and the external load vector is F. The explicit format of the discrete strain-displacement operator, B_s, can be found in, e.g., Ottosen and Petersson (1992). In each element e = 1,…,N_elm in the finite element discretization, we assign a design variable ρ_e.

The design variables, ρ_e, do not directly enter the equilibrium equations, rather they are mapped to the filtered field $\tilde {\rho }$. As per usual, $\tilde {\rho }=0$ denotes locations devoid of material and $\tilde {\rho }=1$ denotes locations filled with solid material. The connection between ρ_e and $\tilde {\rho }$ is the topic of the present paper, and in particular, we are interested in filters which are suitable for large-scale computations. Once $\tilde {\rho }$ is established, the stiffness tensor, D, is evaluated as

$$ \textsf{\textbf{D}} = \left( \tilde{\rho}^{p}(1-\epsilon)+\epsilon\right)\textsf{\textbf{D}}_{o} $$

(2)

where the penalty exponent is taken as p = 3, the uniform elastic isotropic stiffness tensor is denoted by D_o and the residual stiffness factor, 𝜖 = 10^− 9, used to avoid a singular finite element stiffness matrix. In our simulations, we use Young’s modulus E = 1 and Poisson’s ratio ν = 0.3.

2.2 Filters in topology optimization

Here, we compare the PDE filter to the density filter.

2.2.1 Density filtering and padding

The density, i.e., convolution filter was first proposed in Bruns and Tortorelli (2001) and is based on the convolution

$$ \bar{\rho}(\textsf{\textbf{x}}) = \frac{{\int}_{{\Omega}_{f}}w(\textsf{\textbf{y}}-\textsf{\textbf{x}}) \rho(\textsf{\textbf{y}}) dV}{{\int}_{{\Omega}_{f}}w(\textsf{\textbf{y}}-\textsf{\textbf{x}}) dV}, $$

(3)

where Ω_f is the support domain of the filter and w is the weighting kernel function. We denote the convolution filtered density $\bar {\rho }$ to distinguish the results of the standard density filter from that of the PDE filter that is denoted $\tilde {\rho }$. The support domain is given by a sphere with “filter” radius r. Common weight function are the Gaussian bell, hat, and cone functions. In practice, the filtering is performed on the finite element discretization and therefore the filtered density element f is evaluated as

$$ \bar{\rho}_{f}\approx\frac{{\sum}_{e \in {{N}_{f}^{e}}}w(\textsf{\textbf{x}}_{e}-\textsf{\textbf{x}}_{f})\rho_{e} V_{e} }{{\sum}_{e \in {{N}_{f}^{e}}} w(\textsf{\textbf{x}}_{e}-\textsf{\textbf{x}}_{f}) V_{e}}, $$

(4)

where x_e represents the centroid of element e with volume V_e and ${N}_{f}^{e}$ defines the list of elements in the support region of element f. The explicit expression for the weight function used in this work is given by

$$ w(\textsf{\textbf{x}})=\max \left( 0,1-\frac{|\textsf{\textbf{x}}|}{r}\right), $$

(5)

which frequently is referred to as “hat” or “cone” density filter. To eliminate boundary effects, the design domain is padded, by the distance r, so that ${N}_{f}^{e}$ includes elements outside the original design domain, V. The elements in the padding region are either assigned a density of zero or one.

2.2.2 Conventional PDE filter

In the PDE filter, the filtered density $\tilde {\rho }$ is obtained from the nominal design variable density ρ in a competition between (1) the difference between $\tilde {\rho }$ and ρ and (2) the spatial variations in $\tilde {\rho }$. This competition is formulated as a minimization of the potential π defined as

$$ {\varPi}(\tilde{\rho}) = \underbrace{\frac{1}{2}{\int}_{V} {{l}_{o}^{2}} \lvert \boldsymbol{\nabla} \tilde{\rho} \lvert^{2}dV}_{\text{cost for spatial variations in } \tilde{\rho} } + \underbrace{\frac{1}{2}{\int}_{V} (\rho - \tilde{\rho})^{2} dV}_{\text{cost of the difference between } \rho \text{ and } \tilde{\rho}}. $$

(6)

We do not want $\tilde {\rho }$ to be significantly different than ρ and thereby we see that the second integral above is reduced to zero if $\tilde {\rho }=\rho$. But ρ is highly oscillatory so to limit the oscillations in $\tilde {\rho }$ we add the first integral. And thus, regions where ∇ρ≠0, i.e., interface regions, in the domain defined by $\tilde {\rho }$ field are limited. The compromise between these two effects is determined by the (bulk) length scale parameter l_o.

Minimizing π with respect to the filtered density $\tilde {\rho }$, i.e., requiring $\delta {\varPi }(\tilde {\rho }; \delta \tilde {\rho } )=0$$\forall \delta \tilde {\rho }$, allows us to establish the PDE filter that commonly appears in the literature (Lazarov and Sigmund 2011), i.e.,

$$ -{{l}_{o}^{2}} {\Delta} \tilde{\rho} + \tilde{\rho} = \rho, \text{in} \ V, $$

(7)

with the homogeneous Neumann boundary conditions $\boldsymbol {\nabla } \tilde {\rho }\cdot \boldsymbol {n}=0$, where n is the outward normal unit vector to the design domain, V.

3 Augmented PDE filter

From (6), we see that the classical PDE filter associates no cost for placing interfaces along the design domain boundary since $\boldsymbol {\nabla } \tilde {\rho }\cdot \boldsymbol {n}=0$ along ∂V and therefore does not contribute to the cost for spatial variations in $\tilde {\rho }$, cf. (6). Consequently, the PDE filter favors designs having their boundaries coincident with the design domain boundaries rather than interfaces within the design domain. This effect is well-known and clearly seen by optimized designs that “stick” to the design domain boundaries.

Inspired by Wallin and Ristinmaa (2014), we will mitigate this artificial “sticking” by assigning a cost for interfaces that are located along the design domain boundaries. To this end, we add a boundary term to the potential π, i.e.,

$$ \begin{array}{@{}rcl@{}} {\varPi}_{\text{aug}}(\tilde{\rho}) &=& \frac{1}{2}{\int}_{V} {{l}_{o}^{2}} \lvert \boldsymbol{\nabla} \tilde{\rho} \lvert^{2}dV + \frac{1}{2}{\int}_{V} (\rho - \tilde{\rho})^{2} dV\\ &&+ \underbrace{\frac{1}{2}{\int}_{\partial V} l_{s} \tilde{\rho}^{2}dS}_{\text{cost for material along design domain boundaries}}, \end{array} $$

(8)

where l_s is the (surface) length scale parameter. Minimization of (8) results in

$$ \begin{array}{@{}rcl@{}} \delta {\varPi}_{\text{aug}}(\tilde{\rho};\delta \tilde{\rho}) &=& {\int}_{V} {{l}_{o}^{2}} \boldsymbol{\nabla} \tilde{\rho} \boldsymbol{\nabla} \delta\tilde{\rho}dV - {\int}_{V}(\rho - \tilde{\rho})\delta \tilde{\rho}dV\\ &&+ {\int}_{\partial V} l_{s} \tilde{\rho} \delta \tilde{\rho}dS=0, \end{array} $$

(9)

for all $\delta \tilde {\rho }$. Making use of the Green-Gauss theorem on the first volume integral on the right hand side of (9) renders

$$ \begin{array}{@{}rcl@{}} \delta {\varPi}_{\text{aug}}(\tilde{\rho} ;\delta \tilde{\rho} ) &=& - {\int}_{V} {{l}_{o}^{2}} {\Delta} \tilde{\rho}\delta\tilde{\rho}dV - {\int}_{V}(\rho - \tilde{\rho})\delta \tilde{\rho}dV\\ &&+ {\int}_{\partial V}({{l}_{o}^{2}} \boldsymbol{\nabla} \tilde{\rho} \cdot \boldsymbol{n} + l_{s} \tilde{\rho}) \delta \tilde{\rho}dS=0, \end{array} $$

(10)

which should be fulfilled for arbitrary variations, $\delta \tilde {\rho }$. Using the arbitrariness of $\delta \tilde {\rho }$, we find the (Robin) boundary condition

$$ {{l}_{o}^{2}} \boldsymbol{\nabla} \tilde{\rho} \cdot \boldsymbol{n} = - l_{s} \tilde{\rho}, \text{on} \ \partial V, $$

(11)

which ensures that the boundary term in (10) is annihilated. To extract the governing PDE from (10), we again use the arbitrariness of $\delta \tilde {\rho }$ to again obtain (7).

To conclude, instead of solving (7) with homogeneous Neumann boundary conditions $\boldsymbol {\nabla } \tilde {\rho } \cdot \boldsymbol {n} = 0$, we solve (7) with the Robin boundary condition (11). Obviously, by letting $l_{s} \rightarrow 0$, we recover homogeneous Neumann boundary conditions, i.e., the conventional PDE filter is obtained. Similarly, by increasing $l_{s} \rightarrow \infty$, interfaces along external boundaries become prohibitively costly and designs that adhere to the design domain boundaries are eliminated.

3.1 FEM formulation

The governing equations (7) and (11) are discretized using a standard Galerkin-based finite element formulation; i.e., we use the element interpolation $\tilde {\rho }\approx \textsf {\textbf {N}}^{e} \tilde {\boldsymbol {\uprho }}^{e}$ where N^e and ρ^e are the element shape functions and nodal filtered density vectors, respectively. Using Galerkin weight functions, i.e., $\delta \tilde {\rho }=\textsf {\textbf {N}}^{e}\delta \tilde {\boldsymbol {\uprho }}^{e}$, and making use of the arbitrariness of $\delta \tilde {\boldsymbol {\uprho }}$ results in

$$ \Bigl({l}_{o}^{2} \textsf{\textbf{K}} + \textsf{\textbf{M}}^{\text{vol}} + l_{s} \textsf{\textbf{M}}^{\text{surf}}\Bigr)\tilde{\boldsymbol {\uprho}} = \textsf{\textbf{T}}\boldsymbol {\uprho}, $$

(12)

where

(13)

Each N_elm column in T contains

$$ {\int}_{V} \textsf{\textbf{N}}^{eT} dV, $$

(14)

and as per usual, B^e contains the spatial gradient of the shape functions N^e. From (12), we conclude that implementation of the augmented PDE filter only requires minor changes in an existing PDE filter implementation since the new surface term only contributes to the matrix $l_{s} \textsf {\textbf {M}}^{\text {surf}}$. The proposed surface treatment (12) reduces the computational cost slightly compared to the padding approach. However, since the computational cost of the filter is a small fraction of the overall effort that is required to solve the optimization problem, the new scheme and the padding scheme can, computational-wise, be considered to be equal. The primary advantage of this new surface treatment is its simple implementation and its ability to control the attraction towards the boundaries using a single parameter.

¹Our implementations for 2D and 3D minimum compliance topology optimization are provided as Supplementary Material to this article. Both implementations are extensions to widely used open-source codes in Matlab and C++ (Aage et al. 2015; Andreassen et al. 2011).

3.2 Relation between the length scales l_o and l_s

As the two length scales l_o and l_s in (8) are measures of the cost for interfaces within the design domain and interfaces along the boundary of the design domain, they are not independent. To find the connection between them, we consider the 1D version of (7), i.e.,

$$ -{{l}_{o}^{2}}\frac{d^{2} \tilde{\rho}}{dx^{2}}+\tilde{\rho}=\rho, \quad x \in V= \left[-\frac{L}{2}, \ \frac{L}{2} \right] $$

(15)

with

$$ \rho(x)=H(x), $$

(16)

where H(x) is the Heaviside function. Essentially, we view this as a design with boundary at x = 0, and padding region − L/2 < x < 0. Equation (15) is solved with the homogenous Neumann boundary conditions $\frac {d\tilde {\rho }}{dx}=0$ at x = ±L/2, and with l_o = L/50, to compute the conventional PDE filter density $\tilde {\rho }$. This is compared to the convolution filtered density $\bar {\rho }$, obtained using $r=2\sqrt {3}l_{o}$, in Fig. 1. We find that the convolution filter and the PDE filter densities take on equal values $\bar {\rho }=\tilde {\rho }=0.5$ at the interface, x = 0. We also see that the derivatives at x = 0 are $\frac {d\bar {\rho }}{dx}=\frac {1}{r}$ and $\frac {d\tilde {\rho }}{dx}=\frac {1}{2l_{o}}-\frac {1}{2l_{o}(e^{1/l_{o}}+1)}\approx \frac {1}{2l_{o}}$, i.e., the slopes differ by approximately a factor of $\sqrt {3}$ at the interface. This difference is clearly visible in Fig. 1b.

Fig. 1

Unfiltered, convolution, and PDE-filtered densities (a) and their derivatives (b). Design variable ρ (solid blue), convolution filter $\bar {\rho }$ (dashed green), PDE filter $\tilde {\rho }$ (dotted red)

To identify the length scale l_s, we now solve (15) over the trimmed design domain $V=\left [ 0, \ L/2 \right ]$ and enforce Robin boundary condition ${{l}_{o}^{2}}\frac {d{\tilde {\rho }^{a}}}{dx}=l_{s}{\tilde {\rho }^{a}}$ at x = 0. The augmented PDE density filter at the interface equals

$$ \tilde{\rho}^{a}(0)=\frac{\exp(\frac{L}{l_{o}})-1} {\exp(\frac{L}{l_{o}})(1+\xi)+\xi-1}, $$

(17)

where ξ = l_s/l_o. Based on (17), the augmented density at the boundary can for small l_o/L be estimated as

$$ \tilde{\rho}^{a}(0)\approx \frac{ 1 } {\xi +1 }. $$

(18)

From (18), we conclude that if ξ = 1, the value of the filtered density at the interface $\tilde {\rho }^{a}(0)=0.5$ equals the convolution and the conventional PDE filter values $\bar {\rho }(0)=\tilde {\rho }(0)=0.5$ computed over the padded domain. Moreover, upon equating the slopes $\left .\frac {d\tilde {\rho }^{a}}{dx}\right |_{x=0}=\left .\frac {d\tilde {\rho }}{dx}\right |_{x=0}$, we find the condition

$$ \xi=\frac{l_{s}}{l_{o}}= \frac{ \exp(\frac{L}{l_{o}})-1 } { \exp(\frac{L}{l_{o}})+1 }, $$

(19)

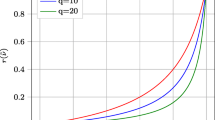
which for small l_o/L suggests that ξ ≈ 1, i.e., l_s ≈ l_o. In conclusion, for the particular choice l_s = l_o, the values of the augmented filtered density and its slope over the domain V = [0, L/2] equal those obtained over the padded domain. To further highlight the influence of l_s = ξl_o, the interface profile $\tilde {\rho }(x)$ for this example is plotted for ξ = 1/30, 1/3, 1, 3, 30.

Again, we conclude that for $\xi =\frac {l_{s}}{l_{o}}=1$, the augmented density profile, $\tilde {\rho }$, coincides with that of the padding procedure, $\bar {\rho }$. Furthermore, in Fig. 2, we see how the choice of ξ affects the maximum filtered value on the boundary. This suggests that the filtered $\tilde {\rho }$ value in the boundary region can take on values from zero to one. Such cases arise when using the robust topology optimization approach that is based on uniform dilations and erosions (Wang et al. 2011).

Fig. 2

Design variable ρ (solid blue), conventional PDE filter $\tilde {\rho }$ (dotted red), and augumented PDE filter $\tilde {\rho }^{a}$ (dashed green) for ξ = 1/30, 1/3, 1, 3, 30

4 Numerical examples

To evaluate the effect of the proposed augmented PDE filter, we apply it to several representative test cases in 2D and 3D. The computations are based on the 88-line Matlab code in Andreassen et al. (2011) and its 82-line PDE filter extension (http://www.topopt.mek.dtu.dk/apps-and-software/efficient-topology-optimization-in-matlabhttp://www.topopt.mek.dtu.dk/apps-and-software/efficient-topology-optimization-in-matlab). The 3D computations are based on the PETSc-based code (Aage et al. 2015), with changes made primarily to the PDEfilter class.

4.1 2D examples

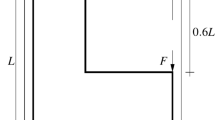
The first topology optimization problem we consider is the well-known MBB beam minimum compliance problem. The geometry and boundary conditions are illustrated in Fig. 3, where the height is L = 100. The design domain is discretized using 300 × 100 4-node plane stress elements and the allowable volume fraction of the design domain is V_f = 0.4. The “standard” parameter settings, as presented in Andreassen et al. (2011) are used, e.g., the penalization exponent is p = 3 and the move limit is m = 0.2. However, in addition to the stopping criteria while change > 0.01, we set the maximum number of design cycles (loop) to 200.

Fig. 3

MBB beam

First, we compare the convolution density filter to the conventional PDE filter. We use the weight function w defined in (5), and we do not impose any explicit modifications to the filter operator over any portion of the domain boundaries including the symmetry face.² For the PDE filter, we apply homogeneous Neumann boundary conditions on all design domain bondaries. The density filter radius is chosen as r = 12, and thus, the PDE filter length scale becomes $l_{o} = r/(2\sqrt {3})$. Figure 4 shows the results generated by running the 88-line and 82-line Matlab codes through top88(100,300,0.4,3,12,2) and top82(100,300,0.4,3,12,2), respectively, with minor modifications for the stopping criteria. Figure 4a and b both show how material “sticks” to the boundary of the domain, and that the design boundaries are forced to be perpendicular to the design domain boundary. These are well-known anomalies which arise both for density and PDE filtering regularization.

Fig. 4

Optimized MBB beam for the a density convolution filter and b PDE filter, using the top88 and top82 Matlab codes, respectively

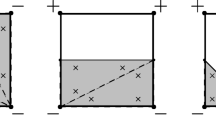
Next, we demonstrate how the encountered anomalies are mitigated via the padding and augmented PDE filter approaches. In the former, the padding thickness equals the filter radius r, no padding adjoins the left symmetry face, and in regions indicated by the dashed and dotted lines in Fig. 5, we assign ρ = 0 and ρ = 1. The width of the latter dotted line regions which encompass the load and support regions is r. We apply the PDE filter with $l_{o} = r/(2\sqrt {3})$ to the padded domain. Again, no special care is given to the symmetry face; i.e., zero Neumann boundary conditions are applied to the entire boundary of the padded domain. Results for this optimization problem are obtained by running the Matlab code top82pad provided in the Supplementary Material. The augmented PDE filter approach is made possible by incorporating Robin boundary conditions into the Matlab top82 code, cf. top82augPDE provided in the Supplementary Material. We specify l_s > 0 on the external boundaries indicated by the dashed lines in Fig. 5, and l_s = 0 on the left symmetry face and dotted boundaries that adjoin the load and support regions.

Fig. 5

MBB beam with padded domain. Dashed and dotted regions represent padding that contain no material and are filled with material, respectively

Figure 6a–c show three density fields, $\tilde {\rho }_{6a}$, $\tilde {\rho }_{6b}$, and $\tilde {\rho }_{6c}$, obtained using the PDE filter. Figure 6a is obtained with homogeneous Neumann boundary conditions (see also Fig. 4b), Fig. 6b with homogeneous Neumann boundary conditions and padding, and Fig. 6c with the augmented PDE filter using ξ = l_s/l_o = 1. In Fig. 6d and e, we plot the filtered element density values across vertical sections of the three topologies, cf. the solid lines and dotted lines at x = 5 and x = 205. As discussed in Section 3.2, we expect the ξ = 1 choice to give $\tilde {\rho } \approx 0.5$ at domain boundaries using the augmented PDE filter. These plots show that both the padding technique (blue line with markers) and the augmented PDE filter (black line) methods give practically identical results and that indeed $\tilde {\rho } \approx 0.5$ on the boundaries. Furthermore, in both of these methods $\nabla \tilde {\boldsymbol {\rho }}\cdot \boldsymbol {n}\neq 0$ at y = 0 and y = 100 and hence the design boundary is not forced to be perpendicular to the design domain boundary. Finally, the filtered density fields $\tilde {\rho }_{6b}$ and $\tilde {\rho }_{6c}$ are compared by evaluating (1) $\frac {1}{V}{\int \limits }_{V} (\tilde {\rho }_{6b} - \tilde {\rho }_{6c})^{2}dV = 2.9 \cdot 10^{-5}$ and (2) the compliance difference, 0.03 %, which further shows that the padding technique and the augmented PDE filter give almost identical results.

Fig. 6

Density fields of the optimized MBB beam. $\tilde {\rho }_{6a}$, $\tilde {\rho }_{6b}$, and $\tilde {\rho }_{6c}$ corresponding to a PDE filter with homogeneous Neumann boundary conditions, b PDE filter with homogeneous Neumann boundary conditions and padding, and c augmented PDE filter with l_s = l_o. Filtered density $\tilde {\rho }_{6a}$, $\tilde {\rho }_{6b}$, and $\tilde {\rho }_{6c}$ at d x = 5 and e x = 205. The compliance values are a 315.8, b 377.3, and c 377.4

4.1.1 Influence of l_s

To further clarify the role of l_s, we also solve the MBB optimization problem using the augmented PDE filter for various choices of ξ = l_s/l_o for fixed $l_{o} = r/(2\sqrt {3})$ and plot the filtered nodal density $\tilde {\rho }$ at (x,y) = (5,0) versus ξ, cf. Fig. 7. It is clearly seen that the results from the optimization practically overlap the 1D PDE solution with Robin boundary condition, cf. (18) (blue dotted line). This result is expected since the design along the x = 5 section cut is nearly one-dimensional. Figure 7 also verifies that the particular choice ξ = 1 gives $\tilde {\rho } \approx 0.5$ at the domain boundary, similar to the padding technique. We also note that as l_s is increased, the filtered density, $\tilde {\rho }(5,0)$, at the boundary decreases. Summarizing, an increase of l_s, gives less filtered material density at the boundary and results in more compliant designs, cf. Table 1.

Fig. 7

Nodal filtered density $\tilde {\boldsymbol {\rho }}(5,0)$ obtained from several optimizations of the MBB beam with the augmented PDE filter (red circles) versus parameter ξ = l_s/l_o, for a fixed l_o. The dotted blue curve shows the function f(ξ) = 1/(1 + ξ), cf. (18)

Table 1 Compliance values of the optimized MBB beam for varying l_s/l_o

4.1.2 2D structure subjected to tensile loading

To connect with the work in Wallin and Ristinmaa (2014), we study the design problem shown in Fig. 8. The two point loads are applied at distances L/4 and 3L/4 from the bottom, respectively, and the left edge of the domain is clamped. The same discretization as used for the MBB beam is used herein, but to obtain topologies similar to those presented in Wallin and Ristinmaa (2014), the filter length scale is reduced to $l_{o} = 4/(2 \sqrt {3})$.

Fig. 8

Design domain with applied loads and boundary conditions of the 2D axially loaded structure

Figure 9 shows optimized topologies using the conventional PDE filter with homogeneous Neumann boundary conditions (Fig. 9a), the conventional PDE filter with homogeneous Neumann boundary conditions and padding over the top and bottom boundaries (Fig. 9b) and the augmented PDE filter with ξ = l_s/l_o = 1 on the top and bottom boundaries and l_s = 0 elsewhere (Fig. 9c). In all three cases, the optimized topology consists of two curved bars connected by a thin vertical bar. In Fig. 9a, we clearly see that the conventional PDE filter favors material along the upper and lower boundaries, whereas this “boundary sticking” is primarily avoided using either the padding or augmented PDE filter approaches, cf. Fig. 9b and c. The compliance values of the latter two designs are almost equal, 39.279 and 39.280, respectively, whereas the 39.674 compliance of the conventional design is worse due to the artificial boundary effect. These results also show that, similar to the results presented in Fig. 6b and c, the padding technique is similar to the augmented PDE filter method with l_s = l_o.

Fig. 9

a Conventional PDE filter with homogeneous Neumann boundary conditions. b Conventional PDE filter with homogeneous Neumann boundary conditions and padding. c Augmented PDE filter with l_s = l_o. The compliance values are a 39.674, b 39.279, and c 39.280

4.2 3D cantilever

In this example, we illustrate the effect of the surface length scale for a 3D case. The particular example is the design of a 2.0 × 1.0 × 1.0 cantilever beam that is fixed on the left face and subjected to a transverse line load at the bottom right edge. We discretize the domain with 256 × 128 × 128 brick elements and set the filter radius to r = 0.05, that is in the range of values explored by Aage et al. (2015). First, we present a reference case using the conventional PDE filter with homogeneous Neumann boundary conditions, essentially reproducing a design similar to those shown in Fig. 3 from Aage et al. (2015). Views of this design from different angles are presented in Fig. 10. One can clearly see the boundary sticking phenomenon.

Fig. 10

Optimized 3D cantilever with conventional PDE filter with homogeneous Neumann boundary conditions. The filtered density distribution has a clear tendency to stick to the domain boundaries. The compliance after 200 design iterations is 6.337

We now repeat the optimization using the augmented PDE filter with l_s = 0 over the support and load boundary regions and l_s > 0 elsewhere. The resulting layouts with l_s = l_o/4, l_s = l_o/2 and l_s = l_o are presented in Figs. 11, 12, and 13. As seen in Fig. 11, the l_s = l_o/4 design is substantially different than the “conventional” Fig. 10 design as the boundaries at $y=y_{{\min \limits } }$ and $y=y_{{\max \limits } }$ are completely avoided. With larger values of l_s, this effect is further exasperated. In the support and load regions where we assign l_s = 0 the structure “sticks” to the boundaries and the filtered density values approach 1.

Fig. 11

Optimized 3D cantilever using the augmented PDE filter with l_s = l_o/4. The filtered density is less than 1 where the “solid” design meets the design domain boundary. The compliance after 200 design iterations is 6.730

Fig. 12

Optimized 3D cantilever using the augmented PDE filter with l_s = l_o/2. The filtered density is approximately 0.5 where the “solid” design meets the design domain boundary, except over the top surface. The compliance after 200 design iterations is 6.874

Fig. 13

Optimized 3D cantilever using the augmented PDE filter with l_s = l_o. The filtered density is 0.5 where the “solid” design meets the design domain boundary. The compliance after 200 design iterations is 6.979

Finally, we repeat this example without the proposed boundary treatment but with the padding method in which both filtering and FEA are performed on the extended domain. This padding choice is selected for its simplicity. For this implementation, we extend the computational domain by d = 0.0625 in − y,+y,−z,+z directions. Note that d is slightly larger than r so that the added number of elements is divisible by 16, and hence 5 multigrid levels can be used for preconditioning of the linear elasticity equations. We do not add padding adjacent to the x = 0 face because of the fixed boundary condition. Finally, we extend the x = 2 face by d = 0.125, again in order to fit 16 elements in the padding region. The region near the load is filled with solid material, whereas all other padding regions are devoid of material. The optimized “padded” design is depicted in Fig. 14, once with and once without the padded elements. We see that the topology is nearly identical to the l_s = l_o design, cf. Fig. 13, thus confirming the suitability of the augmented PDE filter as a means of enforcing a consistent length scale on the domain boundary. Slight differences in the loaded region between the Figs. 13 and 14 designs are observed—this is expected because the solid padding is included in the structural analysis. These differences could be avoided by using separate finite element meshes for the PDE filter and structural computations, i.e., by following the alternative padding method. However, this method requires more extensive changes to the basic PETSc code and which is unnecessary, as the proposed augmented PDE filter gives the same effect with minimal implementation effort.

Fig. 14

Optimized 3D cantilever with physical padding including solids adjacent to the load (left), and presented without the padding layers (right). The topology is nearly identical to that of Fig. 13

5 Conclusions

In this brief paper, we have shown that the PDE filter commonly used in large-scale topology optimization can be easily modified to treat the design domain boundaries in a manner that is consistent with physical padding techniques, without modifying the design domain. The formulation augments the potential that governs the PDE filter with an extra term to accommodate design interfaces located along the design domain boundary. From an implementation point of view, the new boundary term requires minor changes in the PDE filter and it eliminates the need to incorporate padding. To control the penalization of regions adjacent to the design domain boundaries, an additional scalar parameter, l_s, is introduced. By equating l_s to the bulk penalization parameter, l_o, we achieve the same effects of that used in the padding method. Furthermore, l_s can be chosen to accommodate the uniform dilation and erosion of some robust topology optimization techniques.