Multiscale thermal and thermo-structural optimization of three-dimensional lattice structures

Abstract

This paper develops a robust framework for the multiscale design of three-dimensional lattices with macroscopically tailored thermal and thermo-structural characteristics. A multiscale approach is implemented where the discrete evaluations of small-scale lattice unit cell characteristics are converted to response surface models so that the properties exist as continuous functions of the lattice micro-parameters. The derived framework constitutes free material optimization in the space of manufacturable lattice micro-architecture. The optimization of individual lattice member dimensions is enabled by the adjoint method and the explicit expressions of the response surface material property sensitivities. The approach is demonstrated by solving thermal and thermo-structural optimization problems, significantly extending previous work which focused on linear structural response. The thermal optimization solution shows a design with improved optimality compared to the SIMP methodology. The thermo-structural optimization solution demonstrates the method’s capability for attaining a prescribed displacement in response to temperature gradients.

1 Introduction

The advent of additive manufacturing and its rapid evolution is increasingly offering flexibility and precision to the physical realization of advanced materials, potentially expanding the capabilities of some structural and thermal optimization techniques (Sigmund and Maute 2013; Wu et al. 2017; Li et al. 2018; Cheng et al. 2019). In the past, the realization of optimal structural design was limited to manufacturing techniques such as casting and machining processes which constrained the complexity and precision of realizable designs (Brackett et al. 2011). Today, the mechanics of advanced materials have defined a class of optimization techniques that allow free variations of the material properties tailored to meet prescribed macroscale objectives. This concept of freely varying material properties in the domain of a structure towards fulfiling functional objectives, with the capacity for physical realization of optimized structures by additive manufacturing techniques, provides inspiration for this work.

Additive manufacturing has broadened the space of admissible structural designs due to its ability to produce complex geometries at very fine scales. Designs based on topology optimization, concerning the optimal distribution of material within a structure to meet functional objectives, is one such example (Yi et al. 2019). However, a general framework of optimizing directly on a free parameterization of the material tensor, called Free Material Optimization (FMO), is often regarded as the ultimate generalization of the structural optimization problem (Bendsøe et al. 1994; Zowe et al. 1997; Kočvara and Stingl 2007; Kočvara et al. 2008). The FMO framework employs the components of the constitutive material tensor as design variables which are free to vary spatially throughout the domain of the structure. By definition, FMO yields the optimal structural solution as there exist no restrictions on local properties except that the elastic tensor be symmetric and positive semi-definite—a physical constraint (Kočvara and Stingl 2007). Though optimization using the unrestricted set of components of the constitutive material tensor as design variables makes no considerations for the physical realization of local structure, mechanics of advanced materials present a means to integrate admissible local structure within an FMO framework.

Thermal optimization of metamaterials is a subject of notable interest (Dede et al. 2018). Thermal metamaterials, are materials that derive their thermal performance characteristics from their underlying micro-architecture rather than their bulk material composition. The design of these materials to match predefined homogeneous material properties is well developed. However, the integration of these materials into thermal and structural optimization strategies to achieve heterogeneous, spatially varying properties is an active research field (Panetta et al. 2015; Schumacher et al. 2015; Wu et al. 2017). These metamaterials can be incorporated towards attaining optimal heat management within heat diffusers and cooling fins (Roman et al. 2011; Yan et al. 2015; Li et al. 2018). Thermo-structural optimization has been proposed for designing injection moulds that minimize the mould mass while satisfying structural and thermal constraints (Wu et al. 2017). By controlling the geometric parameters of their micro-architectures, metamaterials can be designed to exhibit interesting macroscopic thermal and thermo-mechanical behavior, so that properties of structures built up from these metamaterials can be tailored to satisfy predefined objectives (Lee et al. 2012). Equipped with the free parameterization of thermal and elastic material property driven by the free design of local architecture, an extension to the FMO framework can be derived that delivers manufacturable optimal thermal and thermo-structural designs without sacrificing precision.

The goal of the work described in this paper is to demonstrate a multiscale approach for mechanically and thermally optimized structures using a spatially varying lattice design. A robust optimization framework is derived that executes macroscale thermal and thermo-structural optimization using geometry parameters of constituting micro-architectures, leading to a design of local architecture as well as material layout. Mapping of compatible and connectable micro-architectures is not required, rather, lattice micro-architectures are derived automatically as optimal values of lattice radii parameters are computed. The novelty of this research lies in the use of multiple geometry-based small-scale design parameters for thermal and thermo-structural optimization problems in three-dimensional real space, moving beyond the previously demonstrated structure-only optimized lattice. This allows complex thermo-structural, temperature gradient-based prescribed displacements problems to be demonstrated along with a range of other complex problems. The inclusion of a SIMP-like design variable, controlling whether lattice is present or not, also provides significant improvements in optimum lattice geometry when compared to either SIMP-based topology optimization or continuous lattice-based optimization. The parameterization implemented supports full control over all components of anisotropy with the potential for interesting results. The final outcome is a functional grading of the material of structures, mechanically and thermally tailored to satisfy functional objectives.

2 Overview

This paper extends the framework derived by Imediegwu et al. (2019), that enables functional grading of material properties towards satisfying predefined macroscale objectives using small-scale lattice geometry parameters as control variables. This work builds on this linear structural optimization to include thermal and thermo-structural response, of the lattice. The ability to have no lattice present is also explored with the addition of a SIMP-like variable, significantly improving the response relative to the continuous lattice solution.

The sequential multiscale framework comprises two computational phases. The first phase is an off-line discrete evaluation of effective macroscale properties in the space of microscale lattice geometry parameters. This precomputation involves a parameterization of the small scale that supports a smoothly changing architecture for smooth pertubations of the geometry parameters. A full-factorial design of experiments (DoE) is set up to discretely populate the material space of small-scale parameters by perturbing the geometry parameters over several levels and executing numerical homogenization to derive effective material properties of the corresponding micro-architectures.

The second phase of the framework constitutes the formulation of thermal and thermo-structural optimization at the macroscale using the lattice micro-parameters of the first phase as control variables. Both scales are coupled by polynomial response surface models. The polynomial approximations, constructed as continuous functions to the discrete evaluations of effective material properties, represent functional relationships between the components of the material tensors and lattice geometry parameters in the form of explicit expressions, hence enabling significant savings in computational cost. These polynomial models also facilitate explicit derivations of sensitivities as is demonstrated in this paper.

Though the first phase is associated with significant computational effort, the off-line sampling of the property space needs to be executed only once as the material’s Young’s modulus and thermal conductivity scales linearly with the elastic and conductivity tensor components, respectively (Bendsøe and Sigmund 2003). The microscale parameterization implemented supports all components of anisotropy so that optimization formulations in this work have potential to yield interesting results. It is not claimed that the exploration of the property space is exhaustive given the parameterization scheme employed. However, the truss-like parameterization implemented is known to span broad extents of material property (Hughes et al. 2010), providing a broad range of material behaviors. It also ensures connectivity of adjacent micro-architectures and does not support enclosed voids which is suited to the manufacturing techniques intended for this framework.

Fig. 1

Hierarchical organization of framework illustrating macroscale domain built up of periodic lattice micro-architectures with elastic and thermal properties controlled by lattice micro-parameters

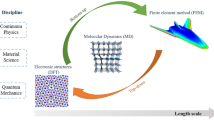
Figure 1 illustrates the hierarchical organization of the framework showing material mechanical and thermal properties of a macroscale problem as functions of lattice geometry parameters.

3 Methodology

In this section, the theory upon which the multiscale framework presented by Imediegwu et al. (2019) is extended to thermal and thermo-structural formulations. Fundamental assumptions are stated to define the class of problems to which this work applies. A process flow chart presents a visual representation of the framework. A description of the theory and numerical implementation of its phases and sub-processes is given. Finally, general mathematical formulations are presented for the macroscale optimization problems of the next section.

Fig. 2

Process flow chart showing the phases and sub-processes of the framework

The thermal formulations of this work are governed by steady-state pure conduction across both scales given by the steady-state heat equation

$$\begin{aligned} \varvec{q}_{i,i} + \varvec{f_{\theta }} = 0 \end{aligned}$$

(1)

and Fourier’s law

$$\begin{aligned} \varvec{q}_i = -\varvec{K}_{ij}~\varvec{\theta }_{,j} \end{aligned}$$

(2)

where $\varvec{q}_i$ is the heat flux vector, $\varvec{f_\theta }$ is heat source per unit volume, $\varvec{K}_{ij}$ is the symmetric thermal conductivity tensor, $\varvec{\theta }$ is temperature difference and $\varvec{\theta }_{,j}$ is the temperature gradient in the direction j for $j =$ 1, 2 and 3. It is also assumed that material thermal conductivity tensor remains unchanged and insensitive to temperature changes.

For large-scale thermo-elastic formulations of this work, the total Cauchy stress tensor is given as

$$\begin{aligned} \varvec{\sigma ^T}_{ij} = \varvec{\sigma }_{ij} + \varvec{\sigma '}_{ij} \end{aligned}$$

(3)

where $\varvec{\sigma ^T}_{ij}$ comprises a linear combination of mechanical strain-induced and thermal strain-induced stresses. The strain-induced stress is given by Hooke’s law

$$\begin{aligned} \varvec{\sigma }_{ij} = \varvec{E}_{ijkl}~\varvec{\varepsilon }_{kl} \end{aligned}$$

(4)

and the thermally induced stress due to a temperature difference, $\varvec{\theta }$, is given as

$$\begin{aligned} \varvec{\sigma '}_{ij} = \varvec{\beta }_{ij}~\varvec{\theta } \end{aligned}$$

(5)

where $\varvec{E}_{ijkl}$ and $\varvec{\beta }_{ij}$ are the 4th-rank elasticity tensor and the thermo-elasticity tensor, respectively. Deformations are governed by the linear elastic theory as presented by Imediegwu et al. (2019). Static equilibrium mechanics is also assumed where applicable. A diagrammatic description of the derived framework is shown in Fig. 2. The framework is sequential consisting of two separate computational phases. A description of the framework now follows.

The first phase is the precomputation phase featuring a one-off development of a microscale model that facilitates the development of the multiscale framework through discrete evaluation of the microscale model at design points in the material property space. It culminates in the generation of continuous functions of material interpolation derived from the precomputed discrete material property evaluations called response surface models or meta-models.

3.1 Micro-architecture parameterization

The objective of the microscale model development is to derive an efficient parameterization of the small-scale geometry that facilitates a robust population of material property spaces.

Fig. 3

Microstructure parameterization: The properties of the micro-architecture are controlled by the components of its vector of normalized radii parameters. Each member has a fixed orientation and the coordinate axes of the microscale are consistent with the macroscale so that the orientations of each member remains unchanged within the large-scale optimization domain

Hughes et al. (2010) and Panetta et al. (2015) demonstrated that parameterization with beam-like structures had the potential to cover large extents of the material property space.

Lattice Unit Cells (LUCs) are employed for the microscale parameterization of this work as presented by Imediegwu et al. (2019). The parameterization provides smoothly changing geometry for slowly changing lattice radii parameters. Sufficient scale separation is an assumption of heterogeneous multiscale methods (Weinan et al. 2007) that validates the homogenization theory as implemented. The scale separation ensures that the micro-architecture length scales are much smaller than the characteristic length over which macroscale field variables change (Geers et al. 2010) so that material property variations are efficiently captured by the smooth variation of microstructure parameters. The parameterization is also suited to the intended manufacturing techniques presenting no enclosed volumes within the unit cell. It should be noted that any parameterization that is periodic, evolves smoothly with smoothly changing micro-parameters, and does not support enclosed volumes or suspended solids is suited to the described framework. The microstructure parameterization chosen is one example of many that satisfy these requirements.

Each LUC is characterized by four strut-like members connecting opposite corners (termed diagonal members) and three similar members connecting opposite face centers (termed face members). The lattice configuration comprises members of circular cross-section as shown in Fig. 3. By varying the radii of each of these lattice members, the material property of the unit cell is altered, hence leading to a parameterization scheme. Each of the seven radii is normalized by the unit cell length. Figure 3 illustrates a typical microstructure with its vector of normalized radii parameters, $\varvec{r}$ as well as its orientation in three-dimensional space. This orientation of the microstructure is preserved for subsequent macroscale analyses.

3.2 Fixed-discretization property assignment

Local property assignment within the LUC is based on the structured element-based material assignment as presented by Imediegwu et al. (2019) so that element-wise Young’s modulus and thermal conductivity is given as

$$\begin{aligned} E_e = n_fE_s + (1 - n_f)E_v \end{aligned}$$

(6)

and

$$\begin{aligned} K_e = n_fK_s + (1 - n_f)K_v \end{aligned}$$

(7)

respectively, where $n_f$ is the node fraction for each element, $E_s = 209~\hbox {GPa}$ and $E_v = 10^{-7}~\hbox {GPa}$ represent the Young’s moduli of the base material and void (modeled as a weak material) respectively and $K_s = 40~\hbox {Wm}^{-1}\hbox {K}^{-1}$ and $K_v = 0.024~\hbox {Wm}^{-1}\hbox {K}^{-1}$ represent the thermal conductivity of the base material and void, respectively. The Poisson’s ratio for both materials is, $\nu = 0.3$. The structured discretization supports the implementation of periodic boundary conditions but also eliminates unstructured mesh-related complications for complex geometries. Mesh convergence studies show convergence for $70^3$ hexahedral finite elements within the LUC. To satisfy geometry periodicity requirements, material assignment for diagonal members 1–4 features an adaptation based on translated centroidal axes for each diagonal member along each of the three orthonormal axes (Imediegwu et al. 2019). Figure 4 shows examples of micro-architectures that can be derived from the parameterization scheme described by Imediegwu et al., along with their fixed-discretization representations. The fixed-discretization representations have been thresholded for visualization at $E_{vis} = 0.01E_s$. Having derived an efficient parameterization, the microscale model is completed by evaluating the effective mechanical and thermal properties of the micro-architectures achievable by the parameterization implemented.

Fig. 4

Example micro-architectures with vector of normalized radii parameters, $\varvec{r}$ :– (0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0.13, 0.13, 0.13), (0.13, 0.13, 0.13, 0.13, 0, 0, 0), (0, 0.19, 0.06, 0, 0.13, 0.06, 0.13), (0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25),(0.38, 0.38, 0.38, 0.38, 0.38, 0.38, 0.38) (left-to-right)

4 Homogenization

In this section, the numerical approach to obtaining the homogenized thermal conductivity tensor, $\varvec{K}^H$ of the lattice-based micro-architecture is summarized. The process follows the principles of asymptotic expansion homogenization which is suited to periodic microstructures as described in (Hollister and Kikuchi 1992; Pinho-da Cruz et al. 2009; Oliveira et al. 2009; Arabnejad and Pasini 2013; Andreassen and Andreasen 2014). The objective of the homogenization process is to substitute the inherent heterogeneities of the lattice microstructure with an equivalent homogeneous media with the benefit of a massive reduction in the degrees of freedom associated with modeling materials composed of architectures. The theory of homogenization as applied to linear elastic structures with periodic micro-architectures is well developed. The fundamental assumption associated with the correct implementation of homogenization is that the macroscale media is built up of periodic representative volume elements (RVEs) at a distinctly separate length scale from the scale of the structure. Mathematically,

$$\varvec{x^{\prime}} = \frac{\varvec{x}}{ \in}$$

(8)

where $\varvec{x^{\prime}}$ and $\varvec{x}$ are the coordinate systems of the microscale and macroscale, respectively. The value of the scale separation parameter, $\epsilon$ is often chosen as $\epsilon<< 1$ so that local microscale field variables vary $1/\epsilon$ times more rapidly than corresponding macroscale field variables. All relevant field variables are therefore approximated by an asymptotic expansion that captures their macroscopic uniform distribution as well as their periodically fluctuating distribution on the microscale.

4.1 Thermal analyses

Extending asymptotic expansion homogenization theory (Pinho-da Cruz et al. 2009; Oliveira et al. 2009) to the determination of effective thermal properties of periodic structures is analogous to the process described by Imediegwu et al. (2019) for mechanical properties. For completeness, the theory is briefly summarized as follows.

The exact temperature field of periodic structures of this work are given as

$$\begin{aligned} \theta ^\epsilon (x_i, x'_i) = \epsilon ^0\theta ^0(x_i, x'_i) + \epsilon \theta ^1(x_i, x'_i) + \epsilon ^2\theta ^2(x_i, x'_i) + ... \end{aligned}$$

(9)

where $\theta ^0$ is the macroscopic uniform temperature field and $\theta ^1$, $\theta ^2$, etc., represent the microscale fluctuations in the field variable as a consequence of underlying heterogeneities of the microscale. A difference is that where displacement is a vector field in elastic theory, temperature is a scalar field as indicated in Eq. 9. Since $\epsilon<< 1$, it suffices to represent the field by a first order approximation. As a consequence, Eq. 9 can be expressed as

$$\begin{aligned} \theta ^\epsilon (x_i, x'_i) = \theta ^0(x_i, x'_i) + \epsilon \theta ^1(x_i, x'_i) \end{aligned}$$

(10)

Derivatives of any of the variables in the multiscale framework follow the chain rule of function differentiation given as

$$\begin{aligned} \dfrac{\partial (~)}{\partial x_i}^\epsilon = \dfrac{\partial (~)}{\partial x_i} + \dfrac{1}{\epsilon }~\dfrac{\partial (~)}{\partial x'_i} \end{aligned}$$

(11)

By Eq. 11 and neglecting terms $\mathcal {O}(\epsilon )$ and higher, temperature gradient based on the multiscale framework is expressed as

$$\begin{aligned} \dfrac{\partial \theta ^\epsilon }{\partial x_i} = \dfrac{\partial \theta ^0}{\partial x_i} + \dfrac{\partial \theta ^1}{\partial x'_i} \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned} \nabla \bar{\theta }_i&= \dfrac{\partial \theta ^0}{\partial x_i}\\\\ \nabla \theta ^*_i&= \dfrac{\partial \theta ^1}{\partial x'_i} \end{aligned} \end{aligned}$$

(13)

are the macroscale average temperature gradient and microscale periodically fluctuating temperature gradient, respectively. As a consequence, Eq. 12 gives the microstructural temperature gradient and can be expressed as

$$\begin{aligned} \nabla \theta _i = \nabla \bar{\theta }_i + \nabla \theta ^*_i \end{aligned}$$

(14)

Substituting the microstructural temperature gradient into the variational form of the Poisson equation for heat conduction gives

$$\begin{aligned} \int _{\varOmega ^\epsilon }\varvec{K}_{ij}~(\nabla w^0_i + \nabla w^1_i)~(\nabla \bar{\theta }_i + \nabla \theta ^*_i)~d\varOmega ^\epsilon = f~w~d\varGamma _f \end{aligned}$$

(15)

where $\nabla w^0_i$ and $\nabla w^1_i$ are the virtual macroscopic and microscopic temperature gradients respectively with f as the heat source on the part of the boundary it acts on, $\varGamma _f$. If the virtual temperature is chosen such that it varies periodically on the microscale but remains constant on the macroscale, Eq. 15 becomes

$$\begin{aligned} \int _{\varOmega ^\epsilon }\varvec{K}_{ij}~\nabla w^1_i~(\nabla \bar{\theta }_i + \nabla \theta ^*_i)~d\varOmega ^\epsilon = 0 \end{aligned}$$

(16)

Taking an integral over the representative volume element, Eq. 16 can be expressed as

$$\begin{aligned} \int _V\varvec{K}_{ij}~\nabla w^1_i~\nabla \theta ^*_i~dV = -\int _V\varvec{K}_{ij}~\nabla w^1_i~\nabla \bar{\theta }_i~dV \end{aligned}$$

(17)

Fig. 5

Unit temperature gradient on the LUC

Provided periodic boundary conditions are imposed on the boundaries of the RVE, Eq. 17 presents the variational form with which the periodically fluctuating temperature gradient, $\nabla \theta ^*_i$ of a representative unit volume of any periodic structure can be derived, given any arbitrary macroscopic temperature gradient, $\nabla \bar{\theta }_i$. The formulation of Eq. 17 can be solved by finite element analysis in its discretized form. Three independent macroscale unit temperature gradients are shown in Fig. 5. The solution to each thermal analysis is the microscale periodic temperature distribution, from which the periodically fluctuating temperature gradient vector is determined. By applying Eq. 14, the microscale temperature gradient vector is derived. Finally, the microscale heat flux vector at each element of the discretized unit cell is given by

$$\begin{aligned} q_i = K_e~(\nabla \theta _i^* + \nabla \bar{\theta }_i) \end{aligned}$$

(18)

where $K_e$ is the element-wise constant thermal conductivity coefficient defined by the fixed-discretization property assignment of Sect. 3.2. The macroscopic heat flux vector is derived from a volume-averaging of the element-wise heat flux vector of Eq. 18 so that

$$\begin{aligned} \bar{q}_i = \dfrac{1}{V}\int _v q_i~dV \end{aligned}$$

(19)

Having obtained $\bar{q}_i$ for each unit macroscopic temperature gradient, $\nabla \bar{\theta }_i$, all 9 terms of the homogenized conductivity tensor is obtained from

$$\begin{aligned} \bar{q}_i = \varvec{K}^H_{ij}~\nabla \bar{\theta }_j \end{aligned}$$

(20)

for i and $j = 1$, 2, and 3. Inherent properties of symmetry must be satisfied by $\varvec{K}^H_{ij}$. Strain deformation analyses to determine the homogenized elasticity tensor, $\varvec{E}^H_{ijkl}$ are analogous to that reported here for thermal analyses and have been described by Imediegwu et al. (2019).

Table 1 Sample micro-architectures enabled by parameterization

4.2 Periodic boundary conditions (PBC)

Considerations for geometry periodicity (Imediegwu et al. 2019) ensures that there is member continuity across neighboring micro-architectures. Periodic boundary conditions (PBC) have also been applied as constraints on the LUC by an association of degrees of freedom on opposite external surface boundaries.

Fig. 6

Coordinate system for PBC implementation

These constraints ensure that the response (structural and thermal) of the unit cell will be representative of the periodic material they form. Imposing PBC ensures that the microstructure boundaries deform identically so that neighboring micro-architectures are compatible. For a hexahedral unit cell in $x'_1 \in [0,~1]$, $x'_2 \in [0,~1]$ and $x'_3 \in [0,~1]$ (See Fig. 6), PBC implementation for thermal problems of this work are temperature constraint equations applied to solve the discretized form of Eq. 17

$$\begin{aligned} \begin{aligned} \theta ^i (0,~x'_2,~x'_3)&= \theta ^i (1,~x'_2,~x'_3)\\ \theta ^i (x'_1,~0,~x'_3)&= \theta ^i (x'_1,~1,~x'_3)\\ \theta ^i (x'_1,~x'_2,~0)&= \theta ^i (x'_1,~x'_2,~1) \end{aligned} \end{aligned}$$

(21)

due to macroscopic temperature gradient, $\nabla \bar{\theta }_i$ in the i-th direction for $i = 1$, 2 and 3.

Table 1 illustrates example micro-architectures enabled by the parameterization scheme employed. The mechanical and thermal properties of all simulated micro-architectures of this work have been determined by the homogenization process described above.

5 Response surface models

In this paper, the mechanical property space population by Imediegwu et al. (2019) is updated to include thermal properties. It involves the determination of a property vector, $\eta _p$, associated with each micro-architecture derived in the full-factorial design of experiments. This constitutes discrete property evaluations within a 7-dimensional space—an evaluation of the components of the stiffness and conductivity matrices as well as volume fraction as functions of the vector of radii parameters. Mathematically, each micro-architecture simulation yields

$$\begin{aligned} \eta _p = (\varvec{E}, \varvec{K}, v_f)_p \end{aligned}$$

(22)

where $p = 1$, 2, ..., $N_T$. The total number of evaluation points, $N_T$ was determined by Imediegwu et al. as 823,543 with a symmetry-based computation reduction as described (Imediegwu et al. 2019).

Table 2 Table of $R^2$-values and RMSEs for 6th-order polynomial meta-models

Response surface models generated for components of elasticity and thermal matrices as well as the volume fraction are consistent with the polynomial approximation functions presented by Imediegwu et al. (2019). These meta-models are differentiable and continuous functions which facilitate the rapid evaluation of local material properties given the vector of radii parameters. They are therefore suited to gradient-based optimization. Table 2 shows the coefficients of determination ($R^2$-values) and root mean square errors (RMSEs) associated with all constructed meta-models.

6 Problem formulation

The optimization phase consists of macroscale optimization formulation in the space of the microscale parameters enabled by the meta-models generated in the preceding section. Equipped with explicit expressions of large-scale (homogenized) properties as functions of the small-scale lattice parameters, functional grading of the material of structures is formulated in the space of the precomputed material properties. The design domain is defined and discretized into finite elements. In contrast to the SIMP approach, where each cell of the discretized domain is assigned an artificial density function as a measure of local stiffness to derive the optimal distribution of material, this framework leverages the continuous functions of material property evaluation derived in the precomputation phase. As a consequence, local properties are controlled at the scale of the lattice micro-architectures by controlling the value of the components of the vector of lattice parameters, $\varvec{r}$ within each cell.

Consider the domain of an externally loaded and constrained initial structure discretized into $N_e$ elements and with $N_n$ nodes. The scale of this structural component defines the macroscale. Recall that an assumption upon which the theoretical concepts of homogenization rely is that there is sufficient separation between the macroscale and the scale of the micro-architectures (Eq. 8). The general formulation of the optimization problems is given as

$$\begin{aligned} \begin{aligned}&\text {minimize:}&J\big (\varvec{u}(\varvec{r}_{\gamma }), \varvec{r}_{\gamma } \big ) \\&\text {subject to:}&F(\varvec{u}(\varvec{r}_{\gamma }), \varvec{r}_{\gamma }) = 0\\&&\int _\varOmega V(\varvec{r}_{\gamma })~d\varOmega \le V_D\\&r_{min} \le r_{i \gamma } \le r_{max}\\&\rho _{min} \le \rho _\gamma \le \rho _{max}\\ \end{aligned} \end{aligned}$$

(23)

for $\gamma = 1$, 2, ...$N_n$ and $i = 1$, 2, ...m where

$$\begin{aligned} \varvec{r}_{\gamma } = [r_{1\gamma },r_{2\gamma },r_{3\gamma },r_{4\gamma },r_{5\gamma },r_{6\gamma },r_{7\gamma }, \rho _\gamma ]^\intercal \end{aligned}$$

(24)

is the stacked vector of control variables with length $8N_n$. The real-valued objective functional, J depends on the solution, $\varvec{u}$, of a PDE that defines the physics of the problem. It also depends on the stacked vector of control variables, $\varvec{r}_{\gamma }$. The solution to the PDE must also satisfy a prescribed equilibrium constraint, $F = 0$. There is an optional cost constraint that controls the overall volume fraction of the optimized structure as shown in Eq. 23 for which the volume fraction meta-model is evaluated at each node as

$$\begin{aligned} V(\varvec{r}_{\gamma }) = \rho _\gamma V(r_{1\gamma },r_{2\gamma },r_{3\gamma },r_{4\gamma },r_{5\gamma },r_{6\gamma },r_{7\gamma }) \end{aligned}$$

(25)

A pseudo-lattice-density variable, $\rho _\gamma$ is introduced in the formulation as shown in Eqs. 24 and 25. Penalizing this variable in a SIMP-like manner discourages intermediate values of the variable so that it defines a macroscale lattice density distribution in the optimal solution. Finally, there exist bound constraints on the components of the stacked vector of control variables as shown in Eq. 23. The lower bound is set based on a limiting computational ability to determine true material behavior with decreasing member radii at the chosen mesh discretization. The lower bound must also satisfy manufacturing constraints as there are limitations to the smallest permissible thickness associated with every base material. Below a specific length scale for a given homogeneous base material, the material properties deviate from documented structural behavior (Doerner et al. 1986; Pantano et al. 2012). The upper bound is set by the highest level of perturbation of the lattice parameters for the micro-architecture to attain the properties of a fully dense block. The bounds of the pseudo-lattice-density variable $\rho _{min} = 0$ and $\rho _{max} = 1$ define the regions of no lattice micro-architecture and lattice-micro-architecture respectively since the variable is penalized to discourage intermediate values. The optimization framework as defined was applied to thermal and thermo-structural problems. The numerical implementation of the derived framework to these classes of optimization problems are described below.

6.1 Thermal optimization

According to the steady-state pure conduction assumptions stated in Sect. 3, the heat equation can be expressed in its variational form as

$$\begin{aligned} \begin{aligned}&\int _{\varOmega } \varvec{q}(\theta ,\varvec{r}_\gamma ):\nabla w~d\varOmega - \int _{\varOmega }\varvec{f_\theta } \cdot w~d\varOmega \\&\quad -\int _{\varGamma }\varvec{T_\theta } \cdot w~d\varGamma = 0 \qquad \forall w \in \mathcal {W} \end{aligned} \end{aligned}$$

(26)

where the heat flux is given as

$$\begin{aligned} \varvec{q}(\theta ,\varvec{r}_\gamma ) = - \varvec{K}(\varvec{r}_\gamma ) \cdot \nabla \theta \end{aligned}$$

(27)

for which $\varvec{K}(\varvec{r}_\gamma ) = \rho _\gamma ^p \varvec{K}(r_{1\gamma },r_{2\gamma },r_{3\gamma },r_{4\gamma },r_{5\gamma },r_{6\gamma },r_{7\gamma })$ is constructed from the meta-models generated in Sect. 5 with a penalization parameter, p on the pseudo-lattice-density function that defines the macroscale lattice density distribution. A test function, w is defined that belongs to the space of all admissible temperature functions $\mathcal {W}$, $\varvec{f_\theta }$ represents the sum of all internal heat sources within the domain of the structure, $\varOmega$, $\varvec{T_\theta }$ represents the sum of all external heat sources on the boundary of the domain, $\varGamma$ and $\theta$ is the solution to the PDE satisfying the steady-state constraint. For thermal compliance minimization problems (average temperature minimization problems), the objective functional for pure thermal conduction problems of this work is given as

$$\begin{aligned} J_{\theta c}\big (\theta (\varvec{r}_{\gamma }), \varvec{r}_{\gamma } \big ) = \int _{\varOmega }\varvec{f_\theta } \cdot \theta ~d\varOmega + \int _{\varGamma }\varvec{T_\theta } \cdot \theta ~d\varGamma \end{aligned}$$

(28)

6.2 Thermo-structural optimization

Based on the assumptions of linear elastic static equilibrium and steady-state pure conduction as presented in Sect. 3, the variational form of a weakly coupled thermo-structural equation for this work is given as

$$\begin{aligned} \begin{aligned}&\int _{\varOmega } \varvec{\sigma ^T}(\varvec{u},\theta ,\varvec{r}_\gamma ):\varvec{\varepsilon }(v)~d\varOmega + \int _{\varOmega } \varvec{q}(\theta ,\varvec{r}_\gamma ):\nabla w~d\varOmega \\&\quad - \int _{\varOmega } \varvec{f} \cdot v~d\varOmega - \int _{\varGamma } \varvec{T} \cdot v~d\varGamma \\&\quad -\int _{\varOmega }\varvec{f_\theta } \cdot w~d\varOmega - \int _{\varGamma }\varvec{T_\theta } \cdot w~d\varGamma = 0 \\&\quad \forall v \in \mathcal {V},~\forall w \in \mathcal {W} \end{aligned} \end{aligned}$$

(29)

where $\varvec{\sigma _T}$ is the total stress induced by mechanical and thermal strains as in Eq. 3 and with all other symbols remaining as denoted in 6.1. Another test function, v is defined that belongs to the space of all admissible displacement functions $\mathcal {V}$. The formulation is referred to as weakly coupled because the temperature field is decoupled from the displacement field, however, the mechanical response depends on the temperature field due to the presence of thermal strains in the thermo-elastic constitutive relation as shown in Eq. 3. The objective functional for the thermo-structural problem of this work is given as

$$\begin{aligned} J_{\varvec{u}\theta d}\big (\varvec{u}(\theta (\varvec{r}_{\gamma })), \varvec{r}_{\gamma } \big ) = \int _{\varGamma } ||\varvec{u} - \varvec{u_D}||^2~d\varGamma \end{aligned}$$

(30)

where $\varvec{u_D}$ is a prescribed target displacement function.

6.3 Filtering of control variables

The direct implementation of the derived framework using low-order finite element discretization is prone to the checker-boarding instability (Bendsøe and Sigmund 2003; Lazarov and Sigmund 2011). It also yields mesh-dependent optimal solutions. Checker-boarding can be minimized by regularization or the use of higher-order finite elements with concomitant increase in computational cost. To eliminate checker-boarded solutions and to ensure mesh-independent optimal results, this work features the filtering of the stacked vector of radii parameters using a Helmholtz-type filter as described by Lazarov and Sigmund (2011). The idea of this filtering technique is to define the control variables at a particular node as a function of the variable field within a support neighborhood defined by a filter radius. The filter is defined implicitly as a solution to the Helmholtz PDE in its strong form as

$$\begin{aligned} -z^2\nabla ^2\varvec{\tilde{r}}_\gamma + \varvec{\tilde{r}}_\gamma = \varvec{r}_\gamma \end{aligned}$$

(31)

where $\varvec{r}_\gamma$ is the unfiltered stacked vector of radii parameters, $\varvec{\tilde{r}}_\gamma$ is the filtered stacked vector of radii parameters and z is the filter radius. Homogeneous Neumann boundary conditions are applied to the boundary of the domain of the structure so that

$$\begin{aligned} \dfrac{\partial \varvec{\tilde{r}}}{\partial \varvec{n}} = 0 \end{aligned}$$

(32)

where $\varvec{n}$ is the unit normal vector. The weak form of Eq. 31 is given as

$$\begin{aligned} \begin{aligned}&\int _{\varOmega } z^2\nabla \varvec{\tilde{r}}_\gamma : \nabla s~d\varOmega \\&\quad + \int _{\varOmega }\varvec{\tilde{r}}_\gamma \cdot s~d\varOmega - \int _{\varOmega }\varvec{r}_\gamma \cdot s~d\varOmega = 0 \qquad \forall s \in \mathcal {S} \end{aligned} \end{aligned}$$

(33)

where $\mathcal {S}$ is the space of all admissible control test functions, s. It should be noted that considerations must be made for design variable filtering order to maintain the correct evaluations of the volume constraint given by

$$V = V(\varvec{\tilde{r}})$$

(34)

The sensitivity of the volume fraction to the stacked vector of radii parameters as well as the sensitivity of the objective functionals of this work make considerations for the implementation of variable filtering as will be clearly demonstrated in Sect. 6.4.

6.4 Sensitivity analyses

The computational cost of evaluating the PDEs of this work motivate the implementation of a gradient-based optimization approach. It follows that the sensitivities of the objective functional to the stacked vector of control parameters, $\dfrac{dJ}{d\varvec{r_\gamma }}$ are to be determined in addition to the value of the objective functional, J so that gradient information is used in the search-direction computations. It is assumed that all derivatives exist and are sufficiently smooth.

Consider the objective functional of the general problem formulation of Eq. 23. Let M denote the dimension of the solution space and $L = 8N_n$ denote the dimension of the parameter space. The objective functional can be written as

$$\begin{aligned} J\big (\varvec{u}(\mathcal {P}(\varvec{\tilde{r}}_\gamma )),\mathcal {P}(\varvec{\tilde{r}}_\gamma ) \big ) \end{aligned}$$

(35)

since the solution of the PDE is dependent on the material properties controlled by the stacked vector of control parameters. Recall that the meta-models generated in Sect. 5 are explicit expressions of material property (structural and thermal) as functions of the stacked vector of control variables so that

$$\begin{aligned} \mathcal {P}(\varvec{\tilde{r}}_\gamma ) = {\left\{ \begin{array}{ll} E_{ij}(\varvec{\tilde{r}}_\gamma ), &{} \text {if elasticity matrix component} \\ K_{pq}(\varvec{\tilde{r}}_\gamma ), &{} \text {if conductivity matrix component} \end{array}\right. } \end{aligned}$$

(36)

where i, $j =$1, 2, ...6 and p, $q =$1, 2 and 3. The sensitivities of J are given as

$$\begin{aligned} \dfrac{dJ}{d\varvec{r}_\gamma } = \dfrac{dJ}{d\mathcal {P}}~\dfrac{d\mathcal {P}}{d\varvec{\tilde{r}}_\gamma }~\dfrac{d \varvec{\tilde{r}_\gamma }}{d \varvec{r}_\gamma } \end{aligned}$$

(37)

The first term of the r.h.s of Eq. 37, $\dfrac{dJ}{d\mathcal {P}}$ is determined by the adjoint method (Farrell et al. 2013). The second term, $\dfrac{d\mathcal {P}}{d \varvec{\tilde{r}}_\gamma }$ is the sensitivity of material property matrices, $(\varvec{E_{ij}}, \varvec{K_{pq}})$ to the filtered stacked vector of control parameters—available as explicit expressions. The sensitivity of the filtered stacked vector of control parameters to the stacked vector of control parameters, $\dfrac{d \varvec{\tilde{r}}_\gamma }{d \varvec{r}_\gamma }$ is a consequence of variable filtering.

The jacobian matrix (the matrix of constraint sensitivities to the unfiltered stacked vector of control parameters) is required for problems with a constraint on the availability of material. This is given as

$$\begin{aligned} \dfrac{dV}{d\varvec{r}_\gamma } = \dfrac{d\varvec{\tilde{r}}_\gamma }{d\varvec{r}_\gamma }~\dfrac{dV}{d\varvec{\tilde{r}}_\gamma } \end{aligned}$$

(38)

All sensitivities are rigorously verified by finite differencing so that the derivative of the objective functional with respect to the i-th component of the stacked vector of control variables is given as

$$\begin{aligned} \dfrac{dJ}{dr_i} = \underset{h \rightarrow 0}{\text {lim}}~ \dfrac{J(\varvec{r}_\gamma + h\xi _i) - J(\varvec{r}_\gamma )}{h} \end{aligned}$$

(39)

where the perturbation is $h = 0.0001$ and $\xi _i$ is the vector of zeros of the same length as $\varvec{r}_\gamma$ with 1 in the i-th entry.

With the ability to evaluate objective functionals constrained by partial differential equations as well as capability for an efficient evaluation of objective functional sensitivities, large-scale optimization was executed in the space of the small-scale design variables. Adjoint sensitivities were obtained using dolfin-adjoint (Farrell et al. 2013). Dolfin-adjoint is a Python library in FEniCS (Logg et al. 2012; Alnæs et al. 2015), the open source finite element solver implemented for the large-scale optimization algorithms of this work.

6.5 Computational implementation of macroscale optimization

Fig. 7

Macroscale optimization loop showing how next design iteration is derived towards attaining optimal design

In its discretized form, Eq. 23 was solved with a robust gradient-based numerical optimizer based on an interior point algorithm, Ipopt Wächter and Biegler (2006). Ipopt is an open source software package for large-scale non-linear optimization. To implement Ipopt within FEniCS, a python connector, PyIpopt was used. PyIpopt uses the definition of the optimization start point from the domain initialization, objective functional evaluation, gradient evaluation, constraint evaluation (if required) and jacobian evaluation (if required) to derive the next design iteration (See Fig. 7). It is important to note that derivatives of the objective and constraint are with respect to the unfiltered stack of control variables. However, the forward solve and global volume fraction are evaluated with the filtered stacked vector of control variables. On an Intel(R) Core(TM) i7-5600U CPU @ 2.60 GHz system with 2 processors, a typical thermal simulation takes approximately 16 hours for 120,000 dofs. A similarly sized thermo-structural problem takes approximately 22 hours. For micro-analyses, it took approximately 5.3 minutes to determine the elasticity matrix (1.8 min to determine the conductivity matrix) of any given microstructure with a single processor. However, by parallelizing the six deformation analyses (or three thermal analyses), the duration for the homogenization process to determine elastic and thermal properties was reduced to approximately 2 minutes and 30 seconds per micro-architecture for deformation and thermal analyses, respectively. The response surface models are evaluated in 0.001 seconds at every dof. It becomes easy to appreciate the efficiency in evaluating material point properties with the response surface models for a 120,000-dof problem over several optimization iterations. The large-scale optimization is terminated when an iterate satisfies the conditions of a firstorder Karush–Kuhn–Tucker (KKT) point, indicating that the solution at the current point is a strict local minimizer of the constrained optimization problem or by a limit on the maximum number of optimization iterations.

7 Results and discussion

Table 3 CHS: Problem definition

In this section, the robustness of the derived optimization framework is investigated by its application to large-scale thermal and thermo-structural optimization problems followed by a discussion of the results obtained. For each sample case, a description of the initial design dimension with thermal loads and boundary constraints is given. The results for each case comprises figures showing the volume fraction distribution within the design domain, the optimal radii distribution for each component of the vector of radii parameters within the design domain as well as a convergence plot of the objective functional through the optimization iterations. The coordinates of large-scale optimization domain coincide with those of the micro-architecture of Fig. 3. This work demonstrates extended capabilities of the framework. The first test case demonstrates that the framework outperforms an equivalent SIMP formulation of a thermal problem that minimizes thermal compliance given a constraint on available material. A second test case features thermo-structural optimization in the space of lattice parameters, yielding a solution beyond the capabilities of optimization strategies based on isotropic material models.

7.1 Case 1: Cylindrical Heat Sink

Fig. 8

CHS: Problem definition

Fig. 9

Cylindrical Heat Sink: non-design region definition

Fig. 10

Cylindrical Heat Sink: temperature, $\theta$ (K) at Iteration 1

Fig. 11

Cylindrical Heat Sink: optimal radii distribution for diagonal members 1–4

Consider the Cylindrical Heat Sink (CHS) with thermal and geometric properties specified in the problem definition of Fig. 8 and Table 3. The design region generates an internal heat source, $F_\theta$ and a heat sink is defined at the internal surface of the hollow cylinder. A non-design region is specified about the internal radius as shown in Fig. 9. The temperature profile of the CHS is shown for the thermal properties specified at the beginning of the optimization search in Fig. 10. The goal of the optimization formulation is to determine the optimal layout of material that minimizes the average temperature (thermal compliance) of the cylinder based on the lattice and SIMP frameworks. This optimization problem is constrained by the PDE that governs steady-state pure heat conduction phenomenon given by Eq. 26. It is also subject to a constraint on the availability of base material such that the volume fraction of the optimized design, $V_D = 0.37$. Bound constraints on the components of the stacked vector of control variables confine the optimization search to the space of precomputed thermal properties. The optimal distribution of radii parameters at termination of the search are displayed in Figs. 11 and 12 for the diagonal and face members, respectively. The solid regions in the solutions depict $r_{i\gamma } \ge 0.25$.

Fig. 12

Cylindrical Heat Sink: optimal radii distribution for face members 5–7

Fig. 13

Cylindrical Heat Sink: section X–X showing temperature evolution through iterations

Fig. 14

Cylindrical Heat Sink: lattice reconstruction

Fig. 15

Cylindrical Heat Sink: lattice-based material distribution and optimization convergence plot

Fig. 16

Cylindrical Heat Sink: SIMP material distribution and optimization convergence plot

It can be observed that radii distributions of Member 1 and 3 (Figs. 11a, 11c) are similar by virtue of their orientation. Similarly, Members 2 and 4 (Figs. 11b, 11d) share similar radii distributions. Member 5 (Fig. 12a) does not contribute significantly to the minimization of objective function since its orientation is co-linear with the centroidal axis. Members with orientations that facilitate the transfer of heat flux from the cylinder body to the heat sink are those to which average temperature is most sensitive and hence the most dominant. Members 6 and 7 (Figs. 12b, 12c) have symmetric distributions differing only based on their respective orientations. The pseudo-lattice-density function (Fig. 12d), describing the macroscale lattice density distribution indicates that lattice is present in most of the design domain. The regions of no-lattice only exist at the radial extremities of the cylinder, where the magnitudes of the radii are mostly at the lower bound. The volume fraction distribution of Fig. 15a shows that, macroscopically, the layout of material corresponding to the radii distributions forms structured projections that link the design region to the sink, with increasing radii magnitude as the radial distance to the sink decreases. Lower member radii values at radial extremities increase the surface area of the members so as to increase the efficiency of heat conduction. The SIMP implementation for the same problem yields the material layout shown in Fig. 16a with finger-like projections branching out into the heat-generating design domain.

The SIMP methodology yields a thermal compliance of 5.34 WK at optimization convergence. The thermal compliance, $J_{\theta c}$ attained at termination for the lattice-based approach is 0.062 WK which corresponds to a further 98.8% reduction in optimal thermal compliance. The optimization convergence plots are shown in Figs. 15b and 16b for the lattice-based and SIMP-based implementations, respectively. It is of note to appreciate the significant improvement enabled by the lattice-based framework in the final objective function. Figure 13 shows the evolution of the temperature distribution against the optimization iterations at a through section X–X of the CHS. Figure 14 shows the lattice reconstruction derived given radii distributions. The reconstruction is based on a marching cubes algorithm that converts volume data generated from radii distribution data to lattice surface mesh (Lewiner et al. 2003; Murphy et al. 2020).

7.2 Case 2: Hollow-pipe section

Table 4 Hollow-pipe section: problem definition

This test case minimizes the structural deformation of specific boundary surfaces of a restricted design domain as the structure expands under thermal load. It demonstrates the multiscale framework’s capability to the class of weakly coupled thermo-structural optimization problems.

Fig. 17

Hollow-pipe section: problem definition

Fig. 18

Hollow-pipe section: non-design region definition

Fig. 19

Hollow-pipe section: temperature, $\theta$ (K) on deformed mesh at Iteration 1

Fig. 20

GE Bracket: optimal radii distribution for diagonal members 1–4

Fig. 21

GE Bracket: optimal radii distribution for face members 5–7

Consider a $25~\hbox {mm}$-section of a square hollow pipe with material properties and Dirichlet boundary conditions specified in the problem definition of Fig. 17 and Table 4. Given the displacement and temperature boundary conditions as shown, the steady-state temperature profile is projected unto the deformed domain mesh according to the displacement distribution—a consequence of the thermo-structural coupling as introduced in Sect. 6.2 (see Fig. 19). Observe that due to the Dirichlet boundary conditions imposed on the near and far-side surfaces, the bottom and top surfaces, $S_1$ and $S_2$ bulge out of the x–z plane as the structure expands under thermal load. The goal of the optimization is to minimize the normal deformation of the target surfaces, $S_1$ and $S_2$. It is assumed that the non-displacement of these surfaces in the y-axis is critical to the optimal design of this section of the pipe and indeed the entire pipe length (not shown). A non-design region surrounds the hollow as shown in Fig. 18.

Fig. 22

Hollow-pipe section: temperature profile (Deformation Scale: 50:1)

Fig. 23

Hollow-pipe section: volume fraction distribution (Deformation Scale: 50:1)

Fig. 24

Hollow-pipe section: lattice reconstruction

Fig. 25

Hollow-pipe section: lattice-based material distribution and optimization convergence plot

The error functional is evaluated as the squared difference between the y-component of the displacement distribution of the target surfaces, $u_y$ and the y-component of a zero-displacement distribution within the domain of the pipe section. Bound constraints have been imposed on the stacked vector of control variables to confine the search within the precomputed mechanical and thermal property spaces. Static equilibrium mechanics as well as pure conduction steady-state phenomenon govern the thermo-structural response of the section. Since there is no constraint on the availability of material, there exists no penalized pseudo-lattice-density function for this problem so that lattice structure exists everywhere within the design domain between the bounds specified in Table 4. The emphasis is on the design of local structure within the macroscale towards satisfying the macroscale objective. The optimal distribution of radii parameters at termination of the search are displayed in Figs. 20 and 21 for the diagonal and face members, respectively. The solid regions in the solutions depict $r_{i \gamma } \ge 0.28$. The pale blue regions depict regions where $r_{min} \le r_{i \gamma } < 0.28$.

The diagonal members demonstrate symmetries by virtue of their orientation as shown by Fig. 20. They also exhibit more dominance than the face members as they yield micro-architectures with properties suited to meeting the macroscale objective. Members 1 and 4 (Figs. 20a, 20d) conduct heat flux towards the bottom-half near-side heat sink as well as the top-half far-side heat sink. Members 2 and 3 (Figs. 20b, 20c) serve a similar purpose but are oriented to conduct heat flux towards the bottom-half far-side heat sink and top-half near-side heat sink. Diagonal members feature off-diagonal components in their conductivity matrices that essentially equips micro-architectures to transfer heat flux in orthonormal directions to temperature gradient. The consequence of this radii distributions can be appreciated in the steady-state temperature distributions of Fig. 22 where the steady-state temperature profile within the design domain is altered with the radii distributions such that the predefined non-displacement objective function is satisfied. The resulting orthotropic lattice micro-architectures offer increased macroscale conductivity towards the heat sink but also feature diagonals that can expand in non-critical directions.

The face members feature much lower radii values as shown in Fig. 21 within the design domain. Member 5 (Fig. 21a) is oriented to conduct heat towards the heat sink but cannot expand under thermal load due to the Dirichlet boundary conditions. Member 6 (Fig. 21b) works against the non-displacement objective, conducting heat flux towards the target surfaces and expanding in the y-direction. Member 7 (Fig. 21c) does not improve conductivity towards the heat sink. The displacement of the target surfaces is also insensitive to the thermal expansion of Member 7. Figure 23 shows the volume fraction distribution at the starting point and the final iteration projected unto a deformed domain. An optimization convergence plot for the problem is shown in Fig. 25b.

This capability exhibited by the orthotropic micro-architectures with diagonals to enhance macroscale conductivity in orthonormal directions to the temperature gradient is key to achieving the prescribed macroscale objective of this problem. This capability cannot be attained by optimization strategies that rely on isotropic material interpolation. Figure 24 shows the lattice reconstruction derived given radii distributions.

8 Conclusion

A robust multiscale framework was derived for the thermal and thermo-structural optimization of printable structures using lattice-based micro-architectures. Structured according to HMM, the framework was derived over two computational phases—a precomputation phase which featured the development of a lattice-based microscale model suited to additive manufacturing constraints and an optimization phase which executed thermal and thermo-structural tailoring of properties in the space of lattice micro-parameters. By exploiting the homogenization theory, structural and thermal properties were derived given microscale lattice geometry parameters so that the properties represented material point properties within a large-scale design domain. The space of material properties covered by the lattice parameterization was populated by a full-factorial design of experiments at only 5% of the computational cost of evaluating the entire full-factorial DoE—facilitated by micro-architecture symmetry considerations. Material property response surface models were generated so that microscale material properties were efficiently integrated into the macroscale optimization framework. By the method of adjoints, sensitivities of prescribed objectives to the lattice micro-architecture parameters were determined, facilitated by the readily differentiable explicit material response surfaces and the chain rule of differentiation. The outcome was the development of free material optimization executed in the space of physically realizable architected material properties. This paper demonstrates the capacity of the framework for thermal and thermo-structural optimization through typical problem cases. Both cases yielded solutions of superior optimality. The lattice-based framework of the first case yielded a 98.8% further reduction in thermal compliance compared to the SIMP-based framework. The second case demonstrates that the framework is capable of full control over local anisotropy—a capability unachievable by optimization strategies based on isotropic material model. The derived solutions are also physically realizable through a process of lattice reconstruction given the optimal distribution of radii parameters. The precision and flexibility of additive manufacturing techniques have inspired the development of the framework and the realization of its optimal solutions.

The derived framework has its limitations. By definition, the theory of homogenization assumes an infinite separation of scales so that the micro-architectures represent material point properties within the macroscale design domain. This work aims for an ‘as-large-as-possible’ separation of scales, however, computational and manufacturing constraints prevent the physical realization of an infinite scale separation. Consequently, the material response of our reconstructed lattice is only an approximation of the numerically computed response. The associated error with this approximation has not been determined in this work since direct numerical simulations on the reconstructed lattice proved an arduous task due to unmanageable mesh sizes. Indeed, such an endeavor has proven computationally intractable - the very challenge this framework circumvents by constructing response models. Experimental validation is currently underway as a viable alternative approach, the results of which will be published in future works. The framework also makes no considerations for local stress constraints which occur at the intersection of the lattice struts (Imediegwu 2020).

Inspired by the limitations of this work and significant advancements in additive manufacturing, the capability of the derived framework should include local stress considerations. Provided local stress data from the microscale deformation analyses is captured, local stress response models can be generated to facilitate the derivation of stress-constrained optimal solutions. This is the subject of current research (Thillaithevan et al. 2021). The principles of heterogeneous multiscale methods can be extended to acoustic, electro-magnetics as well as tailoring of structural properties to predefined resonant frequencies. Extending the methodology to non-linear elastic problems and fully coupled thermo-mechanical formulations has the potential to yield interesting solutions.