1 Introduction

Topology optimization (TO) has gained increasing popularity since the first article by Bendsoe and Kikuchi (1988) and the research is constantly evolving (Deaton and Grandhi 2014). A commonly studied formulation when designing load-carrying structures using TO is to minimize the compliance of the structure subject to a volume restriction. This usually gives a structure which resembles a statically determinate structure with no redundant parts. This implies that if one of the structural members was to break, by for example a brittle failure in the material due to a sudden impact or by an explosion or a similar occurrence, there would not exist any alternative load-paths, and the structure would experience a catastrophic failure. In for example aerospace applications, this is highly unwanted, and a so-called fail-safe design with redundancy in terms of load-paths is required.

According to Niu (1998, 1997), fail-safe can be defined as:

  • A fail-safe structure must support 80–100% limit loads without catastrophic failure.

  • A fail-safe structure must support a single member failed in a redundant structure or partial failure in a monolithic structure.

The present article focuses on the second criteria (for work on the first criteria, see, e.g. Wang et al. (2020)). To satisfy this criteria implies there must exist additional load-paths when one structural member is completely removed or partially damaged. For an a priori discrete structure such as a truss or frame this results in a rather simple design problem—in principle one could simply remove one member at a time and minimize the maximum compliance (see Stolpe (2019) for a practical implementation of this idea). Formulation of the design problem for continuum structures is however not as straightforward. If one were to look at the structure, it would be possible to distinguish a structural member and then say where a damage patch would do a lot of damage, but of course this is not possible if it is going to be implemented into a completely automatic optimization algorithm.

The first article published on fail-safe TO for continua is written by Jansen et al. (2014). In this article, a grid of fixed rectangular damage patches covers the design domain. The optimization problem is then written as a minimization of the compliance under the worst damage, i.e. the damage which gives the maximum compliance. To find the worst damage, all damage patches had to be tested, and since the number of patches is in the range of the number of finite elements the problem becomes very computationally demanding.

To reduce the number of damage patches, Jansen et al. (2014) tried to only include patches which contained material and another approach where only patches which had a non-monotonic density variation were considered. Zhou and Fleury (2016) tried to further decrease the number of patches by having two sets of damage populations in which they increased the number of damage zones until more patches would not do much difference. This was measured by looking at the so-called minimum hideout volume of the added patches.

Ambrozkiewicz and Kriegesmann (2018) examined how well the algorithm by Zhou and Fleury (2016) performed and found that it was sensitive to damage zones which weren’t included in the optimization. They also proposed their own method where they used the stress-state in the structure to divide the structure into knots and beams and each knot and beam was then removed one at at time to simulate a damage to that particular place. This method diverges a bit from the rectangular damage zones seen in previous work.

There are also some research where the fail-safe criterion is formulated in a more implicit way (Wu et al. 2018; Dou 2019). These methods do not include a damage formulation but instead uses local volume constraints which makes the structure get more members and thus increase the redundancy and consequently the damage tolerance. But since fail-safe is not explicitly included the structure has to be tested after optimization.

The most recent article on fail-safe TO is Ambrozkiewicz and Kriegesmann (2020) where the authors first used a local volume method of the type mentioned in the preceding paragraph to get a first draft of a redundant structure and then they used their previous research to divide the structure into knots and beams. The optimization then comes to the second stage where a density-based shape optimization was performed to get the final design. To divide the structure into knots and beams in 2D, the stress-state was examined. This was not possible in 3D with multiple load-cases and thus a visualisation tool was used. The knot and beam formulation is close to that of an MMC but they used it in a different way.

In this article we propose a method to obtain fail-safe designs by using so-called moving morphable components (MMCs) (Guo et al. 2014) to model damage in the structure while using density-based TO to obtain an optimized material layout of the structure. Damage is inflicted on the structure by an MMC which removes material, and the goal of the design problem is to minimize the compliance for the worst possible damage. The worst damage for a given design is sought by optimizing the position of the MMC to maximize the compliance. The smooth but non-convex problem of finding the worst damage is treated using a gradient-based solver by initializing the MMC at multiple locations and taking the maximum of the compliances obtained. This heuristic method does not guarantee that the worst damage is actually found of course, but the numerical results indicate that the method works well in practise.

An advantage of proposed method compared to existing methods for fail-safe design cited above is finite element (FE) mesh independency in the sense that the only connection an MMC has to the mesh is when the MMC is projected onto the FE-mesh for density and gradient calculations. The position of an MMC is thus not bound to the FE-mesh but can move around freely using an optimization solver to find a position where it does the most damage. As will be seen in the numerical examples below, compared to a strategy with fixed damage patches such as in Jansen et al. (2014), the moving patches used herein give more robust structures.

Finally, one issue found in the reviewed literature was that there was very little verification that the structures obtained actually were fail-safe. In the present work, so-called damage maps are used just to show that the optimized structures actually are fail-safe.

2 Background theory

To get an understanding of how the proposed method works, a short explanation of both density-based TO and MMC TO is provided.

2.1 Density-based topology optimization

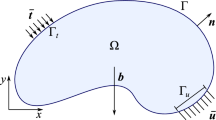
The basic problem considered in this article is to maximize stiffness under a volume constraint. The design is described by a (relative) density function, approximated as element-wise constant and taking values between 0 (no material) and 1 (material). The elemental values ρe are collected in a vector \(\boldsymbol {\rho } \in \mathbb {R}^{m}\), where m is the number of FEs. The Solid Isotropic Material with P+enalization (SIMP) scheme is used to obtain close to binary-valued designs (Christensen and Klarbring 2008; Rietz 2001).

The mathematical formulation of the (FE-discretized) optimization problem is

$$ \begin{cases} \underset{\boldsymbol{\rho}}{\min}\ C(\boldsymbol{\rho})= \boldsymbol{F}^{T}\boldsymbol{U}(\boldsymbol{\rho})\\ \text{s.t.} \begin{cases} V(\boldsymbol{\rho})\leq \alpha V_{0}\\ 0\leq \rho_{e} \leq 1, e=1,\ldots,m, \end{cases} \end{cases} $$

where U(ρ) solves the equilibrium equation K(ρ)U = F, in which K(ρ) is the stiffness matrix, and F is the load-vector. Furthermore, V0 is the volume of the design domain Ω, V (ρ) is the volume of the structure and α is the fraction of volume that the optimized structure is allowed to occupy.

2.1.1 Filtering

To avoid FE mesh dependency and checkerboards for low order FEs (Sigmund and Petersson 1998), a linear filter (Bourdin 2001) is applied to the design variables, giving a filtered design

$$ \tilde{\rho}_{e}=\frac{1}{\sum\limits_{i=1}^{m}Z_{ei}}\sum\limits_{i=1}^{m}Z_{ei}\rho_{i}, \quad e=1,\ldots,m, $$

where \(Z_{ei}=\max \limits (0,R-{{\varDelta }}(e,i))\) is a weight function which smooths the design. Here R is the filter radius and Δ(e,i) the Euclidean distance between the centroid of elements e and i.

2.1.2 Projection for 0/1-designs

When applying a filter, the design becomes gray (intermediate densities) at the boundary of the structure. To instead get a 0/1 boundary without intermediate densities, a so-called projection-filter is often used. Ideally, the Heaviside-function (defined by H(x) = 0 for x < 0 and H(x) = 1 for x ≥ 0) should be used. The discontinuity of this function may however cause problems for gradient-based solvers. To circumvent this, a regularized version of the Heaviside-function (Wang et al. 2011) is used to get the projected density

$$ \bar{\rho}_{e}(\tilde{\rho}_{e}) = \frac{\tanh{(\psi \eta)} +\tanh{(\psi(\tilde{\rho}_{e}- \eta))} }{\tanh{(\psi \eta)}+\tanh{(\psi(1- \eta))} }, $$
(1)

where ψ determines the sharpness of the step. A higher ψ will result in a sharper step but also a more unstable optimization process. Usually, a continuation scheme is used where ψ is gradually increased during the optimization.

A useful feature of the projection is that different values of η can be used for the objective function and the volume constraint. This is used in the present work due to convergence issues seen if the same value for η was used for both objective function and volume constraint. This procedure is known as a robust formulation (Wang et al. 2011) and is used by Jansen et al. (2014). The so-called nominal density \(\bar {\rho }^{(n)}_{e}(\tilde {\rho }_{e})\) is obtained by putting η = 0.5 and the eroded density \(\bar {\rho }^{(e)}_{e}(\tilde {\rho }_{e})\) is obtained by putting η = 0.7. By using the robust formulation, the design becomes more robust to slight changes in the material distribution and thin members vanishes. The densities to be plotted in the following are nominal densities.

2.1.3 The stiffness matrix

Finally, the eroded density is used with a material interpolation scheme to get the stiffness matrix for the structure. Young’s modulus for each element is written as

$$ E_{e}(\rho_{e}) = E_{min}+(E_{0}-E_{min}){(\bar{\rho}^{(e)}_{e})}^{q_{1}}, $$
(2)

where q1 > 1 is the SIMP penalization exponent, E0 is the nominal stiffness of the solid phase, and Emin > 0 is the stiffness of the void phase needed to ensure a non-singular stiffness matrix. The global stiffness matrix is then

$$ \mathbf{K}(\boldsymbol{\rho}) = \sum\limits_{e=1}^{m}E_{e}(\rho_{e})\mathbf{k}_{e}^{0}, $$

where \(\mathbf {k}_{e}^{0}\) is the stiffness of an element with unit Young’s modulus.

2.2 Moving Morphable components

Topology optimization with MMCs is an alternative to the density-based approach which was introduced by Guo et al. (2014) and Zhang et al. (2016).

2.2.1 The mathematical description of a component

In this work, we consider components described by level-set functions of the form

$$ \phi(\boldsymbol{x})=1-\left( \frac{x^{\prime}}{L} \right)^{p_{\phi}}-\left( \frac{y^{\prime}}{f(x^{\prime})} \right)^{p_{\phi}}, $$
(3)

where L is the length of the component, \(f(x^{\prime })\) is a function describing the thickness, and pϕ is a relatively large, even integer. A component with the associated design variables can be seen in Fig. 1. The relation between global xy- and local \(x^{\prime } y^{\prime }\)-coordinates is expressed as

$$ \left\{\begin{array}{ll} x^{\prime}\\ y^{\prime} \end{array}\right\}=\begin{bmatrix} \cos\theta & \sin\theta\\ -\sin\theta & \cos\theta \end{bmatrix} \left\{\begin{array}{ll} x-x_{c}\\ y-y_{c} \end{array}\right\}, $$
(4)

in which xc and yc are the components of the centroid xc. The function f(x) can be defined in different ways depending on what design variables one wants to use. For a quadratically changing width, the function can be written as

$$ f(x^{\prime}) =\frac{t_{1}+t_{2}-2t_{3}}{2L^{2}}(x^{\prime})^{2}+\frac{t_{2}-t_{1}}{2L}x^{\prime}+t_{3}, $$

where the parameters t1, t2, and t3 are defined in Fig. 1.

Fig. 1
figure 1

A moving morphable component together with its design variables

Full size image

If the level-set function is greater than 0 at a point x, then that indicates that the component exists at that position and thus that the elements covered by the component should contain material. If the function is equal to 0, then that defines the boundary of the component and if the function is less than 0, then that means the component is not present at that position and should not contribute with any material. In a more mathematical way, this is written as

$$ \begin{cases} \phi(\boldsymbol{x})>0, & \text{if} \ \boldsymbol{x} \in {{\varOmega}}_{c}\\ \phi(\boldsymbol{x})=0, & \text{if} \ \boldsymbol{x} \in \partial{{\varOmega}}_{c}\\ \phi(\boldsymbol{x})<0, & \text{if} \ \boldsymbol{x} \in {{\varOmega}} \setminus {{\varOmega}}_{c}\\ \end{cases} $$

where Ωc and ∂Ωc are the domain of the component and its boundary, respectively.

Multiple, potentially overlapping components can be combined using the \(\max \limits \)-function to a single function \(\phi ^{s}(\boldsymbol {x})=\max \limits \{\phi _{1}(\boldsymbol {x}),\ldots ,\phi _{n}(\boldsymbol {x})\}\) defining the resulting structure.

2.2.2 The Ersatz material model

To move from a level-set function ϕ to a corresponding (element-wise constant) density distribution ρ, a cheap method is to use the ersatz material model (Guo et al. 2014; Zhang et al. 2016) in which the density of an element e is given by

$$ \rho_{e,MMC}=\frac{{\sum}_{j=1}^{n_{n}} (\widetilde{H}(\phi^{s}(\boldsymbol{x}_{j}))^{q_{2}} }{n_{n}}, $$
(5)

where nn is the number of sampling points xj and \(\tilde {H}\) is a smooth approximation of the Heaviside function specified in Section 3 below. The parameter q2 is used to get a sharper boundary of the structure (Coniglio et al. 2019). Formula (5) is then used in the same manner as in (2), so that the effective Young’s modulus becomes

$$ E_{e,MMC} = E_{min}+(E_{0}-E_{min})\rho_{e,MMC}. $$

2.2.3 Example of MMC TO

To get a better understanding how TO with MMCs actually works we consider and example of optimization of a cantilever beam whose left end is fixed and whose right end is subject to a vertical load. In Fig. 2 (top) one can see the initial configuration of all the 24 MMCs that define the design. The black contour lines indicate ϕ = 0, the green regions are where ϕ > 0, and the white regions are where ϕ < 0 as explained previously. In Fig. 2 (bottom), one can see the final design. In Fig. 3, one can then see how these components are projected onto an (180 × 60) FE-mesh through the Heaviside function.

Fig. 2
figure 2

Initial (top) and final configuration (bottom) of the MMCs

Full size image
Fig. 3
figure 3

Density distribution obtained by projection of the components in the final design in Fig. 2

Full size image

3 Topology optimization for fail-safe designs

We now combine density-based TO with the MMC formulation to obtain fail-safe designs. This is done in the form of a minmax formulation where instead of adding material, one or more MMCs now remove material to model damage on the structure. The goal of the inner maximization problem is thus to find the position, given by the centroid xc, of an MMC that causes the most damage to the structure. The shape of the MMC is taken as a square with rounded corner, more precisely a squircle (sic), but other shapes could of course also be considered (see sections 5.3 and 5.4 below). An example of an optimized, damaged structure can be seen in Fig. 4 (top).

Fig. 4
figure 4

Top: a damage patch located near the lower left corner of the design domain. Bottom: depending on the starting position (dashed lines) a damage patch may end up in different positions

Full size image

Mathematically, the problem of minimizing the worst compliance now reads:

$$ \begin{cases} \underset{\mathbf{\boldsymbol{\rho}}}{\min} \ \underset{\boldsymbol{x}_{c}}{\max}\ \boldsymbol{F}^{T}\mathbf{U}(\boldsymbol{\rho},\boldsymbol{x}_{c}) \\ s.t \ \begin{cases} V(\boldsymbol{\rho}) \leq \alpha V_{0} \\ 0 \leq \rho_{e} \leq 1, \ e=1,\ldots,m\\ \end {cases} \end{cases} $$
(6)

where U(ρ,xc) solves the equilibrium equation

$$ \boldsymbol{K}(\boldsymbol{\rho},\boldsymbol{x}_{c})\boldsymbol{U} = \boldsymbol{F}. $$

Note that no bounds are needed for xc since the worst damage is always obtained for a patch overlapping the design domain. Given a bounded design domain, the optimal centroid is thus confined to a compact set, meaning that the inner problem is well-posed since the objective is continuous in xc.

The non-convexity of the inner maximization problem in (6) is illustrated in Fig. 4 (bottom), where the dotted squares are the initial positions of two different damage patches and the solid squares are the final positions of the damage when optimizing the position. It is thus seen that even if the starting positions of two damage patches are close to each other they do not necessarily end up at the same end position.

While implementing the algorithm it was found that due to the non-convexity of the inner problem, more than one damage patch was needed to make sure that the worst damage was found. (Since we only consider one damage patch at the time however, an alternative point-of-view is that we have one damage patch which is initialized at many different locations. Implementation-wise we get the same problem formulation however.) The objective will therefore be to mitigate the damage from the worst positioned damage obtained for any one of nd damage patches. Introducing the sets \(\mathcal {X}_{i} = \{ \boldsymbol {x}_{ci} | \ \underline {\boldsymbol {x}}_{ci} \leq \boldsymbol {x}_{ci} \leq \overline {\boldsymbol {x}}_{ci} \} \), i = 1,…,nd, the optimization problem is written as:

$$ \begin{cases} \underset{\mathbf{\boldsymbol{\rho}}}{\min} \underset{i=1,\ldots,n_{d}}{\max} \underset{\boldsymbol{x}_{ci} \in \mathcal{X}_{i}}{\max}\ \boldsymbol{F}^{T}\mathbf{U}(\boldsymbol{\rho},\boldsymbol{x}_{ci}) \\ \text{s.t} \ \begin{cases} V(\boldsymbol{\rho})\leq \alpha V_{0}\\ 0 \leq \rho_{e} \leq 1, \ \forall e=1,\ldots,m\\ \end {cases} \end{cases} $$
(7)

The box constraints in the sets \(\mathcal {X}_{i}\) are introduced to make sure that the entire design domain is searched without the patches getting stuck in positions where they do not cause much damage.

3.1 Inner problem

The innermost problem in (7) is to maximize the compliance by moving the i th MMC over a given design ρ. The MMC could be quite complicated as described in (3), but to be able to compare the current algorithm to previous algorithms from the literature a simpler function is used, namely

$$ \phi_{i}(\boldsymbol{x}; \boldsymbol{x}_{ci}) = 1 - \left( \frac{x-x_{ci}}{L}\right)^{p_{\phi}} - \left( \frac{y-y_{ci}}{L}\right)^{p_{\phi}}, $$
(8)

whose zero level set is a (super-ellipse based) squircle. If pϕ is set to 2 a circle is obtained and the higher pϕ used, the sharper the edges on the MMC. For this study, a value of 6 was chosen which yields a square component with rounded corners.

The function ϕi in (8) is then put through a regularized Heaviside function and sampled to get a corresponding density distribution as described in Section 2.2.2. The regularized Heaviside function used in this article is defined as

$$ \widetilde{H}(x) = \frac{1}{2}\big(1+\tanh{(\beta x)}\big), $$
(9)

where β > 0 controls the steepness of the (smooth) step. The stiffness of the structure will now depend on the MMC damage as well as the (eroded) density-distribution ρ̄e = ρ̄e(ρe ~(ρ)) from (1), where the density variable adds material and the MMC removes material. This gives the effective Young’s modulus

$$ \begin{array}{@{}rcl@{}} \widetilde{E}_{e}(\boldsymbol{\rho},\boldsymbol{x}_{c_{i}})&=& E_{min}+ \\ &&(E_{0}-E_{min})\bar{\rho}_{e}^{q_{1}}\left( 1- \frac{{\sum}_{s=1}^{n_{n}} (\widetilde{H}(\phi(\boldsymbol{x}_{s}; \boldsymbol{x}_{ci})))^{q_{2}}}{n_{n}}\right), \end{array} $$
(10)

and thus the stiffness matrix

$$ \boldsymbol{K}(\boldsymbol{\rho},\boldsymbol{x}_{ci})={\sum}_{e=1}^{m}\widetilde{E}_{e}(\boldsymbol{\rho},\boldsymbol{x}_{ci})\boldsymbol{k}_{e}^{0}. $$

3.1.1 Sensitivity analysis

To use a gradient-based algorithm to solve the inner-most problem in (7), the gradient of the compliance \(C_{i} = \boldsymbol {F}^{T}\boldsymbol {U}(\boldsymbol {\rho },\boldsymbol {x}_{ci})\) with respect to the centroid is needed. The only constraints are the box constraints on the centroid and no derivative is needed of these. Differentiating the compliance with respect to the position of the damage-patch using the adjoint method (Christensen and Klarbring 2008), we get

$$ \frac{\partial C_{i}}{\partial x_{c}} = -\boldsymbol{U}(\boldsymbol{\rho},\boldsymbol{x}_{ci})^{T}\frac{\partial \boldsymbol{K}(\boldsymbol{\rho},\boldsymbol{x}_{ci})}{x_{c}}\boldsymbol{U}(\boldsymbol{\rho},\boldsymbol{x}_{ci}), $$

where

$$ \frac{\partial \boldsymbol{K}(\boldsymbol{\rho},\boldsymbol{x}_{ci})}{\partial x_{c}} = \sum\limits_{e=1}^{m}\frac{\partial \widetilde{E}_{e}(\boldsymbol{\rho},\boldsymbol{x}_{ci})}{\partial x_{c}}\boldsymbol{k}_{e}^{0}. $$

The derivative of the regularized Heaviside function from (9) is

$$ \frac{\partial\widetilde{H}}{\partial x_{c}}=\frac{1}{2}\big(1-\tanh^{2}(\beta \phi(\boldsymbol{x}_{s};\boldsymbol{x}_{ci}))\big)\beta\frac{\partial\phi}{\partial x_{c}}, $$

and finally, the derivative of the level-set function from (8) is

$$ \frac{\partial\phi}{\partial x_{c}}= \frac{p_{\phi}}{L}\left( \frac{x^{\prime}}{L}\right)^{p_{\phi}-1} $$

The derivative with respect to yc is obtained analogously.

3.1.2 Extra sampling points

Using too few sampling points in (10) can cause difficulties. For example, a common choice is to use only the FE nodes as sampling points. This can give a good representation of the component itself but not of the derivative with respect to the centroid which is non-zero only in a narrow region at the boundary of the component. To illustrate this, Fig. 5 shows how a component centred at x = 0.5 would look in 1D with a coarse 40-element grid (red), a coarse grid with 3 extra points per element (blue) and how the regularized Heaviside function would actually look (green). As one can see, there is not much difference between extra nodes and no extra nodes. In the bottom plot in Fig. 5; however, the derivative of the component is shown, and here some issues can be seen: the derivative on the coarse grid (red) is almost flat while the derivative with extra nodes (blue) is closer to the actual derivative (green) although averaged over the entire element. Worth noting is that the function is differentiated with respect to xc and not x and thus the derivative is negative on the left side and positive on the right side since material is added on the right side and removed on the left side if the component moves to the right.

Fig. 5
figure 5

Left: the Heaviside function and the sampled Heaviside function in a coarse mesh and a coarse mesh with extra points. Right: the derivative of the component

Full size image

To avoid problems with vanishing derivatives, we use nn = 16 sampling points in our numerical examples. Note that increasing the number of sampling points has negligible effect on the computational time which is dominated by solving the equilibrium equation.

3.2 Outer problem

The outer problem in (7) consists of finding a design which minimizes the worst compliance obtained for any of the damage patches, i.e.

$$ C(\boldsymbol{\rho}) = \underset{i=1,\ldots,n_{d}}{\max} C_{i}(\boldsymbol{\rho})=\boldsymbol{F}^{T}\boldsymbol{U}(\boldsymbol{\rho},\boldsymbol{x}_{ci}^{*}), $$

where \(\boldsymbol {x}_{ci}^{*} = \boldsymbol {x}_{ci}^{*}(\boldsymbol {\rho })\) solves \(\underset {\boldsymbol {x}_{ci} \in \mathcal {X}_{i}}{\max \limits }\ \boldsymbol {F}^{T}\mathbf {U}(\boldsymbol {\rho },\boldsymbol {x}_{ci})\). The optimization problem can thus be written as

$$ \begin{cases} \underset{\boldsymbol{\boldsymbol{\rho}}}{\min} \ C(\boldsymbol{\rho}) \\ s.t \ \begin{cases} V(\boldsymbol{\rho})\leq \alpha V_{0}\\ 0 \leq \rho_{e} \leq 1, & \forall e=1,\ldots,m \end {cases} \end{cases} $$

The \(\max \limits \)-function is non-smooth and therefore the Kreisselmeier-Steinhauser (KS) approximation (Kreisselmeier and Steinhauser 1979) is used to get

$$ C(\boldsymbol{\rho}) \approx C_{KS}(\boldsymbol{\rho}) =\frac{1}{\gamma}\ln{\left( \sum\limits_{i=1}^{n_{d}}\exp\big(\gamma C_{i}(\boldsymbol{\rho})\big)\right)}, $$
(11)

where a higher value of γ makes the approximation closer to the \(\max \limits \)-function.

3.2.1 Sensitivity analysis

The derivative of the KS-approximation with respect to ρe is given by

$$ \frac{\partial C_{KS} }{\partial\rho_{e}} = \frac{{\sum}_{i=1}^{n_{d}}\exp(\gamma C_{i})\frac{\partial C_{i}}{\partial\rho_{e}}}{{\sum}_{i=1}^{n_{d}}\exp(\gamma C_{i})}, $$
(12)

where

$$ \frac{\partial C_{i}}{\partial\rho_{e}} = -\boldsymbol{U}(\boldsymbol{\rho},\boldsymbol{x}_{ci}^{*})^{T}\left( \sum\limits_{j = 1}^{m}\frac{\partial\boldsymbol{K}}{\partial\bar{\rho}_{j}}\frac{\partial\bar{\rho}_{j}}{\partial\tilde{\rho_{j}}}\frac{\partial\tilde{\rho_{j}}}{\partial\rho_{e}}\right)\boldsymbol{U}(\boldsymbol{\rho},\boldsymbol{x}_{ci}^{*}), $$
(13)

in which

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{K}}{\partial \bar{\rho}_{j}} &=& q_{1}(E_{0}-E_{min}) \cdot \\ &&\bar{\rho}_{j}^{{q_{1}}-1}\left( 1-\frac{{\sum}^{n_{n}}_{s=1}(\widetilde{H}(\phi(\boldsymbol{x}_{s}; \boldsymbol{x}_{ci}^{*})))^{q_{2}}}{n_{n}}\right)\boldsymbol{k}_{j}^{0}, \end{array} $$
$$ \frac{\partial \bar{\rho}_{j}}{\partial \tilde{\rho}_{j}} = \frac{\psi (1-\tanh^{2}(\psi(\tilde{\rho}_{j}-\eta)))}{\tanh{(\psi \eta)}+\tanh{(\psi(1- \eta))}}, $$

and \(\partial \tilde {\rho }_{j}/\partial \rho _{e} = Z_{je}/{\sum }_{i=1}^{m}Z_{ji}\).

The expression (13) is valid provided that the i th inner problem \(\underset {\boldsymbol {x}_{ci} \in \mathcal {X}_{i}}{\max \limits }\ \boldsymbol {F}^{T}\mathbf {U}(\boldsymbol {\rho },\boldsymbol {x}_{ci})\) has a unique solution (c.f. Theorem 1 in Klarbring and Strömberg (2012)). That is not necessarily the case in our numerical examples but we nevertheless observe good convergence as shown in Fig. 13 for example.

3.3 The optimization algorithm

Problem (7) is solved using an algorithm which can be seen in the flowchart in Fig. 6.

Fig. 6
figure 6

Flowchart of the optimization algorithm with the inner and outer optimization problem

Full size image

We note that a somewhat similar algorithm was proposed in da Silva et al. (2019) for TO under load uncertainty, and that the inner loop over all damage patches is almost trivial to parallelize if needed. The update of the position of the damage patch was done by the use of the method of moving asymptotes (Svanberg 1987) while the design was updated using the optimality criteria (OC) method (Christensen and Klarbring 2008) as implemented in Andreassen et al. (2011).

4 Numerical examples

The numerical examples in this section are based on the set-up shown in Fig. 7.

Fig. 7
figure 7

Design domain with loads and boundary conditions. To the right are examples of damage patches of two different sizes

Full size image

A “safe-zone” (the region to the right of the blue line in Fig. 7), where no damage can be present, is applied so as to not disconnect the force from the body (which would result in a very large compliance due to the non-zero Young’s modulus Emin > 0 of void regions). Damage patches of two different sizes that will be used are also shown.

The parameter γ in the KS-approximation (11) is taken as 5/Cmax where Cmax is the maximum compliance obtained for a given design (strictly speaking one should then consider Cmax when computing derivatives). Due to big differences in the compliance over the course of the optimization, Cmax is updated every 10th (outer) iteration. The parameter ψ in (1) starts at 2 and is doubled every 50th iteration until a final value of 16. After the 20 first iterations, the design does not change significantly and thus the positions of the MMCs are updated 4 times every iteration the first 20 iterations and thereafter only updated once per iteration to save computational time. The box constraint for each MMC is set to be ± 0.2L in both x − and y-direction starting from the initial position of the MMC. The initial positions for all MMCs are shown for each example below. The mesh size for the cantilever beam was 180 × 60 elements. All other parameters and settings can be found in Table 1.

Table 1 All parameters used in the optimization
Full size table

As initial guess for the design, we use in all cases a uniform density-distribution satisfying the volume and box constraints.

4.1 Damage patch 0.2L

4.1.1 Nominal design with damage

In Fig. 8 (top), one can see how the design looks when it is optimized not considering damage and in the middle plot one can see the worst damage in the structure. To assess the performance of the structure, a so-called damage map, Fig. 8, is constructed by using 360×120 damage patches evenly spread throughout the domain. This yields a map where one can see how the worst compliance varies as a function of the centroid position of a damage patch. The nominal compliance of the nominal design is 202.4 and the compliance for the worst damage is 8627.96. A damage to the optimized structure not considering damage is thus highly detrimental for the performance.

Fig. 8
figure 8

Top: optimized design. Middle: the design with the worst damage. Bottom: damage map for the design

Full size image

4.1.2 Optimized design with stationary damage

To compare to earlier work in Jansen et al. (2014) and Zhou and Fleury (2016), an optimization is performed with stationary damage patches. The optimization was performed with 60 × 180 damage patches uniformly distributed in the domain. The top plot in Fig. 9 shows the optimized design, and the middle plot shows the design with the worst damage obtained from the damage map in the lowermost plot. The undamaged compliance was 245.41 and the worst compliance found during the optimization was 371.28. This is significantly lower than what was found from the damage map where the worst compliance found was 497.46. This shows that even if a large amount of stationary damage patches is used, even a slight change in the position of the damage patches can damage the structure significantly more. Below, we will see that this effect can be avoided almost entirely by using a much smaller number of moving damage patches.

Fig. 9
figure 9

Top: design optimized with stationary damage patches. Middle: design with the worst damage. Bottom: damage map

Full size image

4.1.3 Optimized design with moving damage

Figure 10 shows an optimized design for an initial damage distribution of 5 × 12 damage patches. As can be seen in the middle plot, the worst damage is located near the support at the bottom left part of the domain. The corresponding damage plot is seen in the bottom of Fig. 10.

Fig. 10
figure 10

Top: optimized design with 5 × 12 moving damage patches. Middle: design with the worst damage. Bottom: damage map

Full size image

The initial and final distribution of damage patches for the design in Fig. 10 can be seen in Fig. 11 superimposed onto the respective design. The evolution of the design can be seen in Fig. 12

Fig. 11
figure 11

Initial and final density distribution with the corresponding damage patch distribution (turquoise squares) superimposed

Full size image
Fig. 12
figure 12

The evolution of the design during the first 100 design updates

Full size image

The objective function (the maximum eroded compliance) evolution can be seen in Fig. 13. The general appearance is smooth with jumps at 50, 100, and 150 iterations due to the update of the steepness-parameter ψ for the Heaviside projection filter defined in (1).

Fig. 13
figure 13

The eroded compliance as a function of the iterations during the optimization

Full size image

In Fig. 14a, one can see the design obtained when 3 × 10 = 30 uniformly distributed damage patches were considered during the optimization and in Fig. 14b one can see the design when 5 × 24 = 120 damage patches were considered during the optimization. The undamaged and damaged compliance can be seen in Table 2.

Fig. 14
figure 14

Designs for 3 × 10 = 30 (a) and 5 × 24 = 120 (b) moving damage patches

Full size image
Table 2 Compliance for the cantilever beam example obtained with different settings for the damage size and number of patches
Full size table

The principle appearance, as well as the compliance, of the designs in Figs. 9, 10, 14b and a is similar. If more damage patches were used, then the worst damage found from the optimization is closer to the worst damage found from the damage map. For the 0.2L damage patch, the compliance from the optimization is still close to the worst damage even when only 30 damage patches were used: 431.79 compared to 453.22.

The computational time required for 5×12 moving patches was approximately 23.4 min and for 60×180 stationary patches it was approximately 5542 min. This is thus roughly 240 times faster. This can be compared with it being 180 times more damage patches in the example with the stationary patches. Some additional computational times can be seen in Table 2. The optimization ran on a non-optimized code using MATLAB R1029b on a Intel core i9-9900K @3.60 GHz processor with 64 GB of RAM and using a sparse direct solver for the equilibrium equations. The bottleneck in the calculation is the number times the equilibrium equation needs to be solved.

4.2 Damage patch 0.4L

Figure 15 shows designs obtained with a damage patch of size 0.4L. In Fig. 15a, we see a design for 60 × 180 stationary damage patches, in Fig. 15b, one with 3 × 10 moving damage patches, in Fig. 15c one with 5 × 12 moving damage patches, and in Fig. 15d one with 5 × 24 moving damage patches. The designs here as well are similar to each other and have the same principle design. The compliance for the damaged structure obtained from the damage maps is similar as well except for the optimization with 60 × 180 stationary damage patches. The compliance for the undamaged structures and the compliance for the damaged structure can be found in Table 2. As one can see in Fig. 15, the designs are very similar, but once again the design with stationary damage patches in Fig. 15a has the worst damaged compliance. Here, the moving damage patches make for much better designs at lower computational cost.

Fig. 15
figure 15

Four designs obtained when using 0.4L damage patches. Top left: 60 × 180 stationary damage patches. Top right: 3 × 10 moving damage patches. Bottom left: 5 × 12 moving damage patches. Bottom right: 5 × 24 moving damage patches

Full size image

4.3 Summary

A summary of data for all the designs considered above, including the nominal and worst compliance found during the optimization and the worst compliance found from the damage map, is given in Table 2. As can be seen in the table, the compliance for the structures optimized using a 0.2L damage patch is almost 20 times better than that for the nominal design. The worst compliance found during the optimization is also close to the worst compliance found from the damage map. For the 0.4L damage, the compliance optimized with damage is more than 10 times better than that for the nominal design. Worth noting is that when a low number of damage patches were used, 3 × 10 = 30, the worst compliance was not found during the optimization but the structure is still just as damage tolerant as the designs where the worst damage found during the optimization was close to the worst compliance from the damage map.

5 Additional examples and extensions

To further investigate the capability of the algorithm, some additional examples, namely the MBB beam and the L-bracket, are considered. For these examples, the MMC-damage formulation is the same as in the previous section where only the centroid is used as design variable for the inner problem.

Furthermore, the MMC formulation can easily be modified to include both a change in length, Li, and thickness, ti, as well as rotation, 𝜃i, of the components (c.f. Figure 1). The added variables do make the optimization problem increasingly non-convex and it becomes difficult to verify, with, e.g. a damage map, if the worst damage is found. However, it is clear that the optimized designs are more fail-safe than an optimized design without regarding damage.

If nothing else is stated the parameters are the same as, found in Table 1.

5.1 L-bracket with 0.2L damage patches

For the L-bracket shown in Fig. 16a, a box (in green) was added as a safe zone around the point where the force was applied. This was done to keep the damage from disconnecting the force from the structure. The design domain was 2L × 2L with an inactive zone of L × L in the top right. The number of elements was 120 × 120. The initial damage patches were distributed evenly in the domain and a total of 47 damage patches were considered. The same type of damage patches as in the 0.2L damage cantilever setup was used. The optimized structure can be seen in Fig. 16a, and the worst damage at the inward corner can be seen in Fig. 16b. The compliance for the undamaged structure was 118.66 and for the damaged structure it was 236.23.

Fig. 16
figure 16

The optimized L-bracket (a) and the worst damage (b)

Full size image

5.2 MBB beam with 0.2L damage patches

The other example is the MBB beam with the same setup as for the L-bracket. For the MBB beam, two safe zones (in green) had to be applied to not disconnect the force as well as the support in the bottom right in Fig. 17a since this too would make the compliance tend to infinity. The number of elements was 120 × 40. The total number of damage patches was 72 which were evenly distributed. The optimized structure can be seen in Fig. 17a and the worst damage, located slight below the center of the domain, can be seen in Fig. 17b. The compliance for the undamaged structure was 283.67 and for the damaged structure it was 481.12.

Fig. 17
figure 17

The optimized MBB beam (a) and the worst damage (b)

Full size image

5.3 Varying patch size

In this example, the MMC is allowed to change its position as well as its length, L and width, t. To not get too long, thin damage patches which can cut too many structural members, a bound is put on the length Li ∈ [0.05,0.2] as well as the thickness ti ∈ [0.05,0.2]. Without these bounds, a sufficiently long patch could cut away all the material at the supports and the compliance would tend to infinity in the same manner as disconnecting the force would. To maintain a sensible size of the damage, a bound on the area which it is allowed to cover was added. That is Liti ≤ MaxArea was added into problem (7). This bound is always fulfilled when only varying the centroid and rotation. The maximal area was set to be equal to the area of a square damage patch with side lengths of 0.2L. The amount of damage patches was set to 5 × 12 and they were evenly distributed throughout the domain. The optimized design can be seen in Fig. 18a. The design resembles the designs in. Fig. 15 and this is due to the maximum length of the damage patch being the same as one of the sides of the larger damage patches even though the area covered is smaller in this example. The final damge distribution is shown in Fig. 18b.

Fig. 18
figure 18

The optimized cantilever beam with 4 damage variables (a) and the damage distribution (b)

Full size image

5.4 Varying patch size and orientation

Additionally, one can let the components rotate as stated in (4). The same bounds as in the previous section are used with added bounds on the angle 𝜃 ∈ [−π/2,π/2] for each patch. The damage patches were initially distributed as crosses similar to Fig. 2 to try and capture as many bad damage locations as possible. There were 5 × 12 crosses evenly distributed in the domain resulting in 120 damage patches. Figure 19a shows the optimized structure and Fig. 19b shows the damage distribution. One can see that the damage patches would rather orientate in such a way that they cut as many structural members as possible and not along the structural beams. This is due to the fact that cutting a structural member with a thin damage is almost equally as bad as if the entire beam was removed (if it wasn’t for Emin in (10), ensuring a small stiffness also in voids, it would be exactly as bad).

Fig. 19
figure 19

The optimized cantilever beam with 5 variables (a) and the damage distribution (b)

Full size image

6 Concluding remarks

We have proposed a method for TO of fail-safe structures based on a standard density-based description of the design and a mesh-independent MMC representation of damage. The numerical examples show that the method can be effective for generating fail-safe designs.

When comparing the compliance found during the optimization to the damage map compliance in Sections 4.1 and 4.2, the worst damage was never truly found. However, for a sufficient amount of damage patches, it was close, and for the smaller damage size, it was closer than when using stationary patches. Furthermore, even though the worst damage is not found, the structure still has more than a 10-fold improvement in terms of compliance compared to the nominal design, even for the design with 3 × 10 damage patches of size 0.4L. For the smaller 0.2L damage size, the optimization proved successful at finding the worst damage with as little as 30 damage patches and yielded a 20-fold improvement in worst compliance compared to the nominal design, see Table 2.

As shown in Section 5, the proposed algorithm also works for different examples and it is easy to implement other MMC descriptions in the proposed framework. The structures optimized with additional damage variables, seen in Figs. 18a and 19a, resemble the structures obtained for a 0.4L damage patch seen in Fig. 15 even though each damage only occupies one fourth of the area. The reason is that the damage patches prefer to be as long as possible in one direction to cut as many structural members as possible. More variables added makes it more difficult to know if one has found the worst damage or not but the structures are more fail-safe none the less.