A new stress-based topology optimization approach for finding flexible structures

Abstract

This paper presents a new FE-based stress-related topology optimization approach for finding bending governed flexible designs. Thereby, the knowledge about an output displacement or force as well as the detailed mounting position is not necessary for the application. The newly developed objective function makes use of the varying stress distribution in the cross section of flexible structures. Hence, each element of the design space must be evaluated with respect to its stress state. Therefore, the method prefers elements experiencing a bending or shear load over elements which are mainly subjected to membrane stresses. In order to determine the stress state of the elements, we use the principal stresses at the Gauss points. For demonstrating the feasibility of the new topology optimization approach, three academic examples are presented and discussed. As a result, the developed sensitivity-based algorithm is able to find usable flexible design concepts with a nearly discrete 0 − 1 density distribution for these examples.

1 Introduction

For three decades, the topology optimization has been a fast-developing branch of research. Nowadays, it is a well-established tool in many industrial sectors like automotive or aircraft. The basic idea of this structural optimization method is to find a suitable material distribution within a predefined design space.

Since the publication of the fundamental approach of Bendsøe and Kikuchi (1988) from 1988 about the homogenization method, the topology optimization of continuum structures is an active research area. One year later, Bendsoe published a second strategy, which uses the so-called Solid Isotropic Material with Penalization (SIMP) (Bendsøe and Kikuchi 1988) that is also applied in the present paper. Thus, all further explanations have to be considered in the context of the finite element method (FEM) in combination with the SIMP material law. In this approach, the elasticity tensor E of a finite element is obtained by multiplying the original elasticity tensor E⁰ of the element by the design variable x:

$$ \mathbf{E}(x) = x^{p} \cdot \mathbf{E}^{0}. $$

(1)

Thereby, the design variable is a dimensionless ratio (E/E⁰) which can be varied continuously between a lower boundary x^l and an upper boundary x^u. It represents an artificial density of the element. In the SIMP material model, finite elements with x ≈ 0 represent a void region or for x = 1 a solid region. The dimensionless stiffness ratio may be penalized by the exponent p in (1). Choosing the penalty coefficient p greater than 1 should result in a more discrete design. Ideally, an optimized structure consists of a clear 0 − 1 density distribution. For more details and general discussion, see Bendsøe and Sigmund (2003), Eschenauer and Olhoff (2001), and Rozvany (2009).

Finding a stiff structure within a design space for a certain volume limitation is the most common optimization task in a topology optimization. According to Soto (2001), this optimization target accounts for more than 80% of the optimization tasks in the industry. Often, the simplest objective function for linear elastic problems, the minimization of the compliance is used, which is equal to the maximization of the global stiffness.

During the last 20 years, the interest for finding flexible designs by structural topology optimization grew rapidly (Eschenauer and Olhoff 2001; Soto 2001). According to Lee (2011), there are two research fields which focus on the benefit of flexibility. The first one is the design of compliant mechanisms (CMs) and the second one is the design of energy-absorbing structures.

In contrast to conventional rigid-body mechanisms, CMs have no joints, hinges, or slides, but are elastic single-piece or jointless parts. The transfer of motion, force, or energy is done by elastic deformation of the flexible structural members (Eschenauer and Olhoff 2001; Sigmund 1997). In this way, it is possible to reduce the number of parts. In Gallego and Herder (2009), a detailed overview about the developed synthesis strategies for finding CMs is given. Here, the existing methods are divided into three branches of development (Fig. 1), which are the kinematic, the building blocks, and the structural optimization–based approaches. The third branch includes all topology, shape, and size optimization methods. Here, the focus is on the design of the mechanism. Generally, all included methods of this branch have the same conflict during the optimization: Finding a conceptual monolithic structure which works as a mechanism as well as a structure (Zhu et al. 2019). These are two contrarious optimization goals (rigidity and flexibility) which must be taken into account simultaneously. Commonly, consideration of both goals in one optimization leads to a multi-objective problem.

Fig. 1

Synthesis of compliant mechanisms (figure based on Gallego and Herder (2009))

With the maximization of a mechanical advantage (MA), Sigmund (1997) presents a possible objective function formulation for finding an optimal mechanism. The MA represents a predefined ratio of input and output forces. By optimizing a classical micro-gripping mechanism, Sigmund demonstrates the applicability of this idea. Often, the rigidity of the mechanism is achieved by a minimization of the strain energy and the flexibility by a deflection maximization, as presented by Frecker et al. (1997), where a ratio of mutual potential energy (MPE) (Shield and Prager 1970) and strain energy (SE) is maximized. A weighted linear multi-objective formulation of minimization of SE and maximization of MPE is published by Ananthasuresh et al. (1994). Lin et al. (2010) combine the SIMP material law and the multi-objective formulation of Ananthasuresh with physical programming (PP) (Messac 1996) for finding an optimal jointless mechanism. In their paper, it is demonstrated that this approach is very effective with respect to multi-objective optimization. Lee and Gea (2014) present a similar approach but use a global effective strain for minimization instead of strain energy, which leads to optimized CMs without regions with localized high strains due to one-node-connected hinges as is the case for the classical compliance minimization approach. Other possibilities for avoiding the point flexure drawback are the usage of morphological close-open and open-close density filters (Schevenels and Sigmund 2016) or the control of the stress level with an effective stress constraint formulation (De Leon et al. 2015).

The second field of research where flexibility is a priority is the design of energy-absorbing structures. Such structures have the capacity not only to absorb energy but also to provide stiffness for protection. Consequently, energy-absorbing designs are important in the wide field of transportation to ensure safety of humans in crash situations. A classical example is a frame of a car. In general, the overall optimization goal is to find designs with high crashworthiness. Similar to CMs, the challenge is to optimize stiffness and flexibility at the same time. This is further complicated by the circumstance that many effects resulting from dynamics, nonlinearity of material, and geometry or contacts have to be taken into account during optimization. For more details, see Lee (2011), Mayer et al. (1996), and Ortmann and Schumacher (2013).

The main purpose of our paper is the presentation of a new approach enabling the user to find flexible structures without any knowledge about the structures behavior at the mounting points or their positions (see Figs. 2 and 12). A stress criterion based on principal stress differences is used to distinguish between elements subjected to bending or membrane loading. Our aim is to accelerate the design process of flexible designs by means of a better start design for further optimizations, where only the conditions at the load application point are known.

Fig. 2

Optimization model cantilever beam with design space (green) and non-design space (light gray)

In the literature, stress-related formulations are often used as a constraint for controlling the stress level during the optimization. Duysinx and Bendsoe (1998) presented an ε-relaxation technique which allows the handling of local stress constraints for the topology optimization of continuum structures. Holmberg et al. present in Holmberg et al. (2013) an effective approach based on a design space clustering technique in combination with a modified p-norm for controlling the stress level during the optimization. More rarely is the usage of a stress-based formulation as objective function (Arnout et al. 2012; Yang and Chen 1996). The latter presents a topology optimization process which allows to control the global stress level more effectively by transferring the local stress problem into a global one.

Instead of controlling the stress concentrations during the topology optimization, we use our new stress-based formulation to evaluate finite elements with respect to their type of stress for finding conceptual designs with a dominating state of bending stress. The paper is organized as follows: In Section 2, the motivation and the general new idea will be shown. Section 3 presents the new stress-related objective function and the sensitivity analysis. In Section 4, the feasibility of the new approach is demonstrated for two examples. Finally, Section 5 presents the conclusions of this paper.

2 Motivation and idea

2.1 Motivation

Starting a design process for a new flexible casing part in combination with the question about a good mounting position for the given static structure often leads to unusable solutions, especially using a classical topology optimization objective like compliance (CP) (Lee 2011).

For a demonstration of this difficulty, a two-dimen-sional cantilever beam problem is used (see Fig. 2). The optimization model has a dimension of a × b (with a= 30 mm and b= 10mm) and is discretized with an average element edge length of 0.25mm (4800 linear plane stress continuum elements). The structure is made of steel (Young’s modulus E= 210000 N/mm², Poisson’s ratio ν= 0.3) and has a thickness of 1 mm. The cantilever beam is fixed at the left-hand side and loaded by a single point force of 50N at the right-hand side.

Since the aim is to find a flexible structure, the optimization task CP maximization with a volume fraction constraint v_f = 0.15 is used. Figure 3 shows that this task leads to an unusable (trivial) solution with an objective function value of $f_{CP}^{*} = 1.12e^{8}$N mm since no load path between the load application point and the mounting area exists (displacement at point A tends to $\infty$).

Fig. 3

Result of compliance maximization (legend: , , )

Applying the strategies for finding a general CM design (see Section 1) requires the knowledge about the positions and properties of the boundary conditions in the form of input/output forces or displacements for the description of the mechanism. Especially, the output information is important for most of the CM optimization algorithms (Gallego and Herder 2009; Zhu et al. 2019). Hence, the optimization problem of determining a bending dominated part with an unknown mounting position, described at the beginning, cannot be solved with a simple CM approach.

2.2 Properties of flexible structures

In contrast to stiff structures, flexible structures are able to reduce reaction forces and moments in case of prescribed displacements or decouple the movement of two parts. Such designs are characterized by a varying stress distribution in the structure as shown exemplarily in Fig. 4a for the well-known cantilever beam. A second example is the helical spring in Fig. 4b where a torsional moment reacts in the wire due to the applied forces and causes linearly distributed shear stresses. Both examples illustrate that the available material is no longer used in an optimal way as is the case for stiff structures with a constant stress distribution in their cross section. The fact that flexible parts consist of areas with a varying stress distribution is the basis of the new approach which is presented in the following section.

Fig. 4

Linear stress distribution of cantilever beam (a) and helical spring (b)

3 New approach for finding flexible structures

In this section, firstly, a new objective function for finding flexible structures with the help of topology optimization is presented. Afterwards, the calculation of sensitivities is shown since a gradient-based algorithm is applied for the optimization process. For this, the Augmented Lagrange Multiplier method (ALM) (Vanderplaats 1984) is used for solving the following presented constrained optimization problems. However, it should be noted that this new approach is only implemented for two-dimensional optimization problems at the moment.

3.1 Stress-related objective function

The basic idea of our approach is to make use of the varying stress distribution in the cross section of flexible structures. Therefore, each finite element in the design space must be evaluated with regard to its stress state. The new dominant bending stress (DBS) objective function reads as

$$ f_{DBS}(\mathbf{x},\mathbf{u}(\mathbf{x}))= \frac{1}{N_{ds}} \left( \sum\limits_{i=0}^{N_{ds}} \left( - \frac{\sigma_{ben_{\scriptstyle i}}}{\sigma_{rms_{\scriptstyle i}}} \cdot \frac{{x_{i}^{p}}}{{x_{i}^{q}}} \cdot w_{i} \right) \right) $$

(2)

with ${\sum }_{i=0}^{N_{ds}}$ being a summation over all finite elements of the design space, $\sigma _{ben_{\scriptstyle i}}$ the bending stress of the i-th element, $\sigma _{rms_{\scriptstyle i}}$ the root mean square of Gauss point stress values, x_i the density factor, q a coefficient (q < p) which depends on the SIMP material penalty exponent p, and w_i a weighting factor for the i-th element. The bending stresses are defined as

$$ \begin{array}{@{}rcl@{}} \sigma_{\scriptstyle {ben}} &=& \sigma_{1_{\scriptstyle {ben}}} + \sigma_{2_{\scriptstyle {ben}}}\\ \sigma_{1_{\scriptstyle {ben}}} &=& \sqrt{\frac{2}{m \cdot (m-1)} \sum\limits_{l=1}^{m} \sum\limits_{g=l+1}^{m}\left( {\sigma_{1,l} - \sigma_{1,g}}\right)^{2}} \\ \sigma_{2_{\scriptstyle {ben}}} &=& \sqrt{\frac{2}{m \cdot (m-1)}\sum\limits_{l=1}^{m} \sum\limits_{g=l+1}^{m}\left( {\sigma_{2,l} - \sigma_{2,g}}\right)^{2}}, \end{array} $$

(3)

with ${\sum }_{l=1}^{m} {\sum }_{g=l+1}^{m}$ being a summation over all Gauss point pairs for the principal stresses σ₁ and σ₂ of an element (applied sorting: |σ₁| > |σ₂|). Thus, the defined bending stress σ_ben can become greater than or equal to 0. Depending on σ_ben, the stress state of a finite element may be evaluated (membrane stress state for σ_ben = 0, bending stress state for σ_ben > 0). The variable σ_rms in (2) is defined as

$$ \begin{array}{@{}rcl@{}} \sigma_{\scriptstyle {rms}} &=& \sigma_{1_{\scriptstyle {rms}}} + \sigma_{2_{\scriptstyle {rms}}}\\ \sigma_{1_{\scriptstyle {rms}}} &=& \sqrt{\frac{1}{m}\sum\limits_{l=1}^{m} \left( {\sigma_{1,l}}\right)^{2}} \\ \sigma_{2_{\scriptstyle {rms}}} &=& \sqrt{\frac{1}{m}\sum\limits_{l=1}^{m} \left( {\sigma_{2,l}}\right)^{2}}, \end{array} $$

(4)

with ${\sum }_{l=1}^{m}$ being a summation over all m Gauss points of a finite element. By dividing σ_ben by σ_rms, the bending stress is normalized which has the effect that elements with a high stress state are not preferred to elements with a lower stress level during the optimization. Simply spoken, the new approach prefers elements subjected to bending or shearing to elements subjected to tensile or compressive stresses. The minus sign in (2) results from the used optimization method (ALM method (Vanderplaats 1984)) which can only search for minima.

The second term of the objective function ${{x^{p}_{i}}}/{{x^{q}_{i}}}$ is a relaxation factor and necessary to avoid an overestimation of the stresses in low-density elements (Bruggi 2008). As a result, the effect of the so-called singularity phenomenon (elements with a density tending to 0 tend to finite stress values (Duysinx and Bendsøe 1998; Yang and Chen 1996)) on the optimization result is reduced. Moreover, a possible skipping of the gradient field from iteration to iteration is avoided. Thus, the algorithm is able to find an usable solution with a nearly discrete density distribution.

The term w_i in (2) represents a dimensionless weighting factor for reducing the overestimation of elements in regions of stress singularities (Huang and Labossiere 2002) as well as the overestimation of elements with extremely small stress values. This factor is based on the density function of a trapezoidal distribution (van Dorp and Kotz 2003), determined only once per iteration (iter), and can take values between 0 and 1 (see Fig. 5). The z values required for the case-by-case analysis for computing w_i are calculated as

$$ z_{i} = \frac{\sigma_{rms_{\scriptstyle i}}}{\overline{\sigma}_{rms}}, $$

(5)

with $\overline {\sigma }_{rms}$ being the arithmetical mean value of all finite elements of the design space ($\overline {\sigma }_{rms} = {1}/{N_{ds}} \cdot {\sum }_{i=0}^{N_{ds}} \sigma _{rms_{\scriptstyle i}}$). On this basis, the four limits (A ≤ B ≤ C ≤ D) are defined as

$$ \begin{array}{@{}rcl@{}} &&A = min (z_{i}) \\ &&B = 0.1 \cdot \alpha \\ &&C = 3.0 \cdot \beta \\ &&D = max (z_{i})\\ &&\text{where} \\ && \alpha = \alpha_{(iter - 1)} \cdot 0.95 \\ && \beta = \beta_{(iter - 1)} \cdot 1.05, \end{array} $$

(6)

with α and β being factors which influence the z-distance between the points A and B as well as C and D (initial values are α₀ = β₀ = 1.0). Thereby, the limits B and C are defined in such a way that the overestimated values of the fraction ${\sigma _{ben_{\scriptstyle i}}}/{\sigma _{rms_{\scriptstyle i}}}$ in case of stress singularities or extremely small stresses are filtered out. During the optimization process, the filter effect becomes smaller since α and β are changed such that A = B and C = D after a certain number of iterations which leads to w_i = 1 for all elements. Consequently, the weighting factor which is constant during each iteration influences the optimization process just at the beginning and improves the robustness of the new approach in terms of its applicability.

Fig. 5

Density function w_i(z) of a trapezoidal distribution

The effect of the pq-relaxation in combination with the trapezoidal filter is explained in more detail in Section 4.1 on the basis of an example.

In Table 1, finite element models subjected to pure tension and pure bending are evaluated with respect to the terms used in (2). Following from this, we can conclude that generally the objective function value f_DBS increases for a bigger patch of elements subjected to bending.

Table 1 Evaluation of single finite elements with a single-axle tensile (left) and a single-axle bending load (middle and right)

3.2 Sensitivity-based optimization algorithm

For implementing the approach in a sensitivity-based algorithm, the derivative of (2) is necessary. Based on the calculated gradients, the used optimization algorithm, the Augmented Lagrange Multiplier method, defines the new search direction in every iteration (Firl 2010). The state of the art of sensitivity analysis for topology optimization (large number of design variables and few response functions) is the adjoint formulation which has a high numerical efficiency (Kirsch 1993). The objective function f_DBS(x,u(x)) depends not only directly on the design variables x but also indirectly via the displacements u. By using the product rule we get for the derivative:

$$ \begin{array}{@{}rcl@{}} \frac{\mathrm{d} f_{DBS}}{\mathrm{d} x_{j}} &=& \frac{1}{N_{ds}} \left( \sum\limits_{i=0}^{N_{ds}} w_{i} \cdot \left( - \frac{\sigma_{ben_{\scriptstyle i}}}{\sigma_{rms_{\scriptstyle i}}} \cdot \left( p-q\right) \frac{x_{i}^{p-1}}{{x_{i}^{q}}} \right. \right. \\ && \left. \left. + \frac{\left( \frac{\mathrm{d} \sigma_{rms_{i}}}{\mathrm{d} x_{j}} \cdot \sigma_{ben_{\scriptstyle i}} \right) - \left( \sigma_{rms_{\scriptstyle i}} \cdot \frac{\mathrm{d} \sigma_{ben_{i}}}{\mathrm{d} x_{j}} \right) }{\left( \sigma_{rms_{i}}\right)^{2}} \cdot \frac{{x_{i}^{p}}}{{x_{i}^{q}}} \right) \right). \end{array} $$

(7)

The derivatives ${\mathrm {d} \sigma _{ben_{i}}}/{\mathrm {d} x_{j}}$ and ${\mathrm {d} \sigma _{rms_{i}}}/{\mathrm {d} x_{j}}$ with respect to x_j are calculated with the help of the chain rule (Firl 2010):

$$ \begin{array}{@{}rcl@{}} && \frac{\mathrm{d} \sigma_{ben_{\scriptstyle i}}}{\mathrm{d} x_{j}} = \frac{\partial \sigma_{ben_{\scriptstyle i}}}{\partial x_{j}} + \left( \frac{\partial \sigma_{ben_{\scriptstyle i}}}{\partial \mathbf{u}}\right)^{T} \frac{\partial \mathbf{u}}{\partial x_{j}} \\ && \\ && \frac{\mathrm{d} \sigma_{rms_{\scriptstyle i}}}{\mathrm{d} x_{j}} = \frac{\partial \sigma_{rms_{\scriptstyle i}}}{\partial x_{j}} + \left( \frac{\partial \sigma_{rms_{\scriptstyle i}}}{\partial \mathbf{u}}\right)^{T} \frac{\partial \mathbf{u}}{\partial x_{j}}. \end{array} $$

(8)

The term ∂u/∂x_j can be determined from Ku = f with K being the global stiffness matrix and f being the vector of external forces, by differentiation with regard to the design variable

$$ \begin{array}{@{}rcl@{}} && \frac{\partial \mathbf{K}}{\partial x_{j}} \mathbf{u} + \mathbf{K} \frac{\partial \mathbf{u}}{\partial x_{j}} = \frac{\partial \mathbf{f}}{\partial x_{j}} \\ && \text{as}\\ && \frac{\partial \mathbf{u}}{\partial x_{j}} = \mathbf{K}^{-1}\underbrace{\left( -\frac{\partial \mathbf{K}}{\partial x_{j}} \mathbf{u} + \frac{\partial \mathbf{f}}{\partial x_{j}}\right)}_{\mathbf{f}^{*}}. \end{array} $$

(9)

The expression in the parentheses of (9) can be summarized to the pseudo load vector f^∗. In most cases, the derivative of f is a zero vector since these forces are independent of the design variable. However, if a dependency exists, this term is approximated by a forward finite difference. The determination of ∂K/∂x_j in a topology optimization using the SIMP material model is done by summing up the derivatives of the element stiffness matrices K_eas

$$ \frac{\partial \mathbf{K}}{\partial x_{j}} = \sum\limits_{i=0}^{N_{ds}} \frac{\partial \mathbf{K}_{e_{\scriptstyle i}}}{\partial x_{j}} = \sum\limits_{i=0}^{N_{ds}} p \cdot x_{j}^{p - 1} \mathbf{K}^{0}_{e_{\scriptstyle i}} $$

(10)

By combining (8), (9), and (10), the derivatives ${\mathrm {d}\sigma _{ben_{i}}}/{\mathrm {d} x_{j}}$ and ${\mathrm {d} \sigma _{rms_{i}}}/{\mathrm {d} x_{j}}$ can be computed as

$$ \begin{array}{@{}rcl@{}} && \frac{\mathrm{d} \sigma_{ben_{\scriptstyle i}}}{\mathrm{d} x_{j}} = \frac{\partial \sigma_{ben_{\scriptstyle i}}}{\partial x_{j}} + \underbrace{\left( \frac{\partial \sigma_{ben_{\scriptstyle i}}}{\partial \mathbf{u}}\right)^{T} \mathbf{K}^{-1}}_{\mathbf{\lambda}_{ben}^{T}} \cdot \ \mathbf{f}^{*} \\ && \frac{\mathrm{d} \sigma_{rms_{\scriptstyle i}}}{\mathrm{d} x_{j}} = \frac{\partial \sigma_{rms_{\scriptstyle i}}}{\partial x_{j}} + \underbrace{\left( \frac{\partial \sigma_{rms_{\scriptstyle i}}}{\partial \mathbf{u}}\right)^{T} \mathbf{K}^{-1}}_{\mathbf{\lambda}_{rms}^{T}} \cdot \ \mathbf{f}^{*}. \end{array} $$

(11)

The results of the matrix vector products $\left ({\partial \sigma _{ben_{i}}}/{\partial \mathbf {u}}\right )^{T} \mathbf {K}^{-1}$ and $\left ({\partial \sigma _{rms_{i}}}/{\partial \mathbf {u}}\right )^{T} \mathbf {K}^{-1}$ in (11) are the adjoint variable vectors $\mathbf {\lambda }_{ben}^{T}$ and $\mathbf {\lambda }_{rms}^{T}$. These variables must be calculated only once for every response function f of the optimization per iteration. By inserting this adjoint approach in (7), the absolute derivative of the objective function (2) which is used for the implementation results in:

$$ \begin{array}{@{}rcl@{}} && \frac{\mathrm{d} f_{DBS}}{\mathrm{d} x_{j}} = \frac{1}{N_{ds}} \sum\limits_{i=0}^{N_{ds}} w_{i} \cdot \left( \left[\frac{-\sigma_{ben_{\scriptstyle i}}}{\sigma_{rms_{\scriptstyle i}}} \cdot \left( p-q\right) \frac{x_{i}^{p-1}}{{x_{i}^{q}}} \right] \right. \\ && \qquad \qquad \left. + \left[\left( \frac{\left( \frac{\partial \sigma_{rms_{\scriptstyle i}}}{\partial x_{j}} + \mathbf{\lambda}_{rms}^{T} \cdot \mathbf{f}^{*} \right) \cdot \sigma_{ben_{\scriptstyle i}}}{ \left( \sigma_{rms_{\scriptstyle i}}\right)^{2}} - \right. \right. \right. \\ && \qquad \qquad \qquad \left.\left. \left. \frac{ \left( \frac{\partial \sigma_{ben_{\scriptstyle i}}}{\partial x_{j}} + \mathbf{\lambda}_{ben}^{T} \cdot \mathbf{f}^{*} \right)}{\sigma_{rms_{\scriptstyle i}}} \right) \cdot \frac{{x_{i}^{p}}}{{x_{i}^{q}}} \right]\right). \end{array} $$

(12)

For computing the adjoint variable vectors λ_ben and λ_rms in (12) both partial derivatives ${\partial \sigma _{ben_{i}}}/{\partial \mathbf {u}}$ and ${\partial \sigma _{rms_{i}}}/{\partial \mathbf {u}}$ are replaced by a central finite difference approximation. However, the partial derivatives ${\partial \sigma _{ben_{i}}}/{\partial x_{j}}$ and ${\partial \sigma _{rms_{i}}}/{\partial x_{j}}$ are approximated by forward finite differences because stresses are much more sensitive against variations of displacements than against variations of the density factor. The application of this semi-analytical procedure is driven by the fact that the used FE software is not able to provide the necessary derivatives of stresses with respect to density or displacement.

For demonstrating the functionality of this discrete adjoint sensitivity analysis, the cantilever beam model of Section 2.1 is used. The optimization task for maximizing the flexibility can be formulated as

$$ \begin{array}{@{}rcl@{}} && \min_{x} \ f_{DBS} \\ && \qquad s.t. \ \mathbf{K}(\mathbf{x})\mathbf{u} = \mathbf{f}\\ && \qquad \qquad v_{f} = \sum\limits_{i=0}^{N_{ds}} x_{i} \ v_{i} = 0.15\\ && \qquad \qquad 0 < x^{l} \leq x \leq 1, \end{array} $$

(13)

with f representing the external load vector, u the global displacement vector, K the global stiffness matrix of the system which depends on the vector of design variables, v_i the volume of the i-th finite element, and ${x^{l}_{i}}$ the lower density boundary. The resulting optimized structure is shown in Fig. 6 (objective value $f_{DBS}^{*} = -0.0881$).

Fig. 6

Resulting density distribution (a) and von Mises stress distribution (b) after 63 iterations

Within 63 iterations, the algorithm finds a closed load path with an almost discrete 0 − 1 density distribution. The resulting von Mises stress distribution in Fig. 6b clearly illustrates that the optimized beam has a varying stress distribution in thickness direction.

4 Further examples

In this section, two further examples, a cube loaded by a pair of compressive forces and the well-known L - bracket, demonstrate the feasibility of the new stress-related approach for the topology optimization of flexible structures. Both models are discretized with fully integrated linear plane stress continuum elements. Moreover, all optimizations are performed with a linear elastic isotropic material (Young’s modulus E = 210000 N/mm², Poisson’s ratio ν = 0.3) of thickness 1 mm.

4.1 Cube

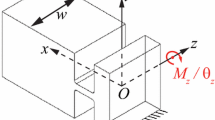
In the first example, a cube which is loaded by a compressive force is studied. The geometry of the problem is presented in Fig. 7. This optimization model has the dimensions a × a (a = 20 mm). All degrees of freedom at the edge of the left non-design space are fixed and forces with a total value of 25N at the edge of the right non-design space are applied. An average element edge length of 0.25 mm results in 6400 linear plane stress continuum elements. During the optimization, the artificial density of each design element may vary between x^l = 0.01 (lower limit) and x^u = 1.0 (upper limit). Furthermore, a linear gradient filter with an influence radius of 0.75 mm is used to overcome the checkerboard effect and to obtain a more discrete 0 − 1 density distribution (Bendsøe and Sigmund 2003; Eschenauer and Olhoff 2001; Masching 2016). The optimization is performed with a constant penalty exponent of p = 2, a coefficient of q = 0.5, and an initial artificial density of x_i = 0.19 for all elements of the design space.

Fig. 7

Optimization model cube with design space (green) and non-design space (light gray)

The optimization task is defined as

$$ \begin{array}{@{}rcl@{}} && \min_{x} \ f_{DBS} \\ && \qquad s.t. \ \mathbf{K}(\mathbf{x})\mathbf{u} = \mathbf{f}\\ && \qquad \qquad v_{f} = \sum\limits_{i=0}^{N_{ds}} x_{i} \ v_{i} = 0.19\\ && \qquad \qquad 0 < x^{l} \leq x \leq 1. \end{array} $$

(14)

After 85 iterations, the algorithm develops a ring-shaped structure as shown in Fig. 8 ($f_{DBS}^{*} = -0.1106$). The stress plot illustrates the dominant bending stress behavior in the structure. Obviously, the new approach is able to make use of the required properties of flexible structures. Moreover, the graph in Fig. 9 shows the stability of the algorithm by its smooth history of the objective function value.

Fig. 8

Density distribution (a) and von Mises stress distribution (b) after 85 iterations

Fig. 9

History of objective function for cube optimization (normalized on the basis of the absolute value of $f_{DBS}^{*} = -0.1106$)

In addition, a mesh study is carried out with this example. Therefore, the optimization model in Fig. 7 is discretized once with an average element edge length of 0.5 mm and once with an average element edge length of 1.0 mm. The results in Fig. 10 show that the optimized structure does not depend on the discretization of the model but the resulting objective function values differ. These different values can be explained with Table 1 since a finer mesh leads to bigger objective function values.

Fig. 10

Mesh study (legend: , , )

The optimization results shown in Fig. 8 as well as the stable optimization behavior result from the used combination of the pq-relaxation and the dimensionless weighting factor w_i which is based on the described trapezoidal filter (Section 3.1). Both methods are necessary in our approach because the gradients in areas with very small stresses or stress singularities would otherwise be overestimated due to the first term of the objective function (2). Since $\sigma _{rms_{\scriptstyle i}}$ may have very small values like in the four corner regions of the cube, the quotient ${\sigma _{ben_{\scriptstyle i}}}/{\sigma _{rms_{\scriptstyle i}}}$ and therefore the gradient may become huge which results in an aggregation of material (see Fig. 11). In a notch region as in the L-Bracket example in Section 4.2, the stress gradient is very high due to the singularity of the geometry which causes the same effect of material aggregation. By this, the density in these corner regions of the models would increase in every iteration, which reduces the influence of the pq-relaxation.

Fig. 11

Density distribution (a) and von Mises stress distribution (b) after 25 iterations without weighting factor w_i

To overcome these so-called corner effects, the trapezoidal filter is implemented which damps out the artificial aggregations at the beginning of the optimization process. Thus, no material is aggregated in these described areas at the beginning. Later, when the influence of the trapezoidal filter is reduced, the pq-relaxation takes over this part and prevents the aggregation of material because of the small densities in the corner regions.

Moreover, the stress-based optimization approach has the capability of avoiding trivial solutions with infinite displacements where no closed path of material between mounting region and load application area exists because such a result would not be an optimal solution in the sense of our objective. This can be simply shown for a single element subjected to some load. In this case, the objective reads

$$ f_{DBS}(\mathbf{x},\mathbf{u}(\mathbf{x}))= - \frac{\sigma_{ben_{\scriptstyle i}}}{\sigma_{rms_{\scriptstyle i}}} \cdot \frac{{x_{i}^{p}}}{{x_{i}^{q}}} $$

(15)

if we neglect for reasons of simplicity the weighting factor. Since p > q is always true and the stresses never become 0 and are always positive, it can be easily seen that the objective function value becomes smaller the bigger the density x_i becomes. This fact can also be shown for the cube example. The objective function value at the end of the optimization process is − 0.1106 because all elements in the design with a high density try to carry load in order to compute significant bending stresses. In contrast, a converged structure without a closed load path would always result in an objective function value close to 0, since the elements with a low density do not contribute to the f_DBS value due to the pq-relaxation. The equality condition of the volume fraction enforces a specific amount of elements with a density close to 1.0. In classical trivial solutions (confer Fig. 3), these elements are arranged as artificial material lumps in the design space. Such elements also do not contribute to the objective function value because these lumps only perform rigid-body motions and thus do not suffer any bending load.

4.2 L - bracket

The L-bracket is a widely studied example in the research field of topology optimization. The model in Fig. 12 has the dimensions a × a (a = 100 mm) with a b × b (b = 60 mm) square cutout. All degrees of freedom at the upper edge are fixed and a single load with F = 10N at the right corner is applied. The model is discretized with an average element edge length of 1 mm (6400 linear plane stress continuum elements). For a smoother result, the same linear gradient filter as for the cube with an influence radius of 4 mm, which corresponds to four times the average element edge length, is used. The initial density value for all design elements is 0.14, a penalty exponent of p = 2 and a coefficient of q = 0.5 is applied. The definition of the optimization task reads as

$$ \begin{array}{@{}rcl@{}} && \min_{x} \ f_{DBS} \\ && \qquad s.t. \ \mathbf{K}(\mathbf{x})\mathbf{u} = \mathbf{f}\\ && \qquad \qquad v_{f} = \sum\limits_{i=0}^{N_{ds}} x_{i} \ v_{i} = 0.14\\ && \qquad \qquad 0 < x^{l} \leq x \leq 1. \end{array} $$

(16)

Fig. 12

Optimization model L-bracket with design space (green) and non-design space (light gray)

Within 94 iterations, the algorithm finds a single arm structure with a dominating state of bending stress, which is shown in Fig. 13 ($f_{DBS}^{*} = -0.0746$). A solution with an almost discrete 0 − 1 density distribution and an existing load path between the load application point and the support structure is obtained. Also, in this example, the stable behavior of the algorithm can be recognized by the smooth course of the objective function which is shown in Fig. 14.

Fig. 13

Resulting flexible L-bracket density distribution (a) and von Mises stress distribution (b) after 94 iterations

Fig. 14

History of objective function for L-bracket optimization (normalized on the basis of the absolute value of $f_{DBS}^{*} = -0.0746$)

Additionally, the influence of two optimization parameters, the volume fraction (P1), and the radius of the linear gradient filter (P2) on the resulting structure should be studied. Therefore, the optimization task (16) with a gradient filter radius of 4 mm is used as a reference. Firstly, the value of P1 is varied between 0.115 and 0.165. In comparison to the reference design in Fig. 13a, it is observed that the variation of P1 only changes the thickness of the flexible arm structure (see Fig. 15).

Fig. 15

Variation of the initial volume fraction (legend: , , )

For the second study, a constant volume fraction of v_f = 0.14 is used. Now, the influence radius of the linear gradient filter is varied. The effect on the optimized structure due to the applied radius sizes of 3.0 mm and 5.0 mm is illustrated in Fig. 16 and shows almost no influence in comparison to the reference solution of Fig. 13a. As a result, both studies confirm a robust behavior for variations of the selected optimization parameters within the defined ranges.

Fig. 16

Variation of the gradient filter radius size (legend: , , )

Finally, an extension of the non-design space at the upper edge of the L-bracket model shows the usability of this stress-based approach with regard to finding a new mounting position. The defined optimization task (16) with the same linear gradient filter settings are also used here. After 98 iterations, the algorithm develops a flexible arm structure ($f_{DBS}^{*} = -0.0678$), but in contrast to the reference solution (see Fig. 13) a different mounting position is chosen by the algorithm. A comparison to the compliance values of both optimization results shows that the mounting point in Fig. 17b leads to a more flexible design ($f_{CP}^{*} = 33.39$ Nmm) than that in Fig. 13a ($f_{CP}^{*} = 12.43$ Nmm).

Fig. 17

Variation of the possible mounting area

5 Conclusions

A new methodology for finding conceptual designs for flexible parts by using the topology optimization has been presented and investigated. Thereby, no knowledge about input-to-output force ratios or displacements as well as mounting positions is necessary. A sensitivity-based algorithm has been successfully implemented in a commercial optimization software. Academic examples illustrate that this new approach could be a useful tool for finding a better initial design for a development process of a flexible part. Furthermore, two studies have shown that the method has a conditional robustness against variation of optimization parameters. It should be noted that the current version supports only two-dimensional plane examples with plane stress continuum elements which have at least four Gauss points but an extension to three dimensions and different finite element formulations is possible.