Topology optimization of compliant mechanisms considering strain variance

Abstract

In this work, compliant mechanisms are designed by using multi-objective topology optimization, where maximization of the output displacement and minimization of the strain are considered simultaneously. To quantify the strain, we consider typical measures of strain, which are based on the p-norm, and a new class of strain quantifying functions, which are based on the variance of the strain. The topology optimization problem is formulated using the Solid Isotropic Material with Penalization (SIMP) method, and the sensitivities with respect to design changes are derived using the adjoint method. Since nearly void regions may be highly strained, these regions are excluded in the objective function by a projection method. In the numerical examples, compliant grippers and inverters are designed, and the tradeoff between the output displacement and the strain function is investigated. The numerical results show that distributed compliant mechanisms without lumped hinges can be obtained when including the variance of the strain in the objective function.

Appendices

Appendix 1 Minimizing global effective strain for compliant gripper example

When the influence of the global effective strain f₁ in the objective function is increased, the lumped hinge at the center shown in Fig. 12a is gradually replaced by a compliant member; see (a) to (d) in Fig. 12.

Fig. 12

Optimized topologies corresponding to the data points shown in Fig. 13. The designs a to j are obtained by varying the weight coefficient w in the objective function g₁

However, new lumped hinges emerge in the central part of the design domain, as shown in Fig. 12 i and j, while f₁ is still relatively small, i.e., the inclusion of the global effective strain f₁ in the objective function does not rule out the possibility of lumped hinges being formed. For all designs in Fig. 12, the volume constraint is active. This is in contrast to the topologies optimized for g₃ (the strain variance function), cf. Fig. 14.

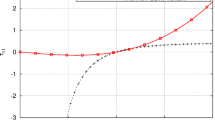
The tradeoff between the output displacement and the global effective strain is seen in Fig. 13. Decreasing the output displacement results in that the global effective strain f₁ is reduced.

Fig. 13

Tradeoff between global effective strain f₁ and output displacement u_out for the Pareto optimal designs in Fig. 12

Appendix 2 Minimizing strain variance function for compliant gripper example

In this example, optimized designs, using the objective function g₃ (the strain variance function) with the weights w = 1, 0.9, 0.8, …, 0.1, are presented in Fig. 14. From Fig. 14, we see that as the strain variance function f₃ decreases, the output displacement u_out decreases. To alleviate strain inhomogeneities, the structure becomes thinner, which leads to that the volume constraint is inactive for w < 0.9. Furthermore, the strain uniformity is increasing with decreasing w. In summary, we conclude that mechanisms transform from lumped to distributed when more emphasis is put on the strain variance function.

Fig. 14

Optimized topologies corresponding to the data points shown in Fig. 15. The designs a to j are obtained by varying the weight coefficient w in the objective function g₃

The tradeoff between the strain variance function f₃ and the output displacement u_out is shown in Fig. 15, and we see that the output displacement decreases as the value of the strain variance function f₃ decreases. It is noted that the strain variance function is significantly reduced with a minor reduction in the output displacement. For example, from point 1 (w = 1) to point 2 (w = 0.4) indicated in Fig. 15, the strain variance function decreased by nearly 50% while the output displacement is decreased by approximately 20%. It is noted that the increase in uniformity of strain distribution vanishes for $\frac{1}{u_{\mathrm{out}}}>1.16$.

Fig. 15

Tradeoff between strain variance function f₃ and output displacement u_out for the Pareto optimal designs in Fig. 14