Optimal archgrids: a variational setting

Abstract

The paper deals with the variational setting of the optimal archgrid construction. The archgrids, discovered by William Prager and George Rozvany in 1970s, are viewed here as tension-free and bending-free, uniformly stressed grid-shells forming vaults unevenly supported along the closed contour of the basis domain. The optimal archgrids are characterized by the least volume. The optimization problem of volume minimization is reduced to the pair of two auxiliary mutually dual problems, having mathematical structure similar to that known from the theory of optimal layout: the integrand of the auxiliary minimization problem is of linear growth, while the auxiliary maximization problem involves test functions subjected to mean-square slope conditions. The noted features of the variational setting governs the main properties of the archgrid shapes: they are vaults over a subregion of the basis domain being the effective domain of the minimizer of the auxiliary problem. Thus, the method is capable of cutting out the material domain from the design domain; this process is built in within the theory. Moreover, the present paper puts forward new methods of numerical construction of optimal archgrids and discusses their applicability ranges.

1 Introduction

Funiculars are planar frameworks which, albeit subject to a transverse and transmissible load, do not undergo flexure, i.e. they remain bending-free and, consequently, are not subject to transverse shear forces, while the axial stress resultants are characterized by a fixed sign: all the bars are in tension (or- in compression). The load is called transmissible, if it follows the design, yet keeping the given (usually vertical) direction and keeping the value of its intensity q(x) measured per unit length of the line orthogonal to the direction of the load [q] = [N/m], cf. Fuchs and Moses (2000). Of the funiculars being fully and uniformly stressed (up to a given limit (equal, say, − σ_C, σ_C being the permissible stress in compression)) one can find one of the least volume. Its rise cannot be too high but also cannot be too small, since big values of thrusts (i.e. horizontal reactions at the pin supports) lead to an inevitable increase of areas of the cross-sections, resulting in the increase of the volume. Thus, the rise should be appropriately chosen. Let z = z(x) represent the shape of the funicular pin supported at A and B at the levels z(0) = h_A, z(l) = h_B.

The optimal rise of the least-volume funicular is determined by the condition

$$ \frac{1}{l} \int\limits_{0}^{l} \left( \frac{\mathrm{d}z}{\mathrm{d}x} \right)^{2} dx = 1+ 2 \left( \frac{h_{B}-h_{A}}{l} \right)^{2} $$

(1)

discovered by Rozvany and Prager (1979) and Rozvany and Wang (1983) and called there: the mean square slope condition. An illustrative example of the optimal funicular corresponding to a particular transverse load is shown in Fig. 1. The level function of a funicular follows the diagram of the bending moment in a simply supported beam with supports of the same ordinates as points A and B and subject to the same load q(x). Thus, for a given vertical transmissible load of intensity q(x), referred to the unit area of the basis plane, one can construct a family of funiculars and select one of the least volume, see Section 6.1 in Lewiński et al. (2019a). The main conclusion is that in a given plane one can construct frameworks, usually having forms of arches, which are simultaneously tension-free and do not undergo bending. Admitting tension leads to Michell-like designs of great complexity, see Darwich et al. (2010). A similar theoretical construction in space is much less obvious. A natural counterpart of a planar bending-free arch is a membrane shell. Of three local equilibrium equations, one is algebraic:

$$ \frac{N_{1}}{R_{1}}+\frac{N_{2}}{R_{2}}+q=0 $$

(2)

where N₁, N₂ represent the membrane stress resultants corresponding to the principal curvature parameterization, while the principal curvatures are denoted by R₁, R₂; q represents intensity of normal load, [q] = [N/m²]. Thus, if the normal load is absent and the curvatures are positive, the stress resultants N₁, N₂ must have opposite signs. At least in this case, a membrane shell cannot be subject only to compression and work in a bending-free state. On the other hand, we remember the solutions of statics of membrane shells of revolution under self-weight: at the pole, both the membrane stress resultants are negative and equal but along the meridian, the diagrams of these stress resultants have different distribution: the meridional force (i.e. its absolute value) increases, while the initially negative circumferential stress resultant increases and, crossing a zero value at a certain circumference, attains positive values along the support, see Flügge (1960). These examples show that, in general, one cannot construct a membrane shell which under a transmissible vertical load would work in a tension-free state. That is why instead of membrane shells, the tension-free grid-shells are preferred in many applications. The grid-shells are tension-free spatial frameworks formed on a single or on several surfaces, their form being selected such that the bending is vastly eliminated, see Richardson et al. (2013) and Jiang et al. (2018).

Fig. 1

The funicular of optimal shape corresponding to the given load. Its level function satisfies the condition (1)

Grid-shells are usually constructed in two steps. First, the geometry of the deformed configuration is found, e.g. by dynamic relaxation, see Day (1965). Then the optimal position of nodes is found to minimize the total weight and impose additional design conditions, see Richardson et al. (2013). The recent paper by Jiang et al. (2018) discusses three more efficient methods of constructing grid-shells: the force density method (FDM) by Linkwitz and Schek (1971) and Schek (1974); the potential energy method (PEM); and the ground structure method (GSM). In the FDM, the values of the member forces are predefined, while the nodal position is determined by the equilibrium conditions in the undeformed state. Thus, the designer has a full control over the values of axial stresses and it is possible to eliminate tension (or compression) a priori. The GSM is also capable of eliminating tension (or compression) but the solution does not constitute a single surface structure; in general, a multi-storey structure appears, cf. Lewiński et al. (2019b).

An alternative method of construction of grid-shells can be inferred from the theory of archgrids, proposed by Rozvany and Prager (1979) and extended in Rozvany et al. (1980, 1982), Rozvany and Wang (1983), and Wang and Rozvany (1983). This theory has been recently revisited in Lewiński et al. (2019a, Sec. 6.3.6; 2019b), Czubacki and Lewiński (2019), and Czubacki et al. (2018). Archgrids are composed of infinitely thin arches formed in the mutually orthogonal planes: x = const., y = const., orthogonal to the basis Ω corresponding to z = 0. The given load of intensity q is transmissible along the z axis and is decomposed into the loads q_x, q_y acting on the arches in y = const. and x = const. planes. The shape of the arches is chosen such that the bending is fully eliminated. Consequently, also the transverse shear forces vanish. Thus, the state of stress in the arches is axial: the only stress components are normal to the cross-sections. One can design the areas of cross-sections of the arches such that the state of stress is fully uniform within the arches and equals − σ_C. Of such uniformly stressed structures, one can find the one of the smallest volume. Rozvany and Prager (1979) discovered that this least volume structure is formed on a single surface. More precisely, if z = z_x(x,y) represents the surface composed of arches formed in y = const. planes, and if z = z_y(x,y) represents the surface composed of arches formed in x = const. planes, then the conditions of minimum volume imply the identity: z_x(x,y) = z_y(x,y) = z(x,y) there, where both the arches are subject to non-zero loads. On the other hand, arches in one direction can also appear and even some part of the basis Ω can be uncovered. The point loads are also allowed and lead to arches of finite cross-sections. Nevertheless, the optimal structure is a grid shell in all cases; the problem of its construction belongs to the class of topology optimization problems.

The numerical solutions shown in the mentioned papers by Rozvany and co-authors have been constructed iteratively, the optimization problem itself had not been explicitly formulated. Czubacki and Lewiński (2019) noted that the archgrid problem reduces to the two mutually dual problems, to some extent similar to those constituting the scalar Beckmann problem, see Santambrogio (2015), forming the Michell’s problem, see Lewiński et al. (2019a) as well as the free material design problems, see Bouchitté and Buttazzo (2001), Czubacki and Lewiński (2015), and Czarnecki and Lewiński (2017). The minimization problem is characterized by the functional of linear growth; its dual version is a maximization problem of the virtual work with locking conditions. Just this decomposition governs the topology optimization features of the setting and of the final form of solutions. Moreover, the numerical and mathematical methods to attack the problem should be appropriately chosen, as for functionals with integrands of linear growth.

The mathematical theory of archgrids evenly supported along the closed contour of the basis domain has been put forward in Czubacki and Lewiński (2019). The present paper is aimed at extensions of this theory towards archgrids unevenly supported. The level of the edge support is determined by the values of the ruled surface given by the equation: z₀(x,y) = a₁xy + a₂x + a₃y + a₄. In the first step, the surfaces z_x(x,y), z_y(x,y) are generated by the family of planar arches in the sections y = const., x = const., supported along the contour Γ of the domain Ω on the level z₀ along Γ. These surfaces determine the grid shells carrying the loads q_x(x,y), q_y(x,y) such that q(x,y) = q_x(x,y) + q_y(x,y). The decomposition of the given load q into q_x,q_y is one of the unknowns of the archgrid theory. Upon introducing the areas of cross-sections for assuring a uniform state of stress in the whole structure, we state the problem of the volume minimization. This leads to various optimality conditions, one of them being the identity z_x(x,y) = z_y(x,y) = z(x,y) valid in these subdomains, where two families of arches carry the load. All the optimality criteria will be discussed and the mathematical formulation of the optimum design problem will be stated; it turns out that the level function z(x,y) of the vault is governed by a well-posed problem composing of two auxiliary mutually dual problems. Upon finding the static unknowns, one can compute the optimal areas of the cross-sections to assure the uniform distribution of stress. The optimum archgrid is the lightest among all statically admissible and fully stressed.

2 The least volume bending-free arch under vertical transmissible load

2.1 Construction of the bending-free arches

The present section shows that for any transverse and transmissible load, one can construct a three-hinge arch which is bending-free.

Consider a three-hinge planar arch subject to a vertical load of intensity $q(\overline {x})$, $0\leq \overline {x}\leq l$, referred to its projection on the horizontal axis x. The hinges at the support lie on the levels: z = h_A and z = h_B, see Fig. 2.

Fig. 2

The three-hinge arch (a) and the simply supported auxiliary beam subject to the same load q (b)

Along with the arch problem, an auxiliary beam supported at points lying below the supports A and B of the arch, of ordinates x = 0 and x = l, is considered. The beam is subject to the same load $q(\overline {x})$, $0\leq \overline {x}\leq l$.

The vertical reaction at the left support A equals

$$ \widehat{V}_{A} = \frac{1}{l} \int\limits_{0}^{l} (l - \overline{x}) q (\overline{x}) d\overline{x} $$

(3)

The bending moment in this beam at the section of ordinate x is expressed by

$$ \widehat{M}(x) = \widehat{V}_{A} x - \int\limits_{0}^{x} (x - \overline{x}) q(\overline{x}) d \overline{x} $$

(4)

The condition of the total equilibrium of the arch reads:

$$ V_{A} l - H(h_{B} - h_{A}) - \int\limits_{0}^{l} (l - \overline{x}) q(\overline{x}) d \overline{x} = 0 $$

(5)

where H represents the horizontal reaction at the support A. We consider only such loads q for which H > 0.

Note that the vertical reactions of the arch and the auxiliary beam are linked by

$$ V_{A} = \widehat{V}_{A} +\tan(\alpha) H $$

(6)

where $\tan (\alpha ) = (h_{B}-h_{A})/l$. The bending moment in the arch at the section of the ordinate x can be expressed by

$$ M(x) = \widehat{M}(x) + H\left[ (\tan(\alpha))x - (z - h_{A}) \right] $$

(7)

The shape of the arch can now be adjusted to the given load by requiring that M(x) = 0 for 0 ≤ x ≤ l. This condition determines the shape of the bending-free arch:

$$ z(x) = h_{A} + (\tan(\alpha)) x + \frac{1}{H} \widehat{M}(x) . $$

(8)

Thus,

$$ \frac{\mathrm{d}z}{\mathrm{d}x} = \tan(\alpha) + \frac{1}{H} \widehat{T}(x), \quad \widehat{T}(x) = \frac{\mathrm{d} \widehat{M}}{\mathrm{d} x} $$

(9)

where $\widehat {T}$ represents the transverse shear force in the auxiliary beam of Fig. 2b. This transverse shear force satisfies the differential equilibrium equation

$$ \frac{\mathrm{d} \widehat{T}}{\mathrm{d} x} +q = 0 $$

(10)

Its variational counterpart has the form

$$ \int\limits_{0}^{l} \widehat{T} \frac{\mathrm{d} v}{\mathrm{d} x} dx = \int\limits_{0}^{l} q v dx \quad \forall v \in \mathcal{V}_{0} $$

(11)

where $\mathcal {V}_{0}$ represents the set of trial functions vanishing at x = 0 and x = l; the regularity conditions involved in the definition of $\mathcal {V}_{0}$ will not be discussed in the present paper.

The equalities (9) and (10) imply

$$ H \frac{\mathrm{d}^{2} z}{\mathrm{d}x^{2}} + q=0 $$

(12)

called the funicular equation.

One can prove that the arch of the form given by the elevation function (8) is not only bending-free but is also not subject to transverse shear. It is subject only to compression. The axial force N(x) in this arch is linked with the horizontal reaction H by the formula

$$ N(x) \cos(\varphi(x)) + H = 0 $$

(13)

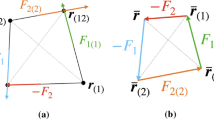
where φ(x) is the angle of inclination of the tangent at point (x,z(x)) to the axis x, hence $\tan (\varphi (x)) = dz/dx,$ cf. Fig. 3. Thus, N(x) < 0 along the whole arch.

Fig. 3

Equilibrium of a segment of the arch, cf. Fig. 2

The areas A(x) of the cross-sections can be chosen such that the normal stresses are made uniform within the whole arch and equal − σ_C, σ_C being the permissible stress in compression. To this end, we assume |N(x)|/A(x) = σ_C, or

$$ A(x) = \frac{H}{{\sigma}_{C} \cos(\varphi(x))} $$

(14)

2.2 The bending-free arch of least volume

Among the arches which are bending-free and uniformly stressed, one can find an arch of the least volume. The volume of the arch of areas of cross-sections given by (14) equals

$$ V = \frac{H}{{\sigma}_{C}} \int\limits_{0}^{l} \frac {1}{\cos^{2}(\varphi(x))} dx $$

(15)

By using the formulas

$$ \begin{array}{@{}rcl@{}} &&{} \frac{1}{\cos^{2}(\varphi(x))} = 1 + \tan^{2}(\varphi(x)),\\ &&{} \tan(\varphi(x)) = \tan(\alpha) + \frac{1}{H} \widehat{T}(x) \end{array} $$

(16)

and considering that the integral of $\widehat {T}(x)$ along the span of the auxiliary beam vanishes, we obtain

$$ {\sigma}_{C} V = \tilde{l} H + \frac{1}{H} \| \widehat{T} \|^{2} $$

(17)

where $\tilde {l} = (1+\tan ^{2}(\alpha )) l$ and ∥⋅∥ stands for the norm¹

$$ \| u \| = \left( \int\limits_{0}^{l} (u(x))^{2} dx \right)^{1/2} . $$

(18)

The optimum design problem ($\mathcal {P}_{0}$)

Among bending-free three-hinge arches corresponding to a given transmissible load q(x) find the least-volume arch.

The solution.

All such arches are characterized by the level functions z(x) given by (8), involving the design variable H. By minimizing the volume V over H, we obtain the optimal value of the horizontal reaction $H = \check {H}$, or

$$ \check{H} = \frac{1}{\sqrt{\tilde{l}}} \| \widehat{T} \| , $$

(19)

while the volume of the lightest arch equals

$$ \check{V} = \frac{2 \sqrt{\tilde{l}}}{{\sigma}_{C}} \| \widehat{T} \| . $$

(20)

Its elevation function $z=\check {z}$ is given by (8) and (19), or

$$ \check{z}(x) = h_{A} + (\tan(\alpha)) x + \frac{\sqrt{\tilde{l}}}{\|\widehat{T}\|} \widehat{M}(x) , $$

(21)

see Fig. 1. Let us differentiate both sides of (21):

$$ \frac{1}{\sqrt{\tilde{l}}} \left( \frac{\mathrm{d}\check{z}}{\mathrm{d}x} -\tan(\alpha) \right) = \frac{1}{\|\widehat{T}\|} \widehat{T}(x) . $$

(22)

The right hand side has the unit norm; consequently, the norm of the left hand side is equal to 1 and this condition leads to, cf. (1)

$$ \frac{1}{l} \int\limits_{0}^{l} \left( \frac{\mathrm{d} \check{z}}{\mathrm{d}x} \right)^{2} dx = 1 + 2 \tan^{2}(\alpha) . $$

(23)

This condition means that the optimal arch cannot be too shallow and also cannot be too high. If it were very shallow, the load would cause great values of the thrust H; consequently, the areas of the cross-sections would be appropriately big to assure a constant normal stress. On the other hand, if an arch is higher and higher than its volume increases. The condition (23) indicates that the rise of the arch should be perfectly chosen. It is worth noting that this is an integral condition and not a point-wise one.² Moreover, note that the bound increases along with the increase of α. Thus, if the difference between the levels of the supports is bigger and bigger, the mean rise increases accordingly. This fact is not obvious and can serve as an hint for a designer.

The arch of minimal volume has the shape given by the elevation function (21), while the areas of its cross-sections are given by (14) and (19). The optimal areas of cross-sections are expressed as below

$$ \check{A} = \frac{1}{{\sigma}_{C} \sqrt{l}} \sqrt{\| \widehat{T} \|^{2} +2 \sin(\alpha) \sqrt{l} \| \widehat{T} \| \widehat{T}(x) + l \left( \widehat{T}(x) \right)^{2}} $$

(24)

Note that $\check {A}$ cannot degenerate along the arch and assumes finite values.

Remark 1

It is worth noting that the optimal volume $\check {V}$ (given by (20)) is proportional to the potential energy of the load, namely

$$ \begin{array}{@{}rcl@{}} \frac{{\sigma}_{C}}{2} \check{V} &=& \int\limits_{0}^{l} q(x) \tilde{z}(x) dx , \\ \tilde{z}(x) &=& \check{z}(x) - \left[ h_{A} + (\tan(\alpha))x \right] \end{array} $$

(25)

The proof runs as follows. Since $\tilde {z}$ vanishes at the ends of the beam, we can choose $v=\tilde {z}$ in (11), which implies

$$ \int\limits_{0}^{l} q\tilde{z} dx = \int\limits_{0}^{l} \widehat{T} \frac{\mathrm{d} \tilde{z}}{\mathrm{d}x} dx $$

(26)

Note that

$$ \frac{\mathrm{d}\tilde{z}}{\mathrm{d}x} = \frac{\mathrm{d}\check{z}}{\mathrm{d}x} - \tan(\alpha) = \frac{\sqrt{\tilde{l}}}{\|\widehat{T}\|}\widehat{T}(x) $$

(27)

Substitution of (27) into (26) gives

$$ \int\limits_{0}^{l} q \tilde{z} dx = \sqrt{\tilde{l}} \| \widehat{T} \| , $$

(28)

which ends the proof.

Remark 2

Consider the following two auxiliary problems of the variational calculus.

Problem ($\mathcal {P}_{0}^{\prime }$)

Find the minimizer $Q = \check {Q}$ of the problem

$$ Z_{1} = \min \left\{ \|Q\| \ \left\vert \ \text{over } Q \text{ such that } \frac{\mathrm{d}Q}{\mathrm{d}x}\! +\! q\! =\! 0 \right. \right\}. $$

(29)

Problem ($\mathcal {P}_{0}^{\prime \prime }$)

Find the maximizer $v = \check {v} \in \mathcal {V}_{0}$ of the problem

$$ \begin{array}{@{}rcl@{}} Z_{2} & =& \max \left\{ \left. \int\limits_{0}^{l} q v dx \ \right\vert \ \text{over } v \text{ such that } \right. \\ &&\left.\qquad\quad \left\| \frac{\mathrm{d} v}{\mathrm{d} x} \right\| \leq 1, \ v \in \mathcal{V}_{0} \vphantom{\int\limits_{0}^{l}}\right\} . \end{array} $$

(30)

If regularity assumptions are appropriately chosen, one can prove that Z₁ = Z₂, cf. Czubacki and Lewiński (2019). Moreover, $\check {v}$ and $\check {Q}$ are linked by

$$ \frac{\mathrm{d} \check{v}}{\mathrm{d} x} = \frac{1}{\| \check{Q} \|} \check{Q}(x) $$

(31)

and $\check {Q}$ represents just the transverse shear force appearing in the auxiliary beam of Fig. 2b, or $\check {Q} =\widehat {T}$. Thus,

$$ \frac{\mathrm{d}\check{v}}{\mathrm{d}x} = \frac{1}{\| \widehat{T} \|}{\widehat{T}(x)}, \quad \check{v}(x) = \frac{1}{\|\widehat{T}\|} \widehat{M}(x) $$

(32)

where $\widehat {M}$ is bending moment in the auxiliary beam of Fig. 2b. Moreover, according to (21), the elevation function of the optimal arch can be expressed by

$$ \check{z}(x) = h_{A} +(\tan(\alpha)) x + \sqrt{\tilde{l}} \check{v}(x) , $$

(33)

which implies $\tilde {z}(x) = \sqrt {\tilde {l}} \check {v}(x)$. It is seen that the field $\check {v}(x)$ attains the bound in the condition involved in (30): $\| \mathrm {d}\check {v} /\mathrm {d}x\| = 1$.

In the problem considered, the variational problems ($\mathcal {P}_{0}^{\prime }$), ($\mathcal {P}_{0}^{\prime \prime }$) are not helpful in construction of the solution, since the solution (21) has been directly constructed. Nevertheless, the formulations of problems ($\mathcal {P}_{0}^{\prime }$), ($\mathcal {P}_{0}^{\prime \prime }$) are inspiration for the construction of the optimal archgrids which are the main subject of the present study.

3 Archgrids unevenly supported along a closed contour

The aim of this section is to put forward a variationally consistent theory of optimal archgrids.

3.1 The stress-based construction of archgrids

The term archgrid is indissolubly bonded with its least-volume property. It will be shown that just the least-volume condition leads to shaping a single surface on which the arches (in the planes x = const., y = const.) are formed. The basis of the archgrids to be designed will be a plane domain Ω parameterized by a Cartesian coordinates system (x,y). Assume that the straight lines y = const. cut the contour Γ of the domain Ω at two points: (x₁(y),y), (x₂(y),y); c ≤ y ≤ d. Similarly, the lines x = const. cut the contour Γ at two points (x,y₁(x)), (x,y₂(x)); a ≤ x ≤ b, cf. Fig. 4. Assume that the domain Ω is included in a rectangle of dimensions a₀ and b₀ and let the point (0,0) be one of its vertices; The sides of the rectangle are given by y = 0, y = b₀, x = 0, x = a₀, see Fig. 4. Let us form over a given rectangle a ruled surface whose elevation function is expressed by

$$ z_{0} (x,y) = \frac{c_{3}-c_{2}+c_{1}-c_{4}}{a_{0} b_{0}}xy+\frac{c_{2}-c_{1}}{a_{0}}x+\frac{c_{4}-c_{1}}{b_{0}}y+c_{1} $$

(34)

Note that

$$ \begin{array}{@{}rcl@{}} z_{0} (0,0) &=& c_{1}, \quad z_{0} (a_{0},0) = c_{2}, \\ z_{0}(a_{0},b_{0}) &=& c_{3}, \quad z_{0}(0,b_{0}) =c_{4} \end{array} $$

(35)

The angles of inclination of the lines x = const., y = const. are expressed by:

$$ \begin{array}{@{}rcl@{}} \tan(\beta(x)) &=& \frac{\partial z_{0}}{\partial y} = \frac{c_{3}-c_{2}+c_{1}-c_{4}}{a_{0} b_{0}}x+\frac{c_{4}-c_{1}}{b_{0}} \\ \tan(\alpha(y)) &=& \frac{\partial z_{0}}{\partial x} = \frac{c_{3}-c_{2}+c_{1}-c_{4}}{a_{0} b_{0}}y+\frac{c_{2}-c_{1}}{a_{0}} \end{array} $$

(36)

The vault will be designed over the basis Ω, along the contour Γ. Its elevation along the contour Γ will be given: z = z₀(x,y) if (x,y) ∈Γ. The elevations of the vault at the points of the contour Γ: (x₁(y),y), (x₂(y),y), (x,y₁(x)), (x,y₂(x)) are denoted by h₁(y), h₂(y), g₁(x), g₂(x), respectively. Thus, we have

$$ \begin{array}{@{}rcl@{}} z_{0}(x_{1}(y),y) =h_{1}(y),\quad z_{0}(x_{2}(y),y)=h_{2}(y)\\ z_{0}(x,y_{1}(x)) =g_{1}(x),\quad z_{0}(x,y_{2}(x))=g_{2}(x) \end{array} $$

The following equalities hold

$$ \begin{array}{@{}rcl@{}} \frac{h_{2}(y)-h_{1}(y)}{l_{x}(y)} &=& \tan(\alpha(y)), \ \ l_{x}(y) = x_{2}(y)-x_{1}(y) \\ \frac{g_{2}(x)-g_{1}(x)}{l_{y}(x)} &=& \tan(\beta(x)), \ \ l_{y}(x) = y_{2}(x)-y_{1}(x) \end{array} $$

(37)

for the subsequent cross-sections y = const., x = const., see Fig. 5.

Fig. 4

The basis Ω of the archgrid and its cross-sections. The domain Ω is enclosed by a rectangle of sides a₀, b₀

The vault to be designed is assumed as an archgrid composed of two families of arches in the directions y = const., x = const., hence formed in the mutually orthogonal planes. The given load q, referred to a unit area of a basis plane, [q] = [N/m²], being transmissible in the z direction (orthogonal to Ω) is decomposed as follows

$$ q(x,y) = q_{x}(x,y) +q_{y}(x,y) . $$

(38)

The arches in the sections y = const., subjected to the vertical load of intensity q_x(x,y), are formed such that they are bending-free with using the method of Section 2. Consider a simply supported beam of length l_x(y). The load q_x(x,y) causes the transverse shear force $\widehat {T}_{x}(x,y)$ and the bending moment $\widehat {M}_{x}(x,y)$. These fields satisfy the differential equations of equilibrium:

$$ \frac{\partial \widehat{T}_{x}}{\partial x} + q_{x} = 0, \quad \widehat{T}_{x} = \frac{\partial \widehat{M}_{x}}{\partial x} . $$

(39)

The level function of the arch is assumed such that the arch is bending-free. Thus, according to (8), the ordinates of the arch formed for y = const. are given by

$$ z_{x}=h_{1}(y) +(\tan(\alpha(y)))x +\frac{1}{H_{x}(y)} \widehat{M}_{x}(x,y) . $$

(40)

In the cross-sections x = const., the optimal arches, subjected to the vertical load of intensity q_y(x,y), are constructed in a similar manner. Consider now simply supported beams of lengths l_y(x). The load of intensity q_y(x,y) causes the fields $\widehat {T}_{y}(x,y)$, $\widehat {M}_{y}(x,y)$ satisfying

$$ \frac{\partial \widehat{T}_{y}}{\partial y} +q_{y} =0, \quad \widehat{T}_{y} = \frac{\partial \widehat{M}_{y}}{\partial y} . $$

(41)

The elevation function of the arch is assumed by the rule (8), or

$$ z_{y} = g_{1}(x) + (\tan(\beta(x)))y +\frac{1}{H_{y}(x)} \widehat{M}_{y}(x,y) $$

(42)

The arch thus constructed is bending-free. The horizontal reactions H_x(y), H_y(x) are assumed to be non-negative.

Fig. 5

The ruled surface z = z₀(x,y) over the rectangle surrounding the basis domain Ω

Note that the fields $\widehat {T}_{x}$, $\widehat {T}_{y}$ satisfy the equilibrium equation

$$ \frac{\partial \widehat{T}_{x}}{\partial x} + \frac{\partial \widehat{T}_{y}}{\partial y} +q = 0 . $$

(43)

At this stage of the study, the designed vault is formed on two surfaces of elevation functions: z_x(x,y), z_y(x,y). Their values coincide along the contour of Γ.

$$ z_{x} \vert_{\varGamma} = z_{y} \vert_{\varGamma} = z_{0} . $$

(44)

The values of z₀ along the contour are determined by the ruled surface (34). In the sequel, our aim is to construct a vault of the minimal volume. It will occur that this condition will result in the identity z_x = z_y within Ω. Just this identity will be interpreted as a junction of both the families of arches to form a one shell-like structure.

The computation of volumes of the both families of arches requires analysis of their slopes. By differentiating (40) and (42), we get

$$ \begin{array}{@{}rcl@{}} \frac{\partial z_{x}}{\partial x} &=& \tan(\alpha(y))+\frac{1}{H_{x}(y)} \widehat{T}_{x} (x,y) , \\ \frac{\partial z_{y}}{\partial y} &=& \tan(\beta(x))+\frac{1}{H_{y}(x)} \widehat{T}_{y}(x,y) . \end{array} $$

(45)

Let φ_x, φ_y represent the inclination of the tangents to the arches in the planes y = const., x = const., respectively, see Fig. 6. Thus,

$$ \tan(\varphi_{x}) = \frac{\partial z_{x}}{\partial x}, \quad \tan(\varphi_{y}) = \frac{\partial z_{y}}{\partial y} $$

(46)

To make the distribution of the axial stress uniform and equal − σ_C, we shall choose the densities of areas of cross-sections in an appropriate manner. By using the rule (14), one obtains

$$ A_{x} = \frac{H_{x}}{{\sigma}_{C} \cos(\varphi_{x})}, \quad A_{y} = \frac{H_{y}}{{\sigma}_{C} \cos(\varphi_{y})} $$

(47)

The elementary volumes of the arches are expressed by

$$ \mathrm{d}V_{x} = A_{x} \mathrm{d} s_{x}, \quad \mathrm{d}V_{y} = A_{y} \mathrm{d} s_{y} $$

(48)

where

$$ \mathrm{d}s_{x} = \frac{\mathrm{d}x}{\cos(\varphi_{x})}, \quad \mathrm{d} s_{y} = \frac{\mathrm{d}y}{\cos(\varphi_{y})} $$

(49)

Substitution of (47), (49) into (48) gives

$$ \begin{array}{@{}rcl@{}} \mathrm{d}V_{x} &=& \frac{H_{x}}{{\sigma}_{C}}(1+\tan^{2}(\varphi_{x})) \mathrm{d}x, \\ \mathrm{d}V_{y} &=& \frac{H_{y}}{{\sigma}_{C}}(1+\tan^{2}(\varphi_{y})) \mathrm{d}y \end{array} $$

(50)

The total volume of the arches parallel to the axis x is expressed by

$$ V_{x} = \frac{1}{{\sigma}_{C}} \int\limits_{c}^{d} \int\limits_{x_{1}(y)}^{x_{2}(y)} H_{x}(y) (1+ \tan^{2}(\varphi_{x})) dxdy $$

(51)

while the total volume of the arches parallel to the axis y equals

$$ V_{y} = \frac{1}{{\sigma}_{C}} \int\limits_{a}^{b} \int\limits_{y_{1}(x)}^{y_{2}(x)} H_{y}(x) (1+ \tan^{2}(\varphi_{y})) dydx $$

(52)

Substitution of (46), (45) into (51) results in

$$ \begin{array}{@{}rcl@{}} {\sigma}_{C} V_{x} &=& \int\limits_{c}^{d} \int\limits_{x_{1}(y)}^{x_{2}(y)} H_{x}(y) \left[\vphantom{\left( \tan(\alpha(y))+\frac{1}{H_{x}(y)} \widehat{T}_{x} (x,y)\right)^{2}} 1 \right.\\ &&+\left. \left( \tan(\alpha(y))+\frac{1}{H_{x}(y)} \widehat{T}_{x} (x,y)\right)^{2} \right] dxdy , \end{array} $$

(53)

which reduces to

$$ {\sigma}_{C} V_{x} = \int\limits_{c}^{d} \tilde{l}_{x}(y)H_{x}(y) dy + \int\limits_{c}^{d} \frac{1}{H_{x}(y)} \int\limits_{x_{1}(y)}^{x_{2}(y)} \left( \widehat{T}_{x} \right)^{2} dxdy $$

(54)

where

$$ \tilde{l}_{x}(y) = l_{x}(y) \left( 1+ \tan^{2}(\alpha(y)) \right) $$

(55)

In a similar manner, we obtain

$$ {\sigma}_{C} V_{y} = \int\limits_{a}^{b} \tilde{l}_{y}(x)H_{y}(x) dx + \int\limits_{a}^{b} \frac{1}{H_{y}(x)} \int\limits_{y_{1}(x)}^{y_{2}(x)} \left( \widehat{T}_{y} \right)^{2} dydx $$

(56)

where

$$ \tilde{l}_{y}(x) = l_{y}(x) \left( 1+ \tan^{2}(\beta(x)) \right) $$

(57)

Now we are ready to formulate the main problem of the present paper, namely the problem of constructing the least-volume archgrid:

Fig. 6

Construction of the archgrid from two families of arches in the planes y = const., x = const.. The auxiliary beams are subject to the loads q_x, q_y, respectively

The minimizing pairs $(\check {H}_{x}, \check {H}_{y})$, $(\check {Q}_{x}, \check {Q}_{y})$ are stationary points of the Lagrangian ${\mathscr{L}}= {\mathscr{L}}(H_{x},H_{y},\widehat {T}_{x},\widehat {T}_{y}, \lambda )$ given by

$$ \mathcal{L} = {\sigma}_{C} (V_{x}+V_{y}) + \int\limits_{\varOmega} \left( \frac{\partial \widehat{T}_{x}}{\partial x} + \frac{\partial \widehat{T}_{y}}{\partial y} +q \right) \lambda(x,y) dxdy $$

(58)

where λ(x,y) is a Lagrangian multiplier corresponding to the equilibrium condition (43) and vanishing along the contour Γ. By integrating by parts, we rearrange the Lagrangian to the form

$$ \mathcal{L} = {\sigma}_{C} (V_{x}+V_{y}) +2 G(v) $$

(59)

where

$$ G(v) = \int\limits_{\varOmega} q v dxdy - \int\limits_{\varOmega} \left( \widehat{T}_{x} \frac{\partial v}{\partial x} + \widehat{T}_{y} \frac{\partial v}{\partial y} \right) dxdy $$

(60)

Let us note that the condition

$$ G(\tilde{v}) =0 \quad \forall \ \tilde{v} \ \text{vanishing}\ \text{on}\ \varGamma $$

(61)

is equivalent to (43). Thus, the fields $\widehat {T}_{x}$, $\widehat {T}_{y}$ involved in (59) will be treated as independent. Moreover, v = λ/2 plays in (59) the role of a Lagrangian multiplier.

We require $\delta {\mathscr{L}} = 0$ with respect to independent variations δv, δH_x, δH_y, $\delta \widehat {T}_{x}$, $\delta \widehat {T}_{y}$. In this way, the stationary conditions of the functional (59) are obtained: the condition (61) and

$$ \begin{array}{@{}rcl@{}} &&{} \frac{\partial v}{\partial x} = \frac{1}{H_{x}(y)} \widehat{T}_{x}, \quad \frac{\partial v}{\partial y} = \frac{1}{H_{y}(x)} \widehat{T}_{y} \end{array} $$

(62)

$$ \begin{array}{@{}rcl@{}} &&{} H_{x}(y) = \frac{1}{\sqrt{\tilde{l}_{x}(y)}} \rho_{y} (\widehat{T}_{x}; x_{1}(y),x_{2}(y) ) \\ &&{} H_{y}(x) = \frac{1}{\sqrt{\tilde{l}_{y}(x)}} \rho_{x} (\widehat{T}_{y}; y_{1}(x),y_{2}(x) ) \end{array} $$

(63)

where the norms ρ_x(⋅ ; ⋅, ⋅), ρ_y(⋅ ; ⋅, ⋅) are defined by

$$ \begin{array}{@{}rcl@{}} \rho_{x}(f;a(x),b(x)) = \left( \int\limits_{\ \ a(x)}^{b(x)} \left( f(x,y) \right)^{2} dy \right)^{1/2} \\ \rho_{y}(f;a(y),b(y)) = \left( \int\limits_{\ \ a(y)}^{b(y)} \left( f(x,y) \right)^{2} dx \right)^{1/2} \end{array} $$

(64)

for a(x) < b(x).

The stationarity conditions (62) and (63) refer to the case of H_x > 0, H_y > 0.

Substitution of the formulas

$$ \widehat{T}_{x} = H_{x}(y) \frac{\partial v}{\partial x}, \quad \widehat{T}_{y} = H_{y}(x) \frac{\partial v}{\partial y} $$

(65)

into (61) leads to:

Problem ($\mathcal {P}_{1}$)

Find v vanishing on the contour Γ such that

$$ a_{H}(v,\tilde{v}) = \int\limits_{\varOmega} q \tilde{v} dxdy \quad \forall \ \tilde{v} \ \text{vanishing on}\ \varGamma $$

(66)

where the bilinear form at the left-hand side reads

$$ a_{H}(u,v)\! =\! \int\limits_{\varOmega} \left[ H_{x}(y) \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} + H_{y}(x) \frac{\partial u}{\partial y} \frac{\partial v}{\partial y} \right] dxdy. $$

(67)

If H_x, H_y are given and H_x > 0, H_y > 0, then the solution v of problem ($\mathcal {P}_{1}$) is unique. This function v determines uniquely the fields $\widehat {T}_{x}$, $\widehat {T}_{y}$ by (65). The formulae (62) may be re-written as

$$ \frac{\partial v}{\partial x} = \frac{1}{H_{x}(y)} \widehat{T}_{x}, \quad \frac{\partial v}{\partial y} = \frac{1}{H_{y}(x)} \widehat{T}_{y} $$

(68)

where now v is the solution to the problem ($\mathcal {P}_{1}$).

By combining (68) with (45), one gets

$$ \frac{\partial}{\partial x} (z_{x} -v ) = \tan(\alpha(y)), \quad \frac{\partial}{\partial y}(z_{y} -v) = \tan(\beta(x)) $$

(69)

hence,

$$ \begin{array}{@{}rcl@{}} z_{x} -v &=& (\tan(\alpha(y))) x + s_{1}(y), \\ z_{y} -v &=& (\tan(\beta(x))) y + s_{2}(x) \end{array} $$

(70)

The functions s₁(y), s₂(x) can be chosen such that z_x = z_y in the whole basis domain including the boundary. Indeed by taking

$$ s_{1}(y) = \frac{c_{4}-c_{1}}{b_{0}} y +c_{1}, \quad s_{2}(x) = \frac{c_{2}-c_{1}}{a_{0}}x+c_{1} $$

(71)

one obtains the identity

$$ (\tan(\alpha(y))) x +s_{1}(y) = (\tan(\beta(x))) y+s_{2}(x) $$

(72)

cf. (36). Since v vanishes on Γ, we note that z = z_x = z_y assumes the values z₀(x,y) for (x,y) lying on Γ. Thus, if H_x(y), H_y(x) are given, then the function

$$ z(x,y)=v(x,y) +z_{0}(x,y) $$

(73)

determines the shape of the vault. To assure that this shape refers to the structure of the minimal volume, the functions H_x(y), H_y(x) should be appropriately selected. The relations (63) make it possible to express the total volume V = V_x + V_y in terms of the fields $\widehat {T}_{x}$, $\widehat {T}_{y}$. The direct substitution of (63) into (54), (56) results in

$$ V = \frac{2}{{\sigma}_{C}} \wp(\boldsymbol{\widehat{\boldsymbol{T}}}) $$

(74)

where for w = (u,v) we define

$$ \begin{array}{@{}rcl@{}} \wp(\boldsymbol{w}) &= & \int\limits_{a}^{b} \sqrt{\tilde{l}_{y}(x)} \rho_{x}(v;y_{1}(x),y_{2}(x)) dx \\ &&+ \int\limits_{c}^{d} \sqrt{\tilde{l}_{x}(y)} \rho_{y}(u;x_{1}(y),x_{2}(y)) dy \end{array} $$

(75)

The vector field $\widehat {\boldsymbol {T}} = (\widehat {T}_{x},\widehat {T}_{y})$ is subject only to the condition (43) (or equivalently: (61)). Now the problem $(\mathcal {P})$ of minimization of the volume of the archgrid can be explicitly formulated as (cf. the theoretical scheme given in Fig. 7):

Fig. 7

The tabular scheme of the theory of optimal archgrids

The problem above is well posed since the set of vector fields Q of given divergence is non-empty. Moreover, let us note that the functional ℘(w) possesses the properties of a norm of a vector function of argument w = (u(x,y),v(x,y)).

Since the functional in (76) is convex and the set of admissible vector fields Q is non-empty, the problem ($\mathcal {P}^{\prime }$) is well-posed. The problem of existence depends on regularity of the data.

Let $\pmb {\check {Q}} = (\check {Q}_{x},\check {Q}_{y})$ be the minimizer of (76). By substituting $\widehat {\boldsymbol {T}} = \pmb {\check {Q}}$ into (63), one obtains the optimal distributions $\check {H}_{x}(y)$, $\check {H}_{y}(x)$ of the boundary forces. Substitution of these results into (67) fixes the coefficients in the bilinear form $a_{\check {H}}(\cdot , \cdot )$ governing the optimal solution. If $\check {H}_{x} >0$, $\check {H}_{y} >0$, then this bilinear form is positive definite and the problem ($\mathcal {P}_{1}$) possesses a unique solution $\check {v}$ which determines the surface of the archgrid by (73).

3.2 The displacement-based construction of the archgrid

It turns out that the stress-based problem ($\mathcal {P}^{\prime }$) has its displacement-based counterpart and just the latter problem will be, usually, easier to solve. The aim of this section is to put forward this dual formulation.

Let us start by noting that the gradient of $\check {v}$ can be computed directly from (62) by putting

$$ H_{x} = \check{H}_{x}, \quad H_{y} = \check{H}_{y}, \quad \widehat{T}_{x}=\check{Q}_{x}, \quad \widehat{T}_{y} = \check{Q}_{y} . $$

(77)

Let us substitute: $H_{x} = \check {H}_{x}$, $H_{y} = \check {H}_{y}$, and

$$ \widehat{T}_{x} = \check{Q}_{x} = \check{H}_{x}(y) \frac{\partial \check{v}}{\partial x}, \quad \widehat{T}_{y} = \check{Q}_{y} = \check{H}_{y}(x) \frac{\partial \check{v}}{\partial y} $$

(78)

into (63). If $\check {H}_{x}>0$, $\check {H}_{y}>0$, then the relations (63) imply

$$ \begin{array}{@{}rcl@{}} \rho_{y} \left( \frac{\partial \check{v}}{\partial x}; x_{1}(y),x_{2}(y) \right) &=& \sqrt{\tilde{l}_{x}(y)} \\ \rho_{x} \left( \frac{\partial \check{v}}{\partial y}; y_{1}(x),y_{2}(x) \right) &=& \sqrt{\tilde{l}_{y}(x)} \end{array} $$

(79)

The field $\check {v}$ determined by the solution of the problem ($\mathcal {P}_{1}$) with the optimal values of the coefficients $H_{x} = \check {H}_{x}$, $H_{y} = \check {H}_{y}$ of the quadratic form (67) is the maximizer of

Indeed, the problems ($\mathcal {P}^{\prime }$), ($\mathcal {P}^{\prime \prime }$) are mutually dual; Z₁ = Z₂, or the duality gap vanishes. For the proof, the reader is referred to Czubacki and Lewiński (2019). The proof applies here since the formal structure of problem ($\mathcal {P}^{\prime \prime }$) and problem (78) in Czubacki and Lewiński (2019) is the same. It is sufficient to replace l_x, l_y with $\tilde {l}_{x}$, $\tilde {l}_{y}$ and if $\pmb {\check {Q}} = (\check {Q}_{x},\check {Q}_{y})$ is the minimizer of (76) and if $\check {v}$ is the maximizer of (80), then these fields are linked by the optimality conditions

Having $\check {Q}_{x}$, $\check {Q}_{y}$, one can find $\nabla \check {v}$ but not vice versa; the relations (81) are non-invertible. Therefore, the construction of the optimal archgrid necessitates solving the two independent problems: ($\mathcal {P}^{\prime }$), ($\mathcal {P}^{\prime \prime }$), while (81) can play the role of a check. Upon finding $\check {v}$, one can construct the level function $\check {z}$ of the optimal archgrid by the rule

$$ \check{z} (x,y) = \check{v} (x,y) + z_{0} (x,y) $$

(82)

where z₀(x,y) is given by (34). One can prove that the function $\check {z}(x,y)$ satisfies the equalities:

$$ \begin{array}{@{}rcl@{}} \int\limits_{x_{1}(y)}^{x_{2}(y)} \left( \frac{\partial \check{z}}{\partial x} \right)^{2} dx = l_{x}(y) \left( 1+ 2\tan^{2}(\alpha(y))\right) \\ \int\limits_{y_{1}(x)}^{y_{2}(x)} \left( \frac{\partial \check{z}}{\partial y} \right)^{2} dy = l_{y}(x) \left( 1+ 2\tan^{2}(\beta(x))\right) \end{array} $$

(83)

These equations are counterparts of the condition (23) known from the theory of planar funiculars. Let us prove the first of the conditions (83). To this end, we insert (cf. (69))

$$ \frac{\partial \check{v}}{\partial x} = \frac{\partial \check{z}}{\partial x} - \tan(\alpha(y)) $$

(84)

into the first of relations (79). One finds

$$ \int\limits_{x_{1}(y)}^{x_{2}(y)} \left( \frac{\partial \check{z}}{\partial x} - \tan(\alpha(y)) \right)^{2} dx = \tilde{l}_{x}(y) . $$

(85)

While computing the l.h.s of (85), one can make use of the formulas:

$$ \begin{array}{@{}rcl@{}} &&{} \check{z} (x_{2}(y),y) - \check{z} (x_{1}(y),y) = l_{x}(y) \tan(\alpha(y)) \\ &&{} x_{2}(y) -x_{1}(y) = l_{x}(y) \end{array} $$

(86)

and thus rearrange (85) to the form of the first of equalities (83).

One can say that the conditions (83) introduce the upper bounds on the slope of the arches in both directions. These bounds are increasing functions of arguments α(y), β(x). The theoretical construction of the optimal archgrids governed by problem ($\mathcal {P}$) is reduced to solving problems ($\mathcal {P^{\prime }}$), ($\mathcal {P^{\prime \prime }}$), their juxtaposition being presented in the diagram in Fig. 7.

Having solved the problems ($\mathcal {P^{\prime }}$), ($\mathcal {P^{\prime \prime }}$), one can determine the areas of arches’ cross-sections, which will be discussed in the sequel.

3.3 Determination of the densities of the areas of arches’ cross-sections

The solution to the problem (80) determines the shape of the optimal archgrid according to (82) but, in general, does not allow for a direct computation of the densities of areas of cross-sections $\check {A}_{x}$, $\check {A}_{y}$ in the optimal structure. These fields are determined by the solution $(\check {Q}_{x},\check {Q}_{y})$ to the problem (76). To find the explicit formulas for the densities of the area cross-sections $\check {A}_{x}$, $\check {A}_{y}$, we shall make use of (47). The forces H_x, H_y involved in these formulas are found by putting $\widehat {T}_{x} =\check {Q}_{x}$, $\widehat {T}_{y} =\check {Q}_{y}$ in (63).

By using (46), (84), and (68), one finds

$$ \begin{array}{@{}rcl@{}} \tan(\varphi_{x}) &=& \tan(\alpha(y)) +\frac{1}{\check{H}_{x}} \check{Q}_{x}, \\ \tan(\varphi_{y}) &=& \tan(\beta(x)) +\frac{1}{\check{H}_{y}} \check{Q}_{y} \end{array} $$

(87)

In this manner, one gets

$$ \begin{array}{@{}rcl@{}} {\sigma}_{C} \check{A}_{x} = \sqrt{\left( \check{H}_{x} \right)^{2} + \left( \check{H}_{x} \tan(\alpha) + \check{Q}_{x} \right)^{2}} \\ {\sigma}_{C} \check{A}_{y} = \sqrt{\left( \check{H}_{y} \right)^{2} + \left( \check{H}_{y} \tan(\beta) + \check{Q}_{y} \right)^{2}} \end{array} $$

(88)

Now the forces $\check {H}_{x}$, $\check {H}_{y}$ can be expressed in terms of $\check {Q}_{x}$, $\check {Q}_{y}$ by putting $\widehat {T}_{x} = \check {Q}_{x}$, $\widehat {T}_{y} = \check {Q}_{y}$ into (63). The final formulae read

$$ \begin{array}{@{}rcl@{}} \check{A}_{x} &=& \frac{1}{{\sigma}_{C}\sqrt{l_{x}}} \left( \left( \rho_{y}(\check{Q}_{x};x_{1},x_{2}) \right)^{2} + l_{x} \left( \check{Q}_{x} \right)^{2} \right. \\ &&\left. + 2 \sin(\alpha) \sqrt{l_{x}} \rho_{y}(\check{Q}_{x};x_{1},x_{2})\check{Q}_{x} \vphantom{\left( \rho_{y}(\check{Q}_{x};x_{1},x_{2}) \right)^{2}}\right)^{1/2} \\ \check{A}_{y} &=& \frac{1}{{\sigma}_{C}\sqrt{l_{y}}} \left( \left( \rho_{x}(\check{Q}_{y};y_{1},y_{2}) \right)^{2} + l_{y} \left( \check{Q}_{y} \right)^{2} \right. \\ &&\left. + 2 \sin(\beta) \sqrt{l_{y}} \rho_{x}(\check{Q}_{y};y_{1},y_{2})\check{Q}_{y} \vphantom{\left( \rho_{y}(\check{Q}_{x};x_{1},x_{2}) \right)^{2}}\right)^{1/2} \end{array} $$

(89)

In the above formulas, the arguments in the functions

$$ \begin{array}{@{}rcl@{}} &&{} l_{x}(y), l_{y}(x), \check{Q}_{x}(x,y), \check{Q}_{y}(x,y), \\ &&{} \alpha(y), \beta(x), x_{1}(y), x_{2}(y), y_{1}(x), y_{2}(x) \end{array} $$

(90)

are omitted. The fields $\check {A}_{x}$, $\check {A}_{y}$ are positive everywhere. Having found the minimizer $\pmb {\check {Q}} = (\check {Q}_{x}, \check {Q}_{y})$ of problem ($\mathcal {P}^{\prime }$) and the maximizer $\check {v}$ of problem ($\mathcal {P}^{\prime \prime }$), one can compute the volume of the lightest archgrid either by

$$ \check{V} = \frac{2}{{\sigma}_{C}} \wp(\pmb{\check{Q}}) $$

(91)

or by

$$ \check{V} = \frac{2}{{\sigma}_{C}} \int\limits_{\varOmega} q \check{v} dxdy , $$

(92)

which shows that the optimal volume is proportional to the potential energy of the loading.

4 Optimal archgrids over rectangular domains—the complete numerical approach with using Legendre polynomials

The present section is aimed at numerical constructions of optimal gridworks over rectangular bases, corresponding to selected transmissible loads including the loads concentrated along curves. The construction is based on tackling simultaneously the problems $(\mathcal {P^{\prime }})$ and $(\mathcal {P^{\prime \prime }})$ along with checking the optimality conditions (81). Both the problems $(\mathcal {P^{\prime }})$, $(\mathcal {P^{\prime \prime }})$ are solved numerically by using Legendre polynomials.

4.1 Construction of the solution to the problem ($\mathcal {P^{\prime \prime }}$)

We confine consideration to the case of the bases being rectangular domains [−L_x,L_x] × [−L_y,L_y], hence x₁(y) = −L_x, x₂(y) = L_x, y₁(x) = −L_y, y₂(x) = L_y.

The n th Legendre polynomial is given by

$$ P_{n}(t)=\frac{1}{2^{n}}\sum\limits_{k=0}^{\left[\frac{n}{2}\right]}(-1)^{k}\binom{n}{k}\binom{2n-2k}{n}t^{n-2k},\ t\in (-1,1), $$

(93)

where $\left [\cdot \right ]$ is a function which rounds down its argument to the nearest integer. Let us introduce polynomials T_n(t), called anti-derivatives of P_n(t), cf. Abedian and Düster (2019), such that:

$$ \frac{d{T_{n}}}{d{t}} = P_{n}(t) , $$

(94)

and T_n(− 1) = T_n(1) = 0 for n ≥ 1. The explicit form of T_n reads

$$ T_{n} = \frac{1}{2n+1}\big(P_{n+1}-P_{n-1}\big), $$

(95)

while T₀(t) = t does not satisfy the above boundary conditions.

The test functions in (80) will be expressed by the truncated series involving the T_n functions, as below

$$ v(x,y) = \sum\limits_{j=1}^{m_{y}}\sum\limits_{i=1}^{m_{x}} v_{ij} T_{i} (\tilde{x}) T_{j}(\tilde{y}) , $$

(96)

with $\tilde {x} = x/L_{x}$, $\tilde {y} = y/L_{y}$; v_ij are unknown coefficients, the numbers m_x, m_y control accuracy of the method. Due to (94) the partial derivatives of v assume the form:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{v}}{\partial{x}} &=& \sum\limits_{j=1}^{m_{y}}\sum\limits_{i=1}^{m_{x}} \frac{v_{ij}}{L_{x}}P_{i}(\tilde{x}) T_{j}(\tilde{y}) , \\ \frac{\partial{v}}{\partial{y}} &=& \sum\limits_{j=1}^{m_{y}}\sum\limits_{i=1}^{m_{x}} \frac{v_{ij}}{L_{y}}T_{i}(\tilde{x}) P_{j}(\tilde{y}) , \end{array} $$

(97)

hence,

$$ \rho_{y}\left( \frac{\partial{v}}{\partial{x}} ; x_{1}(y), x_{2}(y) \right) = \left( \int\limits_{-L_{x}}^{L_{x}} \left( \frac{\partial{v}}{\partial{x}} \right)^{2}dx \right)^{1/2} $$

(98)

or

$$ \begin{array}{@{}rcl@{}} &&\left[ \rho_{y}\left( \frac{\partial{v}}{\partial{x}} ; x_{1}(y), x_{2}(y) \right) \right]^{2} \\ &=& \int\limits_{-L_{x}}^{L_{x}} \left( \displaystyle{\sum}_{j=1}^{m_{y}}{\sum}_{i=1}^{m_{x}} \frac{v_{ij}}{L_{x}}P_{i}(\tilde{x}) T_{j}(\tilde{y}) \right)^{2} dx \end{array} $$

(99)

and the expression $\rho _{x}\left (\frac {\partial {v}}{\partial {y}} ; y_{1}(x), y_{2}(x) \right )$ can be written in a similar manner. Note that a significant number of components at the r.h.s. of (99) cancel by orthogonality of Legendre polynomials:

$$ \int\limits_{-1}^{1} P_{i}(t)P_{j}(t) dt = \frac{2}{2i + 1} \delta_{ij} , $$

(100)

where δ_ij denotes the Kronecker delta. This simplifies the formulation (80) essentially and paves the way for an efficient programming of the maximization problem, see the r.h.s. of Fig. 8. The boundary condition v = 0 on Γ is satisfied identically. The coefficients v_ij are the only unknowns of the problem.

Fig. 8

The numerical flowchart. The unshaded (blank) blocks refer to the steps performed by symbolic computations, while the shaded blocks refer to the steps programmed numerically

The constraints in (80) are satisfied along the lines: x = x_i, $i=1,\dots ,s_{x}$ and along the lines y = y_j, $j=1,\dots ,s_{y}$, where the numbers s_x and s_y are fixed and chosen simultaneously with numbers m_x, m_y. For each x_i, $i=1,\dots ,s_{x}$, the corresponding slopes β(x_i) and the auxiliary lengths $\tilde {l}_{y}(x_{i})$ are computed by (37)₂ and (57) respectively. For each y_j, $j=1,\dots ,s_{y}$, the corresponding slopes α(y_j) and the auxiliary lengths $\tilde {l}_{x}(y_{j})$ are computed by (37)₁ and (55) respectively. In the problems considered in the present paper, the choice: m_x = m_y = m occurred to be efficient.

The numerical approximations to the definite integrals are performed with using the NIntegrate function available in Wolfram Mathematica software.

4.2 Construction of the solution of the problem ($\mathcal {P^{\prime }})$

The unknowns of the problem ($\mathcal {P^{\prime }}$) are expressed by using the Legendre polynomials P_n and their anti-derivatives T_n as follows

$$ \begin{array}{@{}rcl@{}} Q_{x}(x,y) &=& \sum\limits_{j=0}^{n_{y}}\sum\limits_{i=0}^{n_{x}} \frac{Q^{x}_{ij}}{L_{x}} T_{i}(\tilde{x}) P_{j}(\tilde{y}) , \\ Q_{y}(x,y) &=& \sum\limits_{j=0}^{n_{y}}\sum\limits_{i=0}^{n_{x}} \frac{Q^{y}_{ij}}{L_{y}} P_{i}(\tilde{x}) T_{j}(\tilde{y}) , \end{array} $$

(101)

and the vertical load is represented by

$$ q(x,y) = \sum\limits_{j=0}^{n_{y}}\sum\limits_{i=0}^{n_{x}} q_{ij} P_{i}(\tilde{x}) P_{j}(\tilde{y}) , $$

(102)

where

$$ q_{ij} = \left( \frac{2i+1}{2} \right)\! \left( \frac{2j+1}{2} \right) \int\limits_{-L_{y}}^{L_{y}} \int\limits_{-L_{x}}^{L_{x}} q(x,y) P_{i}(\tilde{x}) P_{j}(\tilde{y}) dxdy $$

(103)

The differential condition nested in (76) makes it possible to eliminate the unknowns $Q^{y}_{ij}$ by the algebraic equation

$$ \begin{array}{@{}rcl@{}} Q^{y}_{ij} = - \left( L_{y} q_{ij} + \frac{L_{y}}{L_{x}} Q^{x}_{ij} \right), \end{array} $$

(104)

thus making the unknowns $Q^{x}_{ij}$ the only design variables of the problem. The subsequent steps of the method are schematically shown in the flowchart in Fig. 8. Upon finding the minimizer $Q^{x}_{ij}$, $Q^{y}_{ij}$, one can either compute the volume by (91) or multiplying by the factor 2 the objective function F, see l.h.s. of Fig. 8. This method delivers directly the distribution of the horizontal forces along the edges, see (63). However the method does not provide a direct formula for the optimal level function $\check {z}(x,y)$. To find it, one should integrate the equalities (62) and augment them with the boundary conditions. Let us emphasize that the optimal shape is directly delivered by solving problem ($\mathcal {P^{\prime \prime }}$).

4.3 Archgrids over a rectangular domain for a uniform load

Consider a rectangular domain Ω of side lengths 2L_x = 3L and 2L_y = 2L. The aim is to construct the optimal archgrids over this domain, of the level function z assuming the values z₀ given by (34), now denoted by z_0(λ), with (c₁,c₂,c₃,c₄) = (λL, 0, λL, 0), λ being a parameter, designed for the transmissible uniformly distributed load q = const.; [q] = [N/m²]. Due to symmetries of the problem v_kl = 0 for k, l being even numbers and the integral constraints in (80) are applied only for x_i = $(i-1)\frac {3L}{2s}$ and y_i = $(i-1)\frac {L}{s}$ for $i = 1,\dots ,s$, where s = 2m. Both methods of archgrid constructions are applied according to the flowchart in Fig. 8. The computations based on solving problem ($\mathcal {P^{\prime \prime }}$) are performed for m = 15,45,75; the values of the optimal volumes V_(λ) (for m = 75) increase along with the increase of λ, cf. Table 1. The increase is nonlinear, cf. the last column of this table. The optimal volume for λ = 0 and L_x = L_y compares favourably with the result found in Rozvany and Prager (1979), see Fig. 7 therein, and coincides with the result found in Czubacki and Lewiński (2019) by using: (a) the Fourier series method applied to the problem ($\mathcal {P}^{\prime }$), (b) the Fourier series method applied to the problem ($\mathcal {P}^{\prime \prime }$).

Table 1 The values of the volumes V_(λ)/V_q of the archgrids of Section 4.3 for m = 15,45,75 for subsequent $\lambda = 0, 1/4, \dots , 5/4$ obtained by solving the problem ($\mathcal {P^{\prime \prime }}$), where V_q = qL³/σ_C

For the same case of λ = 0, the results obtained by the method ($\mathcal {P^{\prime }}$), for selected values of n_x = n_y = n, are listed in Table 2. The values of volumes obtained by the method ($\mathcal {P^{\prime \prime }}$) corresponding to the increasing number m_x = m_y = m form an increasing sequence (a lower converging sequence), see the first row in Table 1, while the sequence of volumes obtained by the method ($\mathcal {P^{\prime }}$) for increasing number n_x = n_y = n is a decreasing sequence (an upper converging sequence), see Table 2. Both sequences tend to the same optimal value, thus confirming the duality gap between problems ($\mathcal {P^{\prime }}$) and ($\mathcal {P^{\prime \prime }}$) being zero.

Table 2 The values of the volumes V_(λ= 0)/V_q of the archgrids of Section 4.3, for selected values of n, obtained by solving the problem ($\mathcal {P^{\prime }}$)

Of two methods shown in Fig. 8, the method based on ($\mathcal {P^{\prime }}$) produces the sequence of results converging faster. That is why the results in Table 2 could be confined to n = 30, which corresponds to the accuracy of the method ($\mathcal {P^{\prime \prime }}$) for m = 75.

The method $(\mathcal {P^{\prime \prime }})$ gives the optimal shapes of optimal archgrids directly. They are not concave, cf. Fig. 9. Let us emphasize that $\check {z}_{(\lambda \neq 0)} \neq z_{0(\lambda )} + \check {v}_{(\lambda = 0)}$. On the other hand, the method $(\mathcal {P^{\prime }})$ delivers directly the distribution of the horizontal reactions H_x, H_y and the areas densities A_x, A_y. The method $(\mathcal {P^{\prime \prime }})$ for m = 75 gives the results of the gradient of v of better accuracy than the accuracy with which the method $(\mathcal {P^{\prime }})$ for n = 30 delivers the quotients Q_x/H_x, Q_y/H_y, see Fig. 10 corresponding to the case λ = 0. The same figure shows the precision with which the optimality conditions (81) are fulfilled. To measure the relevant error, the function:

$$ \text{error}_{x}(y) = \frac{ \sqrt{\int\limits_{-L_{x}}^{L_{x}}{ \left( \frac{\partial{v}}{\partial{x}}(x,y) - \frac{Q_{x}(x,y)}{H_{x}(y)} \right)^{2} dx} } }{ \sqrt{ \ \int\limits_{-L_{x}}^{L_{x}}{ \left( \frac{\partial{v}}{\partial{x}}(x,y) \right)^{2} dx}}} $$

(105)

is introduced and the function error_y(x) is defined similarly. These errors, corresponding to the sections x = const., y = const., depend on the distance to the edges. The errors are small far from the edges and increase in the boundary zone, see Table 3. This phenomenon appears because in the problem ($\mathcal {P^{\prime }}$), the boundary conditions are not explicitly imposed.

Fig. 9

The solutions to the problem of Section 4.3 for subsequent values of λ. The optimal level functions $\check {z}$ and their contour plots

Fig. 10

Checking the accuracy of satisfying the optimality conditions (81) for the problem of Fig. 9a. Comparing the plots of the l.h.s and r.h.s of the equalities (81) for selected sections: y = const. (a), x = const. (b). The derivatives of v are computed by the method ($\mathcal {P^{\prime \prime }}$) with m = 75, while the quotients Q_x/H_x, Q_y/H_y are found by the method ($\mathcal {P^{\prime }}$) for n = 30

Table 3 Assessing the accuracy of fulfilling the optimality conditions (81)

5 The optimal archgrids—other illustrative designs

The optimal archgrids to be constructed in this section will be found by solving the problem ($\mathcal {P^{\prime \prime }}$) in order to have directly the optimal level function $\check {z}(x,y)$. Two kinds of vertical loads will be discussed: the load concentrated along a contour of a circle and the load uniformly distributed within a circle.

5.1 The optimal archgrids over a square domain for the load uniformly distributed along a contour of a circle

The optimal archgrids will be constructed over a square domain Ω, of side of length 2L, loaded uniformly along a contour of a circle of origin in the middle of domain and a radius R, see Fig. 11. The load acts along the z axis orthogonal to Ω, the intensity of the load being p = const., [p] = [N/m]. The two cases of the support will be considered:

• (i) z = 0 along Γ

• (ii) z = z₀ along Γ where z₀ is defined by (34) with (c₁,c₂,c₃,c₄) = (L, 0, L, 0), see Fig. 11.

Due to symmetries of the problem v_kl = 0 for k, l being even numbers and v_kl = v_lk due to symmetry of a square domain. Thus, integral constraints in (80) are applied only for x_i = $(i-1)\frac {L}{s}$ for $i = 1,\dots ,s$ and s = 2m.

Fig. 11

The square domain 2L × 2L as a basis and the contour of a circle of radius R = 0.75L along which the load p is applied (a). The archgrid is supported such that z = 0 along Γ(case i), or z = z₀ along Γ, z₀ being shown in (b) (case ii)

The accuracy of the result of the optimal volume is controlled by the number m. For increasing m, the volume tends to

$$ V /V_{p} = 5.295, \quad V_{p} = p L^{2}/{\sigma}_{C} $$

(106)

cf. Table 4.

Table 4 The values of the volumes V/V_p of the archgrids of Section 5.1 corresponding to cases (i) and (ii), for $m=15, \dots , 90$

The shape of the optimal archgrid supported as in case (i) is surprising, see Fig. 12a. The vault is formed not over the whole basis domain; the four squares of the basis: O₁A₁B₁A₈, $\dots$, O₄A₇B₄A₆ are not covered, cf. Fig. 12d. The load acting along the circle is transmitted to the sides of the basis domain by straight arches forming four ruled surfaces over the domains: A₁A₂B₂C₁B₁, $\dots$, A₇A₈B₁C₄B₄, cf. Fig. 13. The net of bars over the interior square B₁B₂B₃B₄ forms a surface of non-zero Gauss curvature, see Fig. 14. This surface is continuously connected with the ruled surfaces mentioned above by the ruled surfaces over the domains: B₁C₁B₂, $\dots$, B₄C₄B₁. Note that although the archgrid is not concave, all the arches are in compression and the stress distribution is uniform, as assured by appropriate design of areas densities (89). Let us stress that the optimization process has determined the position of the load p over the contour C₁C₂C₃C₄. The points $B_{1},\dots , B_{4}$ are at the highest levels (see Fig. 14), which may suggest that the load is concentrated at these vertices, which is obviously not the case. Let us stress here that the exact analytical solution of this result is still pending.

Fig. 12

The shape of the optimal archgrid for the problem (i) of Section 5.1. The axonometric views (a), (b); the side view (c), the upper view of the layout of arches (d)

Fig. 13

The cross-sections of the level function $\check {z}$ of the optimal archgrid shown in Fig. 12 for $y =\frac {i}{25}L$, $i = 0,\dots ,24$. The red dashed lines correspond to non-optimal arches for which the bounds involved in (80) are not saturated

Fig. 14

The contour plot of the optimal solution of problem (i), Section 5.1. The given load of intensity p is applied along the circular contour shown as a red dot-dashed line. The blue dashed lines indicate the directions of the optimal arches

The optimal archgrid for the case (ii) of the support has two symmetry planes, see Figs. 15 and 16, where the cross-sections y = const. are shown. We note that the arches touching the contour of the basis form the ruled surfaces as in case (i). These ruled surfaces and the surface over the interior region B₁B₂B₃B₄ are connected by other four ruled surfaces, see Fig. 17. The optimal volume equals

$$ V /V_{p} = 5.361, \quad V_{p} = p L^{2}/{\sigma}_{C} $$

(107)

and this value is bigger than that of case (i) by 1.26 %. Thus, the construction is heavier, as expected.

Fig. 15

The shape of the optimal archgrid for the problem (ii) of Section 5.1. The axonometric view

Fig. 16

The cross-sections of the level function $\check {z}$ of the optimal archgrid shown in Fig. 15 for $y =\frac {i}{25}L$, $i = 0,\dots ,24$. The red dashed lines correspond to non-optimal arches for which the bounds involved in (80) are not saturated

Fig. 17

The contour plot of the optimal solution of problem (ii), Section 5.1. The given load of intensity p is applied along the circular contour shown as a red dot-dashed line. The blue dashed lines indicate the directions of the optimal arches

5.2 The optimal archgrid over a square domain for the load uniformly distributed within a circle

The aim is to construct an optimal archgrid over a square domain of the side of length 2L for the load of intensity q uniformly distributed within a circle of origin at (0,0) and radius R = 0.75L, see Fig. 18a. The level function $\check {z}$ is constructed by using Legendre polynomials by the method described above.

Fig. 18

The square domain 2L × 2L as a basis and the circular domain of radius R = 0.75L where the uniform load of intensity q is applied (a). The axonometric view of the optimal archgrid (b). The cross-sections of the level functions $\check {z}$ for $y =\frac {i}{25}L$, $i = 0,\dots ,24$. The red dashed lines correspond to non-optimal arches for which the bounds involved in (80) are not saturated (c). The upper view of the layout of arches (d)

The optimal shape of the archgrid (Fig. 18b) is similar to that of Fig. 12a, but now the central part is concave and not convex as before. This structure is composed of four ruled surfaces A₁A₂B₂C₁B₁, $\dots$, A₇A₈B₁C₄B₄ extended towards the interior of the basis domain by the surfaces B₁C₁B₂, $\dots$, B₄C₄B₁—which here are not ruled surfaces—and completed by the surface of non-zero Gauss curvature over the B₁B₂B₃B₄ square (Fig. 19).

Fig. 19

The contour plot of the optimal solution of the problem shown in Fig. 18. The given load of intensity q is applied within the circular contour shown as a red dot-dashed line. The blue dashed lines indicate the directions of the optimal arches

For increasing m, the volume tends to

$$ V /V_{q} = 2.398, \quad V_{q} = q L^{3}/{\sigma}_{C} $$

(108)

cf. Table 5.

Table 5 The values of the volumes V/V_q of the archgrid of Section 5.2 for $m=15, \dots , 75$

6 Final remarks

The theory of optimum design of trusses teaches us that the condition of minimum compliance with a prescribed value of the volume leads to designs in which all the bars are stressed up to the same given limit (cf. Lewiński et al. (2019a), Section 2.1). This suggests that the design optimization of archgrids based on the uniform stress condition should lead to the designs of least compliance. Yet this conjecture needs deeper studies due to issues concerning deformation behaviour of archgrids; note that a single funicular is geometrically variable, which makes the kinematic analysis nontrivial.

The identity of both the surfaces z_x(x,y) = z_y(x,y) of two families of arches shown in Section 3 refers obviously to the undeformed state. Yet the arches of both the families are not connected at nodes on this surface. Consequently, they may form two different surfaces upon deformation. Yet the choice of the areas of the cross-sections of both the families of arches assures uniform stress distribution. We conjecture that this property singles out the rational design which assures the required deformation compatibility. In the forthcoming papers, this question will be addressed by a rationalization of archgrids by replacing them by frames of finite number of arches connected by stiff joints. Like Michell structures (see He and Gilbert (2015)), the archgrids may be effectively rationalized, thus showing their lightness, stiffness, and applicability in the civil engineering practice.

The theory put forward concerns the archgrids composed of two families of arches in x = const and y = const planes. Such constructions can be improved, noting that the load applied close to the corners is better transmitted by arches in the planes going in ± 45^∘ directions, cf. Sec.6.3 in Lewiński et al. (2019a) and examples in Lewiński et al. (2019b) constructed by a discretized version of the archgrid model admitting arches in four directions at the point: 0^∘, 90^∘, ± 45^∘. A continuum model of archgrids composed of arches going in selected directions, or even in all possible planes, is the subject of the current research.